Balanced Neonatal Cry Classification: Integrating Preterm and Full-Term Data for RDS Screening
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
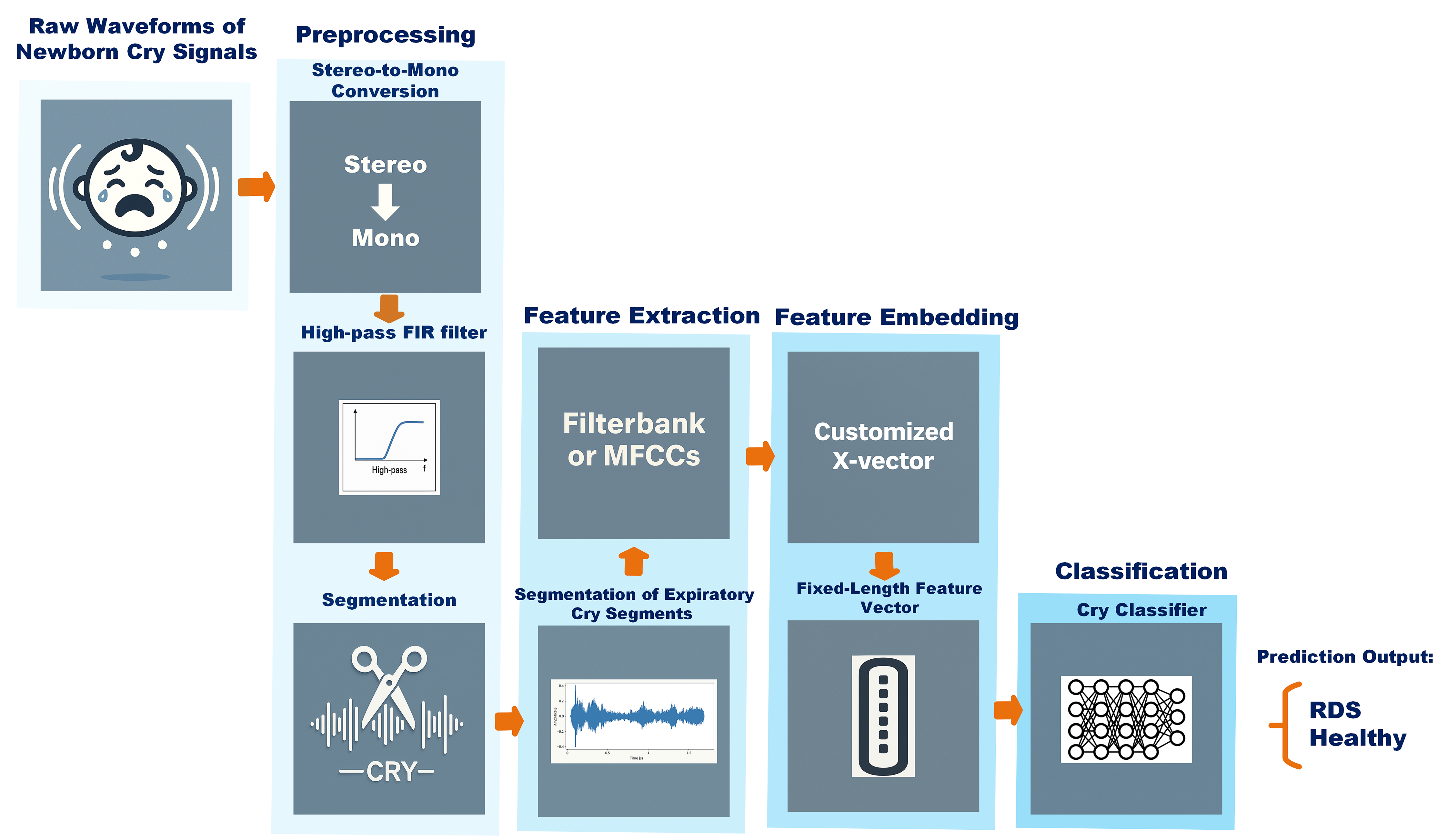
3.1. Data Pipeline
3.1.1. Data Characteristics
3.1.2. Data Implementation
3.2. Feature Extraction
3.2.1. Filterbank Features (FBANKs)
3.2.2. Mel-Frequency Cepstral Coefficients (MFCCs)
3.3. Feature Embedding and Classification
3.4. Training of the Customized X-Vector
3.5. Interpretability Methods
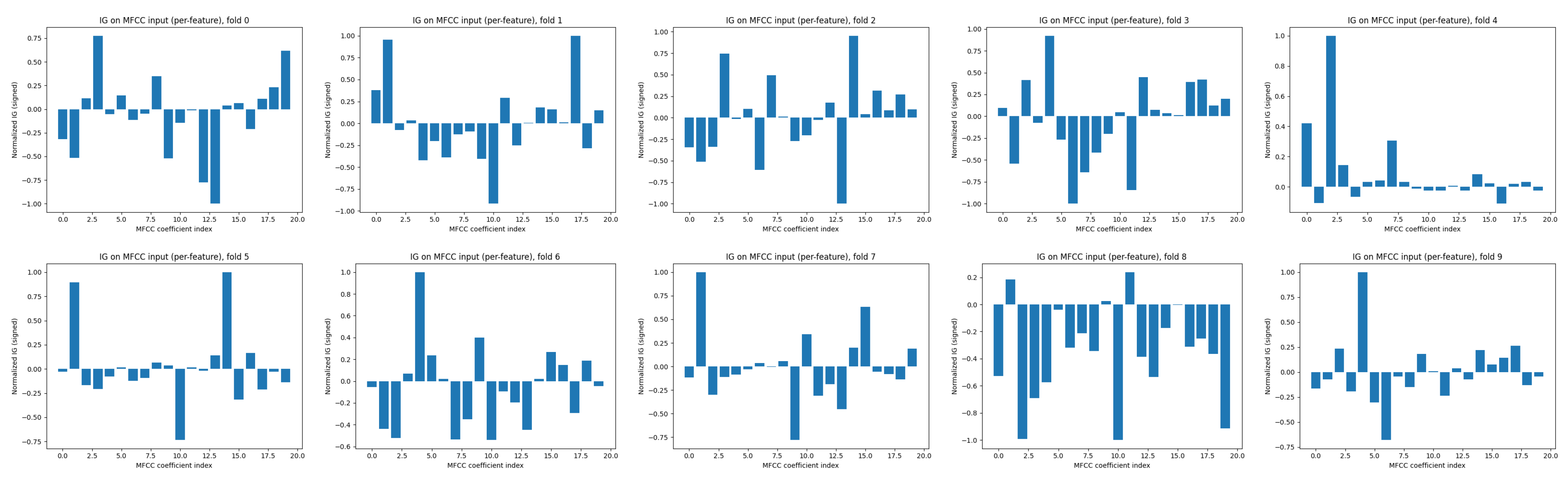
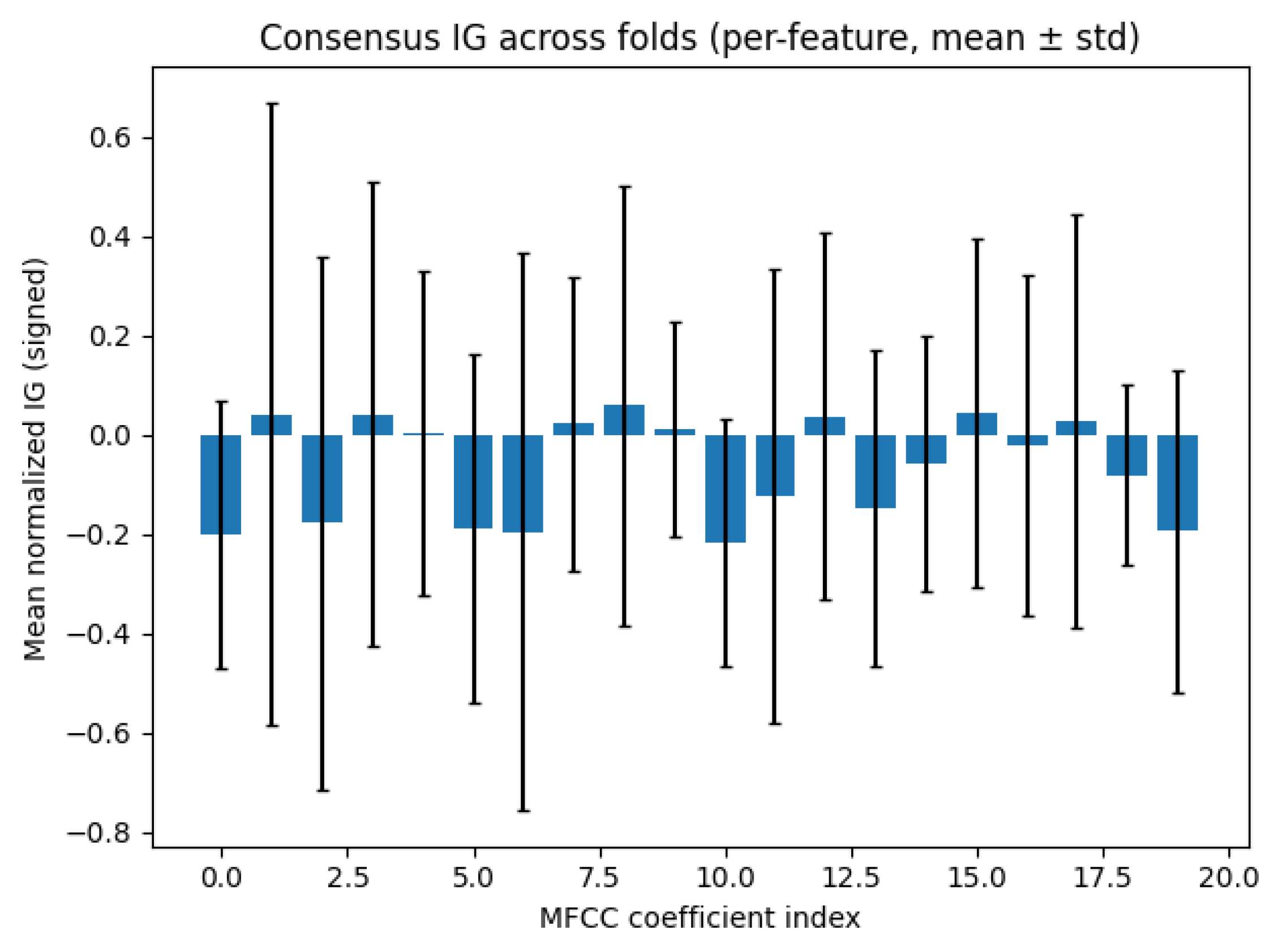
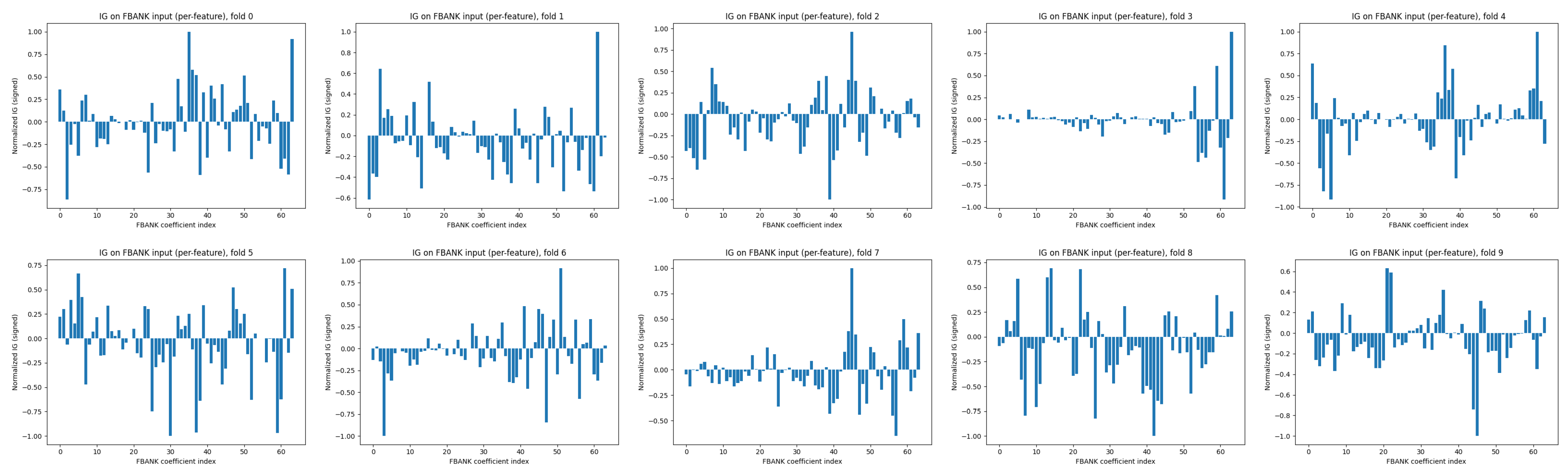
3.5.1. Integrated Gradients (IGs) for MFCC and FBANK
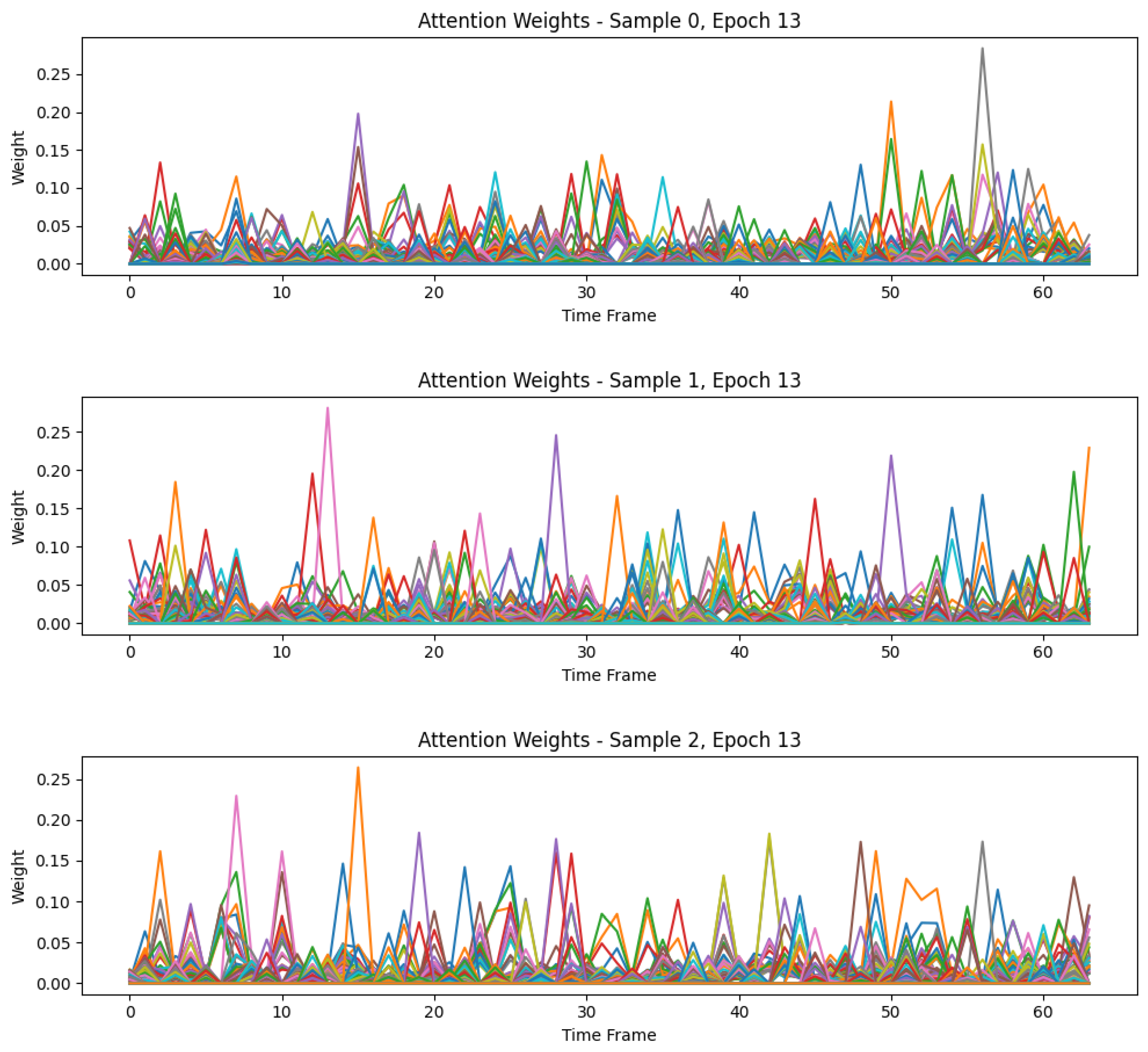
3.5.2. Attention Weight Visualization
3.6. Hyperparameter Optimization and System Configuration
3.7. Experimental Setup and Evaluation Metrics
4. Results and Analysis
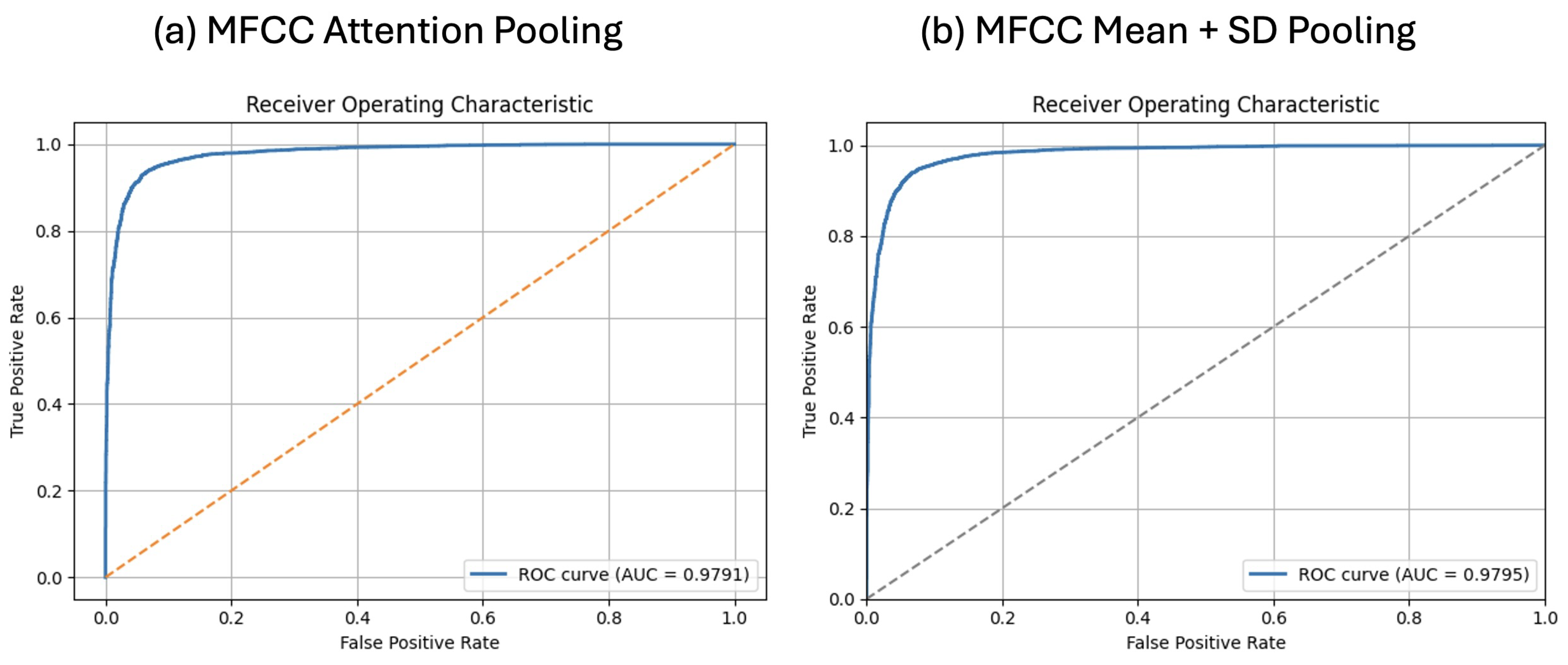
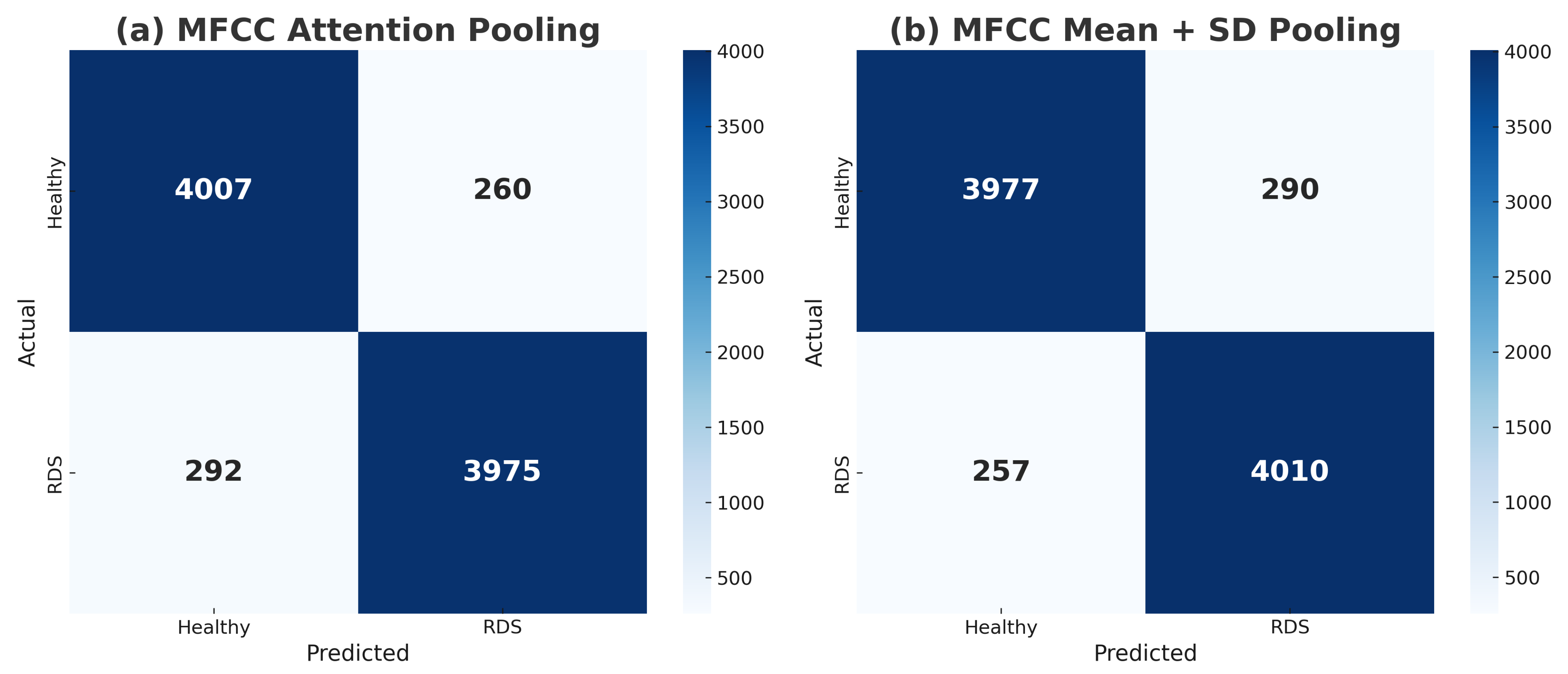
4.1. MFCC Results with Mean + SD and Attention Pooling
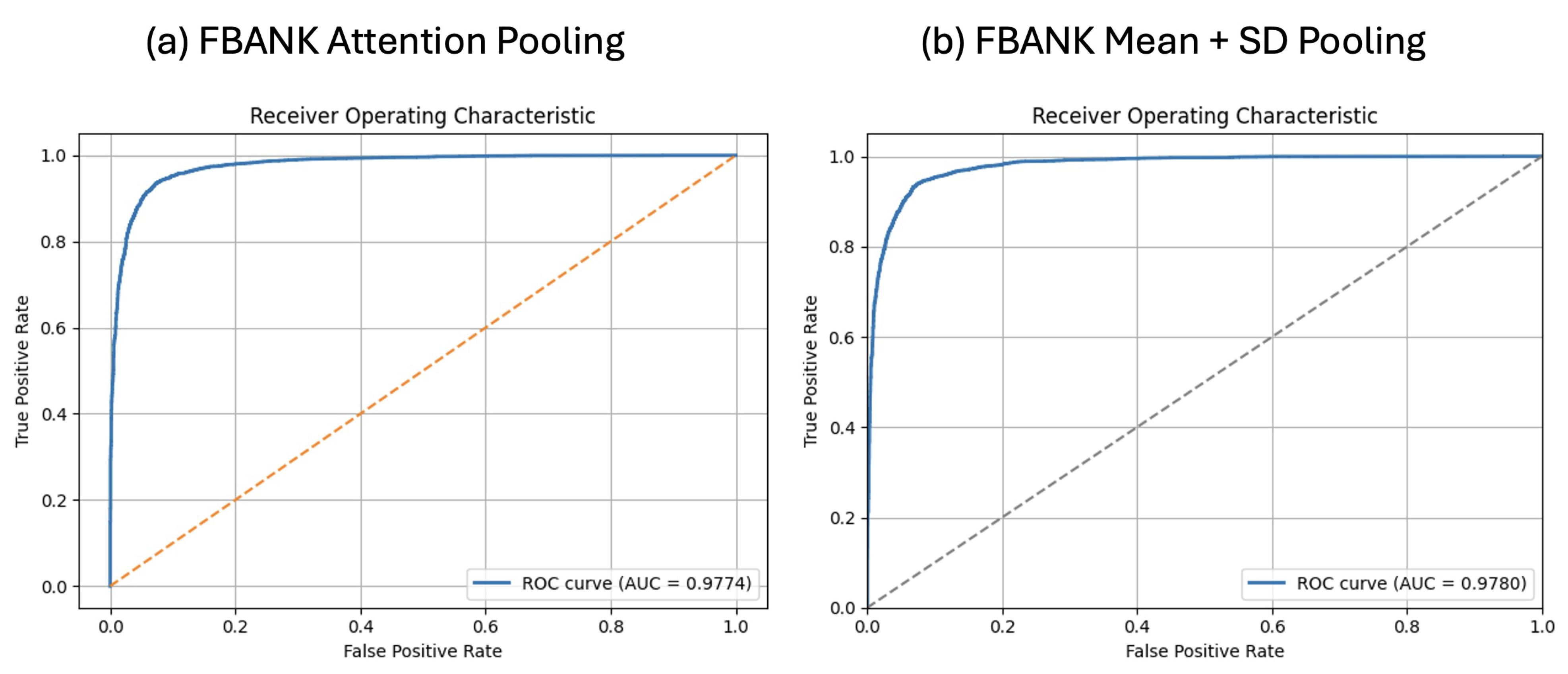
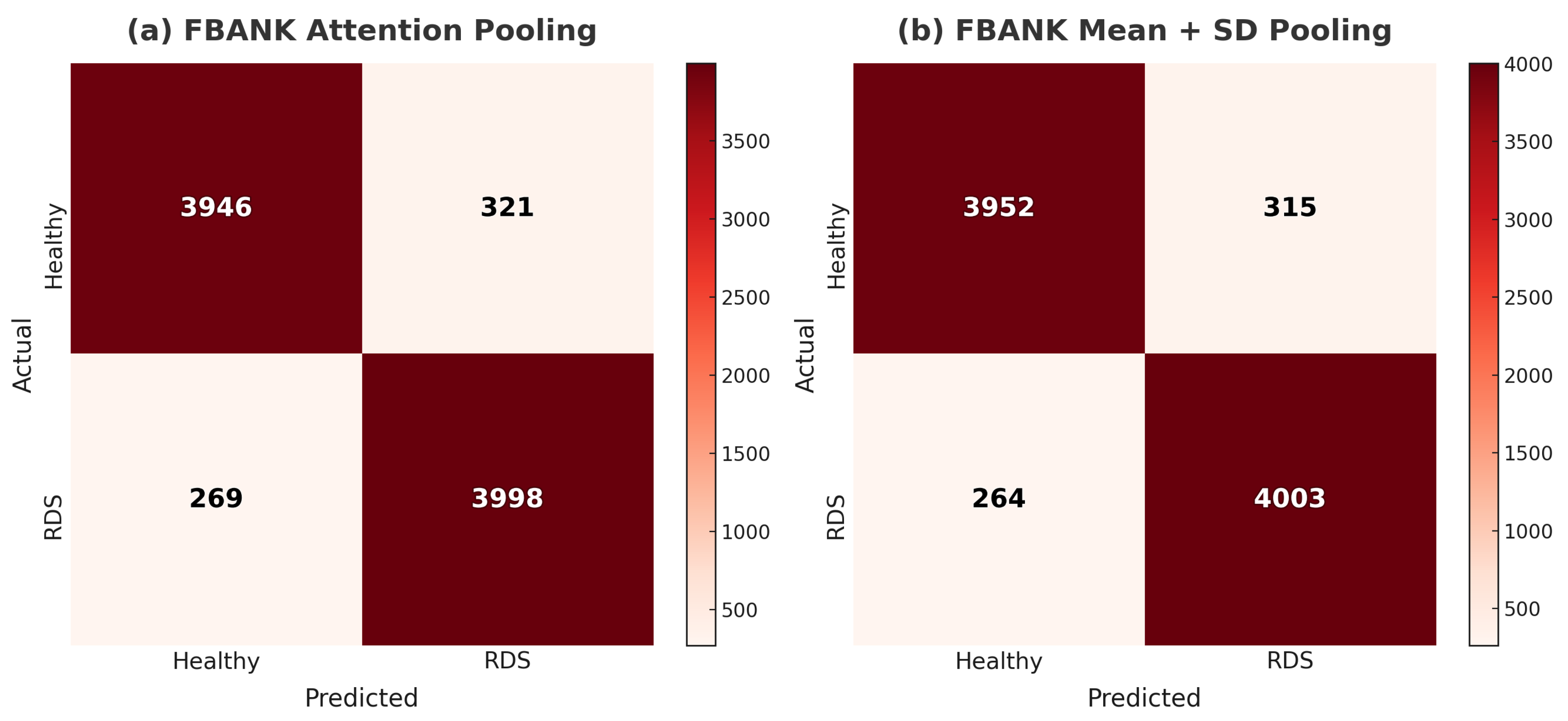
4.2. FBANK Results with Mean + SD and Attention Pooling
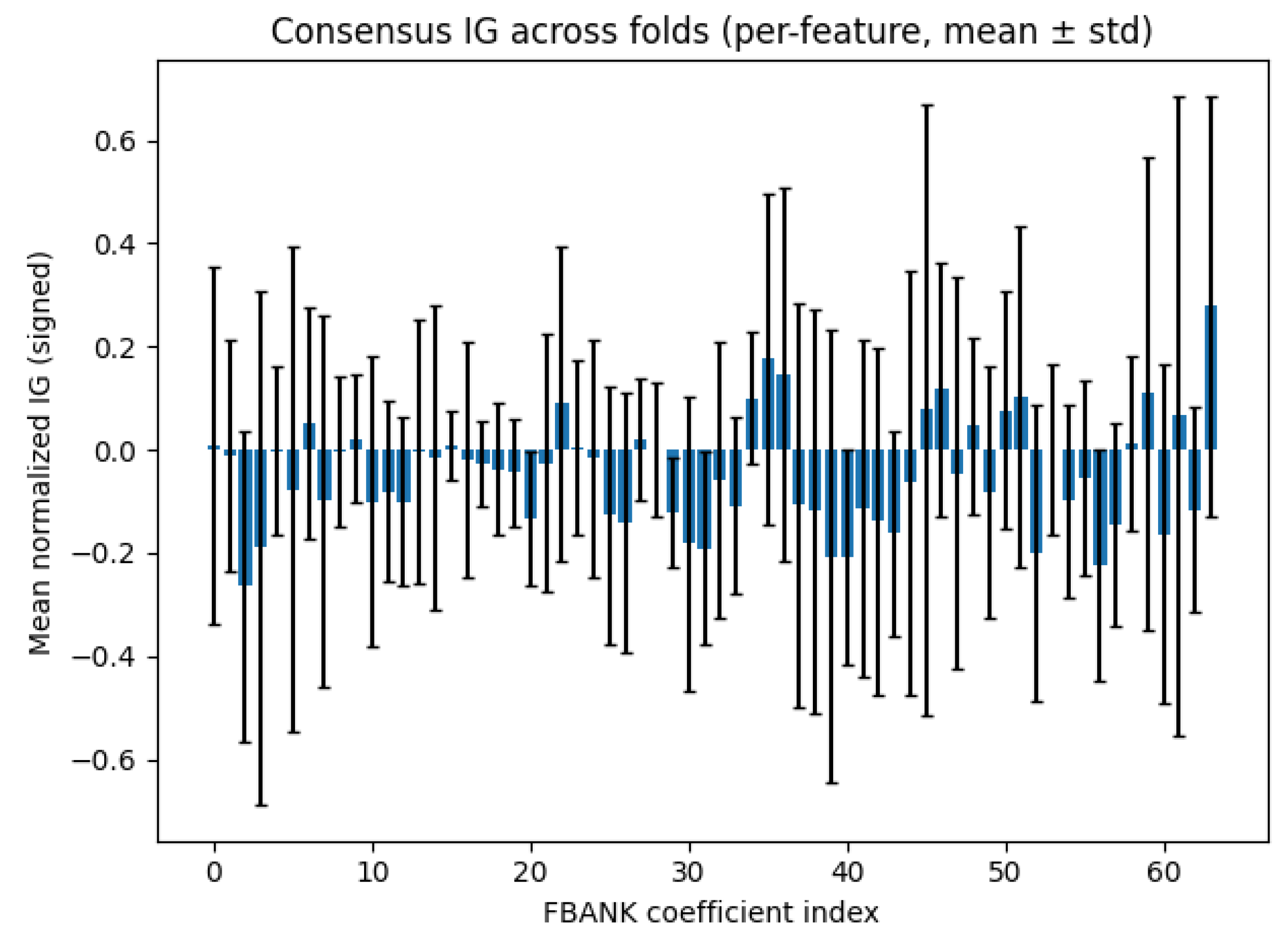
4.3. Interpretability
4.4. Comparison with Previous Studies
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Comparison of X-Vector Architectures
| Component | Original X-Vector [31] | Lightweight-Modified X-Vector (MFCC, Attention) | Lightweight-Modified X-Vector (MFCC, Mean + SD) |
|---|---|---|---|
| Input Features | MFCCs (typically 23–30 dims) | MFCC | MFCC |
| Input Channels | ∼30 | 26 MFCCs | 20 MFCCs |
| TDNN Stack | 5 TDNN layers, fixed dilation | 7 TDNN layers, reduced channels with variable dilation | 7 TDNN layers, reduced channels with variable dilation |
| TDNN Channels | [512, 512, 512, 512, 1500] | [64, 64, 128, 128, 128, 256, 256] | [64, 64, 128, 128, 128, 256, 256] |
| TDNN Kernel Sizes | [5, 5, 7, 9, 1] | [5, 3, 3, 3, 3, 1, 1] | [5, 3, 3, 3, 3, 1, 1] |
| TDNN Dilations | [1, 1, 1, 1, 1] | [1, 1, 2, 2, 3, 1, 1] | [1, 1, 2, 2, 3, 1, 1] |
| Activation Function | ReLU | GELU | LeakyReLU () |
| Normalization | BatchNorm after each TDNN and dense block | Same | Same |
| Pooling | Statistics pooling (mean and std over time) | 4-head self-attention with masking | Statistics pooling (mean and std over time) |
| Embedding Dimension | 512 (after pooling) | 256 (after pooling and linear projection) | 256 (after pooling and linear projection) |
| Fully Connected Layers | FC1: 512, FC2: 1500 | FC1: 256, FC2: 256 | FC1: 256, FC2: 256 |
| Backend / Classifier | PLDA scoring | Feedforward classifier + Sigmoid output | Feedforward classifier + Softmax output |
| Total Trainable Parameters | ∼8.7 M | 641.2 k | 441.6 k |
| Inference Latency Per 1 s Segment (A100, batch = 64) | — | ∼5.5 ms/segment (∼181 seg/s; real-time × 180) | ∼6–7 ms/segment (estimated) |
References
- UNICEF. Neonatal Mortality – UNICEF Data. UNICEF Data Portal. 2024. Available online: https://data.unicef.org/topic/child-survival/neonatal-mortality/ (accessed on 21 July 2025).
- UNICEF. Levels and Trends in Child Mortality: Report 2024. UNICEF Data Portal. 2024. Available online: https://data.unicef.org/resources/levels-and-trends-in-child-mortality-2024/ (accessed on 21 July 2025).
- World Health Organization (WHO). Neonatal Mortality Rate (per 1000 Live Births). WHO Global Health Observatory. 2024. Available online: https://data.who.int/indicators/i/E3CAF2B/A4C49D3 (accessed on 21 July 2025).
- Tochie, J.N.; Chuy, C.; Shalkowich, T.; Olayinka, O.O.; Tanveer, M.; Dondorp, A.M.; Kreuels, B.; Mayhew, S.; Dramowski, A. Global, Regional, and National Trends in the Burden of Neonatal Respiratory Failure: A Scoping Review from 1992 to 2022. J. Clin. Transl. Res. 2023, 8, 637–649. [Google Scholar]
- Legesse, B.; Cherie, A.; Wakwoya, E. Time to Death and Its Predictors Among Neonates with Respiratory Distress Syndrome Admitted at Public Hospitals in Addis Ababa, Ethiopia, 2019–2021: A Retrospective Cohort Study. PLoS ONE 2023, 18, e0289050. [Google Scholar]
- Wasz-Höckert, O.; Valanne, E.; Michelsson, K.; Vuorenkoski, V.; Lind, J. Twenty-Five Years of Scandinavian Cry Research. In Infant Crying: Theoretical and Research Perspectives; Lester, B.M., Boukydis, C.F.Z., Eds.; Plenum Press: New York, NY, USA, 1984; pp. 83–94. [Google Scholar]
- Mukhopadhyay, J.; Saha, B.; Majumdar, B.; Majumdar, A.; Gorain, S.; Arya, B.K.; Bhattacharya, S.D.; Singh, A. An Evaluation of Human Perception for Neonatal Cry Using a Database of Cry and Underlying Cause. In Proceedings of the 2013 Indian Conference on Medical Informatics and Telemedicine (ICMIT), Kharagpur, India, 28–30 March 2013; pp. 64–67. [Google Scholar]
- Owino, G.; Shibwabo, B. Advances in Infant Cry Paralinguistic Classification—Methods, Implementation, and Applications: Systematic Review. JMIR Rehabil. Assist. Technol. 2025, 12, e69457. [Google Scholar] [CrossRef]
- Ji, C.; Mudiyanselage, T.B.; Gao, Y.; Pan, Y. A Review of Infant Cry Analysis and Classification. EURASIP J. Audio Speech Music Process. 2021, 2021, 8. [Google Scholar] [CrossRef]
- Matikolaie, F.S.; Tadj, C. On the Use of Long-Term Features in a Newborn Cry Diagnostic System. Biomed. Signal Process. Control 2020, 59, 101889. [Google Scholar]
- Zayed, Y.; Hasasneh, A.; Tadj, C. Infant Cry Signal Diagnostic System Using Deep Learning and Fused Features. Diagnostics 2023, 13, 2107. [Google Scholar] [CrossRef]
- Mohammad, A.; Tadj, C. Transformer-Based Approach to Pathology Diagnosis Using Audio Spectrograms. J. Pathol. Audio Diagn. 2024, 1, 45–58. [Google Scholar]
- Masri, S.; Hasasneh, A.; Tami, M.; Tadj, C. Exploring the Impact of Image-Based Audio Representations in Classification Tasks Using Vision Transformers and Explainable AI Techniques. Information 2024, 15, 751. [Google Scholar] [CrossRef]
- Shayegh, S.V.; Tadj, C. Deep Audio Features and Self-Supervised Learning for Early Diagnosis of Neonatal Diseases: Sepsis and Respiratory Distress Syndrome Classification from Infant Cry Signals. Electronics 2025, 14, 248. [Google Scholar] [CrossRef]
- Pardede, H.F.; Zilvan, V.; Krisnandi, D.; Heryana, A.; Kusumo, R.B.S. Generalized Filter-Bank Features for Robust Speech Recognition Against Reverberation. In Proceedings of the 2019 International Conference on Computer, Control, Informatics and Its Applications (IC3INA), Tangerang, Indonesia, 23–24 October 2019; pp. 19–24. [Google Scholar]
- Mukherjee, H.; Salam, H.; Santosh, K.C. Lung Health Analysis: Adventitious Respiratory Sound Classification Using Filterbank Energies. Int. J. Pattern Recognit. Artif. Intell. 2021, 35, 2157008. [Google Scholar] [CrossRef]
- Tak, R.N.; Agrawal, D.M.; Patil, H.A. Novel Phase Encoded Mel Filterbank Energies for Environmental Sound Classification. In Proceedings of the 7th International Conference on Pattern Recognition and Machine Intelligence (PReMI 2017), Kolkata, India, 5–8 December 2017; pp. 317–325. [Google Scholar]
- Salehian Matikolaie, F.; Kheddache, Y.; Tadj, C. Automated Newborn Cry Diagnostic System Using Machine Learning Approach. Biomed. Signal Process. Control 2022, 73, 103434. [Google Scholar] [CrossRef]
- Khalilzad, Z.; Tadj, C. Using CCA-Fused Cepstral Features in a Deep Learning-Based Cry Diagnostic System for Detecting an Ensemble of Pathologies in Newborns. Diagnostics 2023, 13, 879. [Google Scholar] [CrossRef] [PubMed]
- Patil, H.A.; Patil, A.T.; Kachhi, A. Constant Q Cepstral Coefficients for Classification of Normal vs. Pathological Infant Cry. In Proceedings of the ICASSP 2022—IEEE International Conference on Acoustics, Speech and Signal Processing, Singapore, 22–27 May 2022; pp. 7392–7396. [Google Scholar]
- Felipe, G.Z.; Aguiar, R.L.; Costa, Y.M.G.; Silla, C.N.; Brahnam, S.; Nanni, L.; McMurtrey, S. Identification of Infants’ Cry Motivation Using Spectrograms. In Proceedings of the 2019 International Conference on Systems, Signals and Image Processing (IWSSIP), Osijek, Croatia, 5–7 June 2019; pp. 181–186. [Google Scholar]
- Farsaie Alaie, H.; Abou-Abbas, L.; Tadj, C. Cry-Based Infant Pathology Classification Using GMMs. Speech Commun. 2016, 77, 28–52. [Google Scholar] [CrossRef]
- Salehian Matikolaie, F.; Tadj, C. Machine Learning-Based Cry Diagnostic System for Identifying Septic Newborns. J. Voice 2024, 38, 963.e1–963.e14. [Google Scholar] [CrossRef]
- Zabidi, A.; Yassin, I.M.; Hassan, H.A.; Ismail, N.; Hamzah, M.M.A.M.; Rizman, Z.I.; Abidin, H.Z. Detection of Asphyxia in Infants Using Deep Learning Convolutional Neural Network (CNN) Trained on Mel Frequency Cepstrum Coefficient (MFCC) Features Extracted from Cry Sounds. J. Fundam. Appl. Sci. 2018, 9, 768. [Google Scholar] [CrossRef]
- Ting, H.-N.; Choo, Y.-M.; Ahmad Kamar, A. Classification of Asphyxia Infant Cry Using Hybrid Speech Features and Deep Learning Models. Expert Syst. Appl. 2022, 208, 118064. [Google Scholar] [CrossRef]
- Ji, C.; Xiao, X.; Basodi, S.; Pan, Y. Deep Learning for Asphyxiated Infant Cry Classification Based on Acoustic Features and Weighted Prosodic Features. In Proceedings of the 2019 International Conference on Internet of Things (iThings), IEEE Green Computing and Communications (GreenCom), IEEE Cyber, Physical and Social Computing (CPSCom), and IEEE Smart Data (SmartData), Atlanta, GA, USA, 14–17 July 2019; pp. 1233–1240. [Google Scholar]
- Wu, K.; Zhang, C.; Wu, X.; Wu, D.; Niu, X. Research on Acoustic Feature Extraction of Crying for Early Screening of Children with Autism. In Proceedings of the 2019 34rd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Guilin, China, 18–20 May 2019; pp. 290–295. [Google Scholar]
- Satar, M.; Cengizler, Ç.; Hamitoğlu, Ş.; Özdemir, M. Audio Analysis Based Diagnosis of Hypoxic Ischemic Encephalopathy in Newborns. Int. J. Adv. Biomed. Eng. 2022, 1, 28–42. [Google Scholar]
- Reyes-Galaviz, O.F.; Tirado, E.A.; Reyes-Garcia, C.A. Classification of Infant Crying to Identify Pathologies in Recently Born Babies with ANFIS. In Proceedings of the International Conference on Computers Helping People with Special Needs (ICCHP 2004), Paris, France, 7–9 July 2004; Lecture Notes in Computer Science, Volume 3118. pp. 408–415. [Google Scholar]
- Hariharan, M.; Sindhu, R.; Vijean, V.; Yazid, H.; Nadarajaw, T.; Yaacob, S.; Polat, K. Improved Binary Dragonfly Optimization Algorithm and Wavelet Packet Based Non-Linear Features for Infant Cry Classification. Comput. Methods Programs Biomed. 2018, 155, 39–51. [Google Scholar] [CrossRef]
- Snyder, D.; Garcia-Romero, D.; Sell, G.; Povey, D.; Khudanpur, S. X-Vectors: Robust DNN Embeddings for Speaker Recognition. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2018), Calgary, AB, Canada, 15–20 April 2018; pp. 5329–5333. [Google Scholar]
- Snyder, D.; Garcia-Romero, D.; Sell, G.; McCree, A.; Povey, D.; Khudanpur, S. Speaker Recognition for Multi-Speaker Conversations Using X-Vectors. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2019), Brighton, UK, 12–17 May 2019; pp. 5796–5800. [Google Scholar]
- Snyder, D.; Garcia-Romero, D.; McCree, A.; Sell, G.; Povey, D.; Khudanpur, S. Spoken Language Recognition Using X-Vectors. In Proceedings of the Odyssey 2018: The Speaker & Language Recognition Workshop, Les Sables d’Olonne, France, 26–29 June 2018; pp. 105–111. [Google Scholar]
- Novotný, O.; Matejka, P.; Cernocký, J.; Burget, L.; Glembek, O. On the Use of X-Vectors for Robust Speaker Recognition. In Proceedings of the Odyssey 2018: The Speaker & Language Recognition Workshop, Les Sables d’Olonne, France, 26–29 June 2018; pp. 111–118. [Google Scholar]
- Karafiát, M.; Veselý, K.; Černocký, J.; Profant, J.; Nytra, J.; Hlaváček, M.; Pavlíček, T. Analysis of X-Vectors for Low-Resource Speech Recognition. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2021), Toronto, ON, Canada, 6–11 June 2021; pp. 6998–7002. [Google Scholar]
- Zeinali, H.; Burget, L.; Černocký, J. Convolutional Neural Networks and X-Vector Embedding for DCASE2018 Acoustic Scene Classification Challenge. In Proceedings of the Detection and Classification of Acoustic Scenes and Events 2018 Workshop (DCASE2018), Surrey, UK, 19–20 November 2018; pp. 202–206. [Google Scholar]
- Janský, J.; Málek, J.; Čmejla, J.; Kounovský, T.; Koldovský, Z.; Žďánský, J. Adaptive Blind Audio Source Extraction Supervised by Dominant Speaker Identification Using X-Vectors. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2020), Barcelona, Spain, 4–8 May 2020; pp. 676–680. [Google Scholar]
- Michelsson, K.; Järvenpää, A.L.; Rinne, A. Sound Spectrographic Analysis of Pain Cry in Preterm Infants. Early Hum. Dev. 1983, 8, 141–149. [Google Scholar] [CrossRef]
- Lester, B.M.; Boukydis, C.F.Z.; Garcia-Coll, C. Neonatal Cry Analysis and Risk Assessment. In Newborn Behavioral Organization and the Assessment of Risk; Lester, B.M., Boukydis, C.F.Z., Eds.; Cambridge University Press: Cambridge, UK, 1992; pp. 137–158. [Google Scholar]
- Mampe, B.; Friederici, A.D.; Christophe, A.; Wermke, K. Newborns’ Cry Melody Is Shaped by Their Native Language. Curr. Biol. 2009, 19, 1994–1997. [Google Scholar] [CrossRef] [PubMed]
- Lind, K.; Wermke, K. Development of the Vocal Fundamental Frequency of Spontaneous Cries during the First 3 Months. Int. J. Pediatr. Otorhinolaryngol. 2002, 64, 97–104. [Google Scholar] [CrossRef]
- Boukydis, C.Z.; Lester, B.M. Infant Crying: Theoretical and Research Perspectives; Plenum Press: New York, NY, USA, 1985. [Google Scholar]
- Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence (IJCAI), Montreal, QC, Canada, 20–25 August 1995; pp. 1137–1143. [Google Scholar]
- Young, S.; Evermann, G.; Gales, M.; Hain, T.; Kershaw, D.; Liu, X.; Moore, G.; Odell, J.; Ollason, D.; Povey, D.; et al. The HTK Book (for HTK Version 3.4); Cambridge University Engineering Department: Cambridge, UK, 2006. [Google Scholar]
- Davis, S.; Mermelstein, P. Comparison of parametric representations for monosyllabic word recognition in continuously spoken sentences. IEEE Trans. Acoust. Speech Signal Process. 1980, 28, 357–366. [Google Scholar] [CrossRef]
- Waibel, A.; Hanazawa, T.; Hinton, G.; Shikano, K.; Lang, K.J. Phoneme Recognition Using Time-Delay Neural Networks. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 328–339. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Okabe, K.; Koshinaka, T.; Shinoda, K. Attentive Statistics Pooling for Deep Speaker Embedding. In Proceedings of the Annual Conference of the International Speech Communication Association (Interspeech), Hyderabad, India, 2–6 September 2018; pp. 2252–2256. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. Available online: https://pytorch.org/ (accessed on 5 September 2025).
- Sundararajan, M.; Taly, A.; Yan, Q. Axiomatic attribution for deep networks. In Proceedings of the 34th International Conference on Machine Learning (ICML), Exeter, UK, 21–23 June 2017; Volume 70, pp. 3319–3328. [Google Scholar]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recogn. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Bradley, A.P. The Use of the Area Under the ROC Curve in the Evaluation of Machine Learning Algorithms. Pattern Recogn. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Tjoa, E.; Guan, C. A Survey on Explainable Artificial Intelligence (XAI): Toward Medical XAI. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4793–4813. [Google Scholar] [CrossRef]
- Digital Research Alliance of Canada. Narval Supercomputing Cluster. Available online: https://alliancecan.ca/en/services/advanced-research-computing/narval (accessed on 5 September 2025).
- Yang, Y.-Y.; Hira, M.; Ni, Z.; Chourdia, A.; Astafurov, A.; Chen, C.; Yeh, C.-F.; Puhrsch, C.; Pollack, D.; Genzel, D.; et al. TorchAudio: An Audio Library for PyTorch. Available online: https://pytorch.org/audio/ (accessed on 5 September 2025).
- McFee, B.; Raffel, C.; Liang, D.; Ellis, D.P.W.; McVicar, M.; Battenberg, E.; Nieto, O. librosa: Audio and Music Signal Analysis in Python. In Proceedings of the 14th Python in Science Conference, Austin, TX, USA, 6–12 July 2015; pp. 18–24. Available online: https://librosa.org/ (accessed on 5 September 2025).
- Ravanelli, M.; Parcollet, T.; Plantinga, P.; Rouhe, A.; Cornell, S.; Lugosch, L.; Subakan, C.; Dawalatabad, N.; Heba, A.; Zhong, J.; et al. SpeechBrain: A General-Purpose Speech Toolkit. arXiv 2021, arXiv:2106.04624. [Google Scholar]
- Ravanelli, M.; Parcollet, T.; Moumen, A.; de Langen, S.; Subakan, C.; Plantinga, P.; Wang, Y.; Mousavi, P.; Della Libera, L.; Ploujnikov, A.; et al. Open-Source Conversational AI with SpeechBrain 1.0. arXiv 2024, arXiv:2407.00463. [Google Scholar]

| Label | RDS | Healthy |
|---|---|---|
| No. of Newborns | 38 | 38 |
| No. of CASs | 93 | 98 |
| No. of EXPs | 4317 | 4267 |
| Sampling Frequency | 44.1 kHz | 44.1 kHz |
| Duration Range (seconds) | [0.040–5.495] | [0.040–6.184] |
| Total Duration (seconds) | 3350.0150 | 3332.2570 |
| Hyperparameter | Tested Values | Optimal (Mean + SD) | Optimal (Attention) |
|---|---|---|---|
| Feature Extraction Parameters | |||
| Window, hop length (ms) | [(10, 3), (15, 5), (20, 6), (25, 10)] | (20, 6) | (20, 6) |
| FFT size | [1024, 2048, 4096] | 2048 | 2048 |
| Number of mel filters | [30, 40, 64, 80] | 80 | 80 |
| Number of MFCC coefficients | [13, 20, 26] | 20 | 26 |
| Deltas | [True, False] | False | False |
| Filter shape | [triangular, gaussian] | triangular | triangular |
| Training Configuration | |||
| Learning rate | [2.5 × 10−4, 5 × 10−4] (step: 0.5 × 10−5) | 4.5 × 10−4 | 4.5 × 10−4 |
| Number of epochs | [10, 12, 14] | 14 | 14 |
| Batch size | [16, 32, 64, 128] | 64 | 64 |
| Weight decay | [, , ] | ||
| Model Architecture | |||
| Activation function | [GELU, SiLU (Swish), ReLU, LeakyReLU] | LeakyReLU | GELU |
| Type of pooling | [Mean + SD, Attention] | Mean + SD | Attention |
| Number of attention heads | [1, 2, 4, 8] | - | 4 |
| Model | Accuracy | Precision | Recall | F1 Score | AUC |
|---|---|---|---|---|---|
| X-vector MFCC + Mean + SD | 93.59 ± 0.48% | 93.27 ± 0.74% | 93.98 ± 1.19% | 93.61 ± 0.50% | 0.9795 |
| X-vector MFCC + Attention | 93.53 ± 0.52% | 93.87 ± 0.72% | 93.16 ± 0.72% | 93.51 ± 0.52% | 0.9791 |
| Hyperparameter | Tested Values | Optimal (Mean + SD) | Optimal (Attention) |
|---|---|---|---|
| Feature Extraction Parameters | |||
| Window, hop length (ms) | [(10, 3), (15, 5), (20, 6), (25, 10)] | (20, 6) | (20, 6) |
| FFT size | [1024, 2048, 4096] | 2048 | 2048 |
| Number of mel filters | [30, 40, 64, 80] | 64 | 80 |
| Deltas | [True, False] | False | False |
| Filter shape | [triangular, Gaussian] | triangular | triangular |
| Training Configuration | |||
| Learning rate | [2.5 × 10−4, 5 × 10−4] (step: 0.5 × 10−5) | 5 × 10−4 | 4.5 × 10−4 |
| Number of epochs | [10, 12, 14] | 12 | 14 |
| Batch size | [16, 32, 64, 128] | 64 | 64 |
| Weight decay | [, , ] | ||
| Model Architecture | |||
| Activation function | [GELU, SiLU (Swish), ReLU, LeakyReLU] | LeakyReLU | GELU |
| Type of pooling | [Mean + SD, Attention] | Mean + SD | Attention |
| Number of attention heads | [1, 2, 4, 8] | - | 4 |
| Model | Accuracy | Precision | Recall | F1 Score | AUC |
|---|---|---|---|---|---|
| X-vector FBANK + Mean + SD | 93.22 ± 0.71% | 92.74 ± 1.48% | 93.81 ± 1.31% | 93.26 ± 0.68% | 0.9780 |
| X-vector FBANK + Attention | 93.09 ± 0.84% | 92.57 ± 1.03% | 93.70 ± 0.93% | 93.13 ± 0.83% | 0.9774 |
| Study | Population | Samples Per Class | Newborns Per Class | Minimum Duration Filter | Input Features | Overall Accuracy |
|---|---|---|---|---|---|---|
| [10] | Full-term | 955 | Unknown * | Not reported | MFCCs, tilt, and rhythm | 73.8% |
| [11] | Full-term | 1132 | Unknown * | Not reported | Spectrograms processed by an ImageNet-pretrained CNN, HR, and GFCC | 97.00% |
| [12] | Full-term | 1300 | Unknown * | <200 ms excluded | Spectrogram | 98.71% |
| [13] | Full-term | 2000 | Unknown * | Not reported | GFCCs, spectrograms, and mel-spectrograms | 96.33% |
| [14] | Full-term | 2799 | 17 | <40 ms excluded | Raw waveform | 89.76% |
| Proposed Method | Full-term and Preterm | 4267 | 38 | No restriction | MFCCs or FBANKs | 93.59% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shayegh, S.V.; Tadj, C. Balanced Neonatal Cry Classification: Integrating Preterm and Full-Term Data for RDS Screening. Information 2025, 16, 1008. https://doi.org/10.3390/info16111008
Shayegh SV, Tadj C. Balanced Neonatal Cry Classification: Integrating Preterm and Full-Term Data for RDS Screening. Information. 2025; 16(11):1008. https://doi.org/10.3390/info16111008
Chicago/Turabian StyleShayegh, Somaye Valizade, and Chakib Tadj. 2025. "Balanced Neonatal Cry Classification: Integrating Preterm and Full-Term Data for RDS Screening" Information 16, no. 11: 1008. https://doi.org/10.3390/info16111008
APA StyleShayegh, S. V., & Tadj, C. (2025). Balanced Neonatal Cry Classification: Integrating Preterm and Full-Term Data for RDS Screening. Information, 16(11), 1008. https://doi.org/10.3390/info16111008






