A Globally Optimal Alternative to MLP
Abstract
1. Introduction
- Investigating and visualizing the challenge encountered by the loss function of an MLP in overcoming to escape local minima to attain the global minimum.
- Deriving the explicit scaling law for MLPs through error bounds and conducting experimental validation on regression tasks.
- Overcoming the limitations of neural networks in fitting multi-frequency data, thereby making LReg more versatile for complex applications.
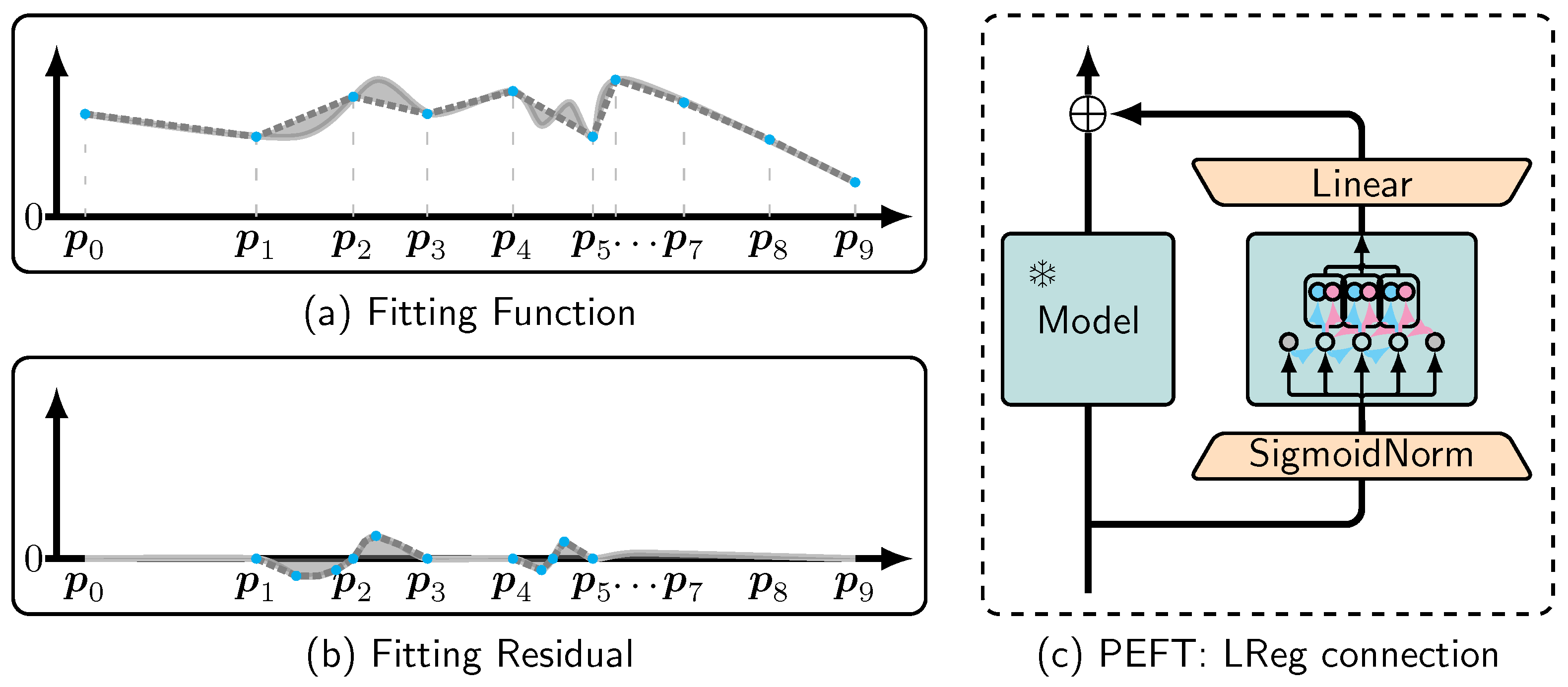
- Applying LReg as a PEFT method for large models (not confined to transformer architectures) to investigate the potential of guiding their loss functions toward global minima, consequently further reducing test loss and improving the performance of pre-trained models.
2. Methods
2.1. Global Minimum and Linear Interpolation
2.2. Preliminary: Function Fitting via MLP
2.3. Optimization: Discrete vs. Continuous Processes
2.4. Lagrange Basis Function
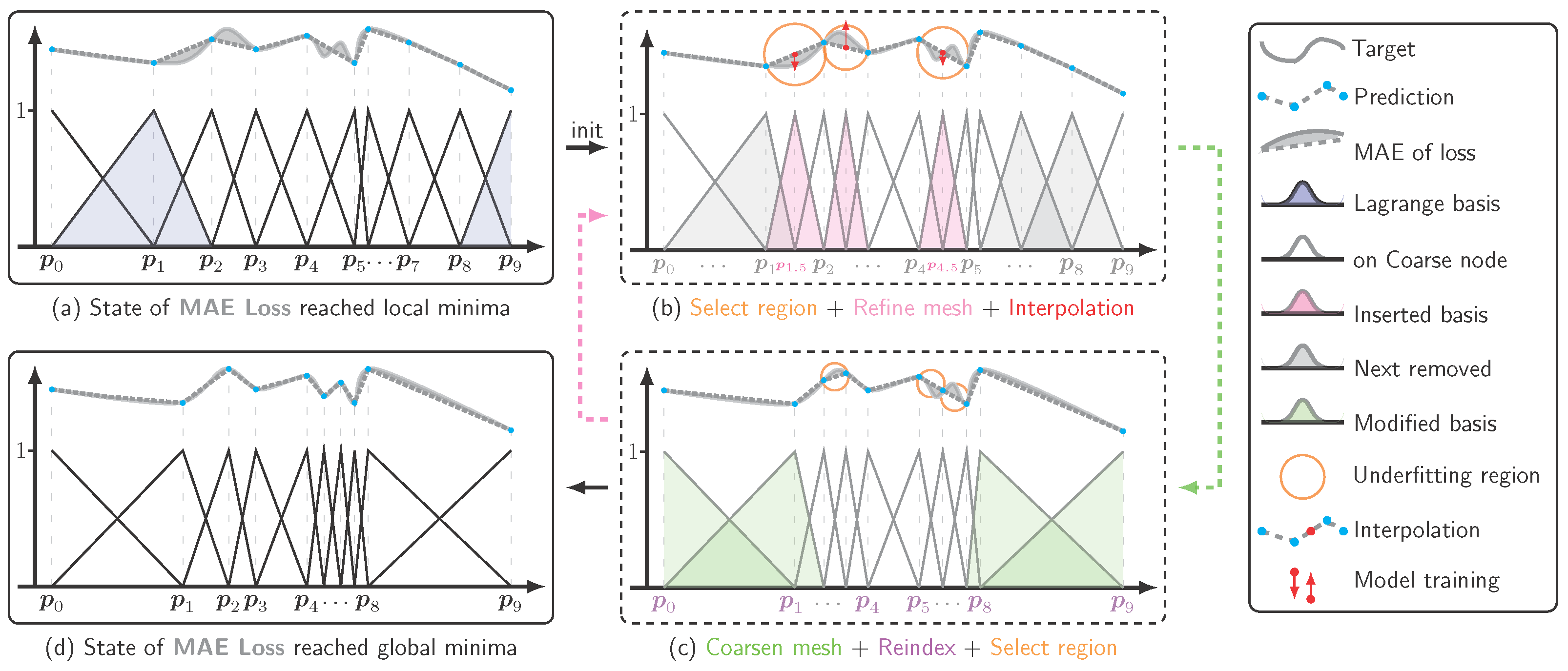
2.5. Mesh-Refinement–Coarsening Loop
| Algorithm 1 Overall 1D Pipeline on the domain [0, 1] |
| Require: Training pairs , initial DoF D, training budget T, top-k selector k Ensure: Final bins and coefficients appended as the model
|
| Algorithm 2 TrainPhase1D (local fit + interval counting) |
| Require: Model f, bins p, coeffs c, selector k; batch size B Ensure: Updated c and accumulated counts
|
| Algorithm 3 MeshUpdate1D (Refine → Coarsen → Reindex) |
| Require: Counts , bins , coeffs , target DoF D, selector k Ensure: Updated ; counts reset
|
2.6. Scaling Law and Error-Bound Formula
2.7. LReg Applied to Large Models
3. Results
3.1. Scaling Law and Addressing Regression Challenges
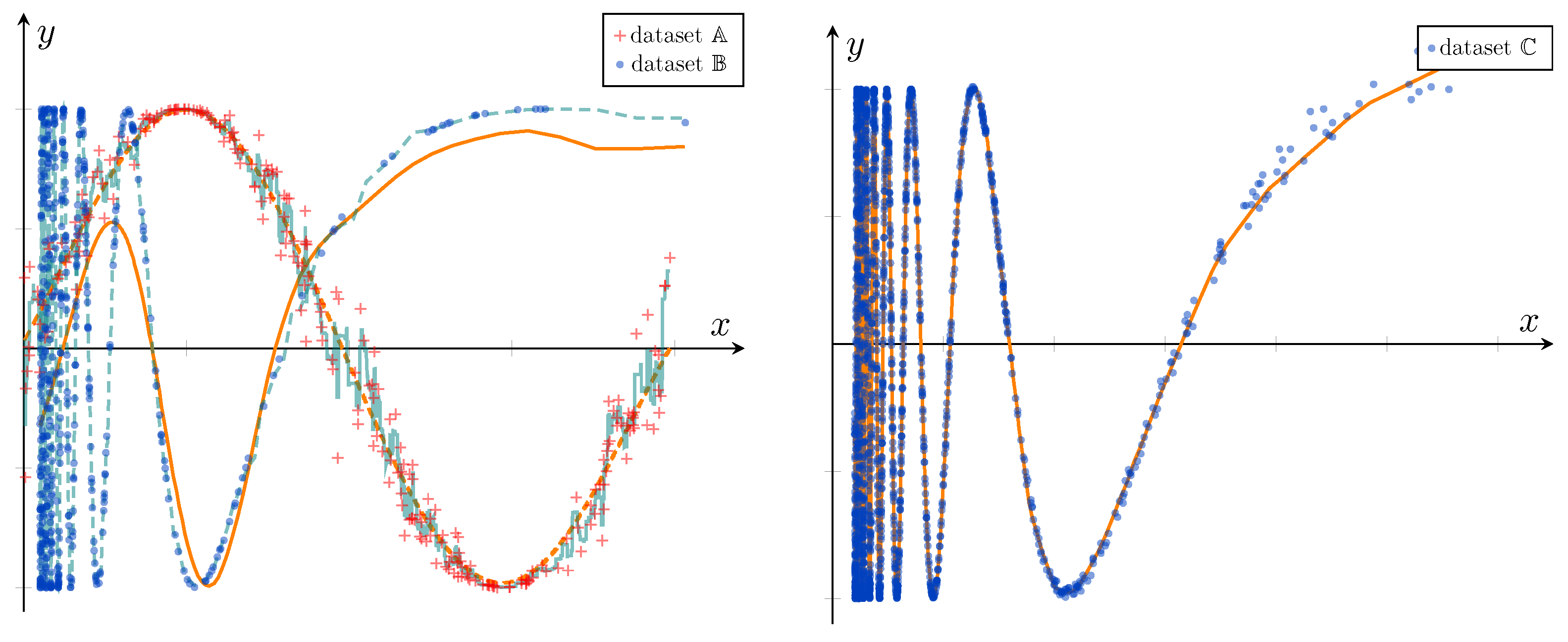
3.2. Comparison with Regressors: Training from Scratch
- : Generated from the distribution , with 1000 training examples and 200 test examples. The LReg was trained with a learning rate of 0.1.
- : Generated from the distribution , with 1000 training examples and 200 test examples. We trained the LReg with a learning rate of 0.9.
- : Generated from the distribution, with 7500 training examples and 1500 test examples. The LReg was trained with a learning rate of 0.1.
- : Generated from the distribution, with 50,000 training examples and 10,000 test examples. Training utilized a learning rate of 0.9.
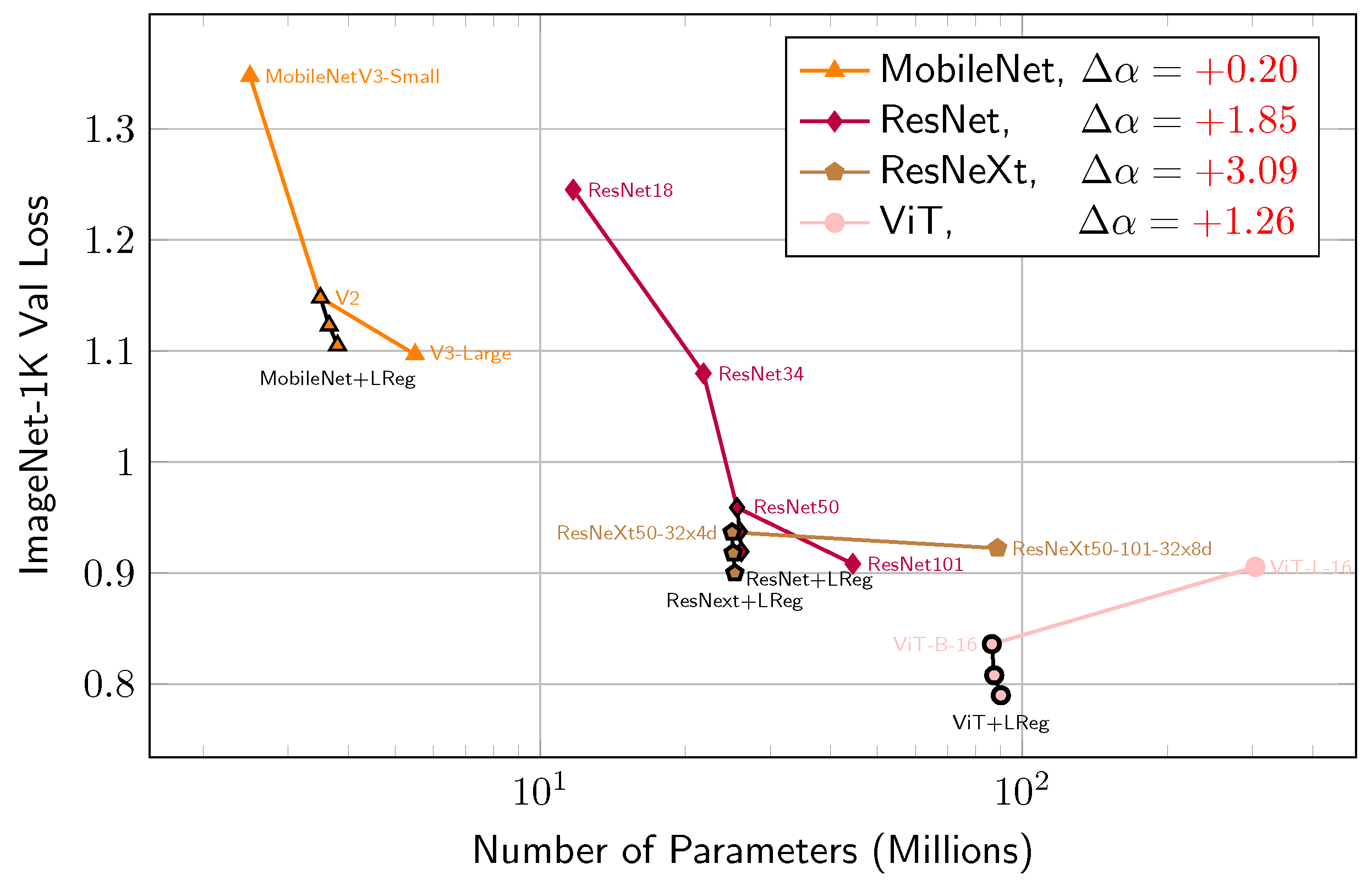
3.3. Improving Pre-Trained Model Performance and Continuously Reducing Loss
3.4. Transfer Learning via LReg Connection
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| LReg | Lagrange Regressor |
| MAE | Mean Absolute Error |
| MLP | Multi-Layer Perceptron |
| MRC | Mesh-Refinement–Coarsening |
| PCA | Principal Component Analysis |
| PEFT | Parameter-Efficient Fine-Tuning |
| SVM | Support Vector Machine |
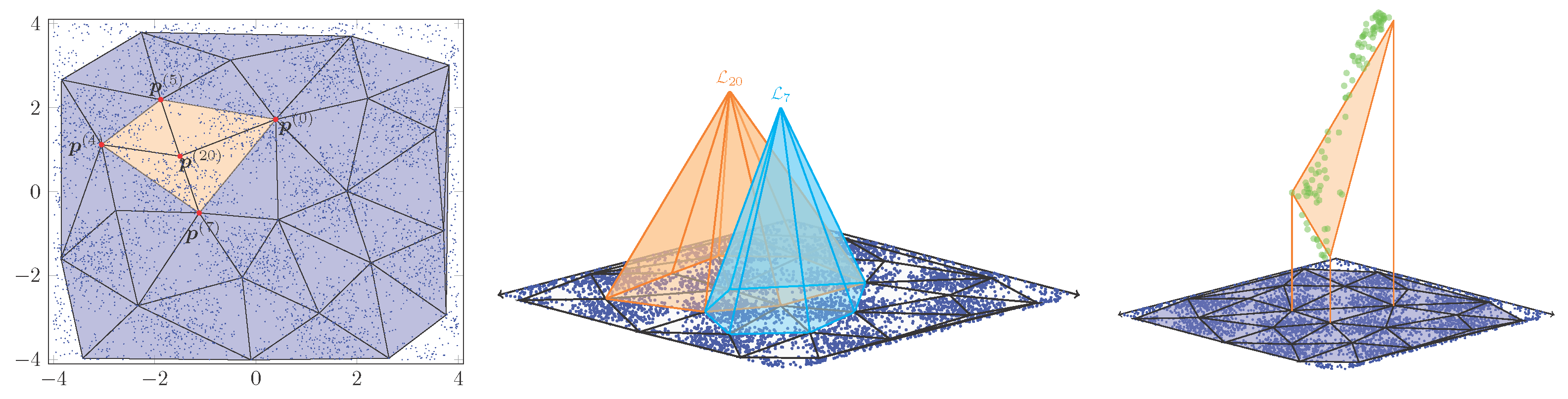
Appendix A. Mesh and Lagrange Basis Function
Appendix A.1. Triangulated Mesh
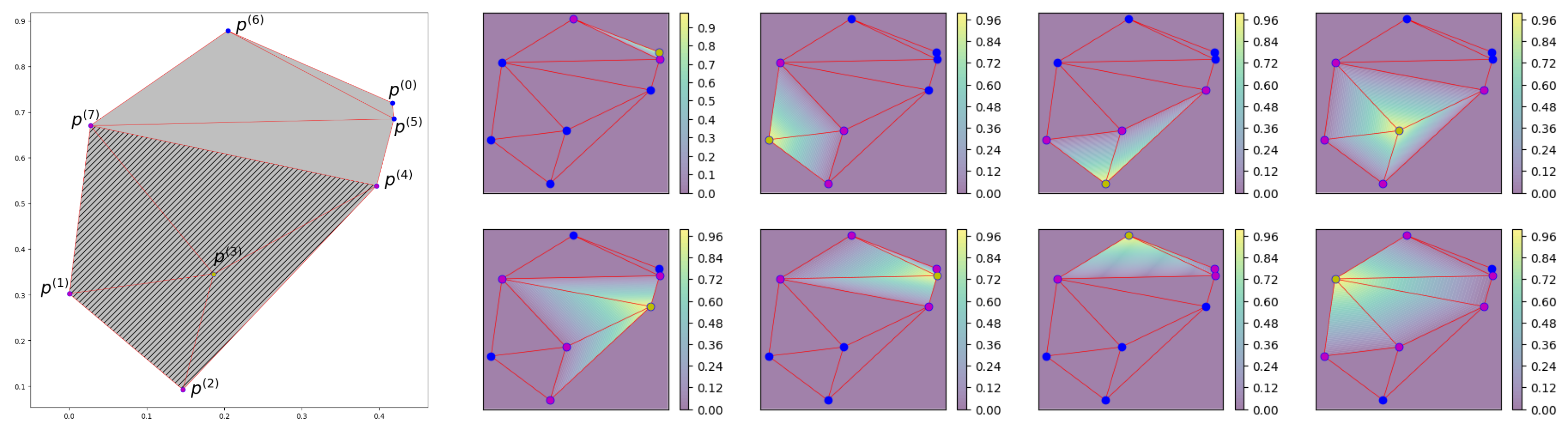
Appendix A.2. Lagrange Basis Function
Appendix A.3. Proof of Lagrange Basis Expression
Appendix A.4. Validation of Lagrange Basis Functions’ Mathematical Expression
Appendix A.5. Visualization of Lagrangian Basis
Appendix B. Additional Experiments
| Model | d | n | # Params | Acc@1 (%) | Acc@5 (%) |
|---|---|---|---|---|---|
| MobileNet-V2 | 32 | 8 | 0.298 M (+8.51%) | ||
| ResNet50 | 32 | 8 | 0.324 M (+1.27%) | ||
| ResNeXt50 | 32 | 8 | 0.324 M (+1.30%) | ||
| ViT-B-16 | 8 | 32 | 1.032 M (+1.19%) |
| Coeff (n, d) | (4, 4) | (4, 8) | (4, 16) | (4, 32) | (8, 4) | (8, 8) | (8, 16) | (8, 32) |
| # Parameters | 36,868 | 69,636 | 135,172 | 266,244 | 73,736 | 139,272 | 270,344 | 532,488 |
| Acc@1 | 76.226 | 76.226 | 76.242 | 76.222 | 76.238 | 76.256 | 76.268 | 76.276 |
| Acc@5 | 92.952 | 92.960 | 92.948 | 92.972 | 92.964 | 92.954 | 92.966 | 92.952 |
| Speed (img/s) | 405.31 | 411.18 | 390.26 | 418.84 | 382.22 | 394.63 | 409.52 | 404.43 |
| Coeff (n, d) | (16, 4) | (16, 8) | (16, 16) | (16, 32) | (32, 4) | (32, 8) | (32, 16) | (32, 32) |
| # Parameters | 147,472 | 278,544 | 540,688 | 1,064,976 | 294,944 | 557,088 | 1,081,376 | 2,129,952 |
| Acc@1 | 76.272 | 76.244 | 76.248 | 76.284 | 76.298 | 76.272 | 76.248 | 76.294 |
| Acc@5 | 92.940 | 92.946 | 92.968 | 92.958 | 92.956 | 92.958 | 92.968 | 92.932 |
| Speed (img/s) | 393.19 | 394.86 | 379.72 | 380.30 | 393.34 | 414.39 | 379.72 | 368.94 |
| Model | Method | # Trainable Parameters | Memory (MB) | GFLOPs | Throughput |
|---|---|---|---|---|---|
| MobileNet-V2 | Baseline | 3.5 M | 2817.5 | 0.60 | 701.51 |
| LReg | 328,720 | 2823.2 | 0.62 | 685.17 | |
| ResNet-50 | Baseline | 25.6 M | 3032.4 | 4.09 | 440.18 |
| LReg | 540,688 | 3039.4 | 4.10 | 411.50 | |
| ResNeXt-50_32x4d | Baseline | 25.0 M | 4238.2 | 4.27 | 334.72 |
| LReg | 135,172 | 4240.6 | 4.27 | 315.33 | |
| ViT-B16 | Baseline | 86.6 M | 4744.4 | 33.0 | 331.02 |
| LReg | 67,076 | 4746.2 | 33.0 | 316.31 | |
| GPT2 | Baseline | 124.4 M | 1428.4 | 0.25 | 6.98 |
| LReg | 0.203 M | 1439.5 | 0.26 | 9.58 | |
| GPT2-Medium | Baseline | 354.8 M | 3428.8 | 0.71 | 3.50 |
| LReg | 0.404 M | 3445.0 | 0.71 | 6.66 | |
| GPT2-Large | Baseline | 774.0 M | 6936.0 | 1.55 | 10.05 |
| LReg | 0.303 M | 6949.9 | 1.55 | 12.37 |
Appendix C. Additional Applications
Appendix C.1. Solve PDEs

Appendix C.2. Fitting High-Noise Data

Appendix C.3. Fitting Multi-Frequency Data

Appendix C.4. Fit a Vector-Valued Function
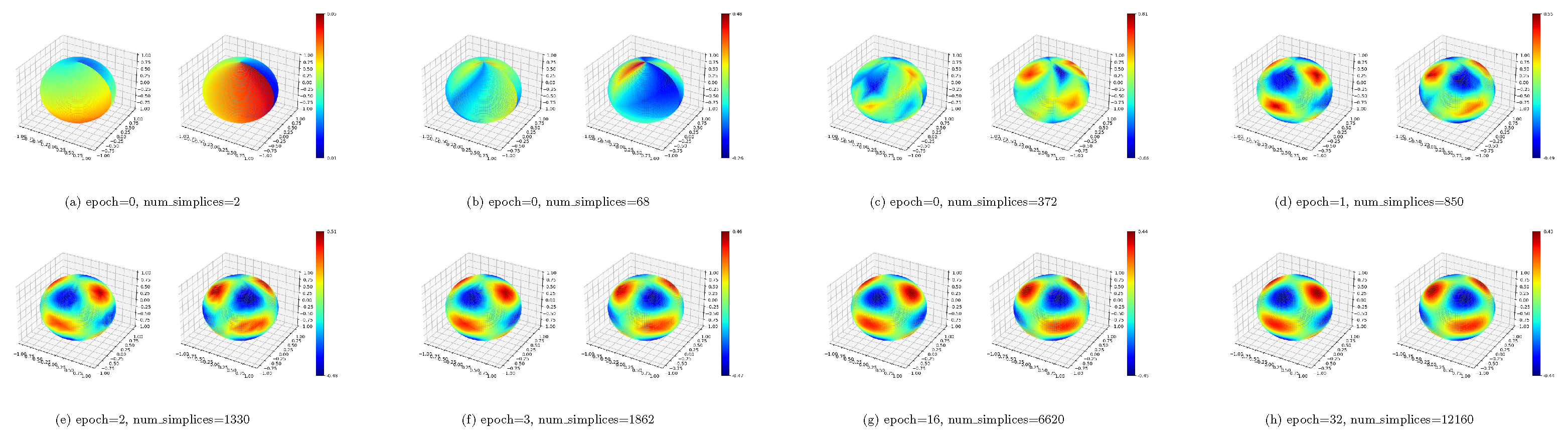
References
- Saxe, A.M.; McClelland, J.L.; Ganguli, S. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. arXiv 2013, arXiv:1312.6120. [Google Scholar]
- Dauphin, Y.N.; Pascanu, R.; Gulcehre, C.; Cho, K.; Ganguli, S.; Bengio, Y. Identifying and attacking the saddle point problem in high-dimensional non-convex optimization. arXiv 2014, arXiv:1406.2572. [Google Scholar]
- Goodfellow, I.J.; Vinyals, O.; Saxe, A.M. Qualitatively characterizing neural network optimization problems. arXiv 2014, arXiv:1412.6544. [Google Scholar]
- Choromanska, A.; Henaff, M.; Mathieu, M.; Arous, G.B.; LeCun, Y. The loss surfaces of multilayer networks. In Proceedings of the Artificial Intelligence and Statistics, PMLR, San Diego, CA, USA, 9–12 May 2015; pp. 192–204. [Google Scholar]
- Kaplan, J.; McCandlish, S.; Henighan, T.; Brown, T.B.; Chess, B.; Child, R.; Gray, S.; Radford, A.; Wu, J.; Amodei, D. Scaling laws for neural language models. arXiv 2020, arXiv:2001.08361. [Google Scholar] [CrossRef]
- Henighan, T.; Kaplan, J.; Katz, M.; Chen, M.; Hesse, C.; Jackson, J.; Jun, H.; Brown, T.B.; Dhariwal, P.; Gray, S.; et al. Scaling laws for autoregressive generative modeling. arXiv 2020, arXiv:2010.14701. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Nithiarasu, P.; Zhu, J. The Finite Element Method; Elsevier: Amsterdam, The Netherlands, 1977; Volume 3. [Google Scholar]
- Xu, Z.Q.J.; Zhang, Y.; Xiao, Y. Training behavior of deep neural network in frequency domain. In Proceedings of the International Conference on Neural Information Processing, Sydney, NSW, Australia, 12–15 December 2019; Springer: Cham, Switzerland, 2019; pp. 264–274. [Google Scholar]
- Platt, J. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Adv. Large Margin Classif. 1999, 10, 61–74. [Google Scholar]
- Thiel, H. A rank-invariant method of linear and polynomial regression analysis. I, II, III. Nederl. Akad. Wetensch. 1950, 53, 386–392. [Google Scholar]
- Cantzler, H. Random Sample Consensus (Ransac); Institute for Perception, Action and Behaviour, Division of Informatics University of Edinburgh: Edinburgh, Scotland, 1981. [Google Scholar]
- Zhang, T. Solving large scale linear prediction problems using stochastic gradient descent algorithms. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; p. 116. [Google Scholar]
- Hilt, D.E.; Seegrist, D.W. Ridge, a Computer Program for Calculating Ridge Regression Estimates; Department of Agriculture, Forest Service, Northeastern Forest Experiment: Washington, DC, USA, 1977; Volume 236.
- Stone, M. Cross-validatory choice and assessment of statistical predictions. J. R. Stat. Soc. Ser. B (Methodol.) 1974, 36, 111–133. [Google Scholar] [CrossRef]
- Jain, P.; Kakade, S.M.; Kidambi, R.; Netrapalli, P.; Sidford, A. Accelerating stochastic gradient descent for least squares regression. In Proceedings of the Conference on Learning Theory, PMLR, Stockholm, Sweden, 6–9 July 2018; pp. 545–604. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, J.; LeCun, Y. Character-level convolutional networks for text classification. arXiv 2015, arXiv:1509.01626. [Google Scholar]
- Wightman, R.; Touvron, H.; Jégou, H. Resnet strikes back: An improved training procedure in timm. arXiv 2021, arXiv:2110.00476. [Google Scholar] [CrossRef]
- Touvron, H.; Vedaldi, A.; Douze, M.; Jégou, H. Fixing the train-test resolution discrepancy. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Touvron, H.; Cord, M.; Douze, M.; Massa, F.; Sablayrolles, A.; Jégou, H. Training data-efficient image transformers & distillation through attention. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 10347–10357. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- TorchVision Contributors. TorchVision Models. 2024. Available online: https://pytorch.org/vision/master/models.html (accessed on 9 August 2024).
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Hu, E.J.; Shen, Y.; Wallis, P.; Allen-Zhu, Z.; Li, Y.; Wang, S.; Wang, L.; Chen, W. Lora: Low-rank adaptation of large language models. arXiv 2021, arXiv:2106.09685. [Google Scholar]
- Hyeon-Woo, N.; Ye-Bin, M.; Oh, T.H. Fedpara: Low-rank hadamard product for communication-efficient federated learning. arXiv 2021, arXiv:2108.06098. [Google Scholar]
- Liu, H.; Tam, D.; Muqeeth, M.; Mohta, J.; Huang, T.; Bansal, M.; Raffel, C.A. Few-shot parameter-efficient fine-tuning is better and cheaper than in-context learning. Adv. Neural Inf. Process. Syst. 2022, 35, 1950–1965. [Google Scholar]
- Zaken, E.B.; Ravfogel, S.; Goldberg, Y. Bitfit: Simple parameter-efficient fine-tuning for transformer-based masked language-models. arXiv 2021, arXiv:2106.10199. [Google Scholar]
- Wang, A. Glue: A multi-task benchmark and analysis platform for natural language understanding. arXiv 2018, arXiv:1804.07461. [Google Scholar]
- Merity, S.; Xiong, C.; Bradbury, J.; Socher, R. Pointer sentinel mixture models. arXiv 2016, arXiv:1609.07843. [Google Scholar] [CrossRef]
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language models are unsupervised multitask learners. OpenAI Blog 2019, 1, 9. [Google Scholar]
- Liu, Y. Roberta: A robustly optimized bert pretraining approach. arXiv 2019, arXiv:1907.11692. [Google Scholar]
- Wolf, T.; Debut, L.; Sanh, V.; Chaumond, J.; Delangue, C.; Moi, A.; Cistac, P.; Rault, T.; Louf, R.; Funtowicz, M.; et al. Transformers: State-of-the-art natural language processing. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing: System Demonstrations, Online, 16–20 November 2020; pp. 38–45. [Google Scholar]

| Method | ||||||||
|---|---|---|---|---|---|---|---|---|
| OLS Linear | 0.037 | 0.042 | 0.963 | 0.951 | 0.085 | 0.092 | 0.984 | 0.984 |
| Theil-Sen | −44.7 | −54.4 | 0.958 | 0.946 | −0.41 | −3.81 | 0.982 | 0.982 |
| RANSAC | −1.21 | −1.43 | 0.963 | 0.951 | −27.0 | −27.1 | 0.983 | 0.983 |
| Huber | 0.036 | 0.041 | 0.962 | 0.949 | 0.085 | 0.092 | 0.984 | 0.984 |
| Ridge | 0.031 | 0.038 | 0.963 | 0.951 | 0.055 | 0.061 | 0.984 | 0.984 |
| RidgeCV | 0.037 | 0.042 | 0.963 | 0.951 | 0.085 | 0.092 | 0.984 | 0.984 |
| SGD | 0.009 | 0.01 | 0.962 | 0.95 | 0.005 | 0.004 | 0.983 | 0.983 |
| KRR | 0.0036 | 0.04 | 0.97 | 0.962 | 0.056 | 0.051 | 0.993 | 0.992 |
| SVR | 0.11 | 0.101 | 0.97 | 0.962 | 0.29 | 0.308 | 0.992 | 0.992 |
| Voting | 0.852 | 0.852 | 0.942 | 0.917 | 0.869 | 0.868 | 0.951 | 0.946 |
| LReg | 1.0 | 1.0 | 0.971 | 0.963 | 0.999 | 0.999 | 0.992 | 0.992 |
| Model | Method | # Trainable Parameters | Acc@1 | Acc@5 | Speed (img/s) | Training Time (Total) |
|---|---|---|---|---|---|---|
| MobileNet-V2 | Baseline * | 3.5 M | 71.878 | 90.286 | 701.51 | 16 h 37 m |
| LReg | 328,720 | 71.934 | 90.268 | 685.17 | 32 m 12 s | |
| ResNet-50 | Baseline * | 25.6 M | 76.130 | 92.862 | 440.18 | 2 d 1 h 15 m |
| LReg | 540,688 | 76.274 | 92.932 | 411.50 | 40 m 42 s | |
| ResNeXt-50_32x4d | Baseline * | 25.0 M | 77.618 | 93.698 | 334.72 | 3 d 1 h 32 m |
| LReg | 135,172 | 77.650 | 93.672 | 315.33 | 51 m 9 s | |
| ViT-B16 | Baseline * | 86.6 M | 81.072 | 95.318 | 331.02 | 3 d 3 h 26 m |
| LReg | 67,076 | 81.082 | 95.316 | 316.31 | 56 m 54 s |
| MNLI | SST-2 | MRPC | QNLI | QQP | RTE | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | # Params | Accuracy | # Params | Accuracy | # Params | Accuracy | # Params | Accuracy | # Params | Accuracy | # Params | Accuracy |
| FT * | 125 M | 87.6 | 125 M | 94.8 | 125 M | 90.2 | 125 M | 92.8 | 125 M | 91.9 | 125 M | 78.7 |
| BitFit * | 0.1 M | 84.7 | 0.1 M | 93.7 | 0.1 M | 92.7 | 0.1 M | 91.8 | 0.1 M | 84.0 | 0.1 M | 81.5 |
| LoRA * | 0.295 M | 87.5±0.3 | 0.295 M | 0.295 M | 0.295 M | 0.295 M | 0.295 M | |||||
| LReg | 0.259 M | 0.259 M | 0.259 M | 0.259 M | 0.259 M | 0.259 M | ||||||
| GPT2 | GPT2-Medium | GPT2-Large | Roberta-Base | |||||||||
| Method | # Params | PPL | Seq/s | # Params | PPL | Seq/s | # Params | PPL | Seq/s | # Params | PPL | Seq/s |
| FT | 124.4 M | 21.4234 | 6.98 | 354.8 M | 15.8900 | 3.50 | 774.0 M | 13.8468 | 1.58 | 124.7 M | 3.6415 | 10.05 |
| LoRA | 0.295 M | 21.4188 | 12.90 | 0.393 M | 15.8873 | 6.29 | 0.737 M | 13.8486 | 1.67 | 0.295 M | 3.6425 | 9.85 |
| LReg | 0.203 M | 21.3401 | 9.58 | 0.404 M | 15.8674 | 6.66 | 0.607 M | 13.8443 | 2.52 | 0.303 M | 3.6414 | 12.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Cheng, J.; Gu, H.H. A Globally Optimal Alternative to MLP. Information 2025, 16, 921. https://doi.org/10.3390/info16100921
Li Z, Cheng J, Gu HH. A Globally Optimal Alternative to MLP. Information. 2025; 16(10):921. https://doi.org/10.3390/info16100921
Chicago/Turabian StyleLi, Zheng, Jerry Cheng, and Huanying Helen Gu. 2025. "A Globally Optimal Alternative to MLP" Information 16, no. 10: 921. https://doi.org/10.3390/info16100921
APA StyleLi, Z., Cheng, J., & Gu, H. H. (2025). A Globally Optimal Alternative to MLP. Information, 16(10), 921. https://doi.org/10.3390/info16100921






