Convolutional Neural Network Acceleration Techniques Based on FPGA Platforms: Principles, Methods, and Challenges
Abstract
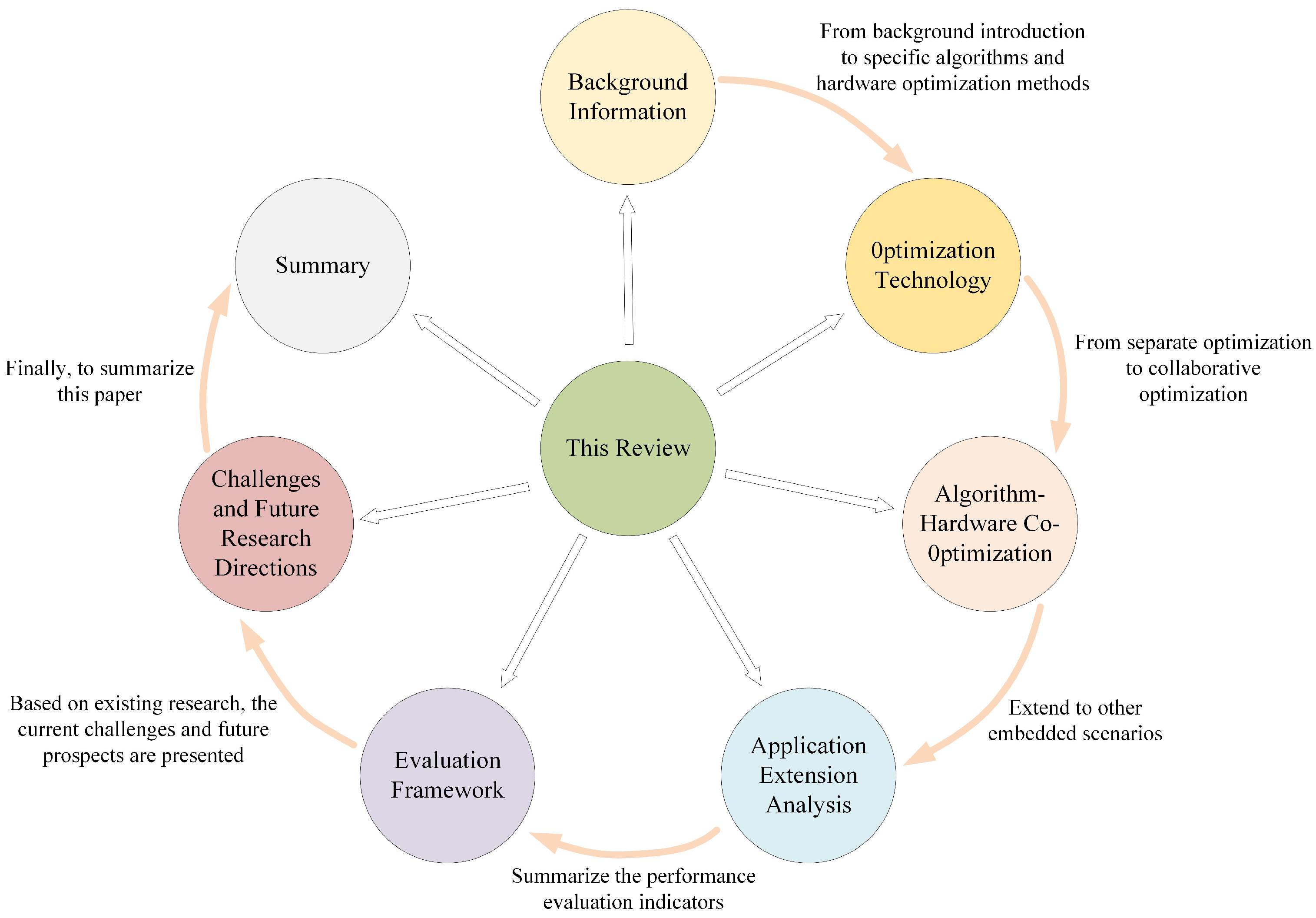
1. Introduction
2. Background Information
2.1. CNN
2.1.1. The Evolution of CNN
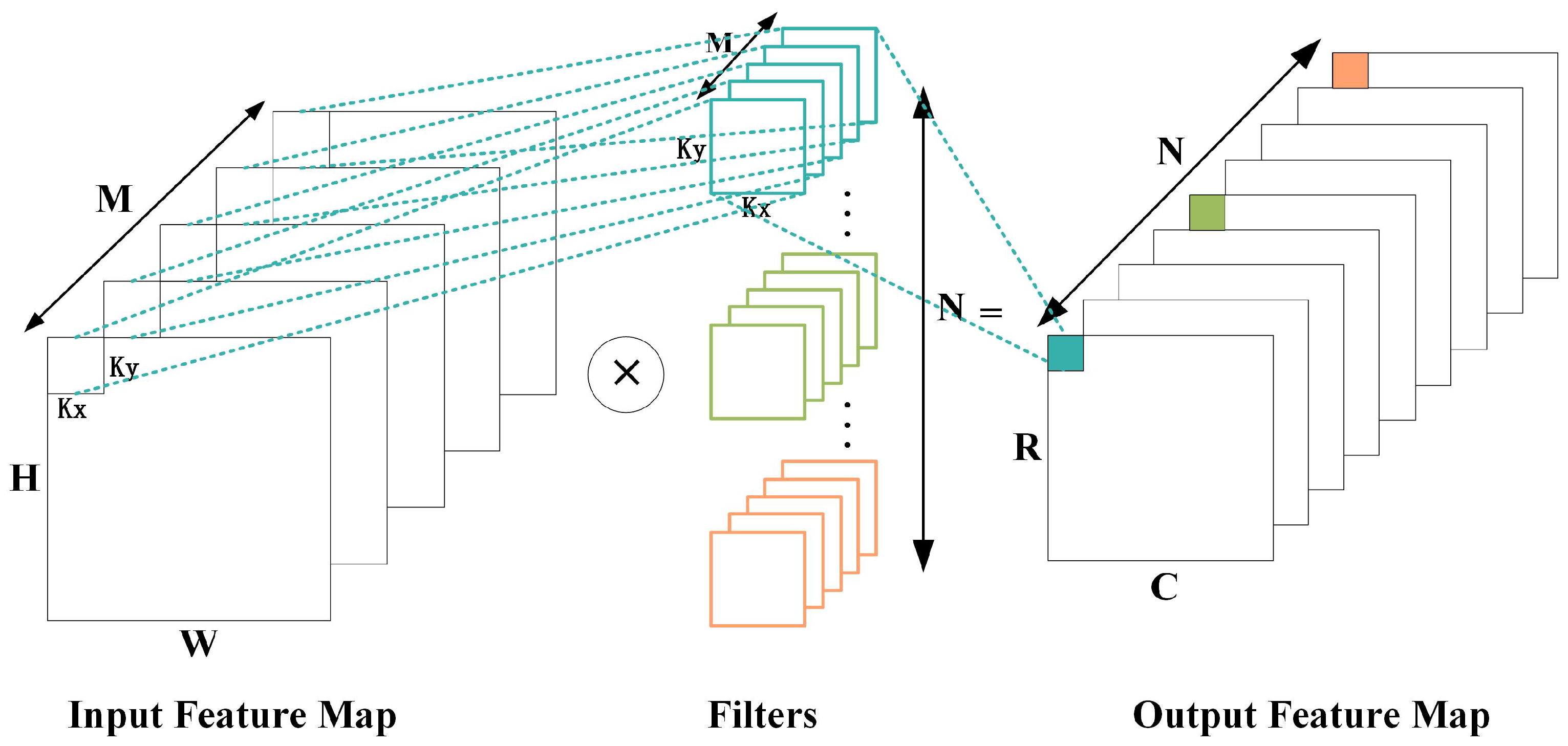
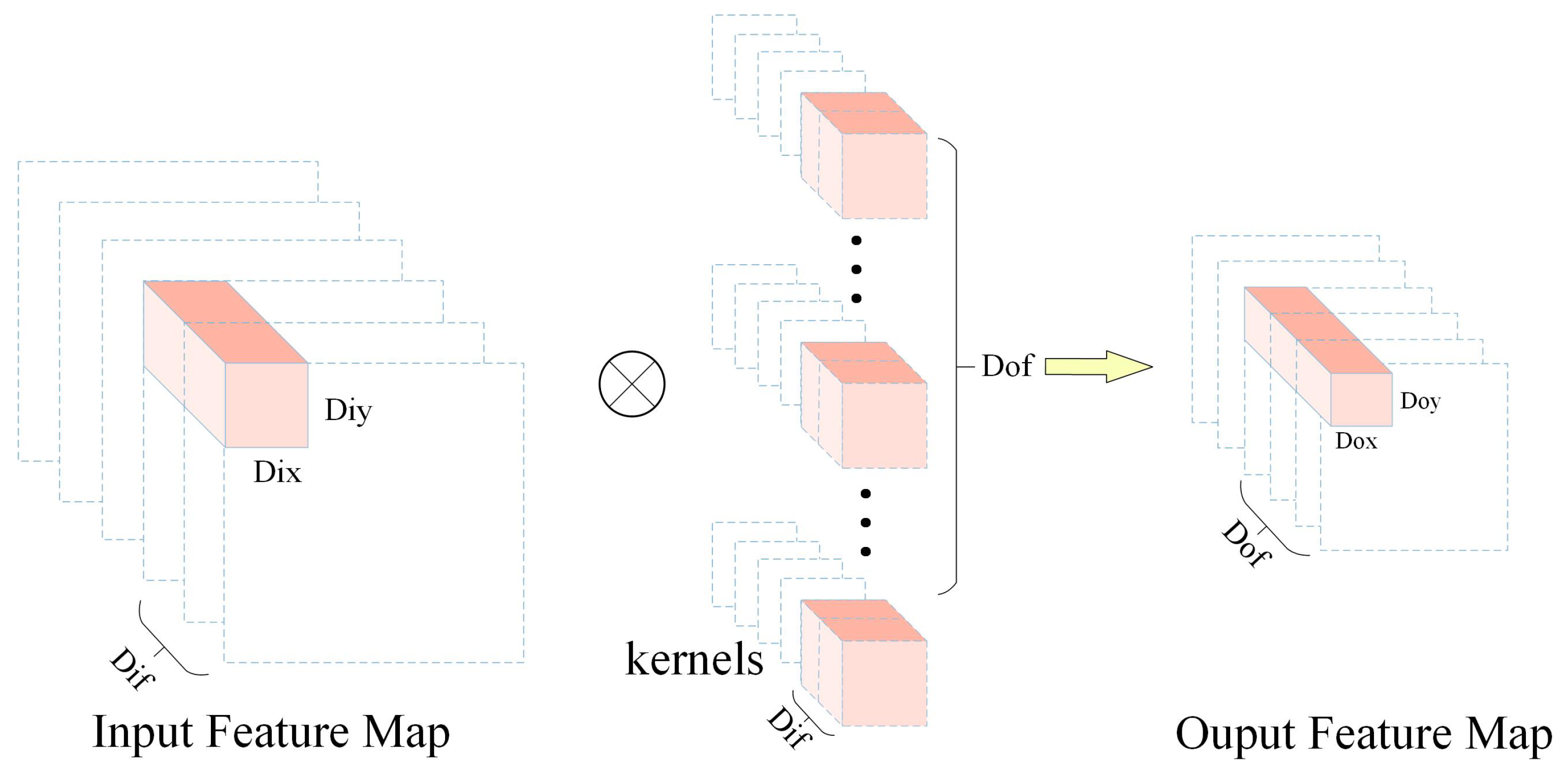
2.1.2. CNN Calculation
2.2. FPGA
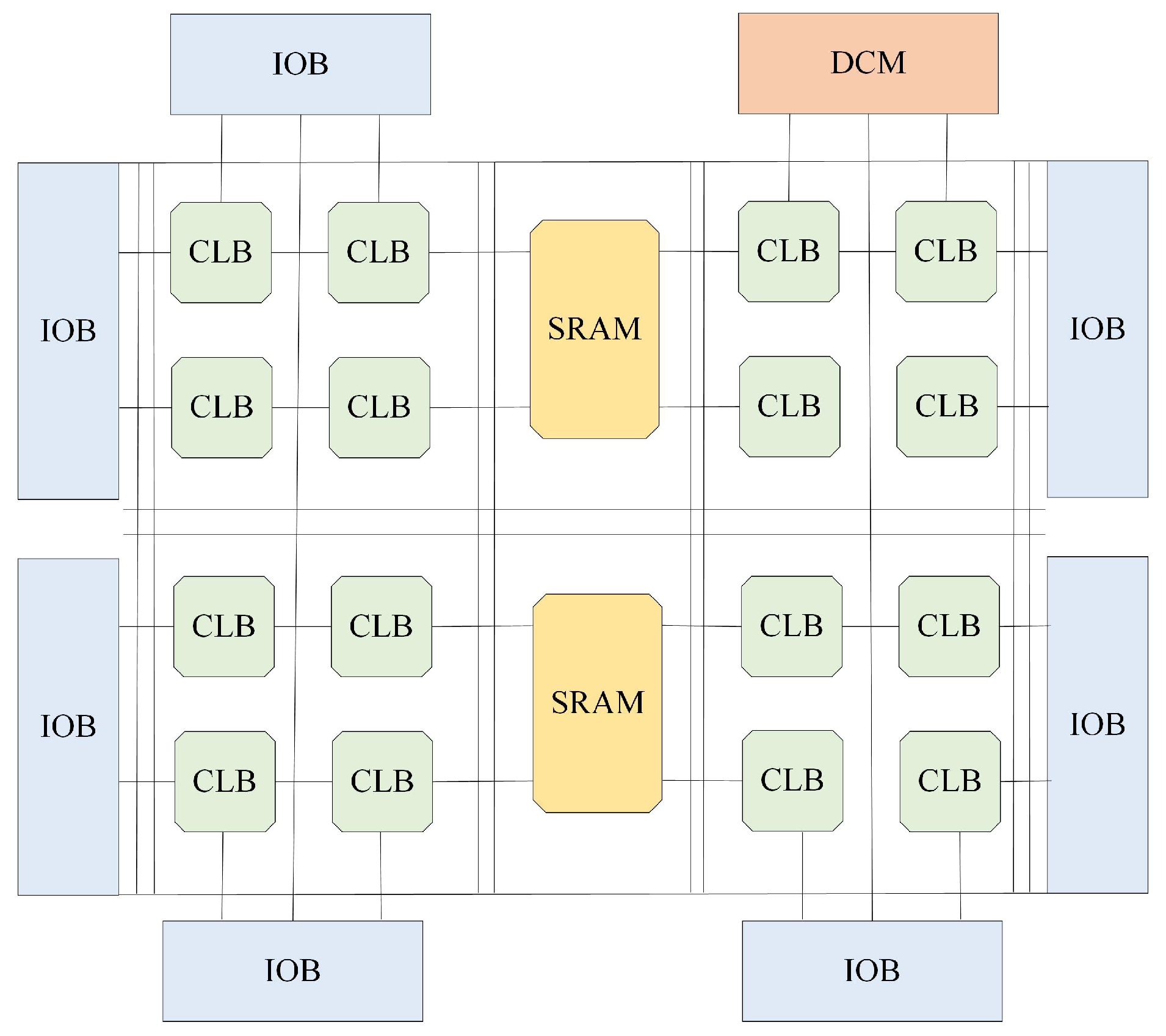
2.2.1. Fundamental Principles of FPGA Technology
2.2.2. Comparison of FPGA with Other Platforms
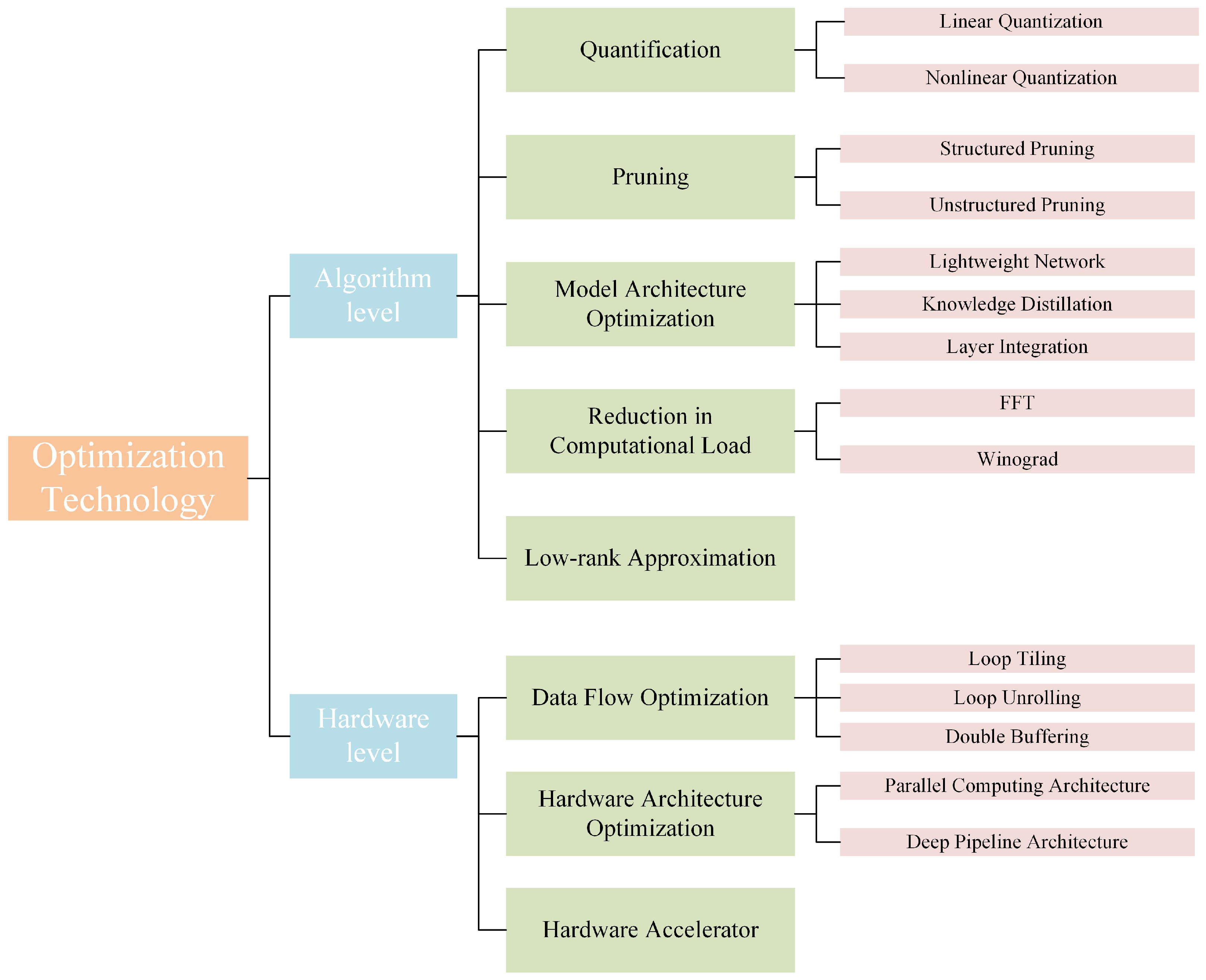
3. Optimization Technology
3.1. Algorithm-Level Optimization
3.1.1. Model Quantification
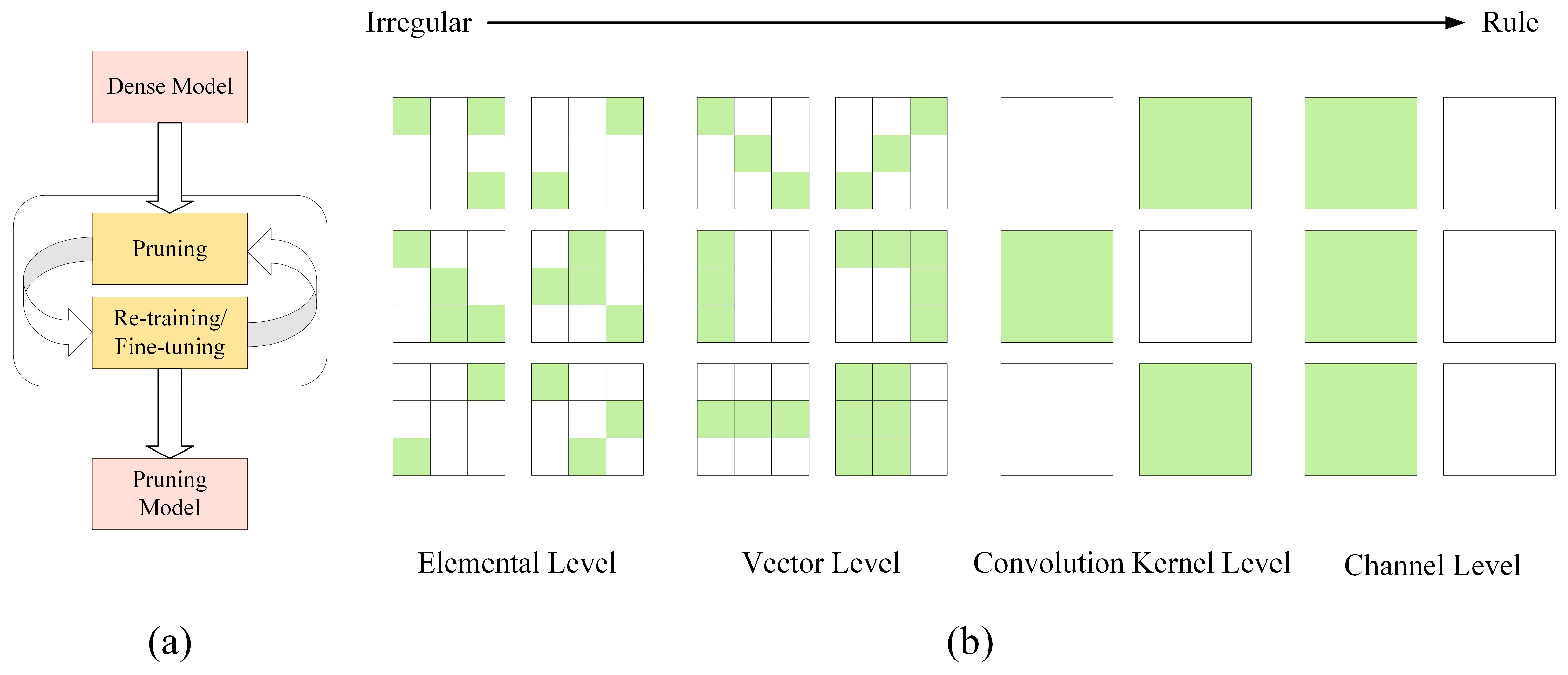
3.1.2. Pruning
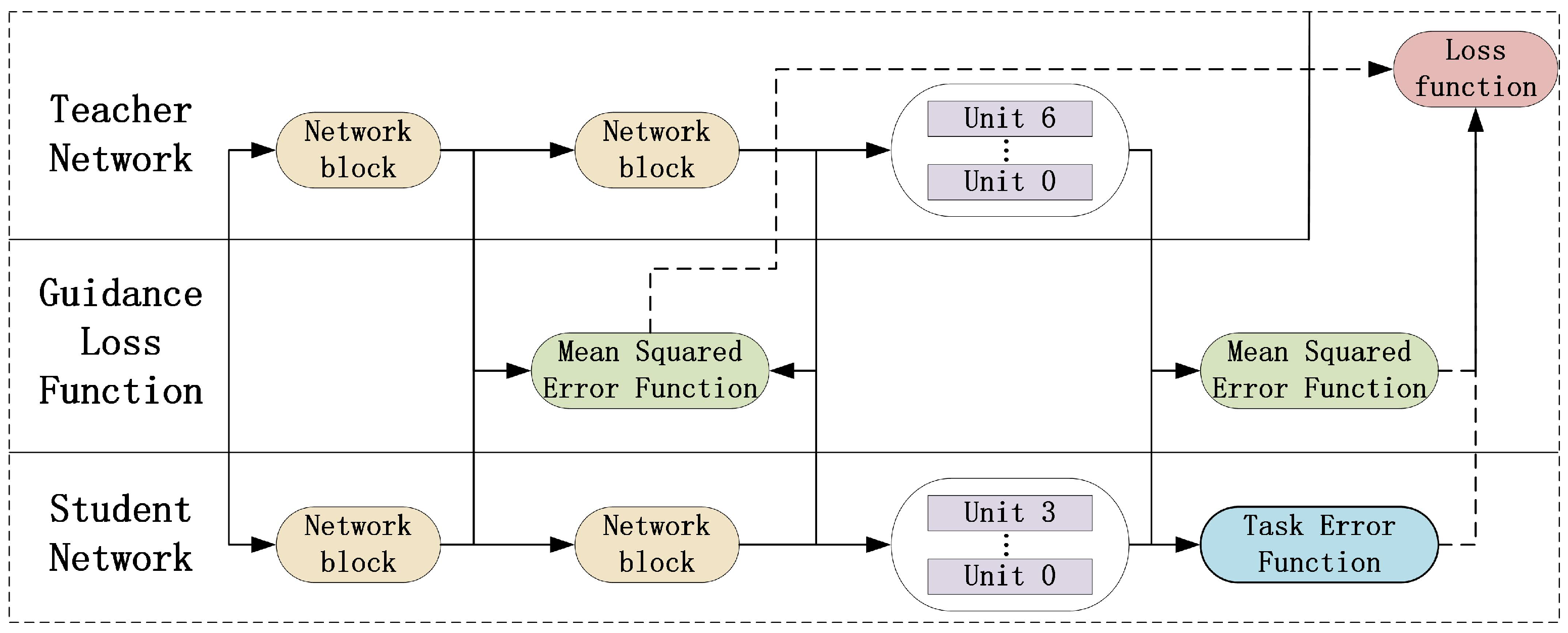
3.1.3. Model Architecture Optimization
3.1.4. Reduction in Computational Load
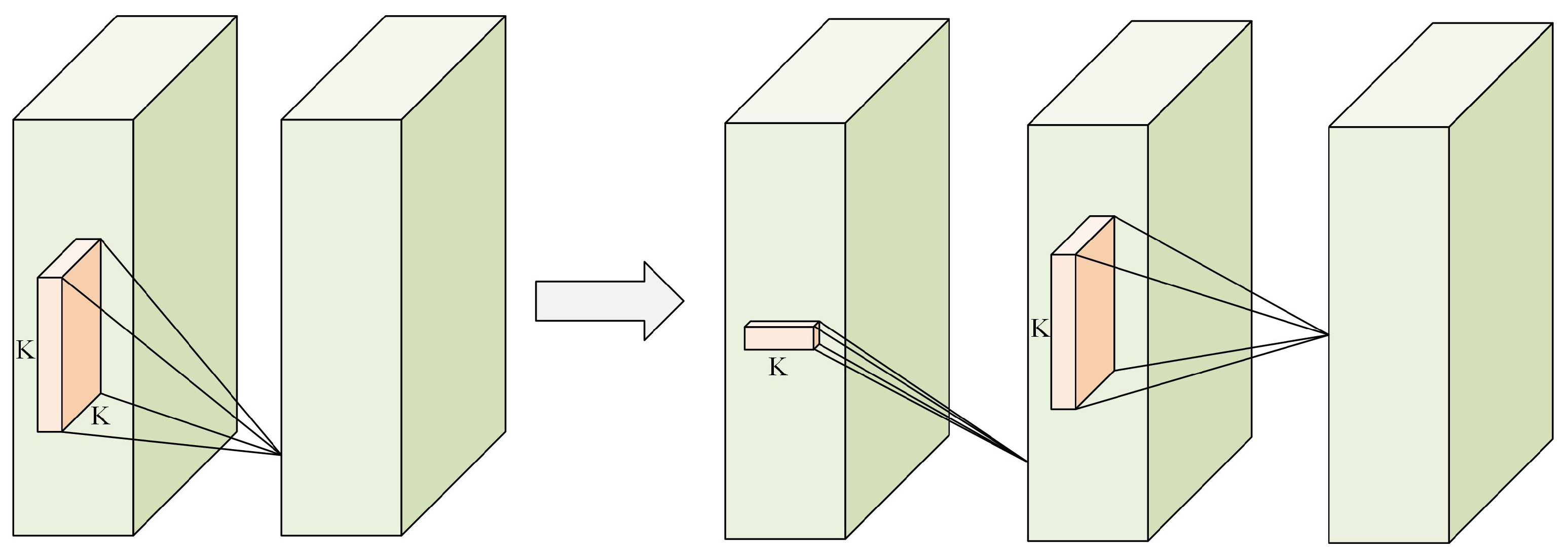
3.1.5. Low-Rank Approximation
3.1.6. Summary
3.2. Hardware-Level Optimization
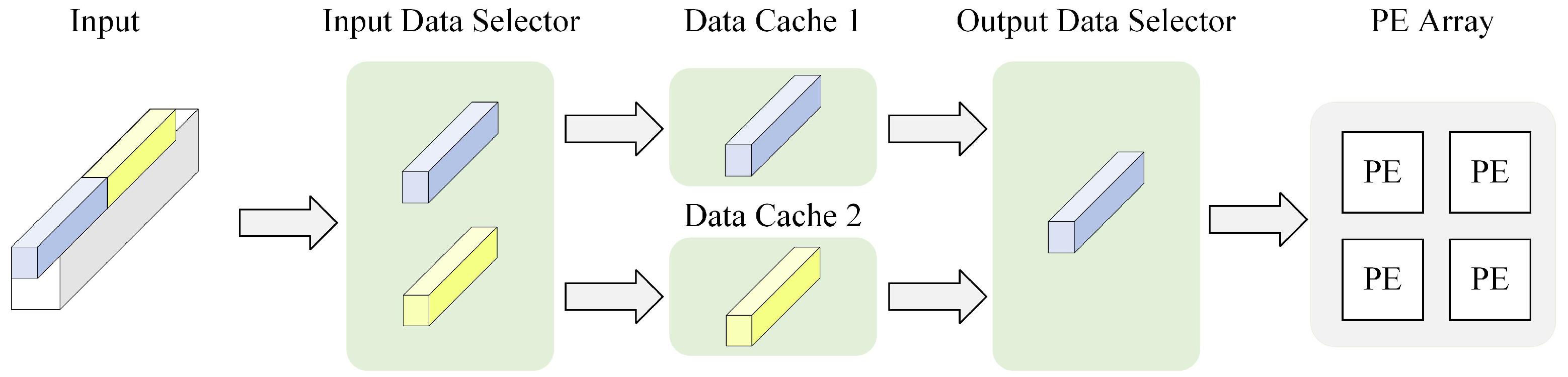
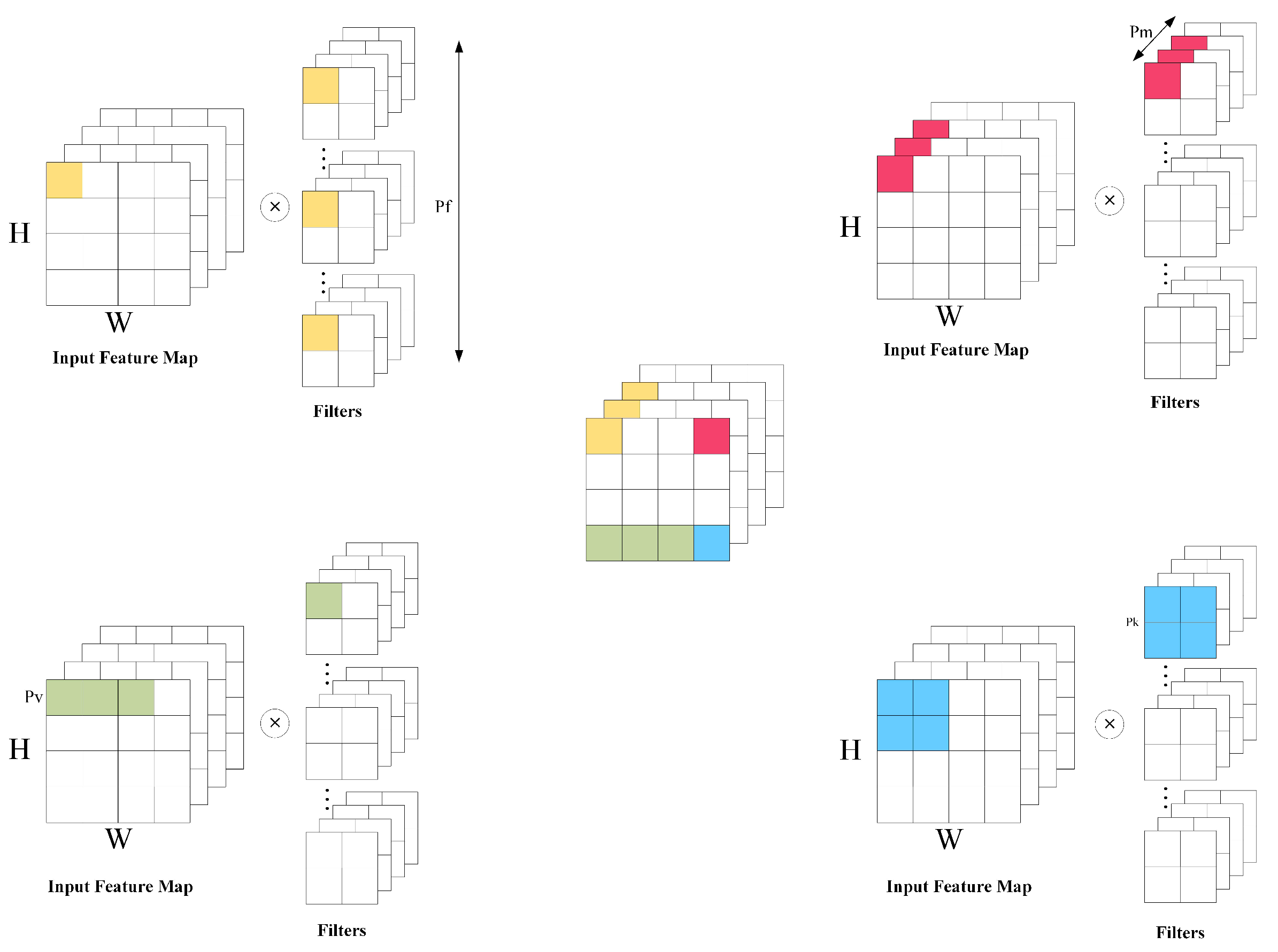
3.2.1. Data Flow Optimization
3.2.2. Hardware Architecture Optimization
3.2.3. Hardware Accelerator
3.2.4. Impact of Different FPGA Platforms on CNN Acceleration Performance
3.2.5. Summary
4. Algorithm–Hardware Co-Optimization
4.1. Algorithm–Hardware Co-Optimization Method
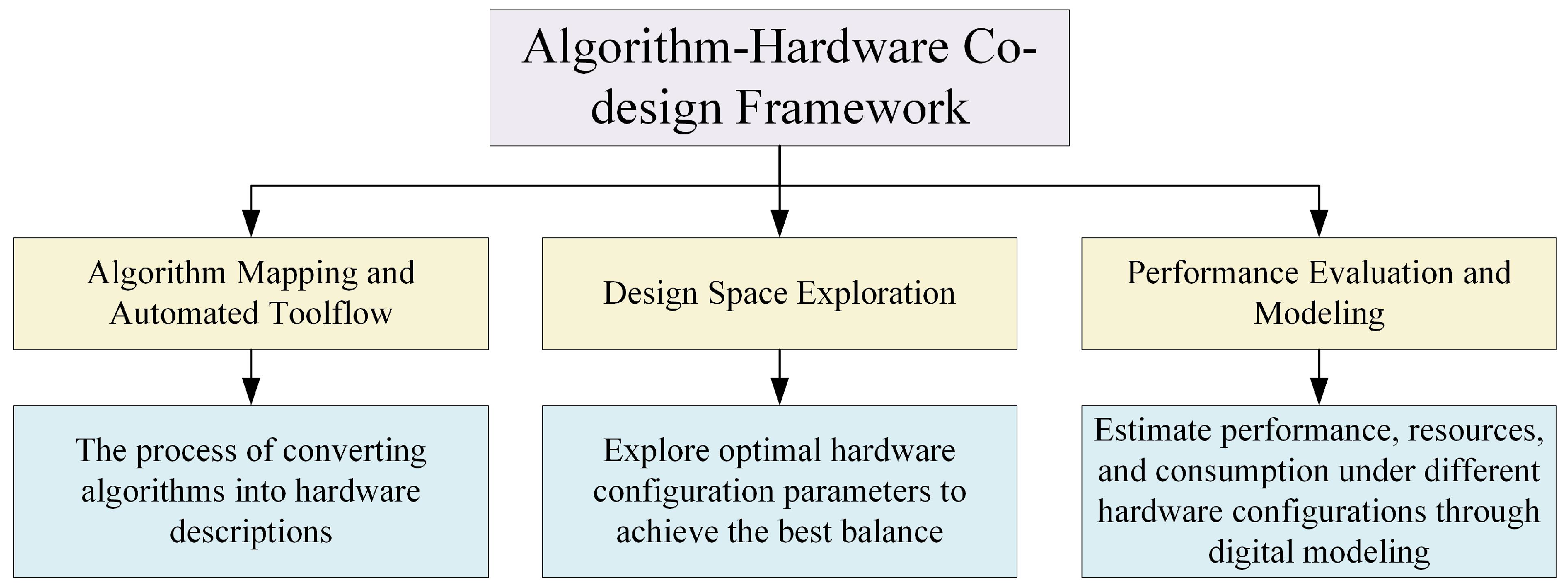
4.2. Algorithm–Hardware Co-Optimization Framework
4.2.1. Algorithm Mapping and Automated Toolflow
4.2.2. Design Space Exploration
4.2.3. Performance Evaluation and Modeling
4.2.4. Case Studies of Collaborative Design
5. Extended Analysis for Diverse Embedded Applications
6. Evaluation Framework
6.1. Network Model Performance Evaluation
6.2. Hardware Acceleration Performance Evaluation
7. Challenges and Future Research Directions
7.1. Challenges
7.2. Future Research Directions
7.3. Limitations of This Paper
8. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, Y.; Liu, Y.; Liu, Z. A Survey on Convolutional Neural Network Accelerators: GPU, FPGA and ASIC. In Proceedings of the 2022 14th International Conference on Computer Research and Development (ICCRD), Shenzhen, China, 7–9 January 2022; pp. 100–107. [Google Scholar]
- Li, Z.; Li, H.; Meng, L. Model compression for deep neural networks: A survey. Computers 2023, 12, 60. [Google Scholar] [CrossRef]
- Kok, C.L.; Zhao, B.; Heng, J.; Teo, T.H. Dynamic Quantization and Pruning for Efficient CNN-Based Road Sign Recognition on FPGA. In Proceedings of the 2025 IEEE International Symposium on Circuits and Systems (ISCAS), London, UK, 25–28 May 2025; pp. 1–5. [Google Scholar]
- Mishra, J.; Sharma, R. Optimized FPGA Architecture for CNN-Driven Voice Disorder Detection. Circuits Syst. Signal Process. 2025, 44, 4455–4467. [Google Scholar] [CrossRef]
- Balasubramanian, K.; Baragur, A.G.; Donadel, D.; Sahabandu, D.; Brighente, A.; Ramasubramanian, B.; Conti, M.; Poovendran; Radha. CANLP: Intrusion Detection for Controller Area Networks using Natural Language Processing and Embedded Machine Learning. IEEE Trans. Dependable Secur. Comput. 2025; early access. [Google Scholar]
- Wu, Y. Review on FPGA-Based Accelerators in Deep learning. In Proceedings of the 2023 IEEE 6th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 24–26 February 2023; Volume 6, pp. 452–456. [Google Scholar]
- Humaidi, A.J.; Kadhim, T.M.; Hasan, S.; Ibraheem, I.K.; Azar, A.T. A generic izhikevich-modelled FPGA-realized architecture: A case study of printed english letter recognition. In Proceedings of the 2020 24th International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 8–10 October 2020; pp. 825–830. [Google Scholar]
- Gołka, Ł.; Poczekajło, P.; Suszyński, R. Implementation of a universal replicable DSP core in FPGA devices for cascade audio signal processing applications. Procedia Comput. Sci. 2024, 246, 2429–2438. [Google Scholar] [CrossRef]
- Zayed, N.; Tawfik, N.; Mahmoud, M.M.; Fawzy, A.; Cho, Y.I.; Abdallah, M.S. Accelerating Deep Learning-Based Morphological Biometric Recognition with Field-Programmable Gate Arrays. AI 2025, 6, 8. [Google Scholar] [CrossRef]
- Guo, K.; Zeng, S.; Yu, J.; Wang, Y.; Yang, H. [DL] A survey of FPGA-based neural network inference accelerators. ACM Trans. Reconfigurable Technol. Syst. 2019, 12, 1–26. [Google Scholar] [CrossRef]
- Shawahna, A.; Sait, S.M.; El-Maleh, A. FPGA-Based Accelerators of Deep Learning Networks for Learning and Classification: A Review. IEEE Access 2019, 7, 7823–7859. [Google Scholar] [CrossRef]
- Mittal, S. A survey of FPGA-based accelerators for convolutional neural networks. Neural Comput. Appl. 2020, 32, 1109–1139. [Google Scholar] [CrossRef]
- Capra, M.; Bussolino, B.; Marchisio, A.; Masera, G.; Martina, M.; Shafique, M. Hardware and Software Optimizations for Accelerating Deep Neural Networks: Survey of Current Trends, Challenges, and the Road Ahead. IEEE Access 2020, 8, 225134–225180. [Google Scholar] [CrossRef]
- Wu, R.; Guo, X.; Du, J.; Li, J. Accelerating neural network inference on FPGA-based platforms—A survey. Electronics 2021, 10, 1025. [Google Scholar] [CrossRef]
- Liu, T.D.; Zhu, J.W.; Zhang, Y.W. A Survey on FPGA-Based Acceleration of Deep Learning. Comput. Sci. Explor. 2021, 15, 2093–2104. [Google Scholar]
- Wang, C.; Luo, Z. A review of the optimal design of neural networks based on FPGA. Appl. Sci. 2022, 12, 10771. [Google Scholar] [CrossRef]
- Dhilleswararao, P.; Boppu, S.; Manikandan, M.S.; Cenkeramaddi, L.R. Efficient Hardware Architectures for Accelerating Deep Neural Networks: Survey. IEEE Access 2022, 10, 131788–131828. [Google Scholar] [CrossRef]
- Amin, R.A.; Obermaisser, R. Towards Resource Efficient and Low Latency CNN Accelerator for FPGAs: Review and Evaluation. In Proceedings of the 2024 3rd International Conference on Embedded Systems and Artificial Intelligence (ESAI), Fez, Morocco, 19–20 December 2024; pp. 1–10. [Google Scholar]
- Hong, H.; Choi, D.; Kim, N.; Lee, H.; Kang, B.; Kang, H.; Kim, H. Survey of convolutional neural network accelerators on field-programmable gate array platforms: Architectures and optimization techniques. J. Real-Time Image Process. 2024, 21, 64. [Google Scholar] [CrossRef]
- Jiang, J.; Zhou, Y.; Gong, Y.; Yuan, H.; Liu, S. FPGA-based Acceleration for Convolutional Neural Networks: A Comprehensive Review. arXiv 2025, arXiv:2505.13461. [Google Scholar]
- Li, R. Dataflow & Tiling Strategies in Edge-AI FPGA Accelerators: A Comprehensive Literature Review. arXiv 2025, arXiv:2505.08992. [Google Scholar]
- Ma, Y.; Cao, Y.; Vrudhula, S.; Seo, J.s. Optimizing loop operation and dataflow in FPGA acceleration of deep convolutional neural networks. In Proceedings of the 2017 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2017; pp. 45–54. [Google Scholar]
- Fukushima, K. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 1980, 36, 193–202. [Google Scholar] [CrossRef]
- Arshad, M.A.; Shahriar, S.; Sagahyroon, A. On the use of FPGAs to implement CNNs: A brief review. In Proceedings of the 2020 International Conference on Computing, Electronics & Communications Engineering (iCCECE), Southend, UK, 17–18 August 2020; pp. 230–236. [Google Scholar]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Peng, X.; Yu, J.; Yao, B.; Liu, L.; Peng, Y. A review of FPGA-based Custom computing architecture for convolutional neural network inference. Chin. J. Electron. 2021, 30, 1–17. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Lee, C.Y.; Gallagher, P.W.; Tu, Z. Generalizing pooling functions in convolutional neural networks: Mixed, gated, and tree. In Proceedings of the Artificial Intelligence and Statistics, Cadiz, Spain, 9–11 May 2016; pp. 464–472. [Google Scholar]
- Chakraborty, S.; Paul, S.; Hasan, K.A. A transfer learning-based approach with deep cnn for covid-19-and pneumonia-affected chest x-ray image classification. SN Comput. Sci. 2022, 3, 17. [Google Scholar] [CrossRef] [PubMed]
- Han, G.; Huang, S.; Ma, J.; He, Y.; Chang, S.F. Meta faster r-cnn: Towards accurate few-shot object detection with attentive feature alignment. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 22 February–1 March 2022; Volume 36, pp. 780–789. [Google Scholar]
- Valdez-Rodriguez, J.E.; Calvo, H.; Felipe-Riveron, E.; Moreno-Armendáriz, M.A. Improving depth estimation by embedding semantic segmentation: A hybrid CNN model. Sensors 2022, 22, 1669. [Google Scholar] [CrossRef]
- Gyawali, D. Comparative analysis of cpu and gpu profiling for deep learning models. arXiv 2023, arXiv:2309.02521. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, M.; Chen, T.; Sun, Z.; Ma, Y.; Yu, B. Recent advances in convolutional neural network acceleration. Neurocomputing 2019, 323, 37–51. [Google Scholar] [CrossRef]
- Beldianu, S.F.; Ziavras, S.G. ASIC design of shared vector accelerators for multicore processors. In Proceedings of the 2014 IEEE 26th International Symposium on Computer Architecture and High Performance Computing, Paris, France, 22–24 October 2014; pp. 182–189. [Google Scholar]
- Jose, A.; Alense, K.; Gijo, L.; Jacob, J. FPGA Implementation of CNN Accelerator with Pruning for ADAS Applications. In Proceedings of the 2024 IEEE 9th International Conference for Convergence in Technology (I2CT), Pune, India, 5–7 April 2024; pp. 1–6. [Google Scholar]
- Wang, J.; He, Z.; Zhao, H.; Liu, R. Low-Bit Mixed-Precision Quantization and Acceleration of CNN for FPGA Deployment. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 9, 2597–2617. [Google Scholar] [CrossRef]
- Lo, C.Y. A Comprehensive Study of FPGA Accelerators for Machine Learning Applications. Ph.D. Thesis, The University of Auckland, Auckland, New Zealand, 2025. [Google Scholar]
- Fata, J.; Elmannai, W.; Elleithy, K. Balancing Performance and Cost—FPGA-Based CNN Accelerators for Edge Computing: Status Quo, Key Challenges, and Prospective Innovations. IEEE Access 2025, 13, 142852–142877. [Google Scholar] [CrossRef]
- Chen, Y.; Luo, T.; Liu, S.; Zhang, S.; He, L.; Wang, J.; Li, L.; Chen, T.; Xu, Z.; Sun, N.; et al. Dadiannao: A machine-learning supercomputer. In Proceedings of the 2014 47th Annual IEEE/ACM International Symposium on Microarchitecture, Cambridge, UK, 13–17 December 2014; pp. 609–622. [Google Scholar]
- Shao, W.; Chen, M.; Zhang, Z.; Xu, P.; Zhao, L.; Li, Z.; Zhang, K.; Gao, P.; Qiao, Y.; Luo, P. Omniquant: Omnidirectionally calibrated quantization for large language models. arXiv 2023, arXiv:2308.13137. [Google Scholar]
- Liu, Z.; Oguz, B.; Zhao, C.; Chang, E.; Stock, P.; Mehdad, Y.; Shi, Y.; Krishnamoorthi, R.; Chandra, V. Llm-qat: Data-free quantization aware training for large language models. arXiv 2023, arXiv:2305.17888. [Google Scholar]
- Zhu, C.; Han, S.; Mao, H.; Dally, W.J. Trained ternary quantization. arXiv 2016, arXiv:1612.01064. [Google Scholar]
- Kosuge, A.; Hsu, Y.C.; Hamada, M.; Kuroda, T. A 0.61-μJ/frame pipelined wired-logic DNN processor in 16-nm FPGA using convolutional non-linear neural network. IEEE Open J. Circuits Syst. 2021, 3, 4–14. [Google Scholar] [CrossRef]
- Liang, S.; Yin, S.; Liu, L.; Luk, W.; Wei, S. FP-BNN: Binarized neural network on FPGA. Neurocomputing 2018, 275, 1072–1086. [Google Scholar] [CrossRef]
- Xu, W.; Li, F.; Jiang, Y.; Yong, A.; He, X.; Wang, P.; Cheng, J. Improving extreme low-bit quantization with soft threshold. Neurocomputing 2022, 33, 1549–1563. [Google Scholar] [CrossRef]
- Chen, P.; Zhuang, B.; Shen, C. FATNN: Fast and accurate ternary neural networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 5219–5228. [Google Scholar]
- Zhong, K.; Ning, X.; Dai, G.; Zhu, Z.; Zhao, T.; Zeng, S.; Wang, Y.; Yang, H. Exploring the potential of low-bit training of convolutional neural networks. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2022, 41, 5421–5434. [Google Scholar] [CrossRef]
- Liu, F.; Zhao, W.; Wang, Z.; Chen, Y.; He, Z.; Jing, N.; Liang, X.; Jiang, L. Ebsp: Evolving bit sparsity patterns for hardware-friendly inference of quantized deep neural networks. In Proceedings of the 59th ACM/IEEE Design Automation Conference, San Francisco, CA, USA, 10–14 July 2022; pp. 259–264. [Google Scholar]
- Yuan, Y.; Chen, C.; Hu, X.; Peng, S. CNQ: Compressor-Based Non-uniform Quantization of Deep Neural Networks. Chin. J. Electron. 2020, 29, 1126–1133. [Google Scholar] [CrossRef]
- Qiu, S.; Zaheer, Q.; Hassan Shah, S.M.A.; Ai, C.; Wang, J.; Zhan, Y. Vector-Quantized Variational Teacher and Multimodal Collaborative Student Based Knowledge Distillation Paradigm for Cracks Segmentation. 2024. Available online: https://ascelibrary.org/doi/10.1061/JCCEE5.CPENG-6339 (accessed on 3 September 2025).
- Wen, W.; Wu, C.; Wang, Y.; Chen, Y.; Li, H. Learning structured sparsity in deep neural networks. Adv. Neural Inf. Process. Syst. 2016, 29. [Google Scholar]
- Huang, Z.; Wang, N. Data-driven sparse structure selection for deep neural networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 304–320. [Google Scholar]
- Lin, S.; Ji, R.; Yan, C.; Zhang, B.; Cao, L.; Ye, Q.; Huang, F.; Doermann, D. Towards optimal structured cnn pruning via generative adversarial learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2790–2799. [Google Scholar]
- Lemaire, C.; Achkar, A.; Jodoin, P.M. Structured pruning of neural networks with budget-aware regularization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9108–9116. [Google Scholar]
- Chen, C.; Tung, F.; Vedula, N.; Mori, G. Constraint-aware deep neural network compression. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 400–415. [Google Scholar]
- Dong, X.; Chen, S.; Pan, S. Learning to prune deep neural networks via layer-wise optimal brain surgeon. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Liu, Z.; Xu, J.; Peng, X.; Xiong, R. Frequency-domain dynamic pruning for convolutional neural networks. Adv. Neural Inf. Process. Syst. 2018, 31. Available online: https://www.semanticscholar.org/paper/Frequency-Domain-Dynamic-Pruning-for-Convolutional-Liu-Xu/c1cbfe55a04916bf65bb7134b2ee02c3c099fd56 (accessed on 14 October 2025).
- Lin, T.; Stich, S.U.; Barba, L.; Dmitriev, D.; Jaggi, M. Dynamic model pruning with feedback. arXiv 2020, arXiv:2006.07253. [Google Scholar] [CrossRef]
- Kim, K.; Kakani, V.; Kim, H. Automatic Pruning and Quality Assurance of Object Detection Datasets for Autonomous Driving. Electronics 2025, 14, 1882. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, K.; Wu, S.; Liu, L.; Liu, L.; Wang, D. Sparse-YOLO: Hardware/software co-design of an FPGA accelerator for YOLOv2. IEEE Access 2020, 8, 116569–116585. [Google Scholar] [CrossRef]
- Ma, X.; Lin, S.; Ye, S.; He, Z.; Zhang, L.; Yuan, G.; Tan, S.H.; Li, Z.; Fan, D.; Qian, X.; et al. Non-structured DNN weight pruning—Is it beneficial in any platform? IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 4930–4944. [Google Scholar] [CrossRef]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for mobilenetv3. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1314–1324. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6848–6856. [Google Scholar]
- Han, K.; Wang, Y.; Tian, Q.; Guo, J.; Xu, C.; Xu, C. Ghostnet: More features from cheap operations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1580–1589. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and< 0.5 MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar] [CrossRef]
- Son, W.; Na, J.; Choi, J.; Hwang, W. Densely guided knowledge distillation using multiple teacher assistants. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 9395–9404. [Google Scholar]
- Lan, X.; Zeng, Y.; Wei, X.; Zhang, T.; Wang, Y.; Huang, C.; He, W. Counterclockwise block-by-block knowledge distillation for neural network compression. Sci. Rep. 2025, 15, 11369. [Google Scholar] [CrossRef]
- Chen, L. Knowledge Distillation Research on CNN Imageclassification Task for Resource-Constrained Devices. Master’s Thesis, Sichuan University, Chengdu, China, 2023. [Google Scholar]
- Luo, D.Y.; Guo, Q.X.; Zhang, H.C. An FPGA implement of ECG classifier using quantized CNN based on knowl-edge distillation. Appl. Electron. Tech. 2024, 50, 97–101. [Google Scholar] [CrossRef]
- Zhu, K.; Yang, H.; Wang, Y. A lightweight fault diagnosis network based on FPGA and feature knowledge distillation. J. Phys. Conf. Ser. 2025, 3073, 012002. [Google Scholar] [CrossRef]
- Qian, W.; Zhu, Z.; Zhu, C.; Zhu, Y. FPGA-based accelerator for YOLOv5 object detection with optimized computation and data access for edge deployment. Parallel Comput. 2025, 124, 103138. [Google Scholar] [CrossRef]
- Zha, Y.; Cai, X. FPGA-Accelerated Lightweight CNN in Forest Fire Recognition. Forests 2025, 16, 698. [Google Scholar] [CrossRef]
- Wu, C.B.; Wu, R.F.; Chan, T.W. Hetero layer fusion based architecture design and implementation for of deep learning accelerator. In Proceedings of the 2022 IEEE International Conference on Consumer Electronics-Taiwan, Taipei, Taiwan, 6–8 July 2022; pp. 63–64. [Google Scholar]
- Nguyen, D.T.; Kim, H.; Lee, H.J. Layer-specific optimization for mixed data flow with mixed precision in FPGA design for CNN-based object detectors. IEEE Trans. Circuits Syst. Video Technol. 2020, 31, 2450–2464. [Google Scholar] [CrossRef]
- Liu, S.; Fan, H.; Luk, W. Accelerating fully spectral CNNs with adaptive activation functions on FPGA. In Proceedings of the 2021 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 1–5 February 2021; pp. 1530–1535. [Google Scholar]
- Xie, Y.; Chen, H.; Zhuang, Y.; Xie, Y. Fault classification and diagnosis approach using FFT-CNN for FPGA-based CORDIC processor. Electronics 2023, 13, 72. [Google Scholar] [CrossRef]
- Malathi, L.; Bharathi, A.; Jayanthi, A. FPGA design of FFT based intelligent accelerator with optimized Wallace tree multiplier for image super resolution and quality enhancement. Biomed. Signal Process. Control 2024, 88, 105599. [Google Scholar] [CrossRef]
- Meng, Y.; Wu, J.; Xiang, S.; Wang, J.; Hou, J.; Lin, Z.; Yang, C. A high-throughput and flexible CNN accelerator based on mixed-radix FFT method. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 72, 816–829. [Google Scholar] [CrossRef]
- Lavin, A.; Gray, S. Fast algorithms for convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4013–4021. [Google Scholar]
- Li, M.; Li, P.; Yin, S.; Chen, S.; Li, B.; Tong, C.; Yang, J.; Chen, T.; Yu, B. WinoGen: A Highly Configurable Winograd Convolution IP Generator for Efficient CNN Acceleration on FPGA. In Proceedings of the 61st ACM/IEEE Design Automation Conference, San Francisco, CA, USA, 23–27 June 2024; pp. 1–6. [Google Scholar]
- Vardhana, M.; Pinto, R. High-Performance Winograd Based Accelerator Architecture for Convolutional Neural Network. Comput. Archit. Lett. 2025, 24, 21–24. [Google Scholar]
- Jaderberg, M.; Vedaldi, A.; Zisserman, A. Speeding up convolutional neural networks with low rank expansions. arXiv 2014, arXiv:1405.3866. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Z.; Lin, J.; Liu, S.; Li, W. Deep neural network acceleration based on low-rank approximated channel pruning. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 1232–1244. [Google Scholar] [CrossRef]
- Yu, Z.; Bouganis, C.S. Svd-nas: Coupling low-rank approximation and neural architecture search. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 2–7 January 2023; pp. 1503–1512. [Google Scholar]
- Yu, Z.; Bouganis, C.S. Streamsvd: Low-rank approximation and streaming accelerator co-design. In Proceedings of the 2021 International Conference on Field-Programmable Technology (ICFPT), Auckland, New Zealand, 6–10 December 2021; pp. 1–9. [Google Scholar]
- Zhou, S.; Kannan, R.; Prasanna, V.K. Accelerating low rank matrix completion on FPGA. In Proceedings of the 2017 International Conference on ReConFigurable Computing and FPGAs (ReConFig), Cancun, Mexico, 4–6 December 2017; pp. 1–7. [Google Scholar]
- Yang, M.; Cao, S.; Zhang, W.; Li, Y.; Jiang, Z. Loop-tiling based compiling optimization for cnn accelerators. In Proceedings of the 2023 IEEE 15th International Conference on ASIC (ASICON), Nanjing, China, 24–27 October 2023; pp. 1–4. [Google Scholar]
- Huang, H.; Hu, X.; Li, X.; Xiong, X. An efficient loop tiling framework for convolutional neural network inference accelerators. IET Circuits, Devices Syst. 2022, 16, 116–123. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Nguyen, T.N.; Kim, H.; Lee, H.J. A high-throughput and power-efficient FPGA implementation of YOLO CNN for object detection. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2019, 27, 1861–1873. [Google Scholar] [CrossRef]
- Basalama, S.; Sohrabizadeh, A.; Wang, J.; Guo, L.; Cong, J. FlexCNN: An end-to-end framework for composing CNN accelerators on FPGA. ACM Trans. Reconfigurable Technol. Syst. 2023, 16, 1–32. [Google Scholar] [CrossRef]
- Deng, Y. Research on FPGA-Based Accelerator forConvolutional Neural Networks. Master’s Thesis, Changchun University of Technology, Changchun, China, 2025. [Google Scholar]
- Liu, Y.; Ma, Y.; Zhang, B.; Liu, L.; Wang, J.; Tang, S. Improving the computational efficiency and flexibility of FPGA-based CNN accelerator through loop optimization. Microelectron. J. 2024, 147, 106197. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Y.c.; Zhao, J. Issm: An Incremental Space Search Method for Loop Unrolling Parameters in Fpga-Based Cnn Accelerators. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4994345 (accessed on 3 September 2025).
- Sengupta, A.; Chourasia, V.; Anshul, A.; Kumar, N. Robust Watermarking of Loop Unrolled Convolution Layer IP Design for CNN using 4-variable Encoded Register Allocation. In Proceedings of the 2024 International Conference on Consumer Electronics-Taiwan (ICCE-Taiwan), Taichung, Taiwan, 9–11 July 2024; pp. 589–590. [Google Scholar]
- Zhang, C.; Li, P.; Sun, G.; Guan, Y.; Xiao, B.; Cong, J. Optimizing FPGA-based accelerator design for deep convolutional neural networks. In Proceedings of the 2015 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2015; pp. 161–170. [Google Scholar]
- Wang, H.; Zhao, Y.; Gao, F. A convolutional neural network accelerator based on FPGA for buffer optimization. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; Volume 5, pp. 2362–2367. [Google Scholar]
- Fan, R. Design of Mobilenet Neural Network AcceleratorBased on FPGA. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2025. [Google Scholar]
- Li, G.; Liu, Z.; Li, F.; Cheng, J. Block convolution: Toward memory-efficient inference of large-scale CNNs on FPGA. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 2021, 41, 1436–1447. [Google Scholar] [CrossRef]
- Fan, H.; Ferianc, M.; Que, Z.; Li, H.; Liu, S.; Niu, X.; Luk, W. Algorithm and hardware co-design for reconfigurable cnn accelerator. In Proceedings of the 2022 27th Asia and South Pacific Design Automation Conference (ASP-DAC), Taipei, Taiwan, 17–20 January 2022; pp. 250–255. [Google Scholar]
- Liu, S.; Fan, H.; Niu, X.; Ng, H.c.; Chu, Y.; Luk, W. Optimizing CNN-based segmentation with deeply customized convolutional and deconvolutional architectures on FPGA. ACM Trans. Reconfigurable Technol. Syst. 2018, 11, 1–22. [Google Scholar] [CrossRef]
- Mao, N.; Yang, H.; Huang, Z. A parameterized parallel design approach to efficient mapping of cnns onto fpga. Electronics 2023, 12, 1106. [Google Scholar] [CrossRef]
- Lai, Y.K.; Lin, C.H. An Efficient Reconfigurable Parameterized Convolutional Neural Network Accelerator on FPGA Platform. In Proceedings of the 2025 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 11–14 January 2025; pp. 1–2. [Google Scholar]
- Liu, S.; Fan, H.; Ferianc, M.; Niu, X.; Shi, H.; Luk, W. Toward full-stack acceleration of deep convolutional neural networks on FPGAs. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 3974–3987. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Duan, X.; Han, J. A design framework for generating energy-efficient accelerator on fpga toward low-level vision. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2024, 32, 1485–1497. [Google Scholar] [CrossRef]
- Yu, Y.; Wu, C.; Zhao, T.; Wang, K.; He, L. OPU: An FPGA-based overlay processor for convolutional neural networks. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2019, 28, 35–47. [Google Scholar] [CrossRef]
- Wu, T.H.; Shu, C.; Liu, T.T. An efficient FPGA-based dilated and transposed convolutional neural network accelerator. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 5178–5186. [Google Scholar] [CrossRef]
- Khan, F.H.; Pasha, M.A.; Masud, S. Towards designing a hardware accelerator for 3D convolutional neural networks. Comput. Electr. Eng. 2023, 105, 108489. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Z.; Hu, J.; Meng, Q.; Shi, X.; Luo, J.; Wang, H.; Huang, Q.; Chang, S. A high-performance pixel-level fully pipelined hardware accelerator for neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 7970–7983. [Google Scholar] [CrossRef]
- Dai, K.; Xie, Z.; Liu, S. DCP-CNN: Efficient acceleration of CNNs with dynamic computing parallelism on FPGA. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2024, 44, 540–553. [Google Scholar] [CrossRef]
- Feng, L. FPGA-Based Design and Implementation for HumanPose Estimation Algorithms. 2025. Available online: https://link.cnki.net/doi/10.27005/d.cnki.gdzku.2025.002354 (accessed on 14 October 2025).
- Fan, H.; Liu, S.; Que, Z.; Niu, X.; Luk, W. High-performance acceleration of 2-D and 3-D CNNs on FPGAs using static block floating point. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 4473–4487. [Google Scholar] [CrossRef]
- Shah, N.; Chaudhari, P.; Varghese, K. Runtime programmable and memory bandwidth optimized FPGA-based coprocessor for deep convolutional neural network. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5922–5934. [Google Scholar] [CrossRef]
- Zhao, R.; Ng, H.C.; Luk, W.; Niu, X. Towards efficient convolutional neural network for domain-specific applications on FPGA. In Proceedings of the 2018 28th International Conference on Field Programmable Logic and Applications (FPL), Dublin, Ireland, 27–31 August 2018; pp. 147–1477. [Google Scholar] [CrossRef]
- Seto, K.; Nejatollahi, H.; An, J.; Kang, S.; Dutt, N. Small memory footprint neural network accelerators. In Proceedings of the 20th International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 6–7 March 2019; pp. 253–258. [Google Scholar] [CrossRef]
- Cui, J.; Zhou, Y.; Zhang, F. Field programmable gate array implementation of a convolutionalneural network based on a pipeline architecture. J. Beijing Univ. Chem. Technol. (Nat. Sci. Ed.) 2021, 48, 111–118. [Google Scholar] [CrossRef]
- Li, T.; Zhang, F.; Wang, S.; Cao, W.; Chen, L. FPGA-Based Unified Accelerator for Convolutional Neural Networkand Vision Transformer. J. Electron. Inf. Technol. 2024, 46, 2663–2672. [Google Scholar]
- Meng, H.; Liu, W. A FPGA-based convolutional neural network training accelerator. J. Nanjing Univ. (Nat. Sci.) 2021, 57, 1075–1082. [Google Scholar] [CrossRef]
- Choudhury, Z.; Shrivastava, S.; Ramapantulu, L.; Purini, S. An FPGA overlay for CNN inference with fine-grained flexible parallelism. ACM Trans. Archit. Code Optim. 2022, 19, 1–26. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Q.; Yan, S.; Cheung, R.C. An efficient FPGA-based depthwise separable convolutional neural network accelerator with hardware pruning. ACM Trans. Reconfig. Technol. Syst. 2024, 17, 1–20. [Google Scholar] [CrossRef]
- Baskin, C.; Liss, N.; Zheltonozhskii, E.; Bronstein, A.M.; Mendelson, A. Streaming architecture for large-scale quantized neural networks on an FPGA-based dataflow platform. In Proceedings of the 2018 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Vancouver, BC, Canada, 21–25 May 2018; pp. 162–169. [Google Scholar]
- Qu, X.; Xu, Y.; Huang, Z.; Cai, G.; Fang, Z. QU Xinyuan, XU Yu, HUANG Zhihong, CAI Gang, FANG Zhen. J. Electron. Inf. Technol. 2022, 44, 1503–1512. [Google Scholar]
- Huang, W.; Luo, C.; Zhao, B.; Jiao, H.; Huang, Y. HCG: Streaming DCNN Accelerator With a Hybrid Computational Granularity Scheme on FPGA. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 18681–18695. [Google Scholar] [CrossRef]
- Jia, X.; Zhang, Y.; Liu, G.; Yang, X.; Zhang, T.; Zheng, J.; Xu, D.; Liu, Z.; Liu, M.; Yan, X.; et al. XVDPU: A high-performance cnn accelerator on the Versal platform powered by the AI engine. ACM Trans. Reconfig. Technol. Syst. 2024, 17, 1–24. [Google Scholar] [CrossRef]
- Rigoni, A.; Manduchi, G.; Luchetta, A.; Taliercio, C.; Schröder, T. A framework for the integration of the development process of Linux FPGA System on Chip devices. Fusion Eng. Des. 2018, 128, 122–125. [Google Scholar] [CrossRef]
- Vaithianathan, M. The Future of Heterogeneous Computing: Integrating CPUs GPUs and FPGAs for High-Performance Applications. Int. J. Emerg. Trends Comput. Sci. Inf. Technol. 2025, 1, 12–23. [Google Scholar] [CrossRef]
- Toupas, P.; Montgomerie-Corcoran, A.; Bouganis, C.S.; Tzovaras, D. Harflow3d: A latency-oriented 3d-cnn accelerator toolflow for har on fpga devices. In Proceedings of the 2023 IEEE 31st Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Marina Del Rey, CA, USA, 8–11 May 2023; pp. 144–154. [Google Scholar] [CrossRef]
- Toupas, P.; Bouganis, C.S.; Tzovaras, D. FMM-X3D: FPGA-based modeling and mapping of X3D for Human Action Recognition. In Proceedings of the 2023 IEEE 34th International Conference on Application-specific Systems, Architectures and Processors (ASAP), Porto, Portugal, 19 July–21 July 2023; pp. 119–126. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Z.; Han, S. Spatten: Efficient sparse attention architecture with cascade token and head pruning. In Proceedings of the 2021 IEEE International Symposium on High-Performance Computer Architecture (HPCA), Seoul, Republic of Korea, 27 February–3 March 2021; pp. 97–110. [Google Scholar] [CrossRef]
- Toupas, P.; Bouganis, C.S.; Tzovaras, D. fpgahart: A toolflow for throughput-oriented acceleration of 3d cnns for har onto fpgas. In Proceedings of the 2023 33rd International Conference on Field-Programmable Logic and Applications (FPL), Gothenburg, Sweden, 4–8 September 2023; pp. 86–92. [Google Scholar] [CrossRef]
- Pacini, T.; Rapuano, E.; Fanucci, L. FPG-AI: A technology-independent framework for the automation of CNN deployment on FPGAs. IEEE Access 2023, 11, 32759–32775. [Google Scholar] [CrossRef]
- Venieris, S.I.; Bouganis, C.S. f-CNNx: A toolflow for mapping multiple convolutional neural networks on FPGAs. In Proceedings of the 2018 28th International Conference on Field Programmable Logic and Applications (FPL), Dublin, Ireland, 27–31 August 2018; pp. 381–3817. [Google Scholar] [CrossRef]
- Sanchez, J.; Sawant, A.; Neff, C.; Tabkhi, H. AWARE-CNN: Automated workflow for application-aware real-time edge acceleration of CNNs. IEEE Internet Things J. 2020, 7, 9318–9329. [Google Scholar] [CrossRef]
- Sledevič, T.; Serackis, A. mNet2FPGA: A design flow for mapping a fixed-point CNN to Zynq SoC FPGA. Electronics 2020, 9, 1823. [Google Scholar] [CrossRef]
- Mousouliotis, P.G.; Petrou, L.P. Cnn-grinder: From algorithmic to high-level synthesis descriptions of cnns for low-end-low-cost fpga socs. Microprocess. Microsyst. 2020, 73, 102990. [Google Scholar] [CrossRef]
- Wan, Y.; Xie, X.; Yi, L.; Jiang, B.; Chen, J.; Jiang, Y. Pflow: An end-to-end heterogeneous acceleration framework for CNN inference on FPGAs. J. Syst. Archit. 2024, 150, 103113. [Google Scholar] [CrossRef]
- Korol, G.; Jordan, M.G.; Rutzig, M.B.; Castrillon, J.; Beck, A.C.S. Design space exploration for cnn offloading to fpgas at the edge. In Proceedings of the 2023 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Foz do Iguacu, Brazil, 20–23 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Lu, W.; Hu, Y.; Ye, J.; Li, X. Throughput-oriented Automatic Design of FPGA Accelerator for Convolutional Neural Networks. J. Comput.-Aided Des. Comput. Graph. 2018, 30, 2164–2173. [Google Scholar]
- Lu, L.; Zheng, S.; Xiao, Q.; liang, Y. FPGA Design for Convolutional Neural Networks. Sci. Sin. 2019, 49, 277–294. [Google Scholar] [CrossRef]
- Wu, R.; Liu, B.; Fu, P.; ji, X.; Lu, W. Convolutional Neural Network Accelerator Architecture Designfor Ultimate Edge Computing Scenario. J. Electron. Inf. Technol. 2023, 45, 1933–1943. [Google Scholar]
- Xu, Y.; Luo, J.; Sun, W. Flare: An FPGA-Based Full Precision Low Power CNN Accelerator with Reconfigurable Structure. Sensors 2024, 24, 2239. [Google Scholar] [CrossRef]
- Ma, Y.; Cao, Y.; Vrudhula, S.; Seo, J.S. Performance modeling for CNN inference accelerators on FPGA. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2019, 39, 843–856. [Google Scholar] [CrossRef]
- Ye, T.; Kuppannagari, S.R.; Kannan, R.; Prasanna, V.K. Performance modeling and FPGA acceleration of homomorphic encrypted convolution. In Proceedings of the 2021 31st International Conference on Field-Programmable Logic and Applications (FPL), Dresden, Germany, 30 August–3 September 2021; pp. 115–121. [Google Scholar] [CrossRef]
- Zhao, R.; Niu, X.; Wu, Y.; Luk, W.; Liu, Q. Optimizing CNN-based object detection algorithms on embedded FPGA platforms. In Proceedings of the International Symposium on Applied Reconfigurable Computing, Delft, The Netherlands, 3–7 April 2017; Springer: Cham, Switzerland, 2017; pp. 255–267. [Google Scholar]
- Juracy, L.R.; Moreira, M.T.; de Morais Amory, A.; Hampel, A.F.; Moraes, F.G. A high-level modeling framework for estimating hardware metrics of CNN accelerators. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 4783–4795. [Google Scholar] [CrossRef]
- Wu, R.; Liu, B.; Fu, P.; Chen, H. A Resource Efficient CNN Accelerator for Sensor Signal Processing Based on FPGA. J. Circuits, Syst. Comput. 2023, 32, 2350075. [Google Scholar] [CrossRef]
- Chen, Y.H.; Yang, T.J.; Emer, J.; Sze, V. Eyeriss v2: A flexible accelerator for emerging deep neural networks on mobile devices. IEEE J. Emerg. Sel. Top. Circuits Syst. 2019, 9, 292–308. [Google Scholar] [CrossRef]
- Blott, M.; Preußer, T.B.; Fraser, N.J.; Gambardella, G.; O’brien, K.; Umuroglu, Y.; Leeser, M.; Vissers, K. FINN-R: An end-to-end deep-learning framework for fast exploration of quantized neural networks. ACM Trans. Reconfig. Technol. Syst. 2018, 11, 1–23. [Google Scholar] [CrossRef]
- Wadekar, S.N.; Chaurasia, A. Mobilevitv3: Mobile-friendly vision transformer with simple and effective fusion of local, global and input features. arXiv 2022, arXiv:2209.15159. [Google Scholar]
- Adibi, S.; Rajabifard, A.; Islam, S.M.S.; Ahmadvand, A. The Science Behind the COVID Pandemic and Healthcare Technology Solutions; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Bengherbia, B.; Tobbal, A.; Chadli, S.; Elmohri, M.A.; Toubal, A.; Rebiai, M.; Toumi, Y. Design and hardware implementation of an intelligent industrial iot edge device for bearing monitoring and fault diagnosis. Arab. J. Sci. Eng. 2024, 49, 6343–6359. [Google Scholar] [CrossRef]
- Wu, B.; Wu, X.; Li, P.; Gao, Y.; Si, J.; Al-Dhahir, N. Efficient FPGA implementation of convolutional neural networks and long short-term memory for radar emitter signal recognition. Sensors 2024, 24, 889. [Google Scholar] [CrossRef]
- Majidinia, H.; Khatib, F.; Seyyed Mahdavi Chabok, S.J.; Kobravi, H.R.; Rezaeitalab, F. Diagnosis of Parkinson’s Disease Using Convolutional Neural Network-Based Audio Signal Processing on FPGA. Circuits Syst. Signal Process. 2024, 43, 4221–4238. [Google Scholar] [CrossRef]
- Liu, Z.; Ling, X.; Zhu, Y.; Wang, N. FPGA-based 1D-CNN accelerator for real-time arrhythmia classification. J. Real-Time Image Process. 2025, 22, 66. [Google Scholar] [CrossRef]
- Vitolo, P.; De Vita, A.; Di Benedetto, L.; Pau, D.; Licciardo, G.D. Low-power detection and classification for in-sensor predictive maintenance based on vibration monitoring. IEEE Sens. J. 2022, 22, 6942–6951. [Google Scholar] [CrossRef]
- Liu, S.; Li, K.; Luo, J.; Li, X. Research on Low-Power FPGA Accelerator for Radar Detection. In Proceedings of the 2024 IEEE 7th International Conference on Electronic Information and Communication Technology (ICEICT), Xi’an, China, 31 July–2 August 2024; pp. 196–199. [Google Scholar] [CrossRef]
- Ahmed, T.S.; Ahmed, F.M.; Elbahnasawy, M.; Youssef, A. Optimized Multi-Radar Hand Gesture Recognition: Robust MIMO-CNN Framework with FPGA Deployment. In Proceedings of the 2025 15th International Conference on Electrical Engineering (ICEENG), Cairo, Egypt, 12–15 May 2025; pp. 1–6. [Google Scholar] [CrossRef]
- Yacouby, R.; Axman, D. Probabilistic extension of precision, recall, and f1 score for more thorough evaluation of classification models. In Proceedings of the First Workshop on Evaluation and Comparison of NLP Systems, Online, 20 November 2020; pp. 79–91. [Google Scholar] [CrossRef]
- Wu, E.; Zhang, X.; Berman, D.; Cho, I.; Thendean, J. Compute-efficient neural-network acceleration. In Proceedings of the 2019 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Seaside, CA, USA, 24–26 February 2019; pp. 191–200. [Google Scholar]

| Literature | Year | Platform Comparison | Quantification, Pruning | Model Architecture Optimization | Reduce Computation | Low-Rank Approximation | Data Flow Optimization | Double Buffering | Hardware Architecture Optimization | Algorithm- Hardware Co-Optimization | Evaluation | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Lightweight | Knowledge Distillation | Layer Integration | Parallelism | Assemblyline | Hardware Accelerator | ||||||||||
| [10] | 2019 | √ | √ | √ | √ | √ | |||||||||
| [11] | 2019 | √ | √ | √ | √ | √ | √ | ||||||||
| [12] | 2020 | √ | √ | √ | √ | √ | √ | ||||||||
| [13] | 2020 | √ | √ | √ | √ | √ | |||||||||
| [14] | 2021 | √ | √ | √ | √ | √ | |||||||||
| [15] | 2021 | √ | √ | √ | √ | ||||||||||
| [16] | 2022 | √ | √ | √ | √ | √ | √ | ||||||||
| [17] | 2022 | √ | √ | √ | √ | √ | |||||||||
| [2] | 2023 | √ | √ | √ | √ | ||||||||||
| [18] | 2024 | √ | √ | √ | √ | √ | |||||||||
| [19] | 2024 | √ | √ | √ | √ | √ | |||||||||
| [20] | 2025 | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||
| [21] | 2025 | √ | √ | ||||||||||||
| ours | 2025 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Stage | Time | Primary Contributor | Content | Significance |
|---|---|---|---|---|
| Theoretical Emergence | 1950s–1980 | David Hubel, Torsten Wiesel | Local receptive field | Establish a theoretical foundation |
| 1980 | Kunihiko Fukushima | Neural cognitive machine | ||
| Modern Foundation | 1998 | Yann LeCun | LeNet-5 | The first modern CNN to achieve end-to-end training |
| Stagnation Period | 2000s–2011 | Deep learning is currently in a trough phase, yet related research continues to advance, laying the theoretical groundwork for future breakthroughs | ||
| Deep Revolution | 2012 | Alex Krizhevsky | AlexNet | Demonstrating the dominance of deep learning, ushering in a new era |
| Diversified Development | 2014–present | VGGNet Team | DataVGGNet | Architecture is mature |
| GooleNet Team | GooleNet | |||
| Kaiming He et al. | ResNet | |||
| Joseph Redmon | YOLO | Application deepening | ||
| Major institutions | MobileNet | |||
| Alexey Dosovitskiy | VIT | Paradigm extension | ||
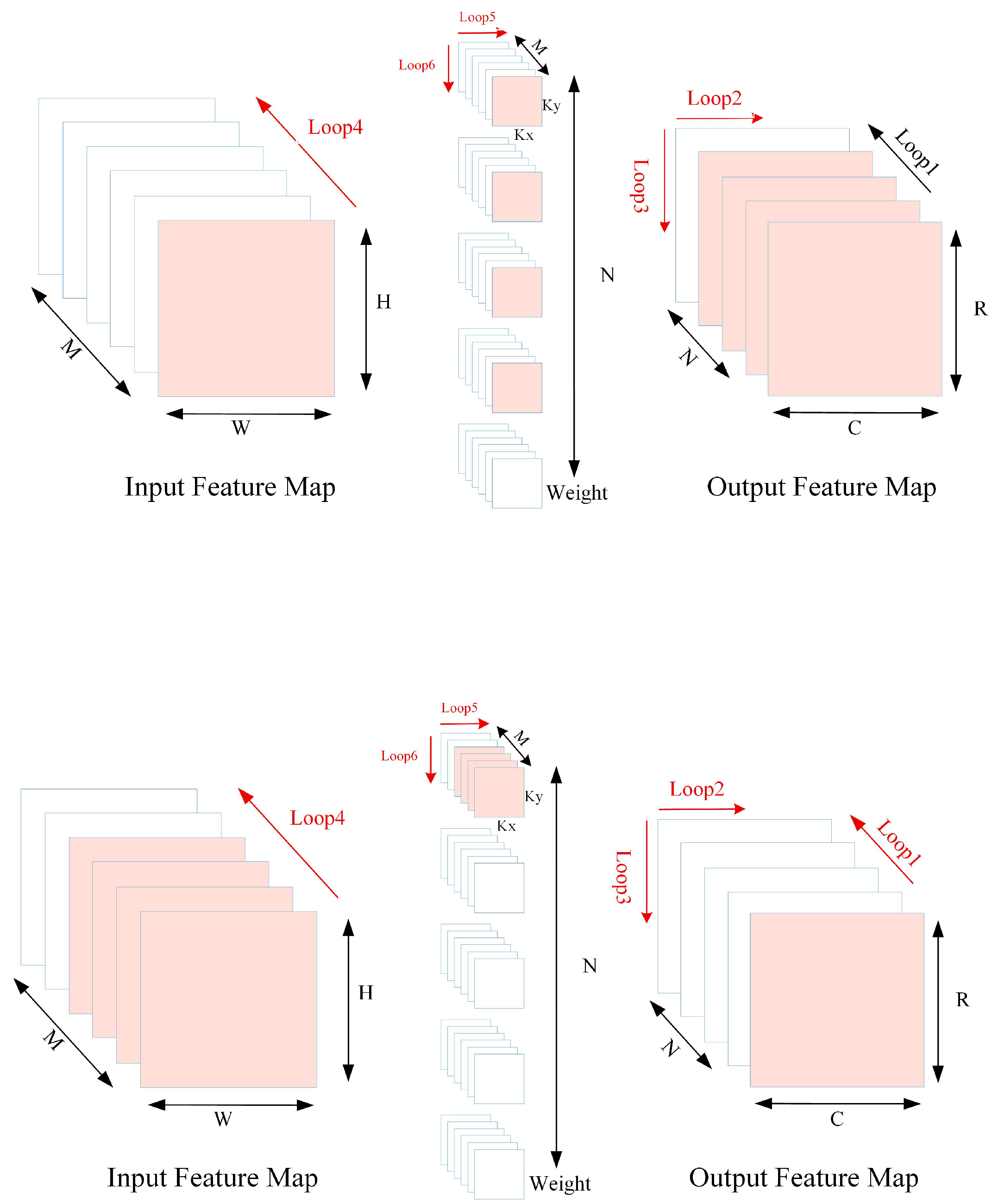
| 1:s = stride # Step length |
| # Nested loops for implementing convolution calculations |
| 2:for n in range(N): # Loop 1: Output feature map channels |
| 3: for c in range(C): # Loop 2:Output feature map row dimension |
| 4: for r in range(R): # Loop 3: Output feature map column dimensions |
| 5: for m in range(M): # Loop 4:Input feature map channel |
| 6: for x in range(Kx): # Loop 5:Convolution kernel row dimension |
| 7: for y in range(Ky): # Loop 6:Convolution kernel column dimension |
| Output _ Feature _ Map[n][r][c] += |
| Input _ Feature _ Map[m][r*s + x][c*s + y] * Filter[n][m][x][y] |
| Platform | Energy Efficiency | Parallel Capability | Flexibility | Development Cycle | Development Costs |
|---|---|---|---|---|---|
| CPU | Low | Low | Maximum | Shortest | High |
| GPU | Midterm | Extremely high | Medium | Short | Maximum |
| ASIC | Highest | Maximum | None | Long | Lower after mass production |
| FPGA | High | High | High | Medium | Relatively low |
| Characteristics | Linear Quantization | Nonlinear Quantization |
|---|---|---|
| Implementation complexity | Low (simple mapping rules) | High (requires more complex algorithms) |
| Hardware-friendly | High (can directly reuse INT ALU) | Moderate (often requires custom logic units) |
| Hardware-friendly | Moderate (significant loss of precision below 4 digits) | Extremely high (supports binary/ternary and other extreme compression) |
| Accuracy Retention | Better (8-bit has been widely validated) | Depending on the method, significant loss of accuracy may occur in extreme cases |
| Application Maturity | Widespread, technologically mature | Emerging, in the research and exploration phase |
| Literature | Quantitative Methods | Model | Achievement |
|---|---|---|---|
| [44] | 16 Bit | CNN | Convert the 32-bit floating-point model to a 16-bit fixed-point model |
| [43] | 8 Bit | CNN | Convert the 32-bit floating-point model to an 8-bit fixed-point model |
| [46] | 4 Bit | CNN | Data-agnostic knowledge distillation |
| [47] | Binary Quantification | DNN | XNOR and shift elimination: bottlenecks in multiplication |
| [49] | Binary Quantification | CNN | Weighting is dualized and implemented using hardware-direct-connect logic |
| [50] | Triple Quantification | CNN | Soft threshold training framework |
| [51] | Triple Quantification | CNN | Implementation through specific 2-bit encoding combined with bit instructions |
| [52] | Quadratic Quantization | CNN | Designing a multi-level scaling tensor data format |
| [53] | Quadratic Quantization | CNN | Train hardware-friendly bit-level sparse patterns |
| [54] | K-means Quantification | CNN | Nonlinear quantization using compressor functions |
| [55] | K-means Quantification | CNN | Teacher model learning generates discrete codebooks |
| Lerature | Literature | Category | Model | Dataset | ComputationalComplexity (FLOPs)/Compression Ratio(CR) | Accuracy | Method |
|---|---|---|---|---|---|---|---|
| [56] | SSL | model | AlexNet | ImageNet | — | Top-1↓0.9% | Structured regularization using Group-Lasso |
| ResNet-20 | CIFAR-10 | — | ↓1.42% | ||||
| [57] | SSS | model | ResNet-50 | ImageNet | FLOPs↓43% | Top-1↑4.3% | Introduce a learnable scaling factor for L1 regularization |
| ResNet-164 | CIFAR-10 | FLOPs↓60% | Top-1 ↑1% | ||||
| [58] | GAL | model | ResNet-50 | ImageNet | FLOPs↓72% | Top-5↑3.75% | Soft mask and Label-free GAN simultaneous pruning |
| ResNet-56 | CIFAR-10 | FLOPs↓60% | ↑1.7% | ||||
| VGGNet | CIFAR-10 | FLOPs↓45% | ↑0.5% | ||||
| [59] | BAR | model | Wide-ResNet | CIFAR-10 | FLOPs↓ | Top-1 ↑0.7% | Apply display constraints using modified functions |
| ResNet-50 | Mio-TCD | FLOPs↓ | — | ||||
| [60] | ECCV | model | AlexNet | ImageNet | CR | Top-1↑3.1% | Correct pruning errors through feedback mechanisms |
| [61] | L-BS | model | LeNet-300-100 | MNIST | CR | ↓0.3% | Pruning via second derivative of hierarchical error |
| LeNet-5 | MNIST | CR | ↓0.3% | ||||
| VGG-16 | ImageNet | CR | Top-1 ↑0.3% | ||||
| [62] | BA-FDNP | model | LeNet-5 | MNIST | CR | — | Frequency domain transformation, dynamic pruning, band- adaptive pruning |
| AlexNet | ImageNet | CR | — | ||||
| ResNet-110 | CIFAR-10 | CR | ↑12% | ||||
| ResNet-20 | CIFAR-10 | CR | — | ||||
| [63] | DPF | model | LeNet-50 | ImageNet | 82.6% Sparse | Top-1↓47% | Correct pruning errors through feedback mechanisms |
| Type | Literature | Method | Result |
|---|---|---|---|
| Quantification | [43] | Quantification, Compression | Memory usage reduced: 66% DSP usage reduction: 78% |
| [46] | Knowledge Distillation, Quantification | Average accuracy increased: 64.5% | |
| [50] | Soft-Threshold Quantization Network | Performance improvement: ; LUT usage reduction: 30% | |
| Pruning | [57] | Sparse Regularization, Pruning | ResNet-164 Acceleration: ; ResNeXt-164 FLOPs Reduction: 60% |
| [59] | Knowledge Distillation, Regularized Pruning | CIFAR-10 FLOPs reduction: ; CIFAR-100 FLOPs reduction: | |
| [62] | Dynamic Pruning, Frequency Domain Transformation | LeNet-5 parameter reduction: ; AlexNet parameter reduction: | |
| Model Architecture Optimization | [76] | Partitioned Knowledge Distillation, Compression Strategies | Accuracy: 88.6%; |
| [78] | Quantization, Knowledge Distillation | Accuracy: 98.5%; LUT usage: 21.52% | |
| [80] | Winograd, PE Optimization | Inference latency: 21.4 ms | |
| Reduction in Computational Load | [86] | FFT, Multiplier Optimization | Accuracy: 98% |
| [90] | Winograd, PE Optimization | Resource usage reduction: 38% | |
| Low-Rank Approximation | [92] | Low-rank Approximations, Channel Pruning | Parameter compression: |
| [93] | Low-rank Approximations, Channel Pruning | FLOPs reduction: 59.17%; parameter reduction: 66.77% |
| Type | Design Methodology | Key Trade-Offs | Specificity | Research Areas |
|---|---|---|---|---|
| Computational Optimization | Quantization, Pruning, Convolution Algorithms | Accuracy vs. Compression Rate | Algorithm level | Model compression, NAS |
| Storage and Data Flow Optimization | Loop optimization, Double buffering | Throughput vs. On-chip resource | Microarchitecture level | Storage subsystem, Compilation scheduling |
| Hardware Architecture Optimization | Deep Pipeline, Computing Unit Array | Performance vs. Logic resources | Macro-architectural level | FPGA/ASIC architecture, EDA tools |
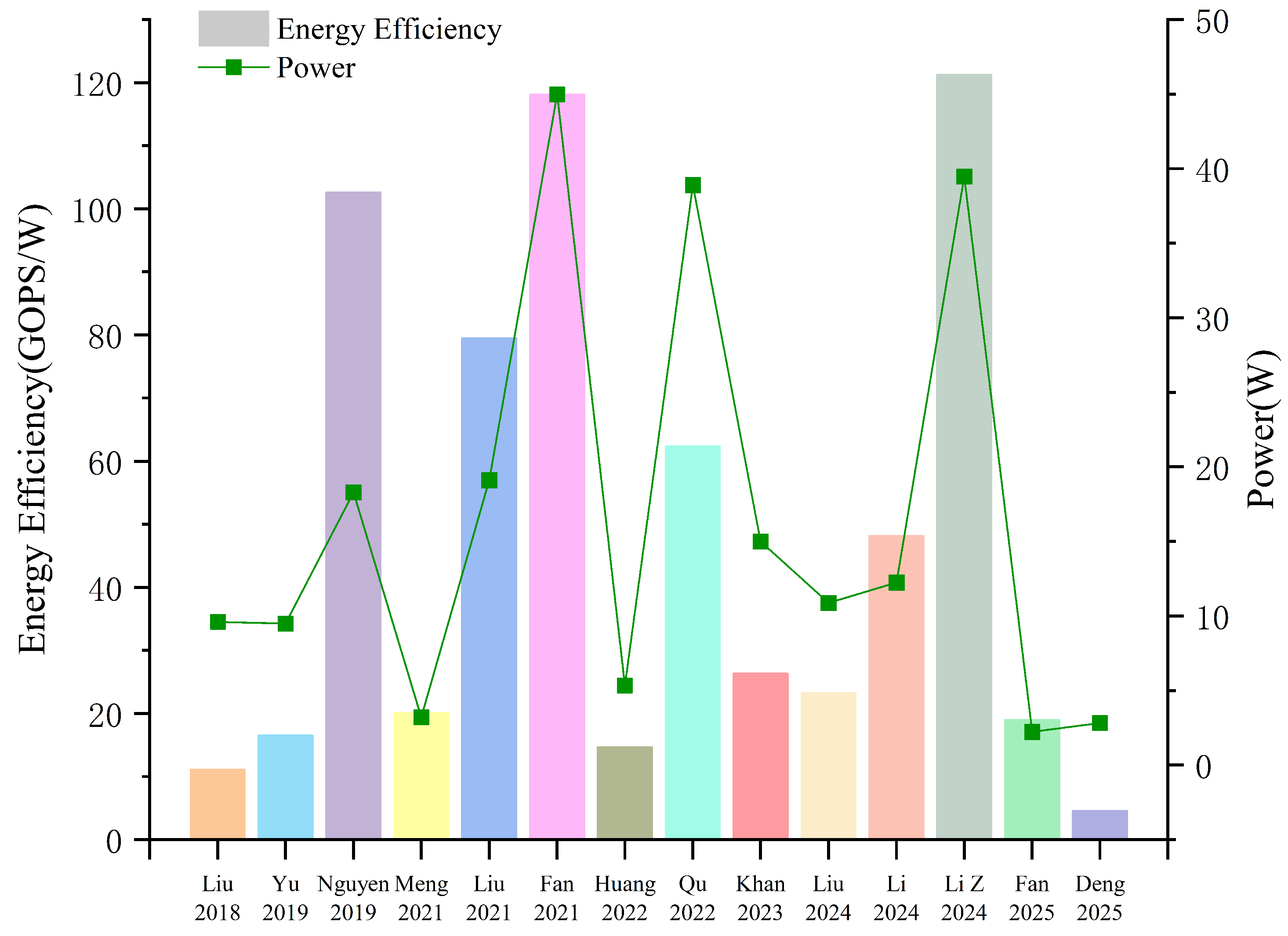
| Literature | Parallelism | Model | Delay (ms) | Throughput (GOP)/S | Computational Efficiency | DSP Resource Utilization Rate | Clock Frequency (MHz) | Energy Efficiency (GOPS/W) |
|---|---|---|---|---|---|---|---|---|
| Pk, Pv, Pf | [109] | U-Net | 58.4 | 107 | — | 71% | 200 | 11.1 |
| Pc, Pf | [110] | LeNet-5 | 0.25 | 3.35 | — | 54.55% | 100 | — |
| [111] | Image Fusion | 192 | 17.7 | — | <40% | 100 | — | |
| [112] | ResNet-50 | 5.07 | 1519 | 92.7% | 97% | 200 | 33.8 | |
| [113] | FSRCNN-light | — | 458 | — | — | 167 | 174.9 | |
| [114] | VGG-16 | — | 397 | 97.79% | 97.26% | 200 | 16.5 | |
| Pc, Pf, Pv | [115] | VGG-16 | — | 2766 | 88.9% | 71% | 190 | 72.7 |
| [116] | I3D | 178.3 | 684 | 99% | 96% | 200 | 26.3 | |
| [117] | MobileNetV1 | 0.6 | 4787.15 | — | 82% | 211 | 121.3 | |
| [100] | YOLOv4-tiny | 427 | 12.01 | — | 99% | 110 | 4.558 | |
| [118] | VGG16 | 0.48 | 807 | 98.5% | 88.9% | 200 | 128.1 | |
| Pc, Pf, Pv, Pk | [119] | OpenPose | 117.07 | 288.3 | — | 23.14% | 250 | 70.3 |
| [120] | ResNet-50 | 8.36 | 1330 | 92.4% | 88.6% | 220 | 118.1 | |
| Pf, Pv | [121] | CIFAR-10 | 0.3 | 162.7 | — | 37% | 150 | 7.2 |
| Type | Description | Particle Size Distribution | Advantages | Applicable Scenarios |
|---|---|---|---|---|
| Arithmetic Pipeline | Processing complex computations between processing units | Fine-grained | Accelerate the computational process between units | Image classification, object detection |
| Inter-layer Assembly Line | Enable different layers of the model to work in parallel | Coarse-grained | Reduce end-to-end latency across the entire network | Autonomous driving, radar monitoring |
| Instruction Pipeline | Implementation in phases directivep | Medium-grained | High flexibility and versatility | Real-time cascaded network applications (such as license plate recognition) |
| Hybrid Assembly Line | Utilizing different pipeline strategies | Mixed particle size | Balance performance, resources, and flexibility | Robotic grasping, remote sensing image processing |
| Type | Advantage | Disadvantage | Applicable Scenarios |
|---|---|---|---|
| Single-engine Architecture | High flexibility and versatility, high hardware reuse rate | Complex control logic and potential performance bottlenecks | Cloud data center |
| Streaming Architecture | Extremely high throughput, relatively straightforward design, stable and predictable performance | Poor flexibility and versatility, uneven resource utilization, and potentially higher resource overhead | Video surveillance, industrial inspection |
| Characteristic Dimension | Xilinx Platform | Altera Platform | Impact on CNN Acceleration Design |
|---|---|---|---|
| Core Computing Resources | DSP58 Module | DSP Block | Designers should optimize quantization strategies based on the native precision supported by the DSP |
| On-Chip Storage Architecture | BRAM | M20K Block | Caching strategy directly affecting weights and feature maps |
| Heterogeneous System Integration | Zynq/Versal Series | Agilex SoC Series | Hardened ARM processors are ideally suited for implementing efficient hardware-software co-design |
| High-level Design Tool | Vitis AI | OpenVINO for FPGA | Directly impacts development efficiency and the ability to rapidly iterate algorithms |
| Type | Calculate Parallelism | Memory Access Efficiency | Energy Efficiency Potential | Resource Consumption |
|---|---|---|---|---|
| Data Flow Optimization | √ | √ √ √ | √ √ | √ |
| Hardware Architecture Optimization | √ √ √ | √ √ | √ √ | √ √ |
| Hardware Accelerator | √ √ | √ √ √ | √ √ √ | √ |
| Name | Organization | Organization | Advantage | Disadvantage | Applicable Scenarios |
|---|---|---|---|---|---|
| Vitis-AI | AMD-Xilinx | Provide a complete model optimization, compilation, and deployment workflow | High development efficiency, mature ecosystem | Less flexible, dependent on DPU architecture | Industrial Vision, ADAS, Medical imaging |
| Intel oneAPI | Intel | Cross-platform inference engine | High platform portability with unified toolchain | Performance may be inferior to solutions optimized for specific purposes | Edge servers, Industrial PC |
| Deep Learning HDL Toolbox | MathWorks | Provide model-to-FPGA prototyping and HDL code generation | Deeply integrated with MATLAB (R2020b and later versions)/software co-simulation. | Relying on the MATLAB commercial software ecosystem | Algorithm–Hardware co-Verification |
| TVM + VTA | Apache | An open-source end-to-end deep learning compilation stack | Fully open-source and highly customizable | Toolchain configuration is complex | Projects requiring deep customization of accelerators |
| hls4ml | Open source | Open-source, from model to automatic HLS code generation | Highly automated, focused on ultra-low latency | Less versatile, with optimization potentially falling short of manual design | Particle physics trigger system, Low-Latency edge inference |
| FINN | Xilinx Research Labs | Open-source, specializing in deep quantitative models | Exceptionally high resource efficiency and performance | Supports only highly quantifiable models, with a high barrier to entry | Embedded FPGA, Micro UAV |
| DNNBuilder | Tsinghua University, MSRA | Automation tools designed to enable an end-to-end workflow for high-performance FPGA implementation. | Highly automated, no RTL programming required | Lack of ongoing commercial-grade support and comprehensive documentation | CNN inference acceleration service |
| FP-DNN | Peking University, UCLA | Automatically generate hardware implementations based on RTL-HLS hybrid templates | End-to-end automation; supports multiple network types with good versatility | Performance optimization may not be as effective as architectures specifically designed for CNN | Large-scale research models, data center FPGA clusters |
| Caffeine | Peking University, UCLA | A Hardware/Software Co-design Library | Focus on optimizing memory bandwidth | Not user-friendly for users of other frameworks | Cloud-Side inference acceleration |
| DeepBurning | Tsinghua University | Automated neural network accelerator generation framework | Highly automated, supporting multiple networks such as CNN and RNN | Lacks robustness and support for the latest networks | Verification projects requiring rapid migration to different FPGA |
| Literature | Name | Development Board | Network Model | Throughput (GOPS) | DSP Resource Utilization |
|---|---|---|---|---|---|
| [140] | f-CNN | Zynq XC7Z045 SoC | VGG16 | 79.63 | — |
| [141] | AWARE-CNN | Xilinx ZCU102 | AlexNet | 271 | — |
| [142] | mNet2FPGA | Zynq Z-7020 | VGG16 | 8.4 | 31% |
| [143] | CNN-Grinder | Xilinx XC7Z020 | SqueezeNet v1.1 | 14.18 | 78.18% |
| [135] | HARFLOW3D | Xilinx ZCU102 | X3D-M | 56.14 | 9.61% |
| [136] | FMM-X3D | Xilinx ZCU102 | X3D-M | 119.83 | 85% |
| [138] | fpgaHART | Xilinx ZCU102 | X3D | 85.96 | 84.43% |
| [144] | Pflow | Ethinker A8000 | SSD-MobileNetV1-300 | 196.08 | 49% |
| [139] | FPG-AI | Xilinx XC7Z045 | MobileNet-V1 | 7.3 | — |
| Method | Core | Advantage | Disadvantage | Literature |
|---|---|---|---|---|
| Exhaustive Search | Exhaustively enumerate all discrete parameter combinations | Ensure global optimization | Long search time, only suitable for extremely small spaces | [125,144,145] |
| Heuristic Search | Simulated Annealing/Genetic Algorithm Gradually Approaches Optimal Solutions | Moderate complexity yields near-optimal results | May get stuck in local optima, resulting in poor interpretability | [135,136,138,146] |
| Deterministic Approach | Rapid estimation using analytical models and mathematical equations | Fast execution | Less flexible | [141,147,148] |
| Mixed Methods | Combining the strengths of multiple strategies to compensate for the shortcomings of a single approach | Fast execution | High implementation complexity | [130,149] |
| Case Study | Target Platform | Algorithm Mapping Critical Decisions | DSE Decision | Performance Evaluation Results | Literature |
|---|---|---|---|---|---|
| HARFLOW3D-X3D | ZCU102 | 3D-CNN decomposed into 3D-Conv + Pool + PW | Genetic Algorithm | Energy efficiency DSP utilization 99.6% Frame latency | [135] |
| SpAtten | Stratix-10 GX | Per-head sparsity threshold for Transformers | Simulated Annealing | Throughput Energy efficiency BERT-Large accuracy | [137] |
| Eyeriss v2 | 65 nm ASIC | 16× structured channel pruning | Mixed Strategy | Energy efficiency Area ResNet-50 only | [155] |
| FINN-R | Zynq-7020 | Extreme 1-bit weight + 2-bit activation | Exhaustive Search | Energy efficiency Power consumption 0.8 W MNIST accuracy 99.2% | [156] |
| MobileViT-v3 | A14 Bionic | ATS+ Linear Attention | Heuristic Search | Inference speed ; Top-1 accuracy | [157] |
| Application Areas | Research Areas | Hardware Platform | Algorithm Optimization | Hardware Optimization | Key Performance Indicators | Literature |
|---|---|---|---|---|---|---|
| Medical Testing | Classification of Respiratory Symptoms | Xilinx Artix-7100t | Low-rank Quantization, Hyperparameter Optimization | Parallel Computing, Logic Unit Optimization | Accuracy | [158] |
| Diagnosis of Parkinson’s Disease | Xilinx Zynq-7020 | Model Compression | Parallel Processing Engine | Accuracy, Latency | [161] | |
| Classification of Arrhythmias | Xilinx Zynq 7020 | Network Architecture Optimization | No-multiplier convolutional unit | Accuracy, Real-time Capability% | [162] | |
| Industrial Maintenance | Bearing Monitoring | Pynq-Z2 FPGA | Partial Binarization | Asynchronous Processing Pipeline | Response Time, System Integration | [159] |
| Sensor-Based Predictive Maintenance | Xilinx Artix-7 | 8-bit quantization, layer fusion | Double-buffered | Power Consumption, Area | [163] | |
| Radar Perception | Radar Transmitter Signal Identification | Xilinx XCKU040 | 16-bit fixed-point quantization | Pulsed Array, Dual-Buffered | Recognition Rate, Energy Efficiency, Throughput | [161] |
| Radar Target Detection | PYNQ-Z1 | 16-bit fixed-point quantization | Loop Optimization | Power Consumption; Accuracy | [164] | |
| Multi-radar Gesture Recognition | Xilinx Kria KR260 | INT8 quantization | DPU Deployment | Accuracy, Speed | [165] |
| Indicator | Calculation Logic | Applicable Scenarios | Relationship with Standard Accuracy |
|---|---|---|---|
| Top-1 Accuracy | The model’s predicted category with the highest probability must perfectly match the actual label to be considered correct | The model must provide a single correct answer | Equivalent to the traditional definition of accuracy |
| Top-5 Accuracy | A true label is considered correct if it appears among the top five categories with the highest predicted probabilities by the model | More tolerant of ambiguous categories | Extended form of traditional accuracy |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Luo, Z.; Wang, L. Convolutional Neural Network Acceleration Techniques Based on FPGA Platforms: Principles, Methods, and Challenges. Information 2025, 16, 914. https://doi.org/10.3390/info16100914
Gao L, Luo Z, Wang L. Convolutional Neural Network Acceleration Techniques Based on FPGA Platforms: Principles, Methods, and Challenges. Information. 2025; 16(10):914. https://doi.org/10.3390/info16100914
Chicago/Turabian StyleGao, Li, Zhongqiang Luo, and Lin Wang. 2025. "Convolutional Neural Network Acceleration Techniques Based on FPGA Platforms: Principles, Methods, and Challenges" Information 16, no. 10: 914. https://doi.org/10.3390/info16100914
APA StyleGao, L., Luo, Z., & Wang, L. (2025). Convolutional Neural Network Acceleration Techniques Based on FPGA Platforms: Principles, Methods, and Challenges. Information, 16(10), 914. https://doi.org/10.3390/info16100914







