Abstract
The subset-sum problem, a foundational NP-hard problem in theoretical computer science, serves as a critical building block for cryptographic constructions. This work introduces novel classical and quantum heuristic algorithms for the random subset-sum problem at density , where exactly one solution is expected. Classically, we propose the first algorithm based on a ternary tree representation structure, inspired by recent advances in lattice-based cryptanalysis. Through numerical optimization, our method achieves a time complexity of and space complexity of , improving upon the previous best classical heuristic result of . In the quantum setting, we develop a corresponding algorithm by integrating the classical ternary representation technique with a quantum walk search framework. The optimized quantum algorithm attains a time and space complexity of , surpassing the prior state-of-the-art quantum heuristic of . Furthermore, we apply our algorithms to information set decoding in code-based cryptography. For half-distance decoding, our classical algorithm improves the time complexity to , surpassing the previous best of . For full-distance decoding, we achieve a quantum complexity of , advancing beyond the prior best quantum result of . These findings demonstrate the broad applicability and efficiency of our ternary representation technique across both classical and quantum computational models.
1. Introduction
The subset-sum problem, also referred to as the knapsack problem, stands as one of the most fundamental and well-known NP-hard problems in theoretical computer science [1]. Owing to its computational intractability, it has been widely employed in the construction of cryptographic systems [2,3,4,5]. Moreover, this problem underpins several cryptographic schemes targeting post-quantum security (see, e.g., ref. [6]) and acts as a key component in certain quantum hidden shift algorithms [7]. These, in turn, are applied in quantum cryptanalysis of isogeny-based protocols [8] and symmetric cryptographic constructions [9].
An instance of the problem is specified by n integers and a target integer . There are two common formulations: the decision version, which is to verify the existence of a subset of summing to s, and the computational version, which requires finding such a subset. The decision subset-sum problem is NP-complete. Moreover, given oracle access to the decision problem, a solution to the computational version can be recovered with n queries. When the instance is uniformly random, the problem is termed the random subset-sum problem (RSSP).
The density of an instance is defined as . For a random instance , the density is closely related to the expected number of solutions. In the high-density regime where , dynamic programming offers an efficient solution [10]. In the low-density setting, Brickell [11] and Lagarias and Odlyzko [12] demonstrated that given oracle access to the shortest vector problem in lattices [13], RSSP can be solved efficiently for densities . Coster et al. [14] and Joux and Stern [15] further raised this bound to . For knapsack instances with density approaching 1, the best known algorithms exhibit exponential-time complexity, rendering them computationally intractable; this inherent difficulty is the reason for their designation as “hard” knapsacks.
This work addresses the random subset-sum problem at density , where exactly one solution is expected to exist. Horowitz and Sahni’s Meet-in-the-Middle approach [16] reduces the time and space complexity from to , avoiding the need for an exhaustive search over all subsets. The idea of the method is to find a collision between two lists of partial sums, each comprising elements. Schroeppel and Shamir [17] refined this approach with a strategy based on merging four lists, which lowered the space complexity to .
A significant heuristic algorithm was proposed by Howgrave-Graham and Joux (HGJ) [18] at EUROCRYPT 2010, solving the RSSP with a time complexity of and a space complexity of , thus breaking the long-standing barrier. Their key innovation was the use of the representation technique, in which the solution is expressed ambiguously as a sum of vectors in . This expands the size of the search space and enables the merging of more lists under arbitrary constraints, leading to improved time efficiency. The time and space complexity is derived via numerical optimization, under the standard heuristic assumption that the individual elements obtained in the merging steps are well-distributed. Becker, Coron, and Joux (BCJ) [19] subsequently reduced the time and space complexity to by introducing representations using vectors from . Later, Bonnetain, Bricout, Schrottenloher, and Shen (BBSS) [20] further reduced the time and space complexity to by relaxing BCJ constraints and permitting representations in . Not only has the representation technique been employed as a tool for the subset-sum problem but it has also been successfully applied to the syndrome decoding problem [21,22,23,24] and the learn-with-errors (LWE) problem [25,26,27,28,29].
Quantum algorithms for the subset-sum problem have also attracted significant attention. The first quantum speedup was achieved by Bernstein, Jeffery, Lange, and Meurer (BJLM) [30], who proposed an algorithm leveraging the HGJ technique, achieving a time and space complexity of . Helm and May (HM) [31] subsequently developed a quantum variant of the BCJ algorithm that obtains a time and space complexity of . Later, Bonnetain et al. [20] introduced a quantum algorithm based on their classical algorithm, attaining the time and space complexity of under the same classical heuristic assumptions.
1.1. Our Contribution
In this work, we introduce a new heuristic algorithm for the subset-sum problem based on a ternary representation technique. The algorithm is further accelerated within a quantum walk search framework, leading to a novel quantum approach.
Representation-based algorithms for the subset-sum problem typically enhance efficiency by increasing the number of representations. These methods inherently exhibit a search tree structure. By recursively constructing parent lists from child lists until reaching a root list that is expected to contain a solution, such algorithms effectively navigate the problem space. To date, all known classical heuristic algorithms employ a binary tree structure. Notably, Lee et al. [29] demonstrated in the context of ternary LWE cryptanalysis that ternary trees significantly increase the number of representations compared to binary trees. Inspired by their idea, we propose the first classical heuristic algorithm for the random subset-sum problem (RSSP) based on a ternary tree structure. Through numerical optimization, we show that our algorithm achieves a time complexity of and a space complexity of , which, to the best of our knowledge, represents the current state of the art among classical heuristic algorithms.
In the quantum setting, we develop a novel quantum algorithm by integrating the proposed classical heuristic with a quantum walk over the Johnson graph, under the MNRS (Magniez–Nayak–Roland–Santha) framework [32]. This quantum algorithm retains the same heuristic foundation as its classical counterpart. After numerical optimization, we demonstrate that it achieves a time and space complexity of , establishing the best-known quantum heuristic performance for RSSP.
A summary of these complexity results is provided in Table 1.

Table 1.
Comparison of complexity exponent of subset-sum algorithms: classical and quantum approaches.
Furthermore, we apply both our classical and quantum algorithms to the decoding problem. Code-based cryptography, which relies on the hardness of decoding random linear codes, is a major candidate for post-quantum cryptography (PQC). Three of the four encryption schemes chosen in the fourth round of the NIST PQC standardization project [33] are code-based schemes, namely, Classic McEliece [34], BIKE [35], and HQC [36]. Among these, only HQC was ultimately selected for standardization. This prominence underscores the importance of rigorous security analysis for such systems.
Our decoding algorithms operate within the framework of information set decoding (ISD). The first classical ISD algorithm was introduced by Prange in 1962 [37]. Subsequent improvements were made by Stern [38] and Finiasz and Sendrier [39]. Later, further advancements were achieved through the use of representation techniques by May, Meurer, and Thomae (MMT) [21] as well as by Becker, Joux, May, and Meurer (BJMM) [22]. These were later enhanced by combining representation techniques with nearest neighbor searches, as proposed by May and Ozerov (MO) [40] and Both and May (BM) [41]. Currently, the Both–May algorithm [41] achieves the optimal time complexity among classical algorithms. Recent work has also explored time–memory trade-offs [42,43,44].
By applying our subset-sum algorithm to half-distance decoding, we improve upon the best-known ISD algorithm by Both–May, reducing the time complexity from to . For full-distance decoding, our algorithm achieves a time complexity of , improving upon the previous [22], which relied solely on representation techniques. Although this result does not surpass the state-of-the-art complexity of attained by BM [41]—which combines both representation and nearest neighbor techniques—we anticipate that integrating our ternary representation approach with nearest neighbor search could lead to further improvements.
Quantum variants of ISD have been less extensively explored: Bernstein [45] analyzed a quantum version of Prange’s algorithm, and Kachigar and Tillich (KT) [23] later proposed several quantum-walk-based ISD algorithms, which currently represent the fastest known quantum ISD algorithms. Kirshanova [24] provided an alternative perspective on the quantum-walk-based KT algorithms and developed a quantum version of the MO algorithm. In this work, we propose a novel quantum ISD algorithm that outperforms the state-of-the-art algorithm by Kachigar and Tillich. A summary of the complexity results for ISD is provided in Table 2.

Table 2.
Comparison of time complexity exponent of ISD: classical and quantum approaches.
1.2. Organization
The remainder of this paper is structured as follows. Section 2 introduces essential preliminary concepts required for our subsequent analysis and illustrates representation techniques, in particular using the HGJ algorithm as an example. In Section 3, we first present our new classical heuristic subset-sum algorithm, detailing its procedure, explaining its correctness, and analyzing its complexity. Then, through rigorous mathematical derivation, we provide a provable probabilistic algorithm that does not rely on heuristics. In Section 4, we turn to quantum algorithms, explaining in detail how the newly proposed classical algorithm is combined with a quantum walk and subsequently analyzing the complexity of the resulting algorithm. In Section 5, we apply our new classical and quantum algorithms to the decoding problem, demonstrating how they can be incorporated into the information set decoding framework. Specifically, the quantum algorithm employs a nested structure combining Grover search and quantum walks. Finally, in Section 6, we conclude with a summary of our new results.
2. Preliminaries
This section introduces the foundational definitions and standard notations for the subset-sum problem, followed by an overview of representation techniques, illustrated through the HGJ algorithm.
2.1. Notations and Conventions
Definition 1
(Distributions of knapsacks). A knapsack (or subknapsack) is a vector where is the digit set. We denote by the set of vectors containing exactly entries equal to , entries equal to 1, and entries equal to 0.
Definition 2
(Random subset-sum instance). Let be chosen uniformly at random, where . For , sample a vector uniformly from , and define . Then the pair is termed a random subset-sum instance. Any vector satisfying is called a solution to the instance.
It is well established that the parameter choice represents the most computationally challenging scenario, as the vector contains an equal proportion of zeros and ones, thereby maximizing combinatorial complexity. Consequently, this paper concentrates exclusively on this specific case.
In asymptotic analysis, we utilize the standard formula given below to estimate the cardinality of vector sets that contain a fixed quantity of certain coefficients.
Lemma 1
(Multinomial approximation). Let be a digit set of cardinality k. Consider vectors in where each digit appears exactly times and the coefficients satisfy . The number of such vectors is asymptotically given by the multinomial coefficient:
where the entropy function is defined as .
We use the notation as a shorthand for the multinomial coefficient , with the dot (·) standing for the remaining term . Similarly, we write for the entropy .
We adopt the soft-O notation, denoted by , to suppress polylogarithmic factors in n. Any rounding is omitted for simplicity.
2.2. Representation Techniques
From a high-level perspective, classical algorithms based on representation techniques recursively generate subknapsack lists and merge them to ultimately obtain a list of solutions to the original knapsack problem.
We use the HGJ algorithm [18] as an example due to its seminal status and relatively simple structure. The tree structure of the HGJ algorithm is illustrated in Figure 1.
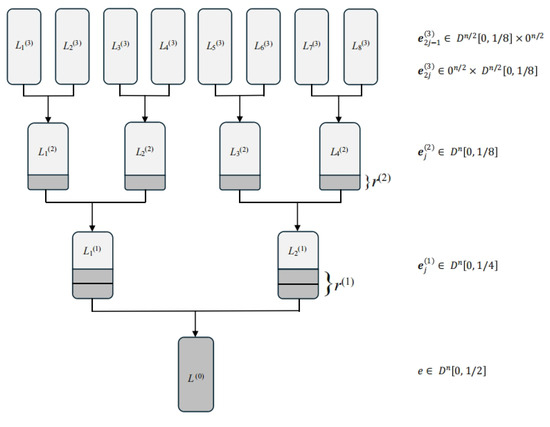
Figure 1.
The tree structure of the HGJ algorithm. The darker regions indicate portions where the modulus constraint has been established.
Consider a subset-sum instance with a solution , meaning , and exactly components of are 1, while the remaining are 0.
The core idea is to represent ambiguously as a sum of vectors in , i.e., with . We call a representation of . The ambiguity introduces representations of , since each of the 1-coordinates in can be represented as or . This paper adopts the notation where a parenthesized superscript corresponds to the depth of a given vector or parameter in the tree.
Since finding even a single representation from this exponential set is adequate to solve the subset-sum problem, the HGJ algorithm’s core principle is to aim for the computation of approximately a fraction of all representations. This targeted approach is designed to yield, in expectation, exactly one valid representation.
This motivates the following strategy. Select a modulus , where , and sample a target value at random . Define the lists
where A collision where , and yields a subset-sum solution. If there are no such collisions, the process is repeated with a new . After polynomially many iterations, the failure probability is negligible.
are constructed recursively, see also Figure 1. We demonstrate the list construction method using as an example. We represent as with . By the same reasoning as before, the number of representations is . Let We compute
for , where .
The level-2 lists are built from the level-3 lists below via a standard Meet-in-the-Middle approach.
Algorithm 1 outlines the HGJ procedure. In summary, the algorithm recursively constructs two lists and that are expected to contain a single representation of . It iteratively performs a merge-and-filter operation across multiple levels, progressively approaching the distribution while incrementally increasing the bit-length of the modular constraint. This continues until the condition is fully satisfied and a solution is found.
Consider two input distributions, and , with a target distribution . Given two lists and , we define the following:
- The merged listwhere is an arbitrary integer,
- The filtered list containing the vectors with the target distribution.
| Algorithm 1 The HGJ algorithm |
|
A central tenet of the standard subset-sum heuristic is the treatment of elements as independent and uniformly distributed under D. The empirically validated heuristic allows for the derivation of classically provable, probabilistic algorithms, thereby corroborating the soundness of the heuristic itself (see Theorem 2 in [19]).
Heuristic 1.
Suppose the input vectors are uniformly distributed over . Then the filtered pairs of vectors are also uniformly distributed over the target set D—or more precisely, over the subset of vectors in D that satisfy the given modular constraint.
By Heuristic 1, the expected size of the merged list is given by , and the average size of the filtered list equals , where pf denotes the probability that a pair , sampled uniformly from , satisfies .
For each level , the size of the corresponding lists is denoted by . Under the same heuristic, the list sizes concentrate sharply around their expectations, leading to the expressions
The time cost is
and the memory cost is . Numerical optimization yields a time complexity of and a space complexity of .
The algorithm of BCJ [19] achieves a time and space complexity of by generalizing the representation technique to include entries from . In later work, Bonnetain et al. further improved this to by relaxing BCJ constraints and allowing 2-coordinates in the representations.
In general, introducing more symbols (, 3, etc.) can increase the parameter search space and improve the optimal time complexity. However, the improvements gained by introducing further symbols are expected to exhibit diminishing returns.
To date, representation-based subset-sum algorithms in the literature exclusively employ binary trees as their search structure. In the following section, we propose new subset-sum algorithms based on ternary trees because ternary trees substantially increase the number of representations over binary trees.
3. A Novel Classical Subset-Sum Algorithm Based on Ternary Representation Techniques
3.1. Heuristic Construction
The proposed classical algorithm, which we refer to as TER, employs a ternary tree structure as illustrated in Figure 2. We encourage the reader to consult the figure for a clearer understanding of the algorithmic workflow. The tree has a depth of 3—a value determined through numerical optimization to be optimal for TER (see Appendix A for details).
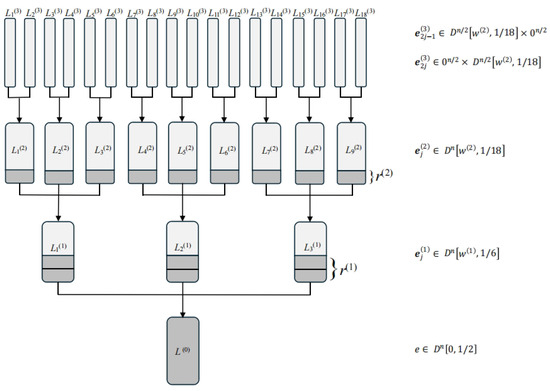
Figure 2.
The ternary tree structure of TER. The darker regions indicate portions where the modulus constraint has been established.
For clarity, we consider a subset-sum instance with a solution . The key idea is to represent as a sum of three vectors in , i.e.,
where . This means each of these three vectors contains exactly entries equal to , entries equal to 1, and entries equal to 0.
We begin by computing the number of representations and establishing the parameter . For each 1-coordinate in , its decomposition via the k-th coordinates of must be one of
Let denote the number of representations for each of the last three types. The total number of representations for the first three types is equal to , because has 1-coordinates.
For each 0-coordinate in , its decomposition via the k-th coordinates of must be one of
excluding the trivial case . Let denote the number of each of these six nontrivial representations.
Table 3 summarizes the counts for each type of level-1 representation.

Table 3.
Count of different level-1 representations.
The total number of representations is given by
where the two factors, respectively, account for the number of representations for 1-coordinates and 0-coordinates in the vector .
The number of -coordinates of for is and the number of 1-coordinates is Let , then for .
To capture a representation of , we choose a modulus where , and random targets . We then define the lists:
where .
A valid solution is found when and . If no collision occurs, new values are sampled. The failure probability becomes negligible after polynomially many attempts.
The expected size of each list is
These lists are constructed recursively. For example, to build , we represent as with .
Let count each of the representations , , and for the 1-coordinates of , and count each of the six nontrivial representations of the 0-coordinates. For the -coordinates, the representations are
Let count each of the last three types. Table 4 provides the counts for each type of level-2 representation.

Table 4.
Count of different level-2 representations.
The number of representations at this level is
The number of -coordinates of for is calculated as
and the number of 1-coordinates of for is calculated as
Let , then for .
Let and choose random targets for . We define
for , where for .
The expected size of each is
The level-2 lists are built from the level-3 lists via a Meet-in-the-Middle approach.
for , each of size
Note that we employ the binary tree only for the top level, because the representation technique is not used in this level.
Algorithm 2 outlines the TER algorithm with a depth of 3. In summary, it recursively constructs three lists that are expected to contain a single representation of . Similar to the HGJ algorithm, this algorithm executes the merge-and-filter operation repeatedly over several levels.
Consider three input distributions, , and , with a target distribution . Given three lists , and , we define the following:
- The merged listwhere is an arbitrary integer,
- The filtered list containing the vectors with the target distribution.
| Algorithm 2 TER with a depth of 3 |
|
Similar to the standard subset-sum assumption, our heuristic assumes that elements in are independently and uniformly sampled from the distribution D.
Heuristic 2.
Suppose the input vectors are uniformly distributed over . Then the filtered pairs of vectors are also uniformly distributed over the target set D—or more precisely, over the subset of vectors in D that satisfy the given modular constraint.
By Heuristic 2, the expected sizes of the merged list is given by , and the average size of the filtered list equals , where pf denotes the probability that a uniformly random triple from satisfies
Theorem 1.
Let be a random subset-sum instance whose solution is a vector . Under Heuristic 2, Algorithm 2 finds in time and space .
Proof.
For each level , the size of the corresponding lists is denoted by . Under Heuristic 2, the list sizes concentrate sharply around their expectations, leading to the expressions
where
and are parameters to be optimized.
Based on the preceding analysis, the time complexity of Algorithm 2 can be derived as follows:
and the space complexity is . Let us focus on the asymptotic exponent in and relative to n. Denote for . Recall that and . Computing the time complexity essentially amounts to solving the following optimization problem, where the objective function is
subject to the following constraints:
Note that Lemma 1 is applied when computing the exponents of the constraints.
Numerical optimization yields the parameters
This results in
which in turn yield list sizes
The time complexity is , determined by the merged list size, and the space complexity is , governed by the filtered list size. □
3.2. Rigorous Analysis of TER
In this subsection, we establish rigorous foundations for Heuristic 2 and present a provable variant of TER that eliminates heuristic assumptions. Our analysis relies on distributional properties of modular sums, as captured by the following fundamental result (Theorem 3.2 in [46]).
Theorem 2.
For any set , the identity
holds, where denotes the probability that for a random drawn uniformly from , i.e.,
The left-hand side of Equation (3) represents the average squared deviation from uniformity across all coefficient vectors and residues . This quantity measures the overall non-uniformity of the distribution. The right-hand side being constant for fixed implies that if certain subset-sum instances exhibit significant deviation from uniformity, others must be exceptionally uniform to maintain the average.
We now extend this result to the Cartesian product setting relevant to our decomposition approach.
Theorem 3.
For any sets and the same coefficient vector , the identity
holds, where denotes the probability that and for random drawn uniformly from .
Proof.
See Appendix C for the full proof. □
We now analyze pathological instances that cause TER to fail. During ternary decomposition (e.g., representing as ), certain coefficient vectors—such as —prevent constructing valid level-1 lists (Equation (1)) with random targets due to sparse residue coverage.
Let and denote the vector sets in the first two parts of the ternary decomposition. We quantify how many residue pairs remain uncovered by . For parameter , define an instance as Type I bad if either covers fewer than residues or covers fewer than residues.
For such bad instances, at least residues lead to zero probability: or . We now establish a lower bound for the variance under bad instances. Without loss of generality, assume that covers fewer than residues. For at least uncovered residues ,
For the remaining at most covered residues , we consider the minimal uniformity scenario: each such residue has a probability of at least (since the total probability sums to 1), and is uniform. Then,
Consequently, the lower bound for the variance is
Let denote the number of Type I bad instances. By Theorem 3,
Since , the fraction of Type I bad instances is
Another failure mode occurs when intermediate lists grow beyond expected sizes, violating the complexity analysis in Theorem 1. We now rigorously analyze list sizes during TER’s execution.
Let be the filtered list in a merge-and-filter operation with distributions D. Let denote all vectors with distribution D. We want for parameter . Define Type II bad instances as those where more than residues c satisfy .
By Theorem 2,
where counts Type II bad instances. Thus,
The fraction of Type II bad instances is at most .
Now consider the merged list size. Let be the merged list in a merge-and-filter operation (definition in Equation (2)). Let contain all sums without modular constraints. Decompose , where represents active moduli from input lists and is the supplementary constraint introduced during construction.
Let denote the target sum for elements in , with , , representing partial sums from the three input lists, respectively, satisfying .
The size of admits the bound
To estimate this quantity, we require bounds on sums of the form
We can extend the relation from Theorem 2 to third moments:
Define Type III bad instances as those where more than values satisfy
Letting count such instances,
which implies
In TER, for construction, so . The fraction of Type III bad instances is at most .
This analysis provides theoretical guarantees for all intermediate lists in TER. Since depth-3 TER uses four ternary decompositions, the total fraction of bad instances is bounded by
By choosing sufficiently large , this fraction becomes negligible.
Excluding three types of bad subset-sum instances, we analyze the success probability of algorithm TER on the remaining good instances, where modulus values are randomly resampled in each ternary decomposition. For good instances, failures fall into three categories:
- Selecting residues that yield zero probability. With at most such residues, the failure probability is .
- The filtered list overflow. With at most residues, the failure probability is .
- The merged list overflow. For each of the three lists to be merged, at most residues cause overflow, and the failure probability here is .
Thus, the overall failure probability is
Using the limit formula , we repeat each ternary decomposition times to ensure a failure probability of at most . Since , and TER involves four ternary decompositions, the overall failure probability is at most . Hence, the success probability is at least . If this success probability is insufficient, a polynomial number of repetitions yields a success probability exponentially close to 1, excluding the bad subset-sum instances. Therefore, this repetition strategy allows us to construct a provable probabilistic version of TER.
4. Improved Subset-Sum Algorithm Based on Quantum Walks
In this section, we begin by introducing the MNRS framework for searching marked vertices on graphs using quantum walks. We then describe how our classical algorithm, TER, is incorporated into this quantum walk framework. Subsequently, we provide a detailed complexity analysis of our quantum algorithm. Through numerical optimization, we derive the optimal parameters and their corresponding complexity values.
4.1. Quantum Walks
Consider an undirected graph that is both connected and regular. Suppose that some vertices of G are “marked.” We denote by the fraction of marked vertices; equivalently, a vertex chosen uniformly at random is marked with probability . Furthermore, let be the spectral gap of G, i.e., the difference between its two largest eigenvalues. For a classical random walk on G starting from any vertex, the number of steps required to approximate the stationary distribution is roughly .
A classical random walk searches for a marked vertex via the following subroutines:
- Setup. Sample a random vertex in time .
- Update. Perform random walk steps, where each step moves to a uniformly random adjacent vertex in time .
- Checking. Check whether the current vertex is marked in time . If not, return to Step 2.
The total time complexity is
In the quantum setting, the walk takes place over a superposition of vertices. The initial state is the uniform superposition . The algorithm proceeds by iterating approximately times, each iteration amplifying the amplitude on marked vertices. Crucially, each such iteration requires only about update steps to sufficiently mix the quantum state. An update step in the quantum walk maps a vertex to a superposition of its neighbors. The MNRS framework [32] enables us to focus on specifying the setup, checking, and update unitaries.
Theorem 4
(Quantum walk on a graph [32]). Given a regular graph with spectral gap , where at least an fraction of the vertices are marked, for a random walk on a graph G with setup, update, and checking costs denoted by , , and , respectively, there exists a quantum algorithm that can find a marked vertex with high probability in time
Johnson graphs are central to the construction of our quantum walk.
Definition 3
(Johnson graph). The Johnson graph, denoted , is an undirected graph whose vertices correspond to all k-element subsets of a universe of size N. Two vertices S and are connected by an edge if and only if . This means can be obtained from S by replacing exactly one element. The spectral gap of is given by
Definition 4
(Cartesian product of Johnson graphs). Let denote the Cartesian product of m copies of the Johnson graph . Each vertex in is an m-tuple of k-element subsets. Two vertices and are adjacent if and only if they differ in exactly one coordinate i, and for that index, . The spectral gap satisfies
Remark 1
(Heuristics on quantum walks [26]). A notable distinction between classical and quantum subroutines is that quantum updates are required to terminate within a specified time limit, whereas classical procedures may run indefinitely in worst-case scenarios, albeit with low probability. This issue was studied in (Section 6 in [47]) and (Section 5 in [20]). It was shown that terminating updates within a polynomial factor of their expected runtime will not significantly impact final quantum states. Hence, up to a polynomial overhead, it is sufficient to analyze the quantum walk complexity using the expected costs.
4.2. Quantum TER (QTER)
Next, we present the quantum version of our classical algorithm TER, termed QTER. Recall the tree structure illustrated in Figure 2. The depth of the tree in our quantum algorithm is also a parameter subject to optimization, and a depth of 3 was found to be optimal for QTER (as detailed in the Appendix A).
In the quantum walk setup, we construct random subsets for , each of size with . The TER algorithm is then executed using these newly formed depth-3 lists .
Let and . For each list , where , we associate a Johnson graph denoted . The overall structure for the random walk is defined on the Cartesian product graph
The vertices of are , with . Denote by the j-th list at level i, which is constructed from according to TER, for . The data structure of a vertex in the graph maintains all such lists . A vertex is considered marked if includes a solution to the initial random subset-sum problem. It can be seen that solving the random subset-sum problem can be transformed into the problem of finding a marked vertex on a graph.
The pseudocode of QTER with depth 3 is given in Algorithm 3.
We now analyze the quantum resources required by Algorithm 3. The quantum circuit width, measured in qubits, comprises three main components: the current vertex registers , the coin register , and the data register .
The tensor product of 18 vertex registers requires qubits. The coin register, which stores superpositions of neighboring vertices, also requires qubits. The data register stores all hierarchical lists constructed from the current vertex, namely, the level-2, level-1, and level-0 lists, requiring qubits in total, where denotes the size of each level-i list. Since the list sizes grow exponentially with the problem parameters, the overall circuit width is dominated by when ignoring polynomial factors.
The circuit depth is determined by three key subroutines. Let , , and represent the circuit depths of the setup, update, and checking operations, respectively. The total circuit depth of Algorithm 3 is given by
which is consistent with Theorem 4. The complexity of QTER therefore depends on the parameters , , , , and .
The checking subroutine achieves through the following procedure: We allocate one ancilla qubit and apply a controlled operation using the register storing as control and the ancilla as target. This operation flips the ancilla qubit if and only if contains a valid solution. The ancilla qubit then facilitates the phase flip for marked vertices. Finally, we uncompute the ancilla by applying the conjugate transpose of the controlled operation. This entire process requires only a polynomial number of quantum gates and one ancilla qubit, ensuring .
We will analyze , , , and in the next subsection to determine the overall complexity of QTER.
| Algorithm 3 QTER with depth 3 |
|
4.3. The Complexity of QTER
From Equation (6), the spectral gap of is
A node v that is marked equivalent to its associated level-0 list is non-empty; that is, it retains at least one representation of that survives all merge-and-filter operations. Note that the parameter selection for the lists within the TER framework ensures that, in expectation, there exists a representation
which persists through all filtering steps up to the root list . Under the QTER construction, the probability that holds simultaneously for all is given by
Hence, the probability that v is marked is .
As shown in Section 3, for TER we obtain the list sizes for each level:
We first calculate the setup cost of QTER with depth 3. The size of the QTER level-3 list is
The level-3 lists can be computed and sorted with respect to the inner products in time for . The level-2 lists contain all elements from their two level-3 children lists that match on the inner products. Thus, we expect elements that match on their inner products.
Analogously, we compute level-1 lists in expected time . However, now we have to filter out all for
Denote as the probability that a uniformly random triple from satisfies , for . The specific calculation formula for can be found in Appendix B.
By leveraging the filtering probability, the size of level-1 lists can be estimated as follows:
The level-0 list can be computed in expected time and
Thus, the setup cost can be bounded as
The update procedure involves inserting and deleting an element from one of the sets , where . For instance, suppose we wish to replace an element in . This update operation on can be performed in constant time, i.e., in .
This update affects the lower-level list if there exist matching elements such that . The expected number of such elements is , applicable to both deletion and insertion operations. At level 1, for the list , each of the elements leads to an expected number of insertions or deletions. A similar reasoning applies to the level-0 list . Overall, the total expected cost of an update is given by
Observe that if we approximate the values of and using their upper bounds, the relation holds. By combining Equations (5), (7) and (8) with , we derive the following expression for the quantum walk runtime:
To balance setup costs with the cost to find a marked node, we set parameter to . This value satisfies the equation . If is greater than , the setup costs increase, leading to a larger overall complexity ; if is smaller than , the cost of the update and checking iterations becomes higher, also resulting in an increase in the overall complexity .
It should be noted that the exponent converges to 1 as the tree depth increases. This implies that QTER degrades to TER as the number of the depth increases. For the QTER algorithm, a depth of 3 is found to be optimal.
This results in
which in turn yield list sizes
The time and space complexity are both .
Theorem 5.
Let be a random subset-sum instance whose solution is a vector . Under the assumption of Heuristic 2, there exists a quantum algorithm (Algorithm 3) that finds in time and space .
5. Application to Decoding
We now turn to the application of our subset-sum techniques to the problem of decoding random binary linear codes. This is a central problem in coding theory and cryptography, and it can be formulated as a subset-sum problem over the additive group rather than .
Definition 5
(Syndrome decoding problem). Let be a uniformly random full-rank matrix, which serves as the parity-check matrix of a random linear code . Let be a received erroneous codeword. The decoding problem is to find an error vector of minimal Hamming weight such that
We denote the syndrome by . The goal is to recover (and hence the codeword ).
Note that if has weight at most , where d is the minimum distance of , then the solution is unique. This is referred to as the half-distance decoding scenario. If , we are in the full-distance decoding setting.
It i s well-known that the relative distance of a random linear code asymptotically meets the Gilbert–Varshamov bound:
where is the inverse of the binary entropy function. Thus, the complexity of decoding can be expressed as a function of the code rate .
A key observation is that the condition can be viewed as a subset-sum instance over : the columns of P form the set of elements, and is the target. The additional constraint is that the solution must be a binary vector of low Hamming weight.
5.1. Information Set Decoding
The core idea of ISD is to reduce the problem dimension via Gaussian elimination.
Let be an permutation matrix over . For any permutation matrix , holds. Let ℓ be a parameter such that . For any ℓ, with constant probability, Gaussian elimination produces an invertible matrix such that
where , , and is the identity matrix of size .
Partition with , , and similarly let . Then the equation becomes
Let us introduce an additional parameter p. We say that a permutation is good if it induces a weight distribution satisfying and . Assume such a good permutation is found, then the decoding problem reduces to finding a vector of weight p such that , and . The complete solution is then given by .
The probability that a randomly chosen permutation is good is
In the following subsection, we show how to solve the resulting subset-sum instance efficiently using a variant of TER, adapted to the binary group setting.
5.2. TER for Decoding
Let us focus on the subset-sum instance with solution , where stands for the jth column of matrix and . We represent as a sum of three vectors, that is, with .
Since the computations are performed in the field , the 1-coordinates of can be represented in the following forms: , , , ; furthermore, the 0-coordinates can be represented as , , , .
For arbitrary , Algorithm 4 gives the pseudocode of TER for decoding with depth h. For each level i (), we define the following quantities:
- Let denote the number of representations of the form ;
- Let denote the number of representations of the form , , or ;
- Let denote the number of 1-coordinates, then .
| Algorithm 4 TER for decoding with depth h (TER-de(h)) |
|
The counts of these representations are summarized in Table 5. For each level i (), we can compute the following quantities:

Table 5.
Count of different level-i representations.
- The number of representations is
- The number of 1-coordinates is
- The list size is
- The time cost iswhere we set for the consistency of the formula.
The level-h list size is
and the level-h runtime is
Then, the overall time complexity is
and the space complexity is
where .
Next, we integrate TER for decoding into the ISD framework. The complete pseudocode of the resulting ISD algorithm is provided in Algorithm 5.
| Algorithm 5 An ISD algorithm that leverages TER |
|
To determine the computational complexity of our algorithm for a fixed code rate and a fixed search tree depth h, we aim to optimize the parameters , and for , such that the expression
is minimized, subject to the following constraints:
In the half-distance decoding scenario, optimization leads to complexities of
under a worst-case code rate of with and the following parameter values:
Our algorithm achieves a runtime of , which represents a polynomial improvement over the previous best runtime of [41].
In the full-distance decoding scenario, optimization leads to complexities of
under a worst-case code rate of with and the following parameter values:
The running time of our algorithm, , is faster than the previous best result of [22] achieved using representation techniques alone. However, it does not outperform the current state-of-the-art algorithm [41], which has a time complexity of and incorporates both representation techniques and nearest neighbor search. We speculate that combining our ternary representation technique with nearest neighbor search could lead to further improvements.
5.3. Improved Quantum ISD Algorithm
In this subsection, we detail the implementation of a quantum version of Algorithm 5. The quantum speedup over the classical algorithm primarily stems from two aspects: first, the accelerated search for a good permutation , and second, the efficient identification of a valid vector that meets the required conditions for a given permutation.
Kachigar and Tillich [23] suggested using Grover’s algorithm to search for good permutations. Grover’s algorithm [48] is an optimal method for unstructured search problems, offering a quadratic speedup over the best classical algorithms. The unstructured search problem involves finding an element x in a set that is marked as “good” by a given oracle function , where indicates that x is good. Let denote the fraction of elements in for which . Grover’s algorithm finds a solution with queries to f—compared to a classical lower bound of —and, assuming an average query time of , the total execution time is .
Algorithm 6 presents the oracle implementation for our quantum ISD algorithm. Specifically, the oracle function within the Grover search is realized through a quantum walk routine. The quantum ISD algorithm then operates by performing transformations on quantum states of the following form (normalization omitted):
The outer search applies Grover’s algorithm over a set of permutations. The validity of a permutation is verified via a quantum walk search, as detailed in Algorithm 6. After approximately steps, the register contains a non-empty level-0 list that yields the correct error vector provided that is a good permutation.
Thus, the total complexity of our quantum ISD algorithm is . Optimization leads to complexities of
under a worst-case code rate of with and the following parameter values:
Our quantum ISD algorithm achieves a runtime of , yielding a polynomial improvement over the previous best quantum runtime of [23].
| Algorithm 6 An oracle for quantum ISD algorithm |
|
6. Conclusions
In this work, we have presented significant advancements in solving RSSP and, by extension, the decoding problem for random linear codes in both the classical and quantum computational settings.
Our primary contribution is the introduction of a novel heuristic algorithm for RSSP based on a ternary tree representation structure. This approach, inspired by techniques in lattice-based cryptanalysis, fundamentally departs from the binary tree structures employed by all previous classical heuristic algorithms. Through meticulous numerical optimization, we demonstrated that our classical algorithm achieves a time complexity of and a space complexity of , establishing a new state of the art for classical heuristic algorithms.
Building upon this classical foundation, we developed a novel quantum algorithm by integrating the ternary representation technique with a quantum walk search framework. The resulting algorithm achieves a time and space complexity of , which, to the best of our knowledge, represents the best-known heuristic performance for RSSP on quantum computers.
We further demonstrated the cryptographic impact of our algorithms by applying them to the decoding problem. For half-distance decoding, our classical algorithm improves upon the state-of-the-art BM algorithm, reducing the time complexity from to . For full-distance decoding, while our result of improves upon pure representation-based approaches like BJMM, it does not surpass the hybrid technique of Both–May. However, this strongly suggests a promising avenue for future work: integrating our ternary representation techniques with nearest neighbor search techniques could potentially lead to further breakthroughs in decoding complexity. In the quantum setting, our proposed ISD algorithm outperforms all previous works, achieving a time complexity of .
Finally, while the quantum algorithms presented in this work achieve improved asymptotic complexities, their practical implementation remains challenging due to the exponential number of qubits required. Recent research directions have explored alternative quantum approaches that utilize only polynomial qubit resources, albeit at the cost of exponential classical memory or higher quantum time complexity [49,50]. Investigating such space-efficient implementations, which may be more amenable to future quantum hardware, represents an interesting direction for future work.
Funding
This work was supported by the Innovation Program for Quantum Science and Technology under Grant No. 2024ZD0300502 and the Beijing Nova Program under Grants No. 20220484128 and 20240484652.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The code associated with this submission is publicly available and can be accessed via the following link: https://gitee.com/li-yang777777/subset-sum (accessed on 22 August 2025).
Acknowledgments
The authors thank the reviewers for their valuable feedback and insightful suggestions, which greatly improved this manuscript.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. TER with Arbitrary Depth
For arbitrary , Algorithm A1 gives the pseudocode of TER with depth d. Following the same analytical approach as in Section 3, we start from the first level and compute the number of representations and expected list sizes for each level up to level d.
For each level i (), we define the following quantities:
- Let denote the number of representations of the form , , or .
- Let denote the number of representations of the form , , , , , or .
- Let denote the number of representations of the form , , or .
- Let denote the number of -coordinates.
- Let denote the number of 1-coordinates.
The result from level 1 is the same as the depth-3 case. Table 3 presents the number of each type of level-1 representations. Thus, , and the number of representations is
Table A1 presents the number of each type of level-i representation. Then, for ,
and the number of representations can be computed as follows:
Let be the size of lists at level i for . Then, under Heuristic 2
The time complexity of Algorithm A1 is
and the space complexity is .
| Algorithm A1 TER with depth d |
|

Table A1.
Count of different level-i representations.
Table A1.
Count of different level-i representations.
| Representations | Count | |
|---|---|---|
| 1-coordinates | ||
| 0-coordinates | ||
| -coordinates | ||
Table A2 presents the time and space complexities of algorithms TER and QTER at various depths.

Table A2.
Time and space complexities of TER and QTER at different depths.
Table A2.
Time and space complexities of TER and QTER at different depths.
| Algorithm | Depth | Time Complexity | Space Complexity |
|---|---|---|---|
| TER | 2 | ||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| QTER | 2 | ||
| 3 | |||
| 4 |
Appendix B. Filtering Probability
In this section, we provide the formula for calculating the filtering probability, which is used in the numerical optimization of QTER.
Lemma A1.
For , let . Then the level-i filtering probability of TER with depth d, denoted , is given by
Proof.
Given a fixed vector , we proceed to count the number of pairs that are compatible with .
We begin by considering the coordinates where has a value of 1. The total number of such coordinates is . According to Table A1, these coordinates are categorized into the following six types based on the values that and take at the same positions:
- Type , which occurs times.
- Type , which occurs times.
- Type , which occurs times.
- Type , which occurs times.
- Type , which occurs times.
- Type , which occurs times.
The number of ways to assign the values of and at these positions, according to the above distribution, is given by the multinomial coefficient:
This corresponds to the first term in Expression (A1).
Similarly, the number of compatible pairs for the coordinates where takes the value 0 is given by the second term in Expression (A1), and the number for the coordinates where equals corresponds to the third term in Expression (A1).
In order to obtain the probability, we divide the first three terms in Expression (A1) by
which corresponds to the total number of all possible pairs . □
Appendix C. Proof of Theorem 3
We proceed to prove the result stated in Theorem 3 of the main text.
Proof.
Following [46], employ exponential sums with and the identity
First prove that for the following identity holds:
Calculate the left side of the above identity
By Equation (A2), if and , the inner sum contributes . If or , assuming without loss of generality:
establishing Equation (A3).
For fixed , independence of and gives
From Equation (A2),
Thus,
The contribution of the term corresponding to is .
Therefore,
The sum over vanishes if or and is equal to M otherwise. Hence,
Applying Equation (A3) yields the result. □
References
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W.H. Freeman: San Francisco, CA, USA, 1979; p. 338. [Google Scholar]
- Merkle, R.; Hellman, M. Hiding information and signatures in trapdoor knapsacks. IEEE Trans. Inf. Theory 1978, 24, 525–530. [Google Scholar] [CrossRef]
- Chor, B.; Rivest, R.L. A knapsack-type public key cryptosystem based on arithmetic in finite fields. IEEE Trans. Inf. Theory 1988, 34, 901–909. [Google Scholar] [CrossRef]
- Impagliazzo, R.; Naor, M. Efficient cryptographic schemes provably as secure as subset sum. J. Cryptol. 1996, 9, 199–216. [Google Scholar] [CrossRef]
- Faust, S.; Masny, D.; Venturi, D. Chosen-ciphertext security from subset sum. In Public-Key Cryptography—PKC 2016; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 35–46. [Google Scholar]
- Lyubashevsky, V.; Palacio, A.; Segev, G. Public-key cryptographic primitives provably as secure as subset sum. In Proceedings of the Theory of Cryptography Conference, Zurich, Switzerland, 9–11 February 2010; Springer International Publishing: Berlin/Heidelberg, Germany, 2010; pp. 382–400. [Google Scholar]
- Bonnetain, X. Improved low-qubit hidden shift algorithms. arXiv 2019, arXiv:1901.11428. [Google Scholar] [CrossRef]
- Bonnetain, X.; Schrottenloher, A. Quantum security analysis of CSIDH. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 10–14 May 2020; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 493–522. [Google Scholar]
- Bonnetain, X.; Naya-Plasencia, M. Hidden shift quantum cryptanalysis and implications. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Brisbane, QLD, Australia, 2–6 December 2018; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 560–592. [Google Scholar]
- Galil, Z.; Margalit, O. An almost linear-time algorithm for the dense subset-sum problem. SIAM J. Comput. 1991, 20, 1157–1189. [Google Scholar] [CrossRef]
- Brickell, E.F. Solving low density knapsacks. In Advances in Cryptology: Proceedings of Crypto 83; Springer US: Boston, MA, USA, 1984; pp. 25–37. [Google Scholar]
- Lagarias, J.C.; Odlyzko, A.M. Solving low-density subset sum problems. J. ACM (JACM) 1985, 32, 229–246. [Google Scholar] [CrossRef]
- Ajtai, M. The shortest vector problem in L2 is np-hard for randomized reductions. In Proceedings of the Thirtieth Annual ACM Symposium on Theory of Computing, Dallas, TX, USA, 24–26 May 1998; Association for Computing Machinery: New York, NY, USA, 1998; pp. 10–19. [Google Scholar]
- Coster, M.J.; LaMacchia, B.A.; Odlyzko, A.M.; Schnorr, C.P. An improved low-density subset sum algorithm. In Proceedings of the Workshop on the Theory and Application of of Cryptographic Techniques, Brighton, UK, 8–11 April 1991; Springer International Publishing: Berlin/Heidelberg, Germany, 1991; pp. 54–67. [Google Scholar]
- Joux, A.; Stern, J. Improving the critical density of the Lagarias-Odlyzko attack against subset sum problems. In Proceedings of the International Symposium on Fundamentals of Computation Theory, Gosen, Germany, 9–13 September 1991; Springer International Publishing: Berlin/Heidelberg, Germany, 1991; pp. 258–264. [Google Scholar]
- Horowitz, E.; Sahni, S. Computing partitions with applications to the knapsack problem. J. ACM (JACM) 1974, 21, 277–292. [Google Scholar] [CrossRef]
- Schroeppel, R.; Shamir, A. A t = O(2n/2), s = O(2n/4) algorithm for certain np-complete problems. SIAM J. Comput. 1981, 10, 456–464. [Google Scholar] [CrossRef]
- Howgrave-Graham, N.; Joux, A. New generic algorithms for hard knapsacks. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 10–14 May 2020; Springer International Publishing: Berlin/Heidelberg, Germany, 2010; pp. 235–256. [Google Scholar]
- Becker, A.; Coron, J.; Joux, A. Improved generic algorithms for hard knapsacks. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 10–14 May 2020; Springer International Publishing: Berlin/Heidelberg, Germany, 2011; pp. 364–385. [Google Scholar]
- Bonnetain, X.; Bricout, R.; Schrottenloher, A.; Shen, Y. Improved classical and quantum algorithms for subset-sum. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Brisbane, QLD, Australia, 2–6 December 2018; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 633–666. [Google Scholar]
- May, A.; Meurer, A.; Thomae, E. Decoding random linear codes in (20.054n). In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Brisbane, QLD, Australia, 2–6 December 2018; Springer International Publishing: Berlin/Heidelberg, Germany, 2011; pp. 107–124. [Google Scholar]
- Becker, A.; Joux, A.; May, A.; Meurer, A. Decoding random binary linear codes in 2n/20: How 1 + 1 = 0 improves information set decoding. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 10–14 May 2020; Springer International Publishing: Berlin/Heidelberg, Germany, 2012; pp. 520–536. [Google Scholar]
- Kachigar, G.; Tillich, J. Quantum information set decoding algorithms. In Proceedings of the International Workshop on Post-Quantum Cryptography, Utrecht, The Netherlands, 26–28 June 2017; Springer International Publishing: Cham, Switzerland, 2017; pp. 69–89. [Google Scholar]
- Kirshanova, E. Improved quantum information set decoding. In Proceedings of the International Workshop on Post-Quantum Cryptography, Utrecht, The Netherlands, 26–28 June 2017; Springer International Publishing: Cham, Switzerland, 2018; pp. 507–527. [Google Scholar]
- May, A. How to meet ternary LWE keys. In Proceedings of the Annual International Cryptology Conference, Virtual, 16–20 August 2021; Springer International Publishing: Cham, Switzerland, 2021; pp. 701–731. [Google Scholar]
- van Hoof, I.; Kirshanova, E.; May, A. Quantum Key Search for Ternary LWE. In Proceedings of the International Workshop on Post-Quantum Cryptography, Utrecht, The Netherlands, 26–28 June 2017; Springer International Publishing: Cham, Switzerland, 2021; pp. 117–132. [Google Scholar]
- Kirshanova, E.; May, A. How to Find Ternary LWE Keys Using Locality Sensitive Hashing. In Proceedings of the IMA International Conference on Cryptography and Coding, Oxford, UK, 14–16 December 2021. [Google Scholar]
- Glaser, T.; May, A. How to Enumerate LWE Keys as Narrow as in Kyber/Dilithium. In Proceedings of the International Conference on Cryptology and Network Security, Singapore, 19–22 December 2023. [Google Scholar]
- Lee, E.; Lee, J.; Son, Y.; Wang, Y. Improved Meet-LWE Attack via Ternary Trees. Cryptology ePrint Archive, Paper 2024/824. Available online: https://eprint.iacr.org/2024/824 (accessed on 23 August 2025).
- Bernstein, D.J.; Jeffery, S.; Lange, T.; Meurer, A. Quantum algorithms for the subset-sum problem. In Proceedings of the International Workshop on Post-Quantum Cryptography, Utrecht, The Netherlands, 26–28 June 2017; Springer International Publishing: Berlin/Heidelberg, Germany, 2013; pp. 16–33. [Google Scholar]
- Helm, A.; May, A. Subset Sum Quantumly in 1.17n. In Proceedings of the 13th Conference on the Theory of Quantum Computation, Communication and Cryptography, Sydney, Australia, 16–18 July 2018; Schloss Dagstuhl–Leibniz-Zentrum für Informatik: Dagstuhl, Germany, 2018; pp. 5:1–5:15. [Google Scholar]
- Magniez, F.; Nayak, A.; Roland, J.; Santha, M. Search via quantum walk. SIAM J. Comput. 2011, 40, 142–164. [Google Scholar] [CrossRef]
- NIST. Status Report on the Fourth Round of the NIST Post-Quantum Cryptography Standardization Process. NIST Internal Report 8545. Available online: https://csrc.nist.gov/projects/post-quantum-cryptography/post-quantum-cryptography-standardization (accessed on 3 March 2025).
- Albrecht, M.R.; Bernstein, D.J.; Chou, T.; Cid, C.; Gilcher, J.; Lange, T.; Maram, V.; Von Maurich, I.; Misoczki, R.; Niederhagen, R.; et al. Classic McEliece: Conservative Code-Based Cryptography. In NIST Post-Quantum Standardization, 4th Round; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022; Available online: https://classic.mceliece.org/nist.html (accessed on 23 October 2022).
- Aragon, N.; Barreto, P.; Bettaieb, S.; Bidoux, L.; Blazy, O.; Deneuville, J.C.; Gaborit, P.; Ghosh, S.; Gueron, S.; Güneysu, T.; et al. BIKE: Bit Flipping Key Encapsulation. In NIST Post-Quantum Standardization, 4th Round; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2024; Available online: https://bikesuite.org/ (accessed on 10 October 2024).
- Gaborit, P.; Aguilar-Melchor, C.; Aragon, N.; Bettaieb, S.; Bidoux, L.; Blazy, O.; Deneuville, J.C.; Persichetti, E.; Zémor, G.; Bos, J.; et al. Hamming Quasi-Cyclic (HQC). In NIST Post-Quantum Standardization, 4th Round; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2025; Available online: https://pqc-hqc.org/resources.html (accessed on 22 August 2025).
- Prange, E. The use of information sets in decoding cyclic codes. IRE Trans. Inf. Theory 1962, 8, 5–9. [Google Scholar] [CrossRef]
- Stern, J. A method for finding codewords of small weight. In Proceedings of the International Colloquium on Coding Theory and Applications, Toulon, France, 2–4 November 1988; Springer International Publishing: Berlin/Heidelberg, Germany, 1988; pp. 106–113. [Google Scholar]
- Finiasz, M.; Sendrier, N. Security bounds for the design of code-based cryptosystems. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Brisbane, QLD, Australia, 2–6 December 2018; Springer International Publishing: Berlin/Heidelberg, Germany, 2009; pp. 88–105. [Google Scholar]
- May, A.; Ozerov, I. On computing nearest neighbors with applications to decoding of binary linear codes. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 10–14 May 2020; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 203–228. [Google Scholar]
- Both, L.; May, A. Decoding linear codes with high error rate and its impact for LPN security. In Proceedings of the International Conference on Post-Quantum Cryptography, Fort Lauderdale, FL, USA, 9–11 April 2018; Springer International Publishing: Cham, Switzerland, 2018; pp. 25–46. [Google Scholar]
- Esser, A.; Zweydinger, F. New time-memory trade-offs for subset sum–improving ISD in theory and practice. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 10–14 May 2020; Springer Nature Switzerland: Cham, Switzerland, 2023; pp. 360–390. [Google Scholar]
- Esser, A. Revisiting nearest-neighbor-based information set decoding. In Proceedings of the IMA International Conference on Cryptography and Coding, Oxford, UK, 14–16 December 2021; Springer Nature Switzerland: Cham, Switzerland, 2023; pp. 34–54. [Google Scholar]
- Furue, H.; Aikawa, Y. An Improved Both-May Information Set Decoding Algorithm: Towards More Efficient Time-Memory Trade-Offs. In Proceedings of the International Conference on Post-Quantum Cryptography, Fort Lauderdale, FL, USA, 9–11 April 2018; Springer Nature Switzerland: Cham, Switzerland, 2025; pp. 104–128. [Google Scholar]
- Bernstein, D.J. Grover vs. mceliece. In Proceedings of the International Workshop on Post-Quantum Cryptography, Utrecht, The Netherlands, 26–28 June 2017; Springer International Publishing: Berlin/Heidelberg, Germany, 2010; pp. 73–80. [Google Scholar]
- Nguyen, P.Q.; Shparlinski, I.E.; Stern, J. Distribution of modular sums and the security of the server aided exponentiation. In Cryptography and Computational Number Theory; Birkhäuser: Basel, Switzerland, 2001; pp. 331–342. [Google Scholar]
- Ambainis, A. Quantum walk algorithm for element distinctness. SIAM J. Comput. 2007, 37, 210–239. [Google Scholar] [CrossRef]
- Grover, L.K. Quantum computers can search arbitrarily large databases by a single query. Phys. Rev. Lett. 1997, 79, 4709–4712. [Google Scholar] [CrossRef]
- Helm, A.; May, A. The power of few qubits and collisions–subset sum below Grover’s bound. In Proceedings of the International Conference on Post-Quantum Cryptography, Fort Lauderdale, FL, USA, 9–11 April 2018; Springer Nature Switzerland: Cham, Switzerland, 2020; pp. 445–460. [Google Scholar]
- Chevignard, C.; Fouque, P.A.; Schrottenloher, A. Reducing the number of qubits in quantum information set decoding. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Brisbane, QLD, Australia, 2–6 December 2018; Springer Nature Singapore: Singapore, 2024; pp. 299–329. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).