A Layered Entropy Model for Transparent Uncertainty Quantification in Medical AI: Advancing Trustworthy Decision Support in Small-Data Clinical Settings
Abstract
1. Introduction
- Opaque Uncertainty Propagation: Traditional FRBS generate a crisp output but fail to reveal how ambiguity from inputs or rules propagates through the reasoning process, leaving users unaware of the decision’s reliability.
- Limited Diagnostic Capability: Conventional systems lack metrics to diagnose the source of uncertainty (e.g., ambiguous inputs vs. conflicting rules), making it difficult to refine the model or knowledge base effectively.
- Absence of a Confidence Metric: There is no integrated, interpretable measure of epistemic confidence, preventing users from distinguishing between a certain outcome and a guess, which is critical for high-stakes decision-making.
- Black-Box Uncertainty Methods: Alternatives like probabilistic deep learning or complex Type-2 fuzzy systems offer uncertainty quantification but at the cost of interpretability, creating a trade-off between transparency and diagnostic power.
2. Materials and Methods
2.1. Alternatives
2.2. Criteria Description
2.3. Suggested Methods
- IME = f1 (Glucose Membership Distribution, BMI Membership Distribution)
- RAE = f2 (IME, Rule Base Activation Strengths)
- SOE = f3 (RAE, Output Aggregation)
3. Results
3.1. Dataset Selection
3.2. Analysis
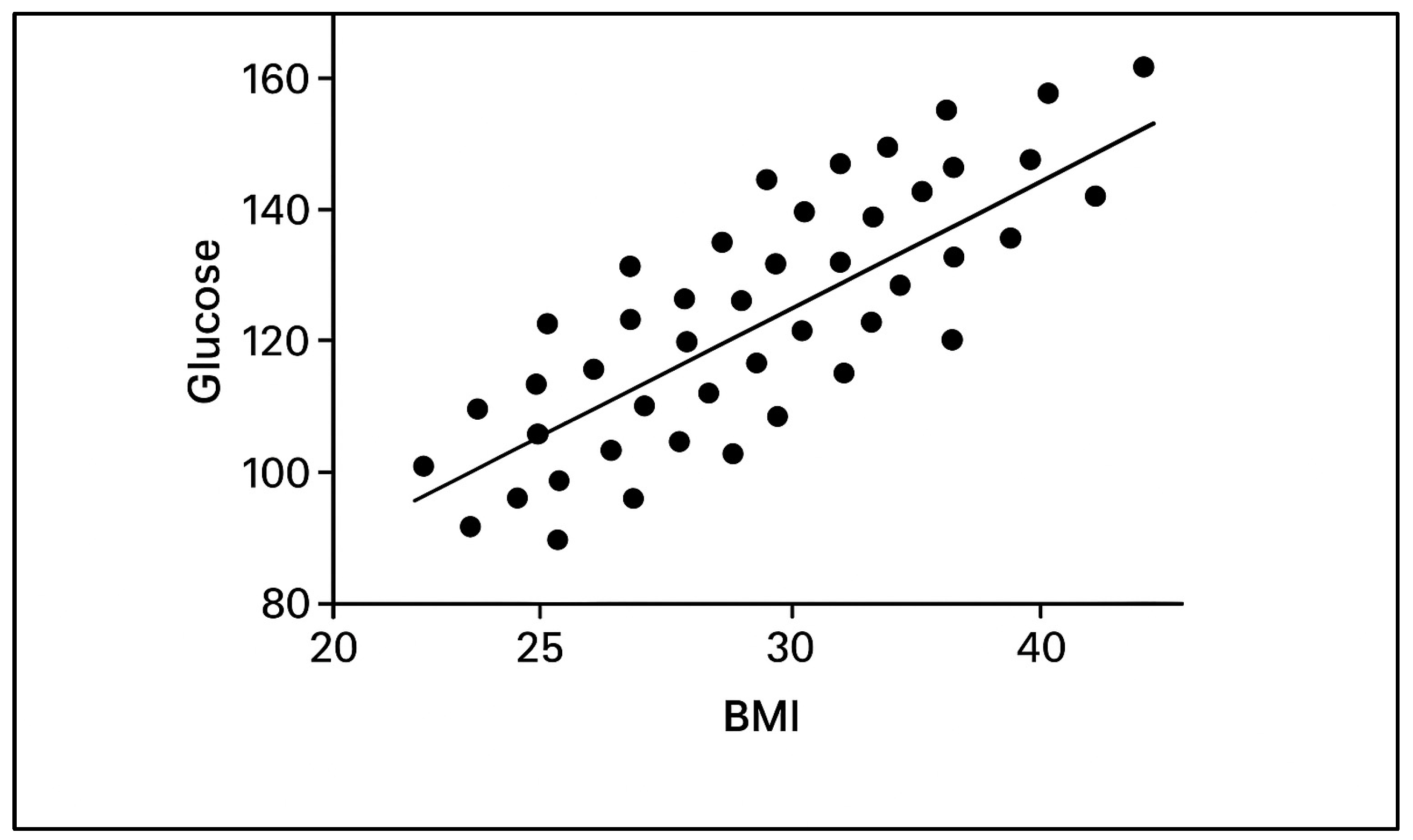
3.2.1. Glucose vs. BMI vs. Diabetes
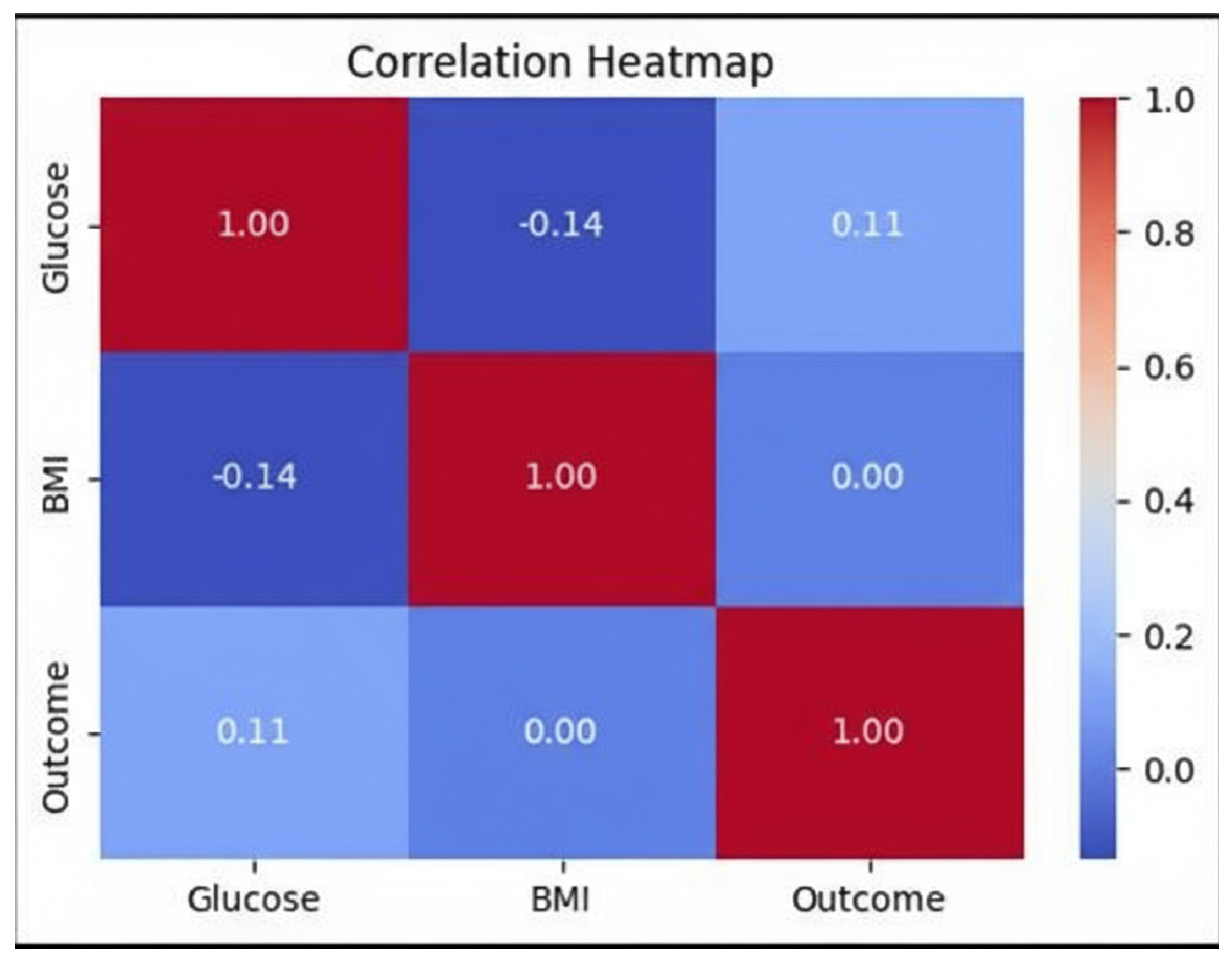
3.2.2. Glucose vs. BMI vs. Outcome Correlation Heatmap
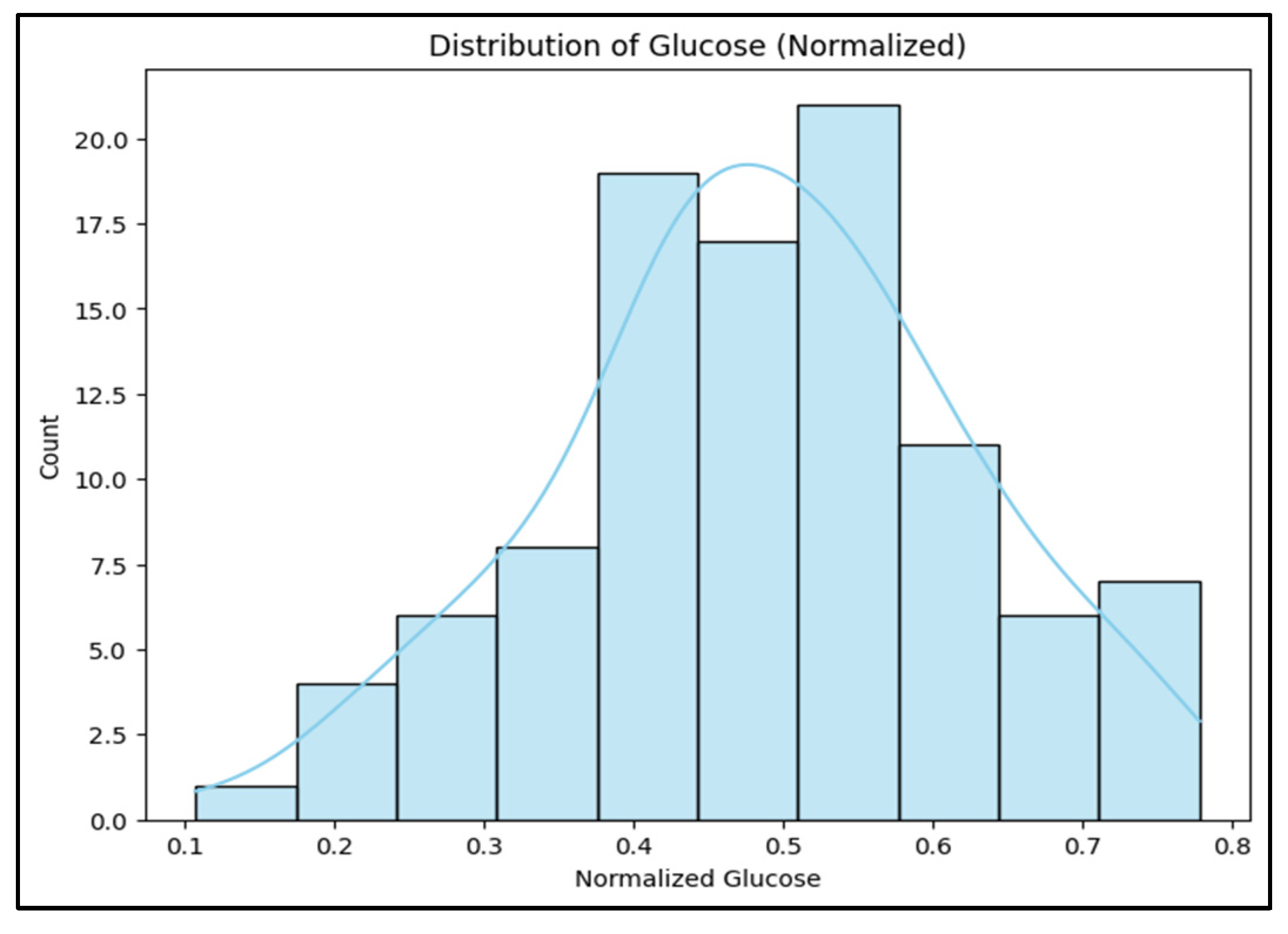
3.2.3. Normalized Glucose
3.2.4. Glucose vs. Simulated Epistemic Confidence Index
3.3. Fuzzy Rule-Based System Design
- Stage 1: In this stage, each input variable was categorized using its normalized range into three linguistic terms of glucose (low, normal, high) and BMI (low, normal, high) (see Table 2).Table 2. Linguistic term partitioning for inputs.
Input Variable Linguistic Term Description Glucose Low Low blood glucose level Glucose Normal Normal glucose concentration Glucose High High blood glucose level BMI Low Low body mass index BMI Normal Normal body mass index BMI High High body mass index
- Stage 2: In stage 2, the output variable “Diabetes Risk Score” was partitioned into low risk, medium risk, and high risk (see Table 3).Table 3. Linguistic term partitioning for output.
Output Variable Linguistic Term Description Diabetes Risk Score Low Risk Minimal likelihood of diabetes onset Diabetes Risk Score Medium Risk Moderate likelihood of diabetes onset Diabetes Risk Score High Risk High likelihood of diabetes onset
- In the 3rd Stage, the rule base was intentionally kept compact and interpretable, to exhibit typical small-data scenarios where domain experts define initial rule sets:
- Rule 1 (R1): IF Glucose is Low AND BMI is Low THEN Risk is Low
- Rule 2 (R2): IF Glucose is Normal AND BMI is Normal THEN Risk is Medium
- Rule 3 (R3): IF Glucose is High AND BMI is High THEN Risk is High
- Rule 4 (R4): IF Glucose is High AND BMI is Low THEN Risk is Medium
3.4. Simulation Protocol
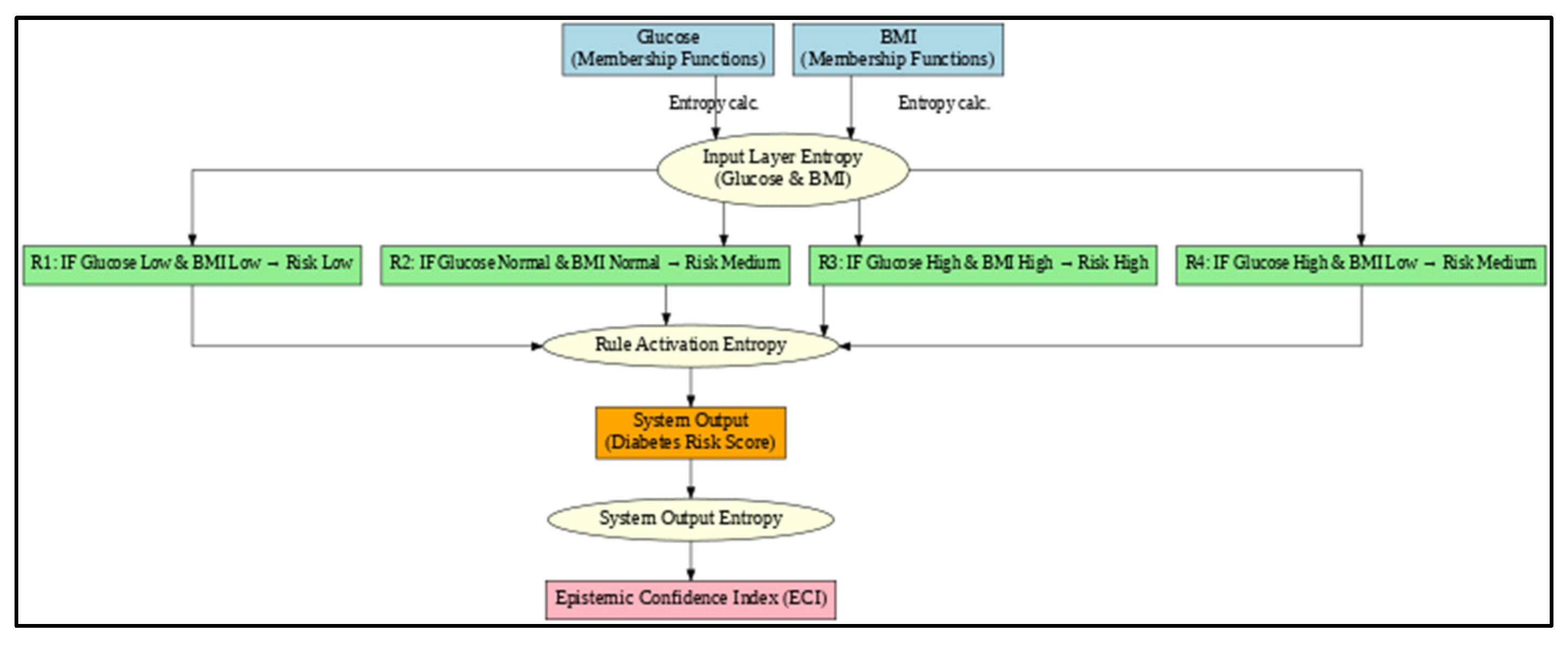
3.5. Layered Entropy Quantification
3.5.1. Membership Function Entropy (Input Layer)—MFE
3.5.2. Rule Activation Entropy (Rule Layer)
- Rule Activation Entropy (RAE) of 0.0000 bits implies complete absence of rule overlapping, thereby reflecting perfect alignment between input conditions and expert rules, while eliminating any rule competition or inferential conflict.
- System Output Entropy (Output Layer)—SOE
3.5.3. Epistemic Confidence Index (Composite)
3.6. Final Results
3.6.1. Membership Values
3.6.2. Rule Activation
3.6.3. Entropy Metrics
3.6.4. Layered Entropy Diagnosis
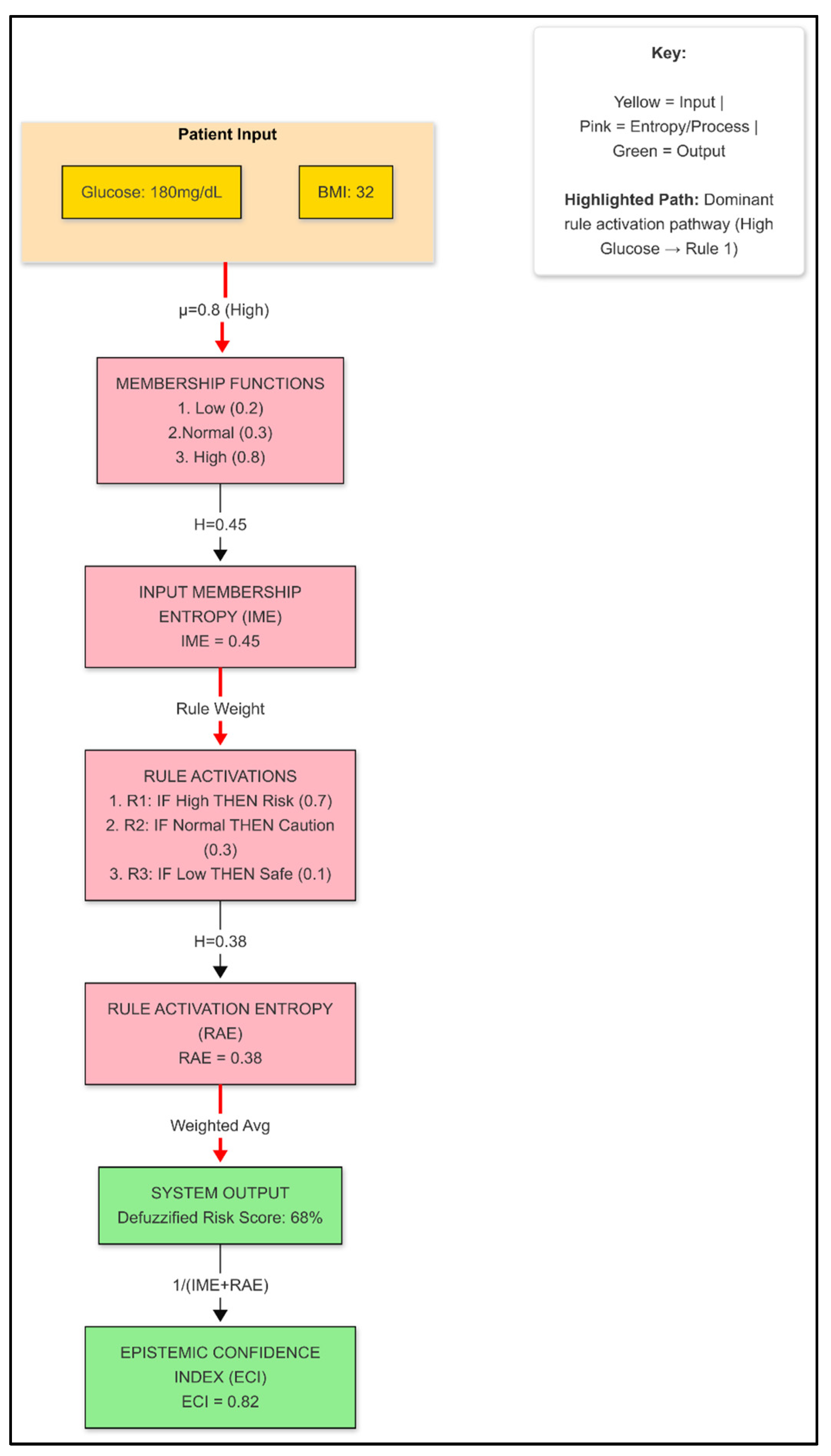
3.6.5. Epistemic Confidence Analysis for Patient Case
3.6.6. Full Layered Entropy Decomposition Flow
3.7. Theoretical Insights
- The input layer entropy that detects uncertainty in the initial fuzzy classification.
- The rule layer entropy imitates the degree of conflict that overlays among contending expert rules.
- The system output entropy computes uncertainty proliferated during stages of inference and aggregation.
3.8. Comparison with Synthetic Simulation
- Real-time patient data highlight strong membership alignment with single rule dominance, presenting high epistemic confidence.
- This comparison suffices the need for identifying epistemic uncertainty- at the input level, rule inference, or defuzzified output, substantiating the presence of a layered entropy framework.
3.9. Generalization Potential
4. Discussion
4.1. Full Transparency in Uncertainty Decomposition
4.2. Implications for Small-Data Decision Models
4.3. Comparison with Existing Fuzzy Uncertainty Models
4.4. Limitations and Future Extensions
- Multi-dimensional entropy landscapes for larger FRBS architectures.
- Dynamic uncertainty monitoring for online or adaptive fuzzy systems.
- Model debugging tools for iterative rule-based refinement.
- Hybrid integration with probabilistic or neural-fuzzy systems to balance knowledge-driven and data-driven uncertainty modeling (Angelov, 2013 [44]).
4.5. Contribution to Explainable AI (XAI)
5. Conclusions
6. Clinical Implications
- Enhanced Trust in AI-Assisted Diagnosis
- 2.
- Improved Safety in High-Risk Decisions
- 3.
- Efficient Small-Data Adaptation for Rare Diseases and Low-Resource Settings
- 4.
- Auditable AI for Medical Liability and Continuous Improvement
- 5.
- Future Clinical Applications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data availability statement
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Mendel, J.M. Fuzzy logic systems for engineering: A tutorial. Proc. IEEE 1995, 83, 345–377. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Fuzzy Sets and Systems: Theory and Applications; Academic Press: Cambridge, MA, USA, 1980. [Google Scholar]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Jang, J.S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Zeng, X.J.; Singh, M.G. Approximation theory of fuzzy systems—MIMO case. IEEE Trans. Fuzzy Syst. 1997, 5, 333–344. [Google Scholar]
- Herrera, F.; Alonso, S.; Chiclana, F.; Verdegay, J.L. A fuzzy decision support system for evaluating the quality of institutional web sites. Int. J. Comput. Intell. Res. 2011, 7, 261–271. [Google Scholar]
- Zimmermann, H.J. Fuzzy Set Theory and Its Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Ross, T.J. Fuzzy Logic with Engineering Applications; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Siler, W.; Buckley, J.J. Fuzzy Expert Systems and Fuzzy Reasoning; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Abraham, A. Neuro-fuzzy systems: State-of-the-art modeling techniques. In Connectionist Models of Neurons, Learning Processes, and Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2005; pp. 269–276. [Google Scholar]
- Angelov, P.; Filev, D. An approach to online identification of Takagi–Sugeno fuzzy models. IEEE Trans. Syst. Man Cybern. B Cybern. 2004, 34, 484–498. [Google Scholar] [CrossRef]
- Cheng, C.H.; Lin, Y.C. Evaluating the best main battle tank using fuzzy decision theory with linguistic criteria evaluation. Eur. J. Oper. Res. 2002, 142, 174–186. [Google Scholar] [CrossRef]
- Kahraman, C.; Cebeci, U.; Ruan, D. Multi-attribute comparison of catering service companies using fuzzy AHP: The case of Turkey. Int. J. Prod. Econ. 2003, 87, 171–184. [Google Scholar] [CrossRef]
- Dincer, I.; Cengel, Y.A. Energy, entropy and exergy concepts and their roles in thermal engineering. Entropy 2001, 3, 116–149. [Google Scholar] [CrossRef]
- Kasabov, N. Evolving Connectionist Systems: The Knowledge Engineering Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Cordón, O.; Herrera, F.; Hoffmann, F.; Magdalena, L. Genetic Fuzzy Systems: Evolutionary Tuning and Learning of Fuzzy Knowledge Bases; World Scientific: Singapore, 2001. [Google Scholar]
- Zhang, Y.; Wang, C.; Huang, Y.; Ding, W.; Qian, Y. Adaptive Relative Fuzzy Rough Learning for Classification. IEEE Trans. Fuzzy Syst. 2024, 32, 6267–6276. [Google Scholar] [CrossRef]
- Torres, A.; Nieto, J.J. Fuzzy logic in medicine and bioinformatics. J. Biomed. Biotechnol. 2006, 2006, 91908. [Google Scholar] [CrossRef]
- Lee, C.S.; Wang, M.H. A fuzzy expert system for diabetes decision support application. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2010, 41, 139–153. [Google Scholar]
- Dhas, J.E.; Kumanan, S. Weld residual stress prediction using artificial neural network and Fuzzy logic modeling. Indian J. Eng. Mater. Sci. 2011, 18, 351–360. [Google Scholar]
- Lee, K.M. Fuzzy logic in control systems: Fuzzy logic controller. IEEE Trans. Syst. Man Cybern. 1990, 20, 404–418. [Google Scholar] [CrossRef]
- Chang, F.J.; Chen, L. Real-coded genetic algorithm for rule-based flood control reservoir management. Water Resour. Manag. 1998, 12, 185–198. [Google Scholar] [CrossRef]
- Carbajal-Hernández, J.J.; Sánchez-Fernández, L.P.; Carrasco-Ochoa, J.A.; Martínez-Trinidad, J.F. Assessment and prediction of air quality using fuzzy logic and autoregressive models. Atmos. Environ. 2012, 60, 37–50. [Google Scholar] [CrossRef]
- Shahnazari, A.; Liu, F.; Andersen, M.N.; Jacobsen, S.E.; Jensen, C.R. Effects of partial root-zone drying on yield, tuber size and water use efficiency in potato under field conditions. Field Crops Res. 2010, 118, 24–31. [Google Scholar] [CrossRef]
- Mendes, W.R.; Araújo, F.M.U.; Dutta, R.; Heeren, D.M. Fuzzy control system for variable rate irrigation using remote sensing. Expert Syst. Appl. 2019, 124, 13–24. [Google Scholar] [CrossRef]
- Pappis, C.P.; Mamdani, E.H. A fuzzy logic controller for a traffic junction. IEEE Trans. Syst. Man Cybern. 1977, 7, 707–717. [Google Scholar] [CrossRef]
- Iqbal, K.; Khan, M.A.; Abbas, S.; Hasan, Z.; Fatima, A. Intelligent transportation system (ITS) for smart-cities using Mamdani fuzzy inference system. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 64–79. [Google Scholar] [CrossRef]
- Bagherian-Marandi, N.; Ravanshadnia, M. Akbarzadeh-TMR Two-layered fuzzy logic-based model for predicting court decisions in construction contract disputes. Artif. Intell. Law 2021, 29, 453–484. [Google Scholar] [CrossRef]
- PIMA Dataset, Retrieved from Datasets/pima-indians-diabetes.data.csv at Master jbrownlee/Datasets, GitHub. 2017. Available online: https://github.com/jbrownlee/Datasets/blob/master/pima-indians-diabetes.data.csv (accessed on 25 August 2025).
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- De Luca, A.; Termini, S. A definition of nonprobabilistic entropy in the setting of fuzzy sets theory. Inf. Control 1972, 20, 301–312. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.I.B. Type-2 fuzzy sets made simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Wu, D.; Mendel, J.M. Aggregation using the linguistic weighted average and interval type-2 fuzzy sets. IEEE Trans. Fuzzy Syst. 2007, 15, 75–90. [Google Scholar] [CrossRef]
- Hagras, H. Type-2 FLCs: A new generation of fuzzy controllers. IEEE Comput. Intell. Mag. 2007, 2, 30–43. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Mendel, J.M. Uncertain Rule-Based Fuzzy Logic Systems: Introduction and New Directions; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Karnik, N.; Mendel, J.M. Centroid of a type-2 fuzzy set. Inf. Sci. 1998, 132, 195–220. [Google Scholar] [CrossRef]
- Inuiguchi, M.; Tanino, T. Fuzzy programming: A survey of recent developments. In Fuzzy Sets in Decision Analysis, Operations Research and Statistics; Slowinski, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 45–87. [Google Scholar]
- Dubois, D.; Prade, H. Possibility Theory: An Approach to Computerized Processing of Uncertainty; Plenum Press: New York, NY, USA, 1993. [Google Scholar]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Hullermeier, E. Fuzzy methods in machine learning and data mining: Status and prospects. Fuzzy Sets Syst. 2007, 156, 387–406. [Google Scholar] [CrossRef]
- Müller, V.C. Ethics of artificial intelligence and robotics. In Stanford Encyclopedia of Philosophy; Stanford University: Stanford, CA, USA, 2019. [Google Scholar]
- Angelov, P. Autonomous Learning Systems: From Data Streams to Knowledge in Real-Time; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Yager, R.R. On the measure of fuzziness and negation. Int. J. Gen. Syst. 1979, 5, 221–229. [Google Scholar] [CrossRef]
- Klir, G.J.; Yuan, B. Fuzzy Sets and Fuzzy Logic: Theory and Applications; Prentice Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Abrahart, R.; Kneale, P.E.; See, L.M. Neural Networks for Hydrological Modeling; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Choi, S.W.; Martin, E.B.; Morris, A.J.; Lee, I.B. Adaptive multivariate statistical process control for monitoring time-varying processes. Ind. Eng. Chem. Res. 2006, 45, 3108–3118. [Google Scholar] [CrossRef]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A survey of methods for explaining black box models. ACM Comput. Surv. 2018, 51, 1–42. [Google Scholar] [CrossRef]
- Doshi-Velez, F.; Kim, B. Towards a rigorous science of interpretable machine learning. arXiv 2017, arXiv:1702.08608. [Google Scholar] [CrossRef]
- Selič, P.; Žnidaršič, A. Explainable fuzzy rule-based systems: State of the art and challenges. Appl. Sci. 2021, 11, 8331. [Google Scholar]
- Hagras, H. A hierarchical type-2 fuzzy logic control architecture for autonomous mobile robots. IEEE Trans. Fuzzy Syst. 2004, 12, 524–539. [Google Scholar] [CrossRef]
- Lipton, Z.C. The mythos of model interpretability. Queue 2018, 16, 31–57. [Google Scholar] [CrossRef]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef]
- European Commission. Ethics Guidelines for Trustworthy, A.I.; European Commission: Brussels, Belgium, 2021. [Google Scholar]



| Pregnancies | Glucose (mg/dL) | Blood Pressure (mmHg) | Skin Thickness (mm) | Insulin (µU/mL) | BMI (kg/m2) | Diabetes Pedigree Function | Age (Years) | Outcome (Binary) | |
|---|---|---|---|---|---|---|---|---|---|
| count | 768 | 768 | 768 | 768 | 768 | 768 | 768 | 768 | 768 |
| mean | 3.845052 | 120.8945 | 69.10547 | 20.53646 | 79.79948 | 31.99258 | 0.471876 | 33.24089 | 0.348958 |
| std | 3.369578 | 31.97262 | 19.35581 | 15.95222 | 115.244 | 7.88416 | 0.331329 | 11.76023 | 0.476951 |
| min | 0 | 0 | 0 | 0 | 0 | 0 | 0.078 | 21 | 0 |
| 25% | 1 | 99 | 62 | 0 | 0 | 27.3 | 0.24375 | 24 | 0 |
| 50% | 3 | 117 | 72 | 23 | 30.5 | 32 | 0.3725 | 29 | 0 |
| 75% | 6 | 140.25 | 80 | 32 | 127.25 | 36.6 | 0.62625 | 41 | 1 |
| max | 17 | 199 | 122 | 99 | 846 | 67.1 | 2.42 | 81 | 1 |
| Rule ID | IF Condition | THEN Output |
|---|---|---|
| R1 | Glucose is Low AND BMI is Low | Risk is Low |
| R2 | Glucose is Normal AND BMI is Normal | Risk is Medium |
| R3 | Glucose is High AND BMI is High | Risk is High |
| R4 | Glucose is High AND BMI is Low | Risk is Medium |
| Input Variable | Membership Entropy (Bits) | Interpretation |
|---|---|---|
| Glucose | 0 | Full membership activation—No ambiguity |
| BMI | 0 | Full membership activation—No ambiguity |
| Rule | Rule Description | Activation Strength | Entropy Contribution (Bits) |
|---|---|---|---|
| R1 | Glucose Low AND BMI Low THEN Risk Low | 0 | 0 |
| R2 | Glucose Normal AND BMI Normal THEN Risk Medium | 1 | 0 |
| R3 | Glucose High AND BMI High THEN Risk High | 0 | 0 |
| R4 | Glucose High AND BMI Low THEN Risk Medium | 0 | 0 |
| Output Variable | System Output Entropy (Bits) | Epistemic Confidence Index (ECI) | Interpretation |
|---|---|---|---|
| Diabetes Risk Score | 0 | 1 | Maximum epistemic confidence (no uncertainty) |
| Variable Pair | Correlation Coefficient | Interpretation |
|---|---|---|
| Glucose vs. BMI | 0.48 | Moderate positive correlation—potential rule overlap zones |
| Variable | Low | Normal | High |
|---|---|---|---|
| Glucose | 0.032 | 0.968 | 0 |
| BMI | 0 | 0.972 | 0.028 |
| Rule | Activation | Normalized |
|---|---|---|
| R1 | 0 | 0 |
| R2 | 0.940896 | 1 |
| R3 | 0 | 0 |
| R4 | 0 | 0 |
| Metric | Value |
|---|---|
| Glucose Entropy | 0.2043 |
| BMI Entropy | 0.1843 |
| Rule Activation Entropy | 0 |
| System Output Entropy | 0 |
| Epistemic Confidence Index (ECI) | 0.7202 |
| Layer | Measure | Value | Interpretation |
|---|---|---|---|
| Input Layer | Glucose Membership Entropy | 0.2043 | Minor fuzziness around membership boundaries (partial overlaps) |
| Input Layer | BMI Membership Entropy | 0.1843 | Slight membership uncertainty in BMI |
| Rule Activation Layer | Rule Activation Entropy | 0 | Single dominant rule fired with no competition |
| Output Layer | System Output Entropy | 0 | Fully determined output aggregation |
| Composite | Epistemic Confidence Index (ECI) | 0.7201 | High epistemic confidence with minor input fuzziness contribution |
| Input Variable | Linguistic Term | Membership Degree |
|---|---|---|
| Glucose | Low | 0.032 |
| Glucose | Normal | 0.968 |
| Glucose | High | 0 |
| BMI | Low | 0 |
| BMI | Normal | 0.972 |
| BMI | High | 0.028 |
| Rule | Antecedent Conditions | Rule Activation Strength |
|---|---|---|
| R1 | Glucose Low and BMI Low | 0 |
| R2 | Glucose Normal and BMI Normal | 0.9409 |
| R3 | Glucose High and BMI High | 0 |
| R4 | Glucose High and BMI Low | 0 |
| Layer/Component | Parameter | Real-Time Patient Data | Synthetic Data (Simulated) | Remarks |
|---|---|---|---|---|
| Input Layer | Glucose (Normalized) | 0.492 | 0.7 | Real-time input near the center of “Normal”; synthetic chosen to explore “High” |
| BMI (Normalized) | 0.507 | 0.3 | Real-time BMI in “Normal”; synthetic chosen to explore “Low” | |
| Membership Functions | Glucose Linguistic Degrees | Low: 0.032, Normal: 0.968, High: 0 | Low: 0, Normal: 0.3, High: 0.7 | Real input shows high certainty in “Normal” |
| BMI Linguistic Degrees | Low: 0, Normal: 0.972, High: 0.028 | Low: 0.7, Normal: 0.3, High: 0 | Synthetic has ambiguity between “Low” and “Normal” | |
| Input Membership Entropy (IME) | Entropy Score | 0.2043 (moderate fuzziness) | ~0.510 (higher fuzziness) | More overlapping memberships in the synthetic input |
| Rule Activation Layer | Fired Rules | R2 (Glucose Normal and BMI Normal) | R4 (Glucose High and BMI Low) | Different dominant rule fired |
| Rule Activation Strength | R2: 0.9409 | R4: ~0.49 | Synthetic case shows partial rule confidence | |
| Rule Activation Entropy (RAE) | Entropy Score | 0.0000 (Single rule dominance) | ~0.32 (mild competition) | Synthetic data shows epistemic ambiguity |
| System Output | Diabetes Risk Output | Medium Risk (Defuzzified) | Medium-High Risk (weighted output) | Output consistent with rule semantics |
| System Output Entropy (SOE) | Entropy Score | 0 | ~0.21 | Output for the synthetic less confident |
| Composite Index | Epistemic Confidence Index | 0.7201 | ~0.48 | Lower ECI for synthetic due to more fuzziness and multiple rule activations |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhattacharjee, S.; Biswas, S. A Layered Entropy Model for Transparent Uncertainty Quantification in Medical AI: Advancing Trustworthy Decision Support in Small-Data Clinical Settings. Information 2025, 16, 875. https://doi.org/10.3390/info16100875
Bhattacharjee S, Biswas S. A Layered Entropy Model for Transparent Uncertainty Quantification in Medical AI: Advancing Trustworthy Decision Support in Small-Data Clinical Settings. Information. 2025; 16(10):875. https://doi.org/10.3390/info16100875
Chicago/Turabian StyleBhattacharjee, Sandeep, and Sanjib Biswas. 2025. "A Layered Entropy Model for Transparent Uncertainty Quantification in Medical AI: Advancing Trustworthy Decision Support in Small-Data Clinical Settings" Information 16, no. 10: 875. https://doi.org/10.3390/info16100875
APA StyleBhattacharjee, S., & Biswas, S. (2025). A Layered Entropy Model for Transparent Uncertainty Quantification in Medical AI: Advancing Trustworthy Decision Support in Small-Data Clinical Settings. Information, 16(10), 875. https://doi.org/10.3390/info16100875







