Explainable Instrument Classification: From MFCC Mean-Vector Models to CNNs on MFCC and Mel-Spectrograms with t-SNE and Grad-CAM Insights
Abstract
1. Introduction
- Section 2 reviews related works on musical instrument classification and the main techniques employed in the literature;
- Section 3 presents the materials and methods, including dataset preparation, feature extraction, and the architecture of the neural models used;
- Section 4 reports the experimental results and evaluation metrics, with particular focus on the explainability techniques adopted to interpret model behavior;
- Section 5, finally, provides conclusions and discusses possible future developments.
2. Related Works
2.1. Early Feature-Based Pipelines (1990–2000)
2.2. First Wave of Large-Scale Studies (2000–2006)
2.3. New Descriptors and Unsupervised Codes (2010–2014)
2.4. Deep-Learning Era (2016–2024)
3. Materials and Methods
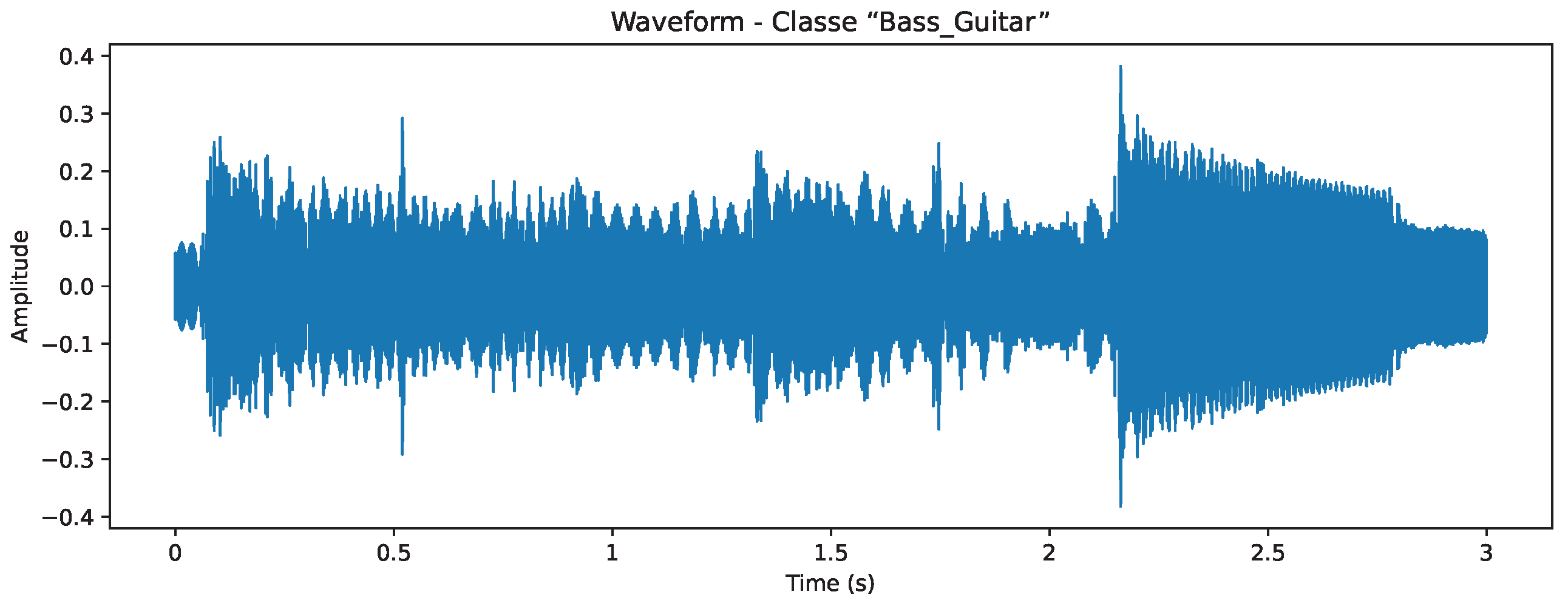
3.1. Dataset
3.2. Libraries
3.3. Data Analysis
3.4. Data Pre-Processing
3.5. Mel Spectrogram and Mel-Frequency Cepstral Coefficients (MFCCs)
3.5.1. Features Extraction
3.5.2. Standardization
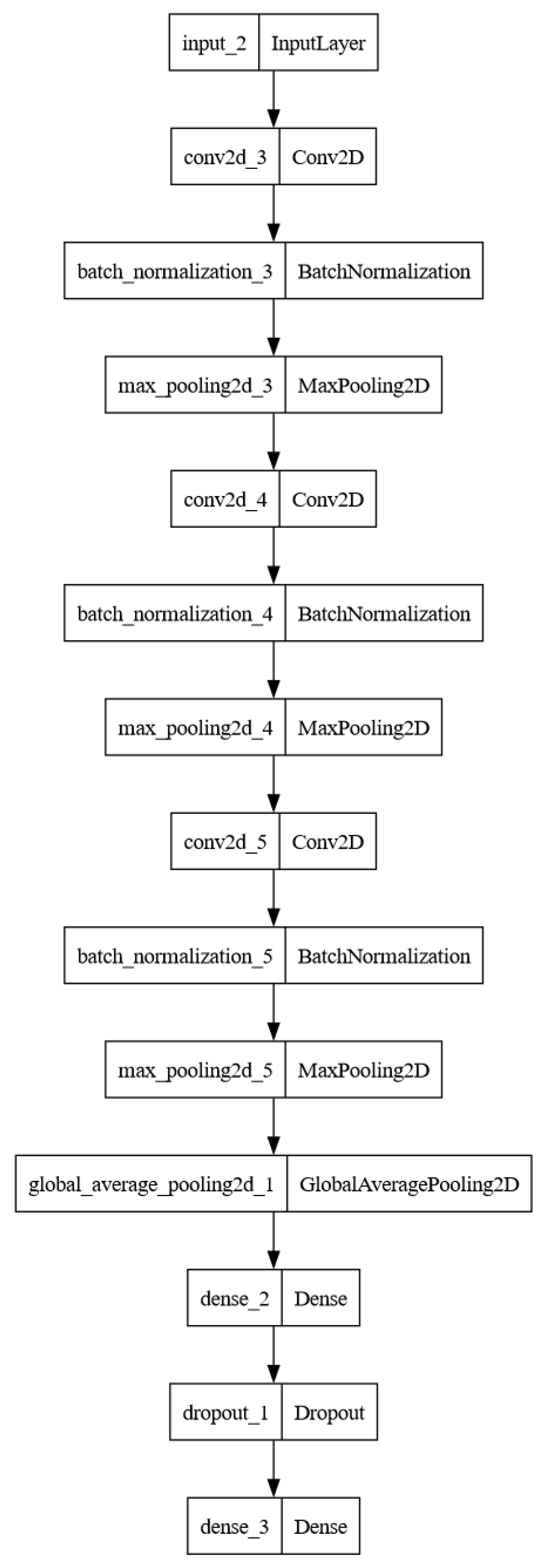
3.6. CNN-Based Models
3.6.1. Model Construction
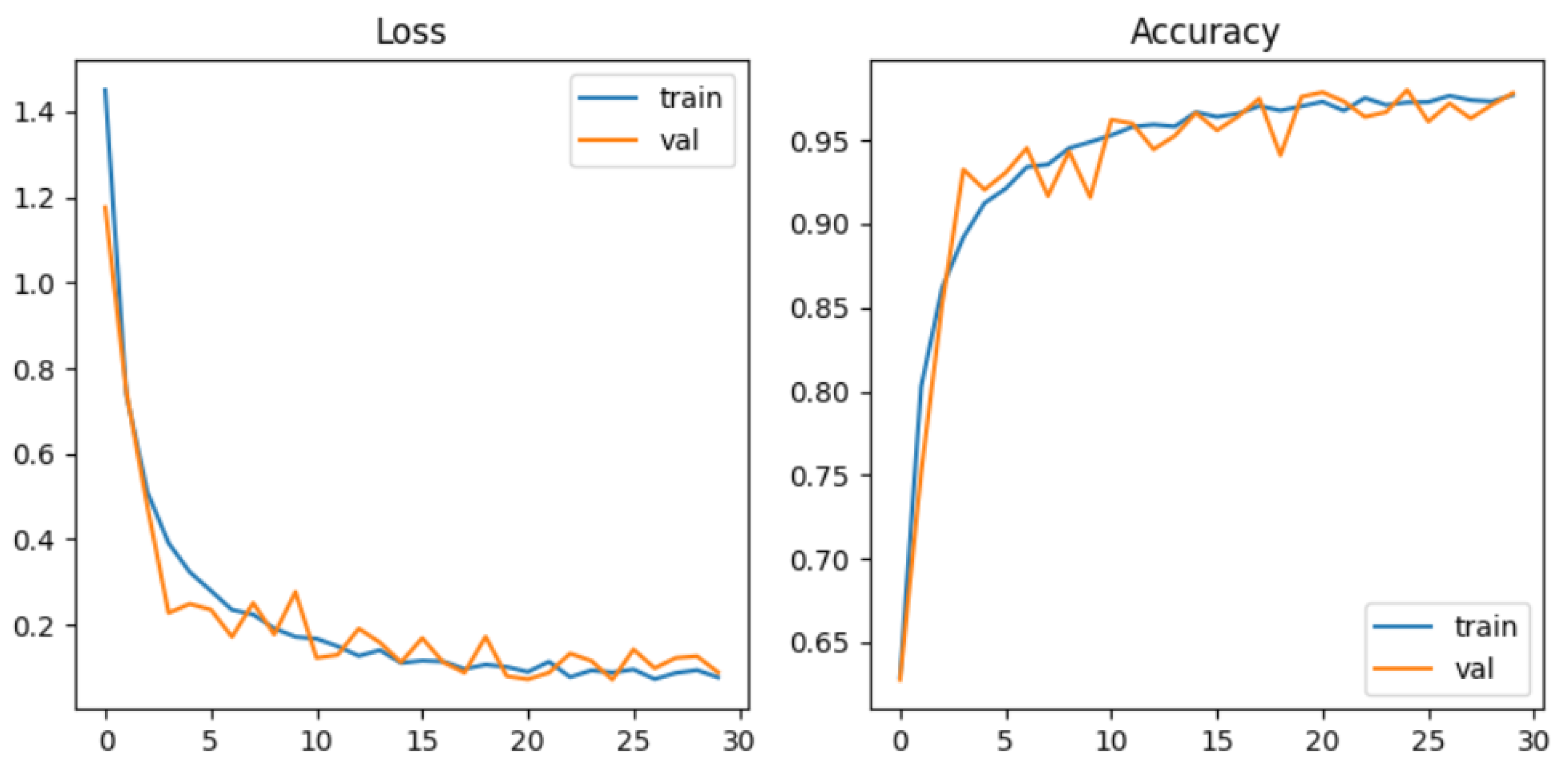
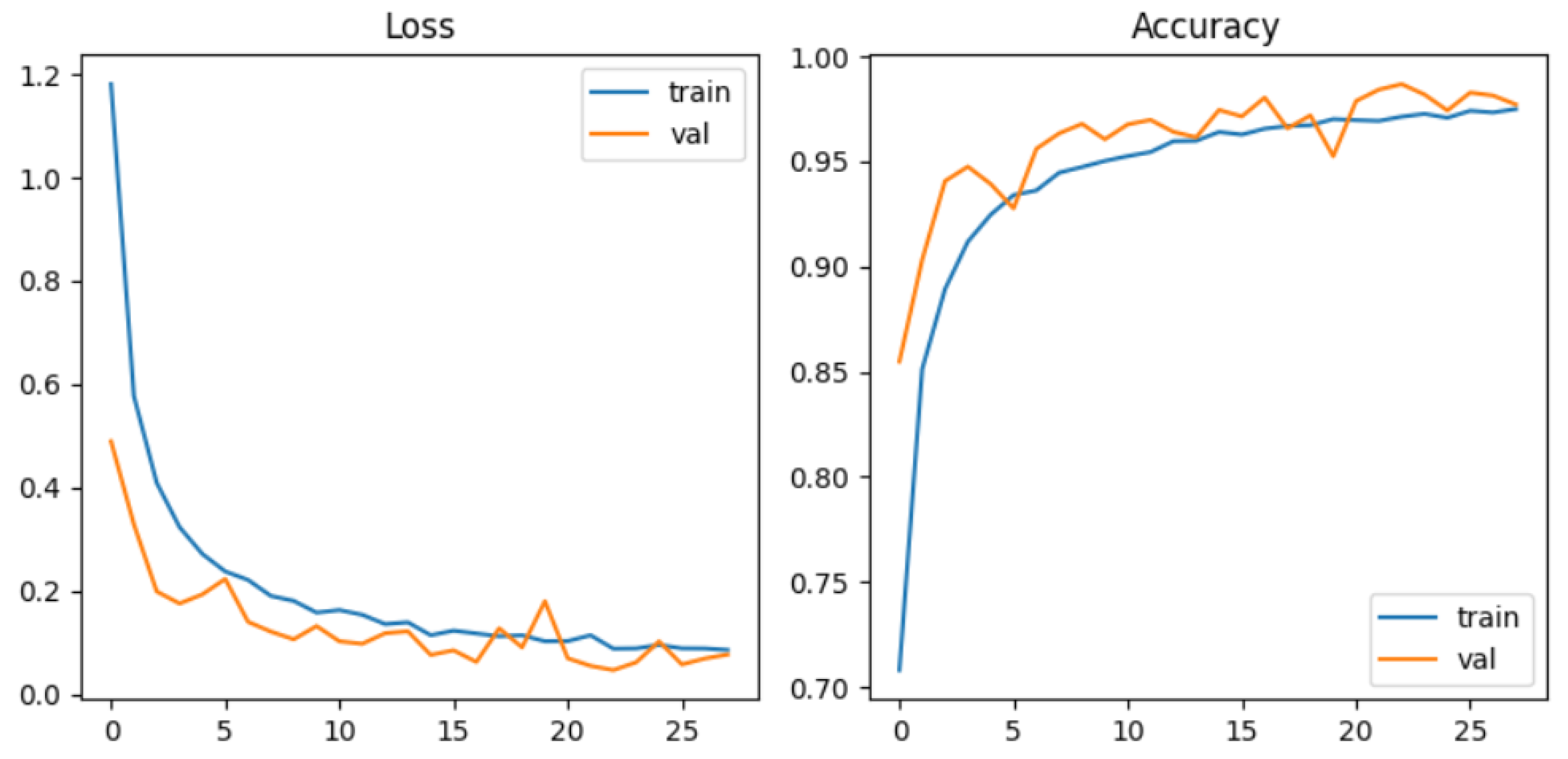
3.6.2. Training
3.6.3. Class Imbalance
3.7. Machine Learning Models
4. Results and Evaluation
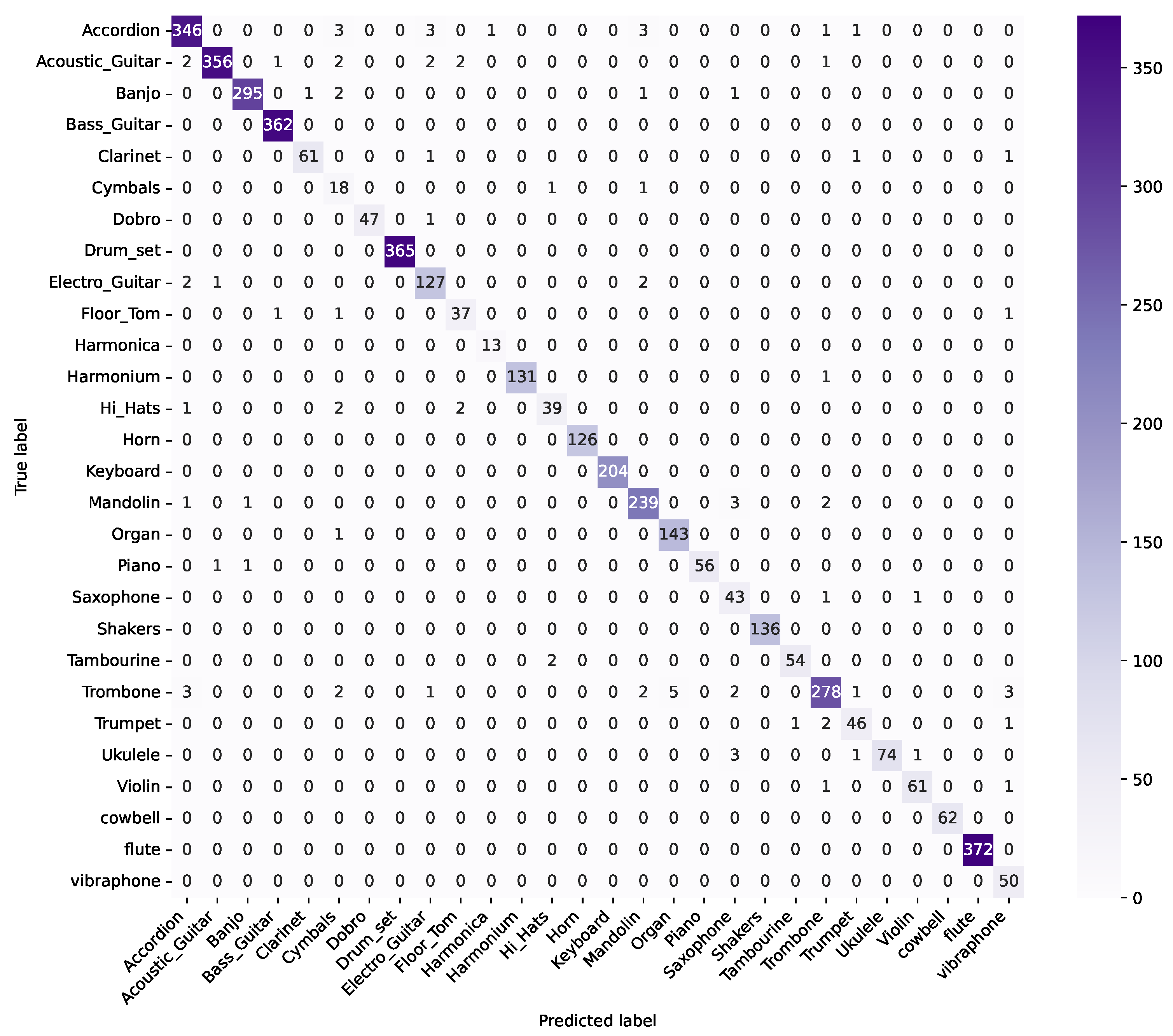
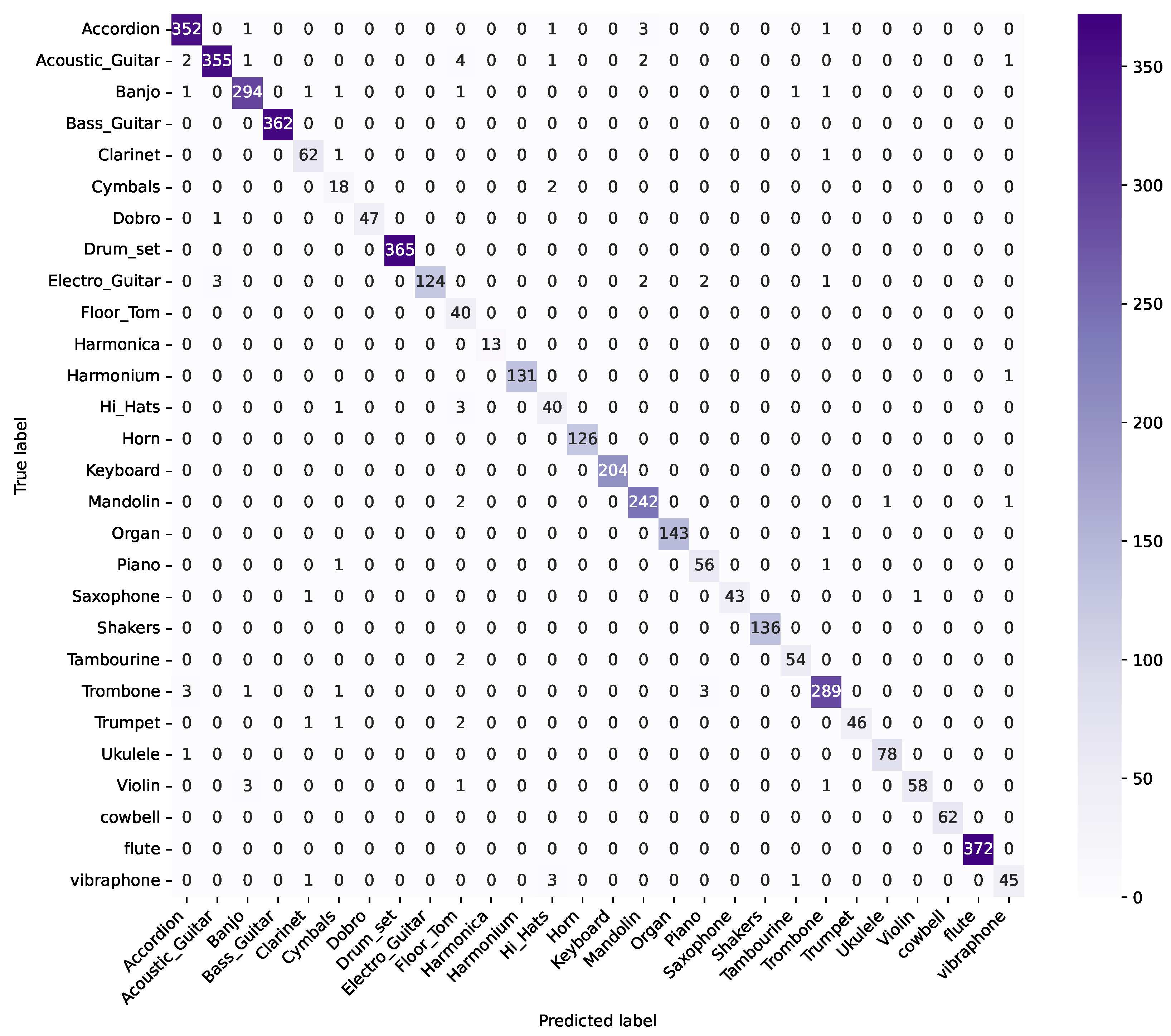
4.1. CNN-Based Models
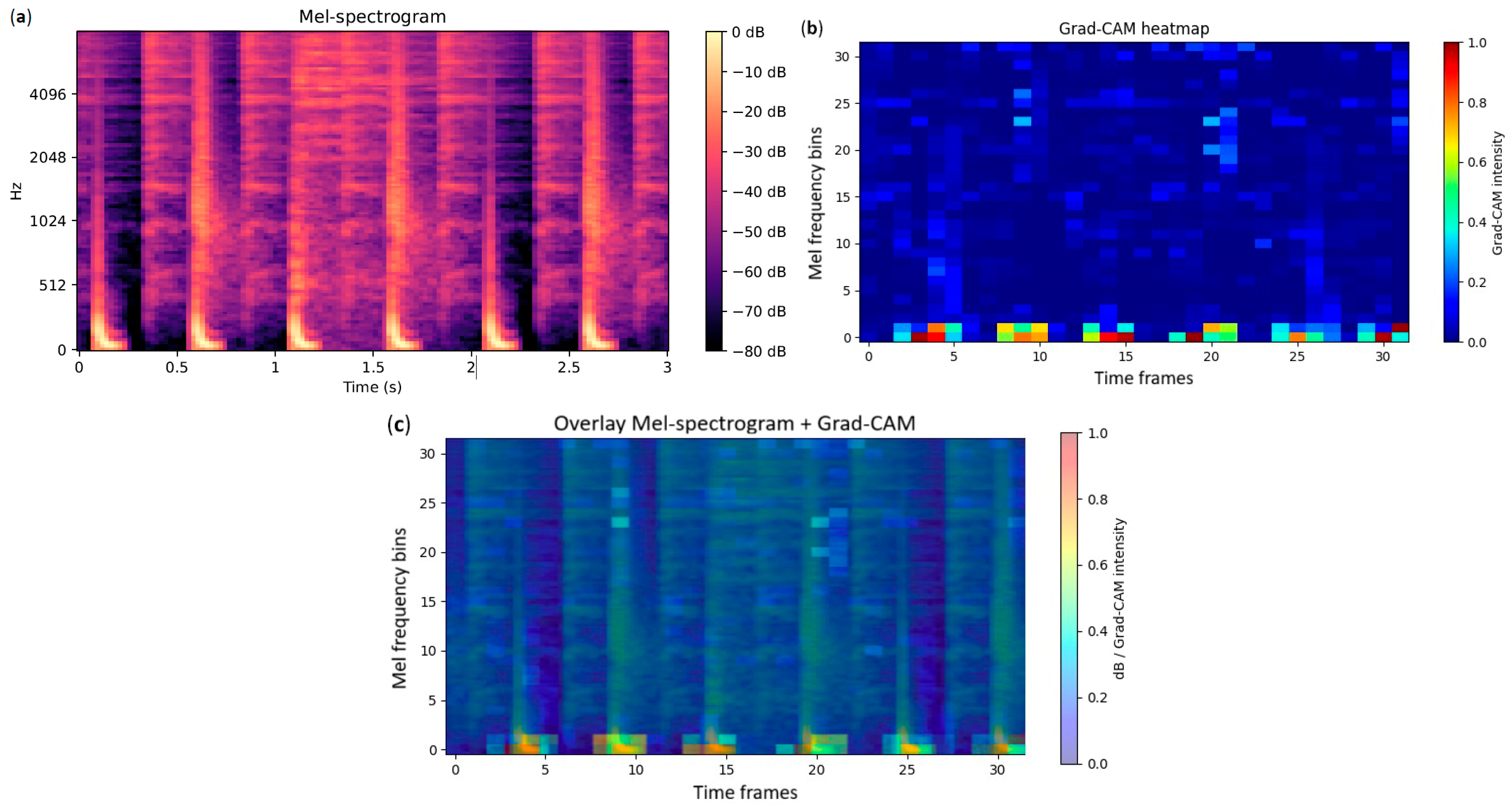
4.2. Explainability
4.3. Machine Learning Models
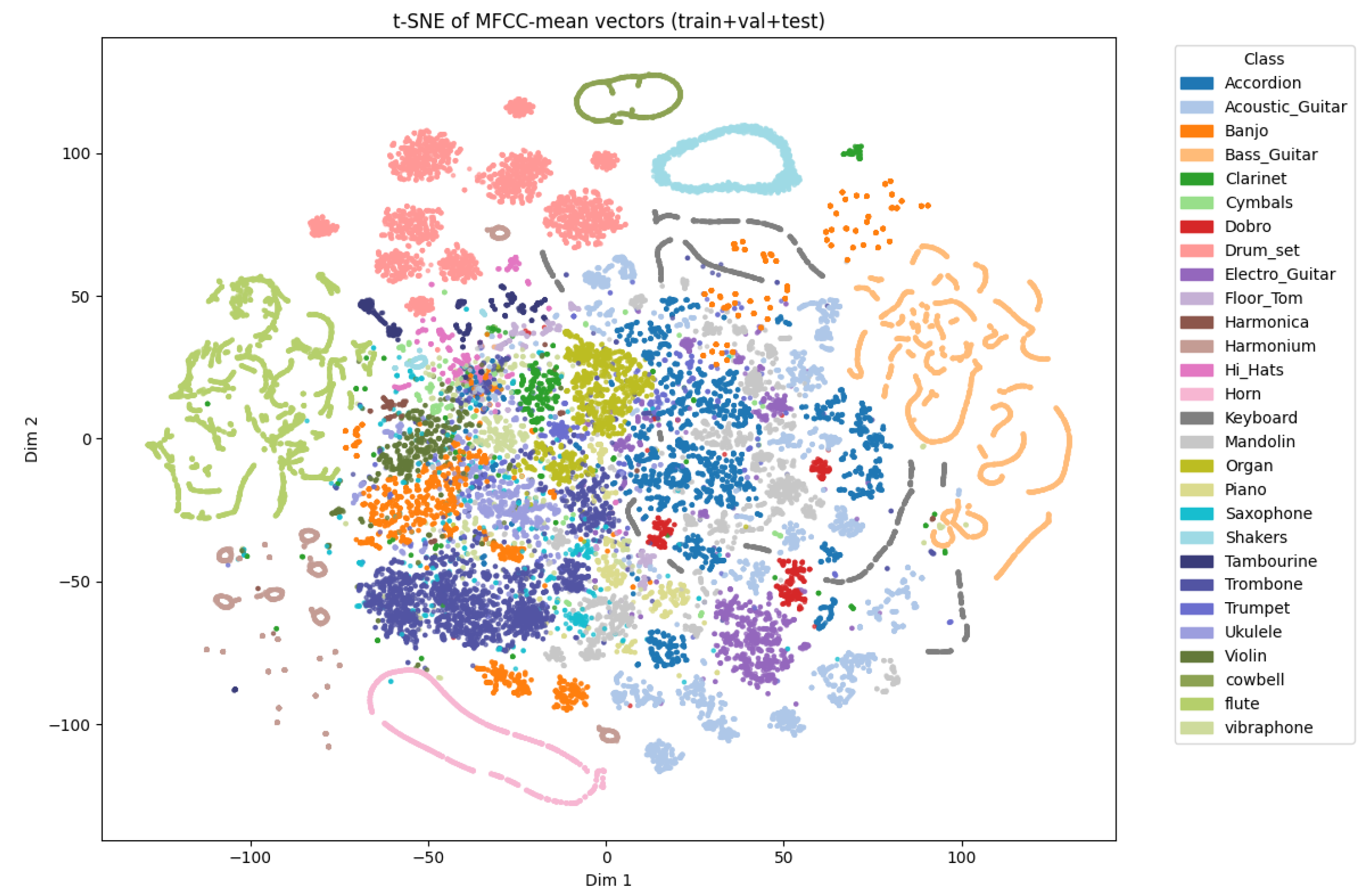
4.4. t-SNE
5. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saggese, A.; Strisciuglio, N.; Vento, M.; Petkov, N. Time-frequency analysis for audio event detection in real scenarios. In Proceedings of the 2016 13th IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS), Colorado Springs, CO, USA, 23–26 August 2016; pp. 438–443. [Google Scholar] [CrossRef]
- Esmaili, S.; Krishnan, S.; Raahemifar, K. Content based audio classification and retrieval using joint time-frequency analysis. In Proceedings of the 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, QC, Canada, 17–21 May 2004; Volume 5, p. V-665. [Google Scholar] [CrossRef]
- Zhang, W.; Xie, X.; Du, Y.; Huang, D. Speech preprocessing and enhancement based on joint time domain and time-frequency domain analysis. J. Acoust. Soc. Am. 2024, 155, 3580–3588. [Google Scholar] [CrossRef] [PubMed]
- Lo Giudice, M.; Mariani, F.; Caliano, G.; Salvini, A. Deep learning for the detection and classification of adhesion defects in antique plaster layers. J. Cult. Herit. 2024, 69, 78–85. [Google Scholar] [CrossRef]
- Lo Giudice, M.; Mariani, F.; Caliano, G.; Salvini, A. Enhancing Defect Detection on Surfaces Using Transfer Learning and Acoustic Non-Destructive Testing. Information 2025, 16, 516. [Google Scholar] [CrossRef]
- Abdul, Z.K.; Al-Talabani, A.K. Mel Frequency Cepstral Coefficient and Its Applications: A Review. IEEE Access 2022, 10, 122136–122158. [Google Scholar] [CrossRef]
- Allamy, S.; Koerich, A.L. 1D CNN architectures for music genre classification. In Proceedings of the 2021 IEEE Symposium Series on Computational Intelligence (SSCI), Orlando, FL, USA, 5–7 December 2021; pp. 1–7. [Google Scholar]
- Zaman, K.; Sah, M.; Direkoglu, C.; Unoki, M. A survey of audio classification using deep learning. IEEE Access 2023, 11, 106620–106649. [Google Scholar] [CrossRef]
- Bose, A.; Tripathy, B. Deep learning for audio signal classification. In Deep Learning—Research and Applications; De Gruyter: Berlin, Germany, 2020; pp. 105–136. [Google Scholar]
- Budyputra, M.A.; Reyfanza, A.; Gunawan, A.A.S.; Syahputra, M.E. Systematic Literature Review of The Use of Music Information Retrieval in Music Genre Classification. Int. J. Comput. Sci. Humanit. AI 2025, 2, 9–14. [Google Scholar] [CrossRef]
- Jenifer, A.E.; Abirami, K.S.; Rajeshwari, M. Enhanced Audio Signal Classification with Explainable AI: Deep Learning Approach in Time and Frequency Domain Analysis. Procedia Comput. Sci. 2025, 258, 2372–2381. [Google Scholar] [CrossRef]
- Becker, S.; Vielhaben, J.; Ackermann, M.; Müller, K.R.; Lapuschkin, S.; Samek, W. AudioMNIST: Exploring Explainable Artificial Intelligence for audio analysis on a simple benchmark. J. Frankl. Inst. 2024, 361, 418–428. [Google Scholar] [CrossRef]
- Lo Giudice, M.; Mammone, N.; Ieracitano, C.; Aguglia, U.; Mandic, D.; Morabito, F.C. Explainable deep learning classification of respiratory sound for telemedicine applications. In Proceedings of the International Conference on Applied Intelligence and Informatics, Reggio Calabria, Italy, 1–3 September 2022; Springer: Cham, Switzerland, 2022; pp. 391–403. [Google Scholar]
- Akman, A.; Schuller, B.W. Audio Explainable Artificial Intelligence: A Review. Intell. Comput. 2024, 3, 0074. [Google Scholar] [CrossRef]
- Kaminskyj, I. Automatic Source Identification of Monophonic Musical Instrument Sounds. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar] [CrossRef]
- Brown, J.C. Computer identification of musical instruments using pattern recognition with cepstral coefficients as features. J. Acoust. Soc. Am. 1999, 105, 1933–1941. [Google Scholar] [CrossRef] [PubMed]
- Marques, J.; Moreno, P.J. A Study of Musical Instrument Classification Using Gaussian Mixture Models and Support Vector Machines. Camb. Res. Lab. Tech. Rep. Ser. CRL 1999, 4, 143. [Google Scholar]
- Eronen, A.; Klapuri, A. Musical Instrument Recognition Using Cepstral Coefficients and Temporal Features. In Proceedings of the 2000 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Istanbul, Turkey, 5–9 June 2000. [Google Scholar] [CrossRef]
- Kostek, B.; Czyżewski, A. Representing Musical Instrument Sounds for Their Automatic Classification. J. Audio Eng. Soc. 2001, 49, 768–785. [Google Scholar]
- Livshin, A.; Rodet, X. The Importance of Cross-Database Evaluation in Sound Classification. In Proceedings of the 4th International Conference on Music Information Retrieval (ISMIR), Washington, DC, USA, 22 October 2003. [Google Scholar]
- Agostini, G.; Longari, M.; Pollastri, E. Musical Instrument Timbres Classification with Spectral Features. EURASIP J. Adv. Signal Process. 2003, 2003, 943279. [Google Scholar] [CrossRef]
- Krishna, A.G.; Sreenivas, T.V. Music Instrument Recognition: From Isolated Notes to Solo Phrases. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Montreal, QC, Canada, 17–21 May 2004; pp. 265–268. [Google Scholar] [CrossRef]
- Essid, S.; Richard, G.; David, B. Musical instrument recognition by pairwise classification strategies. IEEE Trans. Audio Speech Lang. Process. 2006, 14, 1401–1412. [Google Scholar] [CrossRef]
- Diment, A.; Rajan, P.; Heittola, T.; Virtanen, T. Modified Group Delay Feature for Musical Instrument Recognition. In Proceedings of the 10th International Symposium on Computer Music Multidisciplinary Research (CMMR), Marseille, France, 15–18 October 2013. [Google Scholar]
- Yu, L.; Su, L.; Yang, Y. Sparse Cepstral Codes and Power Scale for Instrument Identification. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014. [Google Scholar] [CrossRef]
- Han, Y.; Kim, J.; Lee, K. Deep convolutional neural networks for predominant instrument recognition in polyphonic music. Ieee/Acm Trans. Audio Speech Lang. Process. 2017, 25, 208–221. [Google Scholar] [CrossRef]
- Lee, J.; Kim, T.; Park, J.; Nam, J. Raw Waveform-based Audio Classification Using Sample-level CNN Architectures. arXiv 2017, arXiv:1712.00866. [Google Scholar] [CrossRef]
- Haidar-Ahmad, L. Music and Instrument Classification using Deep Learning Techniques. 2019. Available online: https://cs230.stanford.edu/projects_fall_2019/reports/26225883.pdf (accessed on 1 October 2025).
- Gururani, S.; Sharma, M.; Lerch, A. An Attention Mechanism for Musical Instrument Recognition. arXiv 2019, arXiv:1907.04294. [Google Scholar] [CrossRef]
- Solanki, A.; Pandey, S. Music instrument recognition using deep convolutional neural networks. Int. J. Inf. Technol. 2022, 14, 1659–1668. [Google Scholar] [CrossRef]
- Blaszke, M.; Kostek, B. Musical Instrument Identification Using Deep Learning Approach. Sensors 2022, 22, 3033. [Google Scholar] [CrossRef]
- Reghunath, L.C.; Rajan, R. Transformer-based ensemble method for multiple predominant instruments recognition in polyphonic music. EURASIP J. Audio Speech Music Process. 2022, 2022, 11. [Google Scholar] [CrossRef]
- Chen, R.; Ghobakhlou, A.; Narayanan, A. Interpreting CNN models for musical instrument recognition using multi-spectrogram heatmap analysis: A preliminary study. Front. Artif. Intell. 2024, 7, 1499913. [Google Scholar] [CrossRef] [PubMed]
- McFee, B.; Raffel, C.; Liang, D.; Ellis, D.P.; McVicar, M.; Battenberg, E.; Nieto, O. librosa: Audio and music signal analysis in python. SciPy 2015, 2015, 18–24. [Google Scholar]
- Logan, B. Mel Frequency Cepstral Coefficients for Music Modeling. In Proceedings of the 1st International Symposium Music Information Retrieval, Plymouth, MA, USA, 23–25 October 2000. [Google Scholar]
- Roberts, L. Understanding the Mel Spectrogram. 2021. Available online: https://medium.com/analytics-vidhya/understanding-the-mel-spectrogram-fca2afa2ce53 (accessed on 1 October 2025).
- Mahanta, S.; Khilji, A.; Pakray, D.P. Deep Neural Network for Musical Instrument Recognition Using MFCCs. Comput. Y Sist. 2021, 25, 351–360. [Google Scholar] [CrossRef]


| Class | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| Accordion | 0.97 | 0.97 | 0.97 | 358 |
| Acoustic Guitar | 0.99 | 0.97 | 0.98 | 366 |
| Banjo | 0.99 | 0.98 | 0.99 | 300 |
| Bass Guitar | 0.99 | 1.00 | 1.00 | 362 |
| Clarinet | 0.98 | 0.95 | 0.97 | 64 |
| Cymbals | 0.58 | 0.90 | 0.71 | 20 |
| Dobro | 1.00 | 0.98 | 0.99 | 48 |
| Drum set | 1.00 | 1.00 | 1.00 | 365 |
| Electro Guitar | 0.94 | 0.96 | 0.95 | 132 |
| Floor Tom | 0.90 | 0.93 | 0.91 | 40 |
| Harmonica | 0.93 | 1.00 | 0.96 | 13 |
| Harmonium | 1.00 | 0.99 | 1.00 | 132 |
| Hi Hats | 0.93 | 0.89 | 0.91 | 44 |
| Horn | 1.00 | 1.00 | 1.00 | 126 |
| Keyboard | 1.00 | 1.00 | 1.00 | 204 |
| Mandolin | 0.96 | 0.97 | 0.97 | 246 |
| Organ | 0.97 | 0.99 | 0.98 | 144 |
| Piano | 1.00 | 0.97 | 0.98 | 58 |
| Saxophone | 0.83 | 0.96 | 0.89 | 45 |
| Shakers | 1.00 | 1.00 | 1.00 | 136 |
| Tambourine | 0.98 | 0.96 | 0.97 | 56 |
| Trombone | 0.97 | 0.94 | 0.95 | 297 |
| Trumpet | 0.92 | 0.92 | 0.92 | 50 |
| Ukulele | 1.00 | 0.94 | 0.97 | 79 |
| Violin | 0.97 | 0.97 | 0.97 | 63 |
| Cowbell | 1.00 | 1.00 | 1.00 | 62 |
| Flute | 1.00 | 1.00 | 1.00 | 372 |
| Vibraphone | 0.88 | 1.00 | 0.93 | 50 |
| Accuracy | 0.98 | 4232 | ||
| Macro avg | 0.95 | 0.97 | 0.96 | 4232 |
| Weighted avg | 0.98 | 0.98 | 0.98 | 4232 |
| Class | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| Accordion | 0.98 | 0.98 | 0.98 | 358 |
| Acoustic Guitar | 0.99 | 0.97 | 0.98 | 366 |
| Banjo | 0.98 | 0.98 | 0.98 | 300 |
| Bass Guitar | 1.00 | 1.00 | 1.00 | 362 |
| Clarinet | 0.94 | 0.97 | 0.95 | 64 |
| Cymbals | 0.75 | 0.90 | 0.82 | 20 |
| Dobro | 1.00 | 0.98 | 0.99 | 48 |
| Drum set | 1.00 | 1.00 | 1.00 | 365 |
| Electro Guitar | 1.00 | 0.94 | 0.97 | 132 |
| Floor Tom | 0.73 | 1.00 | 0.84 | 40 |
| Harmonica | 1.00 | 1.00 | 1.00 | 13 |
| Harmonium | 1.00 | 0.99 | 1.00 | 132 |
| Hi Hats | 0.85 | 0.91 | 0.88 | 44 |
| Horn | 1.00 | 1.00 | 1.00 | 126 |
| Keyboard | 1.00 | 1.00 | 1.00 | 204 |
| Mandolin | 0.97 | 0.98 | 0.98 | 246 |
| Organ | 1.00 | 0.99 | 1.00 | 144 |
| Piano | 0.92 | 0.97 | 0.94 | 58 |
| Saxophone | 1.00 | 0.96 | 0.98 | 45 |
| Shakers | 1.00 | 1.00 | 1.00 | 136 |
| Tambourine | 0.96 | 0.96 | 0.96 | 56 |
| Trombone | 0.98 | 0.97 | 0.97 | 297 |
| Trumpet | 1.00 | 0.92 | 0.96 | 50 |
| Ukulele | 0.99 | 0.99 | 0.99 | 79 |
| Violin | 0.98 | 0.92 | 0.95 | 63 |
| Cowbell | 1.00 | 1.00 | 1.00 | 62 |
| Flute | 1.00 | 1.00 | 1.00 | 372 |
| Vibraphone | 0.94 | 0.90 | 0.92 | 50 |
| Accuracy | 0.98 | 4232 | ||
| Macro avg | 0.96 | 0.97 | 0.97 | 4232 |
| Weighted avg | 0.98 | 0.98 | 0.98 | 4232 |
| Class | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| Accordion | 0.81 | 0.65 | 0.72 | 358 |
| Acoustic Guitar | 0.91 | 0.76 | 0.83 | 366 |
| Banjo | 0.85 | 0.85 | 0.85 | 300 |
| Bass Guitar | 1.00 | 1.00 | 1.00 | 362 |
| Clarinet | 0.61 | 0.83 | 0.70 | 64 |
| Cymbals | 0.28 | 0.60 | 0.38 | 20 |
| Dobro | 0.70 | 0.96 | 0.81 | 48 |
| Drum set | 1.00 | 1.00 | 1.00 | 365 |
| Electro Guitar | 0.73 | 0.80 | 0.76 | 132 |
| Floor Tom | 0.56 | 0.88 | 0.68 | 40 |
| Harmonica | 0.87 | 1.00 | 0.93 | 13 |
| Harmonium | 1.00 | 0.99 | 1.00 | 132 |
| Hi Hats | 0.70 | 0.89 | 0.78 | 44 |
| Horn | 1.00 | 1.00 | 1.00 | 126 |
| Keyboard | 1.00 | 1.00 | 1.00 | 204 |
| Mandolin | 0.74 | 0.72 | 0.73 | 246 |
| Organ | 0.95 | 0.97 | 0.96 | 144 |
| Piano | 0.77 | 0.93 | 0.84 | 58 |
| Saxophone | 0.38 | 0.51 | 0.44 | 45 |
| Shakers | 1.00 | 1.00 | 0.99 | 136 |
| Tambourine | 0.90 | 0.93 | 0.91 | 56 |
| Trombone | 0.93 | 0.78 | 0.85 | 297 |
| Trumpet | 0.49 | 0.70 | 0.57 | 50 |
| Ukulele | 0.72 | 0.82 | 0.77 | 79 |
| Violin | 0.93 | 0.79 | 0.85 | 63 |
| Cowbell | 1.00 | 1.00 | 1.00 | 62 |
| Flute | 1.00 | 1.00 | 1.00 | 372 |
| Vibraphone | 0.49 | 0.72 | 0.59 | 50 |
| Accuracy | 0.87 | 4232 | ||
| Macro avg | 0.80 | 0.86 | 0.82 | 4232 |
| Weighted avg | 0.89 | 0.87 | 0.87 | 4232 |
| Class | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| Accordion | 0.95 | 1.00 | 0.98 | 358 |
| Acoustic Guitar | 0.98 | 1.00 | 0.99 | 366 |
| Banjo | 0.93 | 0.99 | 0.96 | 300 |
| Bass Guitar | 1.00 | 1.00 | 1.00 | 362 |
| Clarinet | 0.98 | 0.94 | 0.96 | 64 |
| Cymbals | 0.94 | 0.85 | 0.89 | 20 |
| Dobro | 0.98 | 1.00 | 0.99 | 48 |
| Drum set | 1.00 | 1.00 | 1.00 | 365 |
| Electro Guitar | 0.98 | 0.95 | 0.97 | 132 |
| Floor Tom | 0.80 | 0.97 | 0.88 | 40 |
| Harmonica | 0.87 | 1.00 | 0.93 | 13 |
| Harmonium | 1.00 | 0.99 | 1.00 | 132 |
| Hi Hats | 0.84 | 0.95 | 0.89 | 44 |
| Horn | 1.00 | 1.00 | 1.00 | 126 |
| Keyboard | 1.00 | 1.00 | 1.00 | 204 |
| Mandolin | 0.98 | 0.97 | 0.98 | 246 |
| Organ | 0.96 | 0.99 | 0.97 | 144 |
| Piano | 0.96 | 0.93 | 0.95 | 58 |
| Saxophone | 0.78 | 0.47 | 0.58 | 45 |
| Shakers | 0.99 | 1.00 | 0.99 | 136 |
| Tambourine | 0.98 | 0.95 | 0.96 | 56 |
| Trombone | 0.94 | 0.92 | 0.93 | 297 |
| Trumpet | 0.84 | 0.64 | 0.73 | 50 |
| Ukulele | 0.91 | 0.95 | 0.93 | 79 |
| Violin | 0.93 | 0.84 | 0.88 | 63 |
| Cowbell | 1.00 | 1.00 | 1.00 | 62 |
| Flute | 1.00 | 1.00 | 1.00 | 372 |
| Vibraphone | 1.00 | 0.78 | 0.88 | 50 |
| Accuracy | 0.97 | 4232 | ||
| Macro avg | 0.95 | 0.93 | 0.94 | 4232 |
| Weighted avg | 0.97 | 0.97 | 0.97 | 4232 |
| Class | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| Accordion | 0.95 | 1.00 | 0.97 | 358 |
| Acoustic Guitar | 0.96 | 0.99 | 0.97 | 366 |
| Banjo | 0.95 | 0.98 | 0.96 | 300 |
| Bass Guitar | 1.00 | 1.00 | 1.00 | 362 |
| Clarinet | 0.94 | 0.94 | 0.94 | 64 |
| Cymbals | 1.00 | 0.70 | 0.82 | 20 |
| Dobro | 1.00 | 0.94 | 0.97 | 48 |
| Drum set | 1.00 | 1.00 | 1.00 | 365 |
| Electro Guitar | 0.99 | 0.93 | 0.96 | 132 |
| Floor Tom | 0.91 | 1.00 | 0.95 | 40 |
| Harmonica | 1.00 | 0.92 | 0.96 | 13 |
| Harmonium | 1.00 | 0.99 | 1.00 | 132 |
| Hi Hats | 0.84 | 0.93 | 0.88 | 44 |
| Horn | 1.00 | 1.00 | 1.00 | 126 |
| Keyboard | 1.00 | 1.00 | 1.00 | 204 |
| Mandolin | 0.96 | 0.96 | 0.96 | 246 |
| Organ | 0.96 | 0.99 | 0.97 | 144 |
| Piano | 0.96 | 0.93 | 0.95 | 58 |
| Saxophone | 1.00 | 0.60 | 0.75 | 45 |
| Shakers | 1.00 | 1.00 | 1.00 | 136 |
| Tambourine | 0.96 | 0.93 | 0.95 | 56 |
| Trombone | 0.94 | 0.96 | 0.95 | 297 |
| Trumpet | 0.94 | 0.62 | 0.75 | 50 |
| Ukulele | 0.91 | 0.91 | 0.91 | 79 |
| Violin | 0.91 | 0.94 | 0.92 | 63 |
| Cowbell | 1.00 | 1.00 | 1.00 | 62 |
| Flute | 1.00 | 1.00 | 1.00 | 372 |
| Vibraphone | 0.95 | 0.84 | 0.89 | 50 |
| Accuracy | 0.97 | 4232 | ||
| Macro avg | 0.97 | 0.93 | 0.94 | 4232 |
| Weighted avg | 0.97 | 0.97 | 0.97 | 4232 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senatori, T.; Nardone, D.; Lo Giudice, M.; Salvini, A. Explainable Instrument Classification: From MFCC Mean-Vector Models to CNNs on MFCC and Mel-Spectrograms with t-SNE and Grad-CAM Insights. Information 2025, 16, 864. https://doi.org/10.3390/info16100864
Senatori T, Nardone D, Lo Giudice M, Salvini A. Explainable Instrument Classification: From MFCC Mean-Vector Models to CNNs on MFCC and Mel-Spectrograms with t-SNE and Grad-CAM Insights. Information. 2025; 16(10):864. https://doi.org/10.3390/info16100864
Chicago/Turabian StyleSenatori, Tommaso, Daniela Nardone, Michele Lo Giudice, and Alessandro Salvini. 2025. "Explainable Instrument Classification: From MFCC Mean-Vector Models to CNNs on MFCC and Mel-Spectrograms with t-SNE and Grad-CAM Insights" Information 16, no. 10: 864. https://doi.org/10.3390/info16100864
APA StyleSenatori, T., Nardone, D., Lo Giudice, M., & Salvini, A. (2025). Explainable Instrument Classification: From MFCC Mean-Vector Models to CNNs on MFCC and Mel-Spectrograms with t-SNE and Grad-CAM Insights. Information, 16(10), 864. https://doi.org/10.3390/info16100864







