Addressing Non-IID with Data Quantity Skew in Federated Learning
Abstract
1. Introduction
- We propose an approach introducing MAP-based dynamic adjustment for regularization coefficient in the objective function and orthogonal gradient modulation to adapt to varying degrees of Non-IID distributions. The approach is compatible with existing federated learning frameworks and can be easily integrated.
- We propose a method to evaluate the degree of Non-IID in local datasets and mitigate model drift by adjusting the coefficient of the regularization term in the objective function according to the data heterogeneity.
- We generated three datasets with different degrees of Non-IID: IID, mild Non-IID, and severe Non-IID. Extensive experimental results demonstrate that our approach achieves significant accuracy improvements in both mildly and severely Non-IID scenarios while maintaining a strong performance lower bound.
2. Related Works
2.1. Regularization-Based Approaches
2.2. Biological-Inspired Approaches
3. System Model
3.1. Federated Learning
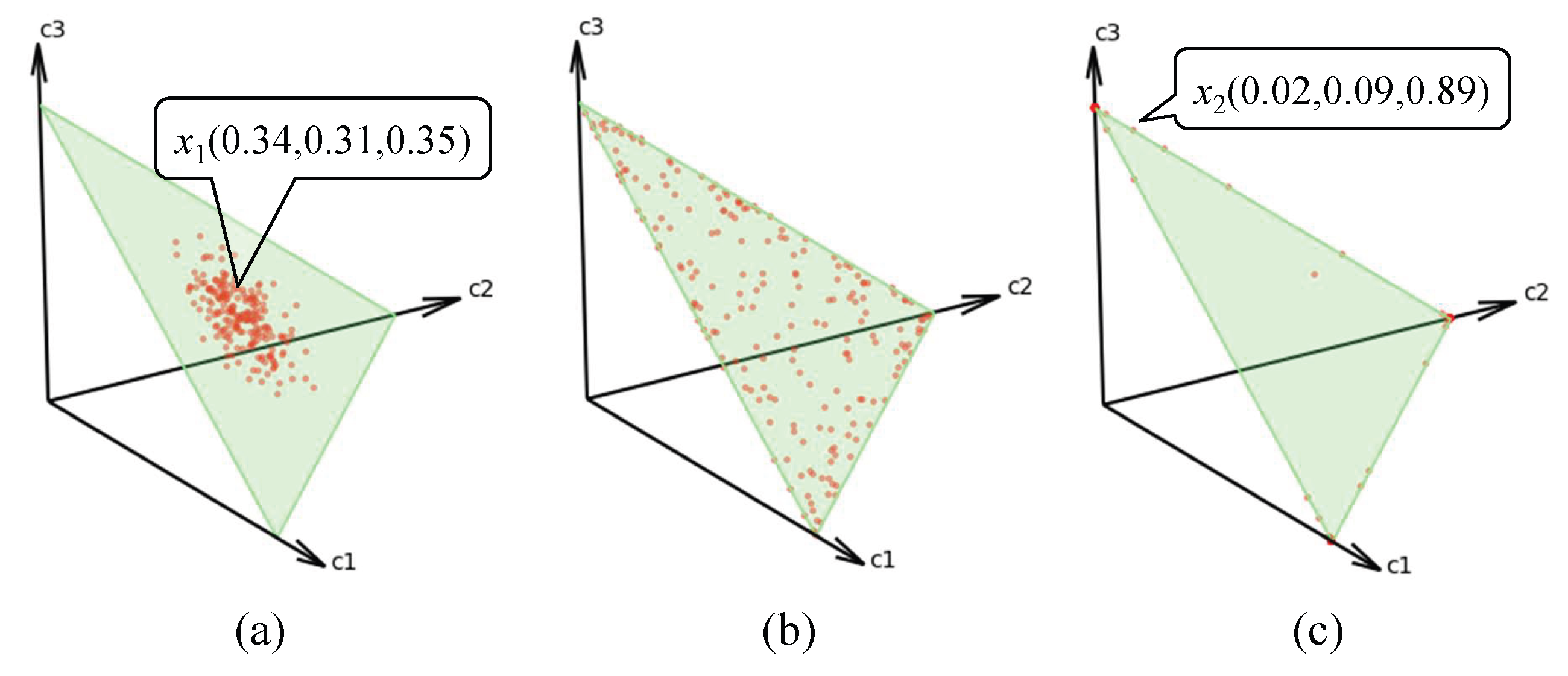
3.2. Evaluation for the Degree of Non-IID of Local Dataset
3.3. Relationship Between and
3.4. Controlling Gradient Coefficient
| Algorithm 1 The pseudocode of the proposal |
|
3.5. Convergence Analysis
- L-smoothness: .
- Strong convex: .
- Bounded gradient:
4. Experiments
4.1. Metrics
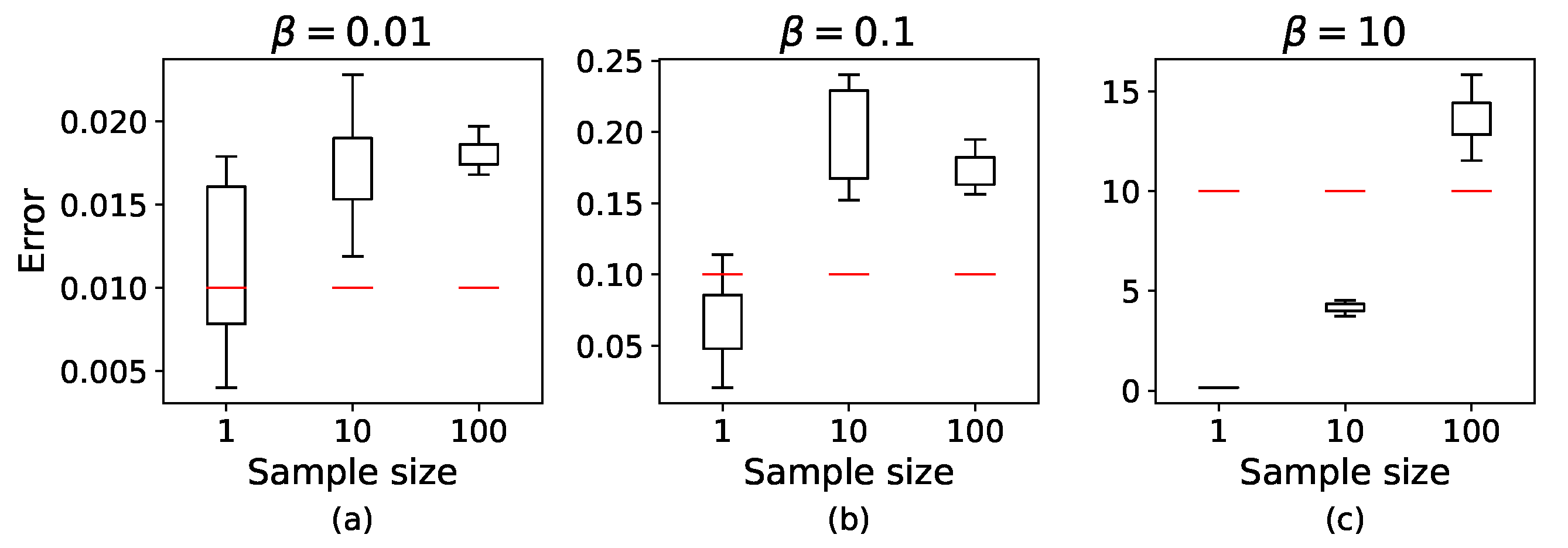
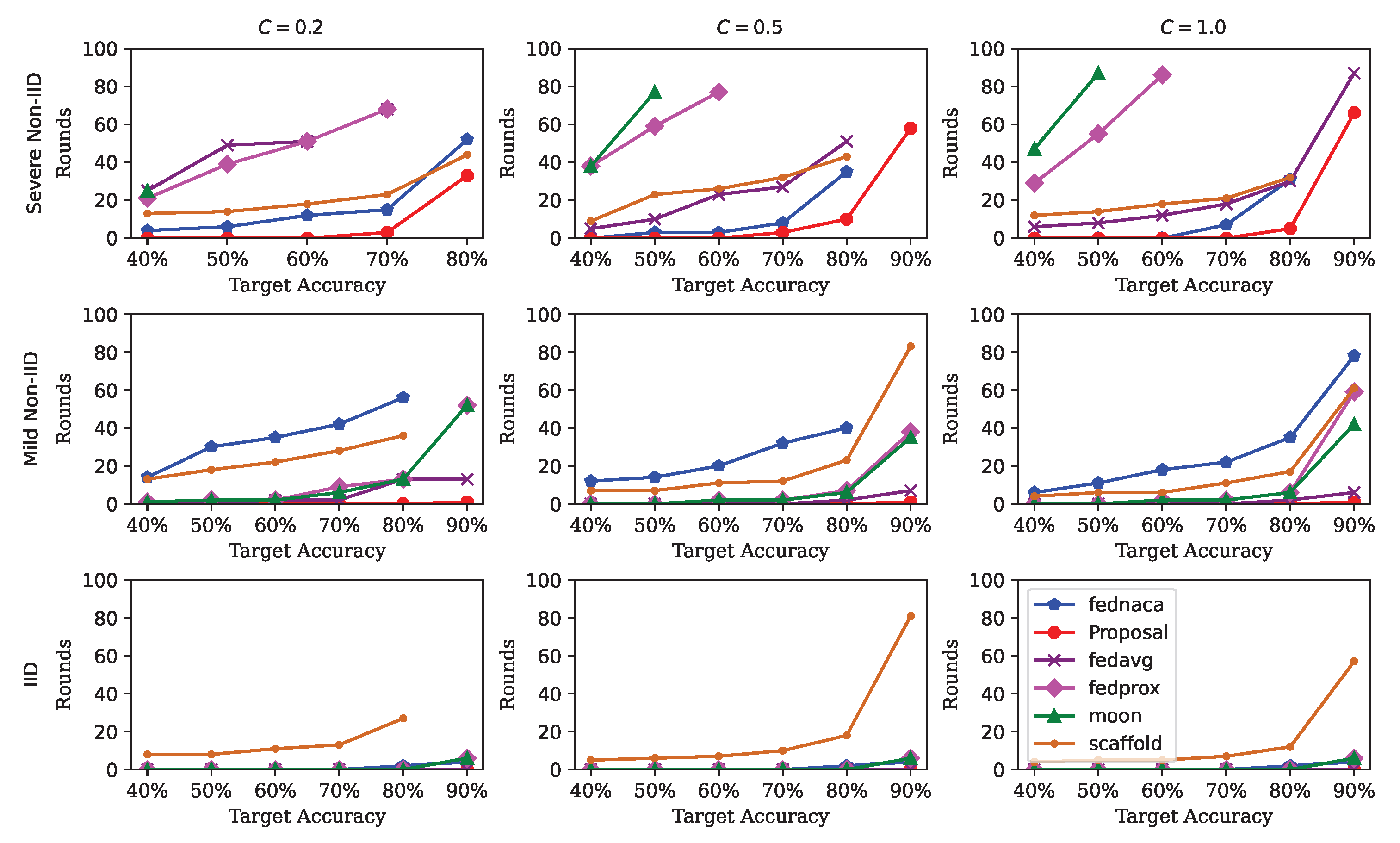
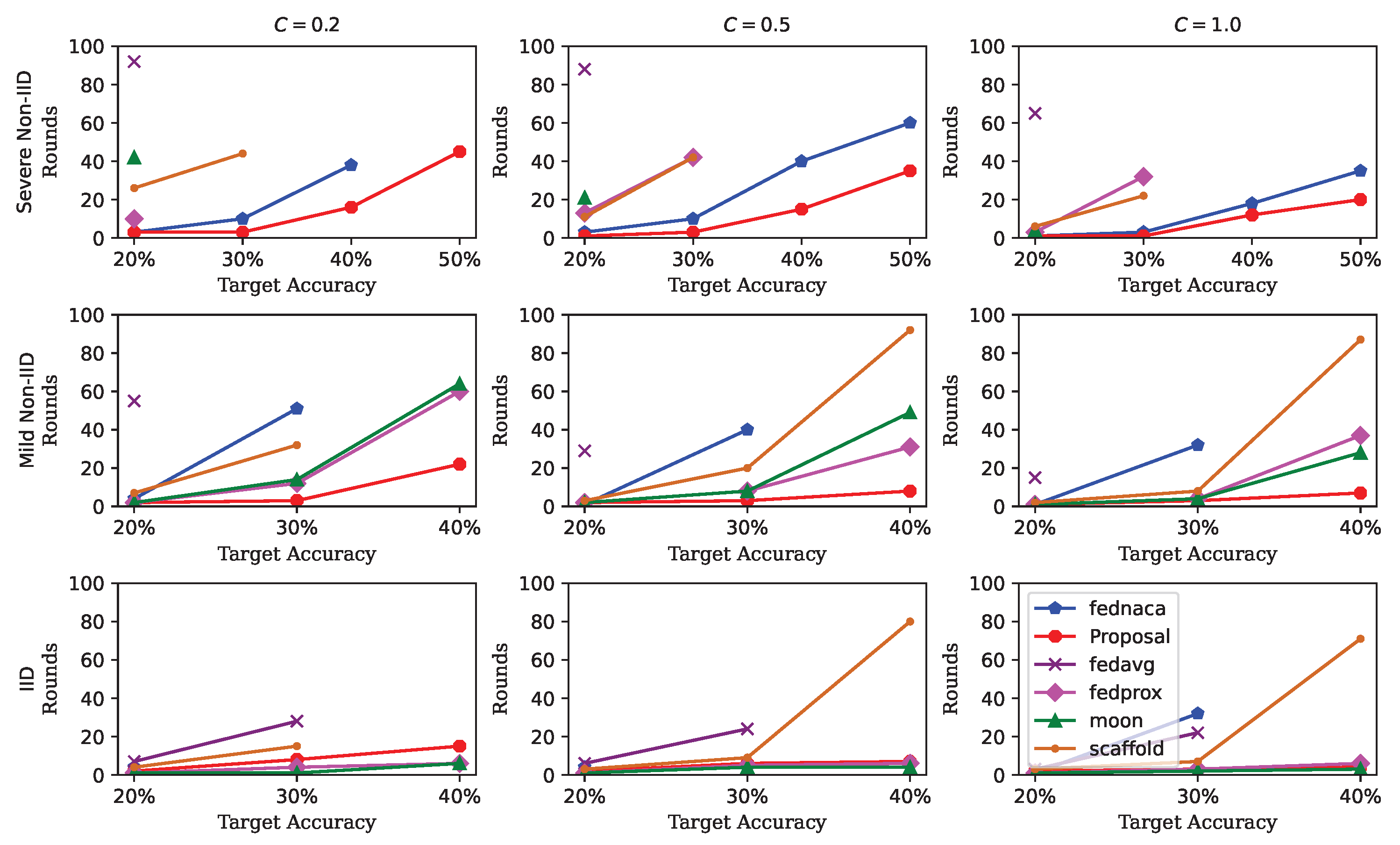
4.2. Results on Non-IID Degree and Client Sampling Ratio C
4.3. Results on Top-1 Accuracy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Generation of Δ (i)

- i
- , where represents the Frobenius inner product, is the Euclidean norm of a matrix. Requiring the Frobenius inner product to be zero implies that corresponding to different classes do not overlap, which can be interpreted as the features of different classes being distinguishable.
- ii
- , for any element of . This condition indicates that the magnitude of a model weight update is less than or equal to the corresponding gradient. When , the corresponding weight will be frozen, implying that this weight does not contribute to the given class. When , the corresponding weight will be updated according to the gradient without any reduction.
- iii
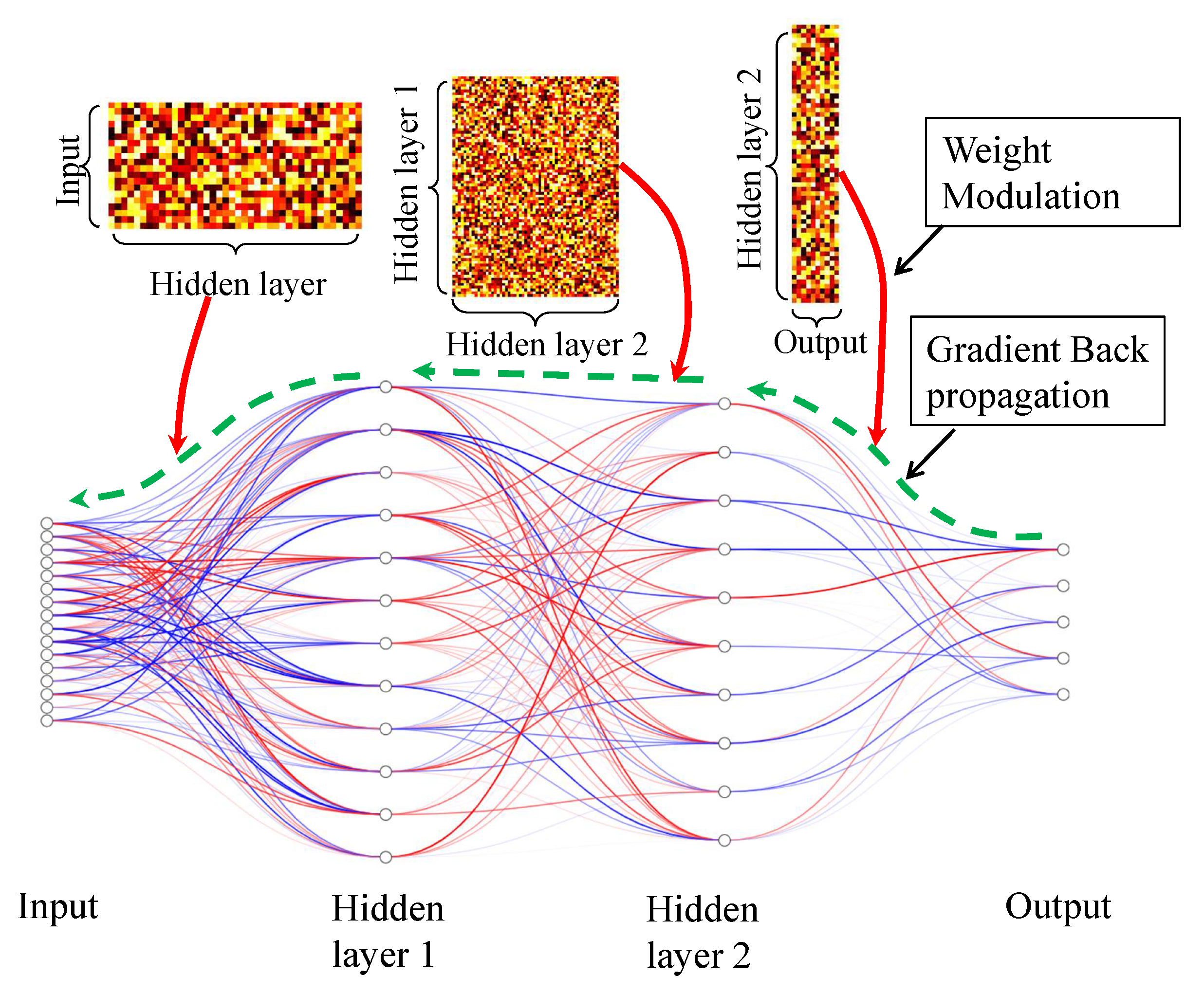
- In , at least, a path connects from input to output, illustrated by the simplified two-layer fully connected network in Figure A1. Similar to the model, also can be decomposed into multiple layers of parameters, represented as multiple tensors, represent the parameters of the first layer, second layer,..., respectively. The path from the input to the output is expressed as , in which there exists at least one element of the multiplication of two tensors , as shown the red line in Figure A1. In our experiments, we set the threshold for the element to ensure the parameters of the model are activated.
| Algorithm A1 the implementation of |
|
| Algorithm A2 Check the transitivity of the tensor |
|
References
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A.y. Communication-Efficient Learning of Deep Networks from Decentralized Data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated machine learning: Concept and applications. Acm Trans. Intell. Syst. Technol. (TIST) 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, M.; Lai, L.; Suda, N.; Civin, D.; Chandra, V. Federated Learning with Non-IID Data. arXiv 2018. [Google Scholar] [CrossRef]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated Optimization in Heterogeneous Networks. In Proceedings of the Machine Learning and Systems (MLSys 2020), Austin, TX, USA, 2–4 March 2020; Volume 2, pp. 429–450. [Google Scholar]
- Li, X.; Jiang, M.; Zhang, X.; Kamp, M.; Dou, Q. FedBN: Federated Learning on Non-IID Features via Local Batch Normalization. arXiv 2021. [Google Scholar] [CrossRef]
- Karimireddy, S.P.; Kale, S.; Mohri, M.; Reddi, S.; Stich, S.; Suresh, A.T. SCAFFOLD: Stochastic Controlled Averaging for Federated Learning. In Proceedings of the 37th International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 5132–5143. [Google Scholar]
- Li, Q.; He, B.; Song, D. Model-Contrastive Federated Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 10713–10722. [Google Scholar]
- Dohare, S.; Hernandez-Garcia, J.F.; Lan, Q.; Rahman, P.; Mahmood, A.R.; Sutton, R.S. Loss of plasticity in deep continual learning. Nature 2024, 632, 768–774. [Google Scholar] [CrossRef]
- Zhang, T.; Cheng, X.; Jia, S.; Li, C.T.; Poo, M.-M.; Xu, B. A brain-inspired algorithm that mitigates catastrophic forgetting of artificial and spiking neural networks with low computational cost. Sci. Adv. 2023, 9. Available online: https://www.science.org/doi/10.1126/sciadv.adi2947 (accessed on 10 August 2025). [CrossRef]
- Peng, J.; Tang, B.; Jiang, H.; Li, Z.; Lei, Y.; Lin, T.; Li, H. Overcoming long-term catastrophic forgetting through adversarial neural pruning and synaptic consolidation. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 4243–4256. [Google Scholar] [CrossRef] [PubMed]
- Abbott, L.F.; Nelson, S.B. Synaptic plasticity: Taming the beast. Nat. Neurosci. 2000, 3, 1178–1183. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, J.; Pascanu, R.; Rabinowitz, N.; Veness, J.; Desjardins, G.; Rusu, A.A.; Milan, K.; Quan, J.; Ramalho, T.; Grabska-Barwinska, A.; et al. Overcoming catastrophic forgetting in neural networks. Proc. Natl. Acad. Sci. USA 2017, 114, 3521–3526. [Google Scholar] [CrossRef] [PubMed]
- Shoham, N.; Avidor, T.; Keren, A.; Israel, N.; Benditkis, D.; Mor-Yosef, L.; Zeitak, I. Overcoming Forgetting in Federated Learning on Non-IID Data. arXiv 2019. [Google Scholar] [CrossRef]
- Kopparapu, K.; Lin, E. FedFMC: Sequential Efficient Federated Learning on Non-iid Data. arXiv 2020. [Google Scholar] [CrossRef]
- Dan, Y.; Poo, M.-M. Spike timing-dependent plasticity of neural circuits. Neuron 2004, 44, 23–30. [Google Scholar] [CrossRef]
- Kheradpisheh, S.R.; Ganjtabesh, M.; Thorpe, S.J.; Masquelier, T. STDP-based spiking deep convolutional neural networks for object recognition. Neural Netw. 2018, 99, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Acar, D.A.E.; Zhao, Y.; Navarro, R.M.; Mattina, M.; Whatmough, P.N.; Saligrama, V. Federated Learning Based on Dynamic Regularization. arXiv 2021. [Google Scholar] [CrossRef]
- Li, Z.; Sun, Y.; Shao, J.; Mao, Y.; Wang, J.H.; Zhang, J. Feature matching data synthesis for non-iid federated learning. IEEE Trans. Mob. Comput. 2024, 23, 9352–9367. [Google Scholar] [CrossRef]
- Luo, M.; Chen, F.; Hu, D.; Zhang, Y.; Liang, J.; Feng, J. No fear of heterogeneity: Classifier calibration for federated learning with non-iid data. In Proceedings of the Annual Conference on Neural Information Processing Systems, virtual, 6–14 December 2021; Volume 34, pp. 5972–5984. [Google Scholar]
- Wang, J.; Liu, Q.; Liang, H.; Joshi, G.; Poor, H.V. Tackling the Objective Inconsistency Problem in Heterogeneous Federated Optimization. In Proceedings of the Annual Conference on Neural Information Processing Systems, virutal, 6–12 December 2020; Volume 33, pp. 7611–7623. [Google Scholar]
- Reddi, S.J.; Charles, Z.; Zaheer, M.; Garrett, Z.; Rush, K.; Konečný, J.; Kumar, S.; McMahan, H.B. Adaptive Federated Optimization. In Proceedings of the International Conference on Learning Representations, ICLR, virutal, 3–7 May 2021; Available online: https://openreview.net/forum?id=LkFG3lB13U5 (accessed on 10 August 2025).
- Dinh, C.T.; Tran, N.; Nguyen, J. Personalized Federated Learning with Moreau Envelopes. In Proceedings of the Annual Conference on Neural Information Processing Systems, virutal, 6–12 December 2020; Volume 33, pp. 21394–21405. [Google Scholar]
- French, R.M. Catastrophic forgetting in connectionist networks. Trends Cogn. Sci. 1999, 3, 128–135. [Google Scholar] [CrossRef]
- Kudithipudi, D.; Aguilar-Simon, M.; Babb, J.; Bazhenov, M.; Blackiston, D.; Bongard, J.; Brna A., P.; Raja, S.C.; Cheney, N.; Clune, J.; et al. Biological underpinnings for lifelong learning machines. Nat. Mach. Intell. 2022, 4, 196–210. [Google Scholar] [CrossRef]
- Minhas, M.F.; Vidya Wicaksana Putra, R.; Awwad, F.; Hasan, O.; Shafique, M. Continual learning with neuromorphic computing: Theories, methods, and applications. arXiv 2024. [Google Scholar] [CrossRef]
- Hebb, D.O. The Organization of Behavior: A Neuropsychological Theory; Psychology Press: East Sussex, UK, 2005. [Google Scholar]
- Tavanaei, A.; Ghodrati, M.; Kheradpisheh, S.R.; Masquelier, T.; Maida, A. Deep learning in spiking neural networks. Neural Netw. 2019, 111, 47–63. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Santoro, A.; Marris, L.; Akerman, C.J.; Hinton, G. Backpropagation and the brain. Nat. Rev. Neurosci. 2020, 21, 335–346. [Google Scholar] [CrossRef] [PubMed]
- Zenke, F.; Poole, B.; Ganguli, S. Continual learning through synaptic intelligence. In Proceedings of the 34th International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 3987–3995. [Google Scholar]
- Wang, L.; Zhang, X.; Li, Q.; Zhang, M.; Su, H.; Zhu, J.; Zhong, Y. Incorporating neuro-inspired adaptability for continual learning in artificial intelligence. Nat. Mach. Intell. 2023, 5, 1356–1368. [Google Scholar] [CrossRef]
- Mei, J.; Meshkinnejad, R.; Mohsenzadeh, Y. Effects of neuromodulation-inspired mechanisms on the performance of deep neural networks in a spatial learning task. Iscience 2023, 26. [Google Scholar] [CrossRef]
- Ellefsen, K.O.; Mouret, J.-B.; Clune, J. Neural modularity helps organisms evolve to learn new skills without forgetting old skills. Plos Comput. Biol. 2015, 11. [Google Scholar] [CrossRef]
- Beaulieu, S.L.E.; Frati, L.; Miconi, T.; Lehman, J.; Stanley, K.O.; Clune, J.; Cheney, N. Learning to Continually Learn. In Proceedings of the European Conference on Artificial Intelligence, ECAI, Santiago de Compostela, Spain, 29 August–8 September 2020; Volume 325, pp. 992–1001. [Google Scholar]
- Velez, R.; Clune, J. Diffusion-based neuromodulation can eliminate catastrophic forgetting in simple neural networks. PloS ONE 2017, 12. [Google Scholar] [CrossRef] [PubMed]
- Miconi, T.; Rawal, A.; Clune, J.; Stanley, K.O. Backpropamine: Training self-modifying neural networks with differentiable neuromodulated plasticity. arXiv 2020. [Google Scholar] [CrossRef]
- Madireddy, S.; Yanguas-Gil, A.; Balaprakash, P. Neuromodulated Neural Architectures with Local Error Signals for Memory-Constrained Online Continual Learning. arXiv 2021. [Google Scholar] [CrossRef]
- Daram, A.; Yanguas-Gil, A.; Kudithipudi, D. Exploring neuromodulation for dynamic learning. Front. Neurosci. 2020, 14. Available online: https://www.frontiersin.org/journals/neuroscience/articles/10.3389/fnins.2020.00928/full (accessed on 10 August 2025). [CrossRef] [PubMed]
- Nishio, T.; Yonetani, R. Client selection for federated learning with heterogeneous resources in mobile edge. In Proceedings of the IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–7. [Google Scholar]
- Li, X.; Huang, K.X.; Yang, W.H.; Wang, S.S.; Zhang, Z.H. On the Convergence of FedAvg on Non-IID Data. In Proceedings of the International Conference on Learning Representations, virtual, 26 April–1 May 2020; Available online: https://openreview.net/forum?id=HJxNAnVtDS (accessed on 10 August 2025).
- Stich, S.U. Local SGD Converges Fast and Communicates Little. arXiv 2018. [Google Scholar] [CrossRef]
- Deng, L. The mnist database of handwritten digit images for machine learning research. IEEE Signal Process. Mag. 2012, 29, 141–142. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. 2009. Available online: http://www.cs.utoronto.ca/~kriz/learning-features-2009-TR.pdf (accessed on 10 August 2025).
- Hsu, T.-M.H.; Qi, H.; Brown, M. Measuring the effects of non-identical data distribution for federated visual classification. arXiv 2019. [Google Scholar] [CrossRef]
- Li, A.; Sun, J.; Zeng, X.; Zhang, M.; Li, H.; Chen, Y. Fedmask: Joint computation and communication-efficient personalized federated learning via heterogeneous masking. In Proceedings of the 19th ACM Conference on Embedded Networked Sensor Systems, Coimbra, Portugal, 15–17 November 2021; pp. 42–55. [Google Scholar]
- Zhou, H.; Lan, T.; Venkataramani, G.P.; Ding, W. Every parameter matters: Ensuring the convergence of federated learning with dynamic heterogeneous models reduction. In Proceedings of the Annual Conference on Neural Information Processing Systems, New Orleans, LO, USA, 10–16 December 2023; Volume 36, pp. 25991–26002. [Google Scholar]
- Zhou, H.; Lan, J.; Liu, R.; Yosinski, J. Deconstructing lottery tickets: Zeros, signs, and the supermask. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 3592–3602. [Google Scholar]




| MNIST | CIFAR10 | ||||||
|---|---|---|---|---|---|---|---|
| C = 0.2 | C = 0.5 | C = 1 | C = 0.2 | C = 0.5 | C = 1 | ||
| Severe Non-IID | FedNACA | 84.09 ± 0.68 | 84.69 ± 0.41 | 84.48 ± 0.22 | 42.88 ± 0.83 | 57.76 ± 0.63 | 58.16 ± 0.45 |
| Proposal | 84.65 ± 0.78 | 91.99 ± 0.38 | 91.54 ± 0.2 | 57.42 ± 0.68 | 58.22 ± 0.61 | 59.21 ± 0.32 | |
| FedAvg | 71.02 ± 0.76 | 89.96 ± 0.69 | 90.86 ± 0.38 | 22.38 ± 1.21 | 25.33 ± 0.98 | 26.37 ± 0.55 | |
| FedProx | 78.17 ± 1.02 | 64.53 ± 0.88 | 62.88 ± 0.65 | 25.96 ± 1.12 | 30.35 ± 0.94 | 30.61 ± 0.89 | |
| MOON | 45.59 ± 1.41 | 53.17 ± 0.9 | 53.69 ± 0.89 | 23.89 ± 1.66 | 27.54 ± 1.32 | 29.44 ± 1.2 | |
| SCAFFOLD | 88.84 ± 0.84 | 88.69 ± 0.7 | 89.62 ± 0.66 | 31.35 ± 1.31 | 33.14 ± 0.97 | 36.39 ± 0.71 | |
| Mild Non-IID | FedNACA | 82.35 ± 0.51 | 84.65 ± 0.31 | 85.66 ± 0.15 | 32.72 ± 0.68 | 33.85 ± 0.45 | 34.48 ± 0.33 |
| Proposal | 96.86 ± 0.44 | 96.46 ± 0.3 | 96.34 ± 0.16 | 44.23 ± 0.53 | 47.28 ± 0.4 | 48.2 ± 0.28 | |
| FedAvg | 96.89 ± 0.52 | 97.21 ± 0.29 | 96.28 ± 0.15 | 23.21 ± 0.66 | 24.01 ± 0.48 | 26.3 ± 0.25 | |
| FedProx | 93.86 ± 0.52 | 93.96 ± 0.3 | 92.61 ± 0.16 | 43.54 ± 0.7 | 44.73 ± 0.42 | 43.9 ± 0.29 | |
| MOON | 94.03 ± 0.61 | 94.58 ± 0.34 | 92.44 ± 0.19 | 41.27 ± 0.73 | 43.16 ± 0.51 | 43.16 ± 0.36 | |
| SCAFFOLD | 88.46 ± 0.48 | 90.52 ± 0.31 | 91.52 ± 0.16 | 36.3 ± 0.68 | 40.11 ± 0.46 | 41.53 ± 0.31 | |
| IID | FedNACA | 92.72 ± 0.22 | 92.82 ± 0.12 | 92.75 ± 0.09 | 28.47 ± 0.56 | 28.61 ± 0.29 | 34.48 ± 0.19 |
| Proposal | 97.51 ± 0.2 | 97.14 ± 0.12 | 96.97 ± 0.11 | 41.37 ± 0.57 | 42.88 ± 0.28 | 43.57 ± 0.21 | |
| FedAvg | 97.57 ± 0.2 | 97.76 ± 0.11 | 97.7 ± 0.1 | 33.01 ± 0.58 | 34.76 ± 0.3 | 35.03 ± 0.22 | |
| FedProx | 96.34 ± 0.19 | 96.39 ± 0.11 | 96.42 ± 0.11 | 48.77 ± 0.52 | 49.43 ± 0.26 | 49.59 ± 0.22 | |
| MOON | 96.46 ± 0.25 | 95.4 ± 0.14 | 94.28 ± 0.13 | 46.6 ± 0.61 | 47.52 ± 0.33 | 46.81 ± 0.24 | |
| SCAFFOLD | 89.12 ± 0.21 | 90.73 ± 0.12 | 92.01 ± 0.11 | 38.87 ± 0.57 | 40.14 ± 0.31 | 41.77 ± 0.22 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cha, N.; Chang, L. Addressing Non-IID with Data Quantity Skew in Federated Learning. Information 2025, 16, 861. https://doi.org/10.3390/info16100861
Cha N, Chang L. Addressing Non-IID with Data Quantity Skew in Federated Learning. Information. 2025; 16(10):861. https://doi.org/10.3390/info16100861
Chicago/Turabian StyleCha, Narisu, and Long Chang. 2025. "Addressing Non-IID with Data Quantity Skew in Federated Learning" Information 16, no. 10: 861. https://doi.org/10.3390/info16100861
APA StyleCha, N., & Chang, L. (2025). Addressing Non-IID with Data Quantity Skew in Federated Learning. Information, 16(10), 861. https://doi.org/10.3390/info16100861






