Mathematical Analysis of Page Fault Minimization for Virtual Memory Systems Using Working Set Strategy
Abstract
1. Introduction
2. Methods
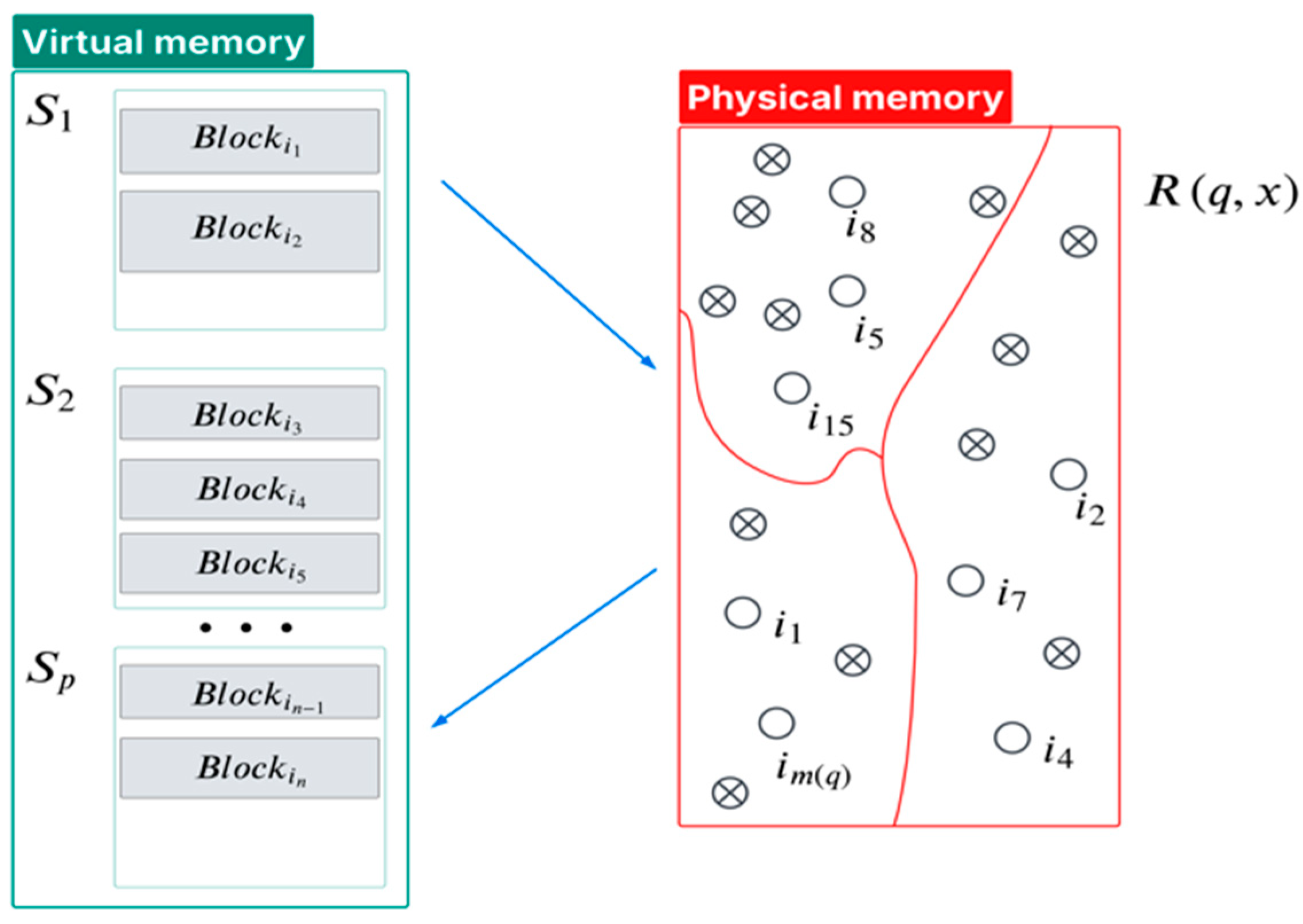
2.1. Geometric Interpretation of the Computational Process
2.2. Functionals and Constraints for
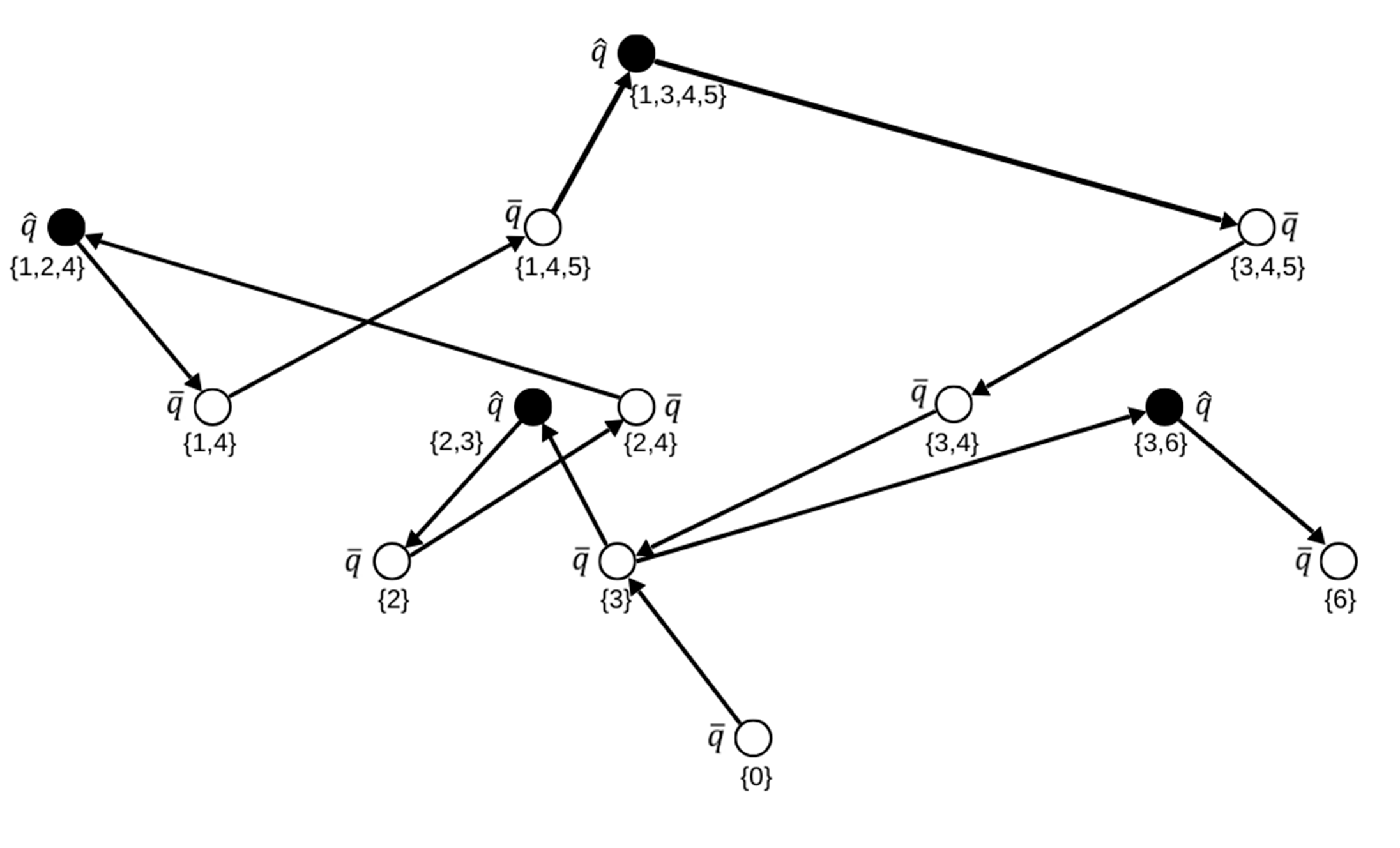
2.3. Reduction in a Number of Inequalities of the Control State in Working Set
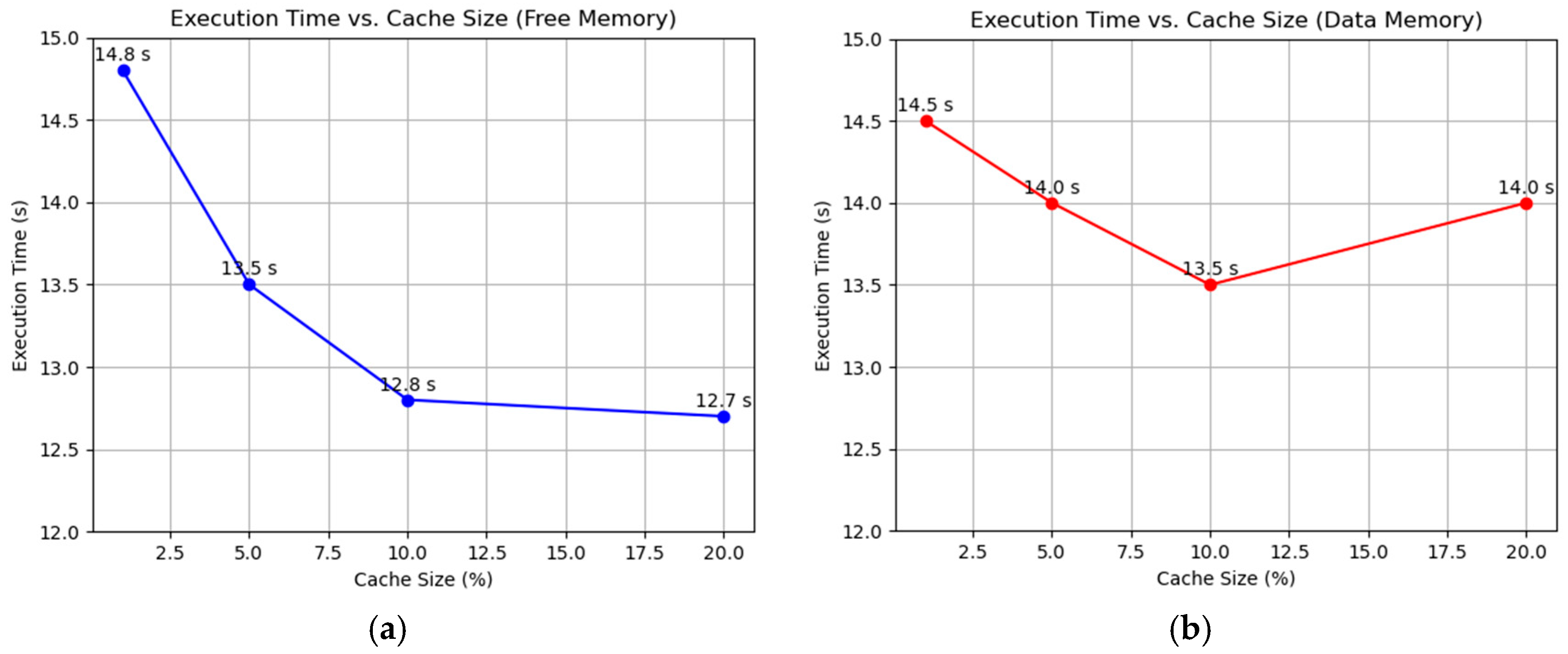
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Allen, T.; Cooper, B.; Ge, R. Fine-Grain Quantitative Analysis of Demand Paging in Unified Virtual Memory. ACM Trans. Archit. Code Optim. 2024, 21, 1–24. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Wu, C.-F.; Chang, Y.-H.; Kuo, T.-W. Exploring Synchronous Page Fault Handling. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2022, 41, 3791–3802. [Google Scholar] [CrossRef]
- Doron-Arad, I.; Naor, J. Non-Linear Paging. In Proceedings of the 51st International Colloquium on Automata, Languages, and Programming (ICALP 2024), Tallinn, Estonia, 8–12 July 2024; Volume 297, pp. 57:1–57:19. [Google Scholar] [CrossRef]
- Wood, C.; Fernandez, E.B.; Lang, T. Minimization of Demand Paging for the LRU Stack Model of Program Behavior. Inf. Process. Lett. 1983, 16, 99–104. [Google Scholar] [CrossRef]
- Dyusembaev, A.E. On one approach to the problem of segmenting programs. Dokl. Akad. Nauk. 1993, 329, 712–723. [Google Scholar]
- Borankulova, G.; Murzakhmetov, A.; Tungatarova, A.; Taszhurekova, Z. Adaptive Working Set Model for Memory Management and Epidemic Control: A Unified Approach. Computation 2025, 13, 190. [Google Scholar] [CrossRef]
- Ngetich, M.K.Y.; Otieno, C.; Kimwele, M.; Gitahi, S. Advancements in Code Restructuring: Enhancing System Quality through Object-Oriented Coding Practices. In Proceedings of the 2023 IEEE 27th International Conference on Intelligent Engineering Systems (INES), Nairobi, Kenya, 26–28 July 2023; IEEE: Nairobi, Kenya, 2023; pp. 000125–000130. [Google Scholar]
- Yegon Ngetich, M.K.; Otieno, D.C.; Kimwele, D.M. A Model for Code Restructuring, A Tool for Improving Systems Quality in Compliance with Object Oriented Coding Practice. IJCATR 2019, 8, 196–200. [Google Scholar] [CrossRef]
- Peachey, J.B.; Bunt, R.B.; Colbourn, C.J. Some Empirical Observations on Program Behavior with Applications to Program Restructuring. IIEEE Trans. Softw. Eng. 1985, SE-11, 188–193. [Google Scholar] [CrossRef]
- Roberts, D.B. Practical Analysis for Refactoring. Ph.D. Thesis, University of Illinois, Champaign, IL, USA, 1999. [Google Scholar]
- Cedrim, D.; Garcia, A.; Mongiovi, M.; Gheyi, R.; Sousa, L.; De Mello, R.; Fonseca, B.; Ribeiro, M.; Chávez, A. Understanding the Impact of Refactoring on Smells: A Longitudinal Study of 23 Software Projects. In Proceedings of the 2017 11th Joint Meeting on Foundations of Software Engineering, Paderborn, Germany, 4–8 September 2017; ACM: Paderborn, Germany, 2017; pp. 465–475. [Google Scholar]
- Agnihotri, M.; Chug, A. Severity Factor (SF): An Aid to Developers for Application of Refactoring Operations to Improve Software Quality. J. Softw. Evolu Process 2024, 36, e2590. [Google Scholar] [CrossRef]
- Agnihotri, M.; Chug, A. Understanding the Effect of Batch Refactoring on Software Quality. Int. J. Syst. Assur. Eng. Manag. 2024, 15, 2328–2336. [Google Scholar] [CrossRef]
- Coelho, F.; Massoni, T.; Alves, E.L.G. Refactoring-Aware Code Review: A Systematic Mapping Study. In Proceedings of the 2019 IEEE/ACM 3rd International Workshop on Refactoring (IWoR), Montreal, QC, Canada, 28 May 2019; pp. 63–66. [Google Scholar]
- Arasteh, B.; Ghanbarzadeh, R.; Gharehchopogh, F.S.; Hosseinalipour, A. Generating the Structural Graph-based Model from a Program Source-code Using Chaotic Forrest Optimization Algorithm. Expert. Syst. 2023, 40, e13228. [Google Scholar] [CrossRef]
- Arasteh, B.; Abdi, M.; Bouyer, A. Program Source Code Comprehension by Module Clustering Using Combination of Discretized Gray Wolf and Genetic Algorithms. Adv. Eng. Softw. 2022, 173, 103252. [Google Scholar] [CrossRef]
- Dyusembaev, A.E. Mathematical Models of Program Segmentation; Fizmatlit/Nauka: Moscow, Russia, 2001. [Google Scholar]
- Sadirmekova, Z.; Murzakhmetov, A.; Abduvalova, A.; Altynbekova, Z.; Makhatova, V.; Akhmetzhanova, S.; Tasbolatuly, N.; Serikbayeva, S. Approach to Automating the Construction and Completion of Ontologies in a Scientific Subject Field. Int. J. Electr. Comput. Eng. 2024, 14, 3064–3072. [Google Scholar] [CrossRef]
- Denning, P.J. The Working Set Model for Program Behavior. In Proceedings of the ACM symposium on Operating System Principles–SOSP ’67, Gatlinburg, TN, USA, 1–4 October 1967; ACM Press: New York, NY, USA, 1967; pp. 15.1–15.12. [Google Scholar]
- Park, Y.; Bahn, H. A Working-Set Sensitive Page Replacement Policy for PCM-Based Swap Systems. J. Semicond. Technol. Sci. 2017, 17, 7–14. [Google Scholar] [CrossRef]
- Sha, S.; Hu, J.-Y.; Luo, Y.-W.; Wang, X.-L.; Wang, Z. Huge Page Friendly Virtualized Memory Management. J. Comput. Sci. Technol. 2020, 35, 433–452. [Google Scholar] [CrossRef]
- Hu, J.; Bai, X.; Sha, S.; Luo, Y.; Wang, X.; Wang, Z. Working Set Size Estimation with Hugepages in Virtualization. In Proceedings of the 2018 IEEE International Conference on Parallel & Distributed Processing with Applications, Ubiquitous Computing & Communications, Big Data & Cloud Computing, Social Computing & Networking, Sustainable Computing & Communications (ISPA/IUCC/BDCloud/SocialCom/SustainCom), Melbourne, VIC, Australia, 11–13 December 2018; IEEE: Melbourne, VIC, Australia, 2018; pp. 501–508. [Google Scholar]
- Nitu, V.; Kocharyan, A.; Yaya, H.; Tchana, A.; Hagimont, D.; Astsatryan, H. Working Set Size Estimation Techniques in Virtualized Environments: One Size Does Not Fit All. In Proceedings of the Abstracts of the 2018 ACM International Conference on Measurement and Modeling of Computer Systems, Irvine, CA, USA, 18–22 June 2018; ACM: Irvine, CA, USA, 2018; pp. 62–63. [Google Scholar]
- Verbart, A.; Stolpe, M. A Working-Set Approach for Sizing Optimization of Frame-Structures Subjected to Time-Dependent Constraints. Struct. Multidisc Optim. 2018, 58, 1367–1382. [Google Scholar] [CrossRef]
- Dyusembaev, A.E. On the Correctness of Algebraic Closures of Recognition Algorithms of the “Tests” Type. USSR Comput. Math. Math. Phys. 1982, 22, 217–226. [Google Scholar] [CrossRef]
- Sadirmekova, Z.; Sambetbayeva, M.; Serikbayeva, S.; Borankulova, G.; Yerimbetova, A.; Murzakhmetov, A. Development of an Intelligent Information Resource Model Based on Modern Natural Language Processing Methods. Int. J. Electr. Comput. Eng. 2023, 13, 5314. [Google Scholar] [CrossRef]
- Pâris, J.-F.; Ferrari, D. An Analytical Study of Strategy-Oriented Restructuring Algorithms. Perform. Eval. 1984, 4, 117–132. [Google Scholar] [CrossRef][Green Version]
- Denning, P.J. Working Set Analytics. ACM Comput. Surv. 2021, 53, 1–36. [Google Scholar] [CrossRef]
- Dyusembaev, A.E. Correct models of program segmenting. J. Pattern Recognit. Image 1993, 3, 187–204. [Google Scholar]
- Mrena, M.; Kvassay, M. Generating Monotone Boolean Functions Using Hasse Diagram. In Proceedings of the 2023 IEEE 12th International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Dortmund, Germany, 7–9 September 2023; IEEE: Dortmund, Germany, 2023; pp. 793–797. [Google Scholar]



| Algorithm | Average Page Faults | Average Locality Factor |
|---|---|---|
| Working Set | 4352 | 0.72 |
| LRU | 4371 | 0.72 |
| FIFO | 4397 | 0.72 |
| Algorithm | Av. Page Fault Time (µs) | Page Fault Frequency (%) | Total Execution Time (s) |
|---|---|---|---|
| WS | 6 | 35 | 13 |
| LRU | 7 | 38 | 14.5 |
| FIFO | 7 | 38 | 14.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murzakhmetov, A.; Borankulova, G.; Bapanov, A.; Altybayev, G. Mathematical Analysis of Page Fault Minimization for Virtual Memory Systems Using Working Set Strategy. Information 2025, 16, 829. https://doi.org/10.3390/info16100829
Murzakhmetov A, Borankulova G, Bapanov A, Altybayev G. Mathematical Analysis of Page Fault Minimization for Virtual Memory Systems Using Working Set Strategy. Information. 2025; 16(10):829. https://doi.org/10.3390/info16100829
Chicago/Turabian StyleMurzakhmetov, Aslanbek, Gaukhar Borankulova, Arseniy Bapanov, and Gabit Altybayev. 2025. "Mathematical Analysis of Page Fault Minimization for Virtual Memory Systems Using Working Set Strategy" Information 16, no. 10: 829. https://doi.org/10.3390/info16100829
APA StyleMurzakhmetov, A., Borankulova, G., Bapanov, A., & Altybayev, G. (2025). Mathematical Analysis of Page Fault Minimization for Virtual Memory Systems Using Working Set Strategy. Information, 16(10), 829. https://doi.org/10.3390/info16100829






