Iterative Optimization of Structural Entropy for Enhanced Network Fragmentation Analysis
Abstract
1. Introduction
2. Methods
2.1. Background: Structural Entropy-Based Node Significance
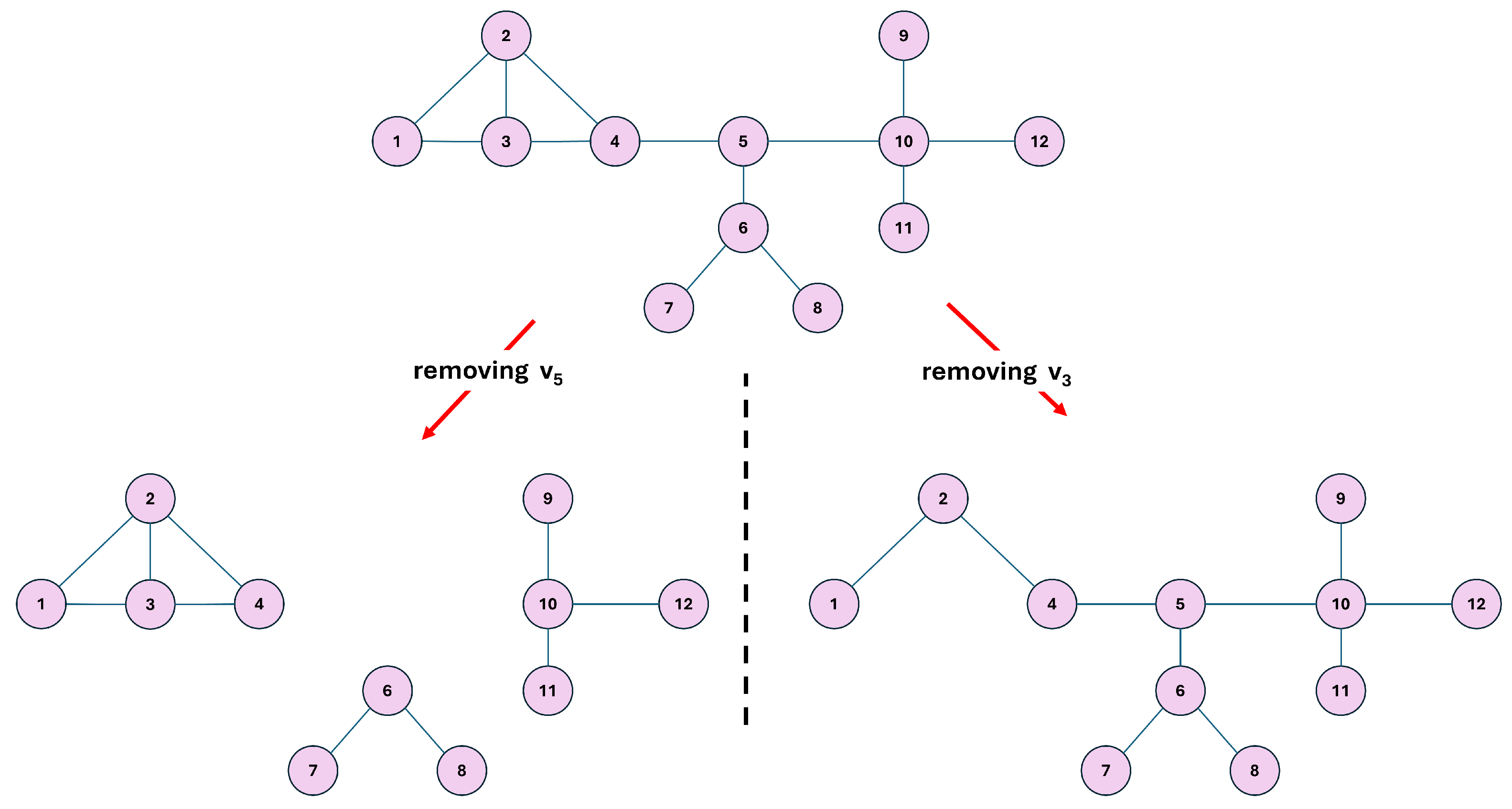
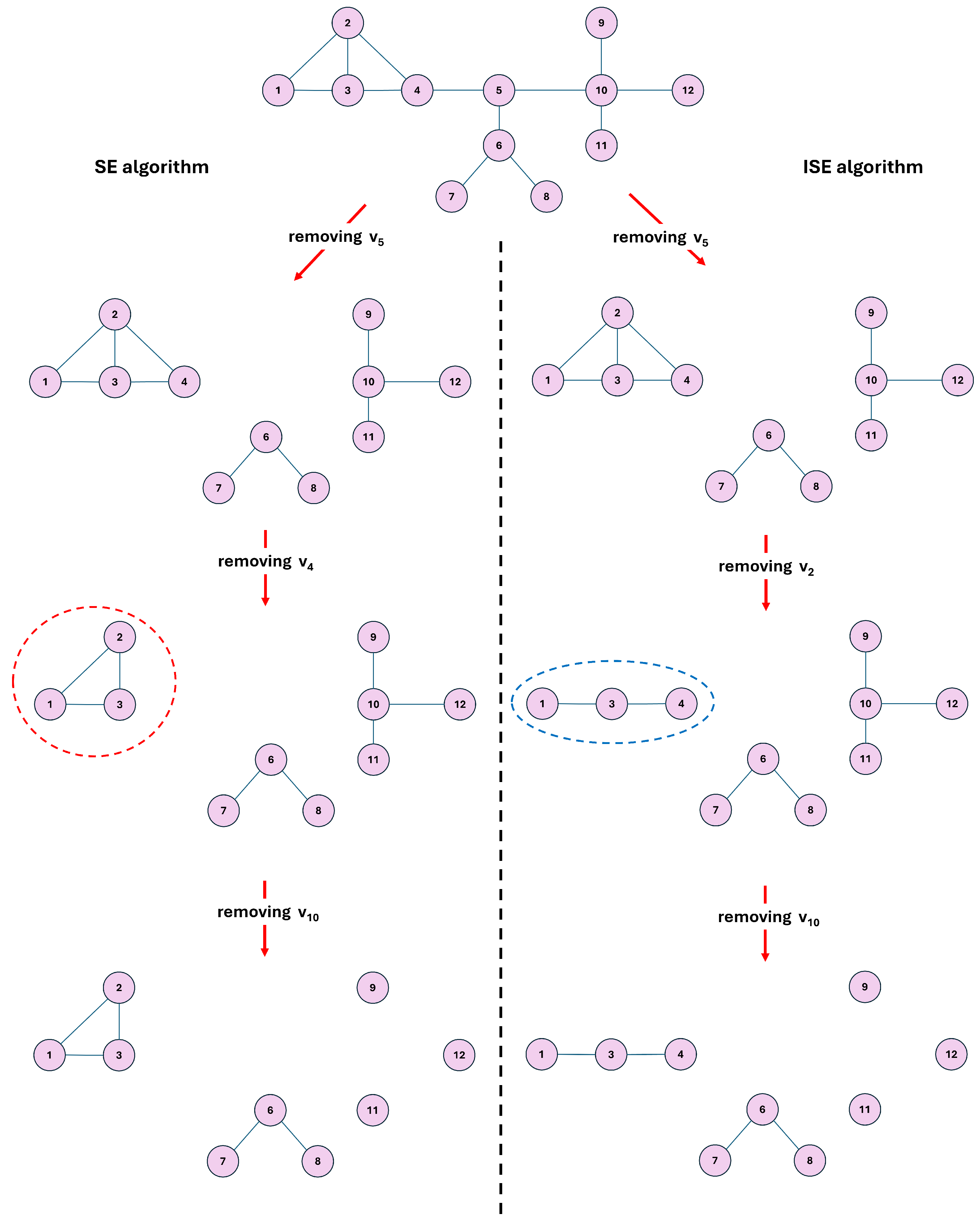
2.2. Our Iterative Optimization Scheme
- Compute for each node in the current graph G using the method described above.
- Identify the node with the lowest value, i.e., the highest significance.
- Remove node from the graph along with its incident edges, resulting in a new graph .
- Record and its significance value.
- Repeat the above steps until the graph becomes empty.
Scope and Motivation for the Iterative Scheme
2.3. Performance Indicators
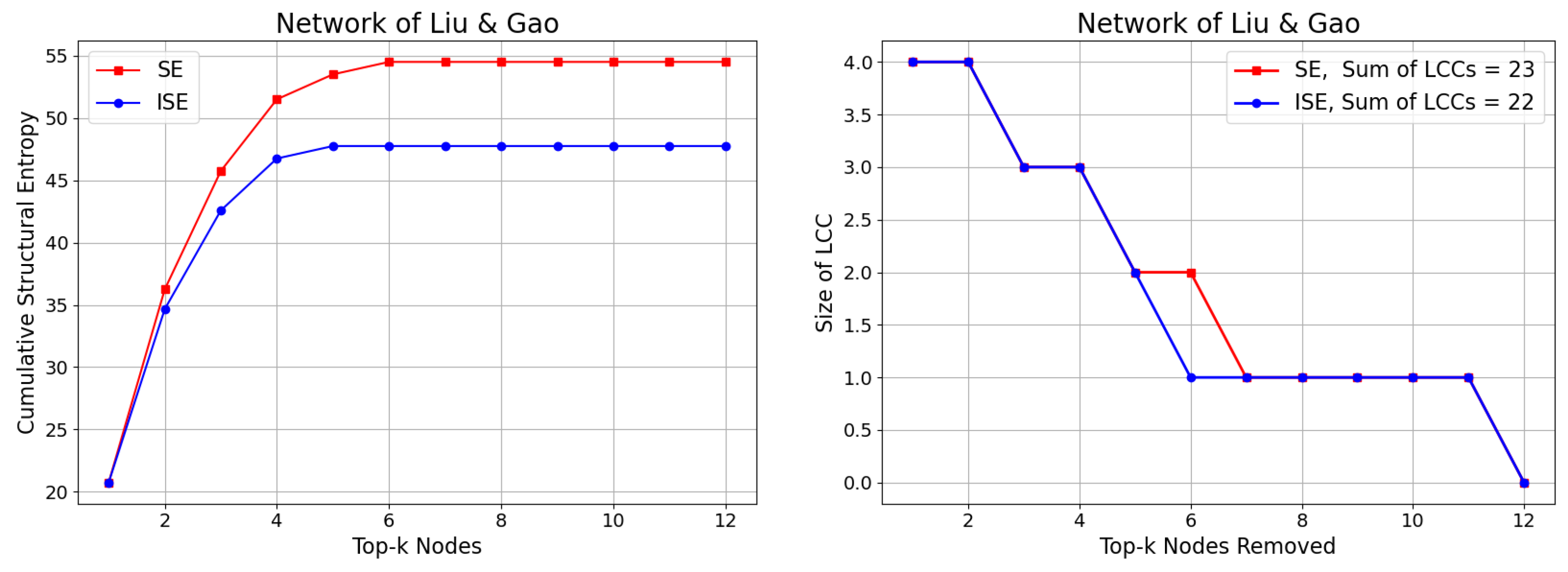
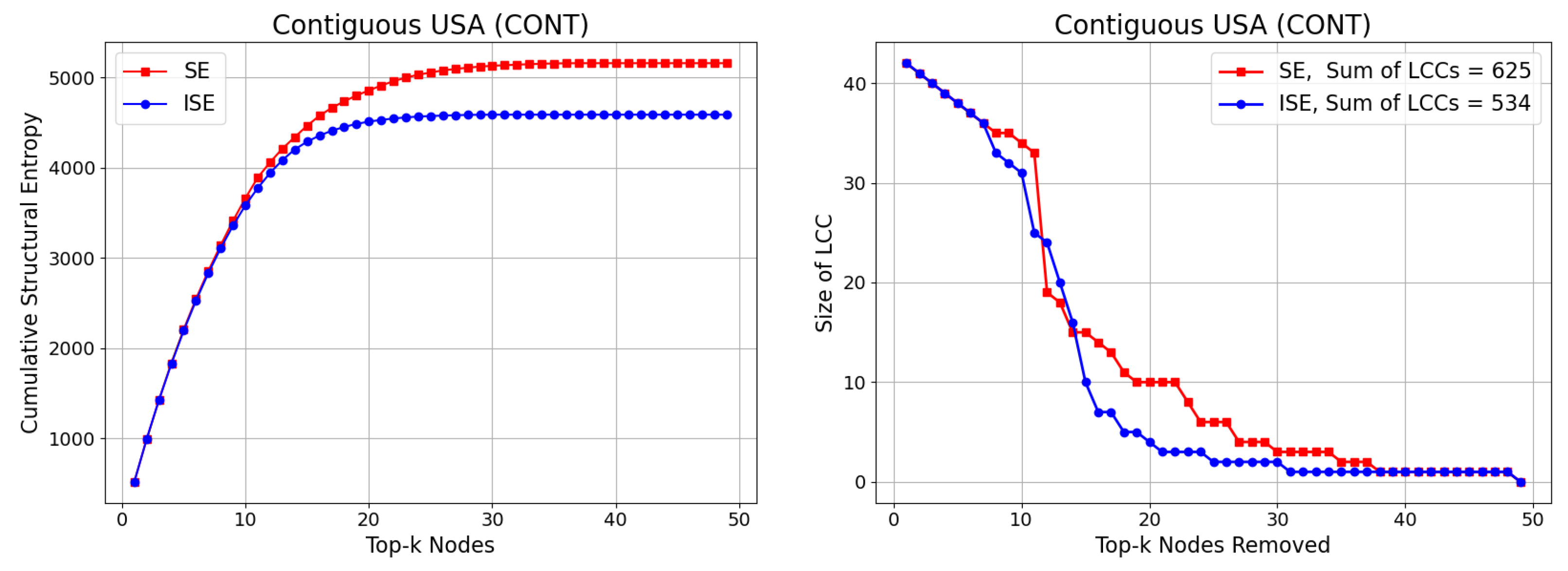
2.3.1. Cumulative Structural Entropy
2.3.2. Size of the Largest Connected Component (LCC)
2.3.3. Fragmentation and Percolation Simulation Protocol
- Removal orders.
- Residual graphs and largest component.
- Panel 1: Average shortest-path length in the LCC.
- Panel 2: Diameter of the LCC.
- Panel 3: Percolation/SIR proxy (expected outbreak size).
- Early stopping rule for the percolation panel.
- Interpretation notes.
- Implementation.
2.3.4. Baseline Centralities (DC, IKS, WR) and Monotonicity M
- Degree centrality (DC).
- Improved k-shell (IKS).
- (i)
- Find the current minimum degree ;
- (ii)
- Remove only the nodes with degree and assign them the current shell index;
- (iii)
- Recompute degrees on the residual graph and repeat.
- Weighted-edge score (WR).
- Monotonicity M.
- Practical convention for zero scores.
3. Results
3.1. Network of Liu and Gao
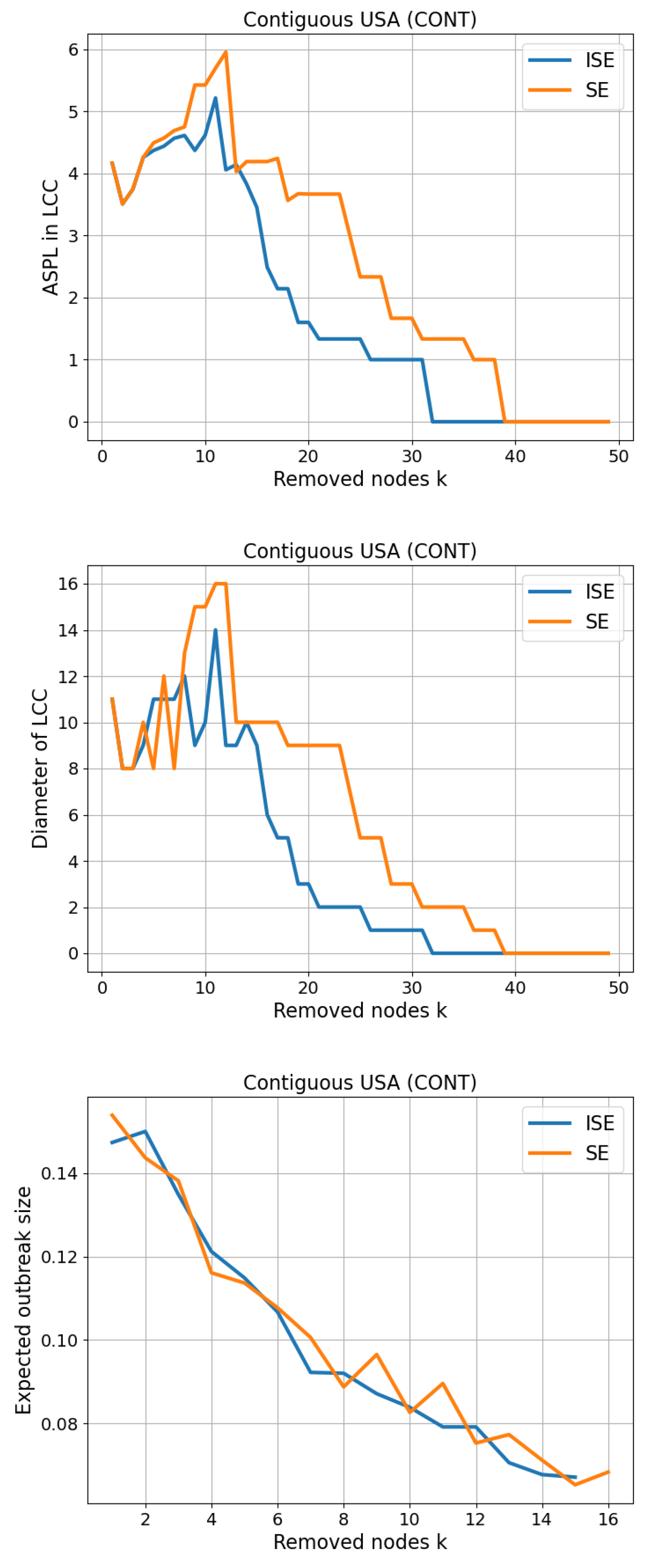
3.2. Contiguous USA (CONT)
3.3. Les Miserables (LESM)
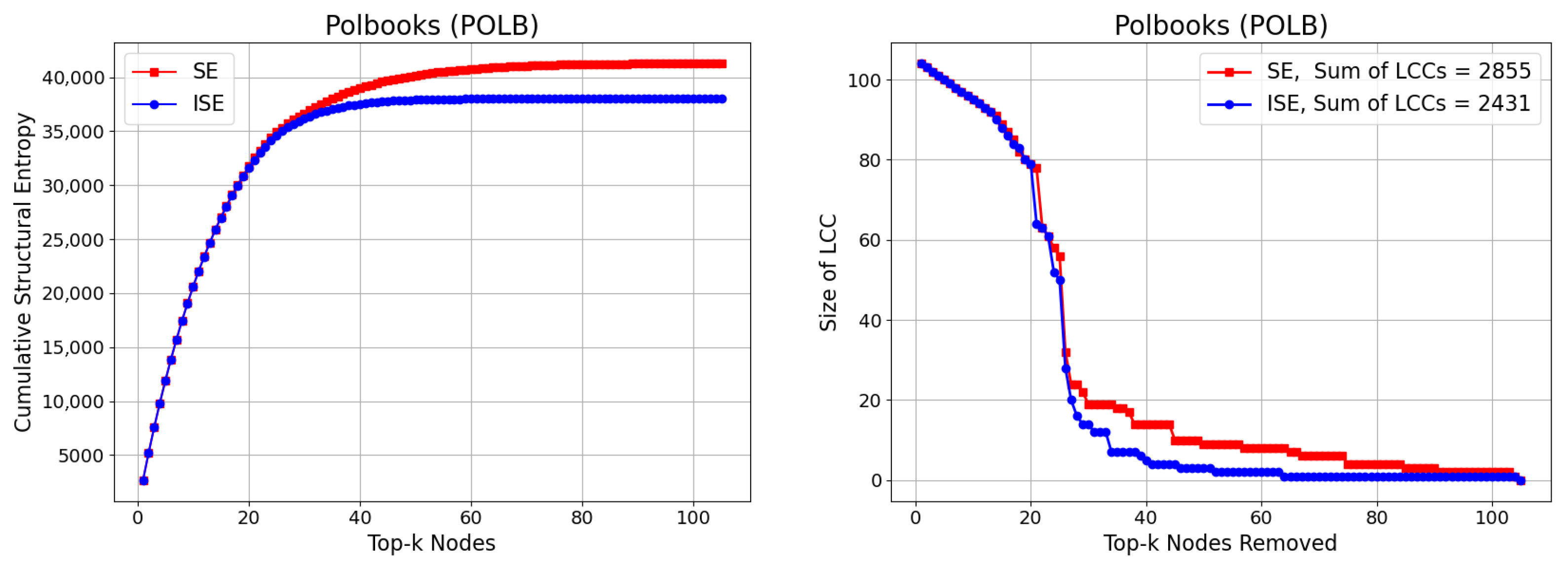
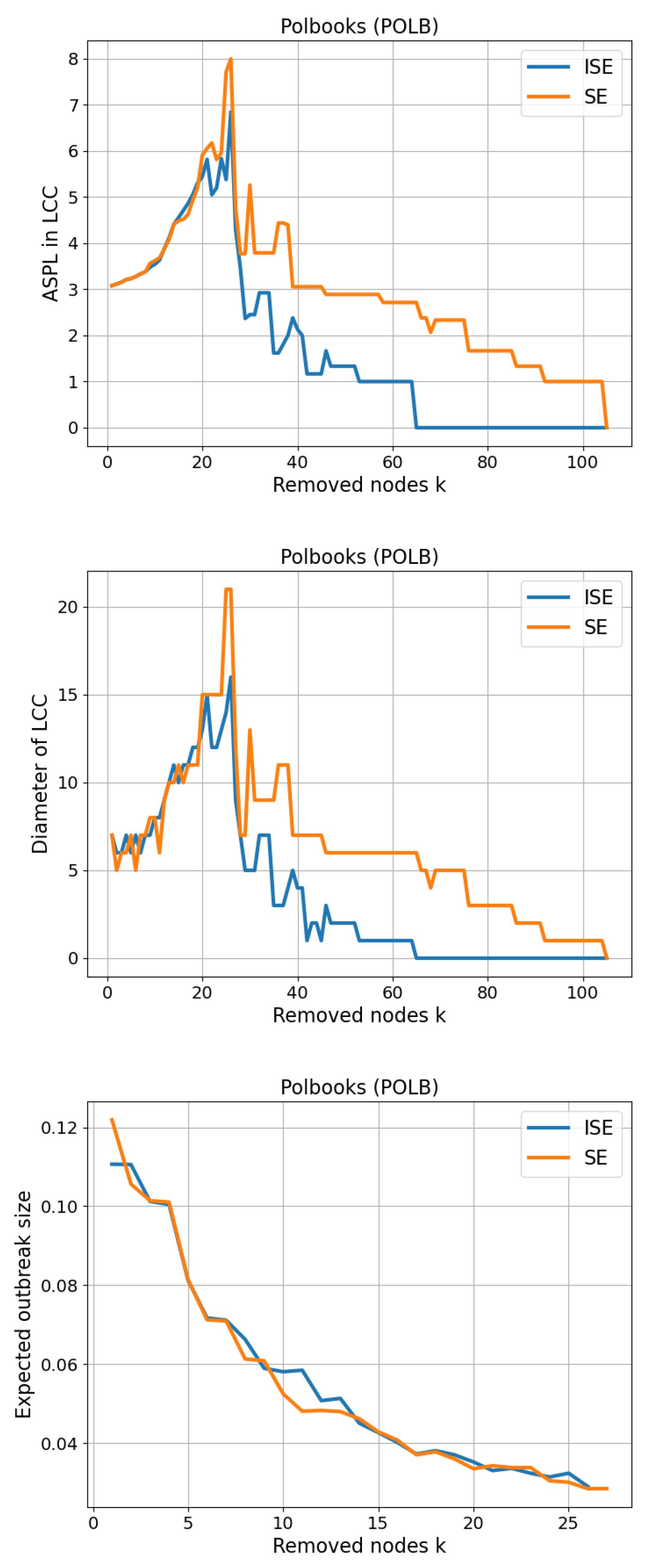
3.4. Polbooks (POLB)
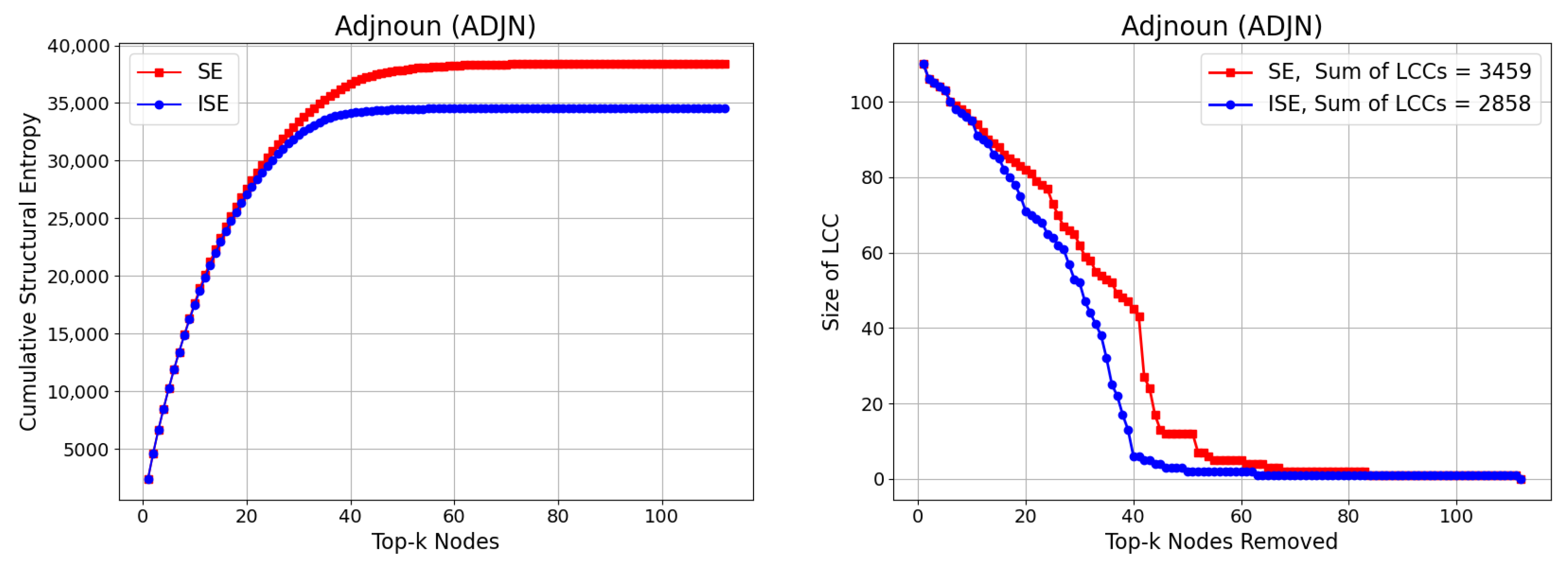
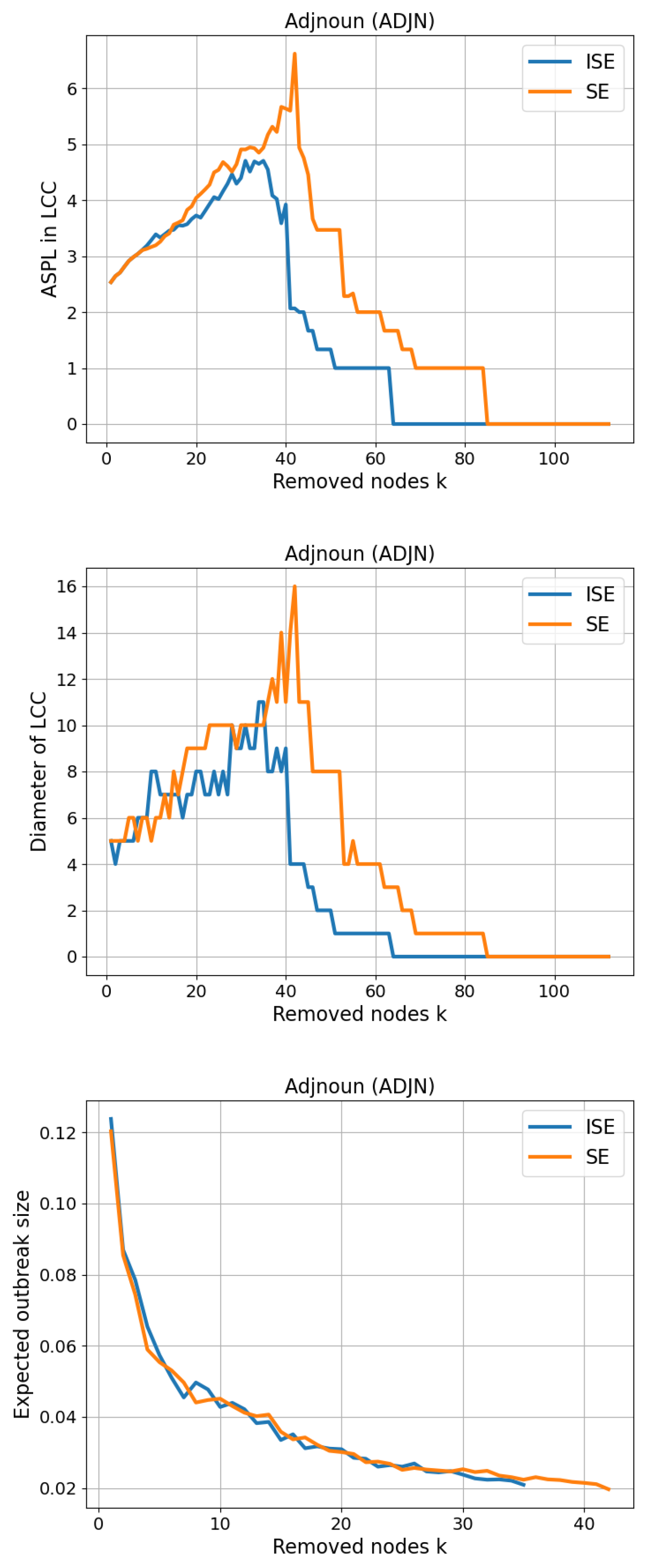
3.5. Adjnoun (ADJN)
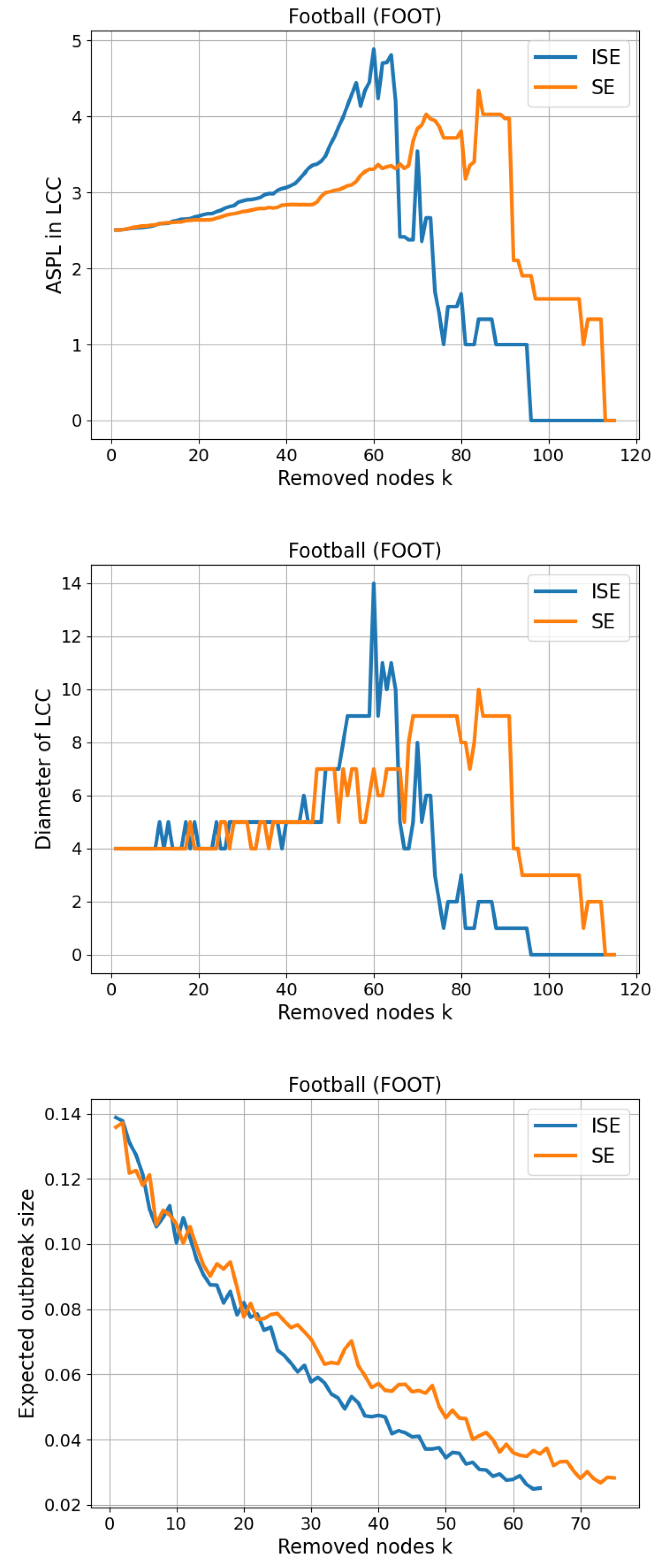
3.6. Football (FOOT)
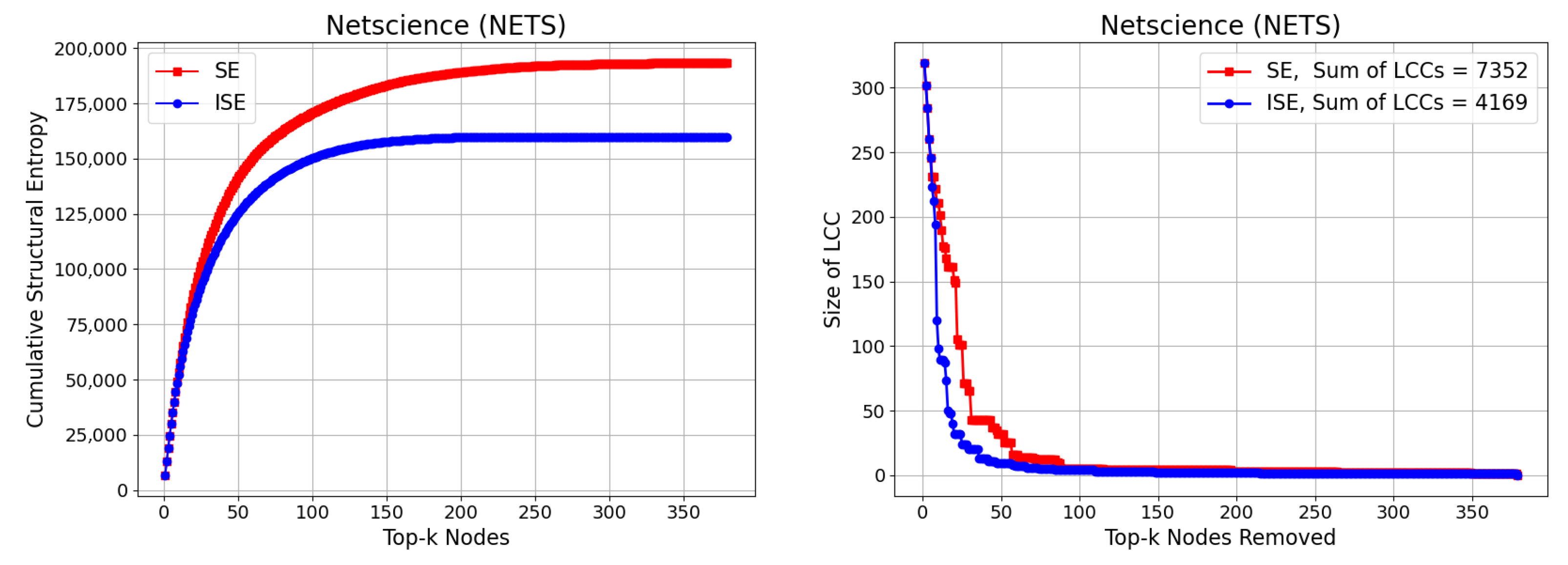
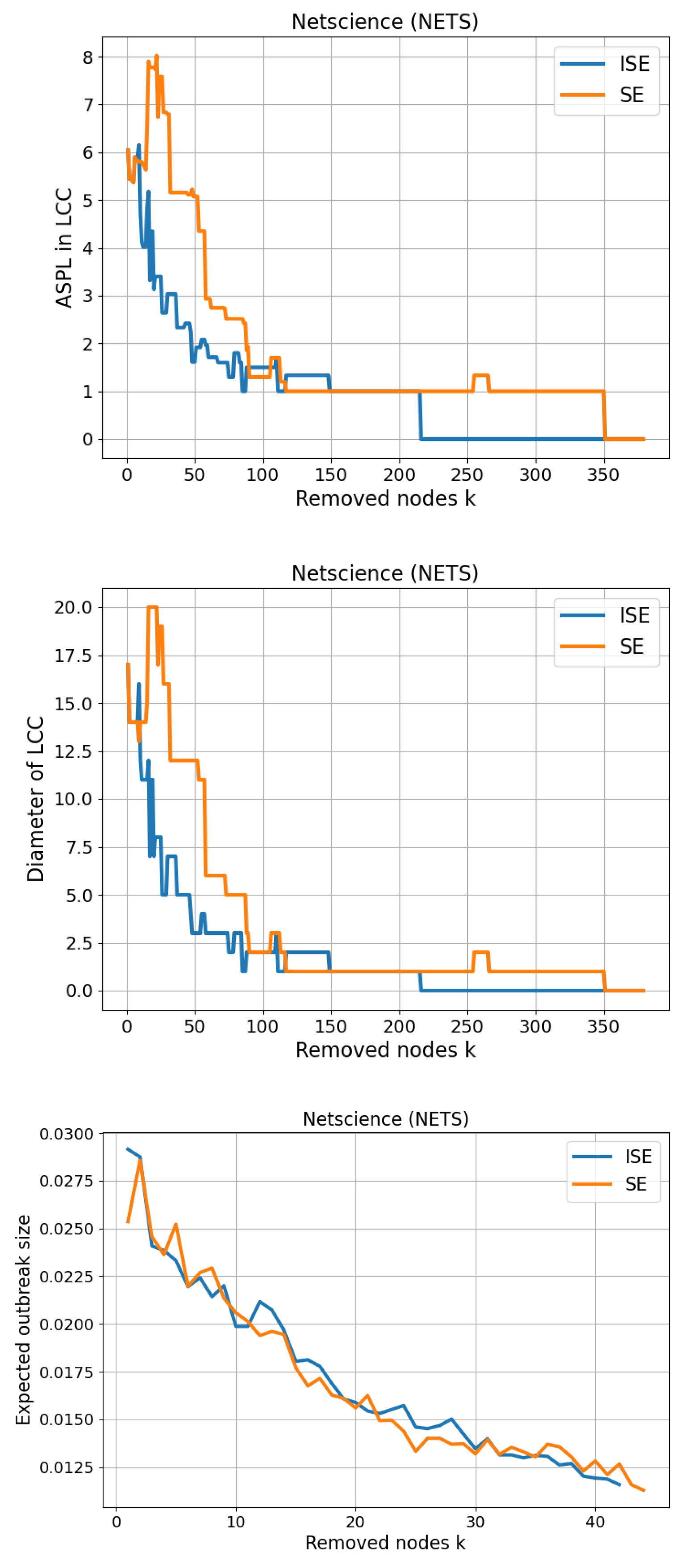
3.7. Netscience (NETS)
3.8. Fragmentation and Percolation Simulation Results
Monotonicity of Score-Induced Rankings
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASPL | Average Shortest-Path Length; |
| CSE | Cumulative Structural Entropy; |
| DC | Degree Centrality; |
| G | Graph; |
| ISE | Iterative Structural Entropy; |
| IKS | Improved k-shell; |
| LCC | Largest Connected Component; |
| Ratio of the Cumulative LCC Sizes under ISE to that under SE; | |
| SE | Structural Entropy; |
| WR | Weighted-edge Score. |
References
- Newman, M.E.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef]
- Lü, L.; Chen, D.; Ren, X.L.; Zhang, Q.M.; Zhang, Y.C.; Zhou, T. Vital nodes identification in complex networks. Phys. Rep. 2016, 650, 1–63. [Google Scholar] [CrossRef]
- Yu, E.Y.; Chen, D.B.; Zhao, J.Y. Identifying critical edges in complex networks. Sci. Rep. 2018, 8, 14469. [Google Scholar] [CrossRef] [PubMed]
- Xie, X.; Zhan, X.; Zhang, Z.; Liu, C. Vital node identification in hypergraphs via gravity model. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 013104. [Google Scholar] [CrossRef]
- Wen, T.; Gao, Q.; Chen, Y.w.; Cheong, K.H. Exploring the vulnerability of transportation networks by entropy: A case study of Asia–Europe maritime transportation network. Reliab. Eng. Syst. Saf. 2022, 226, 108578. [Google Scholar] [CrossRef]
- Ejjbiri, H.; Lubashevskiy, V. Network Robustness Assessment via Edge Criticality Evaluation: Improvement of Bridgeness and Topological Overlap Methods by the Iterative Metrics Re-estimation. In Proceedings of the Asia Simulation Conference; Springer: Berlin/Heidelberg, Germany, 2024; pp. 259–270. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E. Community structure in social and biological networks. Proc. Natl. Scademy Sci. 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Newman, M.E. Spread of epidemic disease on networks. Phys. Rev. E 2002, 66, 016128. [Google Scholar] [CrossRef]
- Yuan, Z.; Chong, W. Identification of essential proteins using improved node and edge clustering coefficient. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 3258–3262. [Google Scholar] [CrossRef]
- Jalili, M.; Salehzadeh-Yazdi, A.; Gupta, S.; Wolkenhauer, O.; Yaghmaie, M.; Resendis-Antonio, O.; Alimoghaddam, K. Evolution of centrality measurements for the detection of essential proteins in biological networks. Front. Physiol. 2016, 7, 375. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, H.; Du, W.; Blanzieri, E.; Viero, G.; Xu, Y.; Liang, Y. Identification of essential proteins based on ranking edge-weights in protein-protein interaction networks. PLoS ONE 2014, 9, e108716. [Google Scholar] [CrossRef]
- Termos, M.; Ghalmane, Z.; Fadlallah, A.; Jaber, A.; Zghal, M. GDLC: A new Graph Deep Learning framework based on centrality measures for intrusion detection in IoT networks. Internet Things 2024, 26, 101214. [Google Scholar] [CrossRef]
- Haque, M.A.; Shetty, S.; Kamhoua, C.A.; Gold, K. Attack graph embedded machine learning platform for cyber situational awareness. In Proceedings of the MILCOM 2022-2022 IEEE Military Communications Conference (MILCOM), Rockville, MD, USA, 28 November–2 December 2022; pp. 464–469. [Google Scholar] [CrossRef]
- Kar, D.; Sahoo, A.K.; Agarwal, K.; Panigrahi, S.; Das, M. Learning to detect SQLIA using node centrality with feature selection. In Proceedings of the 2016 International Conference on Computing, Analytics and Security Trends (CAST), Pune, India, 19–21 December 2016; pp. 18–23. [Google Scholar] [CrossRef]
- Banerjee, A.V.; Chandrasekhar, A.G.; Duflo, E.; Jackson, M.O. Gossip: Identifying Central Individuals in a Social Network; Number w20422; National Bureau of Economic Research: Cambridge, MA, USA, 2014. [Google Scholar]
- Kiss, C.; Bichler, M. Identification of influencers—Measuring influence in customer networks. Decis. Support Syst. 2008, 46, 233–253. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X. Relative superiority of key centrality measures for identifying influencers on social media. Int. J. Intell. Inf. Technol. (IJIIT) 2014, 10, 1–23. [Google Scholar] [CrossRef]
- Kandhway, K.; Kuri, J. Using node centrality and optimal control to maximize information diffusion in social networks. IEEE Trans. Syst. Man, Cybern. Syst. 2016, 47, 1099–1110. [Google Scholar] [CrossRef][Green Version]
- Yelubayeva, P.; Gabdullina, Z. Understanding Media and Information Literacy (MIL) in the Digital Age: A Question of Democracy by Ulla Carlsson. Int. J. Media Inf. Lit. 2024, 9, 491–495. [Google Scholar] [CrossRef]
- Williams, H.T.; McMurray, J.R.; Kurz, T.; Lambert, F.H. Network analysis reveals open forums and echo chambers in social media discussions of climate change. Glob. Environ. Chang. 2015, 32, 126–138. [Google Scholar] [CrossRef]
- Interian, R.; G. Marzo, R.; Mendoza, I.; Ribeiro, C.C. Network polarization, filter bubbles, and echo chambers: An annotated review of measures and reduction methods. Int. Trans. Oper. Res. 2023, 30, 3122–3158. [Google Scholar] [CrossRef]
- De Francisci Morales, G.; Monti, C.; Starnini, M. No echo in the chambers of political interactions on Reddit. Sci. Rep. 2021, 11, 2818. [Google Scholar] [CrossRef]
- Sunstein, C.R. Echo Chambers: Bush v. Gore, Impeachment, and Beyond; Princeton University Press: Princeton, NJ, USA, 2001. [Google Scholar]
- Yurtcicek Ozaydin, S.; Lubashevskiy, V.; Ozaydin, F. Group Polarization and Echo Chambers in# GaijinTwitter Community. Soc. Sci. 2024, 13, 692. [Google Scholar] [CrossRef]
- Sunstein, C.R. Republic: Divided Democracy in the Age of Social Media; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Sunstein, C.R. The law of group polarization. In University of Chicago Law School, John M. Olin Law & Economics Working Paper; University of Chicago Law School: Chicago, IL, USA, 1999. [Google Scholar] [CrossRef]
- Bright, J. Explaining the emergence of political fragmentation on social media: The role of ideology and extremism. J. Comput.-Mediat. Commun. 2018, 23, 17–33. [Google Scholar] [CrossRef]
- Yurtcicek Ozaydin, S.; Nishida, R. Fragmentation and dynamics of echo chambers of Turkish political youth groups on Twitter. J. Socio-Informatics 2021, 14, 17–32. [Google Scholar] [CrossRef]
- Adamic, L.A.; Glance, N. The political blogosphere and the 2004 US election: Divided they blog. In Proceedings of the 3rd International Workshop on Link Discovery, Chicago, IL, USA, 21–25 August 2005; pp. 36–43. [Google Scholar] [CrossRef]
- Ozaydin, F.; Ozaydin, S.Y. Detecting political secession of fragmented communities in social networks via deep link entropy method. In Proceedings of the Asian Conference on Media, Communication & Film, Kyoto, Japan, 9–12 November 2021. [Google Scholar]
- Yurtcicek Ozaydin, S.; Ozaydin, F. Deep Link Entropy for Quantifying Edge Significance in Social Networks. Appl. Sci. 2021, 11, 11182. [Google Scholar] [CrossRef]
- Lubashevskiy, V.; Lubashevsky, I. Evolutionary approach for detecting significant edges in social and communication networks. IEEE Access 2023, 11, 58046–58054. [Google Scholar] [CrossRef]
- Lubashevskiy, V.; Ozaydin, S.Y.; Ozaydin, F. Improved link entropy with dynamic community number detection for quantifying significance of edges in complex social networks. Entropy 2023, 25, 365. [Google Scholar] [CrossRef] [PubMed]
- Lubashevskiy, V.; Ejjbiri, H.; Lubashevsky, I. Iterative assessment of edge criticality: Efficiency enhancement or hidden insufficiency detection. IEEE Access 2025, 13, 60889–60902. [Google Scholar] [CrossRef]
- Rehman, A.U.; Jiang, A.; Rehman, A.; Paul, A.; Din, S.; Sadiq, M.T. Identification and role of opinion leaders in information diffusion for online discussion network. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 15301–15313. [Google Scholar] [CrossRef]
- Jin, B.; Zou, M.; Wei, Z.; Guo, W. How to find opinion leader on the online social network? Appl. Intell. 2025, 55, 624. [Google Scholar] [CrossRef]
- Nian, F.; Zhang, Z. The Influence of Opinion Leaders on Public Opinion Spread and Control Strategies in Online Social Networks. IEEE Trans. Comput. Soc. Syst. 2025; early access. [Google Scholar] [CrossRef]
- Furini, M.; Mariotti, L.; Martoglia, R.; Montangero, M. A Novel Graph-Based Approach to Identify Opinion Leaders in Twitter. IEEE Trans. Comput. Soc. Syst. 2025, 12, 1268–1278. [Google Scholar] [CrossRef]
- Hunt, K.; Gruszczynski, M. “Horizontal” Two-Step Flow: The Role of Opinion Leaders in Directing Attention to Social Movements in Decentralized Information Environments. Mass Commun. Soc. 2024, 27, 230–253. [Google Scholar] [CrossRef]
- Riedl, M.J.; Lukito, J.; Woolley, S.C. Political influencers on social media: An introduction. Soc. Media Soc. 2023, 9, 20563051231177938. [Google Scholar] [CrossRef]
- Liang, H.; Lee, F.L. Opinion leadership in a leaderless movement: Discussion of the anti-extradition bill movement in the ‘LIHKG’web forum. Soc. Mov. Stud. 2023, 22, 670–688. [Google Scholar] [CrossRef]
- Jain, L.; Katarya, R.; Sachdeva, S. Role of opinion leader for the diffusion of products using epidemic model in online social network. In Proceedings of the 2019 Twelfth International Conference on Contemporary Computing (IC3), Noida, India, 8–10 August 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Litterio, A.M.; Nantes, E.A.; Larrosa, J.M.; Gómez, L.J. Marketing and social networks: A criterion for detecting opinion leaders. Eur. J. Manag. Bus. Econ. 2017, 26, 347–366. [Google Scholar] [CrossRef]
- Li, Z.; Chan, C.; Chen, Y.F.; Chan, W.W.H.; Im, U.L. Millennials’ hotel restaurant visit intention: An analysis of key online opinion leaders’ digital marketing content. J. Qual. Assur. Hosp. Tour. 2024, 25, 2074–2103. [Google Scholar] [CrossRef]
- Merola, L.M. Evaluating the legal challenges and effects of counterterrorism policy. In Evidence-Based Counterterrorism Policy; Springer: Berlin/Heidelberg, Germany, 2011; pp. 281–300. [Google Scholar] [CrossRef]
- Wang, M.; Li, W.; Guo, Y.; Peng, X.; Li, Y. Identifying influential spreaders in complex networks based on improved k-shell method. Phys. A Stat. Mech. Its Appl. 2020, 554, 124229. [Google Scholar] [CrossRef]
- Yang, Y.Z.; Hu, M.; Huang, T.Y. Influential nodes identification in complex networks based on global and local information. Chin. Phys. B 2020, 29, 088903. [Google Scholar] [CrossRef]
- Zareie, A.; Sheikhahmadi, A. A hierarchical approach for influential node ranking in complex social networks. Expert Syst. Appl. 2018, 93, 200–211. [Google Scholar] [CrossRef]
- Liu, J.; Xiong, Q.; Shi, W.; Shi, X.; Wang, K. Evaluating the importance of nodes in complex networks. Phys. A Stat. Mech. Its Appl. 2016, 452, 209–219. [Google Scholar] [CrossRef]
- Guo, C.; Yang, L.; Chen, X.; Chen, D.; Gao, H.; Ma, J. Influential nodes identification in complex networks via information entropy. Entropy 2020, 22, 242. [Google Scholar] [CrossRef]
- Liu, Y.; Wei, B.; Du, Y.; Xiao, F.; Deng, Y. Identifying influential spreaders by weight degree centrality in complex networks. Chaos Solitons Fractals 2016, 86, 1–7. [Google Scholar] [CrossRef]
- Chiranjeevi, M.; Dhuli, V.S.; Enduri, M.K.; Hajarathaiah, K.; Cenkeramaddi, L.R. Quantifying node influence in networks: Isolating-betweenness centrality for improved ranking. IEEE Access 2024, 12, 93711–93722. [Google Scholar] [CrossRef]
- Evans, T.S.; Chen, B. Linking the network centrality measures closeness and degree. Commun. Phys. 2022, 5, 172. [Google Scholar] [CrossRef]
- Ruhnau, B. Eigenvector-centrality—A node-centrality? Soc. Netw. 2000, 22, 357–365. [Google Scholar] [CrossRef]
- Bonacich, P. Some unique properties of eigenvector centrality. Soc. Netw. 2007, 29, 555–564. [Google Scholar] [CrossRef]
- Fletcher, R.J., Jr.; Revell, A.; Reichert, B.E.; Kitchens, W.M.; Dixon, J.D.; Austin, J.D. Network modularity reveals critical scales for connectivity in ecology and evolution. Nat. Commun. 2013, 4, 2572. [Google Scholar] [CrossRef] [PubMed]
- Ziv, E.; Middendorf, M.; Wiggins, C.H. Information-theoretic approach to network modularity. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2005, 71, 046117. [Google Scholar] [CrossRef] [PubMed]
- Asif, W.; Lestas, M.; Qureshi, H.K.; Rajarajan, M. Spectral partitioning for node criticality. In Proceedings of the 2015 IEEE Symposium on Computers and Communication (ISCC), Larnaca, Cyprus, 6–9 July 2015; pp. 877–882. [Google Scholar] [CrossRef]
- Yu, Y.; Zhou, B.; Chen, L.; Gao, T.; Liu, J. Identifying important nodes in complex networks based on node propagation entropy. Entropy 2022, 24, 275. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, J.; Liao, Z.; Liu, S.; Zhang, Y. A novel method to rank influential nodes in complex networks based on tsallis entropy. Entropy 2020, 22, 848. [Google Scholar] [CrossRef]
- Liu, S.; Gao, H. The structure entropy-based node importance ranking method for graph data. Entropy 2023, 25, 941. [Google Scholar] [CrossRef]




| SE | ISE |
|---|---|
| Dataset | M(DC) | M(IKS) | M(WR) | M(SE) | M(ISE) |
|---|---|---|---|---|---|
| Liu & Gao | 0.573 | 0.669 | 0.799 | 0.854 | 1.000 |
| CONT | 0.697 | 0.794 | 0.954 | 1.000 | 1.000 |
| LESM | 0.904 | 0.894 | 0.993 | 0.994 | 1.000 |
| POLB | 0.825 | 0.838 | 0.996 | 1.000 | 1.000 |
| ADJN | 0.866 | 0.874 | 0.996 | 0.999 | 1.000 |
| FOOT | 0.363 | 0.941 | 0.928 | 1.000 | 1.000 |
| NETS | 0.764 | 0.761 | 0.983 | 0.995 | 1.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozaydin, F.; Lubashevskiy, V.; Yurtcicek Ozaydin, S. Iterative Optimization of Structural Entropy for Enhanced Network Fragmentation Analysis. Information 2025, 16, 828. https://doi.org/10.3390/info16100828
Ozaydin F, Lubashevskiy V, Yurtcicek Ozaydin S. Iterative Optimization of Structural Entropy for Enhanced Network Fragmentation Analysis. Information. 2025; 16(10):828. https://doi.org/10.3390/info16100828
Chicago/Turabian StyleOzaydin, Fatih, Vasily Lubashevskiy, and Seval Yurtcicek Ozaydin. 2025. "Iterative Optimization of Structural Entropy for Enhanced Network Fragmentation Analysis" Information 16, no. 10: 828. https://doi.org/10.3390/info16100828
APA StyleOzaydin, F., Lubashevskiy, V., & Yurtcicek Ozaydin, S. (2025). Iterative Optimization of Structural Entropy for Enhanced Network Fragmentation Analysis. Information, 16(10), 828. https://doi.org/10.3390/info16100828








