Research on Optimizing Human Resource Expenditure in the Allocation of Materials in Universities
Abstract
1. Introduction
1.1. Background of the Problem
1.2. Problem Formulation
2. Models and Methods
2.1. Problem Analysis
2.1.1. Analysis of Task One
2.1.2. Analysis of Task Two
2.1.3. Analysis of Task Three
2.2. Model Assumptions and Symbols Description
- Assuming that the physical attributes of students are only related to the data table and meet the requirements of the experimental model;
- Assuming that there is no strict adherence to natural speed during student transportation;
- Neglecting objective factors beyond the set conditions during transportation;
- Assuming that the weight of an item can be divided in sufficiently small mass units.
2.3. Establishment and Solution of the Model for Task One
2.3.1. Analysis and Solution of Task One
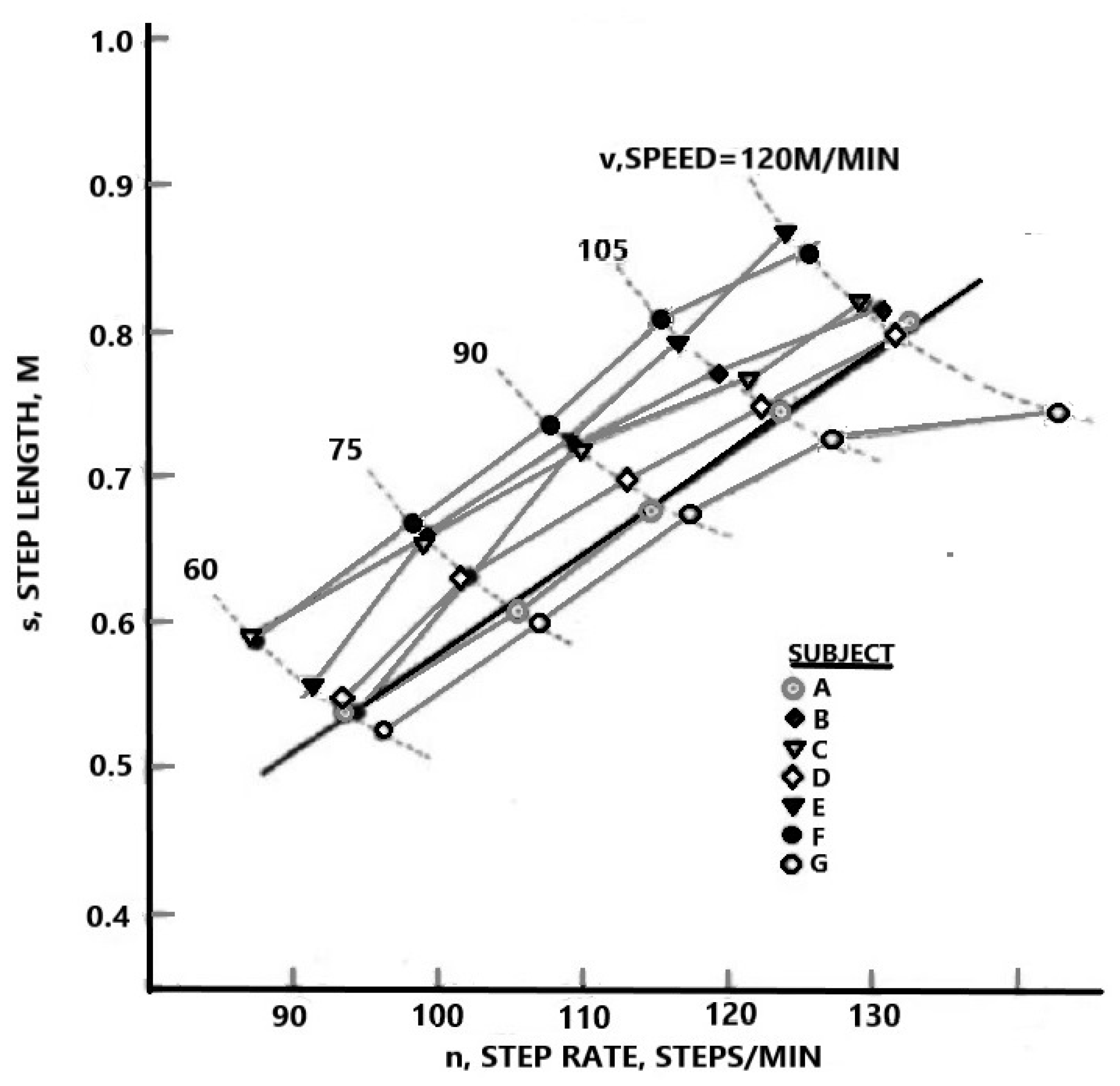
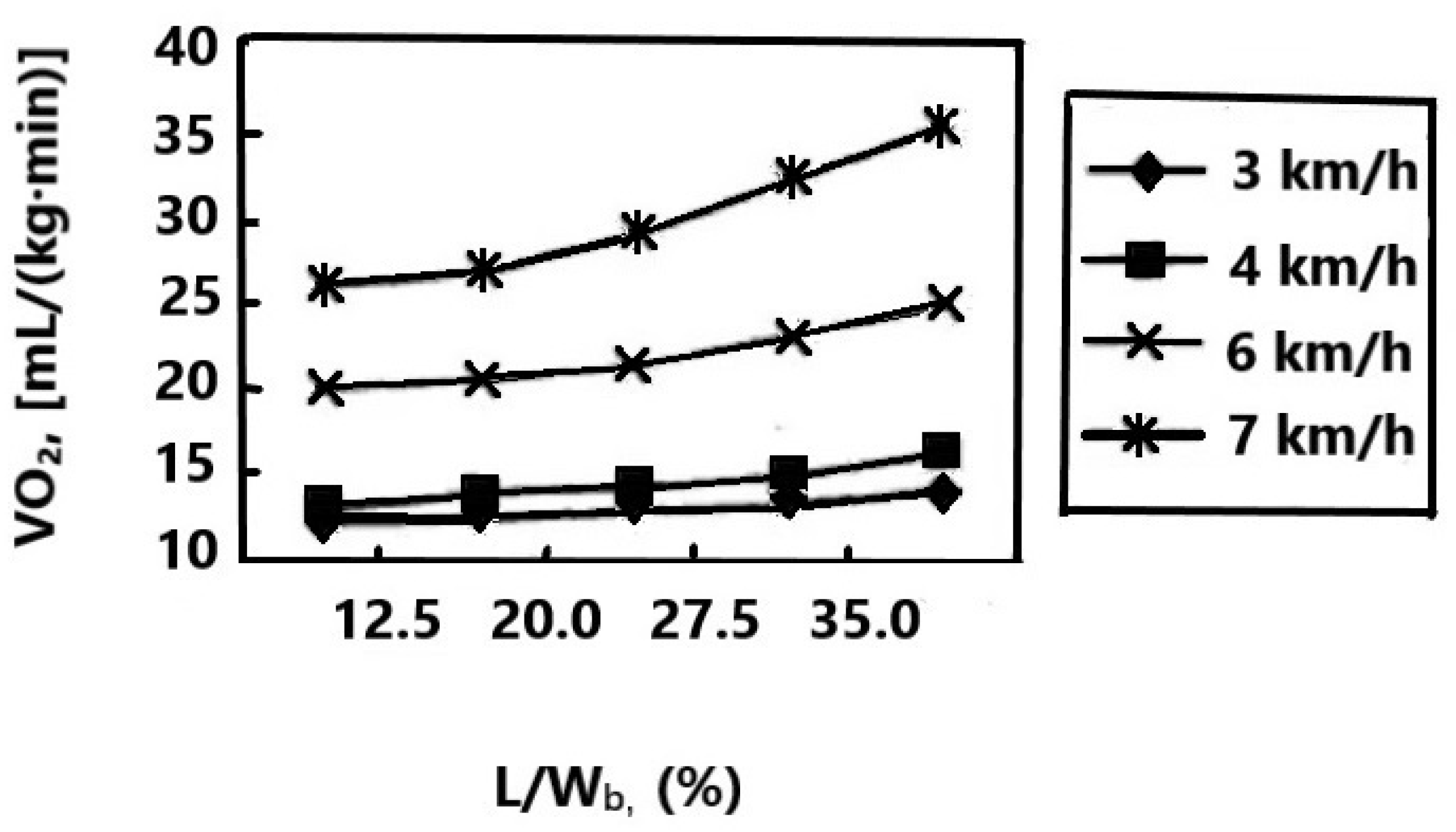
2.3.2. Model Preparation-Energy Consumption Model for Natural Walking
2.4. Establishment of Energy Consumption Model for Load Travel of Task One
2.5. Solving the Model for Task One
2.6. Conclusion of Model for Task One
2.7. Analysis for Task Two
2.8. Model Establishment for Task Two-Data Preprocessing
2.9. Model for Task Two
- (1)
- Establishment of objective functionAs can be seen from the question, the maximum number of transportation packages that require a shelf life rate exceeding 80% is the variable z, which can be recorded as transportation packages with a shelf life rate exceeding 80% in a certain transportation allocation situation, Objective function: T = max (z)
- (2)
- Establishment of restrictive conditionsDue to not considering the impact of item types and time costs, the shelf life rate of the i-th student’s transport bag is , then . The single-objective programming model is as follows:
2.10. Solving the Model for Task Two
2.11. Conclusion for Model of Task Two
3. Evaluation of the Models
3.1. Evaluation of the Model
3.1.1. Advantages of the Models
- (1)
- The model adopts the Monte Carlo simulation algorithm to randomly generate multiple feasible operation plans and compare them pairwise to obtain the optimal plan. This method has a high degree of randomness, and the generated multiple excellent transportation plans can avoid the impact of some students being injured during transportation and unable to transport heavier packages.
- (2)
- The model refers to many widely recognized references within the industry and has great scientific and practical value.
3.1.2. Disadvantages of the Models
3.2. Improvement of the Models
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Student-Item Sample Data (For Test in This Work)
| Item No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| A | 0.16 | 0.10 | 0.06 | 0.19 | 0.02 | 0.13 | 0.04 | 0.10 | 0.21 |
| B | 0.08 | 0.14 | 0.12 | 0.10 | 0.04 | 0.15 | 0.11 | 0.14 | 0.11 |
| C | 0.15 | 0.09 | 0.08 | 0.16 | 0.06 | 0.14 | 0.09 | 0.05 | 0.09 |
| D | 0.11 | 0.09 | 0.08 | 0.03 | 0.15 | 0.13 | 0.13 | 0.14 | 0.13 |
| E | 0.09 | 0.06 | 0.19 | 0.13 | 0.15 | 0.16 | 0.07 | 0.09 | 0.06 |
| F | 0.18 | 0.18 | 0.05 | 0.07 | 0.22 | 0.09 | 0.12 | 0.01 | 0.08 |
| G | 0.01 | 0.16 | 0.05 | 0.05 | 0.20 | 0.06 | 0.06 | 0.15 | 0.25 |
| H | 0.19 | 0.03 | 0.06 | 0.19 | 0.10 | 0.05 | 0.05 | 0.19 | 0.15 |
| I | 0.03 | 0.17 | 0.03 | 0.17 | 0.01 | 0.19 | 0.09 | 0.13 | 0.18 |
| J | 0.16 | 0.01 | 0.06 | 0.15 | 0.17 | 0.02 | 0.11 | 0.15 | 0.16 |
| K | 0.03 | 0.03 | 0.23 | 0.18 | 0.17 | 0.08 | 0.05 | 0.11 | 0.12 |
| L | 0.16 | 0.09 | 0.07 | 0.11 | 0.16 | 0.07 | 0.17 | 0.09 | 0.08 |
| M | 0.02 | 0.01 | 0.03 | 0.01 | 0.16 | 0.07 | 0.17 | 0.09 | 0.08 |
| N | 0.00 | 0.07 | 0.15 | 0.09 | 0.10 | 0.14 | 0.15 | 0.17 | 0.13 |
| O | 0.06 | 0.19 | 0.11 | 0.10 | 0.12 | 0.01 | 0.13 | 0.19 | 0.09 |
| P | 0.03 | 0.15 | 0.17 | 0.00 | 0.00 | 0.03 | 0.22 | 0.15 | 0.25 |
References
- Bertsch, C.; Unger, H.; Winkelmann, W.; Rosenbaum, D. Evaluation of early walking patterns from plantar pressure distribution measurements. Gait Posture 2004, 19, 235–242. [Google Scholar] [CrossRef]
- Eleftherios, K. Plantar pressure distribution during barefoot standing, walking and landing in preschool boys. Gait Posture 2001, 14, 92–97. [Google Scholar]
- Willems, T.; Witvrouw, E.; Delbaere, K.; De Cock, A.; De Clercq, D. Relationship between gait biomechanics and inversion sprains: A prospective study of risk factors. Gait Posture 2005, 21, 379–387. [Google Scholar] [CrossRef]
- Dixon, P.C.; Stebbins, J.; Theologis, T.; Zavatsky, A.B. Spatio-temporal parameters and lower -limb kinematics of turning gait in typically developing children. Gait Posture 2013, 38, 870–875. [Google Scholar] [CrossRef] [PubMed]
- Kerrigan, D.C.; Riley, P.O.; Nieto, T.J.; Della Croce, U. Knee joint torques: A comparison between women and men during barefoot walking. Arch. Phys. Med. Rehabil. 2000, 81, 1162–1165. [Google Scholar] [CrossRef]
- Wang, Y.; Pascoe, D.D.; Weimar, W. Evaluation of book back-pack load during walking. Ergonomics 2001, 44, 858–869. [Google Scholar] [CrossRef]
- Goh, J.H.; Thambyah, A.; Bose, K. Effects of varying backpackloads on peak forces in the lumbosacral spine during walking. Clin. Biomech. 1998, 13 (Suppl. S1), S26–S31. [Google Scholar] [CrossRef]
- Castro, M.P.; Figueiredo, M.C.; Abreu, S.; Sousa, H.; Machado, L.; Santos, R.; Vilas-Boas, J.P. The influenceof gait cadence on the ground reaction forces and plantar pressuresduring load cariage of young adults. Appl. Ergon. 2015, 49, 41–46. [Google Scholar] [CrossRef]
- Stergiou, N.; Moraiti, C.; Giakas, G.; Ristanis, S.; Georgoulis, A.D. The effect of the walking speed on the stability of the anterior cruciate ligament deficient knee. Clin. Biomech. 2004, 19, 957–963. [Google Scholar] [CrossRef]
- Grieve, D.W.; Gear, R.J. The relationship between length of stride, step requency, time ofswing, and speed of walking for children and adults. Ergonomics 1966, 5, 379–399. [Google Scholar] [CrossRef] [PubMed]
- Bobet, J.; Norman, R.W. Effects of load placement on back muscle activity in loadcarriage. Eur. J. Appl. Physiol. 1984, 53, 71–75. [Google Scholar] [CrossRef]
- Weng, J.C.; Hashemi, E.; Arami, A. Natural Walking with Musculoskeletal Models Using Deep Reinforcement Learning. IEEE Robot. Autom. Lett. 2021, 6, 4156–4162. [Google Scholar] [CrossRef]
- Ji, Q.; Fu, S.; Tan, K.; Muralidharan, S.T.; Lagrelius, K.; Danelia, D.; Andrikopoulos, G.; Wang, X.V.; Wang, L.; Feng, L. Synthesizing the optimal gait of a quadruped robot with soft actuators using deep reinforcement learning. Robot. Comput. Integr. Manuf. 2022, 78, 102382. [Google Scholar] [CrossRef]
- Zarrugh, M.Y.; Radcliffe, C.W. Predicting Metabolic Cost of Level Walking. Eur. J. Appl. Physiol. 1978, 38, 215–223. [Google Scholar] [CrossRef]
- Mishra, U.A. Learning Control Policies for Imitating Human Gaits. arXiv 2021, arXiv:2106.15273. [Google Scholar]
- Seay, J.F.; Gregory, V.A.; Frykman, P.N.; Smith, N.I.; Fellin, R.E. Spatiotemporal Comparisons between Male and Female Soldiers While Walking with Heavy Loads:124 Board #5 May 30 9: 30 AM-11: 30 AM. Med. Sci. Sport. Exerc. 2018, 50, 11. [Google Scholar]
- Simpkins, C.; Yang, F. Dynamic Gait Stability and Spatiotemporal Gait Parameters During Overground Walking in Professional Ballet Dancers. J. Danc. Med. Sci. 2024, 28, 28–36. [Google Scholar] [CrossRef]
- Seay, J.F.; Bode, V.G.; Frykman, P.N.; Smith, N.I.; Fellin, R.E. Pelvis and Trunk Motion Comparisons Between Male and Female Soldiers While Walking With Heavy Loads: 85 Board #1 May 29 9:30 AM - 11:30 AM. Med. Sci. Sport. Exerc. 2019, 51, 10. [Google Scholar] [CrossRef]
- Simpson, K.M.; Munro, B.J.; Steele, J.R. Effects of prolonged load carriage on ground reaction forces, lower limb kinematics and spatio-temporal parameters in female recreational hikers. Ergonomics 2012, 55, 316–326. [Google Scholar] [CrossRef]
- Houck, J.R.; Duncan, A.; Haven, K.E.D. Comparison of frontal plane trunk kinematics and hip and knee moments during anticipated and unanticipated walking and side step cutting tasks. Gait Posture 2006, 24, 314–322. [Google Scholar] [CrossRef]
- Yoganandaan, S.; Perumal, V. Effect of Walking with and without LoadIntermittent Walking on Cardio Respiratory EnduranceMuscular Strength and Muscular Endurance of Adolescent Boys. Int. J. Innov. Res. Dev. 2014, 3, 407–409. [Google Scholar]
- Lee, J.S.; Yeon, P.S.; Choi, J.H. Effects of Forest-Walking Exercise on Isokinetic Muscular Strength, Muscular Endurance, and Bone Mineral Density in the Elderly Women. J. Korean Inst. For. Recreat. 2016, 20, 1–9. [Google Scholar] [CrossRef][Green Version]
- Wernbom, M.; Augustsson, J.; Thomeé, R. Effects of vascular occlusion on muscular endurance in dynamic knee extension exercise at different submaximal loads. J. Strength Cond. Res. 2006, 20, 372–377. [Google Scholar] [PubMed]
- Harrison, P.W.; James, L.P.; Jenkins, D.G.; McGuigan, M.R.; Holmberg, P.M.; Kelly, V.G. The Effects of Low-Load Squat Jump and Maximal Isometric Priming Exercise on Muscular Performance and Perceptual State. J. Strength Cond. Res. 2024, 38, 1–9. [Google Scholar] [CrossRef]
- Zarrugh, M.Y.; Todd, F.N.; Ralston, H.J. Optimization of energy expenditure during level walking. Eur. J. Appl. Physiol. 1974, 33, 293–306. [Google Scholar] [CrossRef]
| Symbol | Symbol Description |
|---|---|
| Energy rate per unit weight (J/Min) | |
| s | Step |
| n | Step rate (number/Min) |
| Extreme step size (meter) | |
| Extreme step rate (number/Min) | |
| Natural ultimate speed (M/Min) | |
| T | Time cost (Mins) |
| The i-th student’s j-th load (Kg) | |
| lower limit of load for i-th student (Kg) | |
| Upper limit of load for i-th student (Kg) | |
| The weight of student i’s load (Kg) | |
| Item allocation matrix | |
| i-th student’s item shelf rate (%) |
| Student Code | a | b |
|---|---|---|
| 1 | 3.9638 | 2.0736 |
| 2 | 3.6729 | 1.9214 |
| 3 | 3.4442 | 1.8018 |
| 4 | 8.2578 | 3.5795 |
| 5 | 8.0229 | 3.4777 |
| 6 | 7.5248 | 3.2617 |
| 7 | 13.7822 | 5.1146 |
| 8 | 12.9585 | 4.8089 |
| 9 | 12.1348 | 4.5032 |
| Student Code | First Handling Time Cost/min | Second Handling Time Cost/min | Third Handling Time Cost/min |
|---|---|---|---|
| 1 | 7.5 | 7.77 | 8.05 |
| 2 | 8.00 | 8.29 | 8.59 |
| 3 | 8.50 | 8.81 | 9.12 |
| 4 | 8.80 | 9.12 | 9.45 |
| 5 | 9.00 | 9.32 | 9.66 |
| 6 | 9.50 | 9.84 | 10.20 |
| 7 | 9.60 | 9.95 | 10.30 |
| 8 | 10.00 | 10.36 | 10.73 |
| 9 | 10.50 | 10.88 | 11.27 |
| Item Type | Total Weight (Kg) | Shelf Life Rate |
|---|---|---|
| 1 | 10 | 0.88 |
| 2 | 15 | 0.6 |
| 3 | 7 | 0.93 |
| 4 | 17 | 0.9 |
| 5 | 10 | 0.9 |
| 6 | 14 | 0.78 |
| 7 | 10 | 0.7 |
| 8 | 10 | 0.83 |
| 9 | 13 | 0.95 |
| 10 | 20 | 0.87 |
| 11 | 3 | 0.65 |
| 12 | 20 | 0.75 |
| 13 | 16 | 0.8 |
| 14 | 12 | 0.68 |
| 15 | 10 | 0.87 |
| 16 | 10 | 0.83 |
| Package Code | Parcel Retention Rate |
|---|---|
| 1 | 0.821629 |
| 2 | 0.804405 |
| 3 | 0.801495 |
| 4 | 0.833797 |
| 5 | 0.804377 |
| 6 | 0.809537 |
| 7 | 0.802351 |
| 8 | 0.808308 |
| 9 | 0.812711 |
| Student Size | Running Time of Monte Carlo | Running Time of Integer Prog | Error of Monte Carlo Simulation | Diff. btw. Monte Carlo and Interpolation of Table 3 |
|---|---|---|---|---|
| 7 | 1 min | 30 min | 1.5% | - |
| 8 | 1.5 min | 70 min | 0.9% | - |
| 9 | 2.4 min | 160 min | 1.2% | - |
| 11 | 5 min | 900 min | 0.8% | - |
| 20 | 15 min | - | - | 5.1% |
| 30 | 26 min | - | - | 6.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Wang, Y. Research on Optimizing Human Resource Expenditure in the Allocation of Materials in Universities. Information 2024, 15, 522. https://doi.org/10.3390/info15090522
Zhao L, Wang Y. Research on Optimizing Human Resource Expenditure in the Allocation of Materials in Universities. Information. 2024; 15(9):522. https://doi.org/10.3390/info15090522
Chicago/Turabian StyleZhao, Li, and Ying Wang. 2024. "Research on Optimizing Human Resource Expenditure in the Allocation of Materials in Universities" Information 15, no. 9: 522. https://doi.org/10.3390/info15090522
APA StyleZhao, L., & Wang, Y. (2024). Research on Optimizing Human Resource Expenditure in the Allocation of Materials in Universities. Information, 15(9), 522. https://doi.org/10.3390/info15090522






