Abstract
With the development of the Internet of Things (IoT), IoT nodes with limited energy and computing capability are no longer able to address increasingly complex computational tasks. To address this issue, an Unmanned Aerial Vehicle (UAV)-assisted Wireless Power Transfer (WPT) Mobile Edge Computing (MEC) system is proposed in this study. By jointly optimizing variables such as energy harvesting time, user transmission power, user offloading time, CPU frequency, and UAV deployment location, the system aims to maximize the number of computation bits by the users. This optimization yields a challenging non-convex optimization problem. To address these issues, a two-stage alternating method based on the Lagrangian dual method and the Successive Convex Approximation (SCA) method is proposed to decompose the initial problem into two sub-problems. Firstly, the UAV position is fixed to obtain the optimal values of other variables, and then the UAV position is optimized based on the solved variables. Finally, this iterative process continues until the algorithm convergences, and the optimal solution for the given problem is obtained. The simulation results indicate that the proposed algorithm exhibits good convergence. Compared to other benchmark solutions, the proposed approach performs optimally in maximizing computation bits.
1. Introduction
The rapid evolution and widespread application of IoT devices, alongside advancements in wireless technology, have led to the proliferation of numerous computation-intensive applications, such as online gaming, augmented reality, and online video streaming. However, these new applications often have high sensitivity to latency, necessitating significant computational capabilities in terminal devices for efficient operation [1,2]. Simultaneously, the volume of data generated by these devices and their associated applications has exhibited explosive growth [3]. However, due to limited computing capability and battery capacities, these devices may be unable to handle computation tasks independently, potentially reducing the Quality of Service (QoS) of the applications [4,5].
MEC is widely regarded as a technology that aids in processing compute-intensive, latency-critical tasks at resource-constrained edge devices [6,7]. MEC can provide intensive computing services at the network edge, offering low transmission latency and transmission capability, enabling swift computation result returns and effectively alleviating user task burdens [8]. Although MEC technology can enhance users’ computing capability by assisting in computation, the severely limited energy supply of users significantly restricts computing performance. WPT based on Radio Frequency (RF) signals can effectively solve this problem. Currently, RF-based WPT can transmit a few milliwatts of power over tens of meters [9], which makes it suitable for use with low-power IoT devices [10]. Due to the benefits of WPT and MEC technologies for IoT development, the combination of RF-based WPT and MEC technologies is receiving increasing attention [11].
The integration of MEC and WPT represents an innovative technology in the era of IoT, delivering robust computing capability and sustainable energy to a multitude of low-power mobile devices [12,13]. Therefore, the integration of WPT and MEC can optimize latency, energy consumption, and effectiveness more effectively in real-world environments [14]. The authors in [15] considered a MEC system powered wirelessly that comprises an Access Point (AP) and two mobile devices, utilizing WPT technology to charge users, effectively enhancing the endurance of mobile devices. The authors in [16] considered a multi-user MEC network powered by WPT, where user nodes adopt a binary computation offloading strategy. This strategy aims to maximize the computing rate, i.e., the number of processed bits per second, of all user nodes in the network through joint optimization of the selection of each computation mode and the allocation of system transmission duration. The authors in [17] considered a wireless-powered Mobile Edge Computing (MEC) system comprising a hybrid access point and multiple cooperative fogs. In this system, users within each cooperative fog shared communication and computation resources to enhance their computational performance. Based on the classic time-division multiple-access protocol, the authors proposed a harvest-and-offload protocol to jointly schedule wireless energy transfer and cooperative computation offloading.
The above studies focus exclusively on fixed energy transmitters and MEC servers. However, due to the limited service coverage radius of these fixed servers, additional infrastructure deployment is necessary to cover larger areas and serve more user devices, resulting in substantial cost escalation [18].
Due to their high flexibility, ease of deployment, and low cost, UAV equipped with MEC can serve as aerial base stations for providing computing services to mobile users [19,20]. The authors of [21] considered an UAV-based MEC system where UAVs have strong computing capability, providing edge computing services to users with limited computing capability. The authors in [22] considered an UAV-assisted dynamic environment system, deploying an UAV to provide relay and edge computing services to mobile users. To address the non-convex problem of maximizing system tasks, they proposed a Deep Reinforcement Learning (DRL)-based algorithm. The authors in [23] considered an UAV-assisted MEC framework where UAVs assist user devices in task computation, aiming to minimize the system’s weighted total energy usage. To tackle the non-convex problem in the proposed system, a three-order alternating iterative algorithm was proposed. The authors in [24] considered an UAV-assisted relay MEC network system where UAVs serve as MEC servers to assist mobile users in computing and relay sub-tasks to the ground base station for execution. They achieved this by collectively optimizing communication bandwidth, UAV transmission power, computing resources, and UAV positions in three dimensions to minimize task completion duration in the system. The authors in [25] aimed to minimize the weighted sum of communication consumption, computation consumption, and UAV flight energy within a limited UAV mission duration. This objective is achieved through joint optimization of task allocation ratios, power allocation, and UAV flight paths. The target problem is partitioned into two sub-problems using the Block Coordinate Descent (BCD) method and iteratively solved using the Lagrangian dual method and SCA technique.
The integration of MEC and UAV technologies to provide computing services to mobile users was explored in References [21,22,23,24,25]; however, energy harvesting in the MEC system was not investigated. The authors of [26] considered a novel UAV wireless energy transmission system, utilizing UAV-mounted mobile Energy Transmitters (ET) to transmit sustainable energy to ground Energy Receivers (ER). The optimization of the UAV trajectory aimed to maximize the energy transferred to all user devices within a limited timeframe. The authors of [27] considered an UAV-based MEC wireless-powered system, aiming to maximize the task computation rate while considering constraints related to energy harvesting and UAV speed. The authors of [28] explored time slot optimization for an UAV-assisted wireless-powered cooperative MEC system, which includes an UAV access point and two mobile devices. The goal was to minimize total UAV transmission energy while meeting delay and computation task requirements. The authors of [29] proposed an energy consumption optimization method for UAV-based wireless energy transmission MEC systems. This method optimizes energy harvesting duration, user offloading power, and offloading decisions to minimize overall system energy consumption.
In the above studies, UAVs were equipped with both MEC servers and energy transmitters, capable of edge computing and wireless energy transmission. UAV trajectory optimization was the focus of references [26,27], which did not include optimization of the duration for wireless energy transmission. The optimization of wireless energy transmission duration was considered in references [28,29], but the impact of UAV deployment positions on optimization results was not accounted for.
Therefore, different from these existing works, an optimization method for UAV-assisted MEC is proposed in this study, which optimizes both UAV deployment positions and wireless energy transmission. The detailed differences between our work and the related works are shown in Table 1. By jointly optimizing energy harvesting duration, user offloading power, user offloading duration, CPU frequency, and UAV deployment positions, the method aims to maximize the quantity of computation bits, i.e., the number of bits processed within the entire time slot for all users. The proposed method is suitable in many practical applications. For example, in emergency rescue, due to lack of computing base station, amounts of monitoring data from mobile users are needed to be computed by the optimized deployment of UAVs for timely identifying of survivors and assess of disaster areas. In smart agriculture, the distances between agricultural sensors are usually far, leading to inconvenience to replace batteries of the devices. However, by UAV equipped with MEC and WPT function, electric energy can be transmitted to the agricultural sensors with a non-contact mode. This greatly reduces the human and financing cost. Additionally, the combination of UAV with MEC and WPT technology has also been applied in smart cities, military operation, and so on.

Table 1.
Comparison of related work.
The main contributions of this paper can be summarized as follows:
- An UAV-assisted MEC model is developed to maximize the quantity of computation bits for all users in the system. The UAV provides wireless power supply and task computation assistance. In the partial offloading mode, the model jointly optimizes energy harvesting duration, offloading duration, user transmission power, CPU frequency, and UAV deployment positions to maximize computation bits for all users.
- A two-stage alternating iterative resource allocation method is proposed to decompose the original non-convex problem into two sub-problems. Initially, other variables are optimized with a fixed UAV deployment position, and then the UAV deployment position is optimized based on the variables obtained in the first step. This process iterates alternately until convergence.
- Simulation results demonstrate significant performance improvements using the proposed method in different scenarios (e.g., different user distribution areas, UAV heights, fixed UAV positions, etc.). Compared to other benchmark methods, the proposed method significantly improves the system’s computational amount, enabling more computational tasks to be computed with limited energy conditions. The application of Wireless Power Transfer (WPT) technology in IoT can effectively solve the energy supply problem for distributed IoT devices. It significantly reduces the human and financing cost and is helpful to implement a green IoT ecosystem.
2. System Model
We present an UAV-based Mobile Edge Computing (MEC) system with wireless power transmission in Figure 1. The system consists of a single UAV and fixed-location ground users . The UAV is equipped with an RF energy transmitter and a powerful processor capable of efficiently handling tasks that require significant computational resources, as well as efficiently transmitting energy to ground users and execute computational tasks. The users, as depicted in Figure 1, are equipped with a single antenna and a microprocessor, enabling them to receive energy and handle computational tasks. However, their computing capability are limited, and they can only handle simple computational tasks. As illustrated in Figure 2, each time slot is split into two segments. During the segment of the time slot , the UAV provides energy to the users, who harvest energy using their antennas. In the latter part of the time slot , Orthogonal Frequency Division Multiple Access (OFDMA) technology is utilized. The channel is divided into K equally sized sub-channels using OFDMA technology, and allocated to each user. Users operate in a half-duplex transmission mode, which means they cannot offload data and collect energy simultaneously, However, they can perform local computations and collect energy simultaneously. Assume that the UAV can obtain the channel state information (CSI) and users’ location.
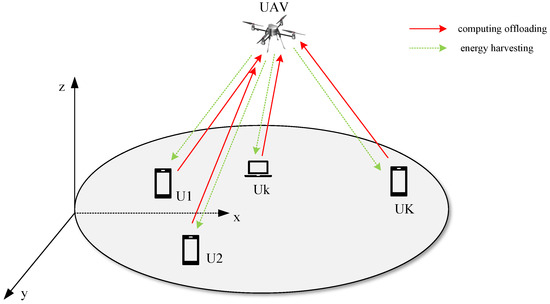
Figure 1.
System model.
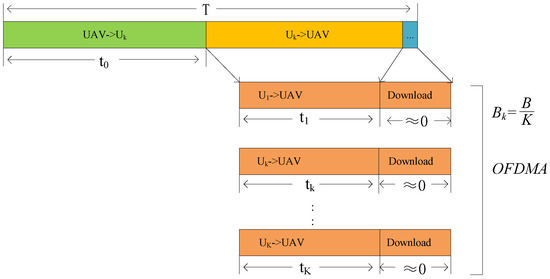
Figure 2.
Frame structure.
2.1. Coordinates and Channel Model
A three-dimensional Cartesian coordinate system is used, where represents the horizontal coordinates of user. All users are fixed on the ground, specifically at height 0. To ensure that the UAV can navigate around all obstacles within the service area, it maintains a fixed height denoted as H, with its horizontal coordinates represented by . Thus, similar to existing works [27,29], it is assumed that there is a line-of-sight (LoS) link between the UAV and each user. Therefore, the channel power gain between the UAV and user k can be expressed as:
where denotes the channel power gain at the reference distance ; denotes the spatial distance between the UAV and the user k, and .
2.2. Computation and Task Offloading Model
A partial offloading model is adopted in this paper. In this mode, each user’s computa-tional task is divided into two parts: one part is computed locally by the user, and the other part is offloaded to the UAV for computation. The UAV’s MEC server handles the offloaded computation. The energy consumed by the user for local computation and task offloading is entirely derived from the energy harvested during the time slot. The energy harvested by each user during the specified period can be formulated as follows:
where represents the energy conversion efficiency, ; represents the UAV’s transmission power. In this study, the UAV transmits at a consistent power. In the partial offloading mode, each user operates as described below.
Local Computing
Let represent the number of CPU cycles needed for task user k to process 1 bit of data, and represent the CPU frequency of user k. The bit count processed locally by user k in time slot T and the energy consumed for local computation can be defined as:
where represents the effective switched capacitance of user k.
2.3. Computation and Task Offloading Model
Users adopt a partial offloading strategy for task offloading. To avoid interference, OFDMA is used for communication between users and the UAV during the offloading stage. The bandwidth B is divided into k sub-bands, with each user allocated one sub-band. Similar to existing work [29], the bit count offloaded by user k to the UAV and the energy consumed for offloading can be expressed as:
where is the sub-bandwidth allocated to user k; is the offloading time for user k; represents the transmission power allocated to user k when offloading tasks to the UAV and denotes the noise power at the user k [29]. Once the UAV receives the offloaded tasks from the users, it performs the computations and then transmits the results back to the user. Due to the UAV’s significantly higher computing capability compared to the users, the bit count related to the computational results is minimal; thus, the computation time and the time required to return the results to the users are neglected. Since each user’s offloading time and energy harvesting time do not exceed the duration of the time slot, the following constraints must be satisfied:
Since the energy expended for local computation and task offloading is entirely derived from the harvested energy, the following energy causality constraint must be satisfied:
The number of computation bits for user k can be expressed as follows:
3. Problem Formulation
This section explores the resource allocation challenge specifically within partial offloading mode. By jointly optimizing the energy harvesting time , user CPU clock frequency , offloading transmission power , offloading time , and UAV deployment position , the goal is to maximize the total computation bits for all users. The objective problem can be formulated as:
where represents the maximum CPU clock frequency for user k, and is the maximum offloading transmission power for user k. The constraint represents the energy causality constraint; ensures that the energy harvesting time and offloading time do not surpass the duration of the time slot; and represents constrain on the CPU clock frequency and offloading transmission power for user k.
Since the variables are coupling, the problem is a non-convex problem. To tackle this issue, we propose a two-stage alternating iterative algorithm. The original issue is broken down into two sub-problems to optimize the CPU clock frequency , energy harvesting time , user offloading transmission power , offloading time , and UAV coordinates . Then, by alternating iterations, the algorithm converges to the optimal solution.
3.1. Fixed UAV Position
In order to deal with the non-convex constraints , Let . Given this fixed UAV position, can be transformed into as described below. Since the problem is a convex optimization problem that can be addressed using the Lagrangian dual method.
Let represent the dual variables corresponding to the constraints , respectively. The Lagrangian function can be formulated as:
Since the problem is a convex optimization problem that can be addressed using the Lagrangian dual method.
Let represent the dual variables corresponding to the constraints , respectively. The Lagrangian function can be formulated as:
where .
The Lagrangian function for problem P1.1 can be expressed as follows:
According to the Lagrangian dyadic function of , the dyadic problem can be expressed as:
To deal with Problem , solve Problem (14) by the given Lagrange multipliers to obtain the optimal variables , and then minimize the function by searching for the optimal dyadic variables.
Thus, given an arbitrary UAV position, the optimal can be guaranteed to satisfy the Karush–Kuhn–Tucker (KKT) condition.
According to the Lagrangian function, the partial derivatives of are obtained flowing the KKT condition, respectively:
From Equation (18), since the energy collection time is linear for the objective function, the problem is addressed using the interior point method in the paper.
For a given UAV position , setting Equation (15) to zero enables us to obtain the optimal CPU clock frequency for the user:
Let Equation (16) be equal to 0. Since and , the case where thus implies . Therefore, the user-optimal transmission power can be expressed as:
where denotes the maximum value between 0 and x.
Let Equation (17) be equal to 0, the optimal unloading time can be obtained by solving Equation (21) using the bisection method.
Then, update the values of according to Formulas (22) and (23) using the sub-gradient method.
where l is the number of iterations, and denote the iteration steps.
3.2. Optimizing UAV Coordinates
The optimal solution is obtained by addressing problem , and then the optimal variables derived from the solution are used to optimize the UAV deployment position. The corresponding sub-problem is expressed as follows:
Due to the presence of in the problem, is a challenging non-convex optimization problem. However, since is a convex function overall, this paper employs the SCA technique for optimizing the problem.
For any given UAV coordinate position , the non-convex term in can be expressed as:
Here, when , Equation (25) holds.
The global lower bound for objective function can be obtained using the SCA technique:
Here, when , Equation (27) holds.
Therefore, based on the above formulas, a convex approximation problem of is obtained, which is expressed as follows:
Problem is a convex problem that can be effectively addressed using the CVX. For problem P, it can be solved by alternately solving the sub-problems and until convergence conditions are met, ultimately obtaining the optimal solution for P1. The Algorithm 1 is summarized in the following steps:
| Algorithm 1 Two-stage alternating iteration algorithm to solve problem P1. |
|
3.3. Complexity Analysis
The time complexity of the proposed method mainly contains four parts. Let M be the number of users, and and be the number of outer and inner iterations, respectively. First, the computation of and has a time complexity of . Second, the bisection method for obtaining the offloading time has a complexity related to the number of iterations. Let be the tolerance for the bisection method, and its complexity is . Third, the time complexity for solving the dual variables , using the subgradient method is , where is the error tolerance for the subgradient method. Finally, the complexity for using CVX to solve the problem is . In conclusion, the total time complexity of Algorithm 1 is: , which is acceptable in general.
4. Simulation Result
The simulation results are obtained by using MATLAB R2021a software. An UAV-assisted wireless powered cooperative MEC system is simulated, in which the number of users is four, and each user is randomly distributed in the region of , with the positions and , respectively, in order. The specific simulation parameters are configured as shown in Table 2.

Table 2.
Simulation parameters.
Figure 3 demonstrates the convergence of the proposed algorithm under various transmission power levels and UAV altitudes. As observed from Figure 3, the algorithm begins to converge after approximately 7 to 8 iterations, indicating good convergence and high efficiency. Furthermore, it is evident that when the UAV’s transmission power is at its maximum and altitude is at its lowest, the maximum number of computational bits can be achieved for all users. Conversely, when the UAV’s transmission power is at its minimum and flight altitude is at its highest, the minimum number of computational bits can be achieved for all users. It is also evident that, for a given UAV transmission power, the total number of computational bits for all users is influenced by the UAV’s altitude; as the altitude decreases, the spatial distance between the UAV and users decreases, thereby improving user service and resulting in a higher total computation bits. When the spatial distance between the UAV and the users is fixed (i.e., the UAV altitude is fixed), higher UAV transmission power enables users to harvest more energy for local computation and task offloading, thereby increasing the total computation bits. This further illustrates that optimizing UAV transmission power and altitude is crucial for enhancing computational capabilities and ensuring efficient task performance in UAV-assisted systems.
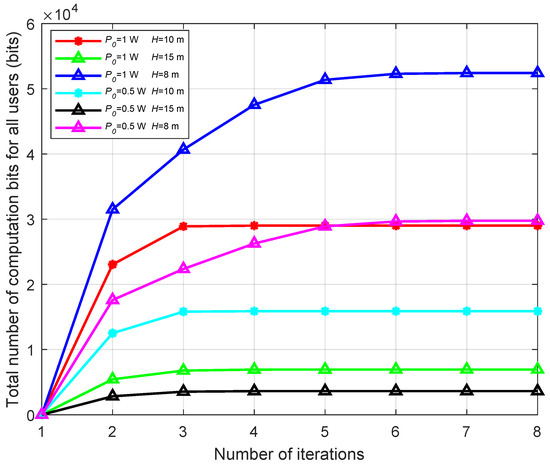
Figure 3.
The total number of computation bits for all the user versus the number of iterations.
Figure 4 illustrates the optimized deployment position of the UAV. The UAV altitude is set to . From Figure 4a, it can be seen that the optimized UAV position is closer to user 1, user 2, and user 3. From Figure 4b, it is evident that the optimized UAV position is closer to user 2, user 3, and user 4. As expected, due to the influence of the channel link, the UAV needs to be closer to the users to better serve them. Therefore, to serve more users and maximize the total computation capacity of the system, the optimized UAV position is closer to the areas with more users. Figure 4c,d show that when user positions are evenly distributed along the edges of a area, the optimized UAV position is near the center of the area. This is because, due to the impact of spatial distance between the UAV and the users, positioning the UAV closer to the center minimizes the distance between the UAV and each user.
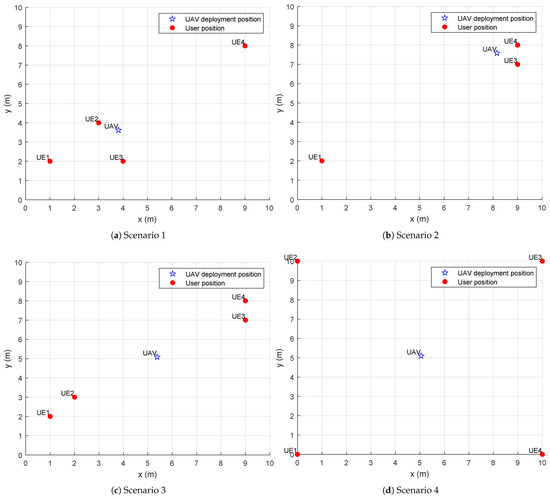
Figure 4.
Optimal deployment position of UAV.
Figure 5 selects Figure 4a to compare the computation bits of each user before and after optimizing the UAV position. The fixed position of the UAV is set to . From Figure 4a, it is evident that the optimized UAV position is closer to user 1, user 2, and user 3, while it is farthest from user 4. Figure 5 shows that the computation bits for user 1, user 2, and user 3 are significantly higher than those for user 4. Meanwhile, it can also be seen from Figure 5 that the number of computed bits for user 2 and user 3 in the fixed UAV position is higher than that for user 1 and user 4, which is because the UAV in the fixed position is closer to user 2 and user 3 and farther away from user 1 and user 4, it can also be seen from Figure 5 that the total number of computed bits of all users after optimizing the UAV position is higher than that in the fixed UAV, which again illustrates the effectiveness of the method implemented in this study.
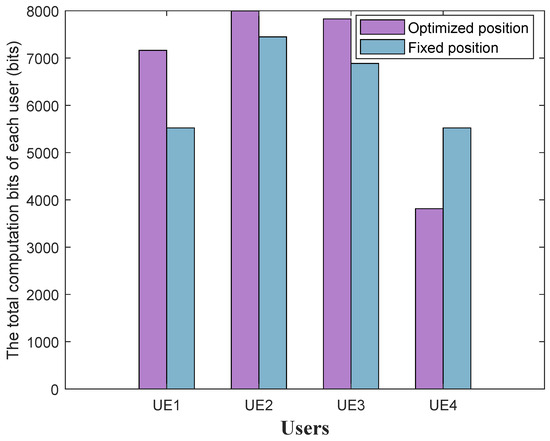
Figure 5.
Comparison of the number of computation bits for each user before and after optimizing the UAV position.
Figure 6 compares the total computation bits of users under different UAV transmission powers and energy conversion efficiencies, with fixed and optimized UAV positions. The UAV altitude is set to H. The UAV transmission power in Figure 6 is set to from 0.1 W to W according to [27]. From the figure, it can be observed that the total computation bits of the users increase with the UAV transmission power. This is because, as the UAV transmission power increases, users can harvest more energy, enabling them to compute more bits. Additionally, Figure 6 demonstrates that the overall computation bits obtained with the optimized UAV deployment position are greater than those obtained with the fixed UAV deployment position. It can also be seen that, for a given UAV position, the higher the energy conversion efficiency, the more energy the users can harvest, resulting in a greater total computation bits for the users
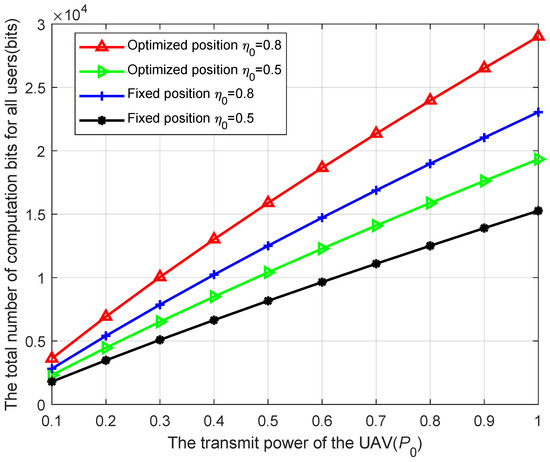
Figure 6.
The UAV transmit power versus the total number of computation bits for all users.
Figure 7 illustrates the relationship involving the average computation bits per user and the number of users. From the figure, it is evident that the average computation capacity per user declines with an increasing number of users. This is because, under the constraints of delay and total bandwidth, the sub-bandwidth allocated to each user decreases as the number of users increases. Consequently, the computation bits that each user can offload to the UAV also decrease, leading to a reduction in the average computation bits per user. It can also be observed that the rate of decrease in average computation bits slows down as the number of users increases. This is because of the limitations of total bandwidth and system total delay. When the sub-bandwidth per user becomes smaller, the offloading time for each user increases, reducing the energy harvesting time. As a result, the amount of energy harvested by the users decreases, affecting their computation bits. Therefore, the average computation bits per user will eventually approach a threshold as the number of users increases. Additionally, Figure 7 further validates that the computation results obtained by optimizing the UAV deployment position are superior to those obtained with a fixed UAV position.
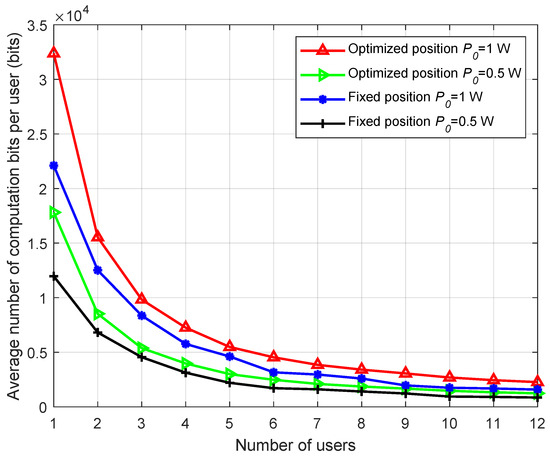
Figure 7.
The average number of computation bits per user versus the number of users.
Figure 8 illustrates the relationship between the total computation bits of users and the system time slot T at different UAV altitudes. From the figure, it can be seen that as T increases, the total computation bits of users also increase. This is because a larger T provides users with more time for energy harvesting and task offloading, thereby in-creasing the total computation bits. As depicted in the figure, an increase in UAV altitude correlates with an increase in the distance between the UAV and the users. This increased distance weakens the channel between the UAV and the users, adversely affecting energy harvesting and task offloading. Consequently, the computation bits of the users decrease as the UAV altitude increases.
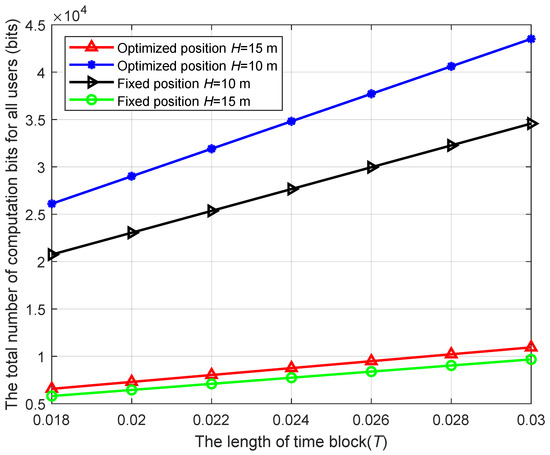
Figure 8.
The total number of computation bits for all users versus UAV altitude.
Figure 9 shows the comparisons of the proposed method with other benchmark methods under different UAV transmission powers. In the fixed UAV position offloading method, the UAV position is fixed at , and other variables are optimized to maximize the total computation bits of the system by using an alternating iterative algorithm. In the fixed energy harvesting duration offloading method, the energy harvesting duration is fixed at , and other variables are optimized using an alternating iterative algorithm. In the fixed energy harvesting duration and UAV position offloading method, both the UAV position and energy harvesting duration are fixed to maximize the computation bits of the system. From Figure 9, it can be seen that as the UAV transmission power increases, the total computation bits obtained by both the proposed method and other benchmark methods increase. This is because when increases, the energy harvested by users also increases, allowing them to handle more tasks. Furthermore, it is evident from the figure that as increases, the energy harvested by users also increases, allowing them to handle more tasks. Furthermore, the proposed method can compute more computation bits compared to other benchmark methods.
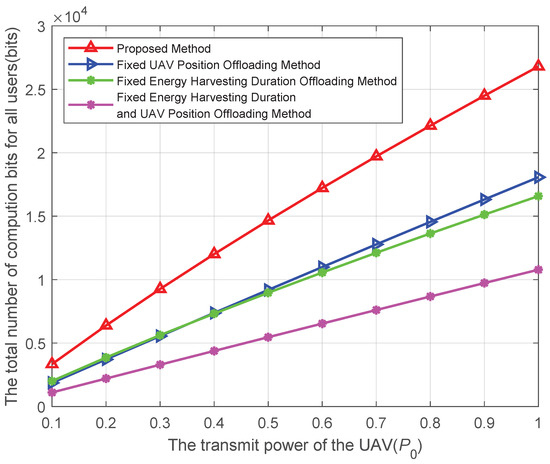
Figure 9.
Computation bits versus the transmission power under different methods.
Figure 10 shows the comparison of the proposed method and other benchmark methods under different T. From Figure 10, it can be seen that as T increases, the computation bits obtained of both the proposed method and the benchmark methods increase. This is because with the increase of T, in both the proposed method and the fixed UAV position offloading method, users have more time to harvest energy, enabling them to handle more computation tasks. For the fixed energy harvesting duration offloading method and the fixed energy harvesting duration and UAV position offloading method, when T increases, the users’ offloading time increases accordingly, allowing more computation tasks to be offloaded to the UAV. Therefore, the total computation tasks of the users increase, too. From Figure 10, it can also be seen that as T increases, the proposed method can compute more computation bits compared to other benchmark methods.
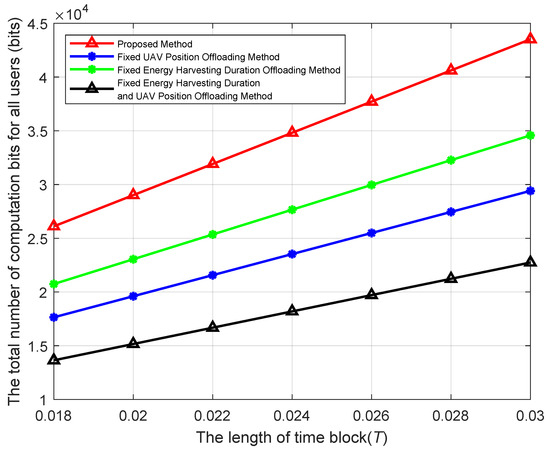
Figure 10.
Computation bits versus the length of time block under different methods.
5. Conclusions
The computation bits of all users in this study are maximized by jointly optimizing the users’ energy harvesting periods, CPU clock frequency, offloading time, offloading power, and UAV deployment position. An objective function was modeled and transformed from the problem. To tackle this non-convex problem, alternating optimization, the Lagrangian dual method, and the SCA technique were employed. The effectiveness of the proposed method in maximizing user computation bits was confirmed by the simulation results. Comparisons are made between the proposed method and the benchmark methods. The results demonstrate that the system computational capability can be significantly enhanced, thereby improving the service quality of various applications. However, due to the joint optimization of multiple variables, the implementation of the proposed algorithom may require high computational capability. Additionally, in practical applications, the assumption of LoS links is not always satisfied. In our future research, non-line-of-sight (NLoS) links will be considered in the complex and changing scenario, and the trajectory of UAV will be optimized in multiple time slots making the method more practical.
Author Contributions
Conceptualization, Z.L. and Y.D.; methodology, Z.L.; software, Z.L.; validation, Z.L.; formal analysis, Z.L. and Y.D.; investigation, S.F. and Z.L.; data curation, Z.L.; writing—original draft preparation, Z.L.; writing—review and editing, S.F. and Z.L.; visualization, Z.L.; supervision, S.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Heilongjiang Natural Science Foundation Joint Guidance Project (No. LH2023F042), Daqing guiding science and technology project (No. zd-2024-34).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Asim, M.; Abd El-Latif, A.A.; ELAffendi, M.; Mashwani, W.K. Energy consumption and sustainable services in intelligent reflecting surface and unmanned aerial vehicles-assisted MEC system for large-scale Internet of Things devices. IEEE Trans. Green Commun. Netw. 2022, 6, 1396–1407. [Google Scholar]
- Porambage, P.; Okwuibe, J.; Liyanage, M.; Ylianttila, M.; Taleb, T. Survey on multi-access edge computing for internet of things realization. IEEE Commun. Surv. Tutor. 2018, 20, 2961–2991. [Google Scholar]
- Wang, F.; Xu, J.; Wang, X.; Cui, S. Joint offloading and computing optimization in wireless powered mobile-edge computing systems. IEEE Trans. Wirel. Commun. 2017, 17, 1784–1797. [Google Scholar]
- Joo, S.; Kang, H.; Kang, J. CoSMoS: Cooperative sky-ground mobile edge computing system. IEEE Trans. Veh. Technol. 2021, 70, 8373–8377. [Google Scholar]
- Hu, X.; Wong, K.K.; Yang, K. Wireless powered cooperation-assisted mobile edge computing. IEEE Trans. Wirel. Commun. 2018, 17, 2375–2388. [Google Scholar]
- Wang, S.; Zhang, X.; Zhang, Y.; Wang, L.; Yang, J.; Wang, W. A survey on mobile edge networks: Convergence of computing, caching and communications. IEEE Access 2017, 5, 6757–6779. [Google Scholar]
- Cao, J.; Bu, Z.; Wang, Y.; Yang, H.; Jiang, J.; Li, H.J. Detecting prosumer-community groups in smart grids from the multiagent perspective. IEEE Trans. Syst. Man, Cybern. Syst. 2019, 49, 1652–1664. [Google Scholar]
- Wu, D.; Wang, F.; Cao, X.; Xu, J. Wireless powered user cooperative computation in mobile edge computing systems. In Proceedings of the 2018 IEEE Globecom Workshops (GC Wkshps), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–7. [Google Scholar]
- Lu, Y.; Xiong, K.; Fan, P.; Zhong, Z.; Letaief, K.B. Robust transmit beamforming with artificial redundant signals for secure SWIPT system under non-linear EH model. IEEE Trans. Wirel. Commun. 2018, 17, 2218–2232. [Google Scholar]
- Saxena, K.; Gupta, N.; Gupta, J.; Sharma, D.K.; Dev, K. Trajectory optimization for the UAV assisted data collection in wireless sensor networks. Wirel. Netw. 2022, 28, 1785–1796. [Google Scholar]
- Lu, X.; Wang, P.; Niyato, D.; Kim, D.I.; Han, Z. Wireless networks with RF energy harvesting: A contemporary survey. IEEE Commun. Surv. Tutor. 2014, 17, 757–789. [Google Scholar]
- Wang, F.; Xu, J.; Cui, S. Optimal energy allocation and task offloading policy for wireless powered mobile edge computing systems. IEEE Trans. Wirel. Commun. 2020, 19, 2443–2459. [Google Scholar]
- Zeng, Y.; Xu, J.; Zhang, R. Energy minimization for wireless communication with rotary-wing UAV. IEEE Trans. Wirel. Commun. 2019, 18, 2329–2345. [Google Scholar]
- Zheng, X.; Zhu, F.; Xia, J.; Gao, C.; Cui, T.; Lai, S. Intelligent computing for WPT–MEC-aided multi-source data stream. EURASIP J. Adv. Signal Process. 2023, 2023, 52. [Google Scholar]
- Ye, Q.; Lu, W.; Hu, S.; Xu, X. Resource optimization in wireless powered cooperative mobile edge computing systems. Sci. China Inf. Sci. 2021, 64, 182303. [Google Scholar]
- Bi, S.; Zhang, Y.J. Computation rate maximization for wireless powered mobile-edge computing with binary computation offloading. IEEE Trans. Wirel. Commun. 2018, 17, 4177–4190. [Google Scholar]
- Mao, S.; Wu, J.; Liu, L.; Lan, D.; Taherkordi, A. Energy-efficient cooperative communication and computation for wireless powered mobile-edge computing. IEEE Syst. J. 2020, 16, 287–298. [Google Scholar]
- Liu, Y.; Xiong, K.; Ni, Q.; Fan, P.; Letaief, K.B. UAV-assisted wireless powered cooperative mobile edge computing: Joint offloading, CPU control, and trajectory optimization. IEEE Internet Things J. 2019, 7, 2777–2790. [Google Scholar]
- Liu, S.; Zhang, X.; Xiao, H.; Li, Z.; Zhang, H. Double-Layer Mobile Edge Computing-Enabled Power Line Inspection in Smart Grid Networks. Information 2022, 13, 167. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, J.; Guo, Y.; Dong, Y.; He, Z. Learning-Based Collaborative Computation Offloading in UAV-Assisted Multi-Access Edge Computing. Electronics 2023, 12, 4371. [Google Scholar] [CrossRef]
- Jeong, S.; Simeone, O.; Kang, J. Mobile edge computing via a UAV-mounted cloudlet: Optimization of bit allocation and path planning. IEEE Trans. Veh. Technol. 2017, 67, 2049–2063. [Google Scholar]
- Tian, K.; Liu, Y.; Chai, H.; Liu, B. Deep Reinforcement Learning-Based Dynamic Offloading Management in UAV-Assisted MEC System. Wirel. Commun. Mob. Comput. 2022, 2022, 2491389. [Google Scholar]
- Hu, X.; Wong, K.K.; Yang, K.; Zheng, Z. UAV-assisted relaying and edge computing: Scheduling and trajectory optimization. IEEE Trans. Wirel. Commun. 2019, 18, 4738–4752. [Google Scholar]
- Xu, Y.; Zhang, T.; Yang, D.; Xiao, L. UAV-assisted relaying and MEC networks: Resource allocation and 3D deployment. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Tang, Q.; Liu, L.; Jin, C.; Wang, J.; Liao, Z.; Luo, Y. An UAV-assisted mobile edge computing offloading strategy for minimizing energy consumption. Comput. Netw. 2022, 207, 108857. [Google Scholar]
- Xu, J.; Zeng, Y.; Zhang, R. UAV-enabled wireless power transfer: Trajectory design and energy optimization. IEEE Trans. Wirel. Commun. 2018, 17, 5092–5106. [Google Scholar]
- Zhou, F.; Wu, Y.; Hu, R.Q.; Qian, Y. Computation rate maximization in UAV-enabled wireless-powered mobile-edge computing systems. IEEE J. Sel. Areas Commun. 2018, 36, 1927–1941. [Google Scholar]
- Zhang, G.; Wang, X.; Shan, M.; Ren, J.; Lu, W. Time allocation improvement method for UAV-based wireless energy transfer cooperative mobile edge. Phys. Commun. 2022, 55, 101861. [Google Scholar]
- Lu, W.; Zhan, Y.; Hua, Q.; Gao, Y.; Cao, J.; Han, H.; Huang, G. Energy consumption optimization in UAV wireless power transfer based mobile edge computing system. J. Electron. Inf. 2022, 44, 899–905. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).