Abstract
The preparation of raw images for subsequent analysis, known as image preprocessing, is a crucial step that can boost the performance of an image classification model. Although deep learning has succeeded in image classification without handcrafted features, certain studies underscore the continued significance of image preprocessing for enhanced performance during the training process. Nonetheless, this task is often demanding and requires high-quality images to effectively train a classification model. The quality of training images, along with other factors, impacts the classification model’s performance and insufficient image quality can lead to suboptimal classification performance. On the other hand, achieving high-quality training images requires effective image preprocessing techniques. In this study, we perform exploratory experiments aimed at improving a classification model of unexposed potsherd cavities images via image preprocessing pipelines. These pipelines are evaluated on two distinct image sets: a laboratory-made, experimental image set that contains archaeological images with controlled lighting and background conditions, and a Jōmon–Yayoi image set that contains images of real-world potteries from the Jōmon period through the Yayoi period with varying conditions. The best accuracy performances obtained on the experimental images and the more challenging Jōmon–Yayoi images are 90.48% and 78.13%, respectively. The comprehensive analysis and experimentation conducted in this study demonstrate a noteworthy enhancement in performance metrics compared to the established baseline benchmark.
1. Introduction
Image preprocessing involves procedures conducted on original images and aims to ready the images for subsequent analysis or further processing [1]. It is an essential step in numerous computer vision applications, such as object detection and image classification. Algorithm efficiency can be enhanced through the application of image preprocessing techniques [2]. During the image preprocessing phase, various techniques are employed, including noise reduction, image segmentation, smoothing, normalization, and compression of image data. These methods contribute to refining and preparing the images for subsequent analysis or applications [3].
Image preprocessing is applied in diverse scenarios. In [4], image preprocessing techniques are implemented in the context of retinal microaneurysm detection in fundus images. They employ specific techniques such as illumination equalization, histogram equalization, and adaptive histogram equalization to address illumination imbalances, enhance the contrast between microaneurysms and the background, and reduce noise. Image preprocessing is used in [5] to prepare computed tomography (CT) scans and X-ray images for COVID-19 detection. Contrast-limited adaptive histogram equalization (CLAHE) is employed in [6] as a preprocessing step in colorectal cancer detection. Weighted mean histogram equalization is utilized in [7] to reduce noise in lung CT images. Likewise, noise removal and contrast enhancement of musculoskeletal radiographs are employed in [8] using CLAHE.
Numerous studies have confirmed the remarkable success of deep learning without requiring handcrafted image features. Nonetheless, several studies report that image preprocessing is still necessary to perform before the training process in deep learning to achieve better performance. In [9], histogram equalization and bilateral filtering are utilized as preprocessing techniques for COVID-19 detection from chest X-ray radiographs. By combining the original image with the two filtered images, they create a pseudo-color image. The experimental results indicate that integrating image preprocessing leads to higher classification accuracy compared to conducting classification without image preprocessing. Histogram equalization is also used in [10] to preprocess face images. Its purpose is to prepare the images for emotion recognition via facial expression classification. In [11], the preparation of the dataset for CNN (convolutional neural network)-based breast cancer classification involves background removal, removal of the pectoral muscle, and application of image enhancements. Similarly, various image preprocessing methods are used in [12] to enhance the conditions of retinal fundus images. These enhancements aim to aid in the identification of diabetic eye disease using multiple deep-learning models.
However, image classification is a challenging task that requires effective image-processing techniques. Images are often subject to noise and distortions, primarily due to the challenging conditions and the potential damage or degradation over time. Furthermore, given that these images may be captured at different moments and locations and with varying acquisition equipment, there can be significant disparities in image quality.
In our previous study, we proposed a framework for archaeological pottery X-ray image classification based on various deep learning architectures, parameters, and techniques [13]. These pottery artifacts contain remnants of various types of food dating back to the Jōmon–Yayoi period. These include ailanthoides, barley, maize weevil, millet, perilla, rice, and wheat. X-ray imaging of these potteries is a non-invasive method to determine the contents and analyze past dietary habits and trade connections. A remaining challenge persists due to the variable conditions under which these images are captured. This issue can be mitigated by image preprocessing, as the inherent nature of radiology images necessitates a preprocessing step [14]. Nevertheless, different image processing techniques may have different effects on different types of archaeological images, depending on their resolution, contrast, noise, etc. Therefore, it is important to investigate and compare various image processing techniques and their impact on image classification, particularly using deep learning.
In this study, we conduct a comprehensive analysis of numerous established image-processing techniques for deep learning-based image classification and discuss the advantages and disadvantages of each preprocessing method. The findings of this study are important for further research in image analysis of various domains, as they provide valuable insights and guidelines for choosing and applying appropriate image processing techniques for different scenarios.
This paper makes several key contributions to the field of image classification as summarized below.
- It investigates the impact of image preprocessing methods on classification accuracy in detail.
- It thoroughly examines image preprocessing techniques on distinct datasets, including controlled laboratory-made images and real-world potsherd objects discovered in archaeological sites.
- It enhances performance compared to the previous study by identifying the most effective image preprocessing method.
2. Materials and Methods
2.1. Image Preprocessing
Image processing refers to the application of algorithms and techniques to manipulate or enhance digital images for various purposes, such as improving visual quality and automated decision-making across a wide array of fields. Image processing can be performed in the spatial domain, involving direct alterations to pixel values, or the transform domain, where adjustments are applied to an input image within a frequency domain [15]. This study examined various image processing techniques within the spatial domain. Techniques in the spatial domain fall into two primary categories: intensity transformation, which manipulates individual pixels within an image, and image filtering, which conducts operations in the neighborhood of each pixel in the image using a filter.
Image filters can be applied to images with different probabilities where . This sets the probability that an image filter will be applied to an input image, and different probabilities bring different effects to the resulting training set. When , an image filter will never be applied to the input image and the original input image will be employed for training. Conversely, when , an image filter will always be applied to the input image, and the original version will never be utilized for training. For values where , there exists a probability that either the original image or the filtered image will be chosen for training. This introduces an element of randomness or variability into the process.
In this study, we employ either or depending on the objective of the filtering. We apply , for instance, in operations like image rotation, flipping, and transposition, so that either the processed images or original images are used in different iterations of the training process, based on that probability. It is important to emphasize that in this mode, the total number of train images remains constant. This mode is referred to as a non-expanding mode.
Conversely, is used for two purposes. Firstly, it standardizes images across all splits. For instance, in the context of the CLAHE, it acts as an image standardization method. Thus, it ensures that only the CLAHE-processed images are considered for training and testing, and the original images are not utilized in this mode. This choice is motivated by the logic that a model trained with images preprocessed using specific filters should also proficiently predict similarly processed images. Secondly, is employed to expand the training set for certain operations. This mechanism is referred to as dataset-expanding mode. For instance, when applied to image flipping, it doubles the resulting training set size as it contains both the original and flipped images. This expanded set is then employed for training the model to enhance the generalizability of the model by providing more training images. Furthermore, several image filters are combined into image processing pipelines, allowing for a comprehensive image enhancement approach.
2.2. Smoothing and Sharpening
Smoothing, as an image transformation technique, aims to reduce sharp intensity transitions that manifest as fine details such as dots and edges within an image [15]. It is frequently utilized to enhance images by reducing noise, given that image noise typically appears as abrupt intensity transitions. Image denoising remains a challenge in the image processing domain [16]. Failure to adequately address issues related to noise can lead to numerous inaccuracies in classifications [17]. Also referred to as low-pass filtering, smoothing has the additional purpose of reducing irrelevant details in images.
In this study, we employ smoothing to investigate whether fine details in the images play a role in archaeological image classification. We utilize Gaussian smoothing, which is the most commonly used image smoothing technique, by convolving the input image with a Gaussian kernel. The standard deviation of the kernel can be adjusted to control the degree of the smoothing, thereby influencing the reduction of fine details. Hence, we can investigate the relationship between the amount of details present in images and its impact on classification accuracy.
As opposed to image smoothing, the objective of image sharpening is to highlight a sharp transition in intensity in an image, which appears as fine details. Image sharpening is employed in this study to examine whether the enhanced details of the image correspond to changes in image quality for classification. By examining the effects of both image smoothing and sharpening, we aim to discern whether it is the fine details or the overall structure of the images that is more important for image classification. In our implementation, the input image is sharpened and superimposed on the original image. The visibility of the sharpened image is adjusted using the parameter where . Specifically, when , only the original image is visible, and when , only the sharpened image is visible. This approach enables the investigation of the relationship between image detail enhancement and its impact on classification results. In the case of image smoothing, Gaussian kernel sizes of 5 and 9 are employed, whereas values of 0.2 and 0.4 are utilized for image sharpening.
2.3. Rotations, Flips, and Transposition
Geometric transformations, including image rotation, flipping, and transposition, are basic image preprocessing methods [18,19]. These methods are recognized for enhancing image classification performance [20]. The rationale is to enhance the diversity of the images within the training set to improve the generalization ability of the models. This is analogous to capturing images of a single object from various angles and perspectives. Hence, these operations are utilized exclusively on the training images. Nevertheless, the choice and execution of geometric transformations require careful consideration. In certain cases, such as with chest X-ray images typically captured in an upright position, these transformations, like rotation and reflection, can potentially distort the images and generate representations that may not align with real-world scenarios. This would consequently lead to a reduction in classification accuracy [21].
We conducted experiments using both , where augmentations occur without expanding the dataset, and where the dataset expands dynamically. In the case of image rotations, various orientations of 90°, 180°, and 270° were employed. When applied using all orientations, the resulting expanded training set quadrupled in size compared to the original set. Furthermore, for image flipping, both vertical and horizontal flips were employed.
2.4. Histogram Equalization
Depending on factors like the objects, lighting conditions, and the image acquisition device, images may display issues such as excessive darkness or brightness, or insufficient contrast, potentially underexposing or overexposing important details in the images. In such instances, histogram equalization proves to be a valuable technique for normalizing and enhancing the contrast of such images by manipulating the histogram values.
Histogram equalization corrects the intensity of a pixel through a transformation function that takes into account the entire image. More specifically, it redistributes the grayscale values across the entire image, ensuring that the result will exhibit a uniform histogram [22]. The transformation is formulated as (1) [4].
Here, N is the number of pixels, is the count of pixels with an intensity of , G stands for the overall number of gray levels, and denotes the cumulative distribution function of .
To process an input image, this method does not require any input parameters. When applied to images with low contrast, this process will effectively enhance the input image by rectifying the overall contrast so that the details in the image will be more apparent. However, it is worth noting that histogram equalization can also drastically alter the appearance of the image and potentially distort image features [23].
2.5. Adaptive Histogram Equalization
In addition to the global histogram equalization mentioned above, another technique known as local histogram equalization, or adaptive histogram equalization, can also be employed. This approach involves dividing the input image into rectangular, non-overlapping blocks and then computing histogram equalization individually in each local block [22]. Therefore, it allows the variation of contrast levels in different regions of an image. Numerous variations of local histogram equalization technique exist, with contrast-limited adaptive histogram equalization (CLAHE) [24] being regarded as one of the most common and effective variations, outperforming global histogram equalization in terms of results [23,25]. It performs effectively for biomedical images such as MRI and mammograms, enhancing image quality through noise removal and preventing excessive noise amplification [26].
CLAHE depends on two important parameters: the number of blocks and the clip limit for contrast limiting. The former specifies how the input image will be divided. This parameter is defined by two values k and l, which partition the image into a grid of non-overlapping blocks. The latter parameter, the clip limit, is designed to control the noise amplification effect by constraining values in the image histogram from surpassing the predetermined threshold [27]. Subsequently, neighboring image regions are blended using bilinear interpolation to eliminate artificially induced boundaries between the regions [28].
2.6. Grid Distortion and Elastic Transformation
Grid distortion changes the spatial arrangement of pixels in an image. It works by employing a grid or mesh that consists of intersecting horizontal and vertical lines overlaid on an input image. This grid divides the input image into blocks. Then the intersection points are shifted randomly along with the pixels surrounding those points. As a result, the shape of objects in an input image will be altered. This method requires two parameters: the number of blocks and the amount of distortion. In our experiment, this operation was exclusively applied to images in the train split to increase the variability of object shapes. This will enhance the model’s robustness and generalization to recognize the same objects that appear in different shapes.
On the other hand, elastic transform also operates using a grid overlaid on an input image. However, instead of shifting the intersection points of the grid individually, elastic transform maps the entire grid itself to a new, random coordinate. The transformation is achieved by implementing affine displacement, denoted as , where the new position of every pixel is determined relative to its original location. For instance, if , it indicates that each pixel’s new location is shifted by 1 to the right. If , the image undergoes scaling by a factor . Since might be a non-integer value, interpolation is essential, typically employing bilinear interpolation [29].
Similar to grid distortion, we utilize elastic transform exclusively to images in the train split. This operation will introduce additional diversity to the train images without substantially altering their semantic content.
3. Experimental Setup
In this work, we aim to enhance the performance of a deep-learning model for classifying archaeological potsherd images. Our focus involves investigating the most effective image preprocessing technique for this purpose.
3.1. Environment Setup
Computations were carried out on an RTX 3090 GPU equipped with 24 GB of GPU memory. The training duration for each model ranged between 30 min to 6 h. The PyTorch framework was employed for model implementation, complemented by functions sourced from the Albumentations library [30] for image processing purposes.
3.2. Classification Model
In this study, we employ ConvNeXt [31] as the classification model, specifically utilizing ConvNeXt-B (base) as our model variant. ConvNeXt is essentially an evolution of the ResNet architecture [32], particularly ResNet-50 and ResNet-200, and was modernized using various design improvements. This development was motivated by the substantial performance gains observed with recent Vision Transformers [33] that outperformed ResNet by a significant margin. Notably, the authors of ConvNeXt reported that its performance exceeds that of the more recent Swin Transformer [34] with similar computation trequirements.
ConvNeXt was fined-tuned for the capability of classifying images in our dataset. Considering the stochastic nature of neural networks, the training was conducted on the same model eight times for each image preprocessing method or pipeline. Code is available at https://github.com/israel-at-aritsugi-lab/archaeological-classification, accessed on 18 April 2024.
We used the Adam optimizer with , , , a weight decay of , and a batch size of 12. Throughout our experiments, the “patience” parameter was set to 30, meaning that the training process would halt if no improvement in performance was observed within 30 epochs. Within the train split, we allocated 10% of the images for validation purposes. The validation portion was selected randomly before the training phase. This train/validation portion was consistently maintained across training iterations, pipelines, and experiments to ensure a fair and objective comparison. Classification performance was measured in terms of accuracy (2).
3.3. Dataset
Our dataset contains 1098 images and consists of two parts. The first part is the Jōmon–Yayoi dataset, which contains X-ray images of ancient potteries from the Jōmon through the Yayoi period, containing a limited set of 64 images. This part is relatively small and insufficient for comprehensively evaluating a classification model. Therefore, we collected the second part of the dataset which we call the experimental dataset, containing X-ray images of a pot made in a laboratory setting. This second part of the dataset is larger, totaling 1034 images. This experimental dataset was collected with the same objects as those contained in the Jōmon–Yayoi dataset. By complementing the Jōmon–Yayoi dataset, it enables the training of the image classification model and enables the model to acquire the characteristics of both image types. We divide these images into train and test splits following a 90:10 ratio, resulting in 929 images for the training split and 105 images for the test split. This dataset configuration remains consistent with that employed in the previous study [13].
The dataset consists of seven classes of images, which are ailanthoides, barley, maize weevil, millet, perilla, rice, and wheat. We arranged the images in such a way that each class in the test split contains an equal number of 15 images, while the train split consists of approximately 130 images per class. However, it is worth noting that the number of images in the Jōmon–Yayoi dataset is not evenly distributed across classes, primarily due to the limited availability of the objects. A breakdown of the dataset’s distribution across splits and classes is provided in Table 1. Additionally, Figure 1 exhibits sample images from each class.

Table 1.
Distribution of the dataset.
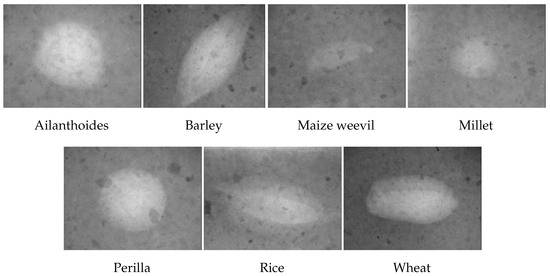
Figure 1.
Images from each class in the dataset.
All images are in grayscale and are stored in either JPG or TIF formats. Most images have dimensions of pixels, while other images are in various dimensions, ranging from to pixels. Each image is resized using bilinear interpolation so that the shortest side of the image becomes 400 pixels while maintaining the original aspect ratio. This allows an input image to be scaled up or down based on its original size. Following this, each image undergoes a center-cropping process to attain a consistent size of pixels. This dimension is determined based on an experiment conducted in [13], which demonstrated the best classification results. All objects are positioned at the center of the images during acquisition. This ensures that this cropping procedure does not truncate the objects. Subsequently, normalization is applied using (3) before the image enters the network. In the formula, and , which represent the mean and standard deviation of our dataset. This normalization procedure is consistently applied across all experiments.
The evaluation of each image processing pipeline’s performance is quantified in terms of accuracy. Since each model is trained eight times, we consider the maximum and the average accuracies achieved from each model.
3.4. Learning Rate
Before experimenting with the image preprocessing methods, we decided on the learning rate to use in those experiments. Learning rate is a hyperparameter that regulates the magnitude of the steps taken in optimizing the weights of a neural network during the training process. Thus, it regulates how quickly or slowly a neural network learns from the data. Properly tuning this hyperparameter is essential for ensuring that the model converges efficiently to optimal or near-optimal solutions. In this experiment, we explored various learning rates, specifically , , , and . No image preprocessing methods were applied during this experiment, except the required pixel resizing, center-cropping, and normalization.
The results are outlined in Table 2, highlighting the best accuracy in bold and the second-best accuracy underlined. Among these learning rates, the highest accuracy was observed with and . On the test split, the learning rate results in a higher accuracy compared to . Conversely, on the Jōmon–Yayoi split, the learning rate yields a higher accuracy. Since the Jōmon–Yayoi split is more challenging compared to the test split, we selected the learning rate of as the most suitable choice from this experiment due to its superior accuracy performance. We utilized this learning rate in the subsequent experiments.

Table 2.
Performance of different learning rate values.
4. Results and Discussion
In this section, we present and analyze the outcomes of each image preprocessing method and their influence on the accuracy of the model. We categorize the methods into two groups: single methods, which employ individual image processing techniques, and combination pipelines, which integrate multiple image processing methods.
4.1. Single Methods
The results of the single methods are detailed in Table 3. Notably, a plus sign (+) denotes the application of a dataset-expanding filter while a “(p)” implies the use of a filter with 0.5 probability in a non-expanding mode. The values next to “CLAHE” mean the clip limit parameter values, while those next to “Smoothing” represent the kernel sizes, and the numbers next to “Sharpen” denote the values.

Table 3.
Accuracy of the single image preprocessing methods.
Additionally, we provide the training and inference times of all models in the table. It is worth noting that the training times represent the average training times of eight models for each preprocessing method. The inference times denote the time required to process the entire test images, rather than just one image. Typically, combination methods require more time than single methods, and the dataset-expanding mode also exhibited a longer runtime compared to the non-expanding mode. However, this was not always the case, as the early stopping mechanism with the specified patience value influenced the training times. For instance, model training without preprocessing (35′15″) took longer to complete than some other single methods.
4.1.1. Histogram Equalization
In this part of the exploration, we employ global histogram equalization across all data splits and aim to achieve a uniform and standardized image distribution. However, this approach did not yield the desired results. On the test split, the average and maximum accuracies were inferior to the original results obtained without any image processing. The average accuracy dropped from 80.48% to 75.24% (−5.24%) and the maximum accuracy decreased from 84.76% to 80% (−4.76%). On the Jōmon–Yayoi split, the maximum accuracy improved from 62.5% to 65.63% (+3.13%) and the average accuracy improved slightly from 60.16% to 60.35% (+0.19%).
Similar outcomes were observed when global histogram equalization was combined with image smoothing, which led to a decrease in both the average accuracy and maximum accuracy on the test split by 10.48% and 10.47%, respectively. On the Jōmon–Yayoi split, the average and maximum accuracy slightly improved by 1.17% and 1.56%, respectively. Based on these results, we decided not to utilize global histogram equalization in any of the further experiments.
Our suspicion arises from the substantial alteration introduced to the original image. This discrepancy becomes evident when examining Figure 2, where the visual appearance of the resulting image differs significantly from the original. This transformation leads to the loss of fine details in certain important image regions, caused by the global equalization carried out through histogram equalization. This challenge could be addressed by adopting localized histogram equalization methods, e.g., contrast limited adaptive histogram equalization (CLAHE).
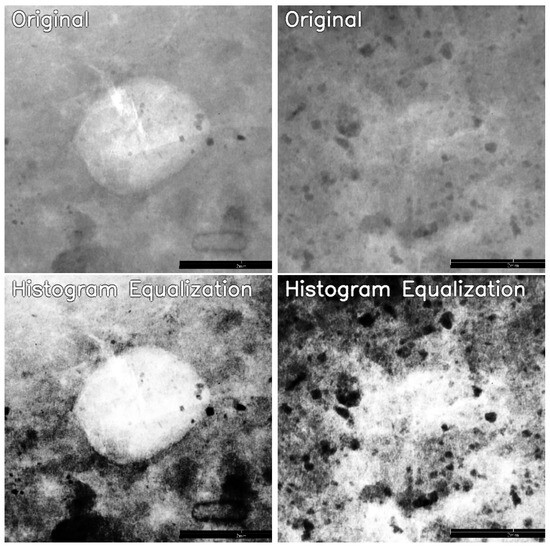
Figure 2.
The effect of histogram equalization. In the bottom row are the processed images from the input images in the top row.
4.1.2. Adaptive Histogram Equalization
This experiment applied contrast-limited adaptive histogram equalization (CLAHE) to all images in all splits. We varied the clip limit values while keeping the number of blocks fixed at . We experimented with values ranging from 2 to 8 for the clip limit parameter.
On the test split, the results revealed a positive correlation between the clip limit values and both the average accuracy and maximum accuracy up to the clip limit value of 7. According to this experiment, the optimal clip limit was 6 which yielded an average accuracy of 81.31% the highest maximum accuracy in this experiment of 85.71%. It was an improvement over the results obtained without preprocessing of 0.83% and 0.95% in terms of average accuracy and maximum accuracy, respectively. For the clip limit of 7, the average accuracy as well as the maximum accuracy declined significantly.
In contrast, the pattern found on the test split does not apply in the Jōmon–Yayoi split, where the positive correlation occurred only up to the clip limit of 5. Interestingly, unlike the test split, positive outcomes were observed in this split. It achieved the highest average accuracy of 65.43% and the highest maximum accuracy of 70.31%. These results outperformed the average accuracy and the maximum accuracy obtained without any image preprocessing by 5.27% and 7.81%, respectively. This aligns with the results presented in [4], where their proposed multi-preprocessing for retinal microaneurysm detection, which incorporates adaptive histogram equalization, demonstrated a higher F-score of 57% compared to the scenario without multi-preprocessing of 48.5%. Similarly, in [35], it was noted that utilizing CLAHE as a preprocessing step led to a substantial accuracy improvement of 17.83% in predicting diabetic retinopathy based on retinal images.
In addition, it is worth noting that the highest accuracy in this study on the test split and Jōmon–Yayoi split was obtained with different clip limit values. This difference arises from the fact that the images in the Jōmon–Yayoi split inherently have higher contrast levels compared to those in the test split. Since a higher clip limit value results in a stronger contrast-enhancing effect, the images in the test split required a higher clip limit value. Consequently, the optimal clip limit value for the test split was higher than that for the Jōmon–Yayoi split. Hence, this highlights opportunities for future research to standardize images with varying conditions, enabling the consistent application of procedures that perform well across all images.
4.1.3. Smoothing
In this part, we varied the kernel sizes to investigate the impact of image detail reduction resulting from image smoothing and its influence on overall classification accuracy. Specifically, we examined kernel sizes of 3, 5, 7, 9, and 11. This smoothing operation was uniformly applied to all images across all data splits to ensure that the models were trained and tested using images processed consistently. On the test split, it appears that the kernel size does not exhibit a clear correlation with the maximum accuracy. However, a positive correlation is observed between the kernel size and the average accuracy. The highest average accuracy of 81.9% was achieved using a kernel size of 9. Conversely, using a kernel size of 11 resulted in a decline in the average accuracy to 80%. However, despite the presence of correlation, both the highest average accuracy and the highest maximum accuracy were lower compared to those achieved without any image preprocessing. This suggests that, for the test split, smoothing removed image details that are essential for accurate classification.
On the other hand, a positive correlation between the kernel size and both the average accuracy and maximum accuracy was found in the Jōmon–Yayoi split. The highest maximum accuracy of 71.88% was achieved when employing a kernel size of 9. This is also the highest accuracy achieved across all experiments on the Jōmon–Yayoi split. The maximum accuracy decreased to 70.31% when using a kernel size of 11. This observation suggests that a kernel size of 11 is excessively large and results in the removal of too many image details. Consequently, we opted to use a kernel size of 9 for combining smoothing with other image preprocessing methods to construct combined image preprocessing pipelines. Moreover, in contrast to the outcomes from the test split, image smoothing led to significantly higher accuracy compared to the results obtained without any image preprocessing. This observation makes sense because our images in the Jōmon–Yayoi split, as depicted in Figure 3, contain a considerable amount of noise which can interfere with the classification process. As a result, smoothing the images recovered their quality and led to an improvement in the classification accuracy. This is one of the significant challenges in this study, due to the different image conditions in the Jōmon–Yayoi images and the experimental images. Future research could focus on developing a method to harmonize these two image types.
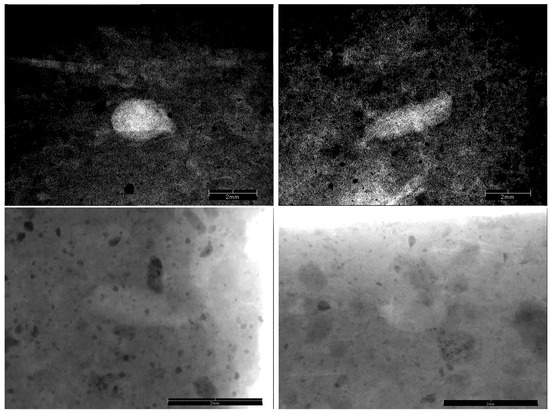
Figure 3.
Images from the Jōmon–Yayoi split (top row) with different conditions from those in the train and test splits (bottom row).
This outcome aligns with findings from other studies that utilized image smoothing/noise reduction which shows its positive impact on overall performance. In [36], image smoothing via bilateral filtering improved the image quality measured in peak signal-to-noise ratio (PSNR) by ∼2 points, while in [37], image denoising improved the system’s accuracy by 1–3 percent.
4.1.4. Sharpening
In this section, different values that control the visibility of the sharpened image on the original image were applied to investigate if there is any relationship between the amount of high frequency on the images and the classification accuracy. We tried values of 0.2, 0.3, 0.4, and 0.5. Similar to smoothing, we uniformly apply sharpening to all images across all data splits.
In the test split, applying sharpening to the images resulted in higher average accuracy and maximum accuracy compared to the accuracy obtained without any image preprocessing. An value of 3 demonstrates the highest average accuracy of 82.5% and the highest maximum accuracy of 84.76%. However, this did not improve the accuracy from that obtained without preprocessing and there was no correlation found between and the accuracy.
On the contrary, this was different from the observation found in the Jōmon–Yayoi split, where a negative correlation was found between the two values. The highest average accuracy of 60.55% and the highest maximum accuracy of 68.75% was obtained using . These were 0.39% and 6.25% higher than the accuracy obtained without image preprocessing. These findings suggest that employing image sharpening with appropriate adjustments in intensity is an effective preprocessing technique for archaeological images. A comparable observation is reported in [5], where it is noted that image sharpening substantially improves the accuracy of chest CT-scan and X-ray image classification.
In addition, distinct impacts of sharpening were evident in the two splits. Accuracy on the test split generally surpassed that achieved through image smoothing. However, in the Jōmon–Yayoi split, the situation was reversed, with accuracy dropping below that of smoothing. This discrepancy arose from the high-frequency nature of images in the Jōmon–Yayoi split, where sharpening adversely affected image quality. In contrast, images in the test split lacked high-frequency elements, leading to improved image quality and subsequently enhanced classification accuracy with sharpening.
4.1.5. Rotations, Flips, and Transposition
Increasing the variability of the train set via image rotations, flips, and transposition demonstrated satisfactory results, which were evident in both the test split and the Jōmon–Yayoi split. Each method was explored in both dataset-expanding and non-expanding modes. Moreover, individual and combined orientations for image rotations and image flips were tested in this experiment.
For the Jōmon–Yayoi split, the best average accuracy and maximum accuracy of 66.80% and 73.44% were obtained using all rotations in dataset-expanding mode. These were 6.64% and 10.94% higher than the average and maximum accuracies attained with no image preprocessing.
Similar positive results were collected using dataset-expanding image transpose and flips. Favorable results were also established in the test split, achieving the highest maximum accuracy and average accuracy across all single methods with 87.62% and 85.48%, which were 2.86% and 5% higher than the no-preprocessing performance. This indicates that image rotations, flips, and transposition were effective as image augmentation techniques and contributed to the improved generalization of the classification model. These outcomes motivated the combination of these methods, which is discussed in Section 4.2.2.
It is noteworthy that combining all directions of image rotations (90°, 180°, and 270°) together resulted in higher maximum and average accuracy than using each direction individually. Similarly, employing both vertical and horizontal flips together tended to lead to higher average accuracy compared to using them separately. This observation held for both the test split and the Jōmon–Yayoi split. In the context of the Jōmon–Yayoi split, employing all directions for image rotations, flips, and transposition in the dataset-expanding mode resulted in superior performance compared to the non-expanding mode.
4.1.6. Grid Distortion and Elastic Transformation
This experiment utilized the dataset-expanding and non-expanding modes for both grid distortion and elastic transformation. On the test split, the highest average accuracy of 81.79% was slightly better compared to that obtained without any image preprocessing, which is 80.48% (+0.83%). The maximum accuracy showed a more substantial improvement, rising to 87.62% from 84.76% (+2.86%). On the Jōmon–Yayoi split, the improvements were even more prominent. The improvements in the average accuracy and maximum accuracy were 5.47% and 10.94%, respectively.
These findings demonstrate the effectiveness of both grid distortion and elastic transformation as valuable image augmentation methods that help improve image variability within the train set. More specifically, the variation introduced by grid distortion and elastic transformation is in terms of the shape of the objects rather than alterations in contrast and illuminance levels. Therefore, higher improvements in the Jōmon–Yayoi split compared to the test split imply that there is higher object shape variation in the Jōmon–Yayoi split, which was collected in real-world conditions, than in the test split, which was acquired in laboratory settings. Therefore, it can be inferred that enhancing the variety of object shapes during training becomes important, particularly when dealing with images that have diverse shapes.
4.2. Combination Methods
The outcomes of the combination methods are detailed in Table 4. The symbols used are consistent with those in Table 3.

Table 4.
Accuracy of the combination image preprocessing pipelines.
4.2.1. Adaptive Histogram Equalization and Smoothing
Next, in this and the subsequent experiments, the combination pipelines are demonstrated. In this experiment, CLAHE was combined with image smoothing where CLAHE was applied first to the input image before smoothing. Based on the experiment in image smoothing, the best kernel size was 9. Thus, the same kernel size was used in this experiment and it was kept fixed. The only variable tested in this experiment was the clip limit of the CLAHE, specifically the clip limit of 2 to 5.
On the Jōmon–Yayoi split, the highest average accuracy was obtained using the clip limit of 2 which achieved 69.92%. This was higher than the highest average accuracy obtained using CLAHE and image smoothing applied individually, which was 65.43% and 67.58%, respectively. It was also significantly higher than the average accuracy and maximum accuracy yielded without any image preprocessing, which was 60.16% and 62.5%, respectively, i.e., an improvement of 9.76% and 7.42%. This suggests that this particular combination is effective.
However, this combination resulted in no improvements in the test split, where the highest maximum accuracy declined to 81.9% and the average accuracy declined by 1.31%. The performance was also inferior to the case when only CLAHE was implemented. This corresponds with the findings from the experiment on image smoothing alone and reveals its unsuitability for the test split, even in conjunction with CLAHE. Image smoothing likely removes crucial details in the images and leads to the observed decrease in classification performance.
4.2.2. Rotations, Flips, and Transposition
Following the favorable outcomes observed with rotations, flips, and transposition applied individually to the train set, they were combined in this experiment. It was also found that better outcomes were observed in a dataset-expanding mechanism than in a non-expanding mode. That is, the size of the train set expanded proportionally with the number of combined methods applied. For instance, when flips (vertical and horizontal) were combined with transposition, the size of the train set would expand by a factor of 4, which would contain the original images, vertically flipped images, horizontally flipped images, and transposed images. Therefore, image rotations, flips, and transposition were applied in a dataset-expanding mode in this experiment. Of these three methods, we experimented with every combination, i.e., rotations and flips, rotations and transposition, flips and transposition, as well as using all three methods together.
On the test split, the best accuracy score was obtained by combining rotations and transposition, attaining 89.52% maximum accuracy and 85.24% average accuracy. The accuracy values from these methods exceeded the accuracy achieved when each method was applied separately. This underscores the effectiveness of combining different methods. Moreover, this performance was among the highest recorded throughout all the experiments.
Furthermore, during the experimentation where two out of the three methods (rotations, flips, and transposition) were utilized, excluding flips and transposition did not result in a performance drop. However, removing image rotations led to an average accuracy decrease of 3%. This suggests that among these three methods, image rotations play the most crucial role in performance enhancement. Indeed, while image rotations are pivotal, it’s essential not to underestimate the significance of image flips and transpositions. As detailed in Section 4.1.5, the experiment demonstrates that relying solely on image rotations yielded lower accuracy compared to combining rotations with flips or transposition. Therefore, the most effective approach is to combine all three of these methods.
On the Jōmon–Yayoi split, among all the combinations, the highest accuracy was obtained from the combination of all three methods. Although not one of the best accuracy throughout all the experiments, the results were positive with 73.44% maximum accuracy and 69.73% average accuracy. This indicates that introducing variations in image orientations proves to be effective in enhancing the diversity of the training set and leads to improved classification performance. Hence, these methods were combined with more image preprocessing methods in the following experiments.
When comparing the results of combinations involving two out of the three methods, it is worth noting that combinations including image flips tended to yield slightly lower maximum accuracy, although the difference was not significant. The presence of size indicators in the bottom-right corners of some images in the Jōmon–Yayoi split might have influenced these results. Even after being resized to a square shape, a portion of these indicators remains in the final image inputted to the network. This can be observed by comparing Figure 3, which depicts the original images before resizing to 400 × 400 pixels, and Figure 2, which displays the images after resizing to 400 × 400. Vertical flips relocated these indicators to the upper part of the image and potentially caused disruptions in the classification process. Therefore, as a part of future work, developing procedures to address this issue could potentially enhance the overall performance of the system.
4.2.3. Rotations, Flips, Transposition, Grid Distortion, and Elastic Transformation
The conducted experiments involving individual image rotations, flips, and transposition, as well as grid distortion and elastic transformation, have yielded promising outcomes. Therefore, in this experiment setup, those methods were combined to verify if their combined application could further augment the results. However, it is noteworthy that grid distortion and elastic transformation were not combined. This decision was made because both methods alter the entire shape of the image significantly, and combining them would result in an alteration that is excessively pronounced.
The combination of image rotations, flips, and transposition, coupled with elastic transformation, reached an accuracy of 71.88% on the Jōmon–Yayoi split and 87.62% on the test split. Meanwhile, when these transformations were employed in conjunction with grid distortion, they showed quite comparable performance on the Jōmon–Yayoi split. However, the combined effect displayed notably improved results on the test split and achieved an accuracy of 88.57%.
4.2.4. Adaptive Histogram Equalization, Smoothing, Rotations, Flips, and Transposition
The combination of CLAHE and image smoothing demonstrated positive results in the previous experimentation, particularly for the Jōmon–Yayoi split. Thus, in this experiment, they were combined with rotations, flips, and transposition, demonstrating one of the highest outcomes in the preceding experiment when they were applied individually. Additionally, it was found that combining rotations, flips, and transposition altogether resulted in the best accuracy. Therefore, the same combination of those methods was employed as well in this experiment. For image smoothing, the kernel size was constantly fixed to 9. Hence, one variable that was examined here is the clip limit of the CLAHE, with values of 2 to 8.
For the test split, as explained in the preceding sections, when CLAHE and smoothing were applied separately and in combination, the average accuracy declined compared to the scenario without image preprocessing. Nonetheless, our interest lies in experimenting with a combination of these two filters along with image rotations, flips, and transposition. The maximum accuracy on the test split was 88.57%, while the highest average accuracy achieved was 84.05%. These results demonstrate that the performance surpasses that of when CLAHE and image smoothing were applied individually. This implies that the combination is effective, and that image rotations, flips, and transposition methods are particularly beneficial for enhancing the performance on the test split.
On the other hand, we achieved the best result for the Jōmon–Yayoi split throughout all experiments with a maximum accuracy of 78.13% and an average accuracy of 71.88%. This was a strong result obtained by incorporating different image preprocessing methods and outperformed the best results from our previous study [13] by 10.13%.
4.2.5. Adaptive Histogram Equalization, Rotations, Flips, and Transposition
The setup in this experiment was identical to the previous one, except that image smoothing was omitted. This was motivated by the results of the experiment on the test split using CLAHE, which demonstrated better compared to when CLAHE was combined with image smoothing. The results confirmed this motivation as both the highest maximum accuracy as well as the highest average accuracy were the highest for the test split throughout this entire study. The highest maximum accuracy and the highest average accuracy were 90.48% and 84.17%, respectively. Furthermore, this experiment reaffirms that image smoothing was not suitable for improving images in the test split.
However, the opposite condition applied in the Jōmon–Yayoi split, as the accuracy scores were lower than that when image smoothing was included in the combination. The best maximum accuracy decreased from 78.13% to 73.44% (−4.69%), while the average accuracy dropped from 71.88% to 69.14% (−2.74%). This suggests that image smoothing was essential to enhance the quality of the images in the Jōmon–Yayoi split, given that many of these images contained excessive high-frequency elements.
4.3. K-Fold Cross-Validation
To validate the results of the system, we conducted a 10-fold cross-validation using the model that yielded the best outcome, comprising the combination of CLAHE (with clip limit value of 3), smoothing, rotations, flips, and transposition. The findings are detailed in Table 5. During the validation process, we observed an average accuracy of 85.43% across the 10 folds for the test split. Although this was slightly lower than the best average accuracy of 85.6% achieved in previous experiments, it still demonstrates the robustness of our model. Similarly, for the Jōmon–Yayoi split, the average accuracy across the 10 folds was 71.72%, which also showed a minor decrease compared to the best average accuracy of 72.46% from previous experiments. These slight variations validate our earlier findings of our experimental outcomes.

Table 5.
Results of 10-fold cross-validation.
4.4. Class Activation Maps (CAMs)
Deep learning architectures present a notable challenge due to the inherent opacity of their derived features and decision-making processes. This lack of transparency often hinders the ability to provide clear explanations for the model’s decisions, making them similar to “black boxes”. A promising approach towards interpretability lies in class activation maps (CAMs), as proposed in [38]. CAMs offer a visual means to unravel this black box by showing specific areas within an image where these architectures concentrate their attention during classification. These maps, depicted as heatmap images, illuminate regions in red, highlighting the network’s focus points.
In Figure 4, two image samples from each class in the dataset are presented alongside the CAM heatmaps generated from the network. These heatmaps originate from the network trained using both preprocessed and non-preprocessed training images. They provide a visual insight into the impact of dataset preprocessing on the network’s attention focus. Specifically, the CAMs derived from the model trained on preprocessed images distinctly reveal an improved emphasis on the objects within the images over their counterparts from the non-preprocessed dataset, for example, in columns (a), (b), and (c). There were some cases in columns (c), (h), and (l) where misclassifications were made by a model trained without image preprocessing which were then corrected by proper image preprocessing.

Figure 4.
Samples of the original images from each class: (a,b) ailanthoides; (c,d) barley; (e,f) maize weevil; (g,h) millet; (i,j) perilla; (k,l) rice; and (m,n) wheat. Below the images on the “input” rows are the true labels. The second and third rows show the class activation map (CAM) heatmaps. Below the images on the “baseline” and “proposed” rows are the predicted labels using the corresponding image preprocessing.
Despite the improvement facilitated by image preprocessing, certain challenges persisted, notably in cases where the model struggled to differentiate between similar objects, as observed in columns (i), (j), and (k) between Perilla and Rice. Thus, while dataset preprocessing enhances the focus within CAMs, it also highlights ongoing challenges and indicates directions for future investigation and improvement in deep learning model architectures.
5. Conclusions
In this study, we thoroughly investigated different image preprocessing techniques for deep learning-based archaeological image classification as well as the combinations. We demonstrated that combining different image processing methods is more effective than applying the methods individually. Our observations indicate that 66% of single methods and 90% of combination methods yielded higher accuracies compared to no image preprocessing. Furthermore, 55% of methods on test images and 98% on Jōmon–Yayoi images led to improved accuracies. This highlights the significance of preprocessing, especially for images with higher noise levels and under challenging conditions.
The best accuracy scores in our experiments for the test split and the Jōmon–Yayoi split were 90.48% and 78.13%, respectively. These were superior to those obtained in our previous study [13] which did not involve any image preprocessing procedures, by 10.13%.
Author Contributions
Conceptualization, H.O. and I.M.; methodology, I.M.; software, R.C.W. and M.D.; validation, R.C.W. and M.D.; formal analysis, M.A.; investigation, M.A.; resources, Y.L. and H.O.; data curation, Y.L. and H.O.; writing—original draft preparation, R.C.W.; writing—review and editing, R.C.W., I.M. and M.A.; visualization, R.C.W.; supervision, M.A.; project administration, I.M. and H.O.; funding acquisition, H.O. All authors have read and agreed to the published version of the manuscript.
Funding
This work was part of the DRA project funded by the Japan Society for the Promotion of Science KAKENHI Grant-in-Aid for Transformative Research Areas (A) titled “Development of cavity detection method and identification method using X-ray equipment” [grant number 20H05810X].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sajedi, H.; Pardakhti, N. Age Prediction Based on Brain MRI Image: A Survey. J. Med. Syst. 2019, 43, 279. [Google Scholar] [CrossRef]
- Ullah, Z.; Farooq, M.U.; Lee, S.H.; An, D. A hybrid image enhancement based brain MRI images classification technique. Med. Hypotheses 2020, 143, 109922. [Google Scholar] [CrossRef]
- ul Rehman, A.; Qureshi, S.A. A review of the medical hyperspectral imaging systems and unmixing algorithms’ in biological tissues. Photodiagnosis Photodyn. Ther. 2021, 33, 102165. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, Y.; Gong, Q.; Yao, J. Automatic detection of microaneurysms in fundus images based on multiple preprocessing fusion to extract features. Biomed. Signal Process. Control 2023, 85, 104879. [Google Scholar] [CrossRef]
- Ahamed, K.U.; Islam, M.; Uddin, A.; Akhter, A.; Paul, B.K.; Yousuf, M.A.; Uddin, S.; Quinn, J.M.; Moni, M.A. A deep learning approach using effective preprocessing techniques to detect COVID-19 from chest CT-scan and X-ray images. Comput. Biol. Med. 2021, 139, 105014. [Google Scholar] [CrossRef]
- Sarwinda, D.; Paradisa, R.H.; Bustamam, A.; Anggia, P. Deep Learning in Image Classification using Residual Network (ResNet) Variants for Detection of Colorectal Cancer. Procedia Comput. Sci. 2021, 179, 423–431. [Google Scholar] [CrossRef]
- Shakeel, P.M.; Burhanuddin, M.; Desa, M.I. Lung cancer detection from CT image using improved profuse clustering and deep learning instantaneously trained neural networks. Measurement 2019, 145, 702–712. [Google Scholar] [CrossRef]
- Mall, P.K.; Singh, P.K.; Yadav, D. GLCM Based Feature Extraction and Medical X-RAY Image Classification using Machine Learning Techniques. In Proceedings of the 2019 IEEE Conference on Information and Communication Technology, Allahabad, India, 6–8 December 2019; pp. 1–6. [Google Scholar]
- Heidari, M.; Mirniaharikandehei, S.; Khuzani, A.Z.; Danala, G.; Qiu, Y.; Zheng, B. Improving the performance of CNN to predict the likelihood of COVID-19 using chest X-ray images with preprocessing algorithms. Int. J. Med. Inform. 2020, 144, 104284. [Google Scholar] [CrossRef]
- Mungra, D.; Agrawal, A.; Sharma, P.; Tanwar, S.; Obaidat, M.S. Pratit: A CNN-based emotion recognition system using histogram equalization and data augmentation. Multimed. Tools Appl. 2019, 79, 2285–2307. [Google Scholar] [CrossRef]
- Beeravolu, A.R.; Azam, S.; Jonkman, M.; Shanmugam, B.; Kannoorpatti, K.; Anwar, A. Preprocessing of Breast Cancer Images to Create Datasets for Deep-CNN. IEEE Access 2021, 9, 33438–33463. [Google Scholar] [CrossRef]
- Sarki, R.; Ahmed, K.; Wang, H.; Zhang, Y.; Ma, J.; Wang, K. Image preprocessing in classification and identification of diabetic eye diseases. Data Sci. Eng. 2021, 6, 455–471. [Google Scholar] [CrossRef] [PubMed]
- Mendonça, I.; Miyaura, M.; Fatyanosa, T.N.; Yamaguchi, D.; Sakai, H.; Obata, H.; Aritsugi, M. Classification of unexposed potsherd cavities by using deep learning. J. Archaeol. Sci. Rep. 2023, 49, 104003. [Google Scholar] [CrossRef]
- Masoudi, S.; Harmon, S.A.A.; Mehralivand, S.; Walker, S.M.; Raviprakash, H.; Bagci, U.; Choyke, P.L.; Turkbey, B. Quick guide on radiology image pre-processing for deep learning applications in prostate cancer research. J. Med. Imaging 2021, 8, 010901. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 4th ed.; Prentice Hall: Hoboken, NJ, USA, 2007. [Google Scholar]
- Wang, S.; Celebi, M.E.; Zhang, Y.D.; Yu, X.; Lu, S.; Yao, X.; Zhou, Q.; Miguel, M.G.; Tian, Y.; Gorriz, J.M.; et al. Advances in Data Preprocessing for Biomedical Data Fusion: An Overview of the Methods, Challenges, and Prospects. Inf. Fusion 2021, 76, 376–421. [Google Scholar] [CrossRef]
- Kaur, C.; Garg, U. Artificial intelligence techniques for cancer detection in medical image processing: A review. Mater. Today Proc. 2023, 81, 806–809. [Google Scholar] [CrossRef]
- Chlap, P.; Min, H.; Vandenberg, N.; Dowling, J.; Holloway, L.; Haworth, A. A review of medical image data augmentation techniques for deep learning applications. J. Med. Imaging Radiat. Oncol. 2021, 65, 545–563. [Google Scholar] [CrossRef] [PubMed]
- Khalifa, N.E.; Loey, M.; Mirjalili, S. A comprehensive survey of recent trends in deep learning for digital images augmentation. Artif. Intell. Rev. 2022, 55, 2351–2377. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Q.; Yang, M.; Tian, X.; Jiang, N.; Wang, D. A Full Stage Data Augmentation Method in Deep Convolutional Neural Network for Natural Image Classification. Discret. Dyn. Nat. Soc. 2020, 2020, 4706576. [Google Scholar] [CrossRef]
- Elgendi, M.; Nasir, M.U.; Tang, Q.; Smith, D.; Grenier, J.P.; Batte, C.; Spieler, B.; Leslie, W.D.; Menon, C.; Fletcher, R.R.; et al. The Effectiveness of Image Augmentation in Deep Learning Networks for Detecting COVID-19: A Geometric Transformation Perspective. Front. Med. 2021, 8, 629134. [Google Scholar] [CrossRef]
- Dhal, K.G.; Das, A.; Ray, S.; Gálvez, J.; Das, S. Histogram equalization variants as optimization problems: A Review. Arch. Comput. Methods Eng. 2020, 28, 1471–1496. [Google Scholar] [CrossRef]
- Alwazzan, M.J.; Ismael, M.A.; Ahmed, A.N. A hybrid algorithm to enhance colour retinal fundus images using a wiener filter and clahe. J. Digit. Imaging 2021, 34, 750–759. [Google Scholar] [CrossRef] [PubMed]
- Pizer, S.M.; Amburn, E.P.; Austin, J.D.; Cromartie, R.; Geselowitz, A.; Greer, T.; ter Haar Romeny, B.; Zimmerman, J.B.; Zuiderveld, K. Adaptive histogram equalization and its variations. Comput. Vision Graph. Image Process. 1987, 39, 355–368. [Google Scholar] [CrossRef]
- Sheet, S.S.M.; Tan, T.S.; As’ari, M.; Hitam, W.H.W.; Sia, J.S. Retinal disease identification using upgraded CLAHE filter and transfer convolution neural network. ICT Express 2022, 8, 142–150. [Google Scholar] [CrossRef]
- Opoku, M.; Weyori, B.A.; Adekoya, A.F.; Adu, K. Clahe-CapsNet: Efficient retina optical coherence tomography classification using capsule networks with contrast limited adaptive histogram equalization. PLoS ONE 2023, 18, e0288663. [Google Scholar] [CrossRef] [PubMed]
- Kuran, U.; Kuran, E.C. Parameter selection for Clahe using multi-objective cuckoo search algorithm for image contrast enhancement. Intell. Syst. Appl. 2021, 12, 200051. [Google Scholar] [CrossRef]
- Hussein, F.; Mughaid, A.; AlZu’bi, S.; El-Salhi, S.M.; Abuhaija, B.; Abualigah, L.; Gandomi, A.H. Hybrid CLAHE-CNN Deep Neural Networks for Classifying Lung Diseases from X-ray Acquisitions. Electronics 2022, 11, 3075. [Google Scholar] [CrossRef]
- Simard, P.; Steinkraus, D.; Platt, J. Best practices for convolutional neural networks applied to visual document analysis. In Proceedings of the Seventh International Conference on Document Analysis and Recognition, 2003, Proceedings, Edinburgh, Scotland, 3–6 August; 2003; pp. 958–963. [Google Scholar]
- Buslaev, A.; Iglovikov, V.I.; Khvedchenya, E.; Parinov, A.; Druzhinin, M.; Kalinin, A.A. Albumentations: Fast and Flexible Image Augmentations. Information 2020, 11, 125. [Google Scholar] [CrossRef]
- Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A ConvNet for the 2020s. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 11966–11976. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Kolesnikov, A.; Dosovitskiy, A.; Weissenborn, D.; Heigold, G.; Uszkoreit, J.; Beyer, L.; Minderer, M.; Dehghani, M.; Houlsby, N.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. In Proceedings of the 9th International Conference on Learning Representations, Virtual, 3–7 May 2021. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 10, Virtual, 19–25 June 2021; pp. 10012–10022. [Google Scholar]
- Alwakid, G.; Gouda, W.; Humayun, M. Deep Learning-Based Prediction of Diabetic Retinopathy Using CLAHE and ESRGAN for Enhancement. Healthcare 2023, 11, 863. [Google Scholar] [CrossRef]
- Chen, S.; Li, Y.; Zhang, Y.; Yang, Y.; Zhang, X. Soft X-ray image recognition and classification of maize seed cracks based on image enhancement and optimized YOLOv8 model. Comput. Electron. Agric. 2024, 216, 108475. [Google Scholar] [CrossRef]
- Xiao, S.; Shen, X.; Zhang, Z.; Wen, J.; Xi, M.; Yang, J. Underwater image classification based on image enhancement and information quality evaluation. Displays 2024, 82, 102635. [Google Scholar] [CrossRef]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning Deep Features for Discriminative Localization. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2921–2929. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).