Secure and Fast Image Encryption Algorithm Based on Modified Logistic Map
Abstract
1. Introduction
- The proposed image encryption method gives a less computationally complex arrangement of the encryption/decryption process, making it lightweight without compromising on the security of the algorithm.
- The key used in the algorithm is the population growth of the modified chaotic logistic map. The keyspace is enhanced in comparison with the original chaotic logistic map.
- One-time substitution is performed in the proposed algorithm, which provides good SAC as compared to classical techniques.
- Various statistical and visual tests prove its resistance to linear and differential attacks.
1.1. Motivation
- Less computationally complex;
- Low-cost;
- Time-efficient;
- Provides lossless encryption.
1.2. Related Work
1.2.1. Importance of CLM
1.2.2. Image Encryption Techniques Based on Permutation
1.2.3. Image Encryption Techniques Based on Substitution
1.2.4. Image Encryption Techniques Based on Transformations
1.3. Objectives of the Research
1.4. Organization of the Paper
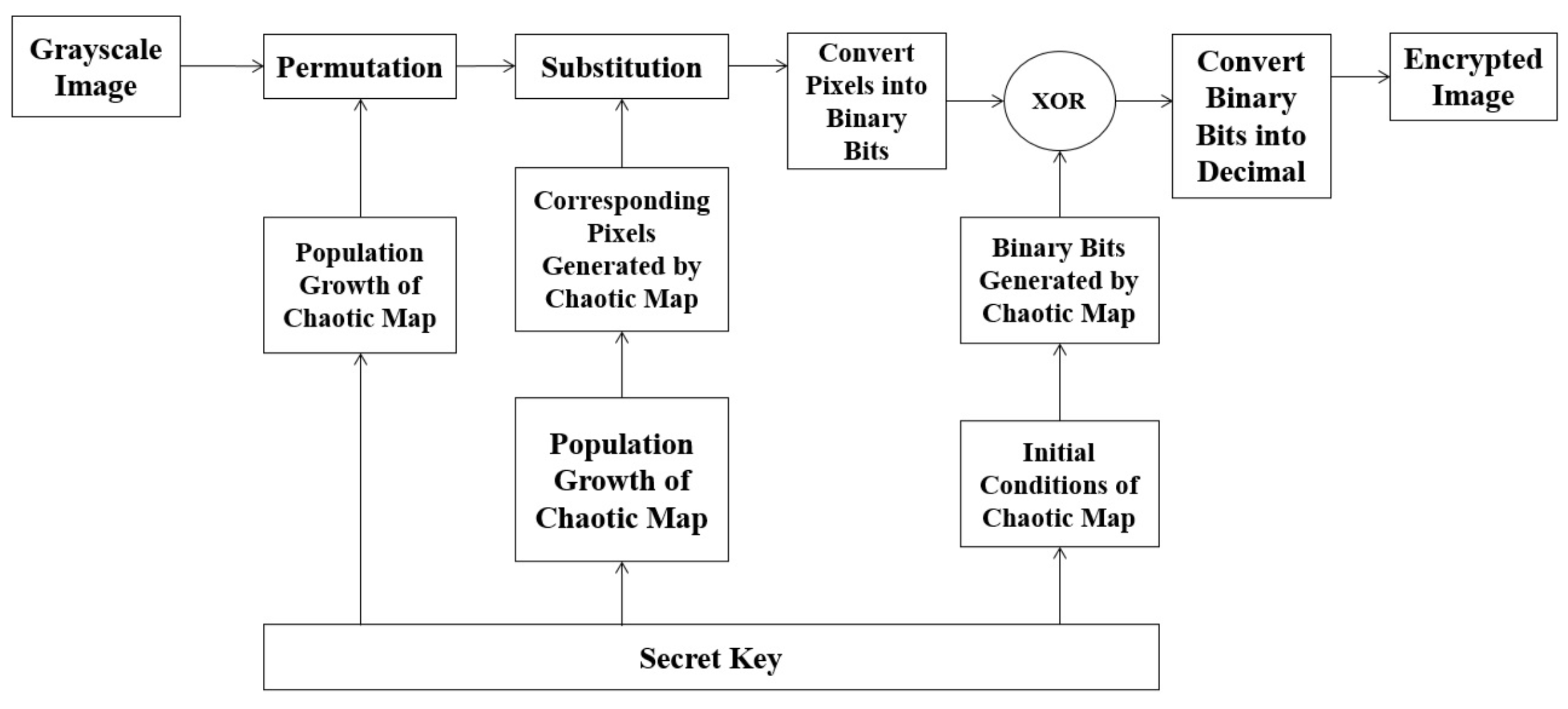
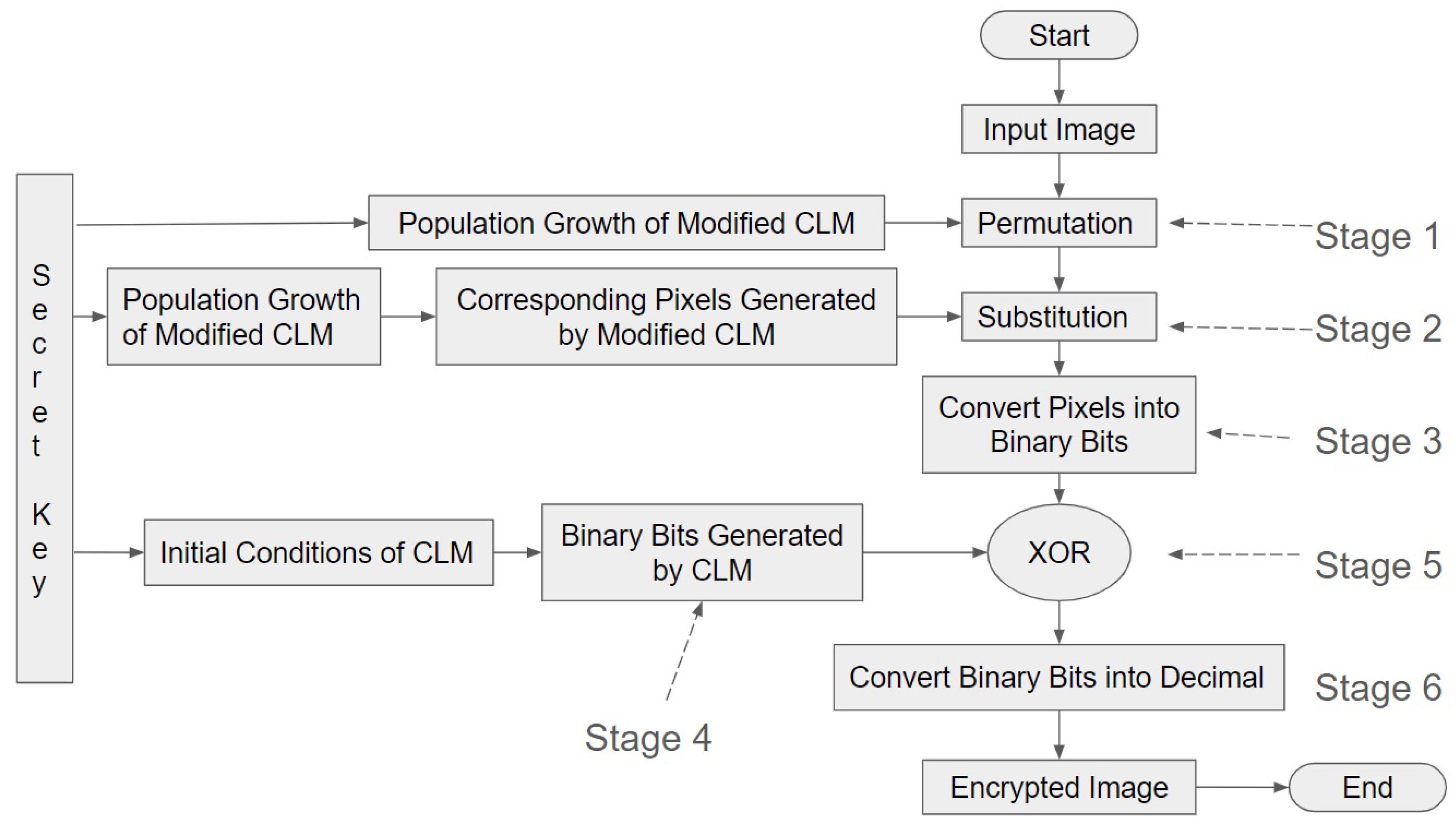
2. Proposed Algorithm
2.1. Permutation
2.1.1. Chaotic Logistic Map
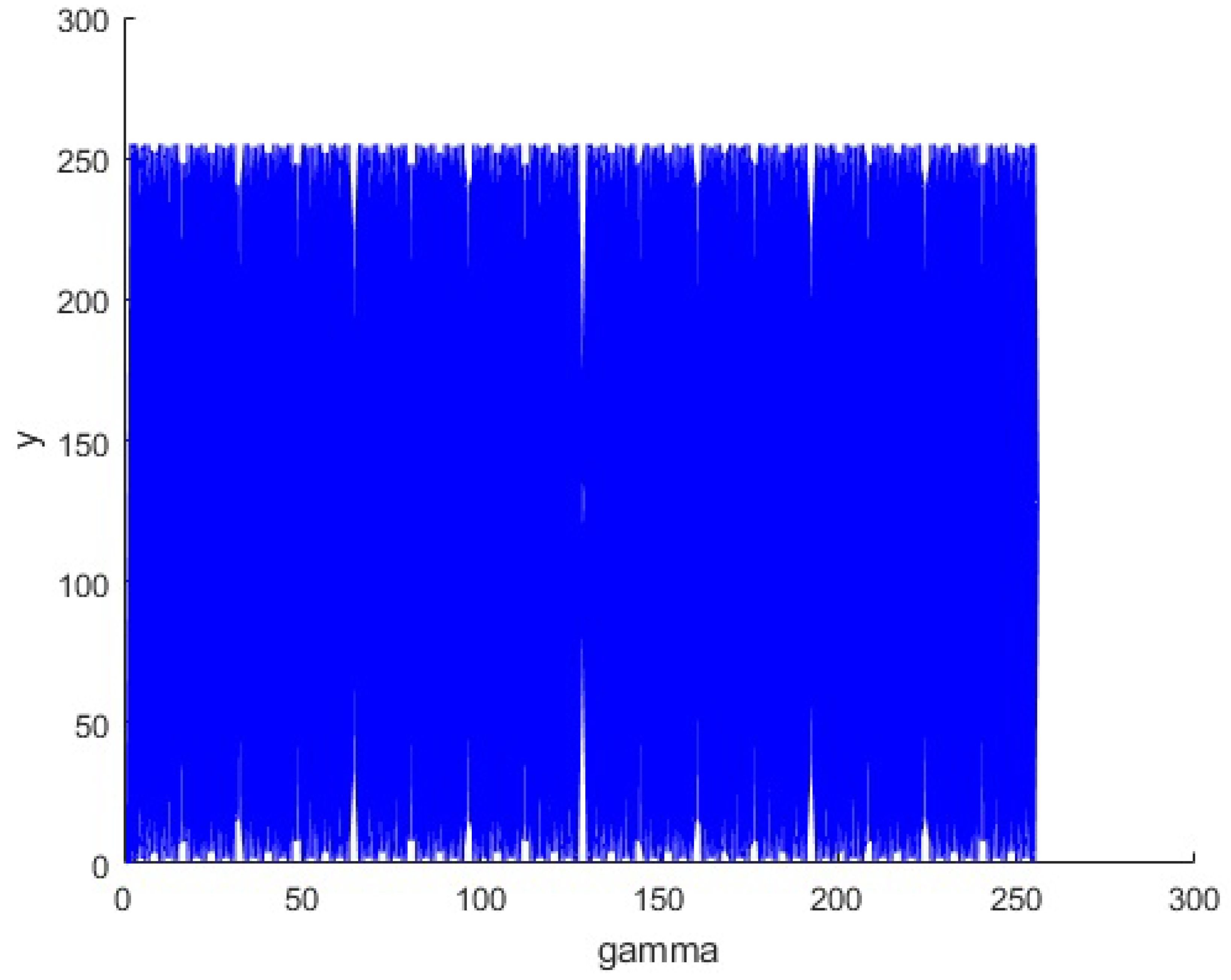
2.2. Behavior of the Modified CLM
2.3. Substitution
2.4. Binary Form of the Image
2.5. Bit Generation
2.6. XOR Operation
2.7. Conversion of Binary Bits to Encrypted Image
3. Pseudocode
3.1. Encryption
- Input image is substituted using modified CLM.
- Substituted image is then permuted using modified CLM.
- Substituted pixels are then converted into binary bits.
- Pseudorandom bits are evaluated from CLM.
- Binary bits from 3. and 4. are XORed together.
- Resultant bits are converted into pixels; therefore, an encrypted image is obtained.
3.2. Decryption
- Encrypted image is converted into binary bits.
- Pseudorandom bits are evaluated from CLM.
- Binary bits from 1. and 2. are XORed together.
- Binary bits are converted into pixels.
- Reverse operation of substitution is applied.
- Reverse operation of permutation is applied; therefore, an input image is obtained.
4. Results
4.1. Computational Analysis
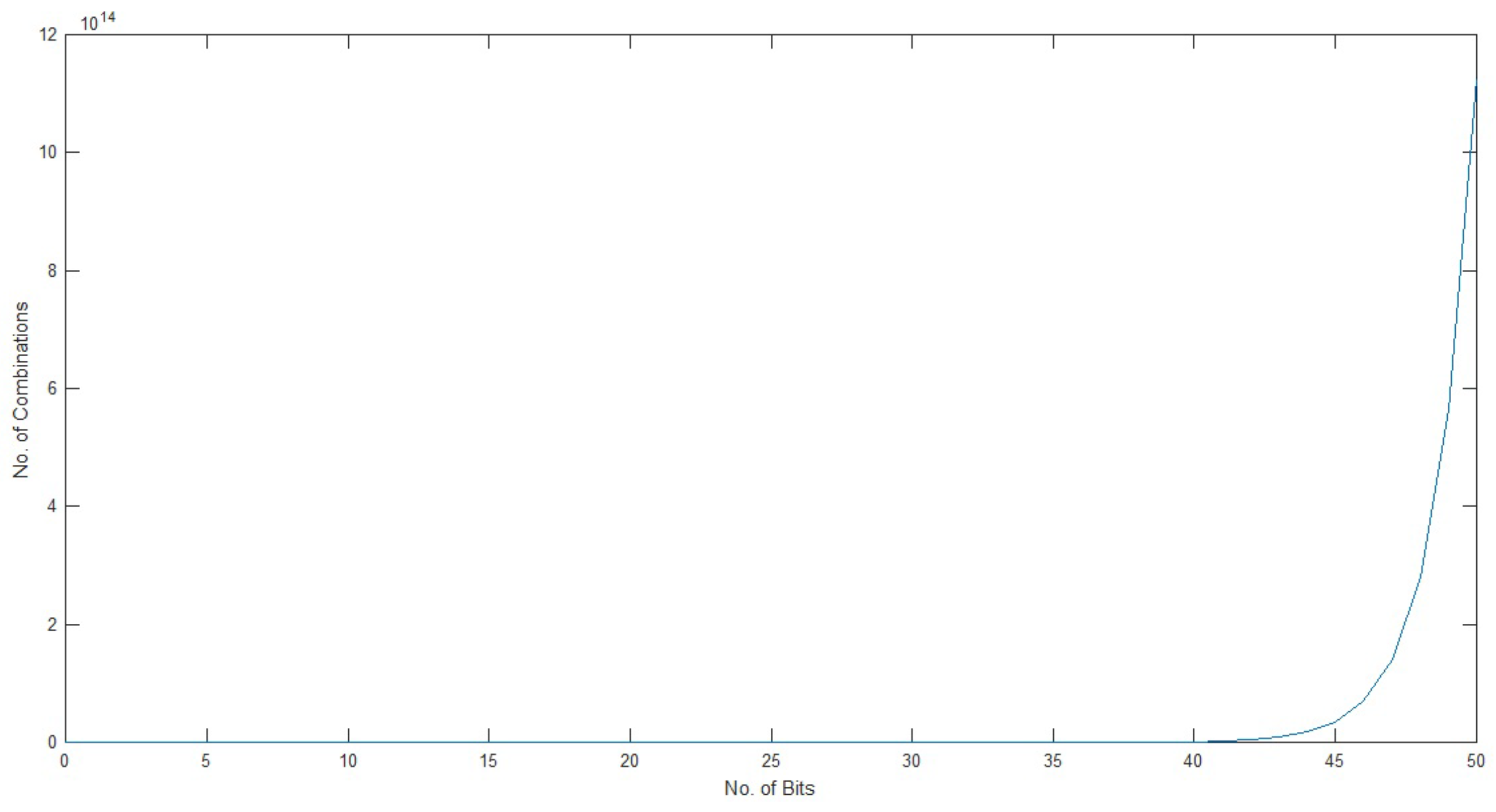
4.1.1. Keyspace Analysis
4.1.2. Complexity Analysis
4.2. Sensitivity Analysis
4.2.1. Number of Pixels Change Rate (NoPCR)
- cipher image of input image;
- cipher image of input image with one-bit change;
- matrix used to calculate difference between and ;
- breadth of the image;
- height of the image.
- x and y represent the positions of the pixel in the horizontal and vertical direction, respectively.
4.2.2. Unified Average Pixel Changing Intensity (UAPCI)
- cipher image of input image;
- cipher image of input image with one-bit change;
- breadth of the image;
- height of the image.
- x and y represent the positions of the pixel in the horizontal and vertical direction, respectively.
4.2.3. Strict Avalanche Criteria (SAC)
- original image;
- cipher image;
- exclusive OR operation.
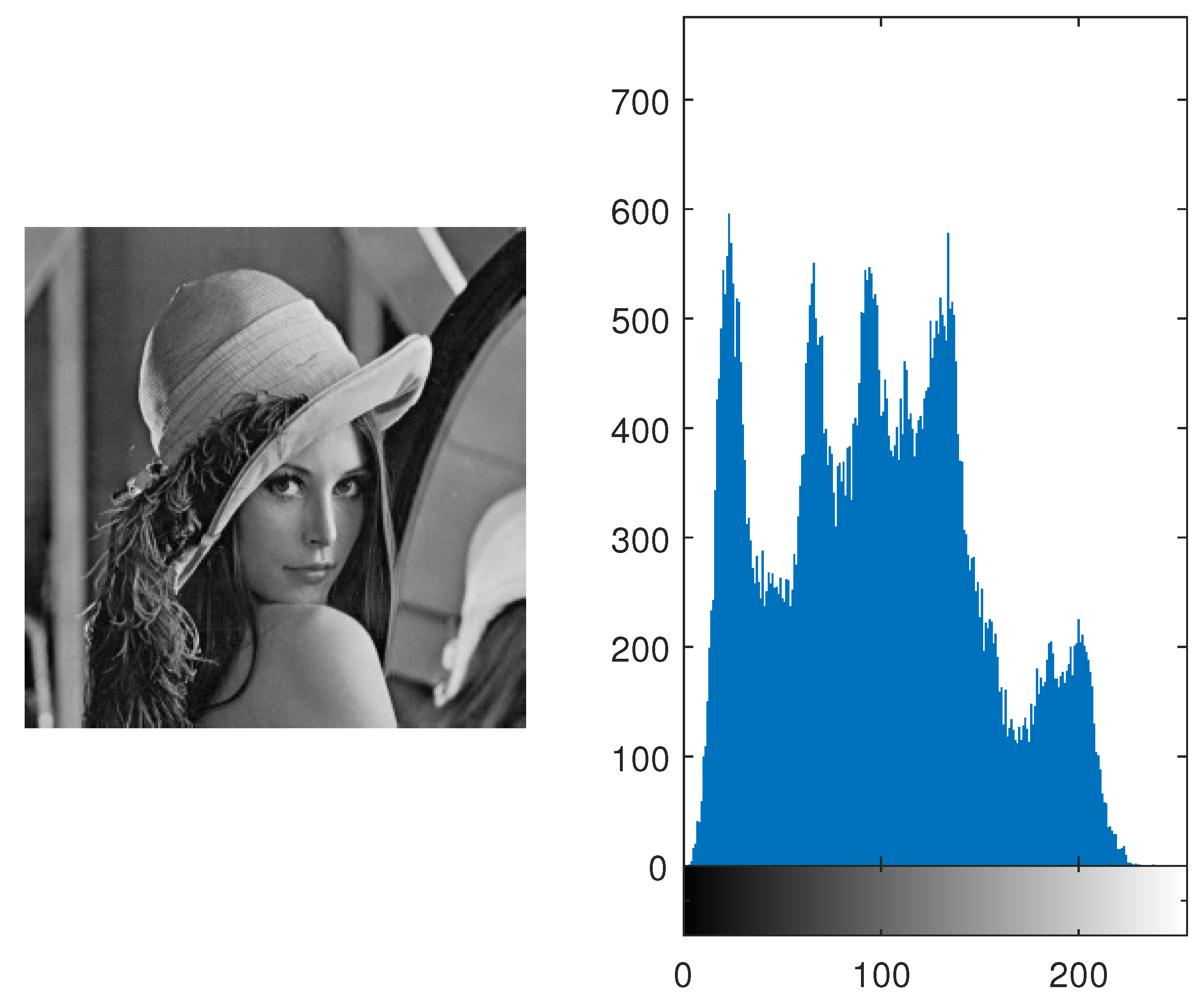
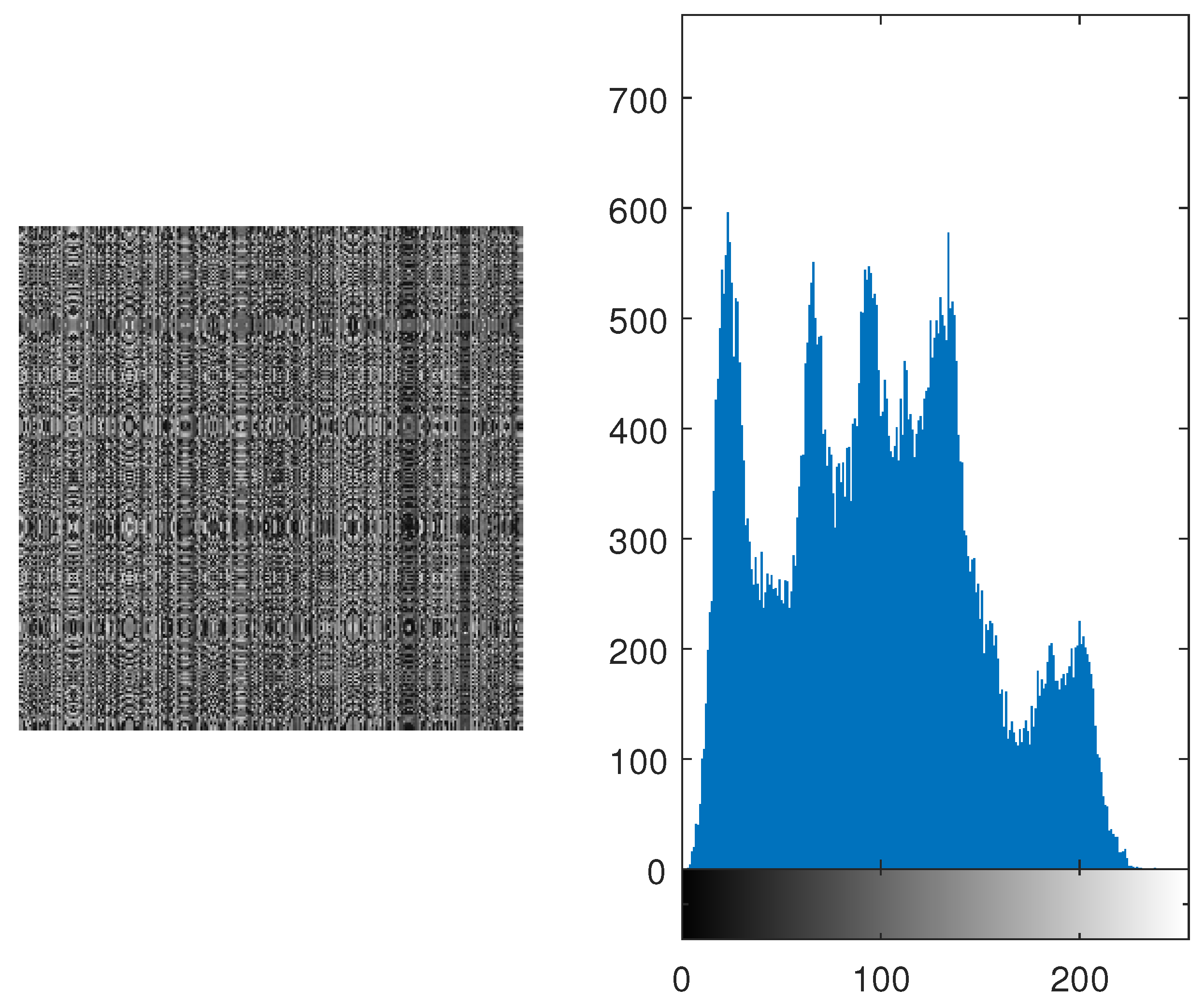
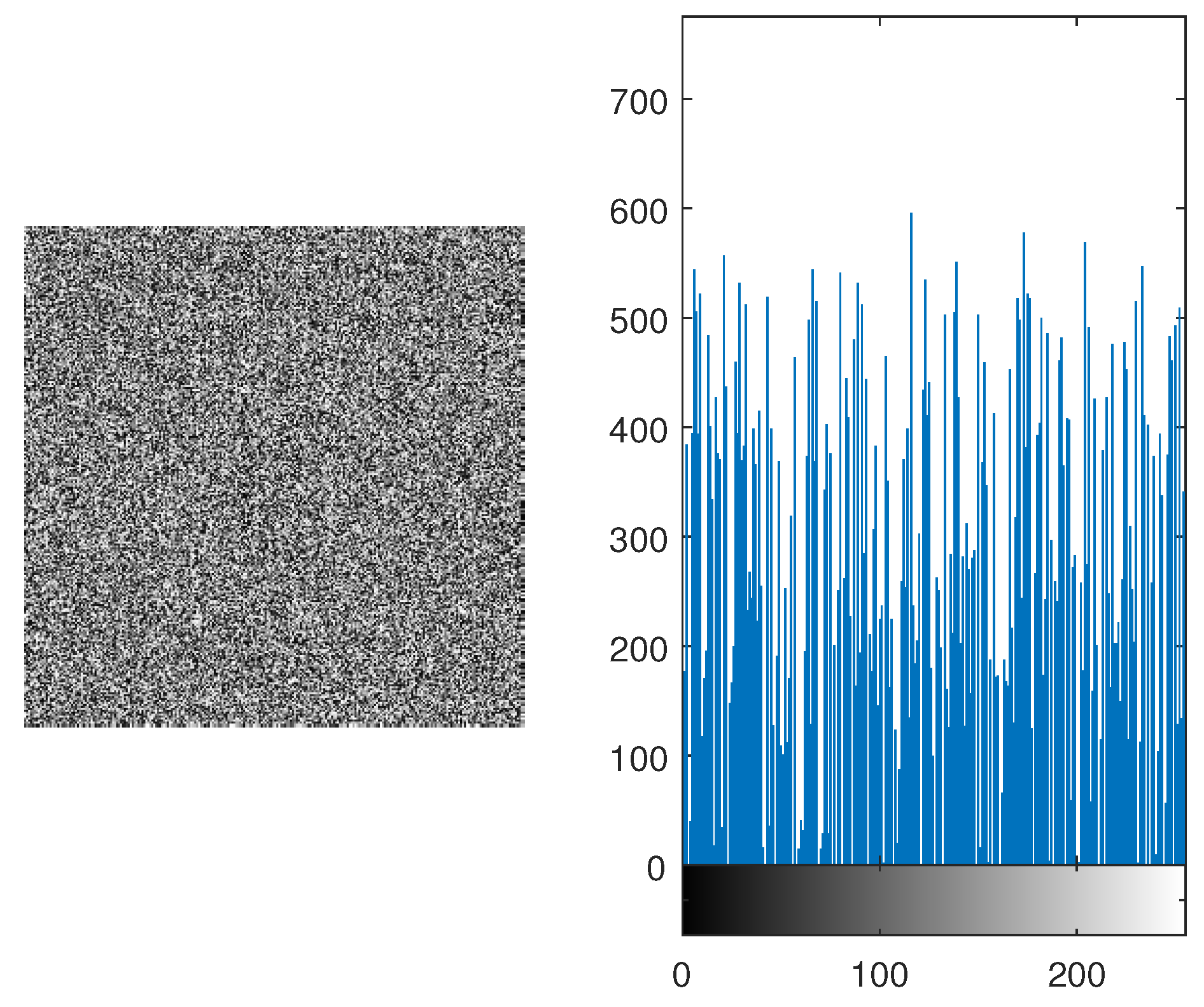
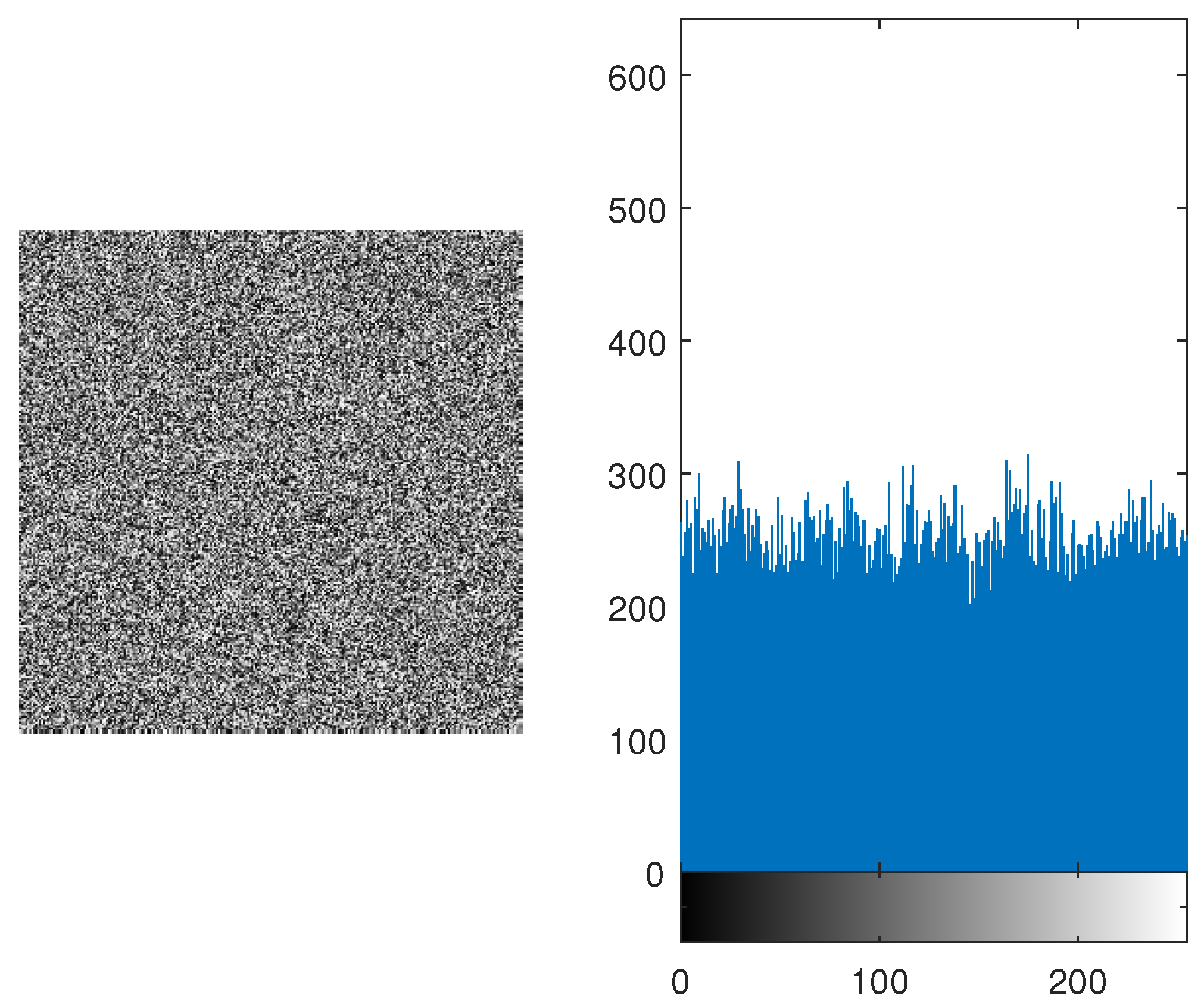
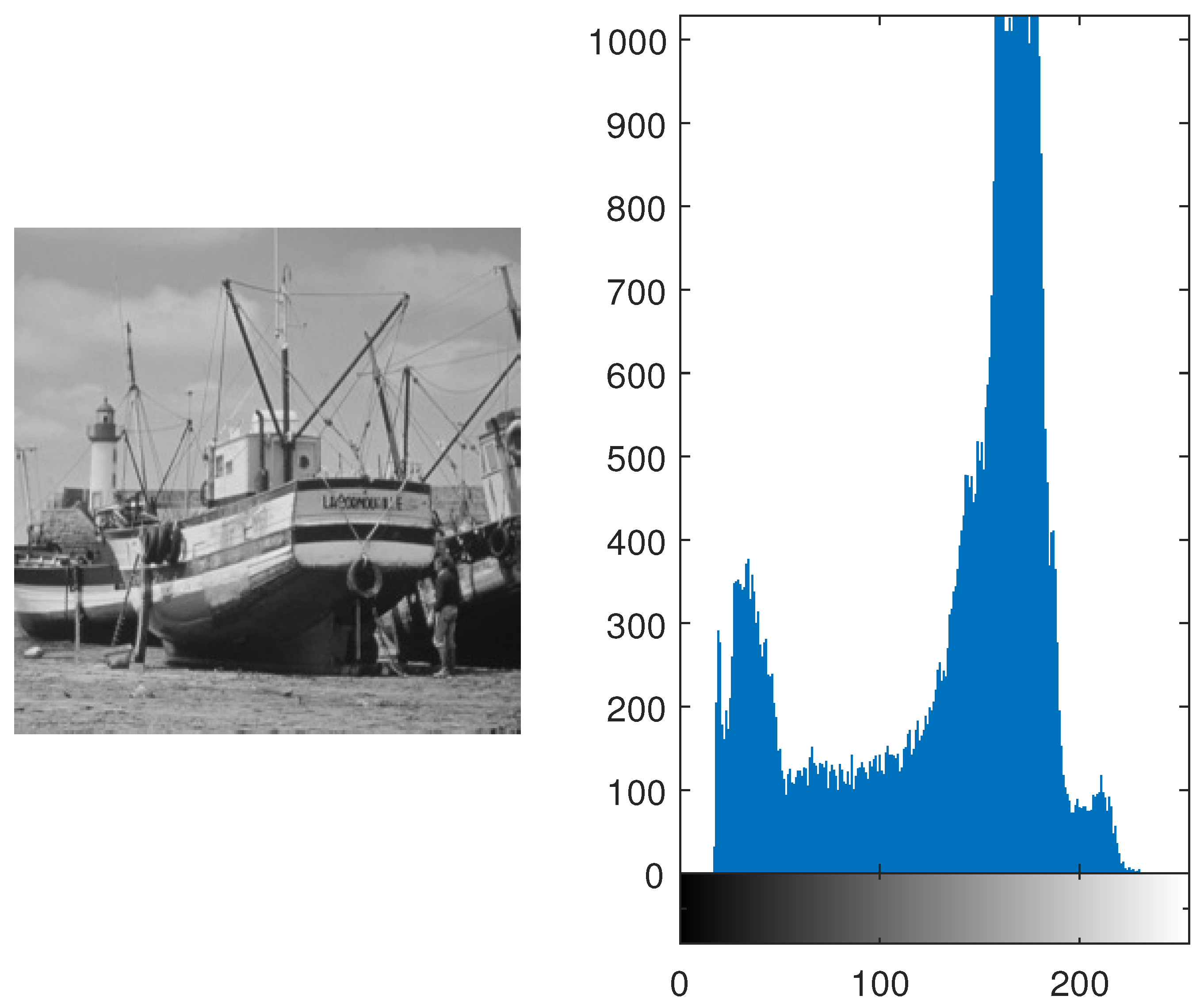
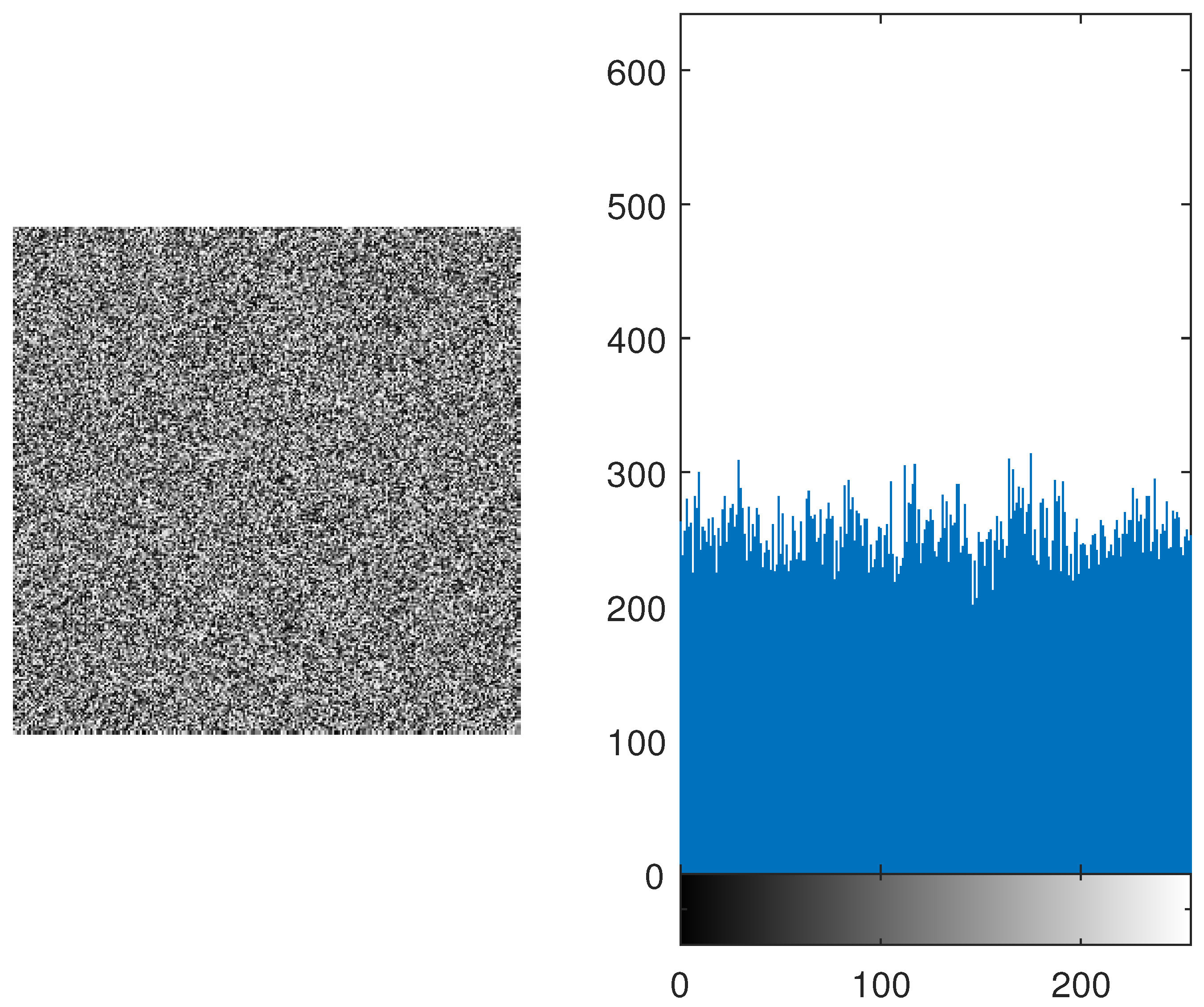
4.3. Histogram Analysis
4.4. Entropy Analysis
4.5. Mean of Absolute Deviation (MAD) Analysis
- pixels of the original image at the position;
- pixels of the encrypted image at the position;
- breadth of the image;
- height of the image.
4.6. Correlation Analysis
- correlation between the original image and its encrypted image;
- original image;
- cipher image;
- mean of the original image;
- mean of the encrypted image;
- expected value operator;
- standard deviation of the original image;
- standard deviation of the cipher image.
4.7. Contrast Analysis
- gray-level co-occurrence matrix;
- breadth of ;
- height of .
- represents the location of elements within .
4.8. Homogeneity
- gray-level co-occurrence matrix.
- represents the location of elements within .
4.9. Comparative Analysis with the Other Encryption Algorithms
- NoPCR of the proposed algorithm proves that 99% of the information inside the input image is scattered in the encrypted image
- UAPCI proves that there is a 10% average change in the encrypted image as compared to others, which are 33%. This makes the encryption algorithm more robust against differential attacks, consequently enhancing its security.
- Correlation is a measure that tells us how an image is related to another. The correlation value of our proposed algorithm is 0.28%, which is very minute. Therefore, it proves that the encryption algorithm is good at hiding information of the input image.
- The encryption time is calculated for a image. The results show that it takes 15 ms to complete the encryption process. Therefore, it is shown here that the algorithm takes less time for the encryption in comparison to others.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MAD | Mean of Absolute Deviation |
| SAC | Strict Avalanche Criteria |
| NoPCR | Number of Pixels Change Rate |
| UAPCI | Unified Average Pixel Changing Intensity |
References
- Su, Z.; Zhang, G.; Jiang, J. Multimedia security: A survey of chaos-based encryption technology. In Multimedia—A Multidisciplinary Approach to Complex Issues; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Wu, W.; Wang, Q. Quantum image encryption based on Baker map and 2D logistic map. Int. J. Theor. Phys. 2022, 61, 64. [Google Scholar] [CrossRef]
- Liu, X.; Xiao, D.; Liu, C. Three-level quantum image encryption based on Arnold transform and logistic map. Quantum Inf. Process. 2021, 20, 1–22. [Google Scholar] [CrossRef]
- Hu, W.W.; Zhou, R.G.; Jiang, S.; Liu, X.; Luo, J. Quantum image encryption algorithm based on generalized Arnold transform and Logistic map. CCF Trans. High Perform. Comput. 2020, 2, 228–253. [Google Scholar] [CrossRef]
- Xu, J.; Li, P.; Yang, F.; Yan, H. High intensity image encryption scheme based on quantum logistic chaotic map and complex hyperchaotic system. IEEE Access 2019, 7, 167904–167918. [Google Scholar] [CrossRef]
- Abd El-Latif, A.A.; Li, L.; Wang, N.; Han, Q.; Niu, X. A new approach to chaotic image encryption based on quantum chaotic system, exploiting color spaces. Signal Process. 2013, 93, 2986–3000. [Google Scholar] [CrossRef]
- Biryukov, A. Substitution–Permutation (SP) Network. In Encyclopedia of Cryptography and Security; van Tilborg, H.C.A., Jajodia, S., Eds.; Springer US: Boston, MA, USA, 2011; p. 1268. [Google Scholar] [CrossRef]
- Biyashev, R.G.; Kapalova, N.A.; Dyusenbayev, D.S.; Algazy, K.T.; Wojcik, W.; Smolarz, A. Development and analysis of symmetric encryption algorithm Qamal based on a substitution-permutation network. Int. J. Electron. Telecommun. 2021, 67, 127–132. [Google Scholar] [CrossRef]
- Ni, Z.; Kang, X.; Wang, L. A novel image encryption algorithm based on bit-level improved Arnold transform and hyper chaotic map. In Proceedings of the 2016 IEEE International Conference on Signal and Image Processing (ICSIP), Beijing, China, 13–15 August 2016; IEEE: Toulouse, France, 2016; pp. 156–160. [Google Scholar]
- Singh, P.; Yadav, A.; Singh, K. Phase image encryption in the fractional Hartley domain using Arnold transform and singular value decomposition. Opt. Lasers Eng. 2017, 91, 187–195. [Google Scholar] [CrossRef]
- Fu, C.; Chen, J.j.; Zou, H.; Meng, W.h.; Zhan, Y.f.; Yu, Y.W. A chaos-based digital image encryption scheme with an improved diffusion strategy. Opt. Express 2012, 20, 2363–2378. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Q.; Wang, X.Y. Spatiotemporal chaos in mixed linear–nonlinear coupled logistic map lattice. Phys. A Stat. Mech. Its Appl. 2014, 402, 104–118. [Google Scholar] [CrossRef]
- Zhu, Z.l.; Zhang, W.; Wong, K.w.; Yu, H. A chaos-based symmetric image encryption scheme using a bit-level permutation. Inf. Sci. 2011, 181, 1171–1186. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y. Image encryption using 2D Logistic-adjusted-Sine map. Inf. Sci. 2016, 339, 237–253. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S. An image encryption algorithm based on Baker map with varying parameter. Multimed. Tools Appl. 2017, 76, 16511–16527. [Google Scholar] [CrossRef]
- Liu, W.; Sun, K.; Zhu, C. A fast image encryption algorithm based on chaotic map. Opt. Lasers Eng. 2016, 84, 26–36. [Google Scholar] [CrossRef]
- Chai, X.; Chen, Y.; Broyde, L. A novel chaos-based image encryption algorithm using DNA sequence operations. Opt. Lasers Eng. 2017, 88, 197–213. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.l. A novel image encryption algorithm based on genetic recombination and hyper-chaotic systems. Nonlinear Dyn. 2016, 83, 333–346. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zhang, Y.Q.; Bao, X.M. A novel chaotic image encryption scheme using DNA sequence operations. Opt. Lasers Eng. 2015, 73, 53–61. [Google Scholar] [CrossRef]
- Zhou, N.; Hu, Y.; Gong, L.; Li, G. Quantum image encryption scheme with iterative generalized Arnold transforms and quantum image cycle shift operations. Quantum Inf. Process. 2017, 16, 1–23. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, X.; Wu, X.; Zhang, Y. Image encryption algorithm based on multiple mixed hash functions and cyclic shift. Opt. Lasers Eng. 2018, 107, 370–379. [Google Scholar] [CrossRef]
- Kulsoom, A.; Xiao, D.; Abbas, S.A. An efficient and noise resistive selective image encryption scheme for gray images based on chaotic maps and DNA complementary rules. Multimed. Tools Appl. 2016, 75, 1–23. [Google Scholar] [CrossRef]
- Wang, L.; Song, H.; Liu, P. A novel hybrid color image encryption algorithm using two complex chaotic systems. Opt. Lasers Eng. 2016, 77, 118–125. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Xu, D.; Liu, C. Image encryption scheme using chaos and simulated annealing algorithm. Nonlinear Dyn. 2016, 84, 1417–1429. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Zhang, H. An effective and fast image encryption algorithm based on Chaos and interweaving of ranks. Nonlinear Dyn. 2016, 84, 1595–1607. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, X.; Zhang, Y. An image encryption algorithm based on Josephus traversing and mixed chaotic map. IEEE Access 2018, 6, 23733–23746. [Google Scholar] [CrossRef]
- Wang, X.; Feng, L.; Zhao, H. Fast image encryption algorithm based on parallel computing system. Inf. Sci. 2019, 486, 340–358. [Google Scholar] [CrossRef]
- Jain, R.; Sharma, J. Symmetric color image encryption algorithm using fractional DRPM and chaotic baker map. In Proceedings of the 2016 IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bangalore, India, 20–21 May 2016; IEEE: Toulouse, France, 2016; pp. 1835–1840. [Google Scholar]
- Wang, X.; Zhang, H.l. A color image encryption with heterogeneous bit-permutation and correlated chaos. Opt. Commun. 2015, 342, 51–60. [Google Scholar] [CrossRef]
- Wu, X.; Wang, D.; Kurths, J.; Kan, H. A novel lossless color image encryption scheme using 2D DWT and 6D hyperchaotic system. Inf. Sci. 2016, 349, 137–153. [Google Scholar] [CrossRef]
- Xu, L.; Li, Z.; Li, J.; Hua, W. A novel bit-level image encryption algorithm based on chaotic maps. Opt. Lasers Eng. 2016, 78, 17–25. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Kadir, A. Image encryption using DNA complementary rule and chaotic maps. Appl. Soft Comput. 2012, 12, 1457–1466. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Wang, X.Y.; Liu, J.; Chi, Z.L. An image encryption scheme based on the MLNCML system using DNA sequences. Opt. Lasers Eng. 2016, 82, 95–103. [Google Scholar] [CrossRef]
- Anees, A.; Siddiqui, A.M.; Ahmed, F. Chaotic substitution for highly autocorrelated data in encryption algorithm. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 3106–3118. [Google Scholar] [CrossRef]
- Arif, J.; Khan, M.A.; Ghaleb, B.; Ahmad, J.; Munir, A.; Rashid, U.; Al-Dubai, A.Y. A novel chaotic permutation-substitution image encryption scheme based on logistic map and random substitution. IEEE Access 2022, 10, 12966–12982. [Google Scholar] [CrossRef]
- Alawida, M. A novel chaos-based permutation for image encryption. J. King Saud Univ. Comput. Inf. Sci. 2023, 35, 101595. [Google Scholar] [CrossRef]
- Hussain, I.; Anees, A.; Al-Maadeed, T.A. A novel encryption algorithm using multiple semifield S-boxes based on permutation of symmetric group. Comput. Appl. Math. 2023, 42, 80. [Google Scholar] [CrossRef]
- Lorenz, E.N. The problem of deducing the climate from the governing equations. Tellus 1964, 16, 1–11. [Google Scholar] [CrossRef]
- Riaz, M.; Ahmed, J.; Shah, R.A.; Hussain, A. Novel secure pseudorandom number generator based on duffing map. Wirel. Pers. Commun. 2018, 99, 85–93. [Google Scholar] [CrossRef]
- Agrawal, V.; Agrawal, S.; Deshmukh, R. Analysis and review of encryption and decryption for secure communication. Int. J. Sci. Eng. Res. 2014, 2, 2347–3878. [Google Scholar]
- SIPI Image Database—Sipi.usc.edu. Available online: http://sipi.usc.edu/database/database.php (accessed on 19 September 2023).
- Mishra, M.; Mankar, V. A Chaotic encryption algorithm: Robustness against Brute-force attack. In Advances in Computer Science, Engineering & Applications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 169–179. [Google Scholar]
- Kamat, V.G.; Sharma, M. Symmetric Image Encryption Algorithm Using 3D Rossler System. Int. J. Comput. Sci. Bus. Inform. 2014, 14, 2145–2152. [Google Scholar]
- Radwan, A.G.; AbdElHaleem, S.H.; Abd-El-Hafiz, S.K. Symmetric encryption algorithms using chaotic and non-chaotic generators: A review. J. Adv. Res. 2016, 7, 193–208. [Google Scholar] [CrossRef]
- Motara, Y.M.; Irwin, B. Sha-1 and the strict avalanche criterion. In Proceedings of the 2016 Information security for South Africa (ISSA), Johannesburg, South Africa, 17–18 August 2016; IEEE: Toulouse, France, 2016; pp. 35–40. [Google Scholar]
- Mar, P.P.; Latt, K.M. New analysis methods on strict avalanche criterion of S-boxes. World Acad. Sci. Eng. Technol. 2008, 48, 25. [Google Scholar]
- Hussain, I.; Shah, T.; Gondal, M.A.; Wang, Y. Analyses of SKIPJACK S-box. World Appl. Sci. J. 2011, 13, 2385–2388. [Google Scholar]
- Zhen, P.; Zhao, G.; Min, L.; Jin, X. Chaos-based image encryption scheme combining DNA coding and entropy. Multimed. Tools Appl. 2016, 75, 6303–6319. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. A novel information entropy based randomness test for image encryption. In Proceedings of the 2011 IEEE International Conference on Systems, Man, and Cybernetics, Anchorage, AK, USA, 9–12 October 2011; IEEE: Toulouse, France, 2011; pp. 2676–2680. [Google Scholar]
- Zeghid, M.; Machhout, M.; Khriji, L.; Baganne, A.; Tourki, R. A modified AES based algorithm for image encryption. Int. J. Comput. Inf. Eng. 2007, 1, 745–750. [Google Scholar]
- Högel, J.; Schmid, W.; Gaus, W. Robustness of the standard deviation and other measures of dispersion. Biom. J. 1994, 36, 411–427. [Google Scholar] [CrossRef]
- Mazumder, S.; Serfling, R. Bahadur representations for the median absolute deviation and its modifications. Stat. Probab. Lett. 2009, 79, 1774–1783. [Google Scholar] [CrossRef]
- Pizolato, J.C., Jr.; Neto, L.G. Phase-only optical encryption based on the zeroth-order phase-contrast technique. Opt. Eng. 2009, 48, 098201. [Google Scholar]
- Bibi, N.; Farwa, S.; Muhammad, N.; Jahngir, A.; Usman, M. A novel encryption scheme for high-contrast image data in the Fresnelet domain. PLoS ONE 2018, 13, e0194343. [Google Scholar] [CrossRef]
- Hua, Z.; Jin, F.; Xu, B.; Huang, H. 2D Logistic-Sine-coupling map for image encryption. Signal Process. 2018, 149, 148–161. [Google Scholar] [CrossRef]
- Gao, S.; Wu, R.; Wang, X.; Liu, J.; Li, Q.; Wang, C.; Tang, X. Asynchronous updating Boolean network encryption algorithm. In IEEE Transactions on Circuits and Systems for Video Technology; IEEE: Toulouse, France, 2023. [Google Scholar]


| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
| 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 |
| 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 |
| 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 |
| 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
| 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 |
| 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 |
| 144 | 145 | 146 | 147 | 148 | 149 | 150 | 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 |
| 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 |
| 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 | 201 | 202 | 203 | 204 | 205 | 206 | 207 |
| 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 |
| 224 | 225 | 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 |
| 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 | 251 | 252 | 253 | 254 | 255 |
| 0 | 245 | 223 | 190 | 146 | 91 | 25 | 204 | 116 | 17 | 163 | 42 | 166 | 23 | 125 | 216 |
| 40 | 109 | 167 | 214 | 250 | 19 | 33 | 36 | 28 | 9 | 235 | 194 | 142 | 79 | 5 | 176 |
| 80 | 229 | 111 | 238 | 98 | 203 | 41 | 124 | 196 | 1 | 51 | 90 | 118 | 135 | 141 | 136 |
| 120 | 93 | 55 | 6 | 202 | 131 | 49 | 212 | 108 | 249 | 123 | 242 | 94 | 191 | 21 | 96 |
| 160 | 213 | 255 | 30 | 50 | 59 | 57 | 44 | 20 | 241 | 195 | 138 | 70 | 247 | 157 | 56 |
| 200 | 77 | 199 | 54 | 154 | 243 | 65 | 132 | 188 | 233 | 11 | 34 | 46 | 47 | 37 | 16 |
| 240 | 197 | 143 | 78 | 2 | 171 | 73 | 220 | 100 | 225 | 83 | 186 | 22 | 103 | 173 | 232 |
| 24 | 61 | 87 | 102 | 106 | 99 | 81 | 52 | 12 | 217 | 155 | 82 | 254 | 159 | 53 | 192 |
| 64 | 181 | 31 | 126 | 210 | 27 | 89 | 140 | 180 | 209 | 227 | 234 | 230 | 215 | 189 | 152 |
| 104 | 45 | 231 | 150 | 58 | 211 | 97 | 228 | 92 | 201 | 43 | 130 | 206 | 15 | 69 | 112 |
| 144 | 165 | 175 | 174 | 162 | 139 | 105 | 60 | 4 | 193 | 115 | 26 | 182 | 71 | 205 | 72 |
| 184 | 29 | 119 | 198 | 10 | 67 | 113 | 148 | 172 | 185 | 187 | 178 | 158 | 127 | 85 | 32 |
| 224 | 149 | 63 | 222 | 114 | 251 | 121 | 236 | 84 | 177 | 3 | 74 | 134 | 183 | 221 | 248 |
| 8 | 13 | 7 | 246 | 218 | 179 | 129 | 68 | 252 | 169 | 75 | 226 | 110 | 239 | 101 | 208 |
| 48 | 133 | 207 | 14 | 66 | 107 | 137 | 156 | 164 | 161 | 147 | 122 | 86 | 39 | 237 | 168 |
| 88 | 253 | 151 | 38 | 170 | 35 | 145 | 244 | 76 | 153 | 219 | 18 | 62 | 95 | 117 | 128 |
| Algorithms | Space Complexity | Permutation Time | ||
|---|---|---|---|---|
| 256 × 256 | 512 × 512 | 1024 × 1024 | ||
| Proposed Algorithm | 1.5 ms | 6 ms | 18 ms | |
| Ref. [15] | 20 ms | 80 ms | 330 ms | |
| Ref. [22] | 4 ms | 16 ms | 68 ms | |
| Ref. [28] | 2.5 ms | 10 ms | 42 ms | |
| Image Name | NoPCR |
|---|---|
| Lena (256,256) | 99.2282 |
| Black Image (All zeros) | 99.2282 |
| Cameraman (256,256) | 99.2282 |
| Baboon (512,512) | 99.4743 |
| White Image (All ones) | 99.2282 |
| Peppers (512,512) | 99.4742 |
| Random Image [0 255] | 99.2282 |
| Barbara (512,512) | 99.4743 |
| Lena (512,512) | 99.4804 |
| Image Name | UAPCI |
|---|---|
| Lena (256,256) | 12.5527 |
| Black Image (All zeros) | 18.5472 |
| Cameraman (256,256) | 12.1591 |
| Baboon (512,512) | 7.2304 |
| White Image (All ones) | 6.5406 |
| Peppers (512,512) | 7.1747 |
| Random Image [0 255] | 12.5526 |
| Barbara (512,512) | 7.2447 |
| Lena (512,512) | 7.1499 |
| S-Boxes | SAC |
|---|---|
| Proposed S-box | 0.491 |
| AES [48] | 0.504 |
| APA [48] | 0.5 |
| Gray [48] | 0.499 |
| S8 AES [48] | 0.504 |
| Skipjack [48] | 0.503 |
| Xyi [48] | 0.502 |
| Prime [48] | 0.516 |
| Image Name | Original Image | Cipher Image |
|---|---|---|
| Lena (256,256) | 7.5683 | 7.9956 |
| Lena (512,512) | 7.4318 | 7.9956 |
| Cameraman (256,256) | 7.0097 | 7.9907 |
| Black Image (All zeros) | 0 | 7.6822 |
| Barbara (512,512) | 7.3925 | 7.9960 |
| White Image (All ones) | 0 | 7.6822 |
| Peppers (512,512) | 7.5700 | 7.9958 |
| Random Image [0 255] | 7.9951 | 7.9972 |
| Baboon (512,512) | 7.2288 | 7.9952 |
| Algorithm | Entropy |
|---|---|
| Proposed Algorithm | 7.9952 |
| AES [51] | 7.91 |
| AES+A5/1 [51] | 7.96 |
| Image Name | MAD |
|---|---|
| Lena (256,256) | 77.90740 |
| Lena (512,512) | 72.82140 |
| Cameraman (256,256) | 79.01410 |
| Black Image (All zeros) | 127.9119 |
| Barbara (512,512) | 72.60550 |
| White Image (All ones) | 127.0529 |
| Peppers (512,512) | 78.51690 |
| Random Image [0 255] | 85.23000 |
| Baboon (512,512) | 69.36040 |
| Image Name | Correlation Value |
|---|---|
| Lena (256,256) | 0.0021 |
| Black Image (All zeros) | NaN |
| Cameraman (256,256) | −0.0048 |
| Baboon (512,512) | 0.001 |
| White Image (All ones) | NaN |
| Peppers (512,512) | −0.0027 |
| Random Image [0 255] | −0.000542209 |
| Barbara (512,512) | 0.0016 |
| Lena (512,512) | −0.0071 |
| Algorithm | Correlation between Various Algorithms |
|---|---|
| Proposed Algorithm | 0.0028 |
| AES [51] | 0.072 |
| AES+A5/1 [51] | 0.067 |
| AES+W7 [51] | 0.025 |
| Image Name | Original Image | Cipher Image |
|---|---|---|
| Lena (256,256) | 235 | 255 |
| Black Image (All zeros) | 0 | 255 |
| Baboon (512,512) | 203 | 255 |
| White Image (All ones) | 0 | 255 |
| Peppers (512,512) | 228 | 255 |
| Lena (512,512) | 217 | 255 |
| Random Image [0 255] | 255 | 255 |
| Barbara (512,512) | 210 | 255 |
| Cameraman (256,256) | 246 | 255 |
| Encryption Algorithm | Contrast |
|---|---|
| Proposed Algorithm | 255 |
| Alawida [37] | 109.2 |
| Hua and Zhou [15] | 109.23 |
| Hua et al. [56] | 109.19 |
| Image Name | Original Image | Cipher Image |
|---|---|---|
| Lena (256,256) | 0.8573 | 0.3874 |
| Black Image (All zeros) | 0.9961 | 0.3828 |
| Baboon (512,512) | 0.7988 | 0.3872 |
| White Image (All ones) | 0.9961 | 0.4345 |
| Peppers (512,512) | 0.8946 | 0.3886 |
| Random Image [0 255] | 0.9961 | 0.4345 |
| Barbara (512,512) | 0.8560 | 0.3880 |
| Cameraman (256,256) | 0.8918 | 0.3907 |
| Lena (512,512) | 0.8813 | 0.3899 |
| Statistical Test | NoPCR | UAPCI | Entropy | Correlation | Encryption Time |
|---|---|---|---|---|---|
| Proposed Algorithm | 99.4804 | 9.5 | 7.9952 | 0.0028 | 0.015 |
| Arif et al. [36] | 99.62 | 33.49 | 7.9994 | 0.0033 | 1.28 |
| Alawida [37] | 99.6125 | 33.4525 | 7.9994 | 0.0004 | 0.25 |
| Anees et al. [35] | 0.0015 | 0.001 | 7.8026 | 0.122 | 1.21 |
| Gao et al. [57] | 99.6102 | 33.4465 | 7.9992 | −0.0001 | 0.2205 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riaz, M.; Dilpazir, H.; Naseer, S.; Mahmood, H.; Anwar, A.; Khan, J.; Benitez, I.B.; Ahmad, T. Secure and Fast Image Encryption Algorithm Based on Modified Logistic Map. Information 2024, 15, 172. https://doi.org/10.3390/info15030172
Riaz M, Dilpazir H, Naseer S, Mahmood H, Anwar A, Khan J, Benitez IB, Ahmad T. Secure and Fast Image Encryption Algorithm Based on Modified Logistic Map. Information. 2024; 15(3):172. https://doi.org/10.3390/info15030172
Chicago/Turabian StyleRiaz, Mamoon, Hammad Dilpazir, Sundus Naseer, Hasan Mahmood, Asim Anwar, Junaid Khan, Ian B. Benitez, and Tanveer Ahmad. 2024. "Secure and Fast Image Encryption Algorithm Based on Modified Logistic Map" Information 15, no. 3: 172. https://doi.org/10.3390/info15030172
APA StyleRiaz, M., Dilpazir, H., Naseer, S., Mahmood, H., Anwar, A., Khan, J., Benitez, I. B., & Ahmad, T. (2024). Secure and Fast Image Encryption Algorithm Based on Modified Logistic Map. Information, 15(3), 172. https://doi.org/10.3390/info15030172







