Abstract
Compressive Sensing (CS) has emerged as a transformative technique in image compression, offering innovative solutions to challenges in efficient signal representation and acquisition. This paper provides a comprehensive exploration of the key components within the domain of CS applied to image and video compression. We delve into the fundamental principles of CS, highlighting its ability to efficiently capture and represent sparse signals. The sampling strategies employed in image compression applications are examined, emphasizing the role of CS in optimizing the acquisition of visual data. The measurement coding techniques leveraging the sparsity of signals are discussed, showcasing their impact on reducing data redundancy and storage requirements. Reconstruction algorithms play a pivotal role in CS, and this article reviews state-of-the-art methods, ensuring a high-fidelity reconstruction of visual information. Additionally, we explore the intricate optimization between the CS encoder and decoder, shedding light on advancements that enhance the efficiency and performance of compression techniques in different scenarios. Through a comprehensive analysis of these components, this review aims to provide a holistic understanding of the applications, challenges, and potential optimizations in employing CS for image and video compression tasks.
1. Introduction
In the era of rapid technological advancement, the sheer volume of data generated and exchanged daily has become staggering. This influx of information, from high-resolution images to bandwidth-intensive videos, has posed unprecedented challenges to conventional methods of data transmission and storage. As we grapple with the ever-growing demand for the efficient handling of these vast datasets, a groundbreaking concept emerges—Compressive Sensing [1].
Traditionally, the Nyquist–Shannon sampling theorem [2] has governed our approach to capturing and reconstructing signals, emphasizing the need to sample at twice the rate of the signal’s bandwidth to avoid information loss. However, in the face of escalating data sizes and complexities, this theorem’s practicality is increasingly strained. Compressive Sensing, as a disruptive force, challenges the assumptions of Nyquist–Shannon by advocating for a selective and strategic sampling technique.
In general, CS is a revolutionary signal-processing technique that hinges on the idea that sparse signals can be accurately reconstructed from a significantly reduced set of measurements. The principle of CS involves capturing a compressed version of a signal, enabling efficient data acquisition and transmission. As the Figure 1 shows, in the field of image processing, numerous works have been proposed in each of various domains, exploring innovative techniques and algorithms to harness the potential of compressive imaging [3,4,5,6,7,8,9,10,11], efficient communication systems [12,13,14,15,16,17,18,19,20], pattern recognition [21,22,23,24,25,26,27,28,29], and video processing tasks [30,31,32,33,34,35,36,37,38]. The versatility and effectiveness of CS make it a compelling area of study with broad implications across different fields of signal processing and information retrieval. Moreover, Figure 2 illustrates the annual publication count of articles related to CS in the four major domains of CS applications in image processing since 2010. It is evident that CS-related research has increasingly become a focal point of attention for researchers. Therefore, a comprehensive and integrated introduction to CS is anticipated. The main contributions of this review are as follows:
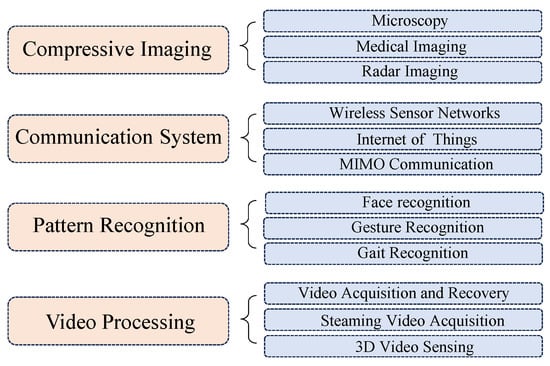
Figure 1.
The applications of compressive sensing in image/video processing.
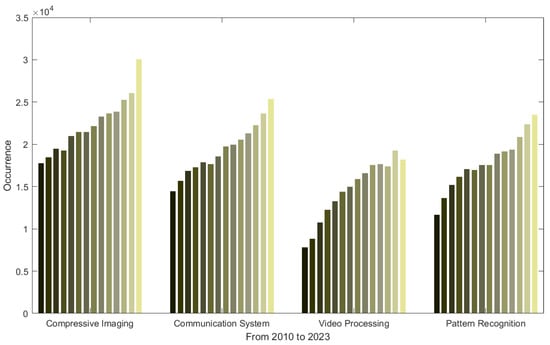
Figure 2.
The paper numbers of compressive sensing research in image processing during the past decade.
- This review emphasizes various sampling techniques, with a focus on designing measurement matrices for superior reconstruction and efficient coding.
- We explore the intricacies of measurement coding, covering approaches like intra prediction, inter prediction, and rate control.
- We provide a comprehensive analysis of CS codec optimization, including diverse reconstruction algorithms, and discuss current challenges and future prospects.
The remainder of this paper is organized as follows: Section 2 presents an overview of the principles of compressive sensing. In Section 3, we introduce algorithms for the sampling part in CS, with a particular emphasis on the measurement matrices designed for better reconstruction quality and those optimized for improved measurement coding. The methods of intra/inter prediction and rate control in measurement coding are elaborated in detail in Section 4. Corresponding to the sampling, the reconstruction methods will be discussed in Section 5, where they are from both traditional and learning-based algorithms. Section 6 provides a detailed discussion on the overall optimization of the CS codec. In Section 7, we discuss the current challenges and future scope of the CS technique. An eventual conclusion of the paper will be given in Section 8.
2. Compressive Sensing Overview
Consider an original signal X, which is an N-length vector that can be sparsely represented as S in a transformed domain using a specific transform matrix , where K-sparse implies that only K elements are non-zero, and the remaining are close to or equal to zero. This relationship is expressed by the equation:
The sensing matrix, also known as the sampling matrix A, is derived by multiplying an measurement matrix by the transform matrix , where :
The sampling rate, or Compressed Sensing (CS) ratio, denoted as the number of measurements M divided by the signal length N, indicates the fraction of the signal that is sampled:
Finally, the measurement vector Y is obtained by multiplying the sensing matrix A with the sparse signal S:
Figure 3 shows the sampling procedure details of CS. We will elaborate the setting and design of the measurement matrix in Section 3.
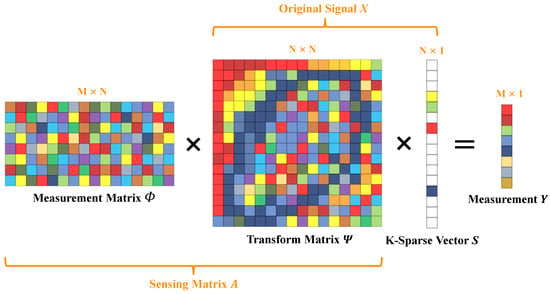
Figure 3.
Procedure of compressive sensing encoder.
Since the CS reconstruction is an ill-posed problem [39], to obtain a reliable reconstruction, the conventional optimization-based CS methods commonly solve an energy function as:
where represents the data-fidelity term for modeling the likelihood of degradation, and the indicates the prior term with a parameter of regularization of . The details for the CS reconstruction will be introduced in Section 5, later.
3. Sampling Algorithms
3.1. Measurement Matrix for Better Reconstructions
One of the fascinating aspects of compressive sensing focuses on the development of measurement matrices. The construction of these matrices is crucial, as they need to meet specific constraints. They should align coherently with the sparsifying matrix to efficiently capture essential information from the initial signal with the least number of projections. On the other hand, the matrix needs to satisfy the restricted isometry property (RIP) to preserve the original signal’s main information in the compression process. However, in the research of [40,41], they verified the possibility that maintaining sparsity levels in a compressive sensing environment does not necessarily require the presence of the RIP, and also demonstrated that it is not a mandatory requirement for adhering to the random model of a signal. Moreover, designing a measurement matrix with low complexity and hardware-friendly characteristics has become more and more crucial in the context of real-time applications and low-power requirements.
In CS-related research a decade ago, random matrices like Gaussian or Bernoulli matrices were often selected as the measurement matrices, which satisfied the RIP conditions of CS. Although these random matrices are easy to implement and contribute to improved reconstruction performance, they come with several notable disadvantages, such as the requirement for significant storage resources and the challenging recovery while dealing with large signal dimensions [42]. Therefore, the issue of the measurement matrix has been widely discussed in recent works.
3.1.1. Conventional Measurement Matrix
Conventional measurement matrices encompass multiple categories, ranging from random matrices to deterministic matrices, each contributing uniquely to the applications in CS. Random matrices are constructed by randomly selecting elements from a certain probability distribution, such as the random Gaussian matrix (RGM) [43] and random binary matrix (RBM) [44]. The well-known traditional deterministic matrices include the Bernoulli matrix [45], Hadamard matrix [46], Walsh matrix [47], and Toplitz matrix [48]. Figure 4 gives an example of two famous deterministic matrices.
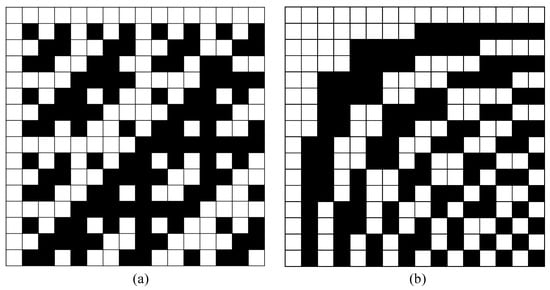
Figure 4.
(a) is Hadamard Matrix and (b) is Walsh Matrix.
Although these deterministic matrices have been extensively researched and successfully applied to the CS camera, because of their good sensing performance, fast reconstruction, and hardware-friendly properties, they are insupportable when applied to the ultra-low CS ratio [49]. Moreover, for instance, in the work of [44], the information of the pixel domain can be obtained by changing a few rows in the matrix, but the modified matrix results in an unacceptable reconstruction performance, posing enormous challenges for practical applications. In recent years, some studies have been carried out to investigate the effect of Hadamard and Walsh projection order selection on image reconstruction quality by reordering orthogonal matrices [50,51,52,53,54]. A Hadamard-based Russian-doll ordering matrix is proposed in [50], which sorts the projection patterns by increasing the number of zero-crossing components. In the works of [51,52], the authors present a matrix, called the cake-cutting ordering of Hadamard, which can optimally reorder the deterministic Hadamard basis. More recently, the work of [54] designs a novel hardware-friendly matrix named the Zigzag-ordered Walsh (ZoW). Specifically, the ZoW matrix uses the zigzag to reorder the blocks from the Walsh matrix, and, finally, vectored them. The illustration of the process is shown in Figure 5.
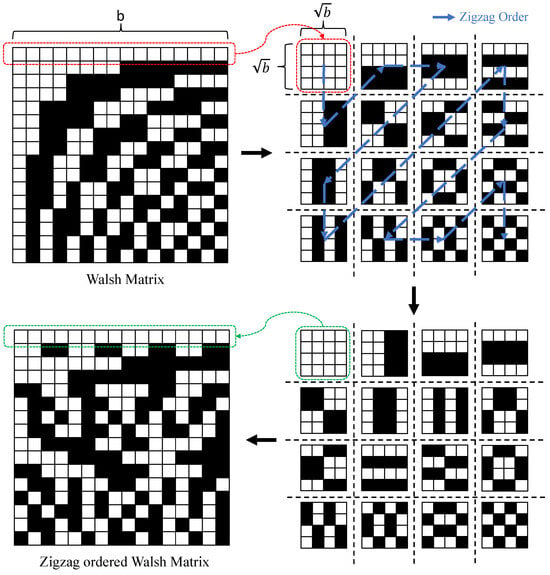
Figure 5.
The illustration of the process from Walsh matrix to ZoW matrix.
In the proposed matrix of [54], the low-frequency patterns are in the upper-left corner, and the frequency increases according to the zigzag scan order. Therefore, across different sampling rates, ZoW consistently retains the lowest frequency patterns, which are pivotal for determining the image quality. This allows ZoW to extract features effectively from low to high-frequency components.
3.1.2. Learning-Based Measurement Matrix
Recently, there has been a surge in the development of image CS algorithms based on deep neural networks. These algorithms aim to acquire features from training data to comprehend the underlying representation and subsequently reconstruct test data from their CS measurements. Therefore, some learning-based algorithms are developed to jointly optimize the sampling matrix and the non-linear recovery operator [55,56,57,58,59,60,61]. Ref. [55]’s first attempt leads into a fully connected layeras the sampling matrix for simultaneous sampling and recovery. In the works of [56,57], the authors present the idea of adopting a convolution layer to mimic the sampling process and utilize all-convolutional networks for CS reconstruction. These methods not only train the sampling and recovery stages jointly but are also non-iterative, leading to a significant reduction in time complexity compared to their optimization-based counterparts. However, only utilizing the fully connected or repetitive convolutional layers for the joint learning of the sampling matrix and recovery operator lacks structural diversity, which can be the bottleneck for a further performance improvement. To address this drawback, Ref. [59] proposes a novel optimization-inspired deep-structured network (OPINE-Net), which includes a data-driven and adaptively learned matrix. Specifically, the measurement matrix is a trainable parameter and is adaptively learned by the training dataset. Two constraints are applied to attain the trained matrix simultaneously. Firstly, the orthogonal constraint is designed into a loss term and then enforced into the total loss, as follows:
where I represents the identity matrix. For the binary constraint, they introduce an element-wise operation, defined below:
Experiments show that their proposed learnable matrix can achieve a superior reconstruction performance with constraint incorporation when compared to conventional measurement matrices.
In general, by learning the features of signals, learning-based measurement matrices can more effectively capture the sparse representation of signals. This personalized adaptability enables learning-based measurement matrices to outperform traditional construction methods in certain scenarios. Another strength of learning-based measurement matrices is their adaptability. By adjusting training data and algorithm parameters, customized measurement matrices can be generated for different types of signals and application scenarios, enhancing the applicability of compressed sensing in diverse tasks. However, obtaining these trainable matrices usually needs a substantial amount of training data and complex algorithms. We believe that the future research focus will revolve around devising more efficient approaches to acquire matrices with better adaptability.
3.2. Measurement Matrix for Better Measurement Coding
It is noticed that the data reduction from the original signal to CS measurement does not completely equal signal compression, and these measurements can indeed be transmitted directly, but still require a substantial bandwidth. To alleviate the transmitter’s load further, the CS-based CMOS image sensor can collaborate with a compressor to produce a compressed bitstream. However, due to the high complexity, the conventional pixel-based compressor is not suitable for CS systems aiming at reducing the computational complexity and power consumption of the encoder [1]. The difference between conventional image sensors and CS-based sensors is shown in Figure 6.
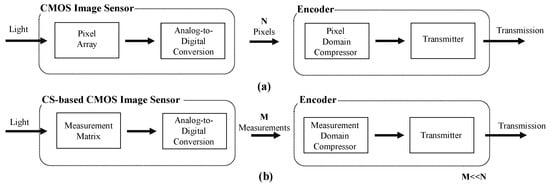
Figure 6.
The illustration of conventional imaging system (a) and CS-based CMOS image sensor (b). The measurement coding is performed on the latter.
Therefore, to further compress measurements, several well-designed measurement matrices for better measurement coding have been recently proposed [62,63]. Wherein, a novel framework for measurement coding is proposed in [63], and designs an adjacent pixels-based measurement matrix (APMM) to obtain measurements of each block, which contains block boundary information as a reference for intra prediction. Specifically, a set of four directional prediction modes is employed to generate prediction candidates for each block, from which the optimal prediction is selected for further processing. The residuals represent the difference between measurements and predictions and undergo quantization and Huffman coding to create a coded bit sequence for transmission. Importantly, each encoding step corresponds to a specific operation in the decoding process, ensuring a coherent and reversible transformation. Extensive experimental results show that [63] can obtain a superior trade-off between the bit-rate and reconstruction quality. Table 1 illustrates the comparison of different introduced measurement matrices that are commonly used in CS.

Table 1.
The PSNR (dB) performance of different matrices on Set5 dataset.
4. Measurement Coding
In addition to designing a measurement matrix to enhance measurement coding, three key aspects further contribute to refining coding advantages: intra prediction, inter prediction, and rate control. Intra prediction involves predicting pixel values within a frame, exploiting spatial correlations to enhance compression efficiency. Inter prediction extends this concept by considering the temporal correlation between consecutive frames, facilitating enhanced predictive coding. Meanwhile, effective rate control mechanisms are essential for balancing compression ratios without compromising the quality of the reconstructed signal. By addressing these aspects in tandem with a well-designed measurement matrix, a comprehensive approach is established for advancing measurement coding capabilities, thereby improving the overall system performance and resource utilization.
4.1. Measurement Intra Prediction
This intra prediction approach in measurement coding aims to reduce the number of measurements needed for accurate signal representation. It is especially valuable when dealing with sparse or compressible signals, where the prediction of one block’s measurements can inform and enhance the prediction accuracy of adjacent blocks.
Hence, some studies are dedicated to this aspect and propose numerous novel algorithms [63,64,65]. In the works of [64], the authors mainly present an angular measurement intra prediction algorithm compatible with CS-based image sensors. Specifically, they apply the idea of an H.264 intra prediction and emulate its computation. More structural rows in the random 0/1 measurement matrix are designed for embedding more precise boundary information of neighbors for intra prediction. Ref. [65] applies the Hadamard matrix instead of the random matrix to sampling and generate predictive candidates, since the pseudo-random cannot guarantee the similarity between the sender and receiver. Moreover, the features of the pixel domain are also utilized to effectively reduce the spatial redundancy in the measurement domain. However, Ref. [65] achieves a good performance but requires high hardware resources. To address this shortcoming, the research of [66] proposes a novel near lossless predictive coding (NLPC) approach to compress block-based CS measurements, which encodes the prediction error measurement between the target and current measurement to attain a lower data size. Furthermore, a complete block-based CS with NLPC with scalar quantization (BCS-NLPC-SQ) is designed in [66] to explore the image quality at varying CS ratios with different blocking sizes. In the previously mentioned work of [63], the authors not only propose a novel matrix APMM for better measurement coding but also present a four-mode intra prediction strategy, which is called the measurement-domain intra prediction (MDIP). An optimal prediction mode for each block is selected from a set of candidates to minimize the difference between the prediction and the current block. Each block is predicted based on the boundary measurements from neighboring and previously encoded blocks. Comparing the sum of absolute differences of four prediction candidates for each block will be utilized to minimize the amount of information to be coded. Combined with the aforementioned APMM, the proposed measurement coding framework demonstrates a superiority in data compression.
4.2. Measurement Inter Coding
Regarding the measurement coding in video-oriented CS, the spatial and temporal redundancy in measurement has become a primary concern that is necessary to further compress. Accordingly, a novel work with inter prediction is proposed to further reduce the spatial redundancy in measurements while still maintaining visual quality [67]. In [67], the authors divide the type of measurement into two portions: static measurement as the non-moving part and dynamic measurement as the moving part in the pixel domain. In general, the information of consecutive frames is similar, resulting in temporal redundancy. To further reduce the bandwidth usage, quantization is a straightforward approach, such as scalar feedback quantization (SFQ). However, the output from CS is represented in a compressed vector, in which an existing video compression algorithm could not be used. Therefore, the work of [67] designs a temporal redundancy reduction method in video CS over the communication channel, which can be shown in Figure 7.
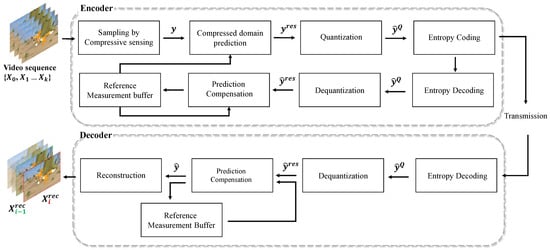
Figure 7.
The intra/inter prediction of measurement coding in compressive sensing.
By utilizing the framework in Figure 7, the proposed method in [67] not only achieves a comparable estimation performance but also effectively reduces sampling costs, easing the burdens on communication and storage. As a result, this straightforward strategy offers a practical solution to mitigate the bandwidth usage.
4.3. Rate Control
On the other hand, the rate control is another critical strategy in CS, involving the allocation of limited measurement resources to ensure the quality of signal recovery. The rate control requires a balance between the design of the measurement matrix, the sampling rate, and the accuracy of signal reconstruction. Optimizing the bit-rate allocation allows for better signal recovery under constrained resources, especially in wireless sensor networks (WSN).
The work of [68] develops a frame adaptive rate control scheme for video CS. Figure 8 illustrates the part of rate control in their proposed framework. In a nutshell, the rate limitation will lead the first frame to find an initial value of QP by their proposed triangle threshold-based quantization method and guide the subsequent frames to adjust the QP based on the predicted QP. The paper of [69] is the extended version of [63] that was described before. In [69], the authors further propose the rate control algorithm using an iterative approach. They consider that the reconstruction quality and the encoded bit-rate mainly rely on two parameters, the CS ratio and the quantization step size. Therefore, they design a rate control algorithm to further process the residuals between measurements and predictions, in order to generate a coded bit sequence for transmitting. As a result, with a component of rate control, their proposed framework can compress the measurements and increase coding efficiency significantly with excellent reconstruction quality, leading to a smaller bandwidth required in communication systems.
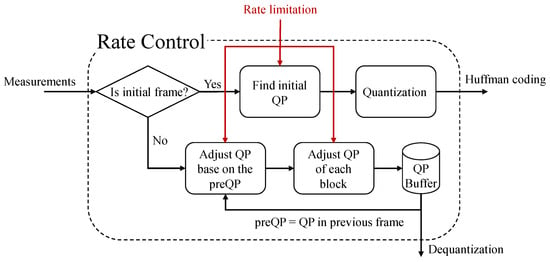
Figure 8.
The flow chart of rate control in the work of [68].
5. Reconstruction Approaches
In CS, reconstruction represents the method to recover the original signal from compressed measurement data. The fundamental idea behind CS reconstruction is to capture signal information with significantly fewer measurements than traditional sampling methods, enabling the efficient compression and subsequent reconstruction of the signal. The reconstruction aims to accurately restore sparse signals from a relatively small number of measurements using mathematical models and prior knowledge about the sparsity of the signal. The objective of the reconstruction approach is to minimize distortions and errors introduced during the measurement process, while preserving the structural integrity of the signal. In the following subsections, we will elaborate on reconstruction methods from both conventional reconstruction methods and deep learning-based reconstruction methods.
5.1. Conventional Reconstruction Methods
There are typically two types of conventional reconstruction methods based on the constraint: L1-norm-based and L0-norm-based algorithms. L1-norm-based CS reconstruction algorithms commonly use the L1-norm as a measure of sparsity. The goal of these algorithms is to find a sparse representation such that the difference between the measured values and the original signal is minimized. Some common algorithms for the L1-norm minimization include the approximate message passing (AMP) [70], iterative shrinkage-thresholding algorithm (ISTA), Fast-ISTA [71], and L1-magic [72,73]. Correspondingly, the L0-norm refers to the number of non-zero elements in a vector, and these methods aim to find a representation with the fewest non-zero elements, essentially seeking the most sparse representation. L0-norm optimization problems are often NP-hard, practical approaches that involve approximate optimization algorithms like greedy algorithms to find an approximate solution. The common greedy algorithms utilized in CS are orthogonal matching pursuit (OMP) [74], L0 gradient minimization (L0GM) [75], and sparsity adaptive matching pursuit (SAMP) [76].
In general, for the conventional reconstruction methods, L1-norm-based algorithms are more common and easier to handle since the optimization problem associated with L1-norm has convex properties. On the other hand, L0-norm-based algorithms can be more complex and computationally challenging. In practical applications, L1-norm is often preferred due to its favorable mathematical properties and computational efficiency.
5.2. Deep Learning-Based Reconstruction Methods
Regarding the conventional compressive sensing reconstruction algorithms, it is crucial to address their inherent limitations. Traditional methods often struggle with the reconstruction of highly complex signals and may encounter challenges in accurately capturing intricate features due to their reliance on fixed mathematical models. Moreover, these approaches typically assume sparsity as a priori information, which might not hold for all types of signals [77]. Recognizing these shortcomings, a paradigm shift has occurred in the form of deep learning-based CS reconstruction algorithms. These innovative approaches leverage the power of neural networks to adaptively learn and model complex signal structures, paving the way for more robust and versatile reconstruction capabilities.
Fueled by the robustness of convolutional neural networks (CNN), numerous learning-based CS reconstruction approaches have been developed by directly learning the inverse mapping from the measurement domain to the original signal domain [55,56,78]. The study conducted by [55] introduces a non-iterative and notably fast algorithm for image reconstruction from random CS measurements. A novel class of CNN architectures called ReconNet is introduced in their work, which takes in CS measurements of an image block as input and outputs the reconstructed image block. In [56], the authors focus on solving the problem of how to design a sampling mechanism to achieve optimal sampling efficiency, and how to perform the reconstruction to obtain the highest quality to achieve an optimal signal recovery. As a result, they design the sampling operator via a convolution layer and develop a convolutional neural network for reconstruction (CSNet+), which learns an end-to-end mapping between the measurement and target image. To preserve more texture details, a dual-path attention network for CS image reconstruction is proposed in the research of [78], which is composed of a structure path, a texture path, and a texture attention module. Specifically, the structure path is designed to reconstruct the dominant structure component of the original image, and the texture path aims to recover the remaining texture details.
Recently, to further enhance the reconstruction performance, a novel neural network structure for CS has been developed, which is called Deep Unfolding Network (DUN). The architecture of DUN is shown in Figure 9.
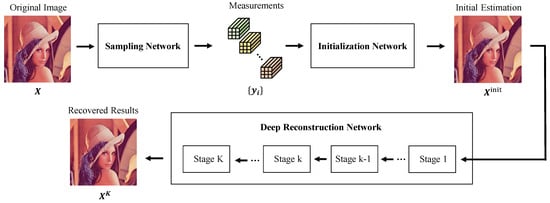
Figure 9.
The architecture of DUN.
The conventional DUN architecture is usually divided into three parts in CS: The sampling network, initialization network, and deep reconstruction network. The sampling network aims to utilize the convolution layers to simulate the sampling operation to obtain the measurements. Before going through deep reconstruction networking, an initialization network is employed to generate the initial estimation of the target image. The image reconstructed at this phase is often of subpar quality and still requires optimization and improvement. The final recovered results will be obtained by a deep reconstruction network. The deep reconstruction network typically consists of multiple stages, each representing an iteration of the traditional iterative reconstruction algorithm. These stages are usually connected sequentially, allowing the network to learn and refine the recovery at each stage. The advantage of deep unfolding lies in its ability to leverage the representation power of deep neural networks to capture complex patterns and dependencies in the data, surpassing the capabilities of traditional iterative methods.
Therefore, the DUN-based image compressive sensing algorithms with good interpretability have been extensively proposed in recent years and have gradually become mainstream [58,61,79,80,81,82]. The work of [79] proposes a cascading network with several incremental detail reconstruction modules and measurements of residual updating modules, which can be regarded as the prototype of DUN. Refs. [58,80] integrate the model-based ISTA and AMP [70] algorithms into the framework of DUN, respectively, achieving a superior performance while retaining commendable flexibility.
More recently, some researchers have started to pay attention to both the size of the network parameters and the speed of the reconstruction process, while retaining the recovered quality [61,81,82]. In general, DUN is composed of a fixed number of stages; the recovered results will be closer to the original images while increasing the unfolding iteration number. The authors from the research [82] perceive that the content of diverse images is substantially different, and it is unnecessary to process all images indiscriminately. Adhering to this perspective, they design a novel dynamic path-controllable deep unfolding network (DPC-DUN). With an elaborate path-controllable selector, their model can adaptively select a rapid and appropriate route for each image and is slimmable by regulating different performance-complexity trade-offs.
6. Codec Optimization of CS
Encoder optimization in the context of CS involves the elaborate selection and transformation of input signals into a compressed form. This phase is critical for capturing the essential information needed for accurate signal reconstruction while discarding non-essential components. One of the challenges lies in striking a balance between compression ratios and the preservation of crucial signal features. On the other hand, decoder optimization plays a pivotal role in the reconstruction of signals from the compressed representations generated by the encoder. The decoder must efficiently recover the original information, addressing challenges such as noise, artifacts, and inherent loss during the compression.
Recently, many researchers have been focusing on the holistic performance of CS and developed numerous optimization approaches for CS codec, which brings the gap between encoder and decoder enhancements. By concurrently refining both components, the CS codec optimization aims to achieve synergistic improvements, unlocking new possibilities for efficient data compression and signal reconstruction.
6.1. Scalable and Adaptive Sampling-Reconstruction
6.1.1. Scalable Sampling-Reconstruction
Although the learning-based algorithms have achieved excellent results, a prevalent limitation among current network-based approaches is that they treat CS sampling-reconstruction tasks separately for various sampling rates. This approach results in the development of intricate and extensive CS systems, necessitating the storage of a multitude of parameters. Such complexity proves to be economically burdensome when considering hardware implementation costs.
Several studies have been proposed to save the CS system memory cost and improve the model scalability [60,83,84]. In the work of [83], a scalable convolutional neural network (SCSNet) is proposed to achieve scalable sampling and scalable reconstruction with only one model. The SCSNet incorporates a hierarchical architecture and a heuristic greedy approach performed on an auxiliary dataset to independently acquire and organize measurement bases. Inspired by the conventional block-based CS methods, Ref. [60] develops a multi-channel deep network for the block-based image CS (DeepBCS) by exploiting inter-block correlations to achieve scalable CS ratio allocation. However, whether the training difficulty and defect of delicacy in [83], or the weak adaptability and structural inadequacy in [60]; both, to some extent, bring the inflexibility and low efficiency of the entire framework. The authors of [84] are devoted to solving the issues of arbitrary-sampling matrices by proposing a controllable network (COAST) and random projection augmentation to promote training diversity, thus realizing scalable sampling and reconstruction with high efficiency.
6.1.2. Adaptive Sampling-Reconstruction
Another optimization aspect of the CS codec is to improve the adaptability while processing different images [85,86]. The key idea is to exploit the saliency information of images, and then allocate more sensing resources to these salient regions but fewer to non-salient regions. Figure 10 demonstrates the illustration of adaptive sampling-reconstruction.

Figure 10.
The illustration of adaptive sampling-reconstruction. The darker the color of the blocks, the higher the allocated CS ratio.
Given that image information is often unevenly distributed, an effective approach to enhance the restored image quality involves optimizing CS ratio allocations based on saliency distribution. The works of [86,87] define saliency as the locations exhibiting a low spatial correlation with their surroundings. As illustrated in Figure 10, the block enclosed in the crimson box should be assigned a higher CS ratio than the one within the light red. This adjustment is justified by the former’s intricate details and richer information content. Being equipped with the optimization-inspired recovery subnet guided by saliency information and a multi-block training scheme that prevents blocking artifacts in [86], this content-aware scalable network (CASNet) can jointly reconstruct the image blocks sampled at various CS ratios with one single model. The PSNR/SSIM and time-consuming results for various CS algorithms on Set11 [55] are shown in Table 2. The results of five CS ratios are provided to further demonstrate the different reconstruct robustness of different methods.

Table 2.
The average PSNR (dB)/SSIM performance comparison among various CS algorithms on Set11 [55] with five different CS ratios. The average parameter and computational complexity are also provided.
The concept of adaptive sampling rates is also widely employed in surveillance video-oriented CS algorithms [88,89,90,91,92,93]. The key idea for these methods is shown in Figure 11.
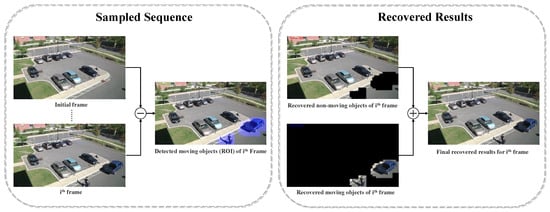
Figure 11.
The concept of adaptive sampling-reconstruction for surveillance video.
The paper of [91] first proposes a low-cost CS with multiple measurement rates for object detection (MRCS). We use another proposed MYOLO3 detector to predict the key objects, and then sample the regions of the key objects as well as other regions using multiple measurement rates to reduce the size of sampled CS measurements. However, the additional detection networking proposed in [91] will inevitably increase the parameters and the complexity of the whole framework, then bring computation and budget constraints. Moreover, the spatial and temporal correlation between successive frames of the sequence cannot be fully utilized.
Since the sampled scenes from surveillance cameras are usually fixed, some works have been developed to tackle these sequences in a straightforward method [88,89,90]. In [90], the first round of sampling will be conducted with a lower CS ratio for the initial frame and the subsequent frames. By comparing the difference between the sampled measurements, thereby locating the position of the moving objects, it also can be regarded as a region-of-interest (ROI). A higher CS ratio will be allocated to these regions for sampling-reconstruction and finally combined with the region that is regarded as background to generate the recovered results. By this background subtraction method, the ROI can be detected without introducing any extra network parameters, but the poor performance in non-ROI can only be served for the video, in which the first frame is the background; this has demonstrated that there is still much room for improvement.
To solve these issues, Ref. [92] proposes a video CS with low-complexity ROI-detection in a compressed domain (VCSL). Different from the work of [90], a binary coordinate is generated after defining ROI and transmitted to the reconstruction, instead of the sampled measurement with the low CS ratio. Moreover, a novel and compact module called a reference frame renewal (RFR) is designed in this work, which states the mechanism for defining a suitable reference, thereby improving the robustness of the framework effectively. Figure 12 shows the test examples from the VIRAT [94] dataset to demonstrate the superior performance while applying [92] to the surveillance system. More recently, Ref. [93] presents an adaptive threshold of ROI detection to replace the conventional and fixed threshold setting manually, which further improves the flexibility of these video-oriented background subtraction methods.

Figure 12.
The comparison of visual results between multi-rate VCS [90] and VCSL [92].
6.2. Pre-Calculation-Based CS Codec
Another aspect of optimizing the CS codec is the pre-calculation, which is developed in the research of [95]. In [95], the authors design a novel codec framework, named the compressive sensing-based image codec with a partial pre-calculation (CSCP). They perceived that in the measurement coding, encoding and decoding are time-consuming, and the quantization has a low complexity but is lossy, leading to a significant degradation of the reconstructed image quality. Therefore, after sampling by CS in the encoder of CSCP, the pre-calculation is performed by another proposal matrix multiplication-based fast reconstruction (MMFR) to attain the frequency domain data, which effectively reduces the processing time of the decoder. Moreover, unlike the existing common CS codecs [65], their proposed codec integrates quantization in the frequency domain after processing the partial pre-calculation. In addition, to simplify the complicated partial pre-calculation, they substitute the complex reconstruction with several add and shift operators relying on the sparsity of the sensing matrix they choose to further decrease the time-consumption.
As a relatively recent work, the research of [95] paves the way for a novel direction in optimizing CS codec more effectively and in help it to be more hardware-friendly. However, a limitation of this work is that the proposed approach can only be applied to a specific-sensing matrix. Developing a more universal framework for a broader range of sensing matrices is desired in the future.
6.3. Down-Sampling Coding-Based CS Codec
The concept of down-sampling-based coding (DBC) proposed in [96] can also be taken into account to optimize the CS codec. As shown in Figure 13, due to the limited bandwidth and storage capacity, videos and images are down-sampled at the encoder and up-sampled at the decoder, which can effectively save data in storage and transmission. The down-sampling, as observed in approaches like Bilinear and Bicubic, serves as a pre-processing step, while up-sampling methods are employed as a post-processing step.

Figure 13.
The concept of down-sampling-based coding.
This type of framework usually achieves a superior rate-distortion while utilizing network-based and high-quality super-resolution algorithms [97,98,99]. However, there are few studies that conduct this idea into CS for codec optimization. Inspired by the concept of DBC, Ref. [100] proposes a novel video compressive sensing reconstruction framework with joint in-loop reference enhancement and out-loop super-resolution, dubbed JVCSR. Specifically, two additional modules are employed to further improve the reconstruction quality: An in-loop reference enhancement module is developed to remove the artifacts and provide a superior-quality frame for motion compensation cyclically. The reconstructed outputs are fed to another proposed out-loop super-resolution module to attain a a higher-resolution and higher-quality video at the lower bit-rates. The experimental results demonstrate that DBC also exhibits coding advantages in CS, especially in low bit-rate transmission. It can be anticipated that this type of method will be more widely applied to some straightforward hardware cameras and is able to provide higher-quality videos while sending the low compressed data.
Finally, Table 3 provides an exhaustive comparison to summarize the various abilities of introduced algorithms.

Table 3.
The comparison of the different learning-based CS sampling-reconstruction approaches.
7. Challenges and Future Scope
The contemporary landscape in data generation is characterized by an unprecedented surge, placing substantial demands on sensing, storage, and processing devices. This surge has led to the establishment of numerous data centers worldwide, grappling with the immense volume of data and resulting in the substantial power consumption during acquisition and processing. The escalating data production underscores the urgent need for innovative concepts in both data acquisition and processing. The emergence and growing popularity of CS have emerged as a substantial contributor to addressing this burgeoning issue, presenting a paradigm shift in how data are acquired, transmitted, and processed.
However, despite its transformative potential, CS encounters a spectrum of challenges and opportunities that warrant a closer examination. The advent of deep neural networks and transformers has given rise to a plethora of learning-based CS algorithms, aimed at achieving superior reconstruction quality. Nevertheless, a notable hurdle lies in the successful implementation of these algorithms in hardware due to the substantial size of the network models. The practical deployment of these algorithms on hardware platforms remains limited, hindering the widespread adoption.
Recent research has recognized the need to balance reconstruction quality with the size of models and processing speed, leading to the development of models that prioritize reduced parameters while maintaining high-quality reconstruction results [81,82]. These endeavors address the practical requirements for real-world applications, particularly in resource-constrained environments. The pursuit of smaller models with preserved reconstruction efficacy emerges as a pivotal research direction for the future, offering promising avenues for practical implementation. Anticipating the continued advancement of technology, the deployment of more optimized CS algorithms across diverse hardware platforms is expected to gain traction. This optimism stems from the ongoing efforts to strike a balance between computational efficiency and reconstruction quality, making CS increasingly applicable in a variety of real-world scenarios.
Beyond conventional applications, the exploration of CS in light field imaging holds immense promise [101,102,103,104]. Light field imaging, renowned for its capability to capture multiple light ray directions and intensities for each point in a scene, seamlessly aligns with the fundamental principles of compressive sensing. This harmonious integration allows for a more efficient harnessing of additional information, thereby enriching the detailed and comprehensive perception of a scene. Furthermore, the reduction in data acquisition requirements achieved through CS in light field imaging introduces significant advantages. This is particularly noteworthy in scenarios involving resource-constrained systems such as sensor networks or mobile devices. The synergy between CS and light field imaging not only enhances the overall quality of the scene perception but also contributes to addressing challenges related to limited resources, paving the way for innovative applications and advancements in these domains.
On the other hand, since the work of [105] had been proposed, several CS systems using chaos filters have been developed recently [106,107,108]. In general, the chaotic CS system is designed to achieve simultaneous compression and encryption. The encryption can provide many significant features, such as security analysis and statistical attack protection, and uses the parameters as the secret key in the reconstruction of the measurement matrix and masking matrix. The advantages of employing chaotic CS systems might surpass the additional algorithmic consumption, given the reduced data transmission requirements. However, the impact on performance under the scenario of a microcontroller operating at a higher frequency, and consequently exhibiting increased consumption, remains an area that requires further investigation in the future. Last but not least, CS, with its capability to substantially reduce the data representation size while preserving essential information, holds promising prospects for applications in many high-level vision tasks, such as object detection [109,110], semantic segmentation [111], and image classification [112,113]. It is imperative to underscore that the potential of CS in these domains is far from fully realized, and there exists substantial room for further advancements and breakthroughs.
8. Conclusions
In this paper, we provide a comprehensive overview of compressive sensing in image and video compression, elaborating it through the lenses of sampling, coding, reconstruction, and codec optimization. Our exploration begins with a detailed discussion of sampling methods, with a particular emphasis on the design of measurement matrices tailored for superior reconstruction quality and optimized for enhanced measurement coding efficiency. We delve into the intricacies of measurement coding, elucidating various approaches such as intra prediction, inter prediction, and rate control. The paper further introduces a spectrum of reconstruction algorithms, encompassing both conventional and learning-based methods. Additionally, we provide a thorough overview of the holistic optimization of the compressive sensing codec. Our discussion extends to the current challenges and future prospects of compressive sensing, offering valuable insights into the evolving landscape of this technique. We believe that this review has the potential to inspire reflection and instigate further exploration within the image and video compression research community. It lays the groundwork for future investigations and applications of compressive sensing in this field.
Author Contributions
Writing—original draft preparation, J.Y.; writing—review and editing, J.Z.; All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by JSPS KAKENHI Grant Number JP22K12101.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to JSPS KAKENHI Grant Number JP22K12101 for the support of this research.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Por, E.; van Kooten, M.; Sarkovic, V. Nyquist–Shannon Sampling Theorem; Leiden University: Leiden, The Netherlands, 2019; Volume 1. [Google Scholar]
- Arildsen, T.; Oxvig, C.S.; Pedersen, P.S.; Østergaard, J.; Larsen, T. Reconstruction algorithms in undersampled AFM imaging. IEEE J. Sel. Top. Signal Process. 2015, 10, 31–46. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Yuan, Y.; Huang, B. Applications of atomic force microscopy in immunology. Front. Med. 2021, 15, 43–52. [Google Scholar] [CrossRef]
- Lerner, B.E.; Flores-Garibay, A.; Lawrie, B.J.; Maksymovych, P. Compressed sensing for scanning tunnel microscopy imaging of defects and disorder. Phys. Rev. Res. 2021, 3, 043040. [Google Scholar] [CrossRef]
- Otazo, R.; Candes, E.; Sodickson, D.K. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn. Reson. Med. 2015, 73, 1125–1136. [Google Scholar] [CrossRef]
- Quan, T.M.; Nguyen-Duc, T.; Jeong, W.K. Compressed sensing MRI reconstruction using a generative adversarial network with a cyclic loss. IEEE Trans. Med. Imaging 2018, 37, 1488–1497. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.M.; Yan, Y.; Wang, S.; Xu, Y.; Shao, L.; Fu, H. Specificity-preserving federated learning for MR image reconstruction. IEEE Trans. Med. Imaging 2022, 42, 2010–2021. [Google Scholar] [CrossRef]
- Zhang, L.; Xing, M.; Qiu, C.W.; Li, J.; Sheng, J.; Li, Y.; Bao, Z. Resolution enhancement for inversed synthetic aperture radar imaging under low SNR via improved compressive sensing. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3824–3838. [Google Scholar] [CrossRef]
- Giusti, E.; Cataldo, D.; Bacci, A.; Tomei, S.; Martorella, M. ISAR image resolution enhancement: Compressive sensing versus state-of-the-art super-resolution techniques. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1983–1997. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, Z.; Wen, C.; Li, J.; Xia, X.G.; Hong, W. An efficient radio frequency interference mitigation algorithm in real synthetic aperture radar data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Priya, G.; Ghosh, D. An Effectual Video Compression Scheme for WVSNs Based on Block Compressive Sensing. IEEE Trans. Netw. Sci. Eng. 2023. [Google Scholar] [CrossRef]
- Rajpoot, P.; Dwivedi, P. Optimized and load balanced clustering for wireless sensor networks to increase the lifetime of WSN using MADM approaches. Wirel. Netw. 2020, 26, 215–251. [Google Scholar] [CrossRef]
- Okada, H.; Suzaki, S.; Kato, T.; Kobayashi, K.; Katayama, M. Link quality information sharing by compressed sensing and compressed transmission for arbitrary topology wireless mesh networks. IEICE Trans. Commun. 2017, 100, 456–464. [Google Scholar] [CrossRef]
- Rao, P.S.; Jana, P.K.; Banka, H. A particle swarm optimization based energy efficient cluster head selection algorithm for wireless sensor networks. Wirel. Netw. 2017, 23, 2005–2020. [Google Scholar] [CrossRef]
- Ali, I.; Ahmedy, I.; Gani, A.; Munir, M.U.; Anisi, M.H. Data collection in studies on Internet of things (IoT), wireless sensor networks (WSNs), and sensor cloud (SC): Similarities and differences. IEEE Access 2022, 10, 33909–33931. [Google Scholar] [CrossRef]
- Gai, K.; Qiu, M. Optimal resource allocation using reinforcement learning for IoT content-centric services. Appl. Soft Comput. 2018, 70, 12–21. [Google Scholar] [CrossRef]
- Garcia, N.; Wymeersch, H.; Larsson, E.G.; Haimovich, A.M.; Coulon, M. Direct localization for massive MIMO. IEEE Trans. Signal Process. 2017, 65, 2475–2487. [Google Scholar] [CrossRef]
- Björnson, E.; Sanguinetti, L.; Wymeersch, H.; Hoydis, J.; Marzetta, T.L. Massive MIMO is a reality—What is next?: Five promising research directions for antenna arrays. Digit. Signal Process. 2019, 94, 3–20. [Google Scholar] [CrossRef]
- Guo, J.; Wen, C.K.; Jin, S.; Li, G.Y. Convolutional neural network-based multiple-rate compressive sensing for massive MIMO CSI feedback: Design, simulation, and analysis. IEEE Trans. Wirel. Commun. 2020, 19, 2827–2840. [Google Scholar] [CrossRef]
- Nagesh, P.; Li, B. A compressive sensing approach for expression-invariant face recognition. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1518–1525. [Google Scholar]
- Andrés, A.M.; Padovani, S.; Tepper, M.; Jacobo-Berlles, J. Face recognition on partially occluded images using compressed sensing. Pattern Recognit. Lett. 2014, 36, 235–242. [Google Scholar] [CrossRef]
- Jaber, A.K.; Abdel-Qader, I. Hybrid Histograms of Oriented Gradients-compressive sensing framework feature extraction for face recognition. In Proceedings of the 2016 IEEE International Conference on Electro Information Technology (EIT), Grand Forks, ND, USA, 19–21 May 2016; pp. 442–447. [Google Scholar]
- Akl, A.; Feng, C.; Valaee, S. A novel accelerometer-based gesture recognition system. IEEE Trans. Signal Process. 2011, 59, 6197–6205. [Google Scholar] [CrossRef]
- Wang, Z.W.; Vineet, V.; Pittaluga, F.; Sinha, S.N.; Cossairt, O.; Bing Kang, S. Privacy-preserving action recognition using coded aperture videos. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar]
- Zhuang, H.; Yang, M.; Cui, Z.; Zheng, Q. A method for static hand gesture recognition based on non-negative matrix factorization and compressive sensing. IAENG Int. J. Comput. Sci. 2017, 44, 52–59. [Google Scholar]
- Sivapalan, S.; Rana, R.K.; Chen, D.; Sridharan, S.; Denmon, S.; Fookes, C. Compressive sensing for gait recognition. In Proceedings of the 2011 International Conference on Digital Image Computing: Techniques and Applications, Noosa, QLD, Australia, 6–8 December 2011; pp. 567–571. [Google Scholar]
- Pant, J.K.; Krishnan, S. Compressive sensing of foot gait signals and its application for the estimation of clinically relevant time series. IEEE Trans. Biomed. Eng. 2015, 63, 1401–1415. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Xu, H. An advanced scheme of compressed sensing of acceleration data for telemonintoring of human gait. Biomed. Eng. Online 2016, 15, 27. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, M.; Torii, A.; Okutomi, M.; Taniguchi, R.i.; Nagahara, H.; Yagi, Y. Deep Sensing for Compressive Video Acquisition. Sensors 2023, 23, 7535. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Ma, S.; Zhang, J.; Xiong, R.; Gao, W. Video compressive sensing reconstruction via reweighted residual sparsity. IEEE Trans. Circuits Syst. Video Technol. 2016, 27, 1182–1195. [Google Scholar] [CrossRef]
- Shi, W.; Liu, S.; Jiang, F.; Zhao, D. Video compressed sensing using a convolutional neural network. IEEE Trans. Circuits Syst. Video Technol. 2020, 31, 425–438. [Google Scholar] [CrossRef]
- Veeraraghavan, A.; Reddy, D.; Raskar, R. Coded strobing photography: Compressive sensing of high speed periodic videos. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 671–686. [Google Scholar] [CrossRef]
- Martel, J.N.; Mueller, L.K.; Carey, S.J.; Dudek, P.; Wetzstein, G. Neural sensors: Learning pixel exposures for HDR imaging and video compressive sensing with programmable sensors. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 1642–1653. [Google Scholar] [CrossRef]
- Dong, D.; Rui, G.; Tian, W.; Liu, G.; Zhang, H. A Multi-Task Bayesian Algorithm for online Compressed Sensing of Streaming Signals. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–5. [Google Scholar]
- Edgar, M.P.; Sun, M.J.; Gibson, G.M.; Spalding, G.C.; Phillips, D.B.; Padgett, M.J. Real-time 3D video utilizing a compressed sensing time-of-flight single-pixel camera. In Proceedings of the Optical Trapping and Optical Micromanipulation XIII, San Diego, CA, USA, 28 August–1 September 2016; Volume 9922, pp. 171–178. [Google Scholar]
- Edgar, M.; Johnson, S.; Phillips, D.; Padgett, M. Real-time computational photon-counting LiDAR. Opt. Eng. 2018, 57, 031304. [Google Scholar] [CrossRef]
- Musarra, G.; Lyons, A.; Conca, E.; Villa, F.; Zappa, F.; Altmann, Y.; Faccio, D. 3D RGB non-line-of-sight single-pixel imaging. In Proceedings of the Imaging Systems and Applications, Munich, Germany, 24–27 June 2019; p. IM2B–5. [Google Scholar]
- Song, J.; Mou, C.; Wang, S.; Ma, S.; Zhang, J. Optimization-Inspired Cross-Attention Transformer for Compressive Sensing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 6174–6184. [Google Scholar]
- Candes, E.J.; Plan, Y. A probabilistic and RIPless theory of compressed sensing. IEEE Trans. Inf. Theory 2011, 57, 7235–7254. [Google Scholar] [CrossRef]
- Foucart, S.; Rauhut, H.; Foucart, S.; Rauhut, H. An Invitation to Compressive Sensing; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Nguyen, T.L.N.; Shin, Y. Deterministic sensing matrices in compressive sensing: A survey. Sci. World J. 2013, 2013, 192795. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Wen, G.; Wang, Z.; Yang, Y. Efficient and secure image communication system based on compressed sensing for IoT monitoring applications. IEEE Trans. Multimed. 2019, 22, 82–95. [Google Scholar] [CrossRef]
- Zhou, J.; Zhou, D.; Guo, L.; Yoshimura, T.; Goto, S. Framework and vlsi architecture of measurement-domain intra prediction for compressively sensed visual contents. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2017, 100, 2869–2877. [Google Scholar] [CrossRef]
- Yu, N.Y. Indistinguishability and energy sensitivity of Gaussian and Bernoulli compressed encryption. IEEE Trans. Inf. Forensics Secur. 2018, 13, 1722–1735. [Google Scholar] [CrossRef]
- Moshtaghpour, A.; Bioucas-Dias, J.M.; Jacques, L. Close encounters of the binary kind: Signal reconstruction guarantees for compressive Hadamard sampling with Haar wavelet basis. IEEE Trans. Inf. Theory 2020, 66, 7253–7273. [Google Scholar] [CrossRef]
- Zhuoran, C.; Honglin, Z.; Min, J.; Gang, W.; Jingshi, S. An improved Hadamard measurement matrix based on Walsh code for compressive sensing. In Proceedings of the 2013 9th International Conference on Information, Communications & Signal Processing, Tainan, Taiwan, 10–13 December 2013; pp. 1–4. [Google Scholar]
- Rauhut, H. Circulant and Toeplitz matrices in compressed sensing. arXiv 2009, arXiv:0902.4394. [Google Scholar]
- Boyer, C.; Bigot, J.; Weiss, P. Compressed sensing with structured sparsity and structured acquisition. Appl. Comput. Harmon. Anal. 2019, 46, 312–350. [Google Scholar] [CrossRef]
- Sun, M.J.; Meng, L.T.; Edgar, M.P.; Padgett, M.J.; Radwell, N. A Russian Dolls ordering of the Hadamard basis for compressive single-pixel imaging. Sci. Rep. 2017, 7, 3464. [Google Scholar] [CrossRef]
- Yu, W.K. Super sub-Nyquist single-pixel imaging by means of cake-cutting Hadamard basis sort. Sensors 2019, 19, 4122. [Google Scholar] [CrossRef]
- Yu, W.K.; Liu, Y.M. Single-pixel imaging with origami pattern construction. Sensors 2019, 19, 5135. [Google Scholar] [CrossRef]
- López-García, L.; Cruz-Santos, W.; García-Arellano, A.; Filio-Aguilar, P.; Cisneros-Martínez, J.A.; Ramos-García, R. Efficient ordering of the Hadamard basis for single pixel imaging. Opt. Express 2022, 30, 13714–13732. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, J.; Peetakul, J.; Zhou, J. Zigzag Ordered Walsh Matrix for Compressed Sensing Image Sensor. In Proceedings of the 2023 Data Compression Conference (DCC), Snowbird, UT, USA, 21–24 March 2023; p. 346. [Google Scholar]
- Kulkarni, K.; Lohit, S.; Turaga, P.; Kerviche, R.; Ashok, A. Reconnet: Non-iterative reconstruction of images from compressively sensed measurements. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 449–458. [Google Scholar]
- Shi, W.; Jiang, F.; Liu, S.; Zhao, D. Image compressed sensing using convolutional neural network. IEEE Trans. Image Process. 2019, 29, 375–388. [Google Scholar] [CrossRef]
- Du, J.; Xie, X.; Wang, C.; Shi, G.; Xu, X.; Wang, Y. Fully convolutional measurement network for compressive sensing image reconstruction. Neurocomputing 2019, 328, 105–112. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Liu, J.; Wen, F.; Zhu, C. AMP-Net: Denoising-based deep unfolding for compressive image sensing. IEEE Trans. Image Process. 2020, 30, 1487–1500. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, C.; Gao, W. Optimization-inspired compact deep compressive sensing. IEEE J. Sel. Top. Signal Process. 2020, 14, 765–774. [Google Scholar] [CrossRef]
- Zhou, S.; He, Y.; Liu, Y.; Li, C.; Zhang, J. Multi-channel deep networks for block-based image compressive sensing. IEEE Trans. Multimed. 2020, 23, 2627–2640. [Google Scholar] [CrossRef]
- Song, J.; Chen, B.; Zhang, J. Memory-augmented deep unfolding network for compressive sensing. In Proceedings of the 29th ACM International Conference on Multimedia, Virtual Event, 20–24 October 2021; pp. 4249–4258. [Google Scholar]
- Gao, X.; Zhang, J.; Che, W.; Fan, X.; Zhao, D. Block-based compressive sensing coding of natural images by local structural measurement matrix. In Proceedings of the 2015 Data Compression Conference, Snowbird, UT, USA, 7–9 April 2015; pp. 133–142. [Google Scholar]
- Wan, R.; Zhou, J.; Huang, B.; Zeng, H.; Fan, Y. Measurement Coding Framework with Adjacent Pixels Based Measurement Matrix for Compressively Sensed Images. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 1435–1439. [Google Scholar]
- Zhou, J.; Zhou, D.; Guo, L.; Takeshi, Y.; Goto, S. Measurement-domain intra prediction framework for compressively sensed images. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017; pp. 1–4. [Google Scholar]
- Peetakul, J.; Zhou, J.; Wada, K. A measurement coding system for block-based compressive sensing images by using pixel-domain features. In Proceedings of the 2019 Data Compression Conference (DCC), Snowbird, UT, USA, 26–29 March 2019; p. 599. [Google Scholar]
- KL, B.R.; Pudi, V.; Appina, B.; Chattopadhyay, A. Image Compression Based On Near Lossless Predictive Measurement Coding for Block Based Compressive Sensing. IEEE Trans. Circuits Syst. II Express Briefs 2023. [Google Scholar] [CrossRef]
- Peetakul, J.; Zhou, J. Temporal redundancy reduction in compressive video sensing by using moving detection and inter-coding. In Proceedings of the 2020 Data Compression Conference (DCC), Snowbird, UT, USA, 24–27 March 2020; p. 387. [Google Scholar]
- Kimishima, F.; Yang, J.; Tran, T.T.; Zhou, J. Frame Adaptive Rate Control Scheme for Video Compressive Sensing. In Proceedings of the International Conference on Image Analysis and Processing, Lecce, Italy, 23–27 May 2022; pp. 247–256. [Google Scholar]
- Wan, R.; Zhou, J.; Huang, B.; Zeng, H.; Fan, Y. APMC: Adjacent pixels based measurement coding system for compressively sensed images. IEEE Trans. Multimed. 2021, 24, 3558–3569. [Google Scholar] [CrossRef]
- Donoho, D.L.; Maleki, A.; Montanari, A. Message-passing algorithms for compressed sensing. Proc. Natl. Acad. Sci. USA 2009, 106, 18914–18919. [Google Scholar] [CrossRef] [PubMed]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Candes, E.; Romberg, J. l1-Magic: Recovery of Sparse Signals via Convex Programming. 2005, Volume 4, p. 16. Available online: www.acm.caltech.edu/l1magic/downloads/l1magic.pdf (accessed on 31 October 2005).
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, C.; Zhao, D.; Gao, W. Image compressive sensing recovery using adaptively learned sparsifying basis via L0 minimization. Signal Process. 2014, 103, 114–126. [Google Scholar] [CrossRef]
- Do, T.T.; Gan, L.; Nguyen, N.; Tran, T.D. Sparsity adaptive matching pursuit algorithm for practical compressed sensing. In Proceedings of the 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–29 October 2008; pp. 581–587. [Google Scholar]
- Li, L.; Fang, Y.; Liu, L.; Peng, H.; Kurths, J.; Yang, Y. Overview of compressed sensing: Sensing model, reconstruction algorithm, and its applications. Appl. Sci. 2020, 10, 5909. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, J.; Liu, Q.; Liu, B.; Guo, G. Dual-path attention network for compressed sensing image reconstruction. IEEE Trans. Image Process. 2020, 29, 9482–9495. [Google Scholar] [CrossRef]
- Chen, J.; Sun, Y.; Liu, Q.; Huang, R. Learning memory augmented cascading network for compressed sensing of images. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 513–529. [Google Scholar]
- You, D.; Xie, J.; Zhang, J. ISTA-NET++: Flexible deep unfolding network for compressive sensing. In Proceedings of the 2021 IEEE International Conference on Multimedia and Expo (ICME), Shenzhen, China, 5–9 July 2021; pp. 1–6. [Google Scholar]
- Chen, W.; Yang, C.; Yang, X. FSOINET: Feature-space optimization-inspired network for image compressive sensing. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 2460–2464. [Google Scholar]
- Song, J.; Chen, B.; Zhang, J. Dynamic Path-Controllable Deep Unfolding Network for Compressive Sensing. IEEE Trans. Image Process. 2023, 32, 2202–2214. [Google Scholar] [CrossRef]
- Shi, W.; Jiang, F.; Liu, S.; Zhao, D. Scalable convolutional neural network for image compressed sensing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 12290–12299. [Google Scholar]
- You, D.; Zhang, J.; Xie, J.; Chen, B.; Ma, S. Coast: Controllable arbitrary-sampling network for compressive sensing. IEEE Trans. Image Process. 2021, 30, 6066–6080. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, B.; Zhang, L. Saliency-based compressive sampling for image signals. IEEE Signal Process. Lett. 2010, 17, 973–976. [Google Scholar]
- Chen, B.; Zhang, J. Content-aware scalable deep compressed sensing. IEEE Trans. Image Process. 2022, 31, 5412–5426. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Wang, B.; Zhang, L. Hebbian-based neural networks for bottom-up visual attention systems. In Neural Information Processing, Proceedings of the 16th International Conference, ICONIP 2009, Bangkok, Thailand, 1–5 December 2009; Proceedings, Part I 16; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–9. [Google Scholar]
- Jiang, H.; Deng, W.; Shen, Z. Surveillance video processing using compressive sensing. arXiv 2013, arXiv:1302.1942. [Google Scholar] [CrossRef]
- Nandhini, S.A.; Radha, S.; Kishore, R. Efficient compressed sensing based object detection system for video surveillance application in WMSN. Multimed. Tools Appl. 2018, 77, 1905–1925. [Google Scholar] [CrossRef]
- Du, J.; Xie, X.; Shi, G. Multi-rate Video Compressive Sensing for Fixed Scene Measurement. In Proceedings of the 2021 5th International Conference on Video and Image Processing, Hayward, CA, USA, 22–25 December 2021; pp. 177–183. [Google Scholar]
- Liao, L.; Li, K.; Yang, C.; Liu, J. Low-cost image compressive sensing with multiple measurement rates for object detection. Sensors 2019, 19, 2079. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Wang, H.; Fan, Y.; Zhou, J. VCSL: Video Compressive Sensing with Low-complexity ROI Detection in Compressed Domain. In Proceedings of the 2023 Data Compression Conference (DCC), Snowbird, UT, USA, 21–24 March 2023; p. 1. [Google Scholar]
- Yang, J.; Wang, H.; Taniguchi, I.; Fan, Y.; Zhou, J. aVCSR: Adaptive Video Compressive Sensing using Region-of-Interest Detection in the Compressed Domain. IEEE MultiMed. 2023, 1–10. [Google Scholar] [CrossRef]
- VIRAT Description. Available online: http://www.viratdata.org/ (accessed on 20 January 2024).
- Xu, J.; Yang, J.; Kimishima, F.; Taniguchi, I.; Zhou, J. Compressive Sensing Based Image Codec With Partial Pre-Calculation. IEEE Trans. Multimed. 2023. [Google Scholar] [CrossRef]
- Shen, M.; Xue, P.; Wang, C. Down-sampling based video coding using super-resolution technique. IEEE Trans. Circuits Syst. Video Technol. 2011, 21, 755–765. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, X.; Zhang, X.; Wang, S.; Wang, R.; Ma, S. A dual-network based super-resolution for compressed high definition video. In Advances in Multimedia Information Processing–PCM 2018, Proceedings of the 19th Pacific-Rim Conference on Multimedia, Hefei, China, 21–22 September 2018; Proceedings, Part I 19; Springer: Berlin/Heidelberg, Germany, 2018; pp. 600–610. [Google Scholar]
- Li, Y.; Liu, D.; Li, H.; Li, L.; Wu, F.; Zhang, H.; Yang, H. Convolutional neural network-based block up-sampling for intra frame coding. IEEE Trans. Circuits Syst. Video Technol. 2017, 28, 2316–2330. [Google Scholar] [CrossRef]
- Khattab, M.M.; Zeki, A.M.; Alwan, A.A.; Bouallegue, B.; Matter, S.S.; Ahmed, A.M. A Hybrid Regularization-Based Multi-Frame Super-Resolution Using Bayesian Framework. Comput. Syst. Sci. Eng. 2023, 44, 35–54. [Google Scholar] [CrossRef]
- Yang, J.; Pham, C.D.K.; Zhou, J. JVCSR: Video Compressive Sensing Reconstruction with Joint In-Loop Reference Enhancement and Out-Loop Super-Resolution. In Proceedings of the International Conference on Multimedia Modeling, Phu Quoc, Vietnam, 6–10 June 2022; pp. 455–466. [Google Scholar]
- Miandji, E.; Hajisharif, S.; Unger, J. A unified framework for compression and compressed sensing of light fields and light field videos. ACM Trans. Graph. (TOG) 2019, 38, 1–18. [Google Scholar] [CrossRef]
- Babacan, S.D.; Ansorge, R.; Luessi, M.; Matarán, P.R.; Molina, R.; Katsaggelos, A.K. Compressive light field sensing. IEEE Trans. Image Process. 2012, 21, 4746–4757. [Google Scholar] [CrossRef]
- Ashok, A.; Neifeld, M.A. Compressive light field imaging. In Proceedings of the Three-Dimensional Imaging, Visualization, and Display 2010 and Display Technologies and Applications for Defense, Security, and Avionics IV, Orlando, FL, USA, 5–9 April 2010; Volume 7690, pp. 221–232. [Google Scholar]
- Guo, M.; Hou, J.; Jin, J.; Chen, J.; Chau, L.P. Deep spatial-angular regularization for compressive light field reconstruction over coded apertures. In Computer Vision–ECCV 2020, Proceedings of the 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part II 16; Springer: Berlin/Heidelberg, Germany, 2020; pp. 278–294. [Google Scholar]
- Linh-Trung, N.; Van Phong, D.; Hussain, Z.M.; Huynh, H.T.; Morgan, V.L.; Gore, J.C. Compressed sensing using chaos filters. In Proceedings of the 2008 Australasian Telecommunication Networks and Applications Conference, Adelaide, SA, Australia, 7–10 December 2008; pp. 219–223. [Google Scholar]
- Sun, Y.; Han, G.; Huang, L.; Wang, S.; Xiang, J. Construction of block circulant measurement matrix based on hybrid chaos: Bernoulli sequences. In Proceedings of the 2020 4th International Conference on Digital Signal Processing, Chengdu, China, 19–21 June 2020; pp. 1–6. [Google Scholar]
- Jabor, M.S.; Azez, A.S.; Campelo, J.C.; Bonastre Pina, A. New approach to improve power consumption associated with blockchain in WSNs. PLoS ONE 2023, 18, e0285924. [Google Scholar] [CrossRef]
- Theu, L.T.; Huy, T.Q.; Quynh, T.T.T.; Tran, D.T. Imaging Ultrasound Scattering Targets using Density-Enhanced Chaotic Compressive Sampling. In Proceedings of the 2023 Asia Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Taipei, Taiwan, 31 October–3 November 2023; pp. 1285–1290. [Google Scholar]
- Ye, D.; Ni, Z.; Wang, H.; Zhang, J.; Wang, S.; Kwong, S. CSformer: Bridging convolution and transformer for compressive sensing. IEEE Trans. Image Process. 2023, 32, 2827–2842. [Google Scholar] [CrossRef]
- Huyan, L.; Li, Y.; Jiang, D.; Zhang, Y.; Zhou, Q.; Li, B.; Wei, J.; Liu, J.; Zhang, Y.; Wang, P.; et al. Remote Sensing Imagery Object Detection Model Compression via Tucker Decomposition. Mathematics 2023, 11, 856. [Google Scholar] [CrossRef]
- Arena, P.; Basile, A.; Bucolo, M.; Fortuna, L. An object oriented segmentation on analog CNN chip. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2003, 50, 837–846. [Google Scholar] [CrossRef]
- Ramirez, J.M.; Torre, J.I.M.; Arguello, H. Feature fusion via dual-resolution compressive measurement matrix analysis for spectral image classification. Signal Process. Image Commun. 2021, 90, 116014. [Google Scholar] [CrossRef]
- Zhou, S.; Deng, X.; Li, C.; Liu, Y.; Jiang, H. Recognition-oriented image compressive sensing with deep learning. IEEE Trans. Multimed. 2022, 25, 2022–2032. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).