1. Introduction
Glioblastoma multiforme (GBM), among the most malignant central nervous system tumors, constitutes a prevalent form of primary brain cancer originating within brain tissue. Studies indicate challenges in complete tumor removal during surgery due to its inherent local invasiveness, with a probability of recurrence in the vicinity of the original tumor location. Its aggressive nature bears a grade IV classification and a bleak prognosis [
1]. Observations in tissue slices of glioblastoma commonly manifest as thrombus formation, microvascular proliferation, and cellular necrosis [
2]. However, the tumor’s substantial heterogeneity implies that absence of these phenomena in tissue slices does not preclude the presence of GBM, posing a challenge to accurate prognosis through histological images.
Traditional survival analysis usually relies on manually extracted features modeled using proportional hazard model. For example, Tibshirani (1997) [
3] utilized clinical data such as gender, age, and treatment methods, and employed the LASSO method to select pertinent features before inputting into the Cox proportional hazards model. This technique adds a penalty term to the loss function during model computation, constraining outputs within a specific range, thereby retaining essential features and reducing complexity while enhancing predictive efficacy.
Early survival analysis methods have since evolved, leveraging machine learning and deep learning techniques, especially in survival prediction based on whole-slide images (WSIs). However, WSIs are extremely high resolution images; feeding them directly into deep learning models is computationally infeasible. Thus, researchers have proposed methods to extract meaningful patches from WSIs as input. For example, Zhu et al. (2016) [
4] addressed the issue by extracting patches from regions of interest (ROIs) annotated by pathologists and trained a deep convolutional neural network (CNN) for lung cancer survival analysis. However, this demands substantial human labor and potentially results in missing insights from other parts of the digital pathology slides.
To mitigate the laborious manual ROI labelling, research studies such as [
5,
6,
7,
8,
9] have proposed to randomly sample patches from different areas of the WSI. Zhu et al. (2017) [
5] then utilized K-means to cluster the sampled patches, and constructed classifiers for each cluster to identify and select the clusters most useful for survival analysis. Li et al. (2018) [
6] and Di et al. (2020) [
8] constructed a graph or hypergraph as a summarized representation of the WSI by placing feature vectors extracted from the patches as node features, and relational features among the patches as edge features. Li et al. (2023), [
10] on the other hand, proposed an entropy-based patch sampling method, and utilized self-supervised learning to alleviate domain gaps from pre-training on natural images. They also introduced an attention-based global-local information fusion strategy to improve prediction accuracy.
However, many of these methods utilized only a fixed subset of all viable patches, even after removing background or distorted patches. Ref. [
5] sampled a fixed area ratio of patches from WSI for training. Ref. [
7] used only patches from selected clusters to train the main classifier. Ref. [
9] sampled a random but fixed 1000 patches from each WSI, while [
10] used only patches with high entropy to train the model. By using only a subset of patches for training, these methods may potentially discard important information from the remaining patches.
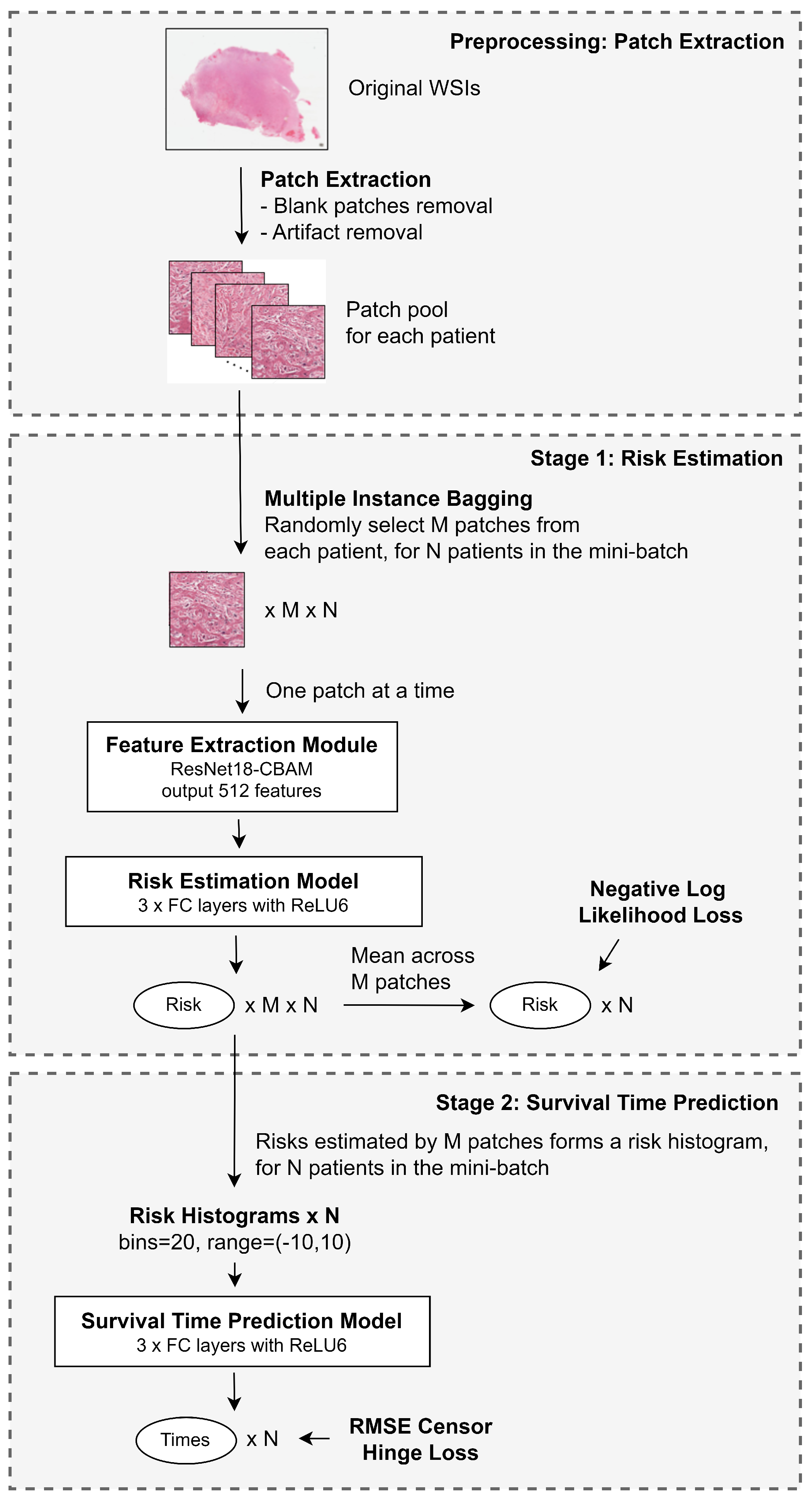
In this study, we propose a method that utilizes all viable patches from the WSI while keeping the training computationally feasible. Additionally, we attempt to predict the exact survival time of patients, beyond the usual risk of death estimation. At the same time, we aim to devise a framework that provides visual explainability for clinicians.
The contributions of this paper can be summarized as follows:
We introduce a multiple instance bagging strategy that enables the utilization of information from the entire WSI while maintaining computational feasibility during training.
We develop a two-stage framework that not only estimates survival risk but also predicts actual survival time.
We propose a new loss function, the Root Mean Square Censor Hinge Loss (RMSCHE), which effectively handles censored data in survival time prediction.
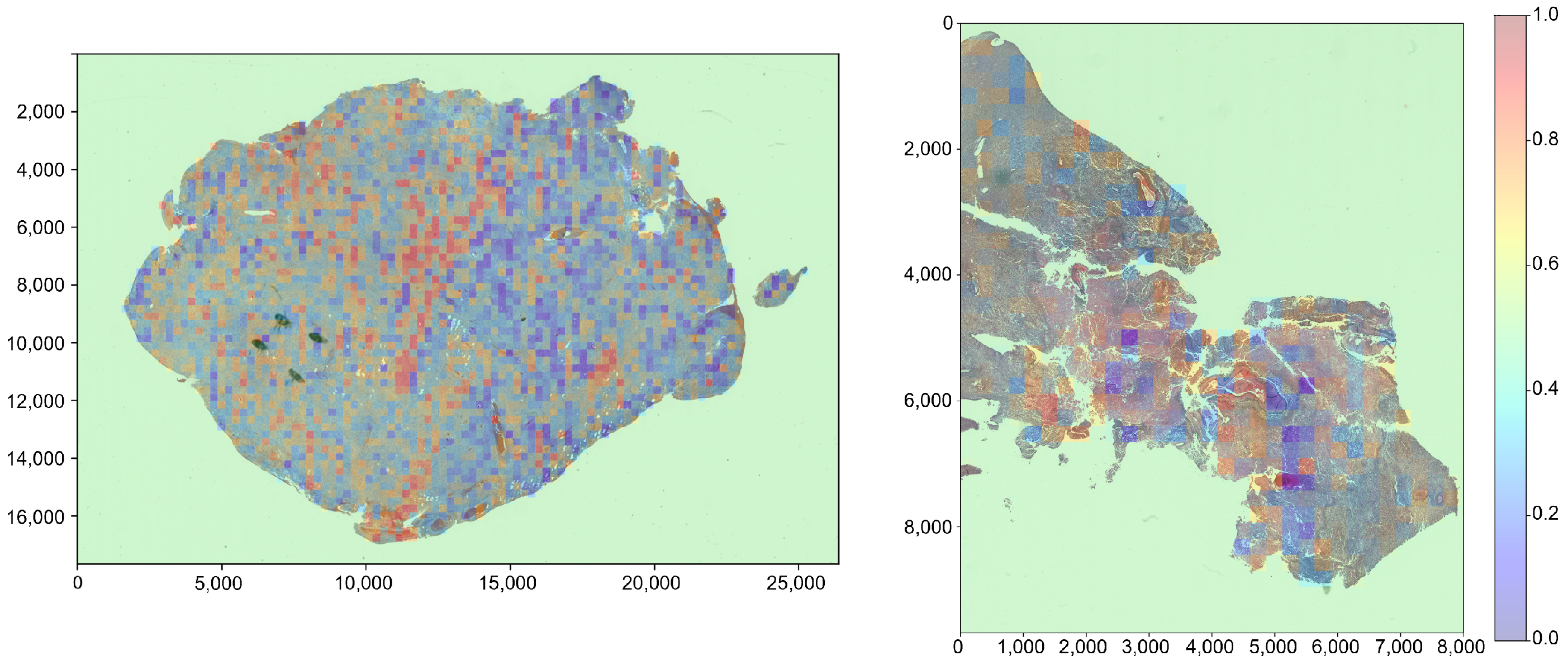
We implement a heatmap visualization method that provides interpretable risk assessments at the patch level, potentially aiding clinicians in identifying high-risk regions within WSIs.
The rest of the paper is organized as follows:
Section 2 introduces the background of survival analysis used in this study.
Section 3 outlines the overall framework and details each stage of the proposed method, including patch extraction, risk estimation, and survival time prediction.
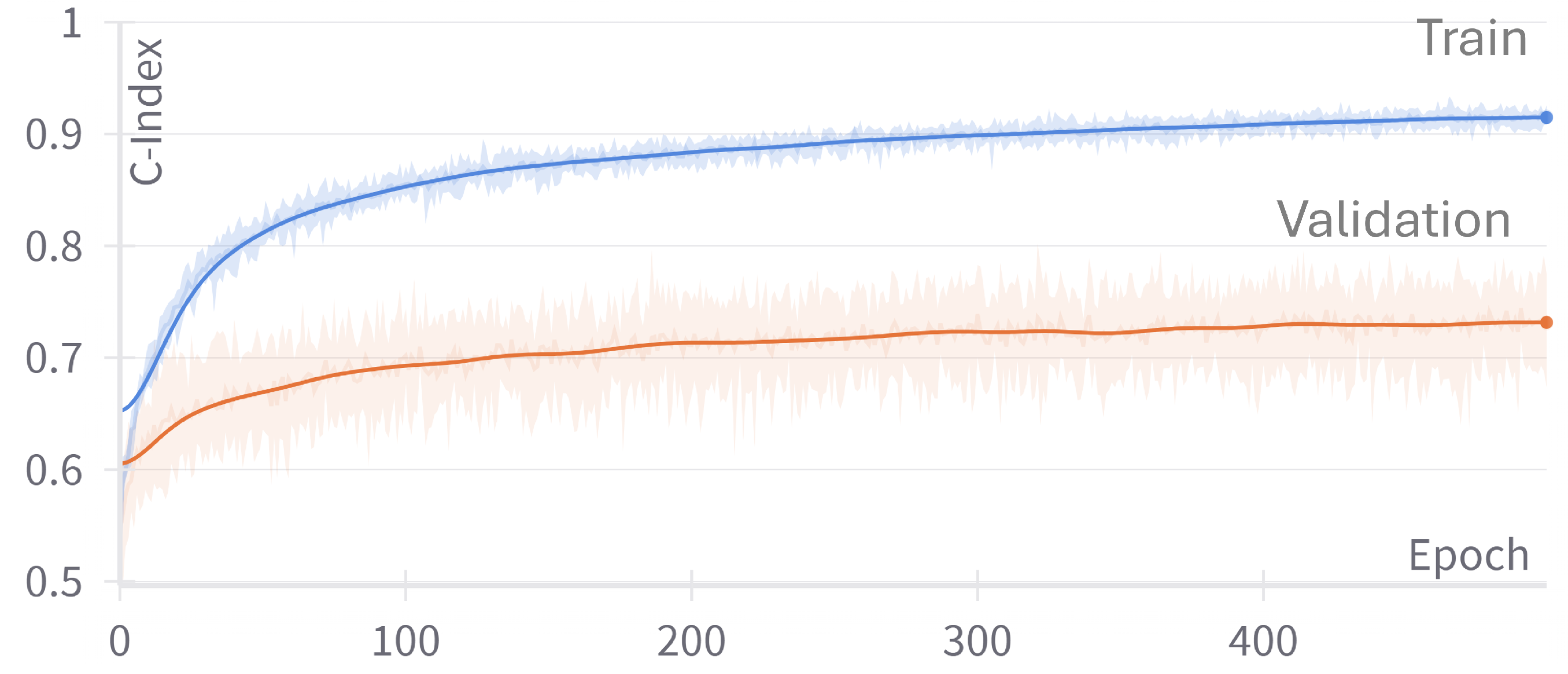
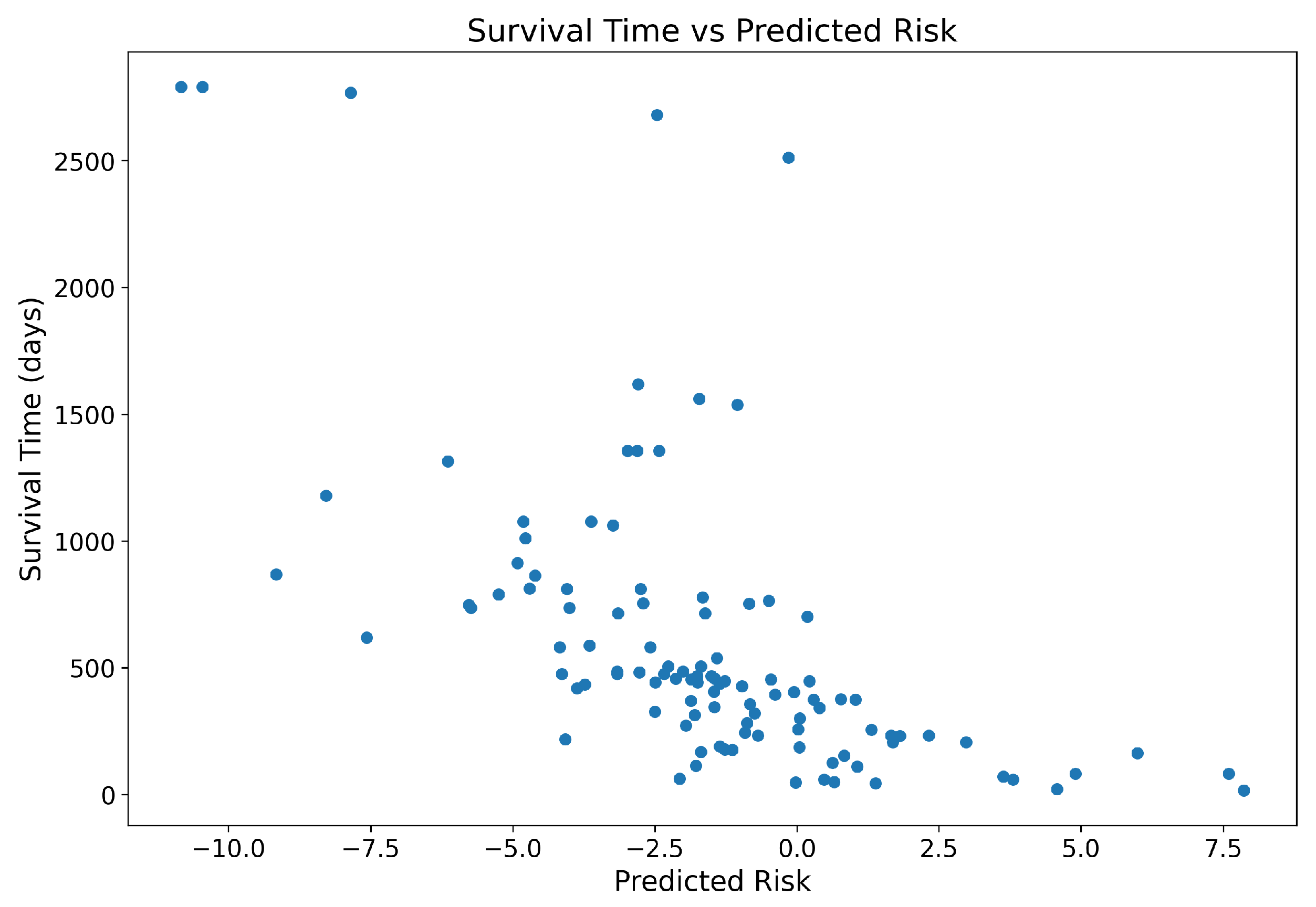
Section 4 presents the experimental setup, including the dataset, evaluation metrics, and implementation details. We also present the results and discuss the findings in this section. Finally,
Section 5 concludes the paper and suggests future research directions.
Author Contributions
Conceptualization, S.-N.Y., Y.P.C. and Y.-C.Y.; Methodology, Y.P.C. and Y.-C.Y.; Software, Y.P.C. and Y.-C.Y.; Writing—Original Draft Preparation, Y.-C.Y. and Y.P.C.; Writing—Review & Editing, Y.P.C.; Visualization, Y.P.C.; Supervision, S.-N.Y.; Project Administration, S.-N.Y.; Funding Acquisition, S.-N.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Ministry of Science and Technology (MOST), Taiwan, under Grant MOST 111-2221-E-194-057; and in part by the Advanced Institute of Manufacturing with High-Tech Innovations (AIM-HI) from the Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the Ministry of Education (MOE) in Taiwan.
Institutional Review Board Statement
Ethical review and approval were waived for this study, as the data used in this study were publicly available and de-identified.
Data Availability Statement
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GBM | Glioblastoma multiforme |
| CNN | Convolutional neural network |
| WSI | Whole-slide images |
| ROIs | Regions of interest |
| CBAM | Convolutional block attention module |
| TCGA | The Cancer Genome Atlas Program |
| C-Index | Concordance index |
References
- Hanif, F.; Muzaffar, K.; Perveen, k.; Malhi, S.; Simjee, S. Glioblastoma Multiforme: A Review of Its Epidemiology and Pathogenesis through Clinical Presentation and Treatment. Asian Pac. J. Cancer Prev. 2017, 18, 3. [Google Scholar] [CrossRef] [PubMed]
- Yu, K.H.; Zhang, C.; Berry, G.J.; Altman, R.B.; Ré, C.; Rubin, D.L.; Snyder, M. Predicting Non-Small Cell Lung Cancer Prognosis by Fully Automated Microscopic Pathology Image Features. Nat. Commun. 2016, 7, 12474. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R. THE LASSO METHOD FOR VARIABLE SELECTION IN THE COX MODEL. Stat. Med. 1997, 16, 385–395. [Google Scholar] [CrossRef]
- Zhu, X.; Yao, J.; Huang, J. Deep Convolutional Neural Network for Survival Analysis with Pathological Images. In Proceedings of the 2016 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Shenzhen, China, 15–18 December 2016; pp. 544–547. [Google Scholar] [CrossRef]
- Zhu, X.; Yao, J.; Zhu, F.; Huang, J. WSISA: Making Survival Prediction from Whole Slide Histopathological Images. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 22–25 July 2017; pp. 6855–6863. [Google Scholar] [CrossRef]
- Li, R.; Yao, J.; Zhu, X.; Li, Y.; Huang, J. Graph CNN for Survival Analysis on Whole Slide Pathological Images. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2018; Frangi, A.F., Schnabel, J.A., Davatzikos, C., Alberola-López, C., Fichtinger, G., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 11071, pp. 174–182. [Google Scholar] [CrossRef]
- Tang, B.; Li, A.; Li, B.; Wang, M. CapSurv: Capsule Network for Survival Analysis With Whole Slide Pathological Images. IEEE Access 2019, 7, 26022–26030. [Google Scholar] [CrossRef]
- Di, D.; Li, S.; Zhang, J.; Gao, Y. Ranking-Based Survival Prediction on Histopathological Whole-Slide Images. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2020; Martel, A.L., Abolmaesumi, P., Stoyanov, D., Mateus, D., Zuluaga, M.A., Zhou, S.K., Racoceanu, D., Joskowicz, L., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 12265, pp. 428–438. [Google Scholar] [CrossRef]
- Fan, L.; Sowmya, A.; Meijering, E.; Song, Y. Cancer Survival Prediction From Whole Slide Images With Self-Supervised Learning and Slide Consistency. IEEE Trans. Med. Imaging 2023, 42, 1401–1412. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Liang, Y.; Shao, M.; Lu, S.; Liao, S.; Ouyang, D. Self-Supervised Learning-Based Multi-Scale Feature Fusion Network for Survival Analysis from Whole Slide Images. Comput. Biol. Med. 2023, 153, 106482. [Google Scholar] [CrossRef]
- Kartsonaki, C. Survival Analysis. Diagn. Histopathol. 2016, 22, 263–270. [Google Scholar] [CrossRef]
- Clark, T.G.; Bradburn, M.J.; Love, S.B.; Altman, D.G. Survival Analysis Part I: Basic Concepts and First Analyses. Br. J. Cancer 2003, 89, 232–238. [Google Scholar] [CrossRef] [PubMed]
- Goel, M.K.; Khanna, P.; Kishore, J. Understanding Survival Analysis: Kaplan-Meier Estimate. Int. J. Ayurveda Res. 2010, 1, 274–278. [Google Scholar] [CrossRef] [PubMed]
- Cox, D.R. Regression Models and Life-Tables. J. R. Stat. Soc. Ser. (Methodol.) 1972, 34, 187–220. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S.; May, S. Applied Survival Analysis: Regression Modeling of Time-to-Event Data, 2nd ed.; Wiley Series in Probability and Statistics; Wiley-Interscience: Hoboken, NJ, USA, 2008. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E.; Eddins, S.L. Digital Image Processing Using MATLAB; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- OpenCV: Laplace Operator. Available online: https://docs.opencv.org/3.4/d5/db5/tutorial_laplace_operator.html (accessed on 1 February 2024).
- OpenCV: Color Conversions. Available online: https://docs.opencv.org/3.4/de/d25/imgproc_color_conversions.html#color_convert_rgb_gray (accessed on 1 September 2024).
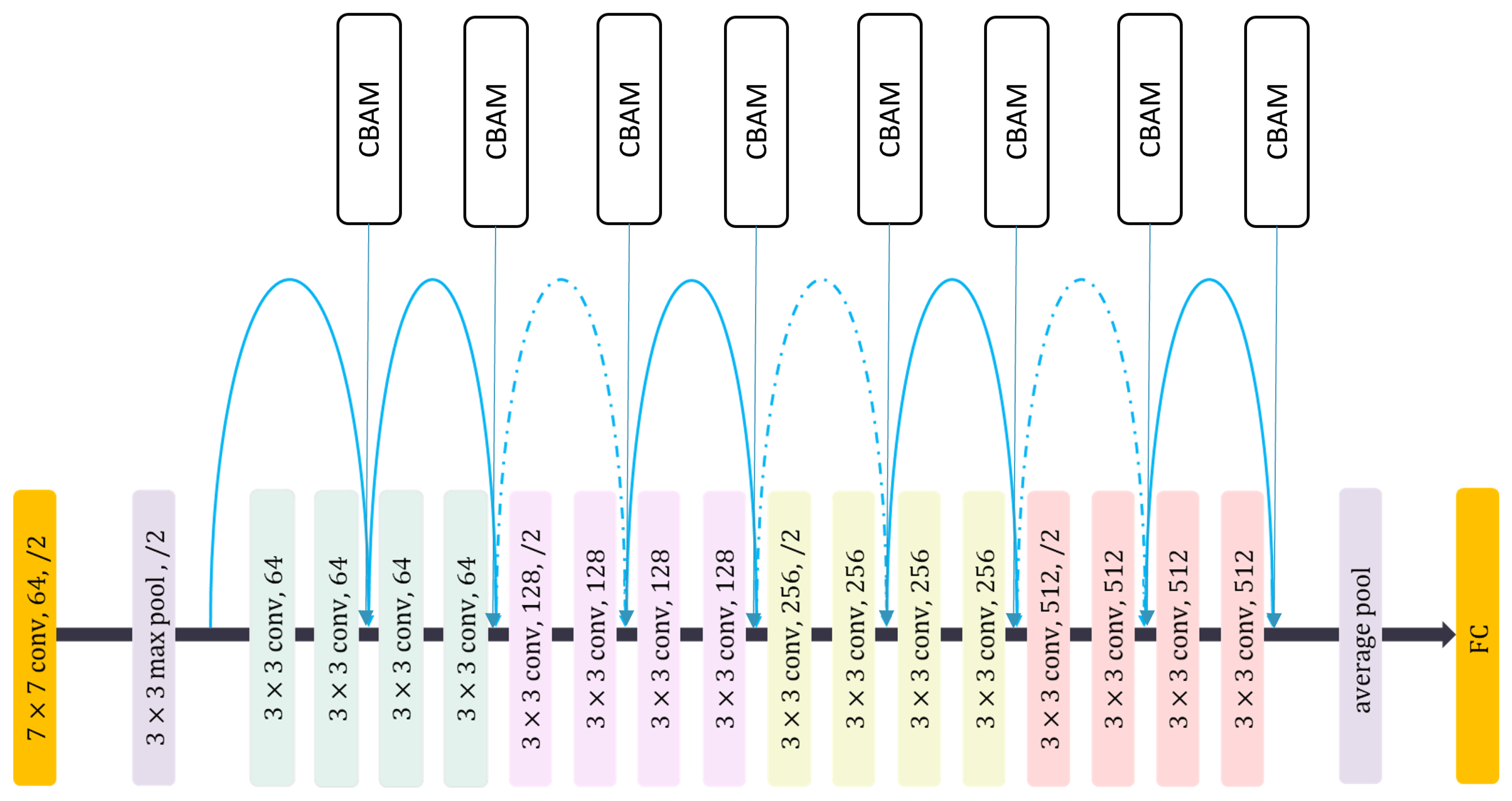
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Computer Vision—ECCV 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 11211, pp. 3–19. [Google Scholar] [CrossRef]
- Scarpace, L.; Mikkelsen, T.; Cha, S.; Rao, S.; Tekchandani, S.; Gutman, D.; Saltz, J.H.; Erickson, B.J.; Pedano, N.; Flanders, A.E.; et al. The Cancer Genome Atlas Glioblastoma Multiforme Collection (TCGA-GBM) (Version 5) [Data set]. 2016. Available online: https://www.cancerimagingarchive.net/collection/tcga-gbm/ (accessed on 1 September 2022).
- Goode, A.; Gilbert, B.; Harkes, J.; Jukic, D.; Satyanarayanan, M. OpenSlide: A Vendor-Neutral Software Foundation for Digital Pathology. J. Pathol. Informatics 2013, 4, 27. [Google Scholar] [CrossRef] [PubMed]
- Sksurv.Metrics. Concordance_index_censored—Scikit-Survival 0.22.2. Available online: https://scikit-survival.readthedocs.io/en/stable/api/generated/sksurv.metrics.concordance_index_censored.html (accessed on 1 February 2024).
- Mantel, N. Evaluation of Survival Data and Two New Rank Order Statistics Arising in Its Consideration. Cancer Chemother. Rep. 1966, 50, 163–170. [Google Scholar] [PubMed]
- Bland, J.M.; Altman, D.G. The Logrank Test. BMJ Br. Med. J. 2004, 328, 1073. [Google Scholar] [CrossRef] [PubMed]
- Bewick, V.; Cheek, L.; Ball, J. Statistics Review 12: Survival Analysis. Crit. Care 2004, 8, 389–394. [Google Scholar] [CrossRef] [PubMed]
- Davidson-Pilon, C. Lifelines: Survival Analysis in Python. J. Open Source Softw. 2019, 4, 1317. [Google Scholar] [CrossRef]
- Farsi, Z.; Allahyari Fard, N. The Identification of Key Genes and Pathways in Glioblastoma by Bioinformatics Analysis. Mol. Cell. Oncol. 2023, 10, 2246657. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Pan, S.; Li, R.; Chen, Z.; Xie, X.; Han, D.; Lv, S.; Huang, Y. Novel Biomarker Genes for Prognosis of Survival and Treatment of Glioma. Front. Oncol. 2021, 11, 667884. [Google Scholar] [CrossRef] [PubMed]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).