Abstract
We present a novel approach to performing fitness approximation in genetic algorithms (GAs) using machine learning (ML) models, focusing on dynamic adaptation to the evolutionary state. We compare different methods for (1) switching between actual and approximate fitness, (2) sampling the population, and (3) weighting the samples. Experimental findings demonstrate significant improvement in evolutionary runtimes, with fitness scores that are either identical or slightly lower than those of the fully run GA—depending on the ratio of approximate-to-actual-fitness computation. Although we focus on evolutionary agents in Gymnasium (game) simulators—where fitness computation is costly—our approach is generic and can be easily applied to many different domains.
1. Introduction
Genetic algorithms (GAs) are population-based metaheuristic optimization algorithms that operate on a population of candidate solutions, referred to as individuals, iteratively improving the quality of solutions over generations. GAs employ selection, crossover, and mutation operators to generate new individuals based on their fitness values, computed using a fitness function [].
GAs have been widely used for solving optimization problems in various domains, such as telecommunication systems [], energy systems [], and medicine []. Further, GAs can be used to evolve agents in game simulators. For example, García-Sánchez et al. [] employed a GA to enhance agent strategies in Hearthstone, a popular collectible card game, and Elyasaf et al. [] evolved high-level solvers for the game of FreeCell.
Algorithm 1 outlines the pseudocode of a canonical GA, highlighting the main fitness–selection–crossover–mutation loop. An accurate evaluation of a fitness function is often computationally expensive, particularly in complex and high-dimensional domains, such as games. In fact, a GA spends most of its time in line 3 of Algorithm 1, computing fitness.
| Algorithm 1 Canonical Genetic Algorithm. |
| Input: problem to solve
|
To mitigate this cost, fitness approximation techniques have been proposed to estimate the fitness values of individuals based on a set of features or characteristics. Specifically, the field of surrogate-assisted evolutionary algorithms (SAEAs) focuses on approximating fitness evaluations in evolutionary algorithms using surrogate models. While there are various types of evolutionary algorithms beyond genetic algorithms (GAs), the vector-based representation of individuals in GAs makes them particularly well suited for surrogate models.
Relying only on approximate fitness scores might cause the GA to converge to a false optimum. To address this, the evolutionary process can be controlled by combining approximate and actual fitness evaluations. This process is referred to as evolution control []. Most surrogate-assisted methods tackle this issue through sampling the population, computing the true fitness scores of the sampled individuals, and retraining the model on these scores []. This approach might not be enough, as the static sampling may be insufficient for the model. As a result, our method incorporates a dynamic transition between true and approximate fitness evaluations to better adapt to the current state of evolution.
We analyze several options for (1) switch conditions between using the actual fitness function and the approximate one, (2) sampling the search space for creating the dataset, and (3) weighting the samples in the dataset.
We present a test case to our method using ridge and lasso machine learning models to evaluate the quality of evolutionary agents on three games implemented by Gymnasium (formerly OpenAI Gym), a framework designed for the development and comparison of reinforcement learning (RL) algorithms. We only use Gymnasium’s game implementations, called environments, for evaluating fitness—we do not use the framework’s learning algorithms.
Our method is not limited to the field of game simulations, and can be applied to any other domain that can incorporate fitness approximation, including robot simulations [], hyperparameter tuning [], neural architecture search [,], and others.
These are the main innovations of our proposed method, which are further detailed in Section 5:
- The use of a switch condition (Section 5.2) favors high flexibility in the experimental setting:
- –
- Different switch conditions can be used according to the domain and complexity of the problem being solved.
- –
- The predefined switch threshold hyperparameter controls the desired amount of trade-off between result quality and computational time.
- A monotonically increasing sample weights function (Section 5.4), which places more emphasis on newer individuals in the learning process.
- The method is generic and can be easily modified, extended, and applied to other domains. Other choices of ML model, switch condition, or sampling strategy can be readily made.

Table 1.
Abbreviations and their meanings.

Table 2.
Notations and their meanings.
The next section surveys the relevant literature on fitness approximation. Section 3 provides brief backgrounds on linear ML models and Gymnasium. Section 4 introduces the problems being solved herein: Blackjack, Frozen Lake, and Monster Cliff Walking. Section 5 describes the proposed framework in detail, followed by experimental results in Section 6. Section 7 presents two extensions to our method, involving novelty search and hidden fitness scores. We end with concluding remarks and future work in Section 8.
2. Fitness Approximation: Previous Work
Fitness approximation is a technique used to estimate the fitness values of individuals without performing the computationally expensive fitness evaluation for each individual. This method allows for an efficient exploration of the search space.
Fitness Inheritance. Smith et al. [] suggested the use of fitness inheritance, where only part of the population has its fitness evaluated—and the rest inherit the fitness values from their parents. This approach allows for a significant reduction in computational costs by minimizing the need for fitness evaluations across the entire population, thus facilitating faster convergence in evolving populations. Their work proposed two fitness inheritance methods: (1) averaged inheritance, wherein the fitness score of an offspring is the average of its parents; and (2) proportional inheritance, wherein the fitness score of an offspring is a weighted average of its parents, based on the similarity of the offspring to each of its parents. Their work was tested on the one-max GA problem and an aircraft routing real-life problem. This approach laid the groundwork for later studies that were built on the principles of fitness inheritance.
Liaw and Ting [] utilized proportional fitness inheritance and linear regression to efficiently solve evolutionary multitasking problems. In the context of GAs, multitasking can lead to better exploration of the solution space, enabling the simultaneous optimization of multiple objectives, which is essential in real-world applications where multiple criteria must be balanced.
Le et al. [] used fitness inheritance and clustering to reduce the computational cost of undersampling in classification tasks with unbalanced data. Their method was tested on 44 imbalanced datasets, achieving a runtime reduction of up to 83% without significantly compromising classifier performance.
Gallotta et al. [] used a neural network and a novel variation of fitness inheritance, termed ‘acquirement’, to predict the fitness of feasible children from infeasible parents in the context of procedural content generation, creating spaceship objects for the game Space Engineers. Acquirement not only considers the fitness of the parents but also incorporates the fitness values of the parents’ previous offspring, enhancing the prediction accuracy.
Kalia et al. [] incorporated fitness inheritance into multi-objective genetic algorithms (MOGAs) to assess the quality of fuzzy rule-based classifiers. The paper addresses the trade-off between classification accuracy and interpretability, which is critical in fuzzy rule-based systems. Their MOGA simultaneously optimizes the accuracy of rule sets and their complexity, the latter being measured in terms of interpretability. The experimental results demonstrate that fitness inheritance can significantly reduce computational costs without compromising the quality of the classifier, achieving competitive results in terms of both accuracy and interpretability.
Although our method does not use fitness inheritance, it does consider solution similarity. As we shall see in Section 6, our method outperforms fitness inheritance in the context of the problems that we tackle.
The surrogate-assisted evolutionary algorithm (SAEA) is the process of using ML models to perform fitness approximation. SAEAs have been an ongoing research topic over the past few years.
Jin [] discussed various fitness approximation methods involving ML models with offline and online learning, both of which are included in our approach. This comprehensive review served as a baseline for many research papers in the field of ML-based fitness approximation.
Dias et al. [] used neural networks as surrogate models to solve a beam angle optimization problem for cancer treatments. Their results were superior to an existing treatment type. They concluded that integrating surrogate models with genetic algorithms is an interesting research direction.
Guo et al. [] proposed a hybrid GA with an extreme learning machine (ELM) fitness approximation to solve the two-stage capacitated facility location problem. The ELM is a fast, non-gradient-based, feed-forward neural network that contains one hidden layer, with random constant hidden-layer weights and analytically computed output-layer weights. The hybrid algorithm included offline learning for the initial population and online learning through sampling a portion of the population in each generation. Our approach is similar to the one suggested in this paper, but it is capable of dynamically transitioning between approximate and true fitness scores.
Yu and Kim [] examined the use of support vector regression, deep neural networks, and linear regression models trained offline on sampled individuals to approximate fitness scores in GAs. Specifically, the use of linear regression achieved adequate results for one-max and deceptive problems.
Livne et al. [] compared two heuristic methods for fitness approximation in context-aware recommender systems to avoid the computational burden of 50,000 deep contextual model training processes, each requiring about one minute. The first approach involved training a multi-layer perceptron (MLP) sub-network, taking about five seconds per individual. The second, more efficient method involved a pre-processing step where a robust single model was trained and individuals were evaluated in just 60 milliseconds by predicting the output of this pre-trained model.
Zhang et al. [] used a deep surrogate neural network with online training to reduce the computational cost of the MAP-Elites (Multi-dimensional Archive of Phenotypic Elites) algorithm for constructing a diverse set of high-quality card decks in Hearthstone. Their work achieved state-of-the-art results.
Li et al. [] addressed agent simulations using evolutionary reinforcement learning (ERL), employing policy-extended value function approximation (PeVFA) as a surrogate for the fitness function. Similarly to our method, their study focused on the domain of agent simulation within the Gym(nasium) environment (see Section 3). However, PeVFA relies on the experience of the RL agent throughout the simulations, and therefore can only be used in the context of RL, unlike our more generic method.
Recent popular ML models were also used in the context of SAEA: Hao et al. [,] used Kolmogorov–Arnold networks (KANs) and multiple large language models (LLMs) as surrogate models. Their approach was tested on the Ellipsoid, Rosenbrock, Ackley, and Griewank functions.
Although deep neural networks have proven to be extremely useful for many tasks in different domains, they require GPU hardware to converge in reasonable time, and are generally considered slower compared to other ML algorithms. Our framework focuses on linear regression, which is commonly used in fitness approximation [].
We chose this simple model because it is fast and—as we shall see—allows for retraining at will, with virtually zero cost.
Table 3 summarizes the previous work.

Table 3.
Summary of literature review for fitness approximation in evolutionary algorithms.
3. Preliminaries
Linear ML models are a class of algorithms that learn a linear relationship between the input features and the target variable(s). We focus on two specific linear models, namely ridge regression (also called Tikhonov) [] and lasso regression (least absolute shrinkage and selection operator) []. These two models strike a balance between complexity and accuracy, enabling efficient estimation of fitness values for individuals in the GA population.
Ridge and lasso are linear regression algorithms with an added regularization term to prevent overfitting. Their loss functions are given by
where is for lasso, is for ridge, X represents the feature matrix, y represents the target variable, w represents the coefficient vector, and represents the regularization parameter.
Regression is commonly used as a surrogate model for fitness evaluations []. A major advantage of linear models with respect to our framework is that they are very fast, enabling us to treat model-training time as virtually zero (with respect to fitness computation time in the simulator). Thus, we could retrain a model as often as we choose. As recently noted by James et al. [], “Historically, most methods for estimating f have taken a linear form. In some situations, such an assumption is reasonable or even desirable.”
It is worth mentioning that our generic method can easily be integrated with other types of ML models.
Gymnasium (formerly OpenAI Gym) [] is a framework designed for the development and comparison of reinforcement learning (RL) algorithms. It offers a variety of simulated environments that can be utilized to evaluate the performance of AI agents. Gymnasium offers a plethora of simulators, called environments (https://gymnasium.farama.org/api/env/, (accessed on 10 November 2024)), from different domains, including robotics, games, cars, and more. Each environment defines state representations, available actions, observations, and how to obtain rewards during gameplay.
A Gymnasium simulator can be used for training an RL agent or as a standalone simulator. Herein, we take the latter approach, using these simulators to test our novel fitness approximation method for an evolutionary agent system.
4. Problems
This section provides details on the three problems from Gymnasium that we will tackle: Blackjack, Frozen Lake, and Monster Cliff Walking (Figure 1).
Figure 1.
Gymnasium environments (or custom modifications of them) that we use for actual fitness-score evaluation.
We specifically sought out simulation problems—where fitness computation is very costly—this required some lengthy behind-the-scenes exploration, testing, and coding, as such simulators are usually not written with GAs in mind.
Blackjack is a popular single-player card game played between a player and a dealer. The objective is to obtain a hand value closer to 21 than the dealer’s hand value—without exceeding 21 (going bust). We follow the game rules defined by Sutton and Barto []. Each face card counts as 10, and an ace can be counted as either 1 or 11. The Blackjack environment (https://gymnasium.farama.org/environments/toy_text/blackjack/, (accessed on 10 November 2024)), of Gymnasium represents a state based on three factors: (1) the sum of the player’s card values, (2) the value of the dealer’s face-up card, and (3) whether the player holds a usable ace. An ace is usable if it can count as 11 points without going bust. Each state allows two possible actions: stand (refrain from drawing another card) or hit (draw a card).
We represent an individual as a binary vector, where each cell corresponds to a game state from which an action can be taken; the cell value indicates the action taken when in that state. As explained by Sutton and Barto [], there are 200 such states; therefore, the size of the search space is .
The actual fitness score of an individual is computed by running 100,000 games in the simulator (the same number of games as in the Gymnasium Blackjack Tutorial (https://gymnasium.farama.org/tutorials/training_agents/blackjack_tutorial/ (accessed on 10 November 2024)), and then calculating the difference between the number of wins and losses. We normalize fitness by dividing this difference by the total number of games. The ML models and the GA receive the normalized results (i.e., scores ), but we will display the non-normalized fitness scores for easier readability. Given the inherent advantage of the dealer in the game, it is expected that the fitness scores will mostly be negative.
Frozen Lake. In this game, a player starts at the top-left corner of a square board and must reach the bottom-right corner. Some board tiles are holes. Falling into a hole leads to a loss, and reaching the goal leads to a win. Each tile that is not a hole is referred to as a frozen tile.
Due to the slippery characteristics exhibited by the frozen lake, the agent might move in a perpendicular direction to the intended direction. For instance, suppose that the agent attempts to move right, after which the agent has an equal probability of to move either right, up, or down. This adds a stochastic element to the environment and introduces a dynamic element to the agent’s navigation.
For consistency and comparison, all simulations will run on the 8 × 8 map presented in Figure 1. In this map, the Frozen Lake environment (https://gymnasium.farama.org/environments/toy_text/frozen_lake/, (accessed on 10 November 2024)), represents a state as a number between 0 and 63. There are four possible actions in each state: move left, move right, move up, or move down. Our GA thus represents a Frozen Lake agent as an integer vector with a cell for each frozen tile on the map, except for the end-goal state (since no action can be taken from that state). Similarly to Blackjack, each cell dictates the action being taken when in that state. Since there are 53 frozen tiles excluding the end goal, the size of the search space is . The fitness function is defined as the percentage of wins out of 2000 simulated games (the same number of games as in the Gymnasium Frozen Lake Tutorial (https://gymnasium.farama.org/tutorials/training_agents/FrozenLake_tuto/, (accessed on 10 November 2024))). Again, we will list non-normalized fitness scores.
Monster Cliff Walking. In Cliff Walking (https://gymnasium.farama.org/environments/toy_text/cliff_walking/, (accessed on 10 November 2024)). the player starts at the bottom-left corner of a 4 × 12 board and must reach the bottom-right corner. All the tiles in the bottom row that are not the starting position or goal are considered cliffs. The player must reach the goal without falling into the cliff.
Since this game can be solved quickly by a GA, we tested a stochastic, more complex version of the game, called Monster Cliff Walking https://github.com/Sebastian-Griesbach/MonsterCliffWalking, (accessed on 10 November 2024). In this version, a monster spawns in a random location and moves randomly among the top three rows of the board. Encountering the monster leads to an immediate loss.
The player performs actions by moving either up, right, left, or down. A state in this environment is composed both of the player’s location and the monster’s location.
There are 37 tiles where an action can be taken by the player (excluding the cliff and end goal) and 36 possible locations for the monster. Therefore, there are 1332 different states in the game. Similarly to Frozen Lake, an agent in Monster Cliff Walking is represented as an integer vector whose size is equal to the number of the states in the game. The size of the search space is , significantly larger than the search spaces of the previous two problems.
Due to stochasticity, each simulation runs for 1000 episodes. An episode ends when one of the following happens: (1) the player reaches the end-goal state; (2) the player encounters the monster; (3) the player performs 1000 steps (we limited the number of steps to avoid infinitely cyclic player routes). Falling into a cliff does not end the episode but only restarts the player’s position.
The fitness function is defined as the average score of all episodes. When an episode ends, the score for the episode is computed as the total rewards obtained during the episode. A penalty of −1 is obtained per step, −100 is added every time the agent falls into a cliff, and −50 is added if the player has encountered the monster (−1000 in the original environment, but we used reward shaping to allow for easier exploration of the search space).
Given the variety of the fitness-function values, the ML model is trained on the natural logarithm of fitness scores, and its predictions are raised to an exponent. More formally,
where is the regression target-value vector in the ML model training, is the vector of true fitness scores sent to the model, is the approximate fitness scores vector sent to the evolutionary algorithm, and is a vector of predictions returned by the model.
5. Proposed Method
This section presents our proposed method for fitness approximation in GAs using ML models. We outline the steps involved in integrating ridge and lasso regressors into the GA framework, and end with a discussion of advantages and limitations of the new method.
5.1. Population Dataset
Our approach combines both offline and online learning, as depicted in Figure 2.
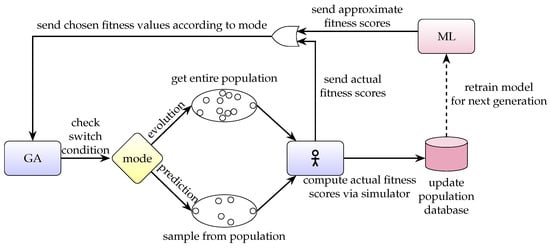
Figure 2.
Flowchart of proposed method. In evolution mode, the algorithm functions as a regular GA. When the switch condition is met, the algorithm shifts to prediction mode: actual (in-simulator) fitness values are calculated only for a sampled subset of the population, while the rest are assigned approximate fitnesses from the ML model. This latter is retrained before moving to the next generation.
The algorithm begins in evolution mode, functioning as a regular GA, where a population evolves over successive generations. However, each time a fitness score is computed for an individual, we update a dataset whose features are the encoding vector of the individual and whose target value is the respective fitness score. An illustration of the dataset is presented in Table 4. The initial population will always be evaluated using the simulator since the population dataset is empty at this stage of the run.

Table 4.
An example of a dataset created during a GA run of the Frozen Lake environment. An individual is a vector of 53 attributes. A total of m fitness computations have been carried out so far.
After a predefined switch condition is met, the algorithm transitions from evolution mode to prediction mode. In prediction mode, actual (in-simulator) fitness scores are computed only for a sampled subset of the population. For the rest of the population, the GA assigns approximate fitness values using a learned ML model that was trained on the existing population dataset. In prediction mode, a sample of the population receives true fitness scores per generation, and the rest of the generation’s individuals receive approximate fitness scores. This method is referred to as individual-based controlled evolution []. The algorithm can switch back and forth between evolution mode and prediction mode, enabling dynamic adaptation to the evolutionary state.
Witness the interplay between the dynamic switch condition and the static (pre-determined) sample rate—a hyperparameter denoting the percentage of the population being sampled. In cases where lower runtimes are preferred, using a relatively lenient switch condition is better, resulting in a higher fitness approximation rate coupled with reduced runtime—at some cost to fitness quality. On the contrary, in cases where accurate fitness scores are preferred, the use of a strict switch condition is advisable to allow for ML fitness approximation only when model confidence is high.
Note that the number of actual, in-simulator fitness computations performed is ultimately determined dynamically by the coaction of the switch condition and sample rate.
In stochastic domains such as ours, the same individual may receive different (actual) fitness scores for every evaluation, and thus appear in the population dataset multiple times—with different target values. This can be prevented by keeping a single copy of each individual in the dataset or by computing an average fitness score of all evaluations of the same individual (or possibly some other aggregate measure). However, since these solutions greatly interfere with the sample weighting mechanism (described in Section 5.4), we decided to remove identical duplicate rows only (i.e., with both equal representations and fitness scores) while keeping individuals with equal representation and different fitness scores in the dataset.
5.2. Switch Condition
Many surrogate-assisted methods, as discussed in Section 2, rely on retraining the model using true fitness scores of sampled individuals to maintain an up-to-date representation of the evolving population []. However, we claim that sampling a fixed number of individuals at each generation fails to account for the dynamic nature of the evolutionary process. Evolutionary changes caused by genetic operators can produce entirely distinct populations across generations. In such cases, the surrogate model may struggle to adapt to these abrupt shifts. To address this limitation, we introduce a fallback mechanism, reverting to the use of exact fitness evaluations to recalibrate the search when necessary.
As discussed in Section 5.1, the entire population receives true fitness evaluation during evolution mode. This strategy allows the model to train on a relatively large amount of data at each generation. However, maintaining the evolution mode for the remainder of the process is undesirable due to the substantial computational cost associated with full fitness evaluations. Consequently, once the model shows high confidence in its predictions for the population, the algorithm transitions back to prediction mode, where only a subset of the population is sampled for true fitness evaluations at each generation. This balance optimizes computational efficiency while retaining model accuracy.
The switch condition plays a crucial role in determining when the algorithm transitions from evolution mode to prediction mode (and vice-versa). Our approach defines the switch condition based on a predefined criterion. The switch condition can be defined in various ways depending on the specific problem and requirements. It may involve measuring the accuracy of the model’s predictions, considering a predefined threshold, or other criteria related to the state of the population and the model. In situations where the model’s accuracy falls below the desired threshold, the algorithm can revert back to evolution mode until the condition for switching to prediction mode is met once again.
Determining an appropriate switch condition is crucial for balancing the trade-off between the accuracy of fitness approximation and the computational efficiency of the algorithm. It requires tuning to find the optimal configuration for a given problem domain. Overall, the switch condition serves as a pivotal component in our approach, enabling a smooth transition between evolution mode and prediction mode based on a predefined criterion.
We defined and tested several different switch conditions, each having a hyperparameter called switch_threshold:
- Dataset size. The simplest solution entailed performing regular evolution until the dataset reaches a certain size threshold, and then transitioning to prediction mode indefinitely. Although simple, this switch condition is less likely to adapt to the evolutionary state due to its inability to switch back to evolution mode.
- Plateau. Wait for the best fitness score to stabilize before transitioning to prediction mode. We consider the best fitness score as stable if it has not changed much (below a given threshold) over the last P generations, for a given P. This method posed a problem, as the model tended to maintain the evolutionary state without significant improvement throughout the run.
- CV error. Evaluate the model’s error using cross-validation on the dataset. We switch to predict mode when the error falls below a predetermined threshold, and vice versa. We will demonstrate the use of this switch condition in the Frozen Lake scenario.
- Cosine similarity. Cosine similarity is a metric commonly used in natural language processing to compare different vectors representing distinct words []. We use this metric to compare the vectors in the GA population with those in the ML dataset. The underlying idea is that the model will yield accurate predictions if the current population closely resembles the previous populations encountered by the model, up to a predefined threshold. Our method utilizes this switch condition in the Blackjack and Monster Cliff Walking scenarios.
Note that there are also two trivial cases of switch conditions (i.e., with no threshold): (1) Permanent Evolution Mode: with this switch condition, the algorithm acts as a traditional GA, ignoring the ML model. (2) Permanent Prediction Mode: in this case, the algorithm uses the ML model to approximate fitness scores, similarly to papers covered in Section 2.
The switch condition is a key component of our method. This section presented the switch conditions tested during our research, yet our method can easily be enhanced with other domain-specific switch conditions.
5.3. Sampling Strategy
Training the ML model on the initial population only is insufficient for performing high-quality approximations: the model needs to be updated throughout the evolutionary process. This can be performed by selecting sample individuals and computing their true fitness score during different stages of the evolutionary run [,].
As mentioned in Section 5.1, during prediction mode, a subset of the population is sampled in each generation. The proportion of sampled individuals is defined by the sample_rate hyperparameter. There are several sampling strategies, and choosing the right strategy can greatly impact the quality of the population dataset. We focus on three strategies that we tested within our method:
- Random sampling. Randomly pick a subset of the population and compute their actual fitness scores while approximating the fitness scores for the rest of the population. Despite its simplicity, this strategy does not leverage any information about the dataset, the population, or the domain.
- Best strategy. Sample the individuals with the best approximated fitness score [,].
- Similarity sampling. Choose the individuals least similar to the population dataset. We assume that this method will improve the diversity of the dataset and hence improve the ability of the model to generalize better to a wider volume of the search space. This strategy is useful for domains where individuals with similar representations receive similar fitness scores, such as our domain. The similarity metric that we chose is the cosine similarity, discussed above.
Our genetic method allows for the seamless integration of additional strategies, such as Latin hypercube sampling [], clustering-based sampling [], and others [].
5.4. Sample Weights
In this section, ‘sample’ refers to a row in the dataset (as is customary in ML)—not to be confused with ‘sampling’ in ‘sampling strategy’, introduced in the previous section.
During the training of the ML model on the dataset, each individual typically contributes equally. However, we preferred the model to pay more attention to recent generations, since recently added individuals are more relevant to the current state of the evolutionary process compared to the individuals at the beginning. To account for this, we tracked the generation in which each individual is added to the dataset and assign weights accordingly.
A similar route was taken by Jin et al. [], except that their approach preferred individuals in the direction of evolution rather than the whole generation. Note that individuals from earlier generations are not ignored by the model and are not removed from the dataset—they only have a smaller impact on the learning process of the model.
In order to pick the most suitable weight function, we performed k-fold cross-validation on the ML models, with different weight functions. The models were trained on datasets of true fitness scores extracted from evolutionary runs. Table 5 compares several weight functions in a dataset of over 16,000 rows, extracted from a Blackjack experiment. We established a square-root relationship between the generation number and its corresponding weight: . We note that the algorithms that we used do not require the weights to sum to one.

Table 5.
Example of sample weight function comparison for Blackjack.
We conclude that the weighting function should avoid excessive steepness (e.g., an exponential function) to ensure that earlier individuals remain relevant. This allows the algorithm to prioritize innovation without greatly discarding insights from prior generations.
5.5. Advantages and Limitations
Our proposed method offers several advantages. It can potentially reduce the computational cost associated with evaluating fitness scores in a significant manner. Rather than computing each individual’s fitness every generation, the population receives an approximation from the ML model at a negligible cost.
The use of models like ridge and lasso helps to avoid overfitting by incorporating regularization. This improves the generalization capability of the fitness approximation model.
Additionally, our approach allows for continuous learning by updating the dataset and retraining the model during prediction mode. The continual retraining is possible because the ML algorithms are extremely rapid and the dataset is fairly small.
There are some limitations to consider. Linear models assume a linear relationship between the input features and the target variable. Therefore, if the fitness landscape exhibits non-linear behavior, the model may not capture it accurately. In such cases, alternative models capable of capturing non-linear relationships may be more appropriate; we plan to consider such models in the future.
Our approach assumes that the individuals are represented by vectors, which are later batched into matrices for training of the machine learning algorithms. Although we employed genetic algorithms (GAs) in our test case, this framework is adaptable to other population-based metaheuristics as long as individuals are represented as vectors. Notable alternatives include differential evolution [], evolutionary strategies [], and particle swarm optimization [].
Beginning generally, our method does not rely on domain-specific knowledge, such as in []. However, it can be adapted to incorporate such knowledge through a domain-specific switch condition, sampling strategy, etc.
Further, the performance of the fitness approximation model heavily relies on the quality and representativeness of the training dataset. If the dataset does not cover the entire search space adequately, the model’s predictions may be less accurate. Careful consideration should be given to dataset construction and sampling strategies to mitigate this limitation. We took this into account when choosing the appropriate switch conditions and sampling strategy, discussed above.
An additional limitation is the choice of the best individual to be returned at the end of the run. Since a portion of the fitness values is approximate, the algorithm might return an individual with a good predicted fitness score, but with a bad actual fitness score. To address this issue, we return the individual with the best fitness from the population dataset (which always holds actual fitness values).
6. Experiments and Results
6.1. Experimental Setup
To assess the efficacy of the proposed approach, we carried out a comprehensive set of experiments aimed at solving the three problems outlined in Section 4. Our objective was to compare the performance of our method against a “full” GA (computing all fitnesses), considering solution quality and computational efficiency as evaluation criteria.
Experiments were conducted using the EC-KitY software [] on a cluster of 96 nodes and 5408 CPUs (the most powerful processors are AMD EPYC 7702P 64-core, although most have lesser specs). A total of 10 CPUs and 3 GB RAM were allocated for each run. Since the nodes in the cluster vary in their computational power, we measured computational cost as the number of actual (in-simulator) fitness computations performed. We excluded the initial-population fitness computation for cleaner percentages (there were 200 initial computations in HEA/FA and 100 computations in the rest of the methods). The average duration of a single fitness computation was 21 s for Blackjack, 6 s for Frozen Lake, and 9 s for Monster Cliff Walking. The source code for our method and experiments can be found at https://github.com/itaitzruia4/ApproxML, (accessed on 10 November 2024).
Both fitness approximation runs and full GA runs included the same genetic operators with the same probabilities: tournament selection [], two-point crossover [], bit-flip mutation for Blackjack, and uniform mutation for Frozen Lake and Monster Cliff Walking [].
6.2. Hyperparameter Setting
The specific linear models utilized in the experiments and their hyperparameters are detailed in Table 6. The values of the approximation-related hyperparameters (switch_condition, switch_threshold, and sample_strategy) were obtained by running full experiments with our approach and comparing them to the traditional GA. As mentioned in Section 5.2, careful consideration and tuning were carried out for the switch threshold in order to find a desired balance between computational cost and solution quality.

Table 6.
Hyperparameters.
The values of the ML hyperparameters (model, alpha, max_iter, and f_weight) were obtained by extracting datasets from traditional GA runs (such as the one described in Table 4) and using k-fold cross-validation in an offline manner, similarly to what was carried out by Yu and Kim []. Since the fitness computations were performed beforehand, and due to the chosen ML models having a fast train and inference time, this approach enables extensive exploration of the ML hyperparameters. We used the linear models provided by scikit-learn []. Hyperparameter tuning was performed using Optuna [].
The values of the GA hyperparameters (population_size, p_crossover, p_mutation, generations, tournament_size, crossover_points, and p_mutation_cell) were taken from EC-KitY tutorials (https://eckity.org, (accessed on 10 November 2024)).
We find that the approximation hyperparameters have a notable impact on the experimental outcomes. This is expected, given that the switch condition and sampling strategy are central elements of our approach, shaping its overall effectiveness and adaptability.
Note the difference between the hyperparameter generations, which designates the number of GA generations, and max_iter, which designates the number of iterations in the ML model training. The latter is relatively negligible in terms of runtime differences due to the short training time of the linear ML models.
6.3. Results
We performed 20 replicates per sample rate, and assessed statistical significance by running a 10,000-round permutation test, comparing the mean scores between our proposed method and the full GA (with full fitness computation). The results are shown in Table 7.

Table 7.
Results. Each row summarizes 20 replicate runs. The last row represents the full GA. Sample rate is the proportion of fitness values computed in prediction mode (Section 5.3). Absolute fitness represents the mean best-of-run fitness values of all replicates. Relative fitness represents the percentage of absolute fitness compared to GA. Absolute computations represents mean number of actual fitness computations performed in simulator across all replicates. Relative computations represents the percentage of absolute computations compared to GA. p-value: result of permutation test. Boldfaced results are those that are statistically identical (meaning statistical insignificance) in performance to full GA, i.e., p-value .
Examining the results reveals an observable rise in fitness scores, along with an increase in the number of fitness computations as the sample rate increases. This is in line with the inherent trade-off within our method, wherein the quality of the results and the runtime of the algorithm are interconnected. Further, there is a strong correlation between the sample rate and the relative number of fitness computations. Notably, as the relative fitness score computation approaches the sample rate, the frequency of individuals with approximate fitness scores increases.
In the Blackjack scenario, fitness–computation ratios closely approximate the sample rates, indicating a strong dominance of the prediction mode. In contrast, computation ratios for Frozen Lake are relatively close to 100%, with the exception of the 20% sample rate, signifying a prevalence of evolution mode in the majority of generations. In Monster Cliff Walking, there is a strong dominance of the prediction mode, except for the 20% sample rate.
These observations shed light on the impact of the switch condition and its predefined threshold hyperparameters on the behavior of the algorithm in approximating fitness scores.
Boldfaced results in Table 7 are those that are statistically identical (meaning statistical insignificance) in performance to the full GA, i.e., p-value .
We observe that results indistinguishable from the full GA can be obtained with a significant reduction in fitness computation.
6.4. Comparison with Previous Work
Table 8, Table 9 and Table 10 show the performance on our three benchmark problems of the four methods discussed in Section 2: KANs pre-selection algorithm (KAN-SPS) [], hybrid evolutionary algorithm with fitness approximation (HEA/FA) [], averaged fitness inheritance (Avg-FI) [], and proportional fitness inheritance (Prop-FI) []. The first two methods perform model-based fitness approximation with a KAN and ELM as a surrogate model and the other two perform similarity-based fitness approximation. We also tested the performance of an ELM as the ML model using our genetic operators, random sampling, and no sample weights, referred to as ELM. Note that these four methods do not use a dynamic switch condition, instead utilizing fitness approximation for the entire GA run. Our method is denoted as ApproxML. Again, boldfaced results are those that are statistically identical (meaning statistical insignificance) in performance to the full GA (last row), i.e., p-value .

Table 8.
Comparison with previous work: Blackjack.

Table 9.
Comparison with previous work: Frozen Lake.

Table 10.
Comparison with previous work: Monster Cliff Walking.
Of the model-based approximation methods presented in Section 2, HEA/FA was the most-similar method to ours. The fitness inheritance methods use our genetic operators (discussed above), while KAN-SPS and HEA/FA use different genetic operators, delineated by Hao et al. [] and Guo et al. [], respectively. For faster training, the KAN was trained on 5 steps in each iteration, as opposed to 50 steps in the original paper. Due to memory issues encountered while running KAN-SPS with Monster Cliff Walking, it was tested only on Blackjack and Frozen Lake.
A key distinction of KAN-SPS is its termination criterion, which is defined by a fixed number of fitness evaluations rather than a fixed number of generations, as seen in other methods. Additionally, unlike other approaches, KAN-SPS does not incorporate a sampling mechanism. To afford fair comparisons, we simulated a sampling rate by setting the termination criterion as the product of the sampling rate and the number of evaluations typically used in the full GA.
KAN-SPS was executed using the pymoo library [], as per the original implementation, whereas all other methods were implemented using EC-KitY [].
Choosing the appropriate competitors for evaluation proved difficult: some papers included only a pseudocode that is complicated to implement (e.g., []), and some papers contained code examples that included major differences in runtime environments—such as GPU usage, different programming languages, and complex simulator integrations (e.g., [,,]). In papers that did not include code implementation, we contacted the authors for the implementation of the papers (unfortunately, they are not available on GitHub) but received no reply, so we implemented the methods ourselves.
KAN-SPS provided poor results. The performance can be improved by altering the genetic operators used or by tuning the model (we used the same operators and hyperparameters as in the original paper).
The HEA/FA algorithm produced unsatisfactory results. We assume that this is due to possible differences between our implementation and the original one, such as the algorithm implementation, the genetic operators, or the hidden-layer size and activation function (these were not given in the paper, and we set them to 100 and ReLU, respectively).
The ELM produced better results, particularly in Frozen Lake, but it did not achieve statistical insignificance for any problem. Although our approach uses a different ML model, this emphasizes the importance of dynamic fitness approximation, as implemented in our architecture.
Prop-FI and Avg-FI performed relatively well, especially in Frozen Lake and Monster Cliff Walking. They achieved statistical insignificance at an 80% sample rate, with a lower computational cost compared to our approach. However, statistical insignificance (i.e., same as the full GA) was only attained at an 80% sample rate in Frozen Lake and Monster Cliff Walking (and not at all in Blackjack), whereas our method achieved statistical insignificance for all problems, and partially for lower sample rates as well, as seen in Table 7.
7. Extensions
7.1. Novelty Search
As mentioned in Section 5.5, the model should cover a large volume of the search space to generalize well to new individuals created by the genetic operators throughout the evolutionary run. We tested an alternative method to initialize the initial population. Instead of randomly generating the initial population, we performed novelty search [].
In novelty search, fitness is abandoned in favor of finding distinct genomes, the idea being to keep vectors that are most distant from their n nearest neighbors in the population (we used ). This causes the individuals to be relatively far from each other at the end of novelty search, and thus cover a larger volume of the search space.
After this new initialization procedure, the algorithm behaves exactly as in Section 5.
The results, shown in Table 11, indicate a minimal difference in fitness scores (cf. Table 7) when using this approach, except for statistical insignificance at the 60% sample rate for Monster Cliff Walking, unlike with random initialization (Table 7). However, this initialization may be useful in other domains, possibly with larger search spaces. Alternatively, other exploration methods can be attempted within this context, e.g., quality diversity [].

Table 11.
Initialization through novelty search: results.
7.2. Hidden Actual Fitness Scores in Prediction Mode
In existing fitness approximation methods, as discussed in Section 2, some individuals in the population have their fitness values approximated, while the rest receive actual fitness scores. Our preliminary investigation, which employed this scheme, suggested that individuals with actual fitness scores might “hijack” the evolutionary process. In cases of pessimistic approximations, the individuals with actual fitness scores are likely to be selected, to then repeatedly reproduce, thus restricting the exploration of the search space [].
In the evolution mode of our baseline method, the actual fitness scores are both given to the GA and added to the ML dataset. Another approach is to hide actual fitness scores from the GA in prediction mode, only adding them to the ML dataset. The sampled individuals still receive approximate fitness scores, even though their actual fitness scores are computed.
This latter approach harms the accuracy of the fitness scores since the approximate fitness scores are usually less accurate than the actual fitness scores. On the other hand, this approach prevents the potential problem described above. In contrast to the baseline method, the calculation of the actual fitness scores and model training in prediction mode is independent of the evolutionary process when true fitness scores are hidden from the GA. As a result, fitness computation and model training can be executed in a separate process in parallel to the evolution, significantly reducing runtime. We plan to perform concrete experiments on this approach in the future.
8. Concluding Remarks and Future Work
This paper presented a generic method for integrating machine learning models in fitness approximation. Our approach is useful for domains wherein the fitness score calculation is computationally expensive, such as running a simulator. We used Gymnasium simulators for evaluating actual fitness scores, and ridge and lasso models for learning the fitness approximation models.
Our analysis includes a rigorous comparison between different methods for (1) switching between actual and approximate fitness, (2) sampling the population, and (3) weighting the samples.
Our results show a significant reduction in GA runtime, with a small price in fitness for low sample rates, and no price for high sample rates.
Further enhancements can be incorporated into our method by employing more complex ML models, such as random forest, XGBoost, or deep networks. While these models have the potential to improve fitness approximation, it is worth noting that they are typically computationally intensive and may not be suitable for domains with limited fitness computation time.
Additionally, our method can be refined by leveraging domain-specific knowledge or additional data science concepts (under-sampling, over-sampling, feature engineering, etc.) to improve the generality of the population dataset and, consequently, the accuracy of the model. These approaches have the potential to enhance the overall performance of our solution.
Author Contributions
Conceptualization, I.T., T.H., M.S. and A.E.; methodology, I.T., T.H., M.S. and A.E.; software, I.T. and T.H.; validation, I.T.; formal analysis, I.T., T.H. and A.E.; investigation, I.T., T.H., M.S. and A.E.; resources, I.T. and T.H.; data curation, I.T. and T.H.; writing—original draft preparation, I.T., M.S. and A.E.; writing—review and editing, I.T., M.S. and A.E.; visualization, I.T.; supervision, M.S. and A.E.; project administration, A.E.; funding acquisition, A.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the following grants: grant #2714/19 from the Israeli Science Foundation; Israeli Smart Transportation Research Center (ISTRC); Israeli Council for Higher Education (CHE) via the Data Science Research Center, Ben-Gurion University of the Negev, Israel.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data was obtained through the public sources whose URLs are given in the text.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Jha, S.K.; Eyong, E.M. An energy optimization in wireless sensor networks by using genetic algorithm. Telecommun. Syst. 2018, 67, 113–121. [Google Scholar] [CrossRef]
- Mayer, M.J.; Szilágyi, A.; Gróf, G. Environmental and economic multi-objective optimization of a household level hybrid renewable energy system by genetic algorithm. Appl. Energy 2020, 269, 115058. [Google Scholar] [CrossRef]
- Hemanth, D.J.; Anitha, J. Modified genetic algorithm approaches for classification of abnormal magnetic resonance brain tumour images. Appl. Soft Comput. 2019, 75, 21–28. [Google Scholar] [CrossRef]
- García-Sánchez, P.; Tonda, A.; Fernández-Leiva, A.J.; Cotta, C. Optimizing Hearthstone agents using an evolutionary algorithm. Knowl.-Based Syst. 2020, 188, 105032. [Google Scholar] [CrossRef]
- Elyasaf, A.; Hauptman, A.; Sipper, M. Evolutionary Design of Freecell Solvers. IEEE Trans. Comput. Intell. AI Games 2012, 4, 270–281. [Google Scholar] [CrossRef]
- Jin, Y.; Olhofer, M.; Sendhoff, B. On Evolutionary Optimization with Approximate Fitness Functions. In Proceedings of the Gecco, Las Vegas, NV, USA, 8–12 July 2000; pp. 786–793. [Google Scholar]
- He, C.; Zhang, Y.; Gong, D.; Ji, X. A review of surrogate-assisted evolutionary algorithms for expensive optimization problems. Expert Syst. Appl. 2023, 217, 119495. [Google Scholar] [CrossRef]
- Hsiao, J.; Shivam, K.; Chou, C.; Kam, T. Shape design optimization of a robot arm using a surrogate-based evolutionary approach. Appl. Sci. 2020, 10, 2223. [Google Scholar] [CrossRef]
- Zhang, M.; Li, H.; Pan, S.; Lyu, J.; Ling, S.; Su, S. Convolutional neural networks-based lung nodule classification: A surrogate-assisted evolutionary algorithm for hyperparameter optimization. IEEE Trans. Evol. Comput. 2021, 25, 869–882. [Google Scholar] [CrossRef]
- Calisto, M.B.; Lai-Yuen, S.K. EMONAS-Net: Efficient multiobjective neural architecture search using surrogate-assisted evolutionary algorithm for 3D medical image segmentation. Artif. Intell. Med. 2021, 119, 102154. [Google Scholar] [CrossRef]
- Fan, L.; Wang, H. Surrogate-assisted evolutionary neural architecture search with network embedding. Complex Intell. Syst. 2023, 9, 3313–3331. [Google Scholar] [CrossRef]
- Smith, R.E.; Dike, B.A.; Stegmann, S. Fitness inheritance in genetic algorithms. In Proceedings of the 1995 ACM Symposium on Applied Computing, Nashville, TN, USA, 26–28 February 1995; pp. 345–350. [Google Scholar]
- Liaw, R.T.; Ting, C.K. Evolution of biocoenosis through symbiosis with fitness approximation for many-tasking optimization. Memetic Comput. 2020, 12, 399–417. [Google Scholar] [CrossRef]
- Le, H.L.; Landa-Silva, D.; Galar, M.; Garcia, S.; Triguero, I. EUSC: A clustering-based surrogate model to accelerate evolutionary undersampling in imbalanced classification. Appl. Soft Comput. 2021, 101, 107033. [Google Scholar] [CrossRef]
- Gallotta, R.; Arulkumaran, K.; Soros, L.B. Surrogate Infeasible Fitness Acquirement FI-2Pop for Procedural Content Generation. In Proceedings of the 2022 IEEE Conference on Games (CoG), Beijing, China, 21–24 August 2022; pp. 500–503. [Google Scholar]
- Kalia, H.; Dehuri, S.; Ghosh, A. Fitness inheritance in multi-objective genetic algorithms: A case study on fuzzy classification rule mining. Int. J. Adv. Intell. Paradig. 2022, 23, 89–112. [Google Scholar] [CrossRef]
- Jin, Y. A comprehensive survey of fitness approximation in evolutionary computation. Soft Comput. 2005, 9, 3–12. [Google Scholar] [CrossRef]
- Dias, J.; Rocha, H.; Ferreira, B.; Lopes, M.d.C. A genetic algorithm with neural network fitness function evaluation for IMRT beam angle optimization. Cent. Eur. J. Oper. Res. 2014, 22, 431–455. [Google Scholar] [CrossRef]
- Guo, P.; Cheng, W.; Wang, Y. Hybrid evolutionary algorithm with extreme machine learning fitness function evaluation for two-stage capacitated facility location problems. Expert Syst. Appl. 2017, 71, 57–68. [Google Scholar] [CrossRef]
- Yu, D.P.; Kim, Y.H. Is it worth to approximate fitness by machine learning? Investigation on the extensibility according to problem size. In Proceedings of the 2018 Genetic and Evolutionary Computation Conference Companion, Kyoto, Japan, 15–19 July 2018; pp. 77–78. [Google Scholar]
- Livne, A.; Tov, E.S.; Solomon, A.; Elyasaf, A.; Shapira, B.; Rokach, L. Evolving context-aware recommender systems with users in mind. Expert Syst. Appl. 2022, 189, 116042. [Google Scholar] [CrossRef]
- Zhang, Y.; Fontaine, M.C.; Hoover, A.K.; Nikolaidis, S. Deep surrogate assisted map-elites for automated hearthstone deckbuilding. In Proceedings of the Genetic and Evolutionary Computation Conference, Boston, MA, USA, 9–13 July 2022; pp. 158–167. [Google Scholar]
- Li, P.; Tang, H.; Hao, J.; Zheng, Y.; Fu, X.; Meng, Z. ERL-Re2: Efficient Evolutionary Reinforcement Learning with Shared State Representation and Individual Policy Representation. In Proceedings of the International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Hao, H.; Zhang, X.; Li, B.; Zhou, A. A First Look at Kolmogorov-Arnold Networks in Surrogate-assisted Evolutionary Algorithms. arXiv 2024, arXiv:2405.16494. [Google Scholar]
- Hao, H.; Zhang, X.; Zhou, A. Large Language Models as Surrogate Models in Evolutionary Algorithms: A Preliminary Study. arXiv 2024, arXiv:2406.10675. [Google Scholar] [CrossRef]
- Tong, H.; Huang, C.; Minku, L.L.; Yao, X. Surrogate models in evolutionary single-objective optimization: A new taxonomy and experimental study. Inf. Sci. 2021, 562, 414–437. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R.; Taylor, J. An Introduction to Statistical Learning with Applications in Python; Springer Texts in Statistics; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Salton, G.; Wong, A.; Yang, C.S. A vector space model for automatic indexing. Commun. ACM 1975, 18, 613–620. [Google Scholar] [CrossRef]
- Bai, F.; Zou, D.; Wei, Y. A surrogate-assisted evolutionary algorithm with clustering-based sampling for high-dimensional expensive blackbox optimization. J. Glob. Optim. 2024, 89, 93–115. [Google Scholar] [CrossRef]
- Wang, X.; Wang, G.G.; Song, B.; Wang, P.; Wang, Y. A novel evolutionary sampling assisted optimization method for high-dimensional expensive problems. IEEE Trans. Evol. Comput. 2019, 23, 815–827. [Google Scholar] [CrossRef]
- Jin, Y.; Olhofer, M.; Sendhoff, B. Managing approximate models in evolutionary aerodynamic design optimization. In Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat. No. 01TH8546), Seoul, Republic of Korea, 27–30 May 2001; Volume 1, pp. 592–599. [Google Scholar]
- Storn, R.; Price, K. Differential evolution: A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Hansen, N.; Auger, B.; Ros, J.B.T.M.T.; Schoenauer, M. Evolution Strategies as a Machine Learning Tool. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation, Hong Kong, China, 1–6 June 2008; pp. 1–8. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Sipper, M.; Halperin, T.; Tzruia, I.; Elyasaf, A. EC-KitY: Evolutionary computation tool kit in Python with seamless machine learning integration. SoftwareX 2023, 22, 101381. [Google Scholar] [CrossRef]
- Blickle, T. Tournament selection. Evol. Comput. 2000, 1, 181–186. [Google Scholar]
- Spears, W.M.; Anand, V. A study of crossover operators in genetic programming. In Proceedings of the International Symposium on Methodologies for Intelligent Systems, Berlin/Heidelberg, Germany, 16–19 October 1991; pp. 409–418. [Google Scholar]
- Lim, S.M.; Sultan, A.B.M.; Sulaiman, M.N.; Mustapha, A.; Leong, K.Y. Crossover and mutation operators of genetic algorithms. Int. J. Mach. Learn. Comput. 2017, 7, 9–12. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Blank, J.; Deb, K. pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Jianye, H.; Li, P.; Tang, H.; Zheng, Y.; Fu, X.; Meng, Z. ERL-Re2: Efficient Evolutionary Reinforcement Learning with Shared State Representation and Individual Policy Representation. In Proceedings of the Tenth International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Lehman, J.; Stanley, K.O. Abandoning objectives: Evolution through the search for novelty alone. Evol. Comput. 2011, 19, 189–223. [Google Scholar] [CrossRef] [PubMed]
- Pugh, J.K.; Soros, L.B.; Stanley, K.O. Quality diversity: A new frontier for evolutionary computation. Front. Robot. AI 2016, 3, 202845. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).