A Note on Equivalent and Nonequivalent Parametrizations of the Two-Parameter Logistic Item Response Model
Abstract
1. Introduction
2. Two-Parameter Item Response Models
2.1. Unipolar IRT Model
2.2. Rational Function Model (RFM)
2.3. 2PL Model with Log-Linear Smoothing
2.4. Ramsay Quotient Model
2.5. Partial Membership Mastery Model
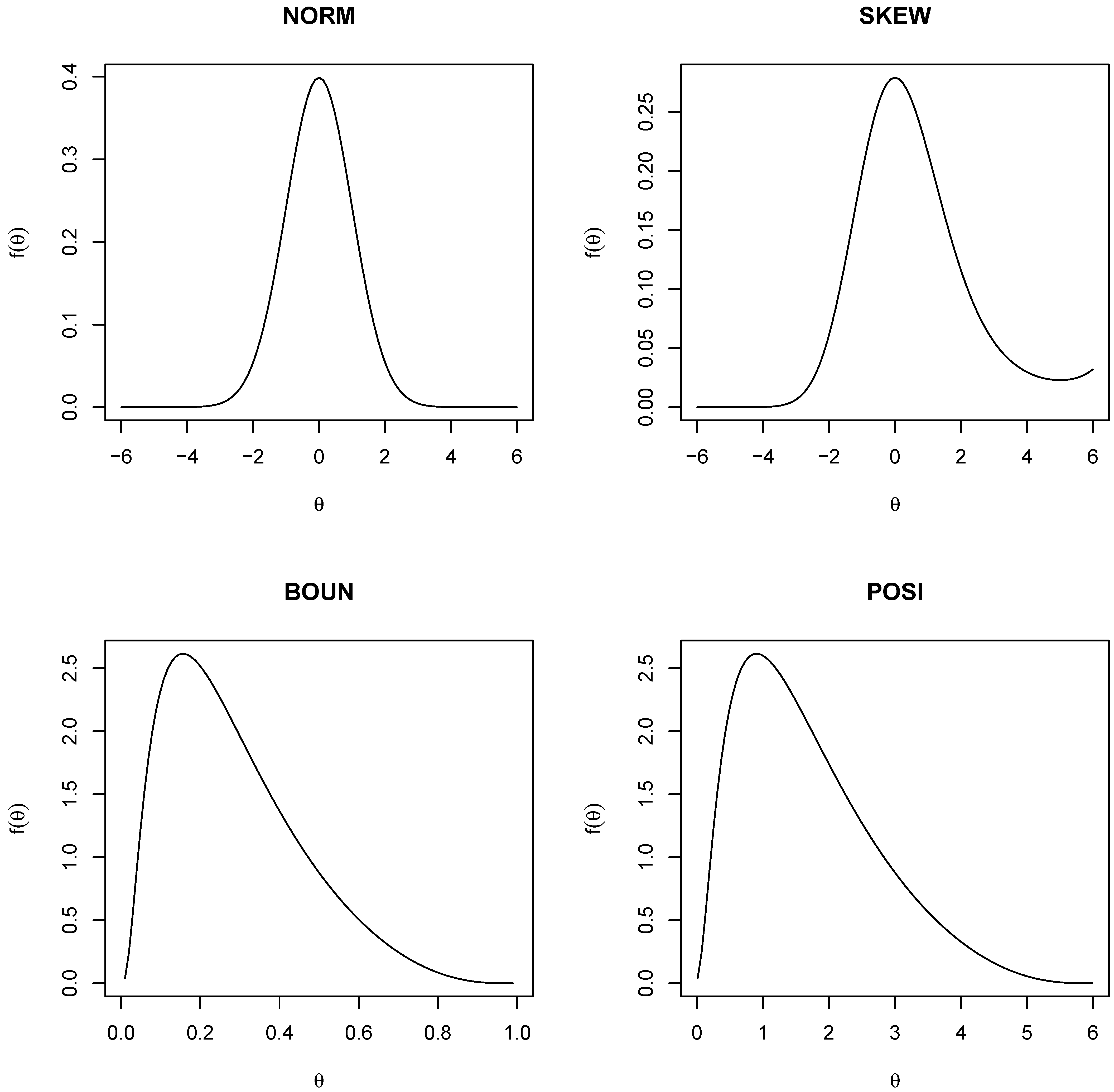
3. Simulation Study
3.1. Method
3.2. Results
4. Empirical Examples
4.1. Method
4.2. Results
5. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AIC | Akaike information criterion |
| 2PL | two-parameter logistic |
| 3PL | three-parameter logistic |
| 4PL | four-parameter logistic |
| DCM | diagnostic classification model |
| DGM | data-generating model |
| GHP | Gilula–Haberman penalty |
| IRF | item response function |
| IRT | item response theory |
| M | mean |
| PMMM | partial membership mastery model |
| RFM | rational function model |
| RQM | Ramsay quotient model |
| SD | standard deviation |
| SK | skewness |
Appendix A. Item Parameters in Simulation Study
| Item | NORM | SKEW | BOUN | POSI | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.85 | −1.55 | 0.54 | −1.85 | 2.67 | −0.06 | 1.34 | 0.14 |
| 2 | 2.01 | −1.76 | 1.54 | −1.97 | 5.65 | −0.14 | 4.67 | 0.41 |
| 3 | 1.69 | −1.22 | 1.19 | −1.29 | 5.07 | −0.03 | 3.28 | 0.52 |
| 4 | 4.05 | −1.01 | 3.15 | −0.96 | 7.85 | 0.03 | 7.53 | 0.62 |
| 5 | 4.77 | −1.12 | 3.91 | −1.10 | 8.27 | 0.02 | 8.52 | 0.56 |
| 6 | 2.38 | −0.89 | 1.69 | −0.84 | 6.64 | 0.05 | 4.71 | 0.64 |
| 7 | 1.56 | −0.79 | 1.04 | −0.70 | 4.60 | 0.06 | 2.76 | 0.67 |
| 8 | 1.61 | −0.31 | 1.00 | 0.00 | 4.77 | 0.18 | 2.53 | 0.87 |
| 9 | 1.27 | −0.32 | 0.81 | 0.03 | 3.95 | 0.20 | 2.15 | 0.87 |
| 10 | 2.20 | 0.32 | 1.29 | 1.01 | 6.28 | 0.35 | 3.02 | 1.19 |
References
- Chen, Y.; Li, X.; Liu, J.; Ying, Z. Item response theory—A statistical framework for educational and psychological measurement. arXiv 2021, arXiv:2108.08604. [Google Scholar]
- Yen, W.M.; Fitzpatrick, A.R. Item response theory. In Educational Measurement; Brennan, R.L., Ed.; Praeger Publishers: Westport, CT, USA, 2006; pp. 111–154. [Google Scholar]
- San Martin, E. Identification of item response theory models. In Handbook of Item Response Theory, Volume 2: Statistical Tools; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 127–150. [Google Scholar] [CrossRef]
- Birnbaum, A. Some latent trait models and their use in inferring an examinee’s ability. In Statistical Theories of Mental Test Scores; Lord, F.M., Novick, M.R., Eds.; MIT Press: Reading, MA, USA, 1968; pp. 397–479. [Google Scholar]
- Woods, C.M. Estimating the latent density in unidimensional IRT to permit non-normality. In Handbook of Item Response Theory Modeling; Reise, S.P., Revicki, D.A., Eds.; Routledge: New York, NY, USA, 2014; pp. 78–102. [Google Scholar] [CrossRef]
- Xu, X.; von Davier, M. Fitting the Structured General Diagnostic Model to NAEP Data; (Research Report No. RR-08-28); Educational Testing Service: Princeton, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Lucke, J.F. Unipolar item response models. In Handbook of Item Response Theory Modeling: Applications to Typical Performance Assessment; Routledge: New York, NY, USA, 2015; pp. 272–284. [Google Scholar] [CrossRef]
- Morales-Vives, F.; Ferrando, P.J.; Hernández-Dorado, A. Modeling maladaptive personality traits with unipolar item response theory: The case of callousness. J. Gen. Psychol. 2024. Epub ahead of print. [Google Scholar] [CrossRef] [PubMed]
- Reise, S.P.; Rodriguez, A.; Spritzer, K.L.; Hays, R.D. Alternative approaches to addressing non-normal distributions in the application of IRT models to personality measures. J. Personal. Assess. 2018, 100, 363–374. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.; Bolt, D.M. Unipolar IRT and the author recognition test (ART). Behav. Res. Methods 2024, 56, 5406–5423. [Google Scholar] [CrossRef]
- Reise, S.P.; Du, H.; Wong, E.F.; Hubbard, A.S.; Haviland, M.G. Matching IRT models to patient-reported outcomes constructs: The graded response and log-logistic models for scaling depression. Psychometrika 2021, 86, 800–824. [Google Scholar] [CrossRef]
- van der Linden, W.J. Unidimensional logistic response models. In Handbook of Item Response Theory, Volume 1: Models; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 11–30. [Google Scholar] [CrossRef]
- Dimitrov, D.M.; Atanasov, D.V. Latent D-scoring modeling: Estimation of item and person parameters. Educ. Psychol. Meas. 2021, 81, 388–404. [Google Scholar] [CrossRef]
- Robitzsch, A. About the equivalence of the latent D-scoring model and the two-parameter logistic item response model. Mathematics 2021, 9, 1465. [Google Scholar] [CrossRef]
- Dimitrov, D. D-scoring Method of Measurement: Classical and Latent Frameworks; Taylor & Francis: Boca Raton, FL, USA, 2023. [Google Scholar] [CrossRef]
- Paisley, J.; Wang, C.; Blei, D.M. The discrete infinite logistic normal distribution. Bayesian Anal. 2012, 7, 997–1034. [Google Scholar] [CrossRef]
- Robitzsch, A. Relating the one-parameter logistic diagnostic classification model to the Rasch model and one-parameter logistic mixed, partial, and probabilistic membership diagnostic classification models. Foundations 2023, 3, 621–633. [Google Scholar] [CrossRef]
- von Davier, M. A general diagnostic model applied to language testing data. Br. J. Math. Stat. Psychol. 2008, 61, 287–307. [Google Scholar] [CrossRef]
- Casabianca, J.M.; Lewis, C. IRT item parameter recovery with marginal maximum likelihood estimation using loglinear smoothing models. J. Educ. Behav. Stat. 2015, 40, 547–578. [Google Scholar] [CrossRef]
- Robitzsch, A. A comprehensive simulation study of estimation methods for the Rasch model. Stats 2021, 4, 814–836. [Google Scholar] [CrossRef]
- Steinfeld, J.; Robitzsch, A. Item parameter estimation in multistage designs: A comparison of different estimation approaches for the Rasch model. Psych 2021, 3, 279–307. [Google Scholar] [CrossRef]
- Ramsay, J.O. A comparison of three simple test theory models. Psychometrika 1989, 54, 487–499. [Google Scholar] [CrossRef]
- van der Maas, H.L.J.; Molenaar, D.; Maris, G.; Kievit, R.A.; Borsboom, D. Cognitive psychology meets psychometric theory: On the relation between process models for decision making and latent variable models for individual differences. Psychol. Rev. 2011, 118, 339–356. [Google Scholar] [CrossRef]
- Robitzsch, A. Relating the Ramsay quotient model to the classical D-scoring rule. Analytics 2023, 2, 824–835. [Google Scholar] [CrossRef]
- Aitkin, M.; Aitkin, I. Investigation of the Identifiability of the 3PL Model in the NAEP 1986 Math Survey; Technical Report; US Department of Education, Office of Educational Research and Improvement National Center for Education Statistics: Washington, DC, USA, 2006; Available online: https://bit.ly/3T6t9sl (accessed on 29 September 2024).
- Aitkin, M.; Aitkin, I. Statistical Modeling of the National Assessment of Educational Progress; Springer: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Lord, F.M.; Novick, R. Statistical Theories of Mental Test Scores; Addison-Wesley: Reading, MA, USA, 1968. [Google Scholar]
- De Ayala, R.J. The Theory and Practice of Item Response Theory; Guilford Publications: New York, NY, USA, 2022. [Google Scholar]
- von Davier, M. Is there need for the 3PL model? Guess what? Meas. Interdiscip. Res. Persp. 2009, 7, 110–114. [Google Scholar] [CrossRef]
- Dayton, C.M.; Macready, G.B. A probabilistic model for validation of behavioral hierarchies. Psychometrika 1976, 41, 189–204. [Google Scholar] [CrossRef]
- DiBello, L.V.; Roussos, L.A.; Stout, W. A review of cognitively diagnostic assessment and a summary of psychometric models. In Handbook of Statistics, Volume 26: Psychometrics; Rao, C.R., Sinharay, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 979–1030. [Google Scholar] [CrossRef]
- von Davier, M.; Lee, Y.S. (Eds.) Handbook of Diagnostic Classification Models; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Rupp, A.A.; Templin, J.; Henson, R.A. Diagnostic Measurement: Theory, Methods, and Applications; Guilford Press: New York, NY, USA, 2010. [Google Scholar]
- de la Torre, J.; Lee, Y.S. A note on the invariance of the DINA model parameters. J. Educ. Meas. 2010, 47, 115–127. [Google Scholar] [CrossRef]
- Huang, Q.; Bolt, D.M. Relative robustness of CDMs and (M)IRT in measuring growth in latent skills. Educ. Psychol. Meas. 2023, 83, 808–830. [Google Scholar] [CrossRef]
- Chen, L.; Gu, Y. A spectral method for identifiable grade of membership analysis with binary responses. Psychometrika 2024, 89, 626–657. [Google Scholar] [CrossRef] [PubMed]
- Erosheva, E.A. Comparing latent structures of the grade of membership, Rasch, and latent class models. Psychometrika 2005, 70, 619–628. [Google Scholar] [CrossRef]
- Manton, K.G.; Woodbury, M.A.; Stallard, E.; Corder, L.S. The use of grade-of-membership techniques to estimate regression relationships. Sociol. Methodol. 1992, 22, 321–381. [Google Scholar] [CrossRef]
- Woodbury, M.A.; Clive, J.; Garson Jr, A. Mathematical typology: A grade of membership technique for obtaining disease definition. Comput. Biomed. Res. 1978, 11, 277–298. [Google Scholar] [CrossRef] [PubMed]
- DeCarlo, L.T. A signal detection model for multiple-choice exams. Appl. Psychol. Meas. 2021, 45, 423–440. [Google Scholar] [CrossRef]
- Erosheva, E.A.; Fienberg, S.E.; Junker, B.W. Alternative statistical models and representations for large sparse multi-dimensional contingency tables. Ann. Fac. Sci. Toulouse Math. 2002, 11, 485–505. [Google Scholar] [CrossRef]
- Erosheva, E.A.; Fienberg, S.E.; Joutard, C. Describing disability through individual-level mixture models for multivariate binary data. Ann. Appl. Stat. 2007, 1, 346–384. [Google Scholar] [CrossRef]
- Finch, H.W. Performance of the grade of membership model under a variety of sample sizes, group size ratios, and differential group response probabilities for dichotomous indicators. Educ. Psychol. Meas. 2021, 81, 523–548. [Google Scholar] [CrossRef]
- Heller, K.A.; Williamson, S.; Ghahramani, Z. Statistical models for partial membership. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 392–399. [Google Scholar] [CrossRef]
- Gruhl, J.; Erosheva, E.A.; Ghahramani, Z.; Mohamed, S.; Heller, K. A tale of two (types of) memberships: Comparing mixed and partial membership with a continuous data example. In Handbook of Mixed Membership Models and Their Applications; Airoldi, E.M., Blei, D., Erosheva, E.A., Fienberg, S.E., Eds.; Chapman & Hall: Boca Raton, FL, USA, 2014; pp. 15–38. [Google Scholar] [CrossRef]
- Ghahramani, Z.; Mohamed, S.; Heller, K. A simple and general exponential family framework for partial membership and factor analysis. In Handbook of Mixed Membership Models and Their Applications; Airoldi, E.M., Blei, D., Erosheva, E.A., Fienberg, S.E., Eds.; Chapman & Hall: Boca Raton, FL, USA, 2014; pp. 101–122. [Google Scholar] [CrossRef]
- Shang, Z.; Erosheva, E.A.; Xu, G. Partial-mastery cognitive diagnosis models. Ann. Appl. Stat. 2021, 15, 1529–1555. [Google Scholar] [CrossRef]
- Robitzsch, A. A comparison of mixed and partial membership diagnostic classification models with multidimensional item response models. Information 2024, 15, 331. [Google Scholar] [CrossRef]
- Barton, M.A.; Lord, F.M. An Upper Asymptote for the Three-Parameter Logistic Item-Response Model; ETS Research Report Series; Educational Testing Service: Princeton, NJ, USA, 1981. [Google Scholar] [CrossRef]
- Loken, E.; Rulison, K.L. Estimation of a four-parameter item response theory model. Br. J. Math. Stat. Psychol. 2010, 63, 509–525. [Google Scholar] [CrossRef] [PubMed]
- Culpepper, S.A. The prevalence and implications of slipping on low-stakes, large-scale assessments. J. Educ. Behav. Stat. 2017, 42, 706–725. [Google Scholar] [CrossRef]
- Robitzsch, A. Four-parameter guessing model and related item response models. Math. Comput. Appl. 2022, 27, 95. [Google Scholar] [CrossRef]
- Zhan, P.; Wang, W.C.; Jiao, H.; Bian, Y. Probabilistic-input, noisy conjunctive models for cognitive diagnosis. Front. Psychol. 2018, 9, 997. [Google Scholar] [CrossRef]
- Zhan, P. Refined learning tracking with a longitudinal probabilistic diagnostic model. Educ. Meas. 2021, 40, 44–58. [Google Scholar] [CrossRef]
- Myszkowski, N.; Storme, M. Data for: A snapshot of g? Binary and polytomous item-response theory investigations of the last series of the standard progressive matrices (SPM-LS). Mendeley Data 2018. [Google Scholar] [CrossRef]
- Myszkowski, N. Analysis of an intelligence dataset. J. Intell. 2020, 8, 39. [Google Scholar] [CrossRef]
- Cavanaugh, J.E.; Neath, A.A. The Akaike information criterion: Background, derivation, properties, application, interpretation, and refinements. WIREs Comput. Stat. 2019, 11, e1460. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2024; Available online: https://www.R-project.org (accessed on 15 June 2024).
- Robitzsch, A. sirt: Supplementary Item Response Theory Models, R Package Version 4.2-73; R Core Team: Vienna, Austria, 2024; Available online: https://github.com/alexanderrobitzsch/sirt (accessed on 7 September 2024).
- Aitkin, M. Expectation maximization algorithm and extensions. In Handbook of Item Response Theory, Volume 2: Statistical Tools; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 217–236. [Google Scholar] [CrossRef]
- Bock, R.D.; Aitkin, M. Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika 1981, 46, 443–459. [Google Scholar] [CrossRef]
- Glas, C.A.W. Maximum-likelihood estimation. In Handbook of Item Response Theory, Volume 2: Statistical Tools; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 197–216. [Google Scholar] [CrossRef]
- George, A.C.; Robitzsch, A.; Kiefer, T.; Groß, J.; Ünlü, A. The R package CDM for cognitive diagnosis models. J. Stat. Softw. 2016, 74, 1–24. [Google Scholar] [CrossRef]
- Robitzsch, A.; George, A.C. The R package CDM for diagnostic modeling. In Handbook of Diagnostic Classification Models; von Davier, M., Lee, Y.S., Eds.; Springer: Cham, Switzerland, 2019; pp. 549–572. [Google Scholar] [CrossRef]
- Templin, J.; Hoffman, L. Obtaining diagnostic classification model estimates using Mplus. Educ. Meas. 2013, 32, 37–50. [Google Scholar] [CrossRef]
- Templin, J.; Bradshaw, L. Hierarchical diagnostic classification models: A family of models for estimating and testing attribute hierarchies. Psychometrika 2014, 79, 317–339. [Google Scholar] [CrossRef] [PubMed]
- Zeileis, A.; Strobl, C.; Wickelmaier, F.; Komboz, B.; Kopf, J. psychotree: Recursive Partitioning Based on Psychometric Models, R Package Version 0.16-1. 2024. Available online: https://CRAN.R-project.org/package=psychotree (accessed on 11 April 2024).
- Strobl, C.; Kopf, J.; Zeileis, A. Rasch trees: A new method for detecting differential item functioning in the Rasch model. Psychometrika 2015, 80, 289–316. [Google Scholar] [CrossRef]
- Myszkowski, N.; Storme, M. A snapshot of g. Binary and polytomous item-response theory investigations of the last series of the standard progressive matrices (SPM-LS). Intelligence 2018, 68, 109–116. [Google Scholar] [CrossRef]
- Myszkowski, N. A Mokken scale analysis of the last series of the standard progressive matrices (SPM-LS). J. Intell. 2020, 8, 22. [Google Scholar] [CrossRef]
- Robitzsch, A. Regularized latent class analysis for polytomous item responses: An application to SPM-LS data. J. Intell. 2020, 8, 30. [Google Scholar] [CrossRef]
- Robitzsch, A.; Kiefer, T.; Wu, M. TAM: Test Analysis Modules, R Package Version 4.2-21. 2024. Available online: https://doi.org/10.32614/CRAN.package.TAM (accessed on 19 February 2024). [CrossRef]
- Su, Y.L.; Choi, K.M.; Lee, W.C.; Choi, T.; McAninch, M. Hierarchical Cognitive Diagnostic Analysis for TIMSS 2003 Mathematics; Technical Report; CASMA Research Report Number 35; University of Iowa: Iowa City, IA, USA, 2013; Available online: https://tinyurl.com/4jrm8mah (accessed on 29 September 2024).
- Skaggs, G.; Wilkins, J.L.M.; Hein, S.F. Grain size and parameter recovery with TIMSS and the general diagnostic model. Int. J. Test. 2016, 16, 310–330. [Google Scholar] [CrossRef]
- Gilula, Z.; Haberman, S.J. Conditional log-linear models for analyzing categorical panel data. J. Am. Stat. Assoc. 1994, 89, 645–656. [Google Scholar] [CrossRef]
- Gilula, Z.; Haberman, S.J. Prediction functions for categorical panel data. Ann. Stat. 1995, 23, 1130–1142. [Google Scholar] [CrossRef]
- Haberman, S.J. The Information a Test Provides on an Ability Parameter; Research Report No. RR-07-18; Educational Testing Service: Princeton, NJ, USA, 2007. [Google Scholar] [CrossRef]
- van Rijn, P.W.; Sinharay, S.; Haberman, S.J.; Johnson, M.S. Assessment of fit of item response theory models used in large-scale educational survey assessments. Large-Scale Assess. Educ. 2016, 4, 10. [Google Scholar] [CrossRef]
- Robitzsch, A. On the treatment of missing item responses in educational large-scale assessment data: An illustrative simulation study and a case study using PISA 2018 mathematics data. Eur. J. Investig. Health Psychol. Educ. 2021, 11, 1653–1687. [Google Scholar] [CrossRef] [PubMed]
- Robitzsch, A. On the choice of the item response model for scaling PISA data: Model selection based on information criteria and quantifying model uncertainty. Entropy 2022, 24, 760. [Google Scholar] [CrossRef] [PubMed]
- Maris, G.; Bechger, T. On interpreting the model parameters for the three parameter logistic model. Meas. Interdiscip. Res. Persp. 2009, 7, 75–88. [Google Scholar] [CrossRef]
- San Martín, E.; González, J.; Tuerlinckx, F. On the unidentifiability of the fixed-effects 3PL model. Psychometrika 2015, 80, 450–467. [Google Scholar] [CrossRef] [PubMed]
- Ho, A.D. A nonparametric framework for comparing trends and gaps across tests. J. Educ. Behav. Stat. 2009, 34, 201–228. [Google Scholar] [CrossRef]
- Fan, J.; Li, R.; Zhang, C.H.; Zou, H. Statistical Foundations of Data Science; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar] [CrossRef]
- Peng, Y.; He, M.; Hu, F.; Mao, Z.; Huang, X.; Ding, J. Predictive modeling of flexible EHD pumps using Kolmogorov–Arnold networks. Biomim. Intell. Robotics 2024, 4, 100184. [Google Scholar] [CrossRef]
- Belov, D.I.; Lüdtke, O.; Ulitzsch, E. Likelihood-free estimation of IRT models in small samples: A neural networks approach. PsyArXiv 2024. [Google Scholar] [CrossRef]
- Gao, L.; Zhao, Z.; Li, C.; Zhao, J.; Zeng, Q. Deep cognitive diagnosis model for predicting students’ performance. Future Gener. Comput. Syst. 2022, 126, 252–262. [Google Scholar] [CrossRef]
- Gu, Y. Going deep in diagnostic modeling: Deep cognitive diagnostic models (DeepCDMs). Psychometrika 2024, 89, 118–150. [Google Scholar] [CrossRef]
- Maris, G.; Bechger, T. Boltzmann machines as multidimensional item response theory models. PsyArXiv 2021. [Google Scholar] [CrossRef]
- Pliakos, K.; Joo, S.H.; Park, J.Y.; Cornillie, F.; Vens, C.; Van den Noortgate, W. Integrating machine learning into item response theory for addressing the cold start problem in adaptive learning systems. Comput. Educ. 2019, 137, 91–103. [Google Scholar] [CrossRef]
- Pokropek, A.; Pokropek, E. Deep neural networks for detecting statistical model misspecifications. The case of measurement invariance. Struct. Equ. Model. 2022, 29, 394–411. [Google Scholar] [CrossRef]
- Tsutsumi, E.; Kinoshita, R.; Ueno, M. Deep item response theory as a novel test theory based on deep learning. Electronics 2021, 10, 1020. [Google Scholar] [CrossRef]
- Yu, J. Neural networks ensemble-based IRT parameter estimation. In Proceedings of the 2009 International Conference on Computational Intelligence and Software Engineering, Wuhan, China, 11–13 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–3. [Google Scholar] [CrossRef]

| DGM | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Analysis Model | Analysis Model | Analysis Model | |||||||||||
| NORM | SKEW | BOUN | POSI | NORM | SKEW | BOUN | POSI | NORM | SKEW | BOUN | POSI | ||
| NORM | 500 | 72.8 | 10.5 | 11.9 | 4.8 | 81.6 | 15.3 | 2.3 | 0.8 | 84.1 | 15.9 | 0.0 | 0.0 |
| 1000 | 74.1 | 12.1 | 11.6 | 2.2 | 84.1 | 15.6 | 0.3 | 0.0 | 83.8 | 16.2 | 0.0 | 0.0 | |
| 2000 | 78.6 | 13.2 | 7.8 | 0.4 | 83.9 | 16.1 | 0.0 | 0.0 | 84.1 | 15.9 | 0.0 | 0.0 | |
| SKEW | 500 | 14.8 | 36.4 | 14.2 | 34.6 | 1.6 | 73.3 | 0.5 | 24.5 | 0.3 | 89.6 | 0.0 | 10.2 |
| 1000 | 3.7 | 55.1 | 9.0 | 32.2 | 0.0 | 86.7 | 0.1 | 13.3 | 0.0 | 99.1 | 0.0 | 0.9 | |
| 2000 | 0.1 | 68.7 | 4.4 | 26.9 | 0.0 | 95.9 | 0.0 | 4.1 | 0.0 | 100.0 | 0.0 | 0.0 | |
| BOUN | 500 | 8.4 | 15.0 | 21.3 | 55.3 | 0.0 | 1.1 | 40.9 | 57.9 | 0.0 | 0.1 | 55.7 | 44.2 |
| 1000 | 0.6 | 8.7 | 24.8 | 65.9 | 0.0 | 0.1 | 55.8 | 44.1 | 0.0 | 0.0 | 60.3 | 39.7 | |
| 2000 | 0.0 | 2.4 | 33.4 | 64.1 | 0.0 | 0.0 | 67.8 | 32.2 | 0.0 | 0.0 | 67.1 | 32.9 | |
| POSI | 500 | 10.8 | 20.6 | 15.4 | 53.2 | 0.4 | 14.4 | 8.3 | 76.9 | 0.0 | 10.2 | 2.8 | 86.9 |
| 1000 | 1.4 | 19.3 | 14.1 | 65.3 | 0.0 | 5.9 | 4.4 | 89.7 | 0.0 | 4.0 | 0.1 | 95.9 | |
| 2000 | 0.0 | 13.5 | 11.2 | 75.3 | 0.0 | 2.5 | 0.6 | 96.9 | 0.0 | 1.5 | 0.0 | 98.5 | |
| DGM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Analysis Model | Analysis Model | Analysis Model | ||||||||
| NORM | BOUN | POSI | NORM | BOUN | POSI | NORM | BOUN | POSI | ||
| SKEW | 500 | 21.3 | 17.2 | 61.6 | 13.9 | 1.5 | 84.7 | 17.9 | 0.0 | 82.1 |
| 1000 | 8.2 | 16.5 | 75.3 | 6.9 | 0.2 | 92.9 | 19.1 | 0.0 | 80.9 | |
| 2000 | 1.2 | 17.1 | 81.7 | 2.7 | 0.0 | 97.3 | 27.8 | 0.0 | 72.2 | |
| Model | Dataset | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| NORM | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| SKEW | −5.9 | −13.6 | −1.4 | −15.8 | −24.6 | −12.0 |
| BOUN | 3.5 | −20.3 | 4.9 | −27.6 | 6.4 | −11.9 |
| POSI | −4.5 | −14.2 | −0.9 | −16.4 | 26.0 | −8.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robitzsch, A. A Note on Equivalent and Nonequivalent Parametrizations of the Two-Parameter Logistic Item Response Model. Information 2024, 15, 668. https://doi.org/10.3390/info15110668
Robitzsch A. A Note on Equivalent and Nonequivalent Parametrizations of the Two-Parameter Logistic Item Response Model. Information. 2024; 15(11):668. https://doi.org/10.3390/info15110668
Chicago/Turabian StyleRobitzsch, Alexander. 2024. "A Note on Equivalent and Nonequivalent Parametrizations of the Two-Parameter Logistic Item Response Model" Information 15, no. 11: 668. https://doi.org/10.3390/info15110668
APA StyleRobitzsch, A. (2024). A Note on Equivalent and Nonequivalent Parametrizations of the Two-Parameter Logistic Item Response Model. Information, 15(11), 668. https://doi.org/10.3390/info15110668






