Protecting Infinite Data Streams from Wearable Devices with Local Differential Privacy Techniques
Abstract
1. Introduction
- (1)
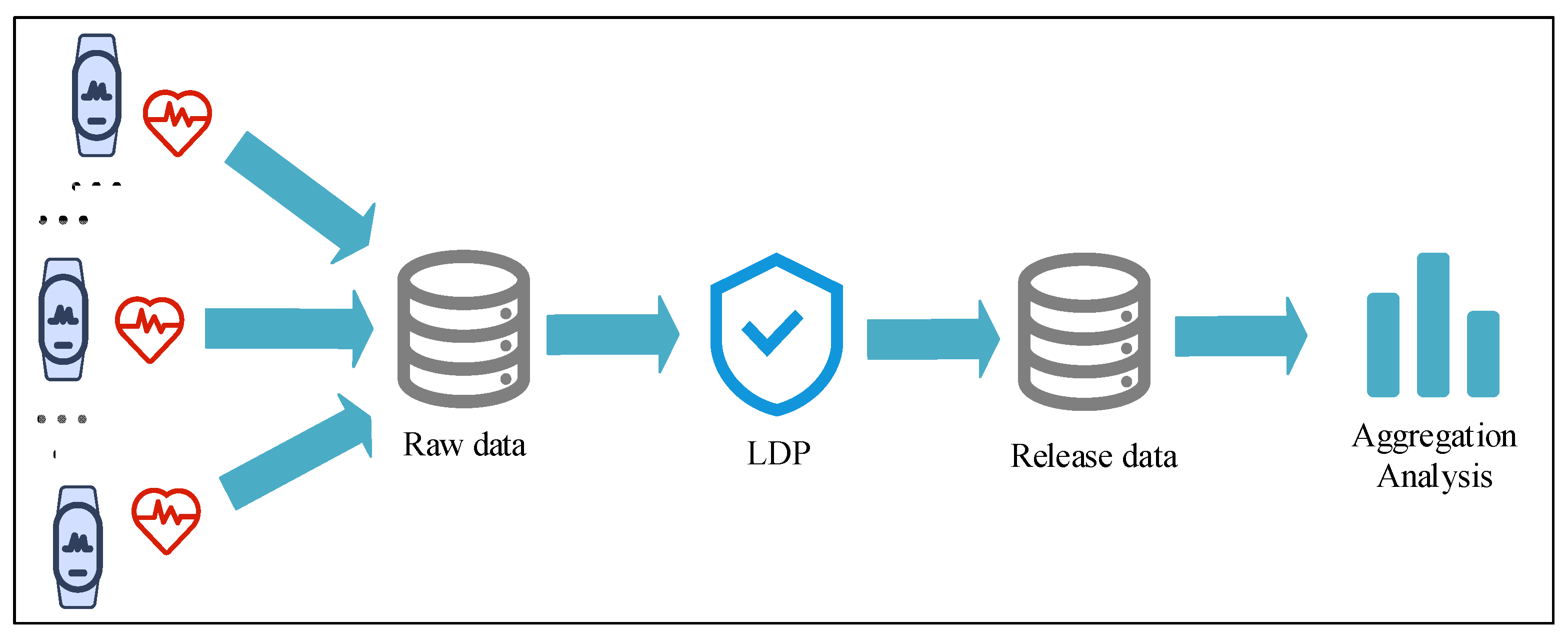
- This paper proposes a local differential privacy protection framework specifically designed for wearable devices, aiming to enhance data availability while safeguarding the privacy of wearable device users.
- (2)
- The adaptive privacy budget mechanism is optimized based on the characteristics of sampling points in the data stream, resulting in a more reasonable allocation of the privacy budget. Additionally, an improved SW mechanism is applied for perturbation, ensuring that data with smaller errors are output with higher probability.
- (3)
- Comparisons with existing methods, using real datasets, demonstrate that this approach not only effectively protects user privacy but also preserves the availability of data streams.
2. Related Work
3. Basic Knowledge
3.1. Infinite Data Streams
3.2. Problem Statement
3.3. Local Differential Privacy
3.4. W-Event Privacy
4. Recommend Method
4.1. WIDS-LDP
4.2. Significant Point Sampling
4.2.1. First-Order Difference Method
4.2.2. LFLS
4.2.3. Dynamic Angle α
| Algorithm 1: Significant point sampling |
| Input: Raw data , |
| Output: |
| for t [2,n] do |
| if then , end Calculate if < end end |
4.3. Budget Allocation and Perturbations
4.3.1. Adaptive Privacy Budget Allocation
| Algorithm 2: Adaptive privacy budget allocation |
| Input: Privacy budget , window size |
| Output: Perturbation data |
| Initialize |
| for do |
| Calculate remaining publication budget end |
4.3.2. Data Perturbations
4.4. Post-Processing Mechanism
| Algorithm 3: Adaptive privacy budget allocation |
| Input: Perturbation data |
| Output: Release data |
| for do |
| |
| end |
4.5. Theoretical Analysis
5. Experiment
5.1. Experimental Environment
5.2. Real Dataset
5.3. Comparison Scheme
5.4. Experiment Indicatorsr
5.5. Experiment Parameters
5.6. Program Utility
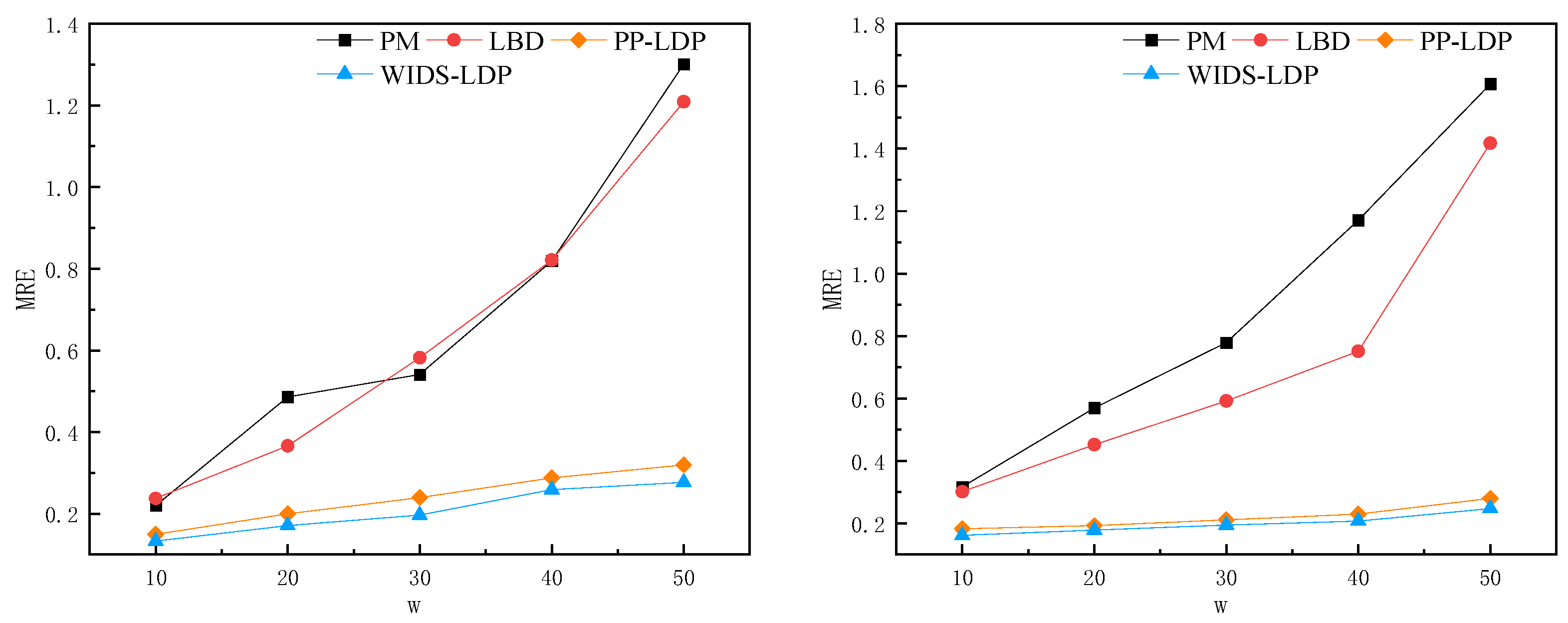
5.6.1. MRE Analysis of Different Window Lengths
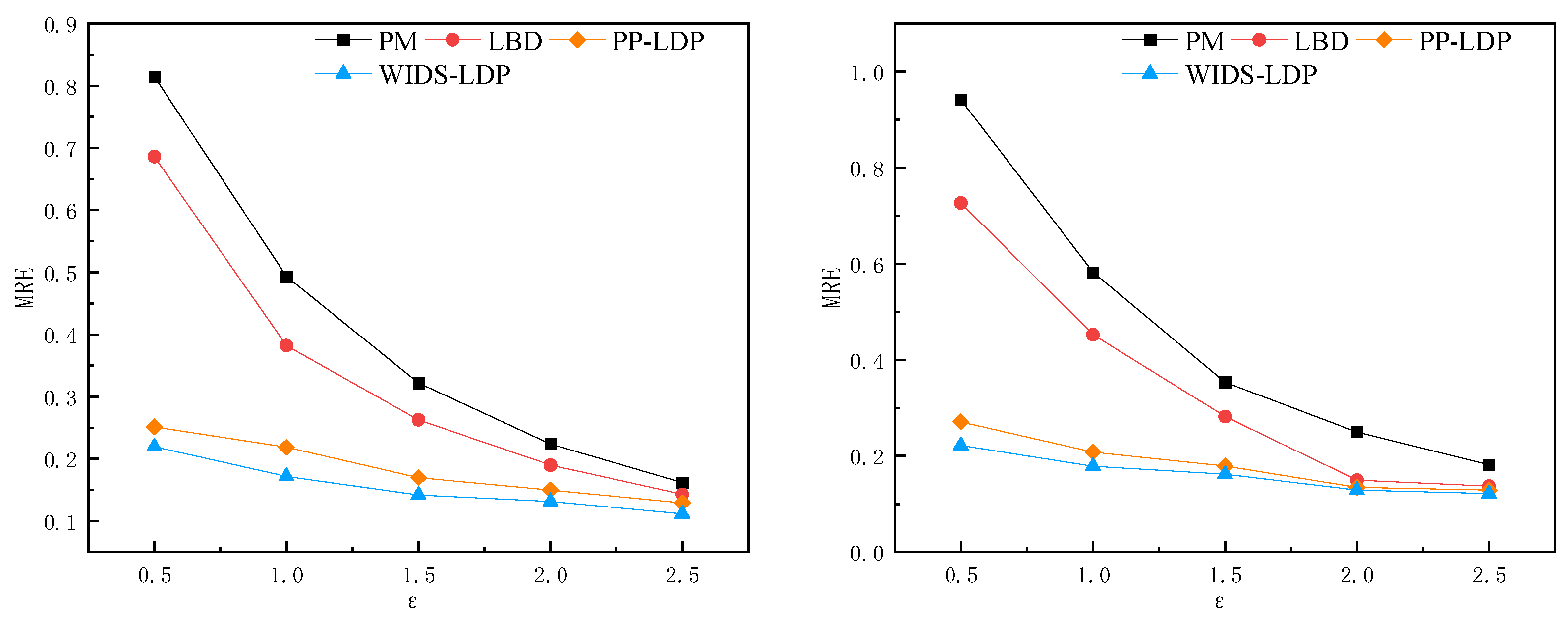
5.6.2. MRE Analysis of Different Privacy Budgets
5.6.3. MRE Analysis of Different Data Lengths
6. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Terminology | Abbreviation | Definition |
| Square wave | SW | A periodic waveform whose value rapidly switches between two fixed levels, commonly used in signal processing and test systems. |
| Kalman filtering | KF | An algorithm for estimating the state of a dynamic system that achieves recursive estimation of the system state by modeling measurement noise and system noise. |
| Mean relative error | MRE | A measure of prediction accuracy that calculates the average of the relative error between the predicted value and the actual value and is used to evaluate the performance of the model. |
| Linear fitting equations with least squares | LFLS | A statistical method that finds the best-fitting line by minimizing the squared difference between the observed data and the fitted model. It is widely used in data analysis and regression modeling. |
| LDP budget distribution | LBD | Refers to the allocation strategy of privacy budget (or noise level) in local differential privacy, aiming to balance the privacy protection and information utility of data. |
| Differential privacy | DP | A method of protecting personal privacy by adding random noise to query results to ensure that individual participation does not significantly affect the overall data analysis results. |
| Local differential privacy | LDP | An implementation of differential privacy that allows users to perturb their data locally, ensuring that the privacy of the data is protected before being transmitted to the server. |
References
- Babu, M.; Lautman, Z.; Lin, X.; Sobota, M.H.; Snyder, M.P. Wearable devices: Implications for precision medicine and the future of health care. Annu. Rev. Med. 2024, 75, 401–415. [Google Scholar] [CrossRef] [PubMed]
- Tu, Z.X.; Liu, S.B.; Xiong, X.X. Differential privacy mean publishing of digital stream data for wearable devices. Comput. Appl. 2020, 40, 6. [Google Scholar]
- Dwork, C.; Mcsherry, F.; Nissim, K. Calibrating noise to sensitivityn in private data analysis. In Proceedings of the Theory of Cryptography: Third Theory of Cryptography Conference, New York, NY, USA, 4–7 March 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 265–284. [Google Scholar]
- Kasiviswanathan, S.P.; Lee, H.K.; Nissim, K. What can we learn privately? SIAM J. Comput. 2011, 40, 793–826. [Google Scholar] [CrossRef]
- Yan, Y.; Chen, J.; Mahmood, A.; Qian, X.; Yan, P. LDPORR: A localized location privacy protection method based on optimized random response. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 101713. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, W.; Pang, X. Towards pattern-aware privacy-preserving real-time data collection. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications, Virtual, 6–9 July 2020; pp. 109–118. [Google Scholar]
- Benhamouda, F.; Joye, M.; Libert, B. A new framework for privacy-preserving aggregation of time-series data. ACM Trans. Inf. Syst. Secur. (TISSEC) 2016, 18, 1–21. [Google Scholar] [CrossRef]
- Zheng, Y.; Lu, R.; Guan, Y. Efficient and privacy-preserving similarity range query over encrypted time series data. IEEE Trans. Dependable Secur. Comput. 2021, 19, 2501–2516. [Google Scholar] [CrossRef]
- Liu, Z.; Yi, Y. Privacy-preserving collaborative analytics on medical time series data. IEEE Trans. Dependable Secur. Comput. 2020, 19, 1687–1702. [Google Scholar] [CrossRef]
- Guan, Z.T.; Lv, Z.F.; Du, X.J.; Wu, L.F.; Guizani, M. Achieving data utility-privacy trade off in Internet of medical things, a machine learning approach. Future Gener. Comput. Syst. 2019, 98, 60–68. [Google Scholar] [CrossRef]
- Song, H.; Shuai, Z.; Qinghua, L. PPM-HDA: Privacy-preserving and multifunctional health data aggregation with fault tolerance. IEEE Trans. Inf. Forensics Secur. 2016, 18, 1940–1955. [Google Scholar]
- Saleheen, N.; Chakraborty, S.; Ali, N.; Rahman, M.M.; Hossain, S.M.; Bari, R.; Buder, E.; Srivastava, M.; Kumar, S. mSieve: Differential behavioral privacy in time series of mobile sensor data. In Proceedings of the 2016 ACM International Joint Conference, Heidelberg, Germany, 12–16 September 2016; ACM: Heidelberg, Germany, 2016; pp. 706–717. [Google Scholar]
- Steil, J.; Hagestedt, I.; Huang, M.X.; Bulling, A. Privacy aware eye tracking using differential privacy. In Proceedings of the ACM. the 11th ACM Symposium, Denver, CO, USA, 20–25 June 2019; ACM: New York, NY, USA, 2019; pp. 1–9. [Google Scholar]
- Bozkir, E.; Günlü, O.; Fuhl, W.; Schaefer, R.F.; Kasneci, E. Differential privacy for eye tracking with temporal correlations. PLoS ONE 2021, 16, e0255979. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.Q.; Li, X.H. Differential privacy medical data publishing method based on attribute correlation. Sci. Rep. 2022, 12, 15725. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.W.; Jang, B.; Yoo, H. Privacy-preserving aggregation of personal health data streams. PLoS ONE 2018, 13, e0207639. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.B.; Wang, B.H.; Li, J.S. Local differential privacy protection for wearable device data. PLoS ONE 2022, 17, e0272766. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Liang, X.; Zhang, Z.; He, S.; Shi, Z. Re-DPoctor: Real-time health data releasing with w-day differential privacy. In Proceedings of the IEEE.GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar]
- Schäler, C.; Hütter, T.; Schäler, M. Benchmarking the Utility of w-Event Differential Privacy Mechanisms-When Baselines Become Mighty Competitors. Proc. VLDB Endow. 2023, 16, 1830–1842. [Google Scholar] [CrossRef]
- Ding, F. Least squares parameter estimation and multi-innovation least squares methods for linear fitting problems from noisy data. J. Comput. Appl. Math. 2023, 426, 115107. [Google Scholar] [CrossRef]
- Gao, W.; Zhou, S. Privacy-Preserving for Dynamic Real-Time Published Data Streams Based on Local Differential Privacy. IEEE Internet Things J. 2023, 11, 13551–13562. [Google Scholar] [CrossRef]
- Li, Z.; Wang, T.; Lopuhaä-Zwakenberg, M.; Li, N.; Škoric, B. Estimating numerical distributions under local differential privacy. In Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data, Portland, OR, USA, 14–19 June 2020; pp. 621–635. [Google Scholar]
- Khodarahmi, M.; Maihami, V. A review on Kalman filter models. Arch. Comput. Methods Eng. 2023, 30, 727–747. [Google Scholar] [CrossRef]
- Shanmugarasa, Y.; Chamikara MA, P.; Paik, H.; Kanhere, S.S.; Zhu, L. Local Differential Privacy for Smart Meter Data Sharing with Energy Disaggregation. In Proceedings of the 2024 20th International Conference on Distributed Computing in Smart Systems and the Internet of Things (DCOSS-IoT), Abu Dhabi, United Arab Emirates, 29 April–1 May 2024; pp. 1–10. [Google Scholar]
- Reiss, A.; Stricker, D. Introducing new benchmarked dataset for activity monitoring. In Proceedings of the IEEE, The 16th International Symposium on Wearable Computers, ISWC 2012, Newcastle Upon Tyne, UK, 18–22 June 2012; pp. 108–109. [Google Scholar]
- Available online: https://www.microsoft.com/en-us/research/publication/t-drive-trajectory-data-sample/ (accessed on 8 September 2024).
- Ren, X.; Shi, L.; Yu, W. LDP-IDS: Local differential privacy for infinite data streams. In Proceedings of the 2022 International Conference on Management of Data, Philadelphia, PA, USA, 12–17 June 2022; pp. 1064–1077. [Google Scholar]
- Wang, N.; Xiao, X.; Yang, Y.; Zhao, J.; Hui, S.C.; Shin, H.; Shin, J.; Yu, G. Collecting and analyzing multidimensional data with local differential privacy. In Proceedings of the 2019 IEEE 35th International Conference on Data Engineering (ICDE), Macao, China, 8–11 April 2019; pp. 638–649. [Google Scholar]


| Tester | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Size | 3000 | 3000 | 3000 | 3000 | 3000 | 3000 | 3000 | 3000 |
| Range | 78~120 | 74~107 | 68~94 | 57~121 | 70~101 | 60~104 | 60~99 | 66~104 |
| Parameter | |||||
| Range | 0.8 | 0.1 | 0.1 | [0.5, 2.5] | [10, 50] |
| Default | 0.8 | 0.1 | 0.1 | 1 | 20 |
| Solution | Advantage | Disadvantage |
|---|---|---|
| PM | Supports multi-value and multi-attribute data | Not applicable for wearable devices; Unable to maintain the data flow pattern |
| LBD | Population division-based and data-adaptive algorithms; Two privacy budget allocation methods are more reasonable | Unable to maintain the dataflow pattern; The perturbation scheme has large errors; Not applicable for wearable devices |
| PP-LDP | Optimized SW data perturbation method; Maintain data flow patterns | Exponentially decreasing privacy budget allocation method |
| WIDS-LDP | A framework suitable for wearable devices; Maintain data flow patterns; LBD privacy budget allocation method | Only supports single-dimensional data |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, F.; Fan, S. Protecting Infinite Data Streams from Wearable Devices with Local Differential Privacy Techniques. Information 2024, 15, 630. https://doi.org/10.3390/info15100630
Zhao F, Fan S. Protecting Infinite Data Streams from Wearable Devices with Local Differential Privacy Techniques. Information. 2024; 15(10):630. https://doi.org/10.3390/info15100630
Chicago/Turabian StyleZhao, Feng, and Song Fan. 2024. "Protecting Infinite Data Streams from Wearable Devices with Local Differential Privacy Techniques" Information 15, no. 10: 630. https://doi.org/10.3390/info15100630
APA StyleZhao, F., & Fan, S. (2024). Protecting Infinite Data Streams from Wearable Devices with Local Differential Privacy Techniques. Information, 15(10), 630. https://doi.org/10.3390/info15100630






