Real-Time Nonlinear Image Reconstruction in Electrical Capacitance Tomography Using the Generative Adversarial Network
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Simulation of the Training Dataset
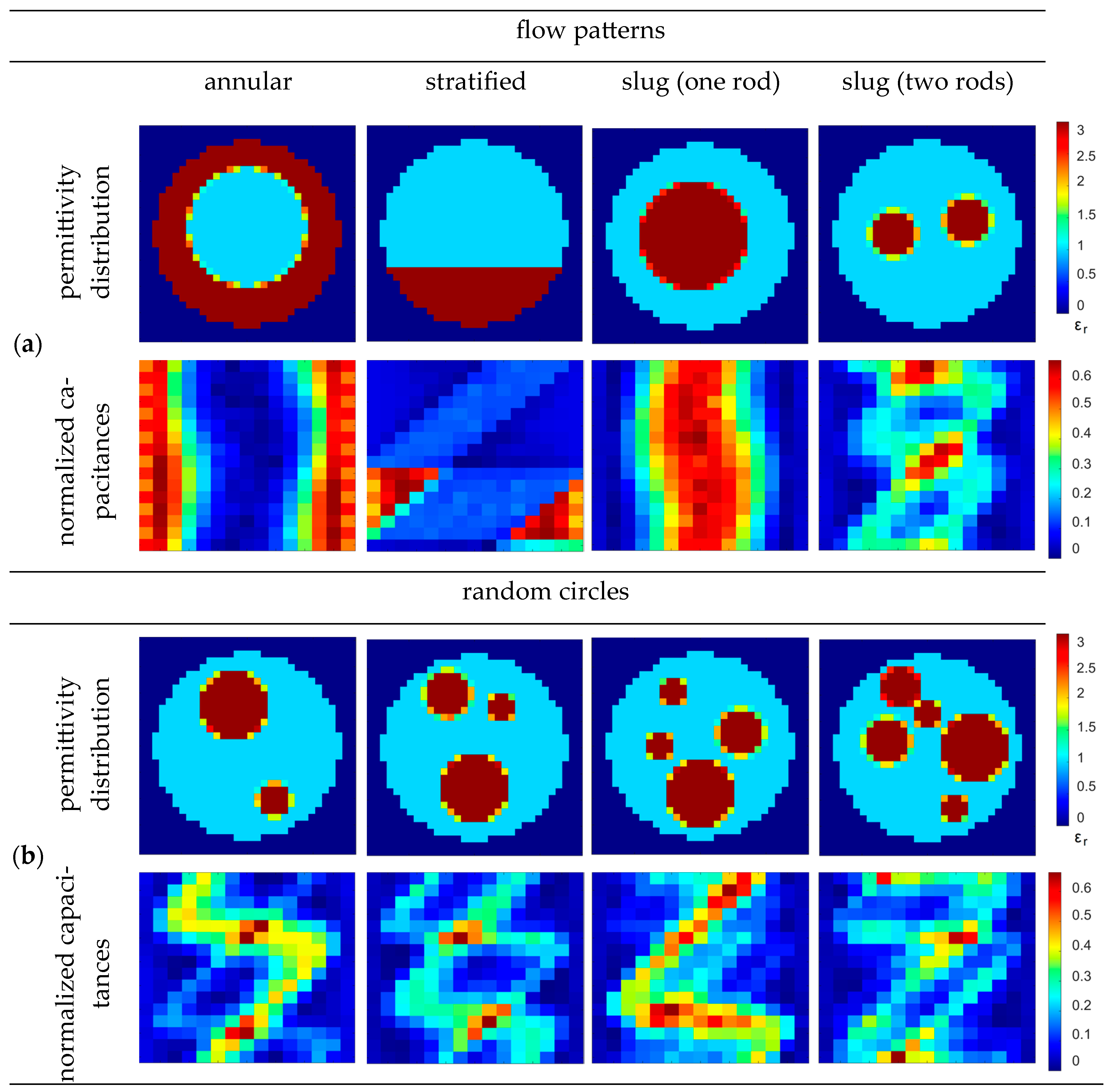
2.2. Training Dataset with the Two-Phase Flow Patterns
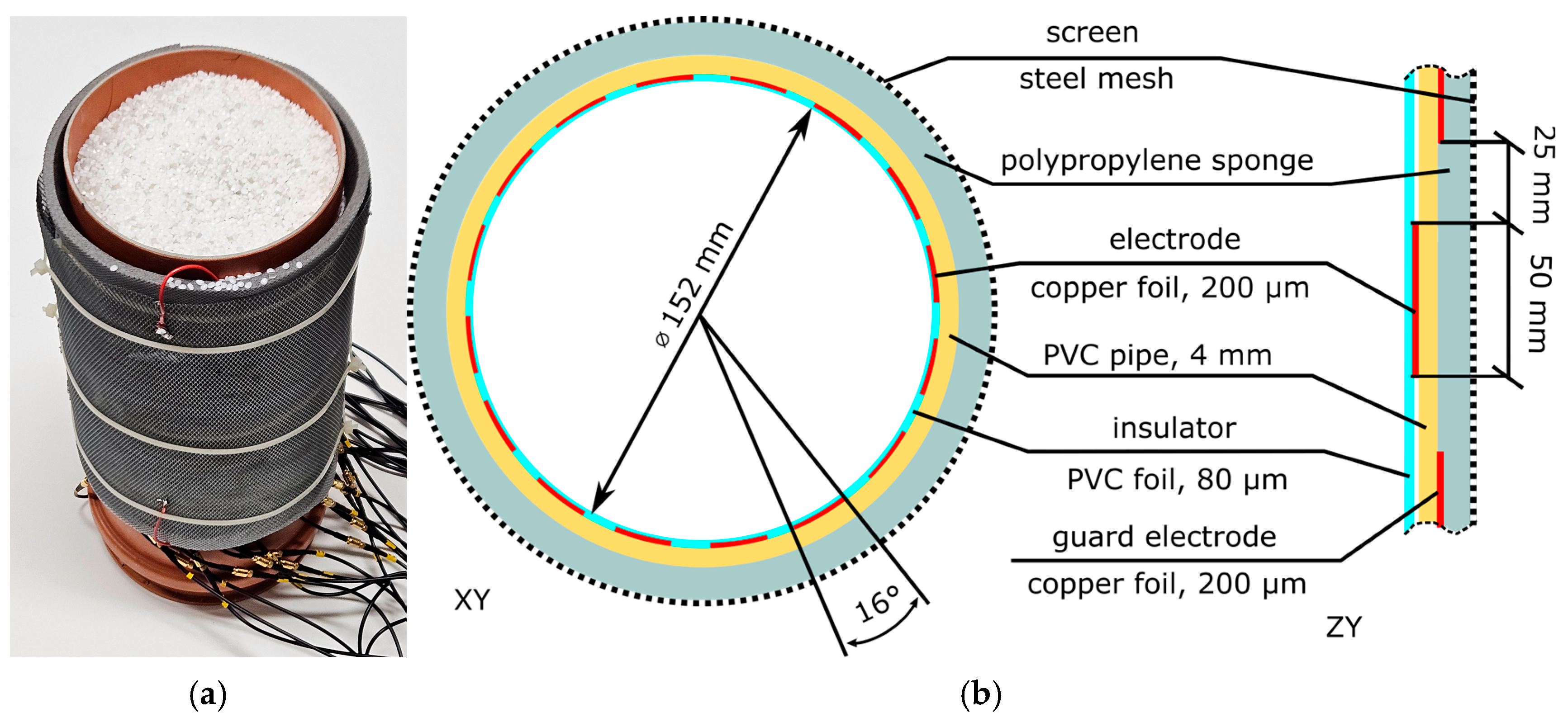
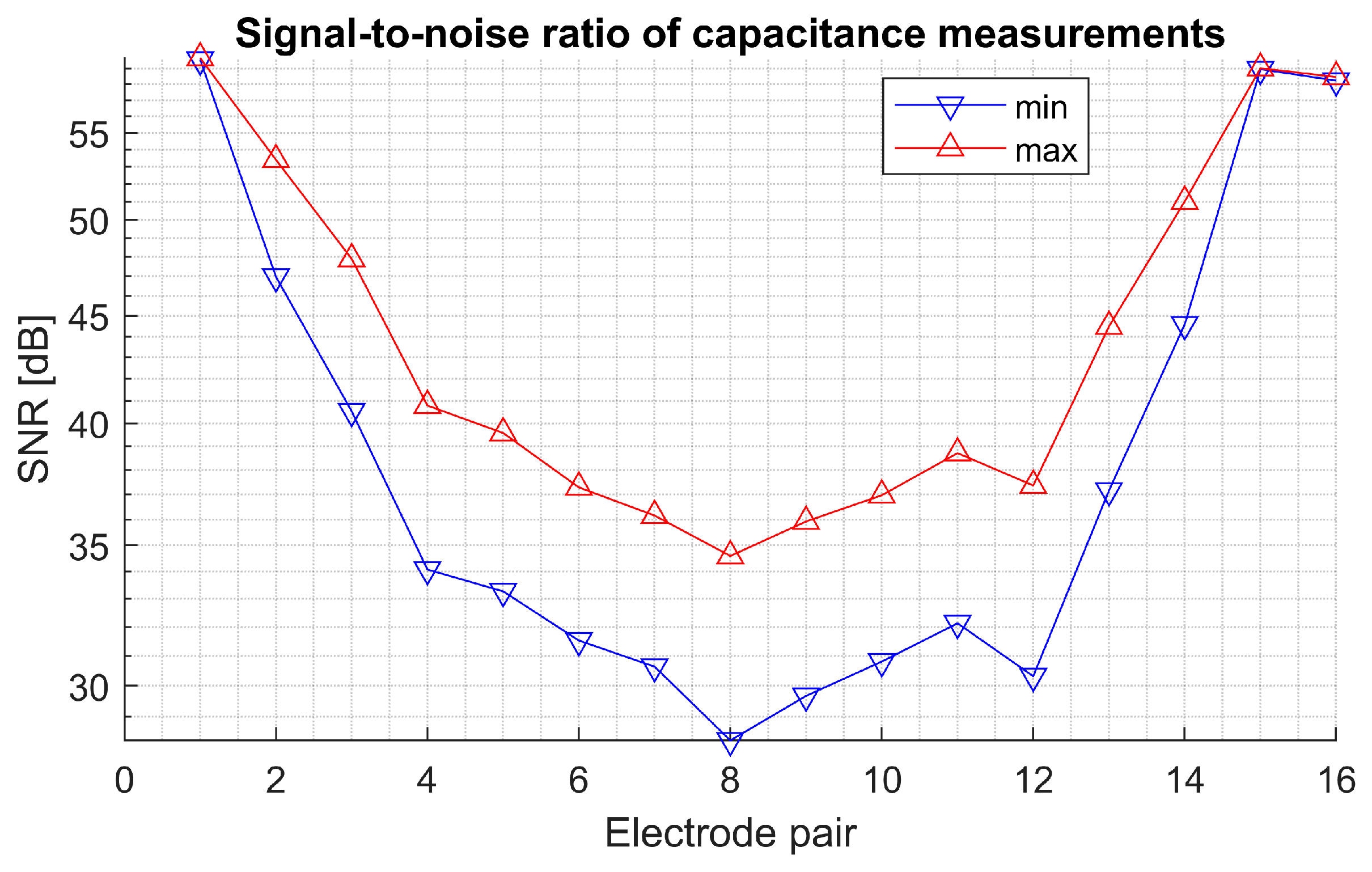
2.3. ECT Sensor and Test Objects for Real Measurements
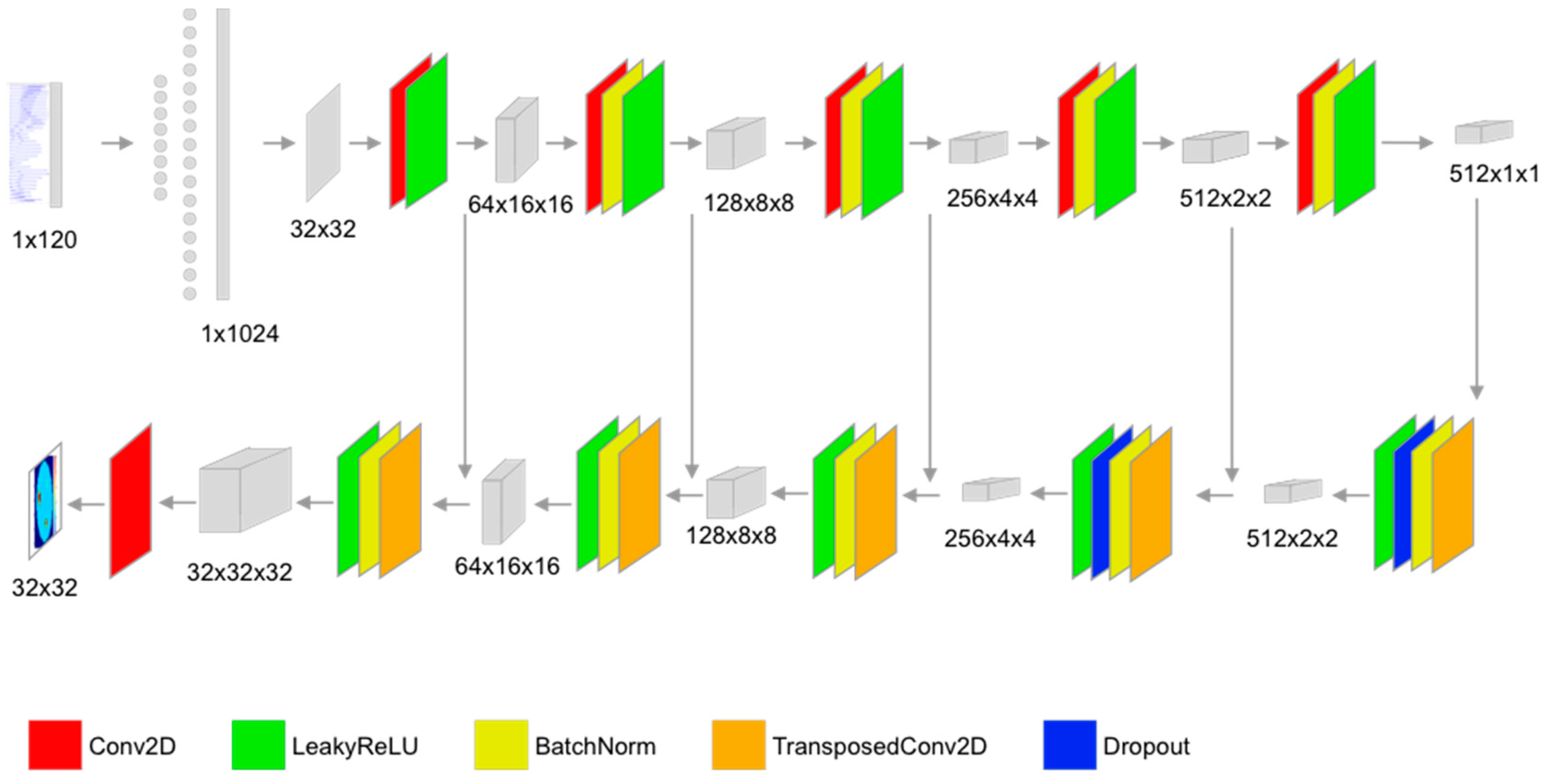
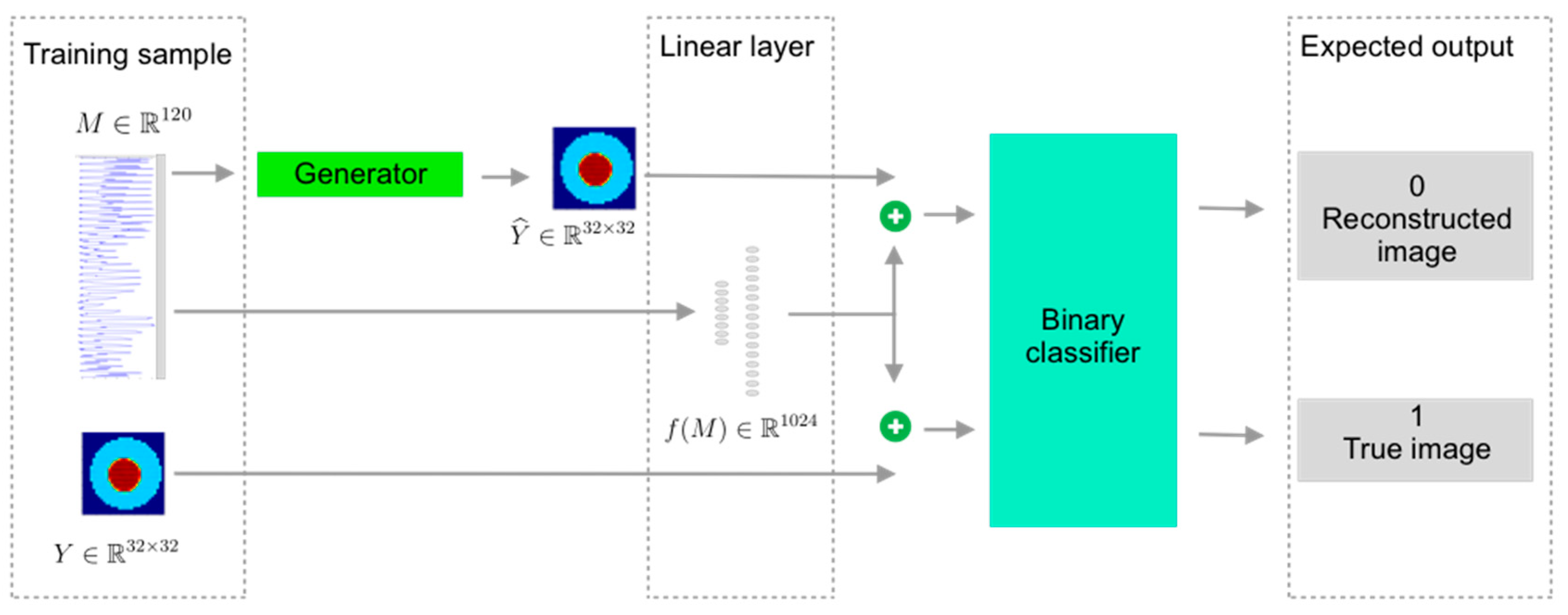
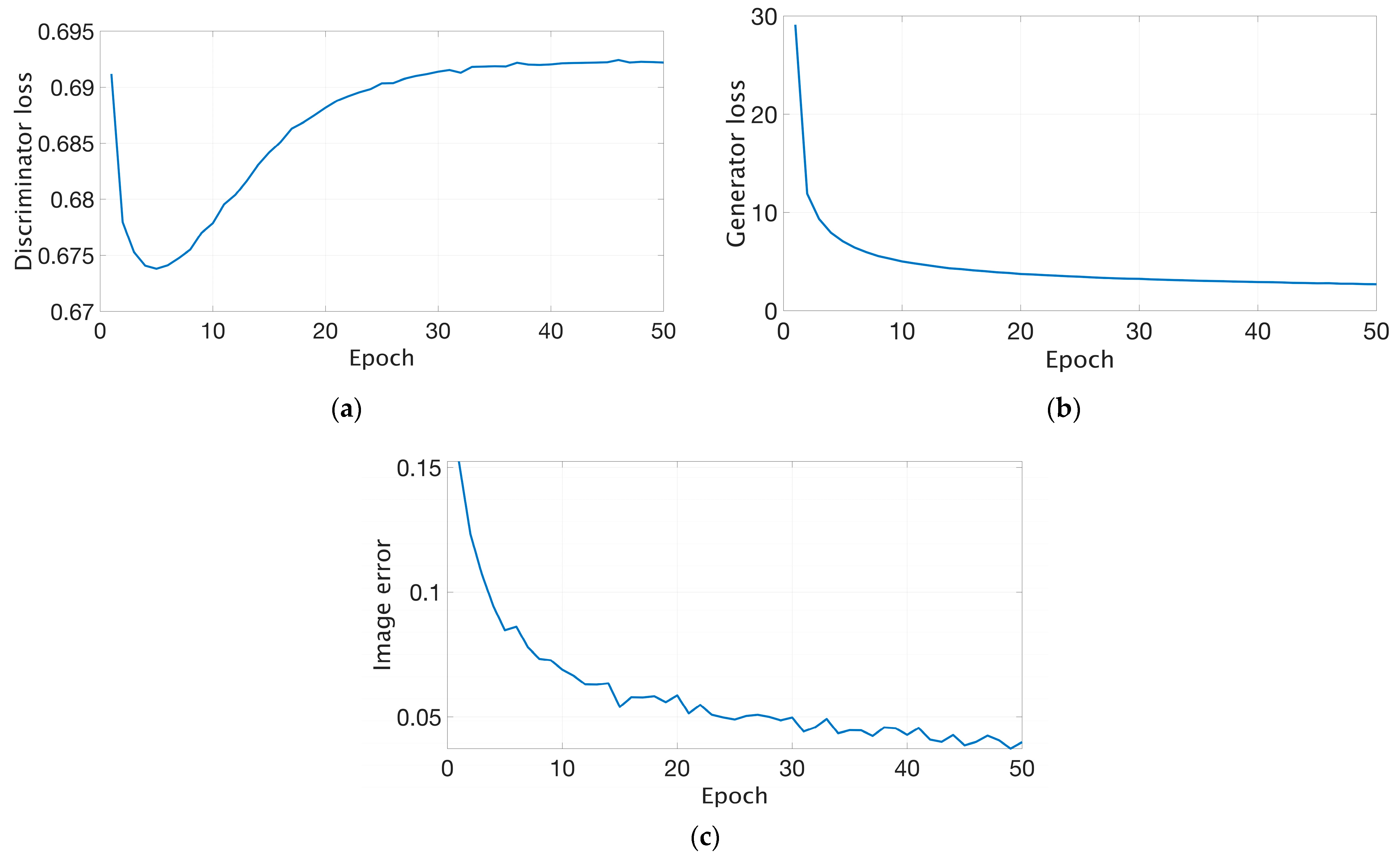
2.4. Neural Network Architecture and Training Procedure
2.5. Reference Image Reconstruction Algorithms
- I.
- The Landweber method, which is given by the formula:where is the self-relaxing step length, is the sensitivity matrix calculated for a uniform distribution inside the sensor, is a vector of measured capacitances, and is the iteration number. A discrepancy norm, given by the formulais calculated in each step of the algorithm. If the error fails to decrease from one iteration to the next, the algorithm may reduce the step size to maintain progress. The calculations are stopped if the step length falls below the assumed minimal level.
- II.
- The simplified Levenberg–Marquardt (sLM) algorithm (also with a self-relaxing step length) is given by the formula:where is a regularization parameter that balances the trade-off between the solution’s stability and accuracy. To optimize the performance of the sLM method, we conducted several reconstructions on the entire validation dataset and determined that a value of yielded the best results. The sensitivity matrix was not updated to reduce computation time, making this a linearized version of the sLM method, which is more comparable in execution time to the neural network-based reconstruction. In the literature, this approach is also called iterative Tikhonov regularization [34]. The stopping criterion is consistent with that used in the Landweber method.
3. Results
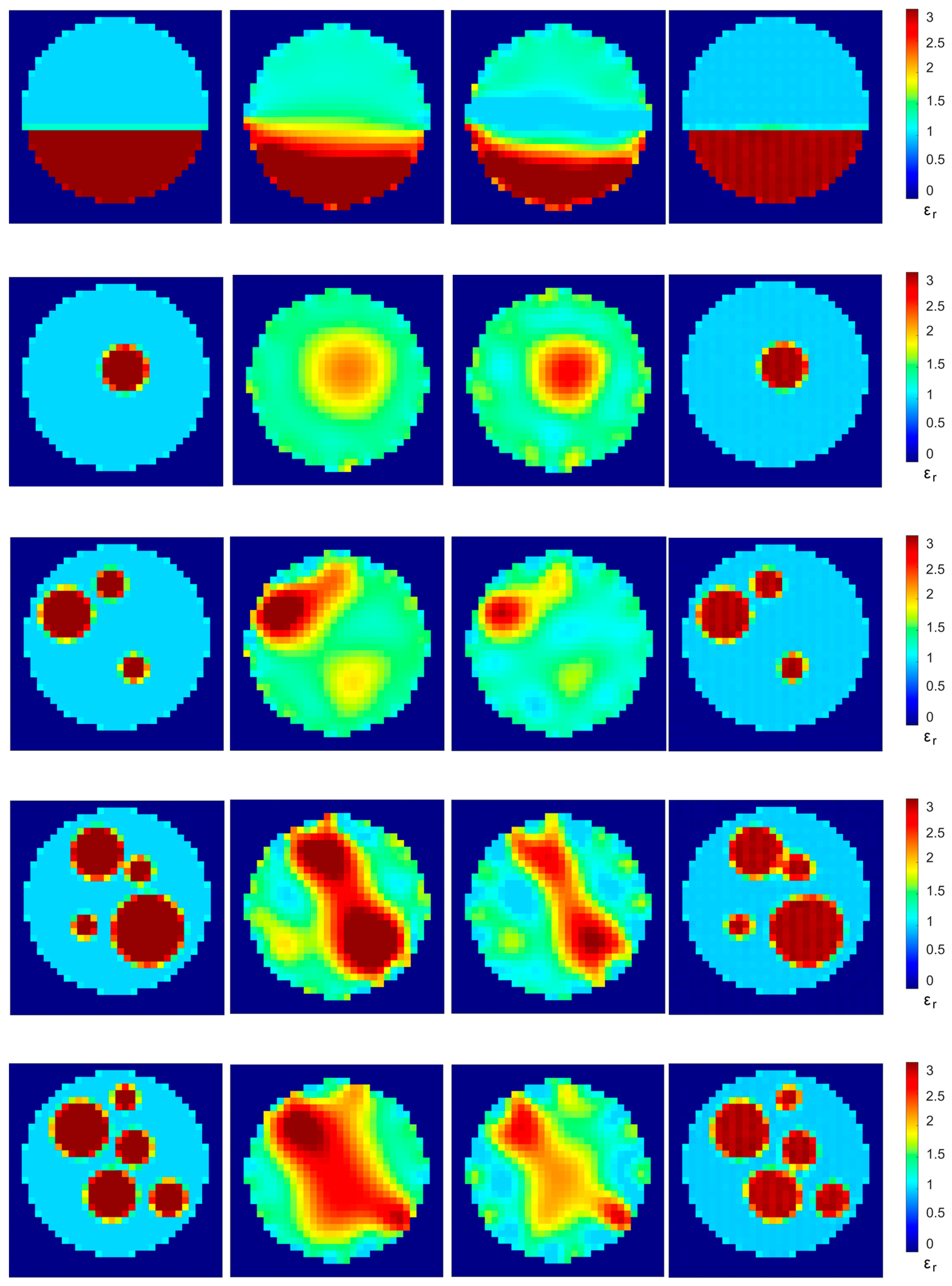
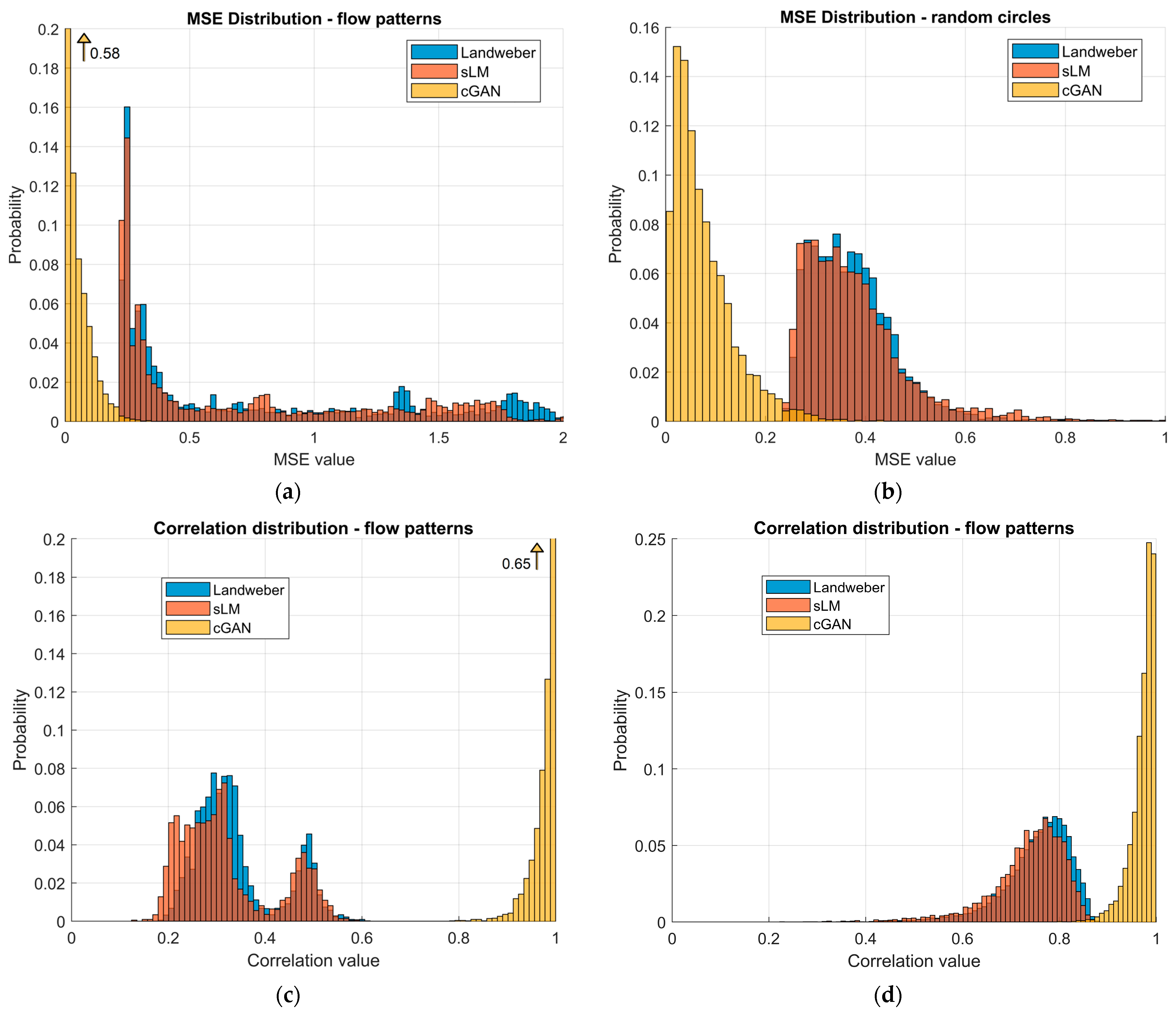
3.1. Analysis of the Simulated Dataset
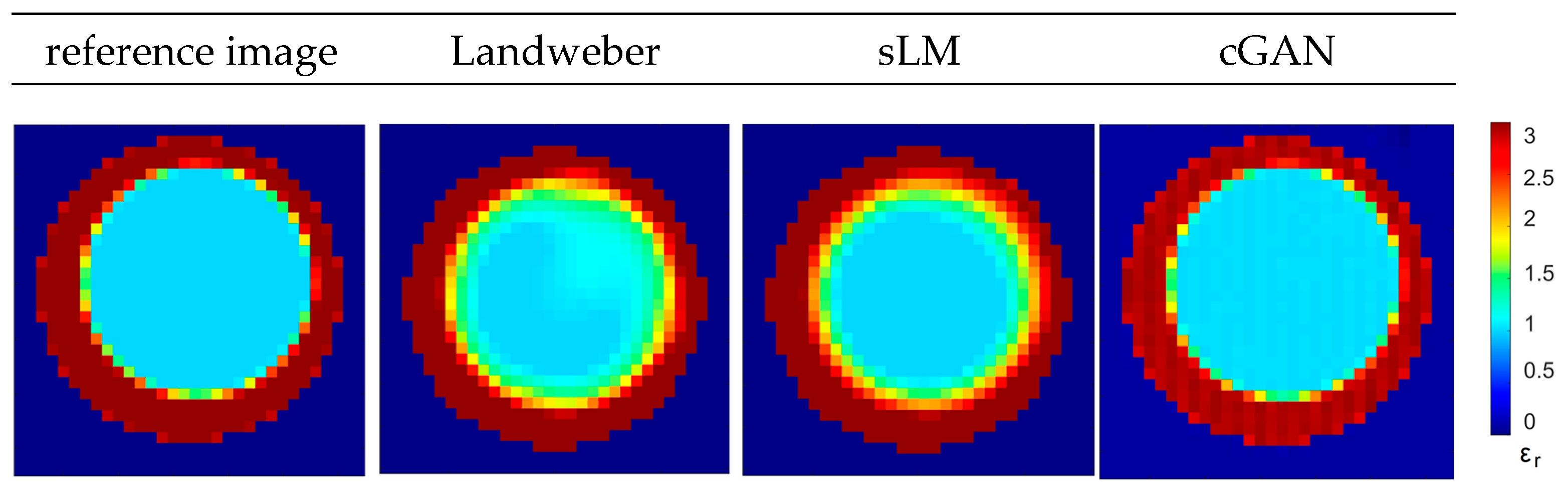
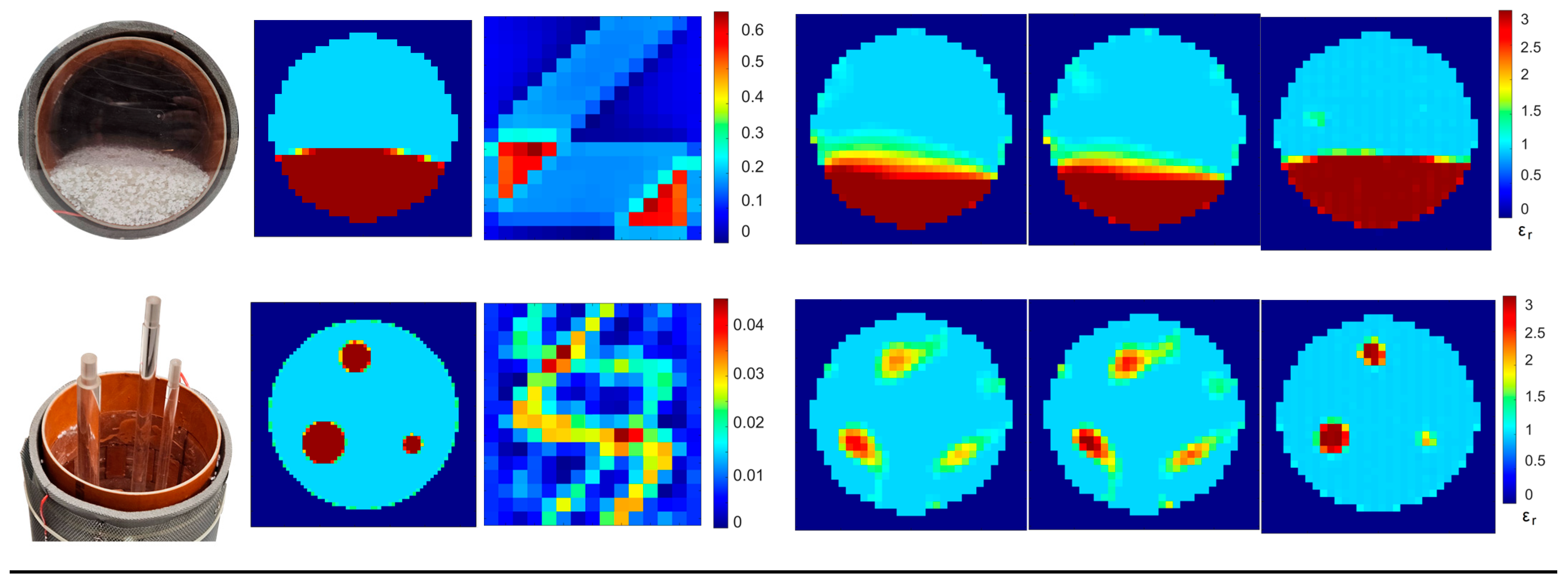
3.2. Reconstruction from Real Measurements
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Plaskowski, A.; Beck, M.S.; Thorn, R.; Dyakowski, T. Imaging Industrial Flows: Applications of Electrical Process Tomography; CRC Press: Boca Raton, FL, USA, 1995; ISBN 9780750302968. [Google Scholar]
- Rymarczyk, T.; Sikora, J. Applying industrial tomography to control and optimization flow systems. Open Phys. 2018, 16, 332–345. [Google Scholar] [CrossRef]
- Zheng, J.; Peng, L. An autoencoder-based image reconstruction for electrical capacitance tomography. IEEE Sens. J. 2018, 18, 5464–5474. [Google Scholar] [CrossRef]
- Rouhani, S.Z.; Sohal, M.S. Two-phase flow patterns: A review of research results. Prog. Nucl. Energy 1983, 11, 219–259. [Google Scholar] [CrossRef]
- Yan, Y.; Mohanarangam, K.; Yang, W.; Tu, J. Experimental measuring techniques for industrial-scale multiphase flow problems. Exp. Comput. Multiph. Flow 2024, 6, 1–13. [Google Scholar] [CrossRef]
- Darnajou, M. A Novel Approach to High-Speed Electrical Impedance Tomography with Frequency Division Multiplexing: Mathieu Darnajou to Cite this Version: HAL Id: Tel-03934574. Ph.D. Dissertation, Ecole Centrale Marseille, Marseille, France, 2023. [Google Scholar]
- Hampel, U.; Babout, L.; Banasiak, R.; Schleicher, E.; Soleimani, M.; Wondrak, T.; Vauhkonen, M.; Lähivaara, T.; Tan, C.; Hoyle, B.; et al. A Review on Fast Tomographic Imaging Techniques and Their Potential Application in Industrial Process Control. Sensors 2022, 22, 2309. [Google Scholar] [CrossRef]
- Bergou, E.H.; Diouane, Y.; Kungurtsev, V. Convergence and Complexity Analysis of a Levenberg–Marquardt Algorithm for Inverse Problems. J. Optim. Theory Appl. 2020, 185, 927–944. [Google Scholar] [CrossRef]
- Husain, Z.; Liatsis, P. A neural network-based local decomposition approach for image reconstruction in Electrical Impedance Tomography. In Proceedings of the IST 2019—IEEE International Conference on Imaging Systems and Techniques, Abu Dhabi, United Arab Emirates, 9–10 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Pinheiro, P.A.T.; Loh, W.W.; Dickin, F.J. Three-dimensional reconstruction algorithm for electrical resistance tomography. IEE Proc. Sci. Meas. Technol. 1998, 145, 85–93. [Google Scholar] [CrossRef]
- Wang, F.; Marashdeh, Q.; Fan, L.S.; Warsito, W. Electrical capacitance volume tomography: Design and applications. Sensors 2010, 10, 1890–1917. [Google Scholar] [CrossRef]
- Nombo, J.; Mwambela, A.; Kisngiri, M. Analysis and Performance Evaluation of Entropic Thresholding Image Processing Techniques for Electrical Capacitance Tomography Measurement System. Tanzan. J. Sci. 2021, 47, 928–942. [Google Scholar] [CrossRef]
- Li, F.; Tan, C.; Dong, F.; Jia, J. V-Net Deep Imaging Method for Electrical Resistance Tomography. IEEE Sens. J. 2020, 20, 6460–6469. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, B.; Liu, K.; Zhu, C.; Pan, H.; Jia, J.; Wu, H.; Yao, J. Shape Reconstruction with Multiphase Conductivity for Electrical Impedance Tomography Using Improved Convolutional Neural Network Method. IEEE Sens. J. 2021, 21, 9277–9287. [Google Scholar] [CrossRef]
- Hamilton, S.J.; Hauptmann, A. Deep D-Bar: Real-Time Electrical Impedance Tomography Imaging with Deep Neural Networks. IEEE Trans. Med. Imaging 2018, 37, 2367–2377. [Google Scholar] [CrossRef] [PubMed]
- Schlemper, J.; Caballero, J.; Hajnal, J.V.; Price, A.N.; Rueckert, D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans. Med. Imaging 2018, 37, 491–503. [Google Scholar] [CrossRef] [PubMed]
- Pelt, D.M.; Batenburg, K.J.; Sethian, J.A. Improving tomographic reconstruction from limited data using mixed-scale dense convolutional neural networks. J. Imaging 2018, 4, 128. [Google Scholar] [CrossRef]
- Hsieh, J.; Liu, E.; Nett, B.; Tang, J.; Thibault, J.-B.; Sahney, S. A New Era of Image Reconstruction: TrueFidelityTM Technical White Paper on Deep Learning Image Reconstruction; General Electric Company: Boston, MA, USA, 2019. [Google Scholar]
- Deabes, W.; Abdel-Hakim, A.E.; Bouazza, K.E.; Althobaiti, H. Adversarial Resolution Enhancement for Electrical Capacitance Tomography Image Reconstruction. Sensors 2022, 22, 3142. [Google Scholar] [CrossRef]
- Zhu, Q.X.; Xu, T.X.; Xu, Y.; He, Y.L. Improved Virtual Sample Generation Method Using Enhanced Conditional Generative Adversarial Networks with Cycle Structures for Soft Sensors with Limited Data. Ind. Eng. Chem. Res. 2022, 61, 530–540. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, M.; Wang, J.; Liu, R.; Shao, Y.; Liu, B.; Tang, Y.; Liu, M.; Yang, W. Imaging irregular structures using electrical capacitance tomography. Meas. Sci. Technol. 2021, 32, 075006. [Google Scholar] [CrossRef]
- Kryszyn, J.; Smolik, W. Toolbox for 3D Modelling and Image Reconstruction in Electrical Capacitance Tomography. Inform. Control Meas. Econ. Environ. Prot. 2017, 7, 137–145. [Google Scholar] [CrossRef]
- Wanta, D.; Smolik, W.T.; Kryszyn, J.; Wróblewski, P.; Midura, M. A Finite Volume Method using a Quadtree Non-Uniform Structured Mesh for Modeling in Electrical Capacitance Tomography. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2021, 92, 443–452. [Google Scholar] [CrossRef]
- Wanta, D.; Smolik, W.T.; Kryszyn, J. ECTsim. Zenodo 2024. [Google Scholar] [CrossRef]
- Kryszyn, J.; Wróblewski, P.; Stosio, M.; Wanta, D.; Olszewski, T.; Smolik, W.T. Architecture of EVT4 data acquisition system for electrical capacitance tomography. Meas. J. Int. Meas. Confed. 2017, 101, 28–39. [Google Scholar] [CrossRef]
- Smolik, W.T.; Kryszyn, J.; Radzik, B.; Stosio, M.; Wróblewski, P.; Wanta, D.; Dańko, L.; Olszewski, T.; Szabatin, R. Single-shot high-voltage circuit for electrical capacitance tomography. Meas. Sci. Technol. 2017, 28, 025902. [Google Scholar] [CrossRef]
- Kryszyn, J.; Wanta, D.M.; Smolik, W.T. Gain Adjustment for Signal-to-Noise Ratio Improvement in Electrical Capacitance Tomography System EVT4. IEEE Sens. J. 2017, 17, 8107–8116. [Google Scholar] [CrossRef]
- Ivanenko, M.; Wanta, D.; Smolik, W.T.; Wróblewski, P.; Midura, M. Generative-Adversarial-Network-Based Image Reconstruction for the Capacitively Coupled Electrical Impedance Tomography of Stroke. Life 2024, 14, 419. [Google Scholar] [CrossRef] [PubMed]
- Ivanenko, M.; Smolik, W.T.; Wanta, D.; Midura, M.; Wróblewski, P.; Hou, X.; Yan, X. Image Reconstruction Using Supervised Learning in Wearable Electrical Impedance Tomography of the Thorax. Sensors 2023, 23, 7774. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: Proceedings of the 18th International Conference, Munich, Germany, 5–9 October 2015; Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics); Springer International Publishing: New York, NY, USA, 2015; Volume 9351, pp. 12–20. [Google Scholar] [CrossRef]
- Cohen, G.; Giryes, R. Generative Adversarial Networks. In Machine Learning for Data Science Handbook, Data Mining and Knowledge Discovery Handbook, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2023; pp. 375–400. [Google Scholar] [CrossRef]
- Deabes, W.; Abdel-Hakim, A.E. CGAN-ECT: Tomography Image Reconstruction from Electrical Capacitance Measurements Using CGANs. arXiv 2022, arXiv:2209.03737. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 5967–5976. [Google Scholar] [CrossRef]
- Yang, W.Q.; Peng, L. Image reconstruction algorithms for electrical capacitance tomography. Meas. Sci. Technol. 2003, 14, R1–R13. [Google Scholar] [CrossRef]
- Xia, Z.; Cui, Z.; Chen, Y.; Hu, Y.; Wang, H. Generative adversarial networks for dual-modality electrical tomography in multi-phase flow measurement. Meas. J. Int. Meas. Confed. 2021, 173, 108608. [Google Scholar] [CrossRef]


| Flow Patterns | Random Circles | ||||||
|---|---|---|---|---|---|---|---|
| Lanweber | sLM | cGAN | Lanweber | sLM | cGAN | ||
| MSE | µ | 0.762 | 0.859 | 0.034 | 0.372 | 0.381 | 0.018 |
| mdn | 0.409 | 0.516 | 0.010 | 0.361 | 0.358 | 0.012 | |
| σ | 0.605 | 0.713 | 0.048 | 0.083 | 0.115 | 0.018 | |
| SSIM | µ | 0.342 | 0.321 | 0.867 | 0.318 | 0.315 | 0.945 |
| mdn | 0.320 | 0.298 | 0.879 | 0.315 | 0.312 | 0.951 | |
| σ | 0.087 | 0.099 | 0.075 | 0.055 | 0.056 | 0.027 | |
| correlation | µ | 0.845 | 0.829 | 0.965 | 0.780 | 0.779 | 0.985 |
| mdn | 0.862 | 0.858 | 0.994 | 0.788 | 0.787 | 0.990 | |
| σ | 0.063 | 0.077 | 0.064 | 0.056 | 0.057 | 0.017 | |
| PSNR | µ | 2.524 | 2.166 | 20.36 | 4.388 | 4.345 | 19.21 |
| mdn | 3.886 | 2.869 | 20.16 | 4.430 | 4.463 | 19.08 | |
| σ | 3.381 | 3.628 | 7.812 | 0.906 | 1.101 | 4.008 | |
| time [ms] | µ | 3.1 | 5.3 | 2.7 | 3.1 | 5.8 | 2.7 |
| mdn | 3.0 | 5.8 | 2.7 | 3.0 | 6.0 | 2.7 | |
| σ | 0.4 | 1.3 | 0.1 | 0.6 | 1.4 | 0.2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wanta, D.; Ivanenko, M.; Smolik, W.T.; Wróblewski, P.; Midura, M. Real-Time Nonlinear Image Reconstruction in Electrical Capacitance Tomography Using the Generative Adversarial Network. Information 2024, 15, 617. https://doi.org/10.3390/info15100617
Wanta D, Ivanenko M, Smolik WT, Wróblewski P, Midura M. Real-Time Nonlinear Image Reconstruction in Electrical Capacitance Tomography Using the Generative Adversarial Network. Information. 2024; 15(10):617. https://doi.org/10.3390/info15100617
Chicago/Turabian StyleWanta, Damian, Mikhail Ivanenko, Waldemar T. Smolik, Przemysław Wróblewski, and Mateusz Midura. 2024. "Real-Time Nonlinear Image Reconstruction in Electrical Capacitance Tomography Using the Generative Adversarial Network" Information 15, no. 10: 617. https://doi.org/10.3390/info15100617
APA StyleWanta, D., Ivanenko, M., Smolik, W. T., Wróblewski, P., & Midura, M. (2024). Real-Time Nonlinear Image Reconstruction in Electrical Capacitance Tomography Using the Generative Adversarial Network. Information, 15(10), 617. https://doi.org/10.3390/info15100617









