Time-Series Neural Network: A High-Accuracy Time-Series Forecasting Method Based on Kernel Filter and Time Attention
Abstract
:1. Introduction
2. Related Work
2.1. Traditional Machine Learning Methods
2.2. Deep Learning Methods
3. Materials and Methods
3.1. Dataset Collection
3.2. Dataset Preprocessing
3.2.1. Outlier Identification and Treatment
3.2.2. Missing Value Treatment
3.2.3. Normalization
3.3. Proposed Methods
3.3.1. Overall
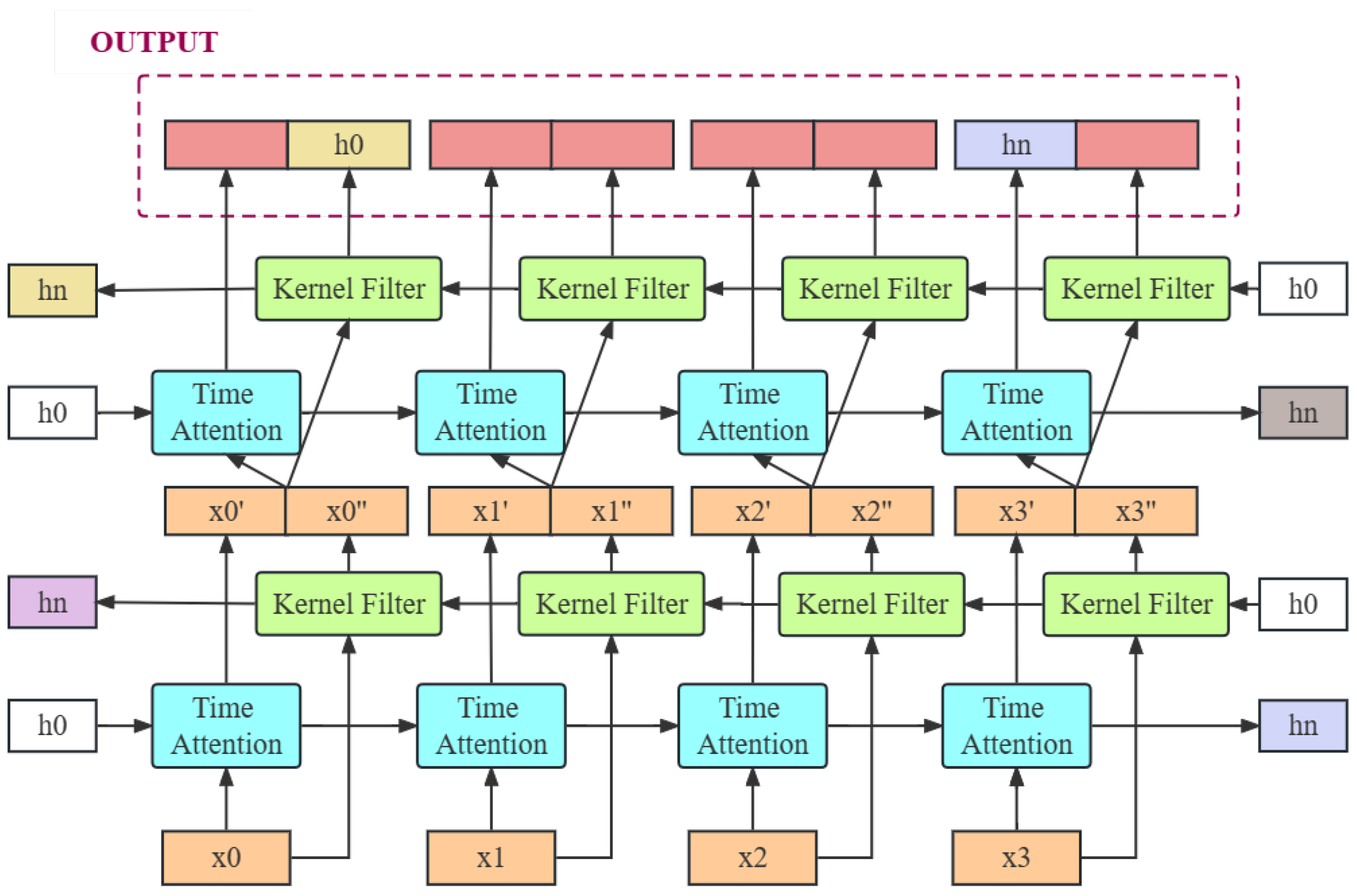
3.3.2. Time-Series Neural Network
3.3.3. Kernel Filter
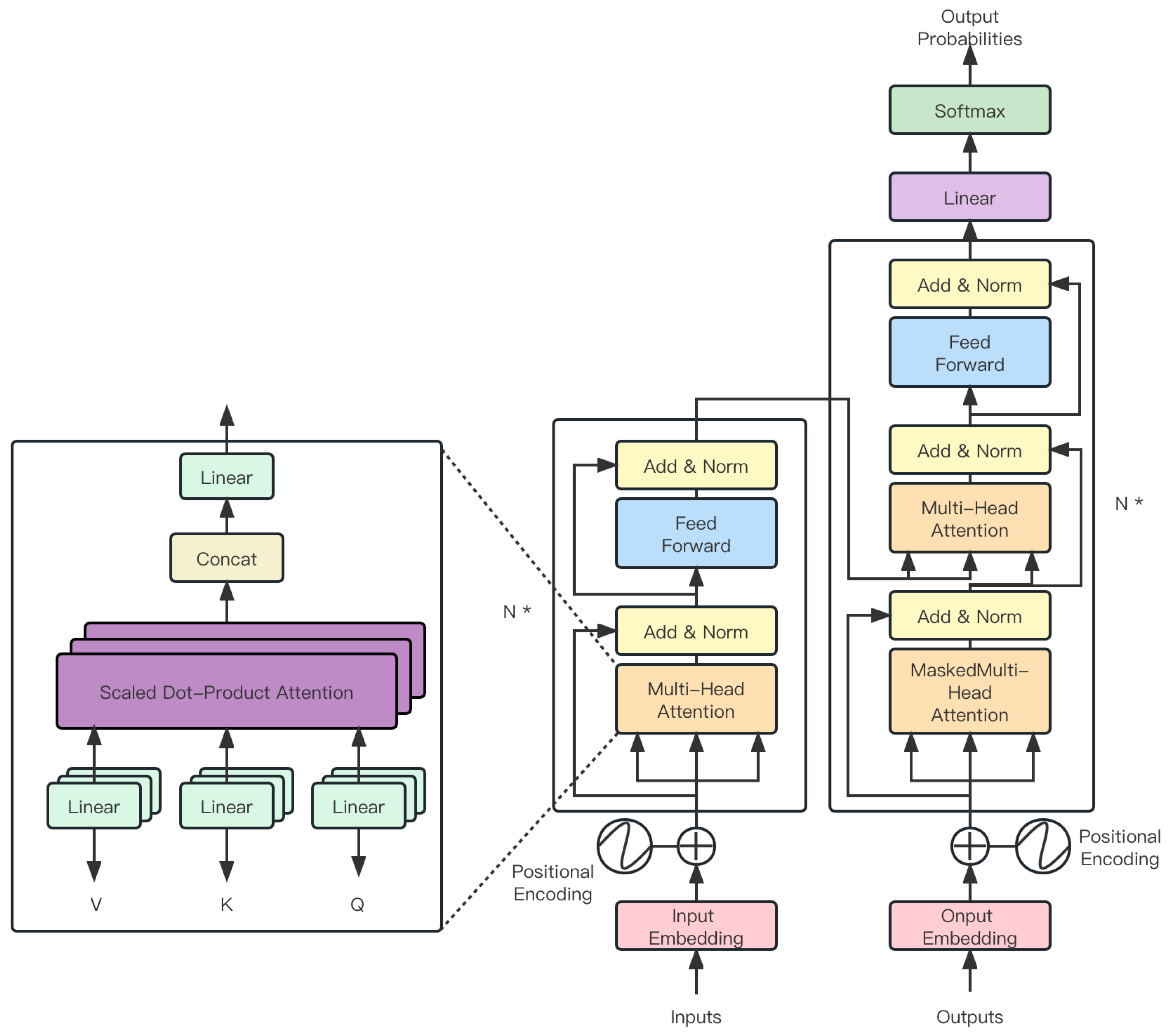
3.3.4. Time Attention
3.4. Experimental Settings
3.4.1. Experiment Designs
3.4.2. Evaluation Metric
4. Results and Discussion
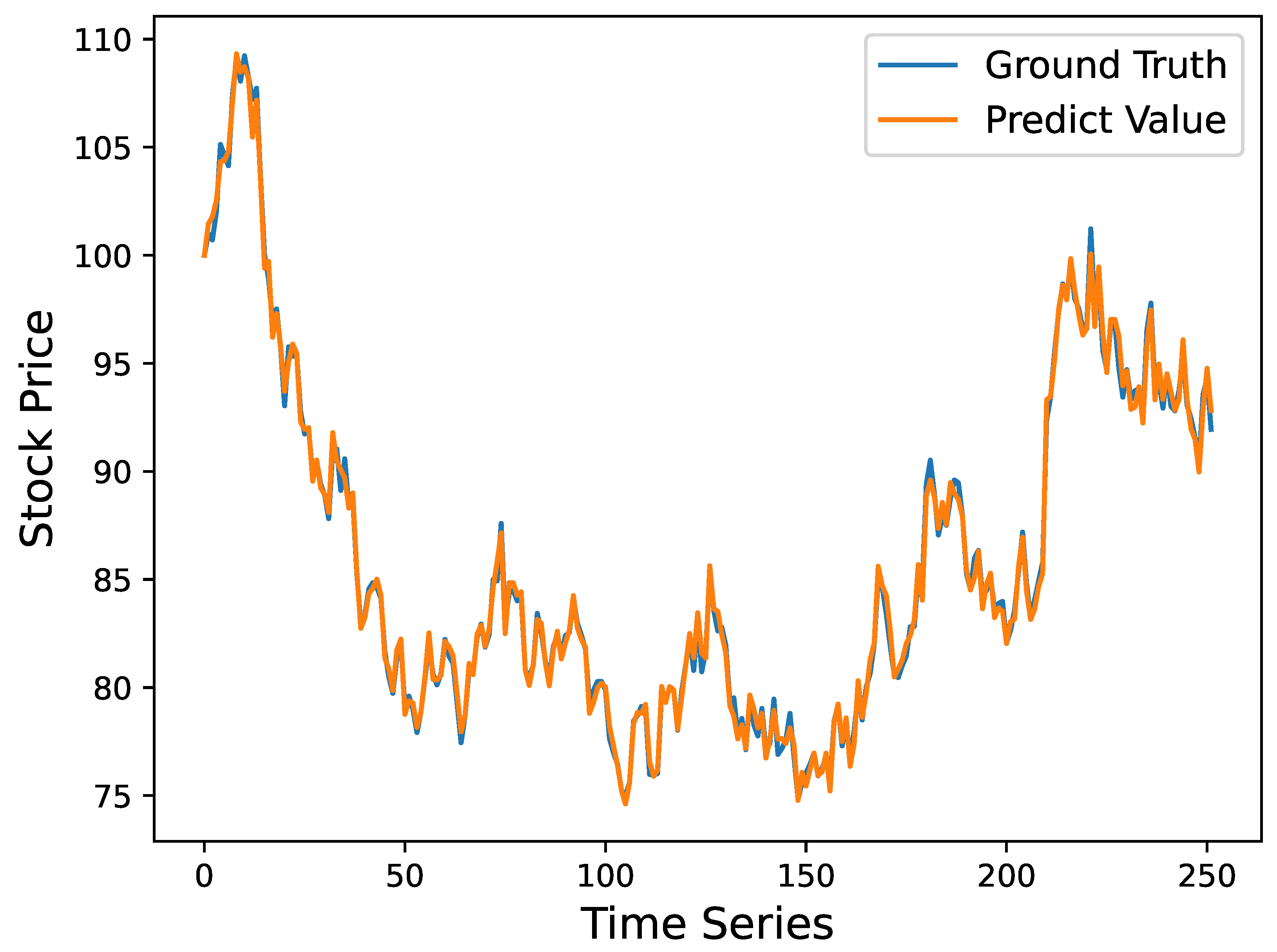
4.1. Results of Time Series Forecasting
4.2. Test on Different Attention Mechanisms
4.3. Test on Kernel Filter
4.4. Limitations and Future Work
- Noise Handling: To mitigate the issue of noise, future research will incorporate various noise filtering and denoising techniques like Kalman filters and median filters.
- Time Slice Flexibility: Future versions of the model will aim to allow dynamic adjustments of time slice spans to meet different application requirements, thereby increasing the model’s adaptability.
- Feature Correlations: Efforts will be undertaken to better uncover and incorporate the intercorrelations among features, with the goal of improving prediction accuracy.
- Evaluation Criteria: Additional metrics such as stability, robustness, and computational efficiency will be introduced to provide a more rounded evaluation of the model’s performance.
- Extended Capabilities: The TNN model will be further developed to capture not just time dependencies but also more complex relationships dependent on the history of changes in incoming parameters, making it more versatile for different types of time-series prediction tasks.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Y.; Wang, H.; Xu, R.; Yang, X.; Wang, Y.; Liu, Y. High-Precision Seedling Detection Model Based on Multi-Activation Layer and Depth-Separable Convolution Using Images Acquired by Drones. Drones 2022, 6, 152. [Google Scholar] [CrossRef]
- Lin, X.; Wa, S.; Zhang, Y.; Ma, Q. A dilated segmentation network with the morphological correction method in farming area image Series. Remote Sens. 2022, 14, 1771. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Wa, S.; Liu, Y.; Kang, J.; Lv, C. GenU-Net++: An Automatic Intracranial Brain Tumors Segmentation Algorithm on 3D Image Series with High Performance. Symmetry 2021, 13, 2395. [Google Scholar] [CrossRef]
- Zhang, Y.; He, S.; Wa, S.; Zong, Z.; Lin, J.; Fan, D.; Fu, J.; Lv, C. Symmetry GAN Detection Network: An Automatic One-Stage High-Accuracy Detection Network for Various Types of Lesions on CT Images. Symmetry 2022, 14, 234. [Google Scholar] [CrossRef]
- Maarif, M.R.; Saleh, A.R.; Habibi, M.; Fitriyani, N.L.; Syafrudin, M. Energy Usage Forecasting Model Based on Long Short-Term Memory (LSTM) and eXplainable Artificial Intelligence (XAI). Information 2023, 14, 265. [Google Scholar] [CrossRef]
- Huo, H.; Guo, J.; Yang, X.; Lu, X.; Wu, X.; Li, Z.; Li, M.; Ren, J. An Accelerated Method for Protecting Data Privacy in Financial Scenarios Based on Linear Operation. Appl. Sci. 2023, 13, 1764. [Google Scholar] [CrossRef]
- Manfre Jaimes, D.; Manuel Zamudio López, M.; Zareipour, H.; Quashie, M. A Hybrid Model for Multi-Day-Ahead Electricity Price Forecasting considering Price Spikes. Forecasting 2023, 5, 499–521. [Google Scholar] [CrossRef]
- Ampountolas, A. Comparative Analysis of Machine Learning, Hybrid, and Deep Learning Forecasting Models: Evidence from European Financial Markets and Bitcoins. Forecasting 2023, 5, 472–486. [Google Scholar] [CrossRef]
- Sedai, A.; Dhakal, R.; Gautam, S.; Dhamala, A.; Bilbao, A.; Wang, Q.; Wigington, A.; Pol, S. Performance Analysis of Statistical, Machine Learning and Deep Learning Models in Long-Term Forecasting of Solar Power Production. Forecasting 2023, 5, 256–284. [Google Scholar] [CrossRef]
- Wood, M.; Ogliari, E.; Nespoli, A.; Simpkins, T.; Leva, S. Day Ahead Electric Load Forecast: A Comprehensive LSTM-EMD Methodology and Several Diverse Case Studies. Forecasting 2023, 5, 297–314. [Google Scholar] [CrossRef]
- Mishra, A.; Dasgupta, A. Supervised and Unsupervised Machine Learning Algorithms for Forecasting the Fracture Location in Dissimilar Friction-Stir-Welded Joints. Forecasting 2022, 4, 787–797. [Google Scholar] [CrossRef]
- Papadimitriou, T.; Gogas, P.; Athanasiou, A.F. Forecasting Bitcoin Spikes: A GARCH-SVM Approach. Forecasting 2022, 4, 752–766. [Google Scholar] [CrossRef]
- Fianu, E.S. Analyzing and Forecasting Multi-Commodity Prices Using Variants of Mode Decomposition-Based Extreme Learning Machine Hybridization Approach. Forecasting 2022, 4, 538–564. [Google Scholar] [CrossRef]
- Carrillo, J.A.; Nieto, M.; Velez, J.F.; Velez, D. A New Machine Learning Forecasting Algorithm Based on Bivariate Copula Functions. Forecasting 2021, 3, 355–376. [Google Scholar] [CrossRef]
- Yasrab, R.; Jiang, W.; Riaz, A. Fighting Deepfakes Using Body Language Analysis. Forecasting 2021, 3, 303–321. [Google Scholar] [CrossRef]
- May, M.C.; Albers, A.; Fischer, M.D.; Mayerhofer; Florian an Schäfer, L.; Lanza, G. Queue Length Forecasting in Complex Manufacturing Job Shops. Forecasting 2021, 3, 322–338. [Google Scholar] [CrossRef]
- Rezazadeh, A. A Generalized Flow for B2B Sales Predictive Modeling: An Azure Machine-Learning Approach. Forecasting 2020, 2, 267–283. [Google Scholar] [CrossRef]
- Claveria, O. Forecasting with Business and Consumer Survey Data. Forecasting 2021, 3, 113–134. [Google Scholar] [CrossRef]
- Shah, V.H. Machine learning techniques for stock prediction. Found. Mach. Learn. Spring 2007, 1, 6–12. [Google Scholar]
- Janiesch, C.; Zschech, P.; Heinrich, K. Machine learning and deep learning. Electron. Mark. 2021, 31, 685–695. [Google Scholar] [CrossRef]
- Murphy, K.P. Probabilistic Machine Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Maulud, D.; Abdulazeez, A.M. A review on linear regression comprehensive in machine learning. J. Appl. Sci. Technol. Trends 2020, 1, 140–147. [Google Scholar] [CrossRef]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Wan, A.; Dunlap, L.; Ho, D.; Yin, J.; Lee, S.; Jin, H.; Petryk, S.; Bargal, S.A.; Gonzalez, J.E. NBDT: Neural-backed decision trees. arXiv 2020, arXiv:2004.00221. [Google Scholar]
- Kurani, A.; Doshi, P.; Vakharia, A.; Shah, M. A comprehensive comparative study of artificial neural network (ANN) and support vector machines (SVM) on stock forecasting. Ann. Data Sci. 2023, 10, 183–208. [Google Scholar] [CrossRef]
- Ma, Y.; Han, R.; Fu, X. Stock prediction based on random forest and LSTM neural network. In Proceedings of the 2019 19th International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 15–18 October 2019; pp. 126–130. [Google Scholar]
- Zaremba, W.; Sutskever, I.; Vinyals, O. Recurrent neural network regularization. arXiv 2014, arXiv:1409.2329. [Google Scholar]
- Graves, A.; Graves, A. Long short-term memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]
- Zhao, J.; Zeng, D.; Liang, S.; Kang, H.; Liu, Q. Prediction model for stock price trend based on recurrent neural network. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 745–753. [Google Scholar] [CrossRef]
- Zhu, Y. Stock price prediction using the RNN model. J. Phys. Conf. Ser. 2020, 1650, 032103. [Google Scholar] [CrossRef]
- Swathi, T.; Kasiviswanath, N.; Rao, A.A. An optimal deep learning-based LSTM for stock price prediction using twitter sentiment analysis. Appl. Intell. 2022, 52, 13675–13688. [Google Scholar] [CrossRef]
- Ma, Q. Comparison of ARIMA, ANN and LSTM for stock price prediction. In Proceedings of the E3S Web of Conferences, Chongqing, China, 20–22 November 2020; Volume 218, p. 01026. [Google Scholar]
- Li, Y.; Zou, C.; Berecibar, M.; Nanini-Maury, E.; Chan, J.C.W.; Van den Bossche, P.; Van Mierlo, J.; Omar, N. Random forest regression for online capacity estimation of lithium-ion batteries. Appl. Energy 2018, 232, 197–210. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.; Kweon, I.S. CBAM: Convolutional Block Attention Module. CoRR 2018. Available online: http://xxx.lanl.gov/abs/1807.06521 (accessed on 6 September 2023).
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. Mar. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. Available online: https://proceedings.neurips.cc/paper_files/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf (accessed on 6 September 2023).

| Model | Time Span | RMSE | MAE | MAPE | |
|---|---|---|---|---|---|
| TNN | 1 day | 0.05 | 0.23 | 0.95 | 1.3% |
| Linear Regression | 1 day | 0.34 | 0.57 | 0.63 | 7.5% |
| Decision Tree | 1 day | 0.36 | 0.60 | 0.61 | 7.8% |
| Random Forest | 1 day | 0.21 | 0.47 | 0.69 | 5.1% |
| SVM | 1 day | 0.23 | 0.48 | 0.67 | 4.1% |
| RNN | 1 day | 0.13 | 0.37 | 0.87 | 2.8% |
| LSTM | 1 day | 0.09 | 0.3 | 0.91 | 1.9% |
| TNN | 7 day | 0.16 | 0.4 | 0.89 | 1.8% |
| Linear Regression | 7 day | 0.67 | 0.81 | 0.35 | 9.6% |
| Decision Tree | 7 day | 0.65 | 0.81 | 0.39 | 8.9% |
| Random Forest | 7 day | 0.56 | 0.75 | 0.43 | 6.3% |
| SVM | 7 day | 0.49 | 0.70 | 0.47 | 5.8% |
| RNN | 7 day | 0.25 | 0.50 | 0.61 | 3.3% |
| LSTM | 7 day | 0.23 | 0.48 | 0.66 | 3.1% |
| TNN | 30 day | 0.14 | 0.37 | 0.91 | 3.7% |
| Linear Regression | 30 day | 0.85 | 0.92 | 0.16 | 11.2% |
| Decision Tree | 30 day | 0.82 | 0.90 | 0.20 | 13.9% |
| Random Forest | 30 day | 0.77 | 0.88 | 0.29 | 10.4% |
| SVM | 30 day | 0.76 | 0.88 | 0.29 | 6.8% |
| RNN | 30 day | 0.27 | 0.52 | 0.63 | 4.9% |
| LSTM | 30 day | 0.28 | 0.53 | 0.58 | 3.7% |
| Attention Model | RMSE | MAE | |
|---|---|---|---|
| SENet [34] | 0.08 | 0.27 | 0.87 |
| CBAM [35] | 0.09 | 0.3 | 0.92 |
| Time Attention | 0.05 | 0.23 | 0.95 |
| Model | RMSE | MAE | |
|---|---|---|---|
| TNN (No Filter) | 0.26 | 0.51 | 0.82 |
| TNN (Kalman Filter) | 0.12 | 0.34 | 0.91 |
| TNN (Kernel Filter) | 0.05 | 0.23 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Wang, R.; Li, Z.; Li, J.; Ge, Y.; Wa, S.; Huang, S.; Lv, C. Time-Series Neural Network: A High-Accuracy Time-Series Forecasting Method Based on Kernel Filter and Time Attention. Information 2023, 14, 500. https://doi.org/10.3390/info14090500
Zhang L, Wang R, Li Z, Li J, Ge Y, Wa S, Huang S, Lv C. Time-Series Neural Network: A High-Accuracy Time-Series Forecasting Method Based on Kernel Filter and Time Attention. Information. 2023; 14(9):500. https://doi.org/10.3390/info14090500
Chicago/Turabian StyleZhang, Lexin, Ruihan Wang, Zhuoyuan Li, Jiaxun Li, Yichen Ge, Shiyun Wa, Sirui Huang, and Chunli Lv. 2023. "Time-Series Neural Network: A High-Accuracy Time-Series Forecasting Method Based on Kernel Filter and Time Attention" Information 14, no. 9: 500. https://doi.org/10.3390/info14090500
APA StyleZhang, L., Wang, R., Li, Z., Li, J., Ge, Y., Wa, S., Huang, S., & Lv, C. (2023). Time-Series Neural Network: A High-Accuracy Time-Series Forecasting Method Based on Kernel Filter and Time Attention. Information, 14(9), 500. https://doi.org/10.3390/info14090500







