Exploring Evaluation Methods for Interpretable Machine Learning: A Survey
Abstract
:1. Introduction
- Fidelity: Does the resulting explanation accurately reflect the computation performed by the original model during the decision-making process? To prevent providing a falsely convincing explanation, the reported explanation must be faithful to what is computed. Generally, unfaithfulness is brought up in post hoc explanations. In this survey, we group all methods that examine this factor under the heading “evaluating correctness”. Additionally, instability is an undesirable phenomenon that undermines our trust in the model’s decision; thus, a further subsection is introduced to examine the robustness of the interpretation.
- Comprehensibility: Are the generated explanations “human-understandable”? This can be determined by designing an experiment in which human assessors judge the understandability or by relying on the findings of prior research that have demonstrated the understandability of a particular model, such as a rule or tree. This factor is discussed in two subsections of this survey: human evaluators and comprehensibility.
2. Background
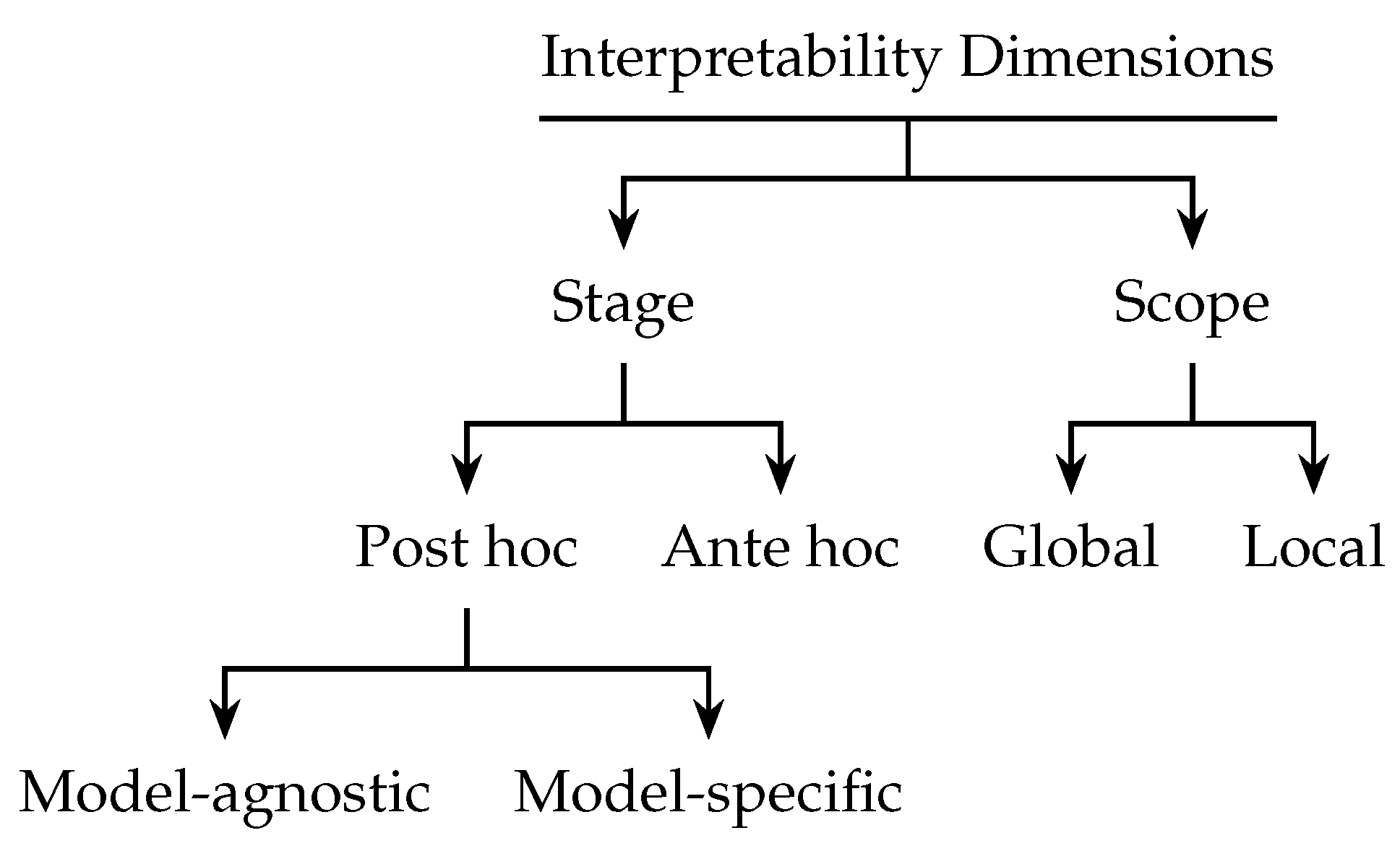
2.1. Interpretability as Stages: Post Hoc vs. Ante Hoc
Post Hoc Interpretability
2.2. Interpretability by Scope
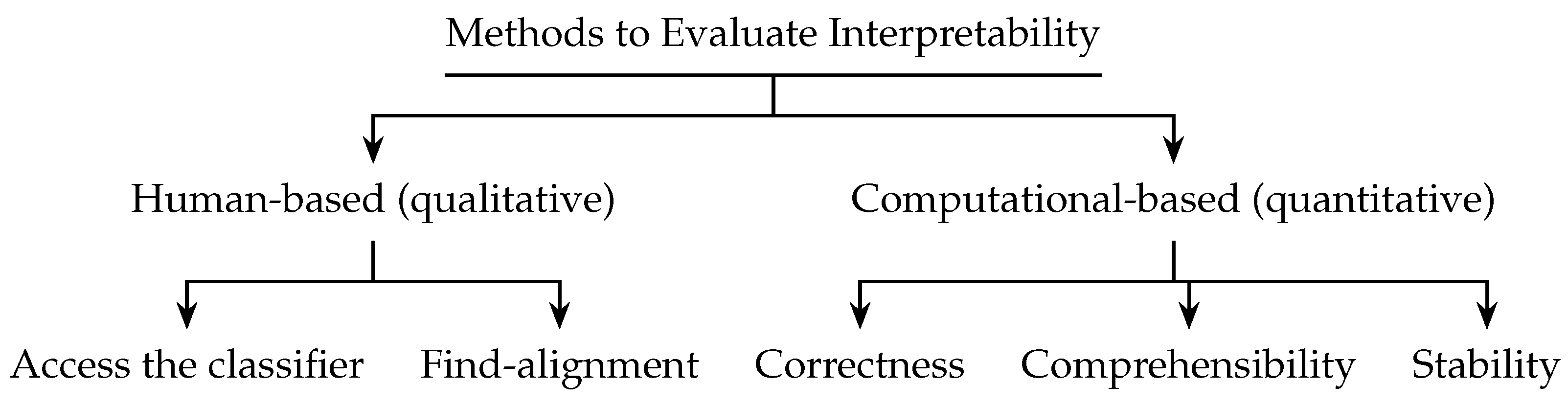
3. Qualitative Evaluation: Human-Based
3.1. Access the Classifier
3.2. Find Alignment
3.3. Discussion
4. Computational Metric: Correctness with Respect to the Original Model/Faithfulness/Fidelity
4.1. Interpretation as Model
4.2. Interpretation as Feature-Attribution (Saliency/Heat-Maps)
4.2.1. Removal-Based Evaluation
- Select features to remove, either randomly or based on their importance.
- Fill in the blanks of features, and this is where the methods vary (either filling the blank with the background, or replacing it with the mean, or ignoring it, etc.)
- Calculating the difference between the presence and absence of a feature to determine its predictive impact (reporting the decline in accuracy relative to the trained model).
4.2.2. Entropy-Based Evaluation
4.2.3. Compare Interpretation with a Ground-Truth
| Ref. | Metric | Data |
|---|---|---|
| [72] | Outside–inside relevance ratio | PASCAL VOC2007 [84] |
| [61] | Outside–inside relevance ratio | A subset from imageNet dataset with segmentation masks, and some images from the Pascal VOC |
| [55,73] | Normalized cross correlation | Computed to compare with disease effect maps in ADNI dataset [85] |
| [80] | Phrase/word correlation Segment AUC | Sentiment analysis: SST dataset [86] Image classification: MS COCO dataset [87] |
| [74] | Explanation accuracy | Synthetic datasets |
| [35] | Comprehensiveness and sufficiency | ERASER: A Benchmark to Evaluate Rationalized NLP Models [35] |
| [82] | Reasoning Graph Accuracy Reasoning Graph Similarity | STREET: Structured Reasoning and Explanation Multi-Task benchmark [82] |
4.3. Discussion
5. Computational Metrics: Comprehensibility
5.1. Rules/Decision Trees
- The number of rules should be as small as possible, since according to Occam’s razor principle, “the best model is the simplest one fitting the system behavior well”. Additionally, rule weights or degrees of plausibility should be avoided.
- For the number of conditions, the rule antecedent should contain only a few conditions limited by distinct conditions.
- For the consistency of the rule set, there are no contradictory rules in the rule set.
- The rule’s redundancy: reducing the number of redundant rules in the rule set improves the rule set’s interpretability.
5.2. Feature Attribution
5.3. Discussion
6. Computational Metric: Stability/Robustness
Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tulio Ribeiro, M.; Singh, S.; Guestrin, C. “Why should i trust you?”: Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Jiao, J. The Pandora’s Box of the Criminal Justice System. 2017. Available online: https://dukeundergraduatelawmagazine.org/2017/09/25/the-pandoras-box-of-the-criminal-justice-system/ (accessed on 18 August 2023).
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Michie, D. Machine learning in the next five years. In Proceedings of the 3rd European Conference on European Working Session on Learning, Glasgow, UK, 3–5 October 1988; Pitman Publishing, Inc.: Lanham, MD, USA, 1988; pp. 107–122. [Google Scholar]
- Biran, O.; Cotton, C. Explanation and justification in machine learning: A survey. In Proceedings of the IJCAI-17 Workshop on Explainable AI (XAI), Melbourne, Australia, 20 August 2017; Volume 8, pp. 8–13. [Google Scholar]
- Miller, T. Explanation in artificial intelligence: Insights from the social sciences. Artif. Intell. 2019, 267, 1–38. [Google Scholar] [CrossRef]
- Doshi-Velez, F.; Kim, B. A Roadmap for a Rigorous Science of Interpretability. Stat 2017, 1050, 28. [Google Scholar]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A survey of methods for explaining black box models. ACM Comput. Surv. (CSUR) 2019, 51, 93. [Google Scholar] [CrossRef]
- Murdoch, W.J.; Singh, C.; Kumbier, K.; Abbasi-Asl, R.; Yu, B. Definitions, methods, and applications in interpretable machine learning. Proc. Natl. Acad. Sci. USA 2019, 116, 22071–22080. [Google Scholar] [CrossRef] [PubMed]
- Molnar, C. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable. 2018. Available online: https://christophm.github.io/interpretable-ml-book/ (accessed on 12 December 2022).
- Gilpin, L.H.; Bau, D.; Yuan, B.Z.; Bajwa, A.; Specter, M.; Kagal, L. Explaining explanations: An overview of interpretability of machine learning. In Proceedings of the 2018 IEEE 5th International Conference on data science and advanced analytics (DSAA), Turin, Italy, 1–3 October 2018; pp. 80–89. [Google Scholar]
- Pearl, J. The seven tools of causal inference, with reflections on machine learning. Commun. ACM 2019, 62, 54–60. [Google Scholar] [CrossRef]
- Bareinboim, E.; Correa, J.; Ibeling, D.; Icard, T. On Pearl’s Hierarchy and the Foundations of Causal Inference; ACM Special Volume in Honor of Judea Pearl (Provisional Title); Association for Computing Machinery: New York, NY, USA, 2020. [Google Scholar]
- Adadi, A.; Berrada, M. Peeking inside the black-box: A survey on explainable artificial intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Gacto, M.J.; Alcalá, R.; Herrera, F. Interpretability of linguistic fuzzy rule-based systems: An overview of interpretability measures. Inf. Sci. 2011, 181, 4340–4360. [Google Scholar] [CrossRef]
- He, C.; Ma, M.; Wang, P. Extract interpretability-accuracy balanced rules from artificial neural networks: A review. Neurocomputing 2020, 387, 346–358. [Google Scholar] [CrossRef]
- Chakraborty, S.; Tomsett, R.; Raghavendra, R.; Harborne, D.; Alzantot, M.; Cerutti, F.; Srivastava, M.; Preece, A.; Julier, S.; Rao, R.M.; et al. Interpretability of deep learning models: A survey of results. In Proceedings of the 2017 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computed, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/CBDCom/IOP/SCI), San Francisco, CA, USA, 4–8 August 2017; pp. 1–6. [Google Scholar]
- Zhou, J.; Gandomi, A.H.; Chen, F.; Holzinger, A. Evaluating the quality of machine learning explanations: A survey on methods and metrics. Electronics 2021, 10, 593. [Google Scholar] [CrossRef]
- Moraffah, R.; Karami, M.; Guo, R.; Raglin, A.; Liu, H. Causal interpretability for machine learning-problems, methods and evaluation. ACM SIGKDD Explor. Newsl. 2020, 22, 18–33. [Google Scholar] [CrossRef]
- Bhatt, U.; Xiang, A.; Sharma, S.; Weller, A.; Taly, A.; Jia, Y.; Ghosh, J.; Puri, R.; Moura, J.M.; Eckersley, P. Explainable machine learning in deployment. In Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency, Barcelona, Spain, 27–30 January 2020; pp. 648–657. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4765–4774. [Google Scholar]
- Craven, M.; Shavlik, J.W. Extracting tree-structured representations of trained networks. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 2–5 December 1996; pp. 24–30. [Google Scholar]
- Craven, M.W. Extracting Comprehensible Models from Trained Neural Networks. Ph.D. Thesis, The University of Wisconsin-Madison, Madison, WI, USA, 1996. [Google Scholar]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Fong, R.C.; Vedaldi, A. Interpretable explanations of black boxes by meaningful perturbation. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3429–3437. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 818–833. [Google Scholar]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. In Proceedings of the International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Henelius, A.; Puolamäki, K.; Boström, H.; Asker, L.; Papapetrou, P. A peek into the black box: Exploring classifiers by randomization. Data Min. Knowl. Discov. 2014, 28, 1503–1529. [Google Scholar] [CrossRef]
- Hu, R.; Andreas, J.; Darrell, T.; Saenko, K. Explainable neural computation via stack neural module networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 53–69. [Google Scholar]
- Ross, A.; Chen, N.; Hang, E.Z.; Glassman, E.L.; Doshi-Velez, F. Evaluating the interpretability of generative models by interactive reconstruction. In Proceedings of the 2021 CHI Conference on Human Factors in Computing Systems, Yokohama, Japan, 8–13 May 2021; pp. 1–15. [Google Scholar]
- Lage, I.; Chen, E.; He, J.; Narayanan, M.; Kim, B.; Gershman, S.J.; Doshi-Velez, F. Human evaluation of models built for interpretability. In Proceedings of the AAAI Conference on Human Computation and Crowdsourcing, Stevenson, WA, USA, 28–30 October 2019; Volume 7, pp. 59–67. [Google Scholar]
- Lage, I.; Chen, E.; He, J.; Narayanan, M.; Kim, B.; Gershman, S.; Doshi-Velez, F. An evaluation of the human-interpretability of explanation. arXiv 2019, arXiv:1902.00006. [Google Scholar]
- Chen, J.; Song, L.; Wainwright, M.; Jordan, M. Learning to explain: An information-theoretic perspective on model interpretation. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 883–892. [Google Scholar]
- DeYoung, J.; Jain, S.; Rajani, N.F.; Lehman, E.; Xiong, C.; Socher, R.; Wallace, B.C. ERASER: A Benchmark to Evaluate Rationalized NLP Models. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 4443–4458. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Anchors: High-precision model-agnostic explanations. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Wang, T. Multi-value rule sets for interpretable classification with feature-efficient representations. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 10858–10868. [Google Scholar]
- Lage, I.; Ross, A.; Gershman, S.J.; Kim, B.; Doshi-Velez, F. Human-in-the-loop interpretability prior. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 10159–10168. [Google Scholar]
- Kim, B.; Khanna, R.; Koyejo, O.O. Examples are not enough, learn to criticize! criticism for interpretability. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 2280–2288. [Google Scholar]
- Samek, W.; Binder, A.; Montavon, G.; Lapuschkin, S.; Müller, K.R. Evaluating the visualization of what a deep neural network has learned. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2660–2673. [Google Scholar] [CrossRef]
- Cong, Z.; Chu, L.; Wang, L.; Hu, X.; Pei, J. Exact and Consistent Interpretation of Piecewise Linear Models Hidden behind APIs: A Closed Form Solution. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; pp. 613–624. [Google Scholar]
- Tsang, M.; Cheng, D.; Liu, H.; Feng, X.; Zhou, E.; Liu, Y. Feature Interaction Interpretability: A Case for Explaining Ad-Recommendation Systems via Neural Interaction Detection. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Lakkaraju, H.; Bach, S.H.; Leskovec, J. Interpretable decision sets: A joint framework for description and prediction. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1675–1684. [Google Scholar]
- Bastani, O.; Kim, C.; Bastani, H. Interpreting Blackbox Models via Model Extraction. arXiv 2017, arXiv:1705.08504. [Google Scholar]
- Huang, Q.; Yamada, M.; Tian, Y.; Singh, D.; Chang, Y. Graphlime: Local interpretable model explanations for graph neural networks. IEEE Trans. Knowl. Data Eng. 2022, 35, 6968–6972. [Google Scholar] [CrossRef]
- Kim, S.S.Y.; Meister, N.; Ramaswamy, V.V.; Fong, R.; Russakovsky, O. HIVE: Evaluating the Human Interpretability of Visual Explanations. In Proceedings of the Computer Vision—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Springer: Cham, Switzerland, 2022; pp. 280–298. [Google Scholar]
- Yang, Y.; Panagopoulou, A.; Zhou, S.; Jin, D.; Callison-Burch, C.; Yatskar, M. Language in a bottle: Language model guided concept bottlenecks for interpretable image classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 19187–19197. [Google Scholar]
- Shrikumar, A.; Greenside, P.; Kundaje, A. Learning important features through propagating activation differences. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 3145–3153. [Google Scholar]
- Herman, B. The promise and peril of human evaluation for model interpretability. arXiv 2017, arXiv:1711.07414. [Google Scholar]
- Poursabzi-Sangdeh, F.; Goldstein, D.G.; Hofman, J.M.; Wortman Vaughan, J.W.; Wallach, H. Manipulating and measuring model interpretability. In Proceedings of the 2021 CHI Conference on Human Factors in Computing Systems, Yokohama, Japan, 8–13 May 2021; pp. 1–52. [Google Scholar]
- Zhong, R.; Shao, S.; McKeown, K. Fine-grained sentiment analysis with faithful attention. arXiv 2019, arXiv:1908.06870. [Google Scholar]
- Fel, T.; Vigouroux, D. Representativity and Consistency Measures for Deep Neural Network Explanations. arXiv 2020, arXiv:2009.04521. [Google Scholar]
- Tan, S.; Caruana, R.; Hooker, G.; Lou, Y. Auditing Black-Box Models Using Transparent Model Distillation with Side Information. 2017. Available online: http://adsabs.harvard.edu/abs (accessed on 27 January 2021).
- Tan, S.; Soloviev, M.; Hooker, G.; Wells, M.T. Tree space prototypes: Another look at making tree ensembles interpretable. In Proceedings of the 2020 ACM-IMS on Foundations of Data Science Conference, Seattle, WA, USA, 18–20 October 2020; pp. 23–34. [Google Scholar]
- Bass, C.; da Silva, M.; Sudre, C.; Tudosiu, P.D.; Smith, S.; Robinson, E. ICAM: Interpretable classification via disentangled representations and feature attribution mapping. Adv. Neural Inf. Process. Syst. 2020, 33, 7697–7709. [Google Scholar]
- Adebayo, J.; Gilmer, J.; Muelly, M.; Goodfellow, I.J.; Hardt, M.; Kim, B. Sanity Checks for Saliency Maps. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Montavon, G.; Samek, W.; Müller, K.R. Methods for interpreting and understanding deep neural networks. Digit. Signal Process. 2018, 73, 1–15. [Google Scholar] [CrossRef]
- Bhatt, U.; Weller, A.; Moura, J.M. Evaluating and aggregating feature-based model explanations. arXiv 2020, arXiv:2005.00631. [Google Scholar]
- Samek, W.; Wiegand, T.; Müller, K.R. Explainable artificial intelligence: Understanding, visualizing and interpreting deep learning models. arXiv 2017, arXiv:1708.08296. [Google Scholar]
- Petsiuk, V.; Das, A.; Saenko, K. Rise: Randomized input sampling for explanation of black-box models. arXiv 2018, arXiv:1806.07421. [Google Scholar]
- Nam, W.J.; Gur, S.; Choi, J.; Wolf, L.; Lee, S.W. Relative attributing propagation: Interpreting the comparative contributions of individual units in deep neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 2501–2508. [Google Scholar]
- Ancona, M.; Ceolini, E.; Öztireli, C.; Gross, M. Towards better understanding of gradient-based attribution methods for deep neural networks. arXiv 2017, arXiv:1711.06104. [Google Scholar]
- Bach, S.; Binder, A.; Montavon, G.; Klauschen, F.; Müller, K.R.; Samek, W. On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLoS ONE 2015, 10, e0130140. [Google Scholar] [CrossRef]
- Rieger, L.; Hansen, L.K. IROF: A low resource evaluation metric for explanation methods. In Proceedings of the Workshop AI for Affordable Healthcare at ICLR 2020, Addis Ababa, Ethiopia, 24–26 April 2020. [Google Scholar]
- Sundararajan, M.; Taly, A.; Yan, Q. Axiomatic attribution for deep networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 3319–3328. [Google Scholar]
- Yeh, C.K.; Hsieh, C.Y.; Suggala, A.; Inouye, D.I.; Ravikumar, P.K. On the (in) fidelity and sensitivity of explanations. Adv. Neural Inf. Process. Syst. 2019, 32, 10967–10978. [Google Scholar]
- Hooker, S.; Erhan, D.; Kindermans, P.J.; Kim, B. A benchmark for interpretability methods in deep neural networks. Adv. Neural Inf. Process. Syst. 2019, 32, 9737–9748. [Google Scholar]
- Yoshikawa, Y.; Iwata, T. Gaussian Process Regression with Local Explanation. arXiv 2020, arXiv:2007.01669. [Google Scholar]
- Ismail, A.A.; Gunady, M.; Corrada Bravo, H.; Feizi, S. Benchmarking deep learning interpretability in time series predictions. Adv. Neural Inf. Process. Syst. 2020, 33, 6441–6452. [Google Scholar]
- Ismail, A.A.; Corrada Bravo, H.; Feizi, S. Improving deep learning interpretability by saliency guided training. Adv. Neural Inf. Process. Syst. 2021, 34, 26726–26739. [Google Scholar]
- Dabkowski, P.; Gal, Y. Real time image saliency for black box classifiers. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6970–6979. [Google Scholar]
- Lapuschkin, S.; Binder, A.; Montavon, G.; Muller, K.R.; Samek, W. Analyzing classifiers: Fisher vectors and deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2912–2920. [Google Scholar]
- Baumgartner, C.F.; Koch, L.M.; Tezcan, K.C.; Ang, J.X.; Konukoglu, E. Visual feature attribution using wasserstein gans. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8309–8319. [Google Scholar]
- Ying, R.; Bourgeois, D.; You, J.; Zitnik, M.; Leskovec, J. Gnnexplainer: Generating explanations for graph neural networks. Adv. Neural Inf. Process. Syst. 2019, 32, 9240. [Google Scholar] [PubMed]
- Dai, J.; Upadhyay, S.; Aivodji, U.; Bach, S.H.; Lakkaraju, H. Fairness via Explanation Quality: Evaluating Disparities in the Quality of Post hoc Explanations. arXiv 2022, arXiv:2205.07277. [Google Scholar]
- Alvarez-Melis, D.; Jaakkola, T.S. Towards robust interpretability with self-explaining neural networks. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 7786–7795. [Google Scholar]
- Meng, C.; Trinh, L.; Xu, N.; Enouen, J.; Liu, Y. Interpretability and fairness evaluation of deep learning models on MIMIC-IV dataset. Sci. Rep. 2022, 12, 7166. [Google Scholar] [CrossRef] [PubMed]
- Jethani, N.; Sudarshan, M.; Aphinyanaphongs, Y.; Ranganath, R. Have We Learned to Explain?: How Interpretability Methods Can Learn to Encode Predictions in their Interpretations. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Virtual, 13–15 April 2021; pp. 1459–1467. [Google Scholar]
- Alangari, N.; Menai, M.; Mathkour, H.; Almosallam, I. Intrinsically Interpretable Gaussian Mixture Model. Information 2023, 14, 164. [Google Scholar] [CrossRef]
- Tsang, M.; Rambhatla, S.; Liu, Y. How does this interaction affect me? interpretable attribution for feature interactions. Adv. Neural Inf. Process. Syst. 2020, 33, 6147–6159. [Google Scholar]
- Hase, P.; Xie, H.; Bansal, M. The out-of-distribution problem in explainability and search methods for feature importance explanations. Adv. Neural Inf. Process. Syst. 2021, 34, 3650–3666. [Google Scholar]
- Ribeiro, D.N.; Wang, S.; Ma, X.; Zhu, H.; Dong, R.; Kong, D.; Burger, J.; Ramos, A.; Huang, Z.; Wang, W.Y.; et al. Street: A Multi-Task Structured Reasoning and Explanation Benchmark. In Proceedings of the Eleventh International Conference on Learning Representations, Vienna, Austria, 7–11 May 2023. [Google Scholar]
- Dai, J.; Upadhyay, S.; Aivodji, U.; Bach, S.H.; Lakkaraju, H. Fairness via Explanation Quality: Evaluating Disparities in the Quality of Post Hoc Explanations. In Proceedings of the AIES ’22, 2022 AAAI/ACM Conference on AI, Ethics, and Society, Oxford, UK, 19–21 May 2021; Association for Computing Machinery: New York, NY, USA, 2022; pp. 203–214. [Google Scholar]
- Everingham, M.; Eslami, S.A.; Van Gool, L.; Williams, C.K.; Winn, J.; Zisserman, A. The pascal visual object classes challenge: A retrospective. Int. J. Comput. Vis. 2015, 111, 98–136. [Google Scholar] [CrossRef]
- Jack, C.R., Jr.; Bernstein, M.A.; Fox, N.C.; Thompson, P.; Alexander, G.; Harvey, D.; Borowski, B.; Britson, P.J.; L. Whitwell, J.; Ward, C.; et al. The Alzheimer’s disease neuroimaging initiative (ADNI): MRI methods. J. Magn. Reson. Imaging 2008, 27, 685–691. [Google Scholar] [CrossRef]
- Socher, R.; Perelygin, A.; Wu, J.; Chuang, J.; Manning, C.D.; Ng, A.Y.; Potts, C. Recursive deep models for semantic compositionality over a sentiment treebank. In Proceedings of the 2013 Conference on Empirical Methods in Natural Language Processing, Seattle, WA, USA, 18–21 October 2013; pp. 1631–1642. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 740–755. [Google Scholar]
- Slack, D.; Hilgard, S.; Jia, E.; Singh, S.; Lakkaraju, H. Fooling lime and shap: Adversarial attacks on post hoc explanation methods. In Proceedings of the AAAI/ACM Conference on AI, Ethics, and Society, New York, NY, USA, 7–8 February 2020; pp. 180–186. [Google Scholar]
- Shahin Shamsabadi, A.; Yaghini, M.; Dullerud, N.; Wyllie, S.; Aïvodji, U.; Alaagib, A.; Gambs, S.; Papernot, N. Washing the unwashable: On the (im) possibility of fairwashing detection. Adv. Neural Inf. Process. Syst. 2022, 35, 14170–14182. [Google Scholar]
- Kindermans, P.J.; Hooker, S.; Adebayo, J.; Alber, M.; Schütt, K.T.; Dähne, S.; Erhan, D.; Kim, B. The (un) reliability of saliency methods. In Explainable AI: Interpreting, Explaining and Visualizing Deep Learning; Springer: Berlin/Heidelberg, Germany, 2019; pp. 267–280. [Google Scholar]
- Nie, W.; Zhang, Y.; Patel, A. A theoretical explanation for perplexing behaviors of backpropagation-based visualizations. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 3809–3818. [Google Scholar]
- Michalski, R.S. A theory and methodology of inductive learning. In Machine Learning; Elsevier: Amsterdam, The Netherlands, 1983; pp. 83–134. [Google Scholar]
- Freitas, A.A. Comprehensible classification models: A position paper. ACM SIGKDD Explor. Newsl. 2014, 15, 1–10. [Google Scholar] [CrossRef]
- Bodenhofer, U.; Bauer, P. A formal model of interpretability of linguistic variables. In Interpretability Issues in Fuzzy Modeling; Springer: Berlin/Heidelberg, Germany, 2003; pp. 524–545. [Google Scholar]
- Cordón, O.; Herrera, F. A proposal for improving the accuracy of linguistic modeling. IEEE Trans. Fuzzy Syst. 2000, 8, 335–344. [Google Scholar] [CrossRef] [PubMed]
- Casillas, J.; Cordon, O.; Herrera, F.; Magdalena, L. Finding a balance between interpretability and accuracy in fuzzy rule-based modelling: An overview. In Trade-Off between Accuracy and Interpretability in Fuzzy Rule-Based Modelling, Studies in Fuzziness and Soft Computing, Physica, Heidelberg; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Jin, Y.; Von Seelen, W.; Sendhoff, B. An approach to rule-based knowledge extraction. In Proceedings of the 1998 IEEE International Conference on Fuzzy Systems Proceedings, IEEE World Congress on Computational Intelligence (Cat. No. 98CH36228), Anchorage, AK, USA, 4–9 May 1998; Volume 2, pp. 1188–1193. [Google Scholar]
- Ishibuchi, H.; Nozaki, K.; Yamamoto, N.; Tanaka, H. Selecting fuzzy if-then rules for classification problems using genetic algorithms. IEEE Trans. Fuzzy Syst. 1995, 3, 260–270. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Murata, T.; Türkşen, I. Single-objective and two-objective genetic algorithms for selecting linguistic rules for pattern classification problems. Fuzzy Sets Syst. 1997, 89, 135–150. [Google Scholar] [CrossRef]
- Carrizosa, E.; Kurishchenko, K.; Marín, A.; Morales, D.R. On clustering and interpreting with rules by means of mathematical optimization. Comput. Oper. Res. 2023, 154, 106180. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Yamamoto, T. Interpretability issues in fuzzy genetics-based machine learning for linguistic modelling. In Modelling with Words; Springer: Berlin/Heidelberg, Germany, 2003; pp. 209–228. [Google Scholar]
- Mikut, R.; Jäkel, J.; Gröll, L. Interpretability issues in data-based learning of fuzzy systems. Fuzzy Sets Syst. 2005, 150, 179–197. [Google Scholar] [CrossRef]
- Nauck, D.D. Measuring interpretability in rule-based classification systems. In Proceedings of the FUZZ’03, 12th IEEE International Conference on Fuzzy Systems, St. Louis, MI, USA, 25–28 May 2003; Volume 1, pp. 196–201. [Google Scholar]
- Pedrycz, W. Expressing relevance interpretability and accuracy of rule-based systems. In Interpretability Issues in Fuzzy Modeling; Springer: Berlin/Heidelberg, Germany, 2003; pp. 546–567. [Google Scholar]
- Stefanowski, J.; Vanderpooten, D. Induction of decision rules in classification and discovery-oriented perspectives. Int. J. Intell. Syst. 2001, 16, 13–27. [Google Scholar] [CrossRef]
- Rajapaksha, D.; Bergmeir, C.; Buntine, W. LoRMIkA: Local rule-based model interpretability with k-optimal associations. Inf. Sci. 2020, 540, 221–241. [Google Scholar] [CrossRef]
- Fu, T.; Gao, T.; Xiao, C.; Ma, T.; Sun, J. Pearl: Prototype learning via rule learning. In Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, Niagara Falls, NY, USA, 7–10 September 2019; pp. 223–232. [Google Scholar]
- Alonso, J.M.; Magdalena, L.; Guillaume, S. HILK: A new methodology for designing highly interpretable linguistic knowledge bases using the fuzzy logic formalism. Int. J. Intell. Syst. 2008, 23, 761–794. [Google Scholar] [CrossRef]
- Nguyen, A.p.; Martínez, M.R. On quantitative aspects of model interpretability. arXiv 2020, arXiv:2007.07584. [Google Scholar]
- Jacovi, A.; Goldberg, Y. Towards Faithfully Interpretable NLP Systems: How Should We Define and Evaluate Faithfulness? In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 4198–4205. [Google Scholar]
- Jacovi, A.; Goldberg, Y. Aligning faithful interpretations with their social attribution. Trans. Assoc. Comput. Linguist. 2021, 9, 294–310. [Google Scholar] [CrossRef]
- Feldman, J. Minimization of Boolean complexity in human concept learning. Nature 2000, 407, 630–633. [Google Scholar] [CrossRef] [PubMed]
- Lavrač, N. Selected techniques for data mining in medicine. Artif. Intell. Med. 1999, 16, 3–23. [Google Scholar] [CrossRef] [PubMed]
- Allahyari, H.; Lavesson, N. User-oriented assessment of classification model understandability. In Proceedings of the 11th Scandinavian Conference on Artificial Intelligence, Trondheim, Norway, 24–26 May 2011. [Google Scholar]
- Barron, A.; Rissanen, J.; Yu, B. The minimum description length principle in coding and modeling. IEEE Trans. Inf. Theory 1998, 44, 2743–2760. [Google Scholar] [CrossRef]
- Domingos, P. Occam’s two razors: The sharp and the blunt. In Proceedings of the Fourth International Conference on Knowledge Discovery & Data Mining (KDD-98), New York, NY, USA, 27–31 August 1998; pp. 37–43. [Google Scholar]
- Miller, G.A. The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychol. Rev. 1956, 63, 81. [Google Scholar] [CrossRef] [PubMed]
- Ghorbani, A.; Abid, A.; Zou, J. Interpretation of neural networks is fragile. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar]
- Dombrowski, A.K.; Alber, M.; Anders, C.; Ackermann, M.; Müller, K.R.; Kessel, P. Explanations can be manipulated and geometry is to blame. Adv. Neural Inf. Process. Syst. 2019, 32, 13589–13600. [Google Scholar]
- Kuznetsov, S.O.; Makhalova, T. On interestingness measures of formal concepts. Inf. Sci. 2018, 442, 202–219. [Google Scholar] [CrossRef]
- Chen, J.; Wu, X.; Rastogi, V.; Liang, Y.; Jha, S. Robust attribution regularization. Adv. Neural Inf. Process. Syst. 2019, 32, 1–11. [Google Scholar]
- Tsipras, D.; Santurkar, S.; Engstrom, L.; Turner, A.; Madry, A. Robustness May Be at Odds with Accuracy. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Engstrom, L.; Ilyas, A.; Santurkar, S.; Tsipras, D.; Tran, B.; Madry, A. Adversarial robustness as a prior for learned representations. arXiv 2019, arXiv:1906.00945. [Google Scholar]
| Lay | Expert | Lay + Expert | |
|---|---|---|---|
| Specific | - Understand internal reasoning process [30] - Reconstruct target instance [31] | ||
| All models | - Verification [32,33] - Counterfactual [32] | - Alignment between human and model [21,34,35] | - Forward Simulation [6,7,30,32,36,37,38,39] - Select the best explanation [7,21,26,30,36,40,41,42] - Describe the class characteristics [43,44] |
| Agnostic | - Select the best classifier [1,25,45,46] - Improve a classifier [1] - Alignment between human and model [46,47] | - Identify classifier irregularities [1] |
| References | Validation Approach | Explanation Type |
|---|---|---|
| [22,44,53,54] | Separate test-set | Global models (post hoc) |
| [43,55] | Ablation studies | Global models (intrinsic) |
| [34,40,41,48,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,71] | Removal-approach | All feature attribution approaches |
| [35,55,61,72,73,74,75] | Compare interpretation with ground-truth | All types when data are available |
| Ref. | Metric Name | Proxy Model | How the Faithfulness Measured |
|---|---|---|---|
| [22] | Fidelity | Decision tree | The percentage of test-set examples on which the classification made by a tree agrees with black-box (NN) counterpart. |
| [53] | Fidelity | Linear model, iGAM | Compare the output of both black-box with transparent models on test-sets |
| [44] | Accuracy relative to the complex model | Decision tree | Find the match between the two models on test-sets |
| [55] | - | Global prototypes per class | Use prototypes in nearest-prototype classifier |
| Ref. | Metric Name | Removal | Approaches |
|---|---|---|---|
| [56] | Fidelity | Remove | Measure the drop in probability after the perturbation |
| [57] | Faithfulness | Replace by baseline values | Find subset features perturbation to a baseline |
| [58] | Explanation selectivity | Remove | Measure the drop in probability after remove important feature |
| [40] | AOPC | Remove | The same as [58], on patch of size 9 × 9 |
| [59] [60] | - | Replace by random sample from uniform distribution | Same as [58] |
| [61] | AOPC | Remove | Extended AOPC to evaluate negative attributions to irrelevant regions |
| [62] | - | Replacing with zero | Same as [40], one pixel at a time |
| [41] | (CPP) and (NLCI) | Replace positive by 0, and negative by 1. | Find the change of prediction probability and the number of label-changed instance |
| [63] | Pixels flipping | Flip the pixels | Change pixels with highly scores then evaluate the effect |
| [64] | - | Iterative removal | Remove the segment with highly score then, find the drop in AOC |
| [48] | - | Required change to flip the class (erase) | Find log-odds score change between original image and perturbed image in another class |
| [65] | Completeness | Baseline | Sum of features’ attribution should sum up to difference in prediction wrt baseline |
| [62] | Sensitivity-n | Baseline | Quantify the attributions difference when remove a subset of features |
| [66] | Infidelity | Baseline, noisy baseline, and multiple baselines | Same as [62], with different perturbations |
| [67] | - | Remove | Re-train models on the perturbed instances before find the drop |
| [68] | - | Remove features one-by-one | Find the differences and correlation |
| [34] | Post hoc accuracy | Zero padding | Compute accuracy level between original and padded instance |
| [69,70] | Precision and recall | Masking with uninformative from original distribution | Utilize AUP and AUR |
| [71] | Saliency metric | Cropping relevant region | Utilize entropy to validate the classifier ability to recognize class |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alangari, N.; El Bachir Menai, M.; Mathkour, H.; Almosallam, I. Exploring Evaluation Methods for Interpretable Machine Learning: A Survey. Information 2023, 14, 469. https://doi.org/10.3390/info14080469
Alangari N, El Bachir Menai M, Mathkour H, Almosallam I. Exploring Evaluation Methods for Interpretable Machine Learning: A Survey. Information. 2023; 14(8):469. https://doi.org/10.3390/info14080469
Chicago/Turabian StyleAlangari, Nourah, Mohamed El Bachir Menai, Hassan Mathkour, and Ibrahim Almosallam. 2023. "Exploring Evaluation Methods for Interpretable Machine Learning: A Survey" Information 14, no. 8: 469. https://doi.org/10.3390/info14080469
APA StyleAlangari, N., El Bachir Menai, M., Mathkour, H., & Almosallam, I. (2023). Exploring Evaluation Methods for Interpretable Machine Learning: A Survey. Information, 14(8), 469. https://doi.org/10.3390/info14080469





