Abstract
The rapid growth in greenhouse gases (GHGs), the lack of electricity production, and an ever-increasing demand for electrical energy requires an optimal reduction in coal-fired thermal generating units (CFTGU) with the aim of minimizing fuel costs and emissions. Previous approaches have been unable to deal with such problems due to the non-convexity of realistic scenarios and confined optimum convergence. Instead, meta-heuristic techniques have gained more attention in order to deal with such constrained static/dynamic economic emission load dispatch (ELD/DEELD) problems, due to their flexibility and derivative-free structures. Hence, in this work, the elephant herd optimization (EHO) technique is proposed in order to solve constrained non-convex static and dynamic ELD problems in the power system. The proposed EHO algorithm is a nature-inspired technique that utilizes a new separation method and elitism strategy in order to retain the diversity of the population and to ensure that the fittest individuals are retained in the next generation. The current approach can be implemented to minimize both the fuel and emission cost functions of the CFTGUs subject to power balance constraints, active power generation limits, and ramp rate limits in the system. Three test systems involving 6, 10, and 40 units were utilized to demonstrate the effectiveness and practical feasibility of the proposed algorithm. Numerical results indicate that the proposed EHO algorithm exhibits better performance in most of the test cases as compared to recent existing algorithms when applied to the static and dynamic ELD issue, demonstrating its superiority and practicability.
1. Introduction
1.1. Overview
One of the key issues with the power dispatch system is the ELD, which aims to schedule the active power of the CFTGU as efficiently as possible while adhering to certain equality and inequality constraints. The efficient allocation of generators leads to minimizing electricity costs for the end consumer, which is achieved via the effective solution methodology []. Various approaches have frequently been applied to the ELD problem in the past, such as genetic algorithms (GA), sequential quadratic programming (SQP) and evolutionary programming (EP) [,]. These approaches are fast and require derivatives of their fitness function, but cannot successfully solve large and complex problems such as ELD with VPE and ramp rate limits, as the Hessian or Gradient matrix is too difficult to form [,]. Additionally, EPs involve long computational times while handling composite constraints. In view of this, quantum bits can be incorporated into EP to overcome composite constraints and to avoid local minima in the solution []. Likewise, in the recent past, algorithms such as an improved genetic algorithm with multiplier updating (IGAMU) [], self-tuning hybrid differential algorithm (HDE) [], anti-predatory particle swarm optimization (AP-PSO) [], and EP with mutations (MEP) [] have gained importance in solving the ELD problem. Further, algorithms such as PSO [], evolutionary strategy optimization (ESO) [] artificial bee colony (ABC) algorithm [], hybrid quantum mechanics-inspired PSO (Q-PSO) [], biogeography optimization (BBO) [], and hybrid differential evolution with BBO [] have been utilized to solve the complex ELD problem considering valve point effects (VPE) and transmission losses (TL). Even though these techniques are the most fitting choices for nonlinear optimization, they inherently suffer from lower convergence rates, tendencies toward local minima, and are highly sensitive to the control parameters.
The methods used in the past provide reasonable solutions, but search efficiency drops and higher times for convergence are required when utilizing ELD with valve point effects [,,]. Due to the above limitations, the hybridized techniques, such as Q-PSO [], hybrid PSO (HPSO) [], gravitational search algorithm (GSA) [], enhanced multi–objective cultural algorithm (EMOCA) [], improved orthogonal design PSO (IDPSO) [], modified kill herd algorithm (MKHA) [], modified crow search algorithm (MCSA) [], a self-adapted across neighborhood search (SA-ANS) [], flooding-based topology discovery algorithm (FBTDA) [], JAYA with self-adaptive multi-population and levy flights (JAYA-SML) [], JAYA with teaching learning-based optimization (JAYA-TLBO) [], hybrid grey wolf optimization (HGWO) [], kernel tricks (KSO) [], an improved Q-PSO [], emended salp swarm algorithm (ESSA) [,], exchange market algorithm method (EMAM) [], peafowl optimization algorithm (POA) [], and modified H-PSO with BAT algorithm-inspired acceleration coefficients (BAAC) [] have been proposed in order to solve the ELD problem. The above algorithms do not always achieve the global best, but generally tend to reach near to the global optimal value [,]. The traditional static ELD problem seeks to minimize the generation cost of CFTGU for a certain load in a given time-period by satisfying limitations such as power balance and generation limits. Additionally, when the load demand fluctuates significantly, it becomes more challenging to solve the ELD problem due to the ramp rate constraints of the CFTGUs.
Another suitable actual power dispatch requirement is the DEELD, which uses the dynamic dispatching for a load cycle of a 24 h period. The DEELD problem has been tackled in a number of different ways to date. At first, mathematical methods such as lambda step, optimal point, participation coefficients, and gradient-based approaches have generally been utilized for the DEELD problem. However, mathematical methods have drawbacks such as excessive memory utilization and being less accurate when addressing a highly complex problem. As a result, numerous artificial intelligence techniques (AIT) have since been used to tackle the DEELD problem and produce successful dispatch outcomes. In this context, to solve the multi-objective DEELD (MO-DEELD) problem, the dynamic non-sorted biogeography-based optimization (Dy-NSBBO) algorithm is suggested in reference []. Similarly, the algorithms such as the multi-objective virus colony search (MO-VCS) algorithm [], moth–flame optimization with position disturbance updating strategy (MFO-PDU) [], improved tunicate swarm algorithm (ITSA) [], and improved sailfish algorithm (ISFO) [] were created in order to solve the DEELD problem in the recent past. In [], the authors noted that the DEELD problem is more challenging address as it involves both fuel and pollution costs.
Similarly, in [], an improved bacterial foraging algorithm (IBFA) was implemented in order to solve the DEELD problem. In [], the DEELD problem was solved using a multi-objective BAT optimization algorithm, which considers slope rate constraints and valve point effects. In [], the convergence performance was not confirmed when the orthogonal-PSO algorithm was implemented to solve the DEELD problem. Likewise, many works have not addressed the emissions objectives when attempting to solve the DEELD problem []. In sum, even though the previous algorithms have been successfully applied to the DEELD problem, various drawbacks, such as higher convergence rates, a tendency to become stuck at local optimum values, and addressing only limited objectives, can be identified as major gaps.
On the other hand, the elephant herd optimization (EHO) algorithm has a strong potential of achieving a global optimal solution, with robustness and fast convergence speed; it is a newly proposed intelligent algorithm (see [] and []). It has proven its ability to achieve the global optimal solution by implementing it in various standard test functions []. Likewise, the EHO has proven its ability to obtain the optimal solution using lower convergence rates when subjected to the design of the optimal PI controller for the control of the grid-tied four-phase switched reluctance generator (SFG) []. Furthermore, the discrete EHO (DEHO)-based partial transmit sequence (PTS) method is recommended to improve the peak-to-average power ratio of universal filtered multicarrier (UFMC) signals to minimum levels. The recent literature describing the static/dynamic ELD problem and a summary of the implemented algorithms are presented in Table 1.

Table 1.
Literature review describing the methodology and associated problem of interest.
1.2. Research Contributions
The major contributions of this work are as follows:
- An artificial intelligence algorithm, namely, elephant herd optimization (EHO), is implemented in order to solve a critical engineering problem.
- The algorithm is implemented in order to solve both the convex static and dynamic EELD problems of power systems.
- The predictability of the proposed algorithm is evaluated by implementing the algorithm on three different systems, such as 6-, 10-, and 40-unit systems.
- The obtained results are compared to the recent available algorithms in the literature to demonstrate the efficacy of the proposed approach.
1.3. Organization of the Present Work
Section 2 outlines the basic ELD problem formulations with various constraint scenarios. Section 3 illustrates the modeling of DEELD problem with constraints. Section 4 discusses the mathematical modeling of the EHO algorithm. Finally, Section 5 deliberates on the results, and Section 6 presents the conclusions drawn from the present work.
2. Problem Formulation for the Basic ELD Problem
2.1. Objective Function
The basic ELD problem comprises a fitness function along with various practical constraints. In the basic form, the fitness function is a quadratic function that describes the various cost functions of participating generators [] on a hourly basis. The mathematical form of the fitness function for the BELD problem is shown below:
The ELD problem consists of minimizing is subject to the following constraints.
2.2. Constraints
2.2.1. Power Balance Constraints
The total power generated should be equal to the sum of the total load on the system and total transmission line network losses []. The mathematical form for the power balance constraint is shown below:
The transmission loss may be represented using B coefficients []:
2.2.2. Generator Capacity Constraints
The output delivered from the generators maintained to be within their lower and upper limits, as shown below:
2.2.3. Ramp Rate Limits Constraints
The power delivered by the generator in a period is to be maintained within certain up-ramp and down-ramp limits [], with respect to the previous . This is shown below:
and
and
The fitness function (1) is subject to real power balance constraints (2), generator capacity constraints (4), and ramp rate limit constraints (7).
3. Problem Formulation for Dynamic EELD Problem
In this section, we provide the mathematical formulations for the DEELD problem. We assume that the network has dispatchable power generators, . The control variables of the DEELD problem are collected in the vector at each hour , where and is the vector collecting the generations for all . Let the function be the positive valued, differentiable, non-decreasing, and convex objective function that captures the generation cost for the DEELD problem. Let the be the partial derivative with respective to the control variable and the constraints imply that for all []. The cost function for the DEELD problem comprises a fuel cost function and an emission dispatch function , which are shown as follows:
3.1. Fuel Cost Function
The 24 h fuel cost function for all is represented as quadratic costs valued in USD []. The fuel cost function utilized in this work is shown as below:
3.2. Emission Dispatch Function
The next fitness function is the emission pollutants in (kgs). It has a straight relationship with the output generated from the gth conventional generator. The emissions include CO2, nitrogen oxide (NOx) and sulfur oxide (SOx), which are caused by the burning of fossil fuels []. The can be expressed as follows:
The above functions are minimized, as they are subject to various constraints, i.e., limits on active power generations, ramp rate limits, power balance constraints, and transmission loss constraints. The next sub-section discloses the constraints considered in this work.
3.3. Constraints
Transmission losses: The loss at any time segment tth, including B-coefficients, is given as follows:
Active Power Balance Constraints: The power generated at any tth time segment is utilized to supply the demand and transmission losses at the given time segment. This is mathematically represented as follows:
Limits on active power generation: The active power generation at time segment is restricted by the prescribed upper and lower limits. Figure 1 shows the pictorial representation of the maximum and minimum limits of a 6-unit system. This is mathematically represented as follows:
Figure 1.
Thermal generator maximum and minimum limits.
Ramp Rate Limits: This is specified as follows []:
3.4. Weighted Fitness Function to Obtain the Optimal Scheduling Strategy
The weighted fitness function has been utilized in order to find the optimum fuel cost and emission dispatch of the generators. The weighted multi-objective function is discussed as follows:
where and are the weighting factors, set as 0.5 in this work.
Constraint Handling
The power balance constraints, including the real power generations, load demand, and charging/discharging, are handled by including a penalty factor to the objective function (17) as shown below:
where
The fitness function (17) is subjected to real power balance constraints (10), limits on active power generation (11), and ramp rate limits specified in (13)–(15).
4. Elephant Herd Optimization
In 2015, Wang et al. [] created the EHO algorithm, taking inspiration from the social behaviors of elephant herds observed in nature. Even though elephants demonstrate intelligent behavior in real life, the EHO algorithm was created using the following idealized rules. The elephant population is divided into clans containing a constant number of elephants in each clan. One elephant in each tribe guides the others as they look for food and water. Additionally, as generations pass, some elephants of a particular age leave their clan to live independently in distant areas far from the family group they belong to. On this basis, the basic EHO algorithm is designed to have two main phases, namely clan updating and separation.
Clan Updating Operator
As previously stated, each of the elephants is led by a matriarch in their respective clan. Thus, matriarch authority influences the next position of each elephant in the clan . For instance, elephant in clan is updated as follows:
Here, uniform conveyance is utilized. No group’s fittest elephant can be replenished by Equation (18). For the finest elephant, the clan is updated as shown below:
We can observe a new individual, , in Equation (19), which is produced by the data obtained by all the elephants in the clan . for the aspect may be calculated as follows:
The center of clan , can be determined through the D estimations using Equation (20). Using the process above, the group refreshing administrator can be uncovered. When they reach puberty, the male elephants in each clan will depart from their group and live independently. When handling improvement-related concerns, an administrator can serve as an example of this isolating cycle. Let us assume that the elephants with the worst health will act as the isolating administrator at every age in order to improve the search capability of the EHO strategy. This mechanism is shown in Equation (21).
The pseudo-codes for the clan updating operator and separating operator are shown in Figure 2 below.

Figure 2.
Pseudo-codes for the EHO algorithm.
5. Case Study
5.1. Description of Systems
In this study, the EHO algorithm is used to minimize the total fuel cost for both static and dynamic ELD problems of the power system. The results are evaluated on three different test systems to assess the effectiveness of the proposed approach. Concisely, the flow chart in Figure 3 illustrates the internal mechanism of the proposed algorithm along with process of achieving results.
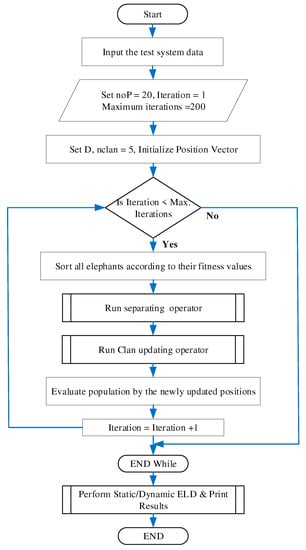
Figure 3.
Flow chart for proposed EHO algorithm for ELD/DEELD problems.
5.1.1. Test System 1
Test system 1 utilized in the present study is a six-unit system. The details such as generator cost coefficients, generator limits, and the loss matrix of the test system 1 are shown in Table 2 below, which are taken from reference [].

Table 2.
Data for the six-unit system.
5.1.2. Test System 2
Similarly, in this study, test system 2 is a 40-unit system. The details related to this system are taken from references [,].
5.1.3. Test System 3
Similarly, in this study, test system 3 is a 10-unit system. The details related to this system are taken from reference [].
5.2. Parameter Setting and System Configurations
The proposed EHO algorithm for solving static/dynamic ELD problems was implemented using MATLAB on a 64-bit laptop with a 2.60 GHz CPU and 8 GB RAM. Meanwhile, to evaluate their effectiveness, the results obtained from the proposed EHO algorithm at every stage are compared with standard algorithms, such as BAT [], ALO [], and those from other recently published works. The algorithm was tested on each test system 20 times to minimize the statistical errors, and the obtained results were compared with the previous literature. Further, the weighting factors, such as and in (17), are set to 0.5 in order to provide the equal preferences for the considered objectives []. Before proceeding to the simulated calculation, the careful selection of parameter settings is important to produce a competent result. The selection of the parameters, such as , considerably affects the performance of the EHO in terms of the present problem of interest. To successfully implement the EHO, the values of were varied, namely as 100, 200, and 500 in order to obtain the best parameter setting. The results of this are presented in Table 3 for test system 1. Based on the results from Table 3, it can be observed that the EHO algorithm provides the best results when for test system 1.

Table 3.
Parameter setting of EHO algorithm for test system 1.
5.3. Computation Results and Comparisons
5.3.1. Test System 1
In this case, a six-unit static ELD problem considering losses is used to test the effectiveness of the proposed EHO algorithm. A general load demand of 1263 MW is considered in the present test case. Twenty trials were utilized to evaluate each algorithm and the results were analyzed based on the best, worst, and standard deviation values obtained. Based on the static results obtained in Table 3 and to validate these, the was set to 200 for the proposed EHO, ALO, and BAT algorithms, as shown in Table 4. The optimization results of the proposed and other reported approaches are shown in Table 5. The best fuel cost in this case is achieved through the EHO algorithm at 15,286.47 (USD/h), which is low compared to 15,443.0 (USD/h), 15,796.02746 (USD/h), and 15,814.97355 (USD/h) achieved by MKHA, ALO, and BAT algorithms, respectively. It is also clear from Table 5 that the proposed EHO algorithm provides a much better solution with less computational time compared to MKHA, ALO, and BAT algorithms. Furthermore, the convergence curves obtained by the proposed EHO and other reported approaches are shown in Figure 4. It can be observed that the EHO algorithm converges at a low number of iterations, which reinforces the superiority of the proposed approach. In addition, the results have been evaluated and validated using a medium-sized test bus system.

Table 4.
Parameters considered for the reported algorithms.

Table 5.
Comparative results of the six-unit system with MW.
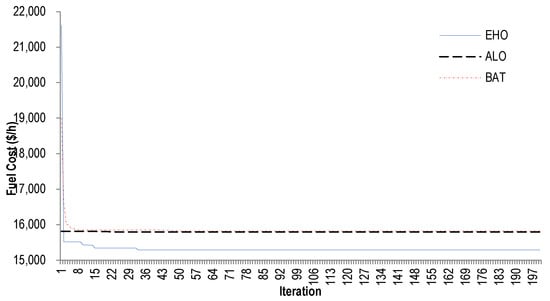
Figure 4.
Convergence curve for various algorithms for a six-unit system with MW.
5.3.2. Test System 2
This case study consists of 40 generators, meeting a demand of MW. The optimal scheduling of the generators in this case by the EHO, ALO, and BAT algorithms is shown in Figure 5. Similarly, the results obtained in this case by the EHO algorithm are compared with recent similar approaches, such as KSO [], HDE [], Beta-HC-GWO [], and CBPSO-RVM [], and are shown in Table 6. From the comparisons shown in Table 6, it can be seen that, among the reported algorithms such as BAT, ALO, and EHO, EHO performs well in respect to fuel costs. Furthermore, amongst all other algorithms listed, EHO performs better while producing minimum fuel costs as well as time consumptions. The convergence curves for the algorithms EHO, BAT, and ALO are shown in Figure 6. The micro-level examination of the figure reveals that the proposed EHO algorithm converges in the early stage (before 80 iterations), while the other two only settled with difficulty. The results demonstrate the superiority and practicability of the proposed EHO over the large test systems. Furthermore, to confirm the feasibility of the proposed EHO algorithm, the problem involving a dynamically varying load is discussed in the next section.
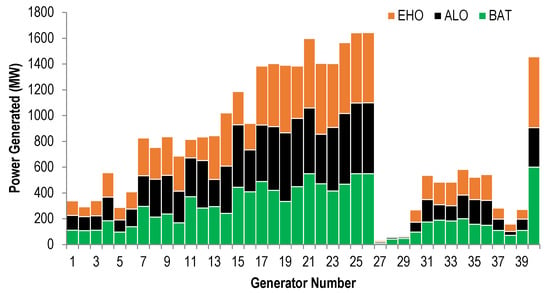
Figure 5.
Active power generation of a 40-unit system with MW.

Table 6.
Comparative results of a 40-unit system with MW.
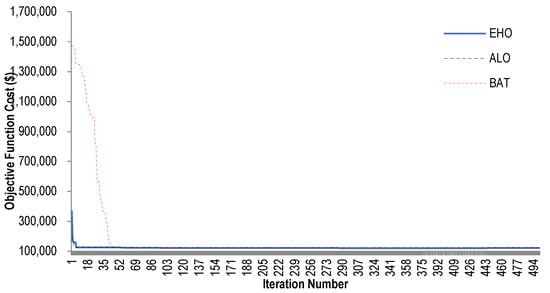
Figure 6.
Convergence curve for various algorithms for a 40-unit system with MW.
5.3.3. Test Case 3
In this case, a 10-unit DEELD problem is used to evaluate the 24 h period fuel cost utilizing the proposed EHO algorithm. The data-related costs and up/down limits of the 10-unit system are taken from []. The general load profile referred to by most recent works such as [] and [] is depicted in Figure 7 below. Here also, in order to obtain the best setting of , itermax has been varied as 100, 200 and 500. The results of this are presented in Table 7 for test system 2. Based on the results from Table 6, it can be observed that the EHO algorithm provides the best results when the (as in test system 2).
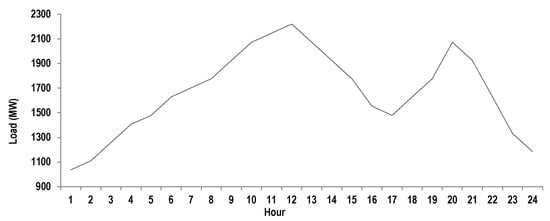
Figure 7.
Load profile for a 10-unit system.

Table 7.
Parameter setting of EHO algorithm for test system 3.
The optimal dispatch of the 10-unit system in a period of 24 h by the proposed EHO algorithm is shown in Figure 8. The results, such as fuel costs and emissions on an hourly basis, are depicted in Table 8. It can be observed that the total fuel costs, , and total emissions, , for a period of 24 h, obtained by the proposed EHO algorithm, are 1,013,950 (USD) and 648,085 (kg) respectively. Furthermore, the comparative analysis of the obtained results with those of the previous benchmark approaches, such as ICA [], CDE [], DE [], AIS [], ECE [], IPSO [], DGPSO [], BAT, ALO, SOA-SQP [], PSO-SQP [], MHEP-SQP [], AIS-SQP [], and CS-DE [] algorithms, are shown in Table 9. From the table, it can be declared that the proposed EHO algorithm outperforms the previous approaches. In addition, the convergence characteristics of the proposed EHO and other reported approaches, such as ALO and BAT, are shown in Figure 9. From the figure, it can be seen that the proposed approach converges in a smaller number of iterations, as compared to other reported approaches. The comprehensive result analysis also demonstrates that the proposed approach has a remarkable impact on both static and dynamic EELD problems.
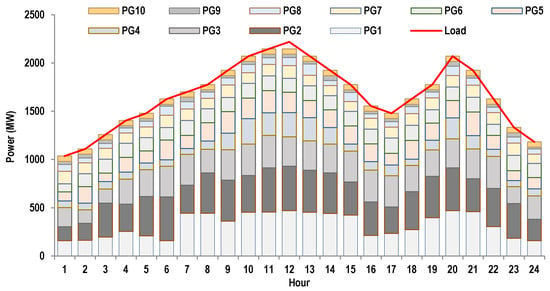
Figure 8.
Hourly generation and the corresponding load of DEED problem via the EHO algorithm.

Table 8.
Cost-based results for test system 3.

Table 9.
Comparative results of a 10-unit system with dynamic loading.
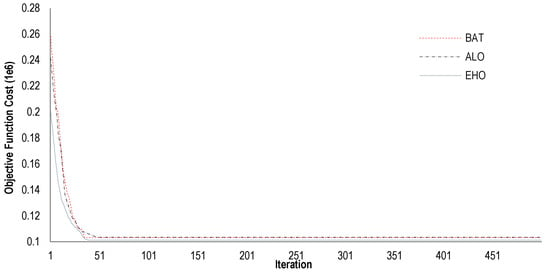
Figure 9.
Convergence curve for various algorithms for the 10-unit system DEED problem.
6. Conclusions
In this study, a novel EHO method was used to resolve the power system’s static and dynamic EELD problems. For both small- and large-scale test systems, the performance of the EHO algorithm was investigated in a variety of instances, involving both the static ELD and dynamic EELD problems. The numerical simulation demonstrates that the suggested EHO method is capable of finding the best scheduling for the test systems in regard to static and dynamic EELD problems. The comparative analysis of the fuel cost function value obtained by the EHO algorithm, with respect to the BAT and ALO algorithms, demonstrates its superiority and could save billions of USD annually by making the generating units eco-friendlier.
Furthermore, the convergence results also demonstrate that the proposed approach provides a significant reduction in fuel costs and convergence time for both small- and large-scale test systems, while solving complicated optimization problems in power systems. Finally, it can be concluded that the proposed approach is a superior alternative for power system operators to obtain an improved dispatch schedule for static and dynamic EELD problems in small- and large-scale systems, irrespective of their complexities.
Author Contributions
Conceptualization, R.P., Y.K.N. and S.R.S.; methodology, S.K.W., R.P. and S.R.S.; software, R.P. and S.K.W.; validation, R.P., Y.K.N. and S.R.S.; formal analysis, Y.K.N., S.K.W.; investigation, R.P., S.K.W. and S.R.S.; resources, R.P. and S.R.S.; data curation, R.P. and S.R.S.; writing—original draft preparation, R.P. and S.K.W.; writing—review and editing, R.P., S.K.W. and S.R.S.; visualization, R.P. and Y.K.N.; supervision, R.P., S.K.W. and S.R.S.; project administration, Y.K.N. and S.K.W.; funding acquisition, R.P. and S.R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funding support from Woosong University’s Academic Research Funding—2023.
Data Availability Statement
The data used to support the findings of this study are publicly available online, and any further information required is available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| The quadratic cost function of gth generator in | |
| , and | The cost coefficients of the gth generator in |
| The active power output from the gth generator in | |
| The total number of CFTGU | |
| The power demand at the load in | |
| The loss coefficient matrices | |
| Maximum limit of active power generation of gth generator | |
| Minimum limit of active power generation of gth generator | |
| Recently refreshed for elephant in clan | |
| Recently refreshed for elephant in clan | |
| Matriarch which is the fittest elephant individual in clan | |
| Random value between [0, 1] | |
| Random value between [0, 1] | |
| Total dimension | |
| Quantity of elephants in clan | |
| The dth elephant individual of | |
| The upper bound of the position of elephant individual | |
| The lower bound of the position of elephant individual | |
| Worst elephant individual in clan | |
| Centre of clan | |
| A real between the range [0 1] |
Acronyms
| GHGs | Greenhouse Gases |
| ELD | Economic Load Dispatch |
| DEELD | Dynamic Economic Emission Load Dispatch |
| EHO | Elephant Herd Optimization |
| CFTGU | Coal-Fired Thermal Generating Unit |
| VPE | Valve Point Effects |
| PTS | Partial Transmit Sequence |
| SFG | Switched Reluctance Generator |
| UFMC | Universal Filtered Multicarrier |
| GA | Genetic Algorithm |
| EP | Evolutionary Programming |
| SQP | Sequential Quadratic Programming |
| PSO | Particle Swarm Optimization |
| TL | Transmission Losses |
| IGAMU | Improved Genetic Algorithm with Multiplier Updating |
| HDE | Self-Tuning Hybrid Differential Algorithm |
| AP-PSO | Anti-Predatory PSO |
| ESO | Evolutionary Strategy Optimization |
| Q-PSO | Quantum Mechanics Inspired PSO |
| BBO | Biogeography Optimization |
| HPSO | Hybrid PSO |
| GSA | Gravitational Search Algorithm |
| EMOCA | Enhanced Multi-Objective Cultural Algorithm |
| IDPSO | Improved Orthogonal Design PSO |
| MKHA | Modified Kill Herd Algorithm |
| MCSA | Modified Crow Search Algorithm |
| SA-ANS | Self-Adapted Across Neighborhood Search |
| FBTDA | Flooding Based Topology Discovery Algorithm |
| HGWO | Hybrid Grey Wolf Optimization |
| ESSA | Emended Salp Swarm Algorithm |
| EMAM | Exchange Market Algorithm Method |
| POA | Peafowl Optimization Algorithm |
| Dy-NSBBO | Dynamic Non-Sorted Biogeography-Based Optimization |
| MO-VCS | Multi-Objective Virus Colony Search |
| MFO-PDU | Moth–Flame Optimization with Position Disturbance Updating Strategy |
| ITSA | Improved Tunicate Swarm Algorithm |
| ISFO | Improved Sailfish Algorithm |
| IBFA | Improved Bacterial Foraging Algorithm |
References
- Wu, M.; He, Q.; Liu, Y.; Zhang, Z.; Shi, Z.; He, Y. Machine Learning Techniques for Decarbonizing and Managing Renewable Energy Grids. Sustainability 2022, 14, 13939. [Google Scholar] [CrossRef]
- Mei, P.; Wu, L.; Zhang, H.; Liu, Z. A Hybrid Multi-Objective Crisscross Optimization for Dynamic Economic/Emission Dispatch Considering Plug-In Electric Vehicles Penetration. Energies 2019, 12, 3847. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L.F. An Exact MINLP Model for Optimal Location and Sizing of DGs in Distribution Networks: A General Algebraic Modeling System Approach. Ain. Shams. Eng. J. 2019, 11, 409–418. [Google Scholar] [CrossRef]
- Subathra, M.S.P.; Easter Selvan, S.; Aruldoss Albert Victoire, T.; Hepzibah Christinal, A.; Amato, U. A Hybrid with Cross-Entropy Method and Sequential Quadratic Programming to Solve Economic Load Dispatch Problem. IEEE Syst. J. 2015, 9, 1031–1044. [Google Scholar] [CrossRef]
- Jabr, R.A. Solution to Economic Dispatching with Disjoint Feasible Regions via Semidefinite Programming. IEEE Trans. Power Syst. 2012, 27, 572–573. [Google Scholar] [CrossRef]
- Sailesh Babu, G.S.; Bhagwan Das, D.; Patvardhan, C. Real-Parameter Quantum Evolutionary Algorithm for Economic Load Dispatch. IET Gener. Transm. Distrib. 2008, 2, 22–31. [Google Scholar] [CrossRef]
- Chiang, C.L. Genetic-Based Algorithm for Power Economic Load Dispatch. IET Gener. Transm. Distrib. 2007, 1, 261–269. [Google Scholar] [CrossRef]
- Wang, S.K.; Chiou, J.P.; Liu, C.W. Non-Smooth/Non-Convex Economic Dispatch by a Novel Hybrid Differential Evolution Algorithm. IET Gener. Transm. Distrib. 2007, 1, 793–803. [Google Scholar] [CrossRef]
- Selvakumar, A.I.; Thanushkodi, K. Anti-Predatory Particle Swarm Optimization: Solution to Nonconvex Economic Dispatch Problems. Electr. Power Syst. Res. 2008, 78, 2–10. [Google Scholar] [CrossRef]
- Sinha, N.; Chakrabarti, R.; Chattopadhyay, P.K. Evolutionary Programming Techniques for Economic Load Dispatch. IEEE Trans. Evol. Comput. 2003, 7, 83–94. [Google Scholar] [CrossRef]
- Gaing, Z.L. Particle Swarm Optimization to Solving the Economic Dispatch Considering the Generator Constraints. IEEE Trans. Power Syst. 2003, 18, 1187–1195. [Google Scholar] [CrossRef]
- Pereira-Neto, A.; Unsihuay, C.; Saavedra, O.R. Efficient Evolutionary Strategy Optimisation Procedure to Solve the Nonconvex Economic Dispatch Problem with Generator Constraints. IEE Proc. Gener. Transm. Distrib. 2005, 152, 653. [Google Scholar] [CrossRef]
- Hemamalini, S.; Simon, S.P. Artificial Bee Colony Algorithm for Economic Load Dispatch Problem with Non-Smooth Cost Functions. Electr. Power Compon. Syst. 2010, 38, 786–803. [Google Scholar] [CrossRef]
- Meng, K.; Wang, H.G.; Dong, Z.Y.; Wong, K.P. Quantum-Inspired Particle Swarm Optimization for Valve-Point Economic Load Dispatch. IEEE Trans. Power Syst. 2010, 25, 215–222. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Chattopadhyay, P.K. Biogeography-Based Optimization for Different Economic Load Dispatch Problems. IEEE Trans. Power Syst. 2010, 25, 1064–1077. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Chattopadhyay, P.K. Hybrid Differential Evolution with Biogeography-Based Optimization for Solution of Economic Load Dispatch. IEEE Trans. Power Syst. 2010, 25, 1955–1964. [Google Scholar] [CrossRef]
- Li, L.; He, D.; Jin, J.; Yu, B.; Gao, X. Multi-Objective Load Dispatch Control of Biomass Heat and Power Cogeneration Based on Economic Model Predictive Control. Energies 2021, 14, 762. [Google Scholar] [CrossRef]
- Tao, S.; Zhang, Y.; Yuan, M.; Zhang, R.; Xu, Z.; Sun, Y. Behavioral Economics Optimized Renewable Power Grid: A Case Study of Household Energy Storage. Energies 2021, 14, 4154. [Google Scholar] [CrossRef]
- Mahdy, A.; El-Sehiemy, R.; Shaheen, A.; Ginidi, A.; Elbarbary, Z.M.S. An Improved Artificial Ecosystem Algorithm for Economic Dispatch with Combined Heat and Power Units. Appl. Sci. 2022, 12, 1773. [Google Scholar] [CrossRef]
- Chakraborty, S.; Senjyu, T.; Yona, A.; Saber, A.Y.; Funabashi, T. Solving Economic Load Dispatch Problem with Valve-Point Effects Using a Hybrid Quantum Mechanics Inspired Particle Swarm Optimisation. IET Gener. Transm. Distrib. 2011, 5, 1042–1052. [Google Scholar] [CrossRef]
- Lu, H.; Sriyanyong, P.; Song, Y.H.; Dillon, T. Experimental Study of a New Hybrid PSO with Mutation for Economic Dispatch with Non-Smooth Cost Function. Int. J. Electr. Power Energy Syst. 2010, 32, 921–935. [Google Scholar] [CrossRef]
- Güvenç, U.; Sönmez, Y.; Duman, S.; Yörükeren, N. Combined Economic and Emission Dispatch Solution Using Gravitational Search Algorithm. Sci. Iran. 2012, 19, 1754–1762. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, J.; Mo, L.; Ouyang, S.; Liao, X. Economic Environmental Dispatch Using an Enhanced Multi-Objective Cultural Algorithm. Electr. Power Syst. Res. 2013, 99, 18–29. [Google Scholar] [CrossRef]
- Qin, Q.; Cheng, S.; Chu, X.; Lei, X.; Shi, Y. Solving Non-Convex/Non-Smooth Economic Load Dispatch Problems via an Enhanced Particle Swarm Optimization. Appl. Soft Comput. J. 2017, 59, 229–242. [Google Scholar] [CrossRef]
- Kaur, A.; Singh, L.; Dhillon, J.S. Modified Krill Herd Algorithm for Constrained Economic Load Dispatch Problem. Int. J. Ambient. Energy 2022, 43, 4332–4342. [Google Scholar] [CrossRef]
- Mohammadi, F.; Abdi, H. A Modified Crow Search Algorithm (MCSA) for Solving Economic Load Dispatch Problem. Appl. Soft Comput. J. 2018, 71, 51–65. [Google Scholar] [CrossRef]
- Shen, X.; Wu, G.; Wang, R.; Chen, H.; Li, H.; Shi, J. A Self-Adapted Across Neighborhood Search Algorithm with Variable Reduction Strategy for Solving Non-Convex Static and Dynamic Economic Dispatch Problems. IEEE Access 2018, 6, 41314–41324. [Google Scholar] [CrossRef]
- Li, F.; Qin, J.; Kang, Y. Multi-Agent System Based Distributed Pattern Search Algorithm for Non-Convex Economic Load Dispatch in Smart Grid. IEEE Trans. Power Syst. 2019, 34, 2093–2102. [Google Scholar] [CrossRef]
- Yu, J.T.; Kim, C.H.; Wadood, A.; Khurshaid, T.; Rhee, S.B. Jaya Algorithm with Self-Adaptive Multi-Population and Lévy Flights for Solving Economic Load Dispatch Problems. IEEE Access 2019, 7, 21372–21384. [Google Scholar] [CrossRef]
- Mokarram, M.J.; Niknam, T.; Aghaei, J.; Shafie-Khah, M.; Catalão, J.P.S. Hybrid Optimization Algorithm to Solve the Nonconvex Multiarea Economic Dispatch Problem. IEEE Syst. J. 2019, 13, 3400–3409. [Google Scholar] [CrossRef]
- Tai, T.C.; Lee, C.C.; Kuo, C.C. A Hybrid Grey Wolf Optimization Algorithm Using Robust Learning Mechanism for Large Scale Economic Load Dispatch with Vale-Point Effect. Appl. Sci. 2023, 13, 2727. [Google Scholar] [CrossRef]
- Dong, R.; Wang, S. New Optimization Algorithm Inspired by Kernel Tricks for the Economic Emission Dispatch Problem with Valve Point. IEEE Access 2020, 8, 16584–16594. [Google Scholar] [CrossRef]
- Xin-gang, Z.; Ji, L.; Jin, M.; Ying, Z. An Improved Quantum Particle Swarm Optimization Algorithm for Environmental Economic Dispatch. Expert Syst. Appl. 2020, 152, 113370. [Google Scholar] [CrossRef]
- Kansal, V.; Dhillon, J.S. Emended Salp Swarm Algorithm for Multiobjective Electric Power Dispatch Problem. Appl. Soft Comput. J. 2020, 90, 106172. [Google Scholar] [CrossRef]
- Azeem, M.; Malik, T.N.; Muqeet, H.A.; Hussain, M.M.; Ali, A.; Khan, B.; Rehman, A. Combined Economic Emission Dispatch in Presence of Renewable Energy Resources Using CISSA in a Smart Grid Environment. Electron 2023, 12, 715. [Google Scholar] [CrossRef]
- Hagh, M.T.; Kalajahi, S.M.S.; Ghorbani, N. Solution to Economic Emission Dispatch Problem Including Wind Farms Using Exchange Market Algorithm Method. Appl. Soft Comput. 2020, 88, 106044. [Google Scholar] [CrossRef]
- Ali, M.H.; El-Rifaie, A.M.; Youssef, A.A.F.; Tulsky, V.N.; Tolba, M.A. Techno-Economic Strategy for the Load Dispatch and Power Flow in Power Grids Using Peafowl Optimization Algorithm. Energies 2023, 16, 846. [Google Scholar] [CrossRef]
- Ellahi, M.; Abbas, G.; Satrya, G.B.; Usman, M.R.; Gu, J. A Modified Hybrid Particle Swarm Optimization with Bat Algorithm Parameter Inspired Acceleration Coefficients for Solving Eco-Friendly and Economic Dispatch Problems. IEEE Access 2021, 9, 82169–82187. [Google Scholar] [CrossRef]
- Xu, M.; Li, W.; Feng, Z.; Bai, W.; Jia, L.; Wei, Z. Economic Dispatch Model of High Proportional New Energy Grid-Connected Consumption Considering Source Load Uncertainty. Energies 2023, 16, 1696. [Google Scholar] [CrossRef]
- Kurundkar, K.M.; Vaidya, G.A. Stochastic Security-Constrained Economic Dispatch of Load-Following and Contingency Reserves Ancillary Service Using a Grid-Connected Microgrid during Uncertainty. Energies 2023, 16, 2607. [Google Scholar] [CrossRef]
- Ma, H.; Yang, Z.; You, P.; Fei, M. Multi-Objective Biogeography-Based Optimization for Dynamic Economic Emission Load Dispatch Considering Plug-in Electric Vehicles Charging. Energy 2017, 135, 101–111. [Google Scholar] [CrossRef]
- Zou, Y.; Zhao, J.; Ding, D.; Miao, F.; Sobhani, B. Solving Dynamic Economic and Emission Dispatch in Power System Integrated Electric Vehicle and Wind Turbine Using Multi-Objective Virus Colony Search Algorithm. Sustain. Cities Soc. 2021, 67, 102722. [Google Scholar] [CrossRef]
- Liu, Z.F.; Li, L.L.; Liu, Y.W.; Liu, J.Q.; Li, H.Y.; Shen, Q. Dynamic Economic Emission Dispatch Considering Renewable Energy Generation: A Novel Multi-Objective Optimization Approach. Energy 2021, 235, 121407. [Google Scholar] [CrossRef]
- Li, L.L.; Liu, Z.F.; Tseng, M.L.; Zheng, S.J.; Lim, M.K. Improved Tunicate Swarm Algorithm: Solving the Dynamic Economic Emission Dispatch Problems. Appl. Soft Comput. 2021, 108, 107504. [Google Scholar] [CrossRef]
- Li, L.L.; Shen, Q.; Tseng, M.L.; Luo, S. Power System Hybrid Dynamic Economic Emission Dispatch with Wind Energy Based on Improved Sailfish Algorithm. J. Clean. Prod. 2021, 316, 128318. [Google Scholar] [CrossRef]
- Kheshti, M.; Ding, L.; Ma, S.; Zhao, B. Double Weighted Particle Swarm Optimization to Non-Convex Wind Penetrated Emission/Economic Dispatch and Multiple Fuel Option Systems. Renew. Energy 2018, 125, 1021–1037. [Google Scholar] [CrossRef]
- Pandit, N.; Tripathi, A.; Tapaswi, S.; Pandit, M. An Improved Bacterial Foraging Algorithm for Combined Static/Dynamic Environmental Economic Dispatch. Appl. Soft Comput. J. 2012, 12, 3500–3513. [Google Scholar] [CrossRef]
- Liang, H.; Liu, Y.; Li, F.; Shen, Y. Dynamic Economic/Emission Dispatch Including PEVs for Peak Shaving and Valley Filling. IEEE Trans. Ind. Electron. 2019, 66, 2880–2890. [Google Scholar] [CrossRef]
- Al-Bahrani, L.T.; Horan, B.; Seyedmahmoudian, M.; Stojcevski, A. Dynamic Economic Emission Dispatch with Load Dema Nd Management for the Load Demand of Electric Vehicles during Crest Shaving and Valley Filling in Smart Cities Environment. Energy 2020, 195, 116946. [Google Scholar] [CrossRef]
- Behera, S.; Behera, S.; Barisal, A.K. Dynamic Combined Economic Emission Dispatch Integrating Plug-in Electric Vehicles and Renewable Energy Sources. Int. J. Ambient. Energy 2022, 43, 4683–4700. [Google Scholar] [CrossRef]
- Wang, G.G.; Deb, S.; Coelho, L.D.S. Elephant Herding Optimization. In Proceedings of the 2015 3rd International Symposium on Computational and Business Intelligence (ISCBI), Bali, Indonesia, 7–9 December 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, G.G.; Deb, S.; Gao, X.Z.; Dos Santos Coelho, L. A New Metaheuristic Optimisation Algorithm Motivated by Elephant Herding Behaviour. Int. J. Bio-Inspired Comput. 2016, 8, 394–409. [Google Scholar] [CrossRef]
- Li, W.; Wang, G.G.; Alavi, A.H. Learning-Based Elephant Herding Optimization Algorithm for Solving Numerical Optimization Problems. Knowl.-Based Syst. 2020, 195, 105675. [Google Scholar] [CrossRef]
- El-Naggar, M.F.; Mosaad, M.I.; Hasanien, H.M.; AbdulFattah, T.A.; Bendary, A.F. Elephant Herding Algorithm-Based Optimal PI Controller for LVRT Enhancement of Wind Energy Conversion Systems. Ain. Shams. Eng. J. 2021, 12, 599–608. [Google Scholar] [CrossRef]
- Tariq, F.; Alelyani, S.; Abbas, G.; Qahmash, A.; Hussain, M.R. Solving Renewables-Integrated Economic Load Dispatch Problem by Variant of Metaheuristic Bat-Inspired Algorithm. Energies 2020, 13, 6225. [Google Scholar] [CrossRef]
- Mukherjee, V.; Verma, S. Optimal Real Power Rescheduling of Generators for Congestion Management Using a Novel Ant Lion Optimiser. IET Gener. Transm. Distrib. 2016, 10, 2548–2561. [Google Scholar] [CrossRef]
- Peesapati, R.; Yadav, V.K.; Kumar, N. Flower Pollination Algorithm Based Multi-Objective Congestion Management Considering Optimal Capacities of Distributed Generations. Energy 2018, 147, 980–994. [Google Scholar] [CrossRef]
- Wulandhari, L.A.; Komsiyah, S.; Wicaksono, W. Bat Algorithm Implementation on Economic Dispatch Optimization Problem. Procedia Comput. Sci. 2018, 135, 275–282. [Google Scholar] [CrossRef]
- Al-Betar, M.A.; Awadallah, M.A.; Krishan, M.M. A Non-Convex Economic Load Dispatch Problem with Valve Loading Effect Using a Hybrid Grey Wolf Optimizer. Neural Comput. Appl. 2020, 32, 12127–12154. [Google Scholar] [CrossRef]
- Mohammadi-ivatloo, B.; Rabiee, A.; Soroudi, A.; Ehsan, M. Imperialist Competitive Algorithm for Solving Non-Convex Dynamic Economic Power Dispatch. Energy 2012, 44, 228–240. [Google Scholar] [CrossRef]
- Lu, Y.; Zhou, J.; Qin, H.; Wang, Y.; Zhang, Y. Chaotic Differential Evolution Methods for Dynamic Economic Dispatch with Valve-Point Effects. Eng. Appl. Artif. Intell. 2011, 24, 378–387. [Google Scholar] [CrossRef]
- Balamurugan, R.; Subramanian, S. Differential Evolution-Based Dynamic Economic Dispatch of Generating Units with Valve-Point Effects. Electr. Power Compon. Syst. 2008, 36, 828–843. [Google Scholar] [CrossRef]
- Hemamalini, S.; Simon, S.P. Dynamic Economic Dispatch Using Artificial Immune System for Units with Valve-Point Effect. Int. J. Electr. Power Energy Syst. 2011, 33, 868–874. [Google Scholar] [CrossRef]
- Immanuel Selvakumar, A. Enhanced Cross-Entropy Method for Dynamic Economic Dispatch with Valve-Point Effects. Int. J. Electr. Power Energy Syst. 2011, 33, 783–790. [Google Scholar] [CrossRef]
- Yuan, X.; Su, A.; Yuan, Y.; Nie, H.; Wang, L. An Improved PSO for Dynamic Load Dispatch of Generators with Valve-Point Effects. Energy 2009, 34, 67–74. [Google Scholar] [CrossRef]
- Victoire, T.A.A.; Jeyakumar, A.E. Deterministically Guided PSO for Dynamic Dispatch Considering Valve-Point Effect. Electr. Power Syst. Res. 2005, 73, 313–322. [Google Scholar] [CrossRef]
- Sivasubramani, S.; Swarup, K.S. Hybrid SOA–SQP Algorithm for Dynamic Economic Dispatch with Valve-Point Effects. Energy 2010, 35, 5031–5036. [Google Scholar] [CrossRef]
- Victoire, T.A.A.; Jeyakumar, A.E. Reserve Constrained Dynamic Dispatch of Units with Valve-Point Effects. IEEE Trans. Power Syst. 2005, 20, 1273–1282. [Google Scholar] [CrossRef]
- Victoire, T.A.A.; Jeyakumar, A.E. A Modified Hybrid EP–SQP Approach for Dynamic Dispatch with Valve-Point Effect. Int. J. Electr. Power Energy Syst. 2005, 27, 594–601. [Google Scholar] [CrossRef]
- Basu, M. Hybridization of Artificial Immune Systems and Sequential Quadratic Programming for Dynamic Economic Dispatch. Electr. Power Compon. Syst. 2009, 37, 1036–1045. [Google Scholar] [CrossRef]
- He, D.; Dong, G.; Wang, F.; Mao, Z. Optimization of Dynamic Economic Dispatch with Valve-Point Effect Using Chaotic Sequence Based Differential Evolution Algorithms. Energy Convers. Manag. 2011, 52, 1026–1032. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).