Condition Monitoring and Fault Detection in Small Induction Motors Using Machine Learning Algorithms

Abstract

Electric induction motors are one of the most important and widely used classes of machines in modern industry. Large motors, which are commonly process-critical, will usually have built-in condition-monitoring systems to facilitate preventive maintenance and fault detection. Such capabilities are usually not cost-effective for small (under ten horsepower) motors, as they are inexpensive to replace. However, large industrial sites may use hundreds of these small motors, often to drive cooling fans or lubrication pumps for larger machines. Multiple small motors may further be assigned to a single electrical circuit, meaning a failure in one could damage other motors on that circuit. There is thus a need for condition monitoring of aggregations of small motors. We report on an ongoing project to develop a machine-learning-based solution for fault detection in multiple small electric motors. Shallow and deep learning approaches to this problem are investigated and compared, with a hybrid deep/shallow system ultimately being the most effective.

1. Introduction

Induction motors are a hugely important class of electrical machines, shouldering much of the task of transforming energy into useful work in modern industry [1]. As such, the maintenance of these often-critical machines is of paramount importance. Over 40 years of research have shown that many types of faults can be detected in motor sensor data before they cause a failure; there has thus been great interest in using this fact to reduce the losses such failures cause.

Condition Monitoring (CM) is the use of non-destructive testing or sensed data to detect changes within a monitored system. While earlier approaches could only flag the occurrence of a change, more modern approaches can identify a causative fault, its location, and the damage completed so far [2]. These are largely inferential sensing approaches (the estimation of a complex, time-varying system state based on reading from simpler sensors [3,4,5]); some examples include [6,7,8,9]. Some adaptive systems can even attempt self-repair based on that information [2]. CM today is a well-known, economical approach to maintaining large and expensive systems, allowing for predictive maintenance before a fault worsens or causes failure [10,11].

Condition monitoring for small electric motors (rated at 10 HP or less) is not commonly practiced as they are inexpensive and not directly process-critical. However, a large industrial site may contain hundreds of these motors. There is an increasing recognition that their failure also impacts the plant’s operation as they often operate important subcomponents of, or protection systems for, high-value systems. These can include operating cooling/lubrication/HVAC equipment that protects those larger systems. Clearly, any CM solution for these motors must be very cheap. The most sensible approach would thus be to monitor entire groups of small motors at once (e.g., on a common electrical circuit).

This study focuses on detecting faults in multiple small motors. We believe that machine learning approaches would be particularly effective in designing a low-cost solution. Thus, after designing and performing an experimental characterization of damaged small motors, we construct inferential sensors based on ML algorithms. We view CM as an instance of the anomaly detection problem, in which the goal is to induce a model of “normal” behavior and alert on any deviations from it [12]. We have experimented with both shallow and deep learning algorithms for the normal model while we focus on shallow algorithms for the anomaly detector itself. We found that a design using a one-dimensional Convolutional Neural Network (CNN) as the normal model, and a random forest as the anomaly detector, yielded the strongest performance (TPR = 0.948, FPR = 0.033) on a multi-motor dataset.

The remainder of this paper is organized as follows. In Section 2, we discuss the equipment and methodology for our characterization experiments. We present our CM experimental methodology in Section 3, then we present and discuss the results in Section 4. We offer a summary and discussion of future work in Section 5.

2. Background and Related Work

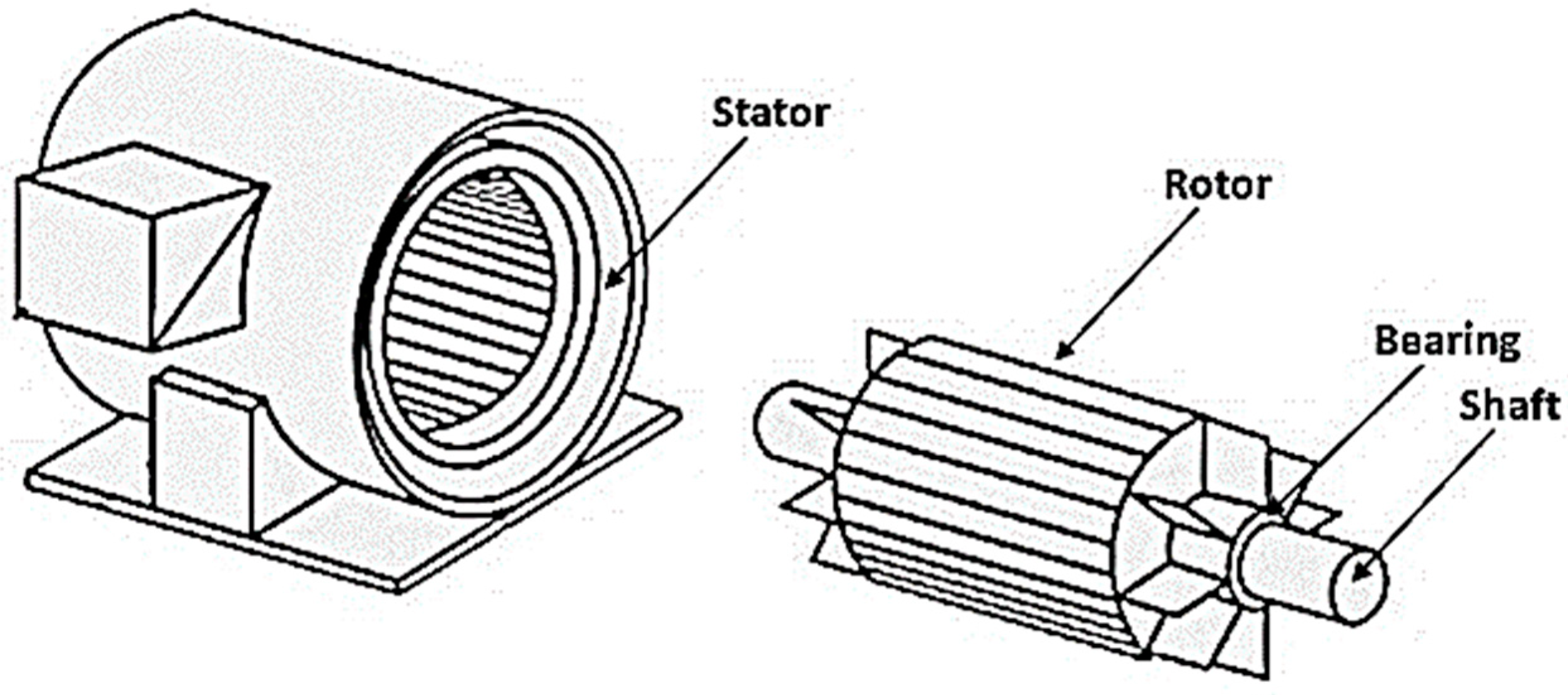
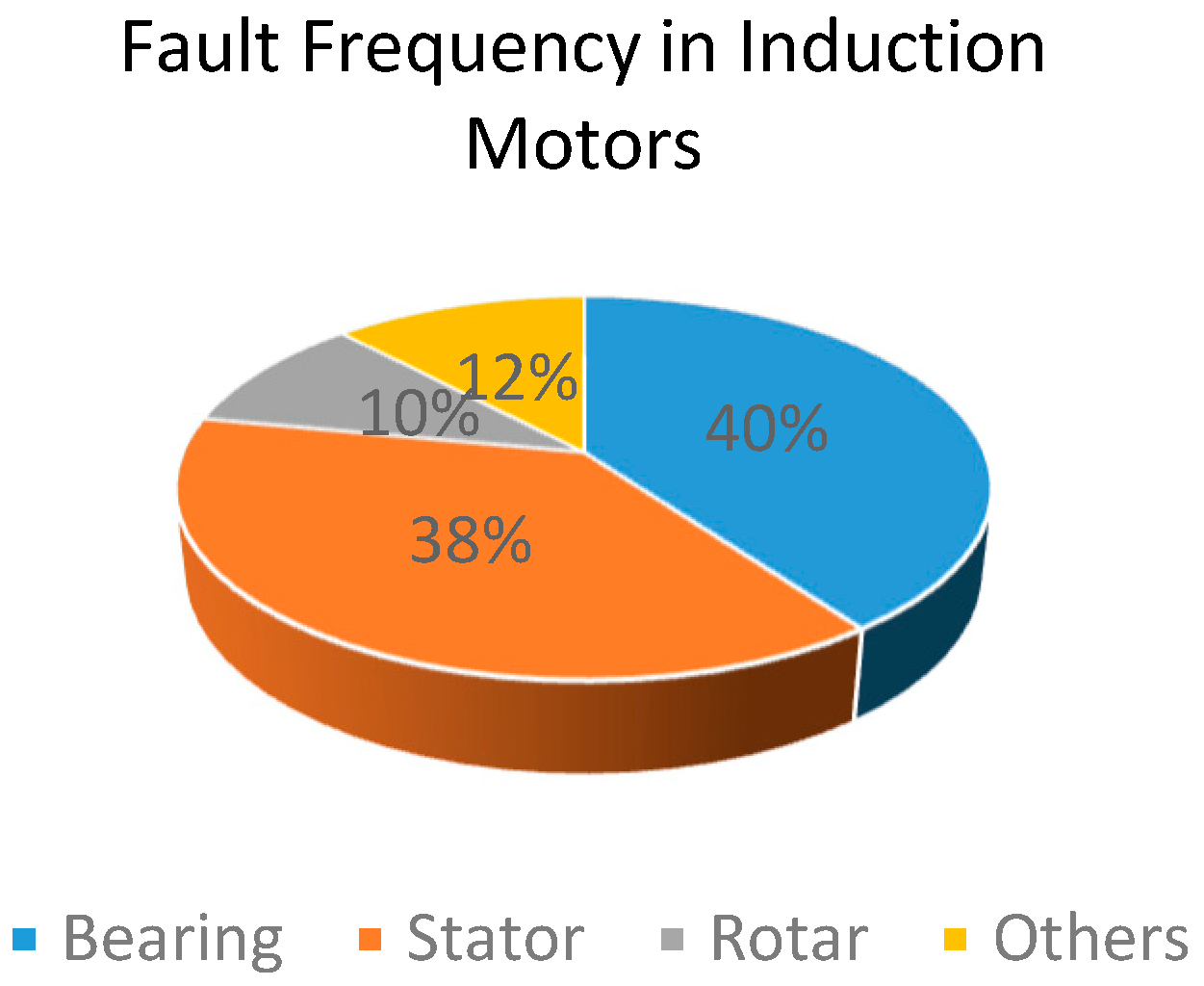
2.1. Condition Monitoring in Electric Motors

A simplified view of a typical induction motor is depicted in Figure 1. The wire windings in the stator form a set of electromagnets. With different phases applied to different windings, this produces a rotating magnetic field. The rotating field induces a current within the windings of the rotor, in turn creating a magnetic field that opposes the rotation of the stator magnetic field. As the rotor and attached shaft are free to turn within the stator, that opposing force results in rotation. Bearings provide lubricated support to the rotor and shaft as they spin, and the rotating shaft is thus able to perform useful work.

The most common faults that occur in induction motors are bearing faults, stator inter-turn faults, and cracked rotor bars [13,14]. Bearing failures account for about 40% of faults in induction motors [3], while stator, rotor, and other faults comprise roughly 38%, 10%, and 12% of the faults, respectively (see Figure 2) [15]. In a more detailed breakdown, [16] classifies induction motor failures as arising from mechanical or electrical faults. Mechanical faults include bearing failures (caused by incorrect lubrication, mechanical stresses, incorrect assembling, misalignment, etc. [14]), gearbox failures (for motors with gearboxes), and eccentricity (the rotor is not centered with respect to the stator and/or its rotation is not aligned with the central axis of the stator). Electrical faults may be associated with the stator or rotor. Stator faults include damage to the stator windings (especially insulation) or the drive (speed controller). Rotor faults include broken rotor bars, damage to rotor windings, and broken end rings.

Numerous sensing modalities have been explored for detecting faults. A review in 2005 found that axial electromagnetic flux monitoring, current and voltage monitoring, thermal/infrared sensors, vibration sensors, acoustic sensors, and chemical analysis of motor oil [17] had all been explored. Many of these remain in use today. One recent innovation is the use of novel magnetic-flux sensors to examine both leakage flux and the air-gap flux between the stator and rotor. Recent reviews of this technology may be found in [18,19]. Vibration analysis was reviewed in [20], while [21] also reviews these various modalities, and partial-discharge analysis. Recent work has often focused on current analysis, particularly current harmonics; this is a non-invasive, in-operation modality. Characteristic frequency responses for various faults have been derived from machine physics [22], and empirical studies of inferential sensors using current analysis usually show high accuracy [23].

Considering that induction motors are rotating machines, a number of the signals indicating incipient or actual faults are periodic. Thus, frequency-domain analysis has been a major approach to motor fault detection for decades. Fourier transforms were studied first, but more modern approaches examine combined time-frequency domain signals. These include wavelet transforms, Empirical Mode Decomposition, short-term Fourier transforms, Hilbert transforms, singular value decomposition, Park’s Vector Analysis, and the Wigner-Ville distribution, among others [16,24]. Some faults are easily detected and diagnosed in the frequency domain, but more commonly, the time-frequency band coefficients are passed as features to a classifier algorithm in the usual inferential-sensing approach [16,24].

A 2022 review in [21] found that there were three fundamental approaches to classifier design for CM: model-based, signal-based, and data-driven algorithms. Model-based approaches require a reference system (either a physical copy or a physics-based simulation) against which observations of the monitored system are compared. Deviations from the reference system, if large enough, raise an alarm. Alternatively, a known mathematical model (be it an exact formulation, a finite-element approximation, or the results of a system identification algorithm) can be combined with observed data to perform state estimation for the monitored system. A key advantage of model-based classifiers is that the reference model embodies “normal” behavior; deviations from normal behavior very often signal incipient or actual faults, even when the nature of the fault is unexpected or unknown. They are thus capable of detecting unexpected faults [21].

Signal-based classification refers generally to the detection and diagnosis of faults directly from a spectral analysis (or related technique in time-frequency domains). Bearing, stator, and rotor are most easily diagnosed in this fashion, as they create abnormal harmonics in the motor. For instance, motor current analysis using the Fast Fourier Transform was state-of-the-art in the late 20th Century. However, modern systems usually employ automated classifiers to detect subtler fault signals [21].

Automated classifiers, as above, form the third (data-driven) class of CM algorithms. Observed signals from the monitored system (which have often, but not always, been transformed from the time domain to a frequency or time-frequency domain as above) are used to recognize examples of the “normal” and “faulty” classes (for fault detection), or to recognize examples of different types of faults in fault diagnosis. The two main approaches to designing classifiers are statistical modeling (e.g., ARIMA, ANOVA, etc.) and inductive machine learning. The latter divides into supervised learning (where an adequate number of examples of each class must be available) and unsupervised learning (most commonly clustering). Some recent work in deep learning for CM looked at Generative Adversarial Network designs, in which one network tried to mimic a signal that competes with another network that tries to distinguish real signals from the generated ones [21]. Machine learning (ML) approaches for fault detection and diagnosis of complex machines have been explored in [1,25]; deep learning in particular has been applied to fault diagnosis in, e.g., [26,27,28,29].

The review in [21], and several recent papers proposing intelligent CM algorithms [16,30,31], make an assumption about supervised data-driven algorithms: that fault detection can be treated as a standard classification problem. However, supervised machine-learning classifiers require adequate examples of both healthy and faulty operation in order to separate the two classes in feature space (technically, the classifiers inductively determine a boundary between regions in feature space corresponding to each class). They are thus unable to detect unexpected faults (as a model-based algorithm would be able to), as there are no examples of the unexpected faults to define a boundary for. However, this neglects the class of intelligent anomaly detection algorithms [12], which have been studied for many years. These algorithms operate by inducing a model of normal behavior, then detecting deviations from it; in essence, a data-driven version of model-based classifiers. Anomaly-detection approaches the fault-detection problem in CM have been studied by numerous authors, with some recent examples being [28,29].

2.2. Anomaly Detection and Deep Learning

Following the vast success of deep learning in various fields, a few deep anomaly detections (AD) methods have also been studied, with promising results [32,33]. Nonetheless, this is still an underexplored topic [33]. With regard to the training approach and the availability of data, these methods can be categorized as supervised, semi-supervised, and unsupervised deep AD.

Supervised AD approaches required labeled data from both normal and anomaly classes for training a deep classifier. Such methods are usually composed of two components: a deep feature extractor (e.g., a deep autoencoder) followed by a classifier. Deep supervised models require a substantial amount of training data. Therefore, these approaches are not as appealing as semi-supervised and unsupervised approaches due to the difficulty and/or expense of acquiring a sufficient volume of labeled data (with fault data usually the most difficult to come by) [33]. Semi-supervised techniques only require data that belongs to one class, typically the normal class. These models generate a boundary around the normal instances and consider the points outside that boundary as anomalies [34,35]. These approaches can take advantage of the (usually) large amounts of available normal data. Unsupervised methods model intrinsic attributes of the data, such as distances or densities [36]. Cost-effectiveness is the main benefit of such methods, as there is no necessity for labeled data. However, unsupervised models are highly vulnerable to noise and faulty data and often do not perform as well as supervised or semi-supervised approaches [33].

One-class neural networks are a good example of semi-supervised anomaly detectors. They integrate the one-class objective function within the layers of deep neural networks. These models create boundaries that separate normal and anomaly instances, such as a hypersphere (Deep Support Vector Data Description or Deep SVDD [37]) or a hyperplane (OC-NN [38]). These studies show that one-class neural networks are among the most effective anomaly detection approaches, in particular for complex datasets. However, long training times seem to be their main issue [33].

One-class adversarial networks (OCAN [39]) are an end-to-end one-class anomaly detector architecture that employs the concept of bad GANs [40] to generate anomalous instances based on normal data. “Anomalous” here indicates that the generator’s distribution output differs from the true data distribution. Hence, the generated data will complement the training dataset, which results in improved generalization for a semi-supervised anomaly detection algorithm.

3. Data Collection and Dataset Generation

To the best of our knowledge, there are no publicly available CM datasets representing multiple electric motors. Furthermore, there are no available datasets for CM of small electric motors that (1) include multiple failure modes across multiple instances of a common motor type; (2) simultaneously record current, voltage, and temperature; and (3) do so at sampling rates up to 10 kHz. The first would allow us to compare CM solutions for both fault detection and fault identification in a constant motor design; the second and third points offer the opportunity to study both high-rate features, such as current harmonics and low-rate ones, such as power profiles. Thus, our first task was to design an experimental apparatus and procedures to collect such a dataset.

An Edmonton-area motor manufacturer donated a set of 20 identical three-phase motors, each rated at 1 HP. A mount was manufactured to hold a motor with the rotor horizontal and couple it to a dynamometer. Electrical and thermal sensors, along with data loggers, were then attached. Our basic experimental design is to run the motors under no-load and full-load conditions in an undamaged state. Then, after all the undamaged data has been collected, each motor will be damaged in a particular manner, and the tests repeated (clearly, they would terminate if the motor failed catastrophically; this, however, did not occur).

3.1. Hardware and Instruments

Our experimental apparatus is depicted in Figure 3. The motors used in our experiments were stainless steel 3-phase one-horsepower motors with 6205 sized drive and fan bearings. They are rated at both 208 V and 480 V line-to-line, but for this application, we ran them at 208 V. This gave a maximum current of 3.8 A at full load, with a maximum rated speed of 1145 RPM. A digital multimeter measured the current (a static value) for the line-to-line locked rotor tests. For all other tests, we sampled the motor current at 10 kHz using the dSPACE DS1104 board. The dynamometer controller was set to create a maximum (full load) torque of 5.624 N$·$m and was used to measure the shaft’s rotational speed in RPM when the motor was coupled to the dynamometer. For the no-load uncoupled tests, the tachometer was used to record this shaft speed.

The oscilloscope used for this project is capable of sampling at 100 MHz but was used to sample at 500 KHz for every test except the inrush test. For the inrush test, the oscilloscope was set to sample at 12.5 MHz. The thermal camera used for this project was connected via an Ethernet switch to a desktop where the video feed was saved. Video of the entire experimental sequence was saved for each test, including the 2.5 h warming period for each “hot” test (i.e., sensed data is collected once the motor has reached steady state heat). Finally, a custom mount was built out of aluminum to hold the dynamometer, rails for the mount to slide on, two mounts to bolt the motors onto, and an adjustable rotor lock so that a locked rotor test could be run.

3.2. Controlled Variables

The controlled variables in our experiments were motor temperature, applied load, motor alignment, rotor locking, dynamometer coupling, and motor damage. The motor temperature was either cold (the motor had been stopped and allowed to cool to room temperature) or hot (the motor had run under full load for 2.5 h, reaching steady-state temperature; this length of time was empirically determined using the thermal imager). The applied load was either full (dynamometer set to 5.624 N∙m) or no load. Motor alignment is either centered (default condition) or twisted (the drive end bearings were under uneven lateral pressure). Rotor lock is a binary variable indicating whether the rotor lock we designed is applied, in which case the rotor cannot rotate. Dynamometer coupling is also binary, indicating whether or not the motor is coupled to the dynamometer. Finally, each motor will either be undamaged or will have been damaged in one way; thus, for each motor, there are two possible values of this variable.

3.3. Experimental Design

We now discuss the experiments run on the apparatus above. Our basic design is a complete factorial experiment for each motor (considering that the motor will only have one type of damage). We begin with trial runs of healthy motors, refining our observation procedures, and troubleshooting the data collection systems. Once those were complete, we executed the no-damage (“healthy”) portion of the experimental design. We then damage the motors and execute the “damage” portion of the design. In the next subsection, we detail the types of faults we induce, our rationale for selecting them, and the specific manner in which the damage is caused.

3.3.1. Stator Short

Within the 38% of failures caused by stator faults, the overwhelming majority of them are caused by shorts in the stator [15]. In order to test if we were able to detect a stator short, motor 3 was opened, and a Dermal was used to strip away some of the insulation between two wires in a winding, and the two wires were soldered together. The solder can be seen outlined by the red box in Figure 4. The motor was then reassembled and run through the same full tests as would be completed in a “hot” test. However, it was also subject to a number of short tests that were run to gather data on the change in impedance from the short caused.

3.3.2. Bearing Faults

It is unknown exactly why the majority of bearings fail in industry settings, but experience indicates that the majority are caused by the following:

• Foreign materials entering the bearing and causing increased wear and pitting on the balls, cage, and inner or outer tracks.
• Under-greasing, or not putting any grease in the bearing, which could cause the bearing to overheat. This could cause the bearings and tracks to deform or warp if they are too hot under load or are going through multiple heating and cooling phases.
• Over-greasing the bearing, causing the seal to be broken, which subsequently causes all of the grease to leak out. This would lead to the same problem as under-greasing the bearing.
• Unbalanced loads on the motor can cause one side of the bearing to wear at a much greater rate than another side, which can lead to static eccentricity.
• Simple friction wear caused by running the motor over many working hours.

To simulate these faults, multiple bearings were put through different types of damage:

• To simulate foreign materials entering the bearing and causing increased wear and pitting, multiple silica carbide beads were packed into the bearing. The bearing was then run on a lathe with the outer ring held stationary at 150 rpm for 40 min. As a side note, after the bearing was run through a full test with the 2.5 h warming period, it was found that the cage holding the bearing balls in place was broken. This cage was not broken before the test was run. The carbide beads were not extensively cleaned out before running the motor for all of its tests, nor was the motor re-greased after the damage was caused.
• To simulate overheating caused by lack of grease, the bearing inner track was heated to a cherry red glow with an acetylene torch. This caused all of the grease to be burned off and left the bearing slightly warped, which caused irregular damage on the inner and outer tracks and the ball bearings. The bearing very clearly ran rough after the damage was caused, and no grease was placed back in the bearing. Running the bearing through the 2.5 h warming period did not seem to cause additional apparent damage.
• The last damage type that was created was a 3 mm hole in the outer track. While this is unlikely to appear in industry, it was completed to compare our results to other research paper’s results as they focused primarily on single point bearing faults, such as a drilled hole in the inner or outer track. The reason they focused on this type of damage is because the damage is supposed to appear at specific frequencies as opposed to general noise increases that random damage causes. Additional bearings were damaged by hitting a bearing’s inner track with a hammer once and multiple times and creating a score on the outer track.

The individual datasets we collected for each motor, and the combined dataset discussed in this paper, are available via Github https://github.com/abso2021 (accessed on 31 May 2023).

4. Methodology

As discussed, our CM design is an anomaly detector, as in Figure 5. It has two components: a model of normal behavior that predicts the current observation from previous ones and an anomaly detector that identifies when the actual and predicted observations differ substantially [12,41].

Our normal model is a one-step-ahead time series forecasting algorithm applied to the current and voltage time series across all three phases (giving six variates total). The essential idea is to estimate the current observation vector $\overrightarrow{x_n}$ given previous values $\overrightarrow{x_{n-1}}$. As this model is supposed to predict the next value with the assumption that our system is in the healthy state, it is trained on healthy data only.

The anomaly detector is responsible for comparing the six values predicted by the normal model with the actual observed values for the next time step. Similar in structure to a classifier, the models designed for this part take 12 inputs and have only 1 binary output, indicating the occurrence of a failure.

We have explored both shallow learning and deep learning approaches for designing our anomaly detector. Both were applied to a dataset constructed from multiple experimental runs in the laboratory setup above, performed on three separate motors (in order to guard against over-specialization of the models to one motor’s particular behavior). Healthy runs are grouped together first, followed by the runs after the motors were individually damaged. We use the method of delay embedding [42] to convert the multivariate time series from each motor into a form suitable for machine learning, then conduct parameter exploration studies for each of the normal model/anomaly detector combinations we have tested.

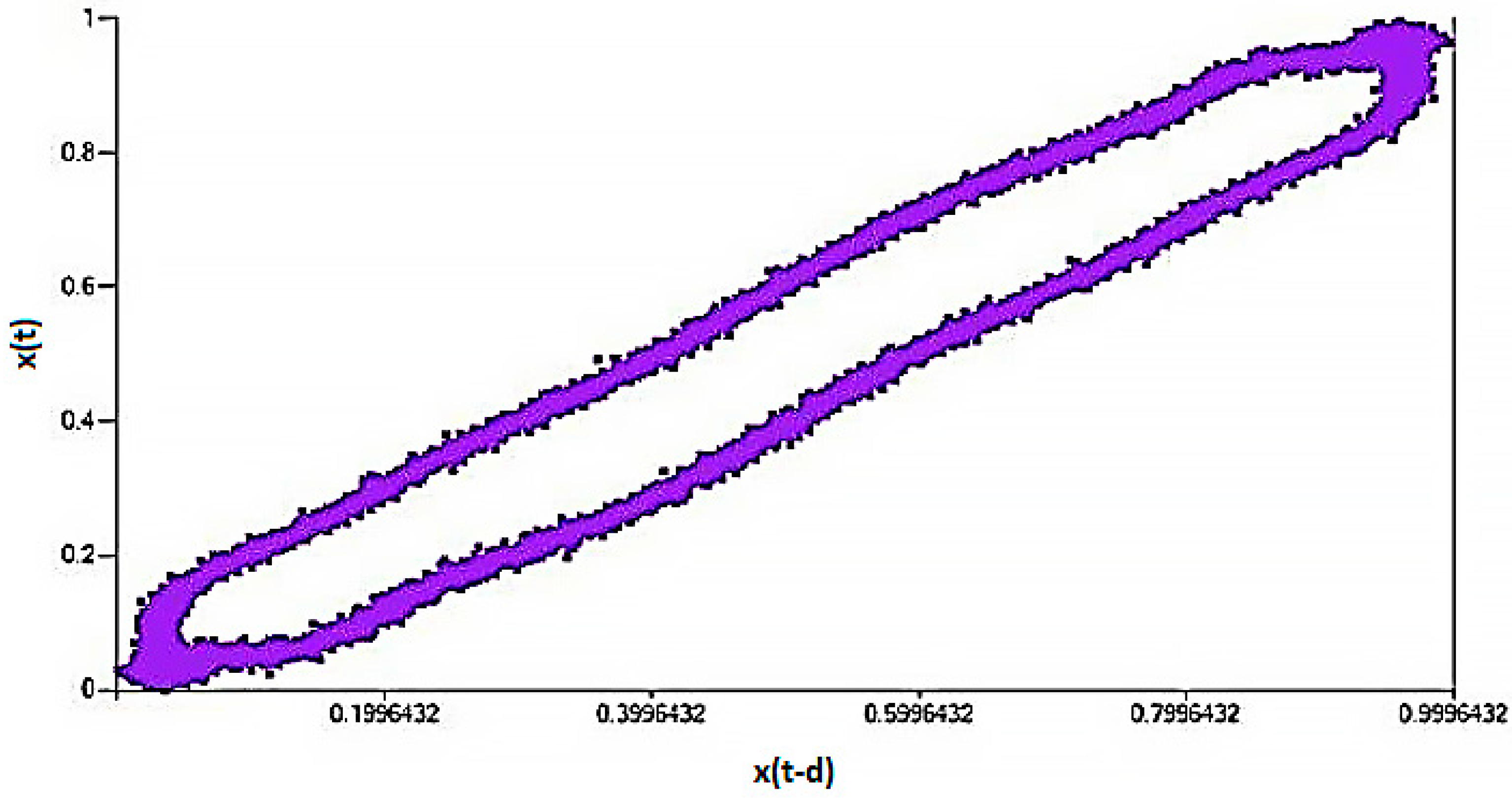
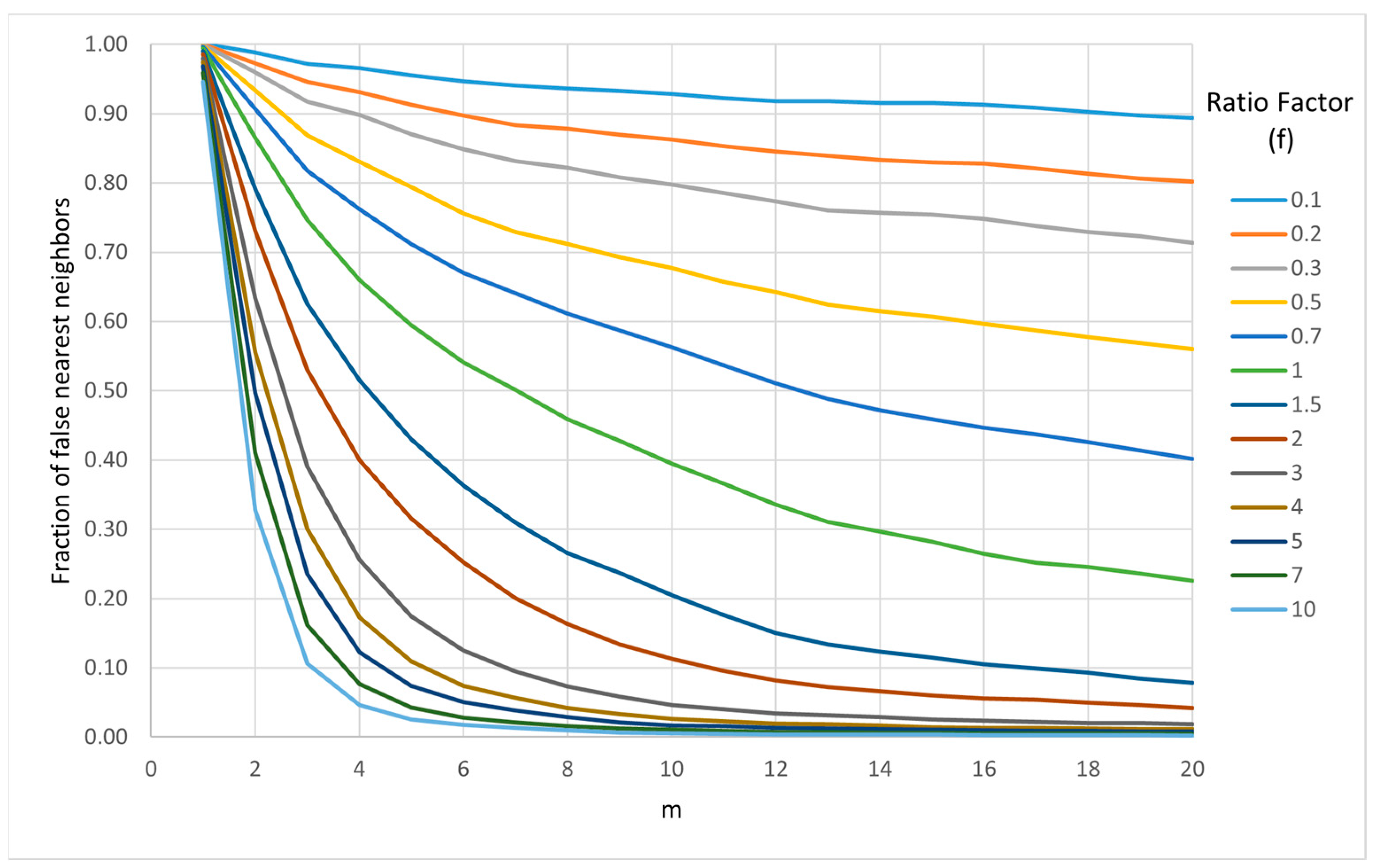
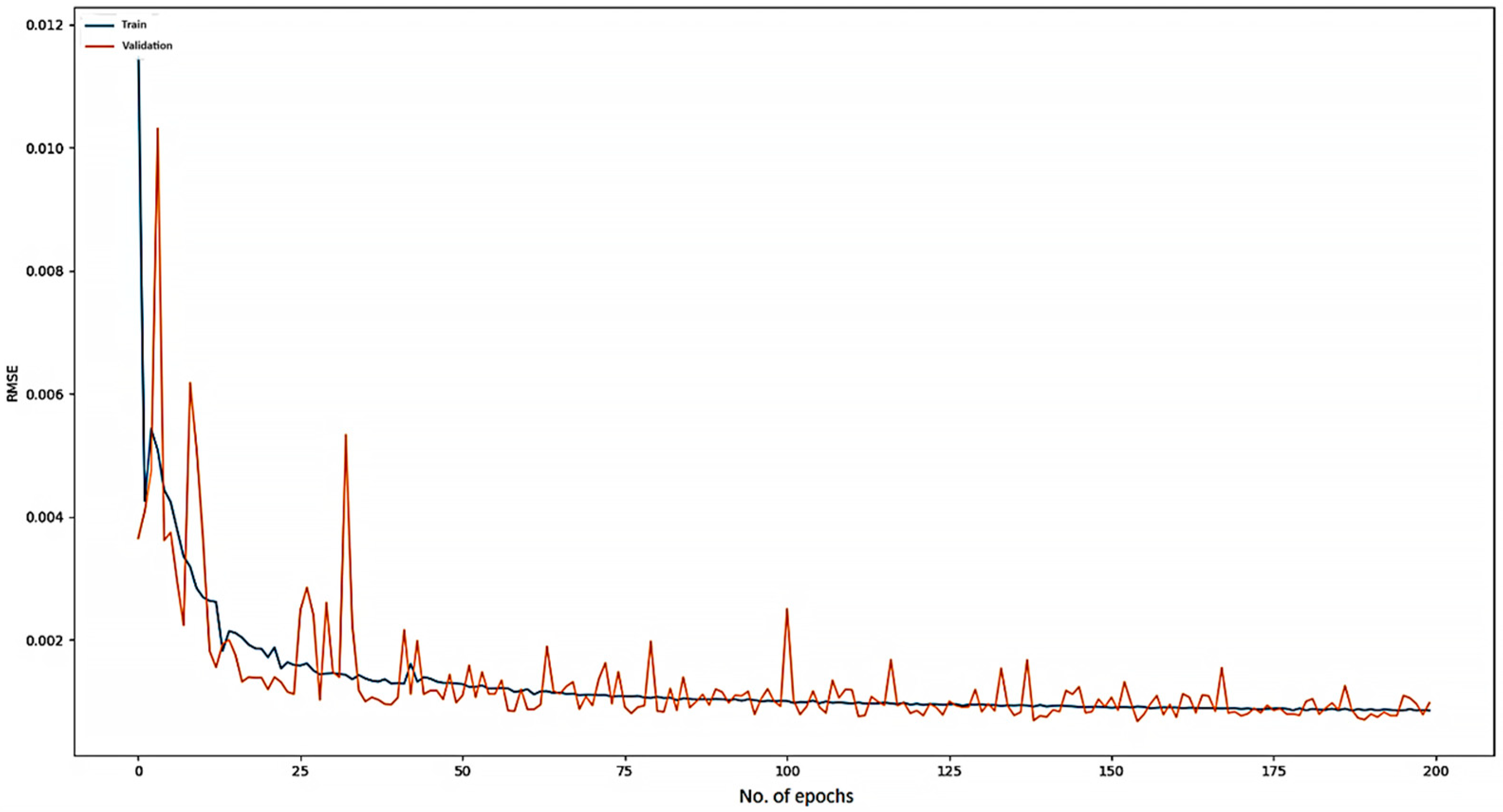
4.1. Data Preprocessing

We begin by normalizing each variate within the data using the positive linear transform:

$$X_n=\frac{x-x_{min}}{x_{max}-x_{min}}$$

(1)

where $x_{min}$ is the minimal and $x_{max}$ the maximal observed value for the variate X, while x is the current value. We then split the data into training and out-of-sample test partitions, assigning the chronologically earliest 70% of the dataset to the training partition and the remaining 30% for testing. This is the chronologically ordered single-split design commonly used in time series forecasting experiments.

After the data are partitioned, they need to be converted from a multivariate time series into a suitable form for general (table-oriented) machine learning algorithms. One common approach is delay embedding (also known as the lagged representation) [43]. The current observation in a time series, and multiple prior observations, are concatenated into a vector. Takens showed that this vector is isomorphic to the (unrecoverable) state vector of the system the time series was observed from at that time instant [43]. The form of a delay vector in a univariate time series is [44]:

$$\overrightarrow{x_n}=\left(x_{n-\left(m-1\right)d},x_{n-\left(m-2\right)d},\dots ,x_n\right)$$

(2)

where $x_i$ is the i-th element of the time series. The embedding is repeated for every $x_i$ in the time series (save those at the beginning for which insufficient former examples are available). For a multivariate time series, the embedding process is repeated for each variate, and the delay vectors for each are concatenated together. Per Equation (2), creating a delay vector comes down to finding two important parameters: the delay (d) and the dimensionality (m). Finding d allows us to get an optimal level of autocorrelation within each delay vector (by taking each successive value, or every second, every third, etc.) [45]. d is determined heuristically, guided by taking the first minimum of the time-delayed mutual information statistic [42]. A phase plot using that d is then computed to check if there are clear spatial relationships in the data. For example, Figure 6 presents our phase plot for d = 6, in which an elliptical structure is clearly visible. The dimensionality m of the delay vector is mathematically critical; Takens’ result above only holds if m is large enough (at least twice the actual dimensionality of the original state space). The value of m can be determined heuristically by using the false-nearest neighborhood algorithm [46,47]. In this algorithm, we systematically survey the data points and their neighbors in dimension d = 1, then d = 2, and so on. As the state-space attractor is unfolded, some points originally close together will abruptly separate; these are termed “false nearest neighbors”. The algorithm works by setting a threshold for how large of a sudden separation constitutes a false neighbor, and the heuristic is to find a value m for which the fraction of false neighbors plateaus at a low value across many values of this threshold [48]. The fraction of false neighbors versus dimensionality m is plotted for our dataset in Figure 7.

4.2. The Condition Monitoring Dataset

The data obtained from each test consist of six columns (currents and voltages for each of phases, a, b, and c; I_a, I_b, I_c, V_a, V_b, V_c) and about 130,000 records. Each of these files was normalized and converted to delay vectors (note that doing so has the effect of removing data skews between different motors). We then combined the tests for three of our motors (all of which were assigned to the damaged-bearings treatment) together to test whether our CM algorithm is effective on a population of motors rather than individual ones. This dataset contains 109 features after delay embedding (including one class label) and about 1,800,000 records.

4.3. Subsection

There are, of course, many shallow and deep algorithms that can be employed in our normal model and anomaly detector. We focus our search on well-known approaches that have worked well in many other domains. We test both shallow and deep learning approaches for the normal model, choosing ones that perform well in time series forecasting. For shallow learning, we have chosen to explore Radial Basis Function Networks (RBFNs) implemented in WEKA, while we have chosen 1-dimensional CNNs in Tensorflow as a deep learner. The RBFN contains one hidden layer whose neurons implement the Gaussian transfer function:

$$\phi \left(r\right)=\exp \left(\frac{r^2}{2{\sigma }^2}\right)$$

(3)

where r is the Euclidean distance from a feature vector to the center point of the Gaussian function, and σ is the standard deviation of the Gaussian. In the WEKA implementation [49], the hidden layer neuron centers and widths are determined via k-means clustering. The output layer takes a weighted sum of the hidden layer outputs, with the weights determined via least-squares estimation, and passes the result through a logistic function. In our parameter search, we vary the number of neurons from 1 to 500, and the standard deviation within the {set 10⁻⁵, 10⁻⁴, 10⁻³, 10⁻², 10⁻¹} [50].

CNNs are a well-known class of deep neural networks, with some recent architectures reaching dozens or hundreds of layers in depth. They are commonly applied to signal-processing problems (with image and video recognition being particularly prominent). As with other deep neural networks, the CNN architecture can be viewed as two sequential components: an automated feature extractor (in this case called the convolutional component [50]), followed by one or more layers of densely-connect neurons that form the classifier component. The latter is common across many shallow and deep architectures (notably the multilayer perceptron), and we will not discuss it further. The convolutional component, in its basic form, is made up of convolutional and pooling layers inspired by the Neocognitron architecture [51]. The former executes several instances of the familiar convolution operation from image processing over the input signal. The latter then reduces the spatial resolution of the input signal. These layers are stacked to form the full convolutional component.

Automated feature extraction generally implies a mapping from input-domain features to a new feature set in which object classes are more readily distinguished. In a CNN, this is accomplished by convolving the input f with a spatially constrained impulse function (or kernel) g. For the two-dimensional (image) case, this is [52]:

$$h\left[i,j\right]={{\displaystyle \sum }}_{k=1}^m{{\displaystyle \sum }}_{l=1}^{n}f\left[k,l\right]·g\left[i-k,j-l\right]$$

(4)

where i, j are the row and column coordinates for an image, and h is the image that results after the convolution has been applied to every pixel (i,j). In image processing, this operation is realized by sliding a convolution window over every pixel in the image and calculating the value of h[i,j] as a weighted sum of the pixels under the window. Edge detectors are a good example; a new image containing information derived from the original is produced and used in further processing.

A CNN realizes the convolution operation via neurocomputing [48]. A neuron is defined for each point h[i,j]; that neuron’s receptive field is exactly the set of pixels that would be covered by the convolution window centered at (i,j). The entire set of neurons representing the convolution h will share weights, ensuring that the same convolution is applied to every pixel; this set of neurons is referred to as a feature map. (Sharing weights also has the effect of dramatically reducing the number of free parameters in a CNN). Unlike an edge detector, however, the weights for each element of the convolution window are learned rather than predefined [50].

Pooling layers are employed to reduce the spatial resolution of a feature map so that in the next stacked layer, the convolution window (which is kept a constant size) covers a larger patch of the original image. Most commonly, the resolution of an image is reduced by a factor of two in each pooling layer, with the maximum value of a 4-pixel patch selected as the single pixel in the new image.

The 1-dimensional CNN is a variation on the CNN architecture for the case of a 1-dimensional signal (e.g., a univariate time series). In Figure 8, a time series (top left) is input to a 1D convolutional layer. A 3-element sliding window implementing the convolution (with weights w1, w2, and w3) is passed over the time series, producing a feature map (bottom left. A single convolutional layer is usually made up of several independent feature maps, each produced by its own kernel (right side). Max-pooling in this architecture will select the larger of two consecutive elements of the time series.

In order to determine the hyper-parameters for our models, we need a validation dataset to prevent overfitting on the final out-of-sample test set. For the RBFN, due to the limitations of the WEKA package, our parameter explorations will also be single-split designs. After the chronologically ordered split in Section 3.1, we will further partition 30% of the training data as the validation dataset, while the test set of Section 3.1 will be set aside for the final evaluation of the whole model. The 1-dimensional CNN is trained on an NVIDIA Titan Xp GPU using Tensorflow, and so we use a tenfold cross-validation design (again, only within the training set) for parameter exploration.

For the anomaly detector, we have chosen to examine only shallow architectures, as there will only be twelve inputs for the n-th observation vector (one predicted and one actual value of each component). Thus, deep learning algorithms do not seem to be a good match for this problem. We have selected multilayer perceptrons [48] (implemented in WEKA [49]), decision trees (Breiman’s CART [53]), and random forests [54] implemented in Scikit-learn [55]. All hyper-parameters of the models are explored. For the multilayer perceptron, these include the number of hidden layers, number of neurons in each layer, activation functions, and initialization methods. For the decision tree and random forest models, the hyperparameters include the minimum number of samples required at a leaf node and the maximum depth of the tree [55].

5. Results

We first examine and present our results for shallow learning of the normal model in

Table 1. Forecast Accuracy for Shallow Normal Model.

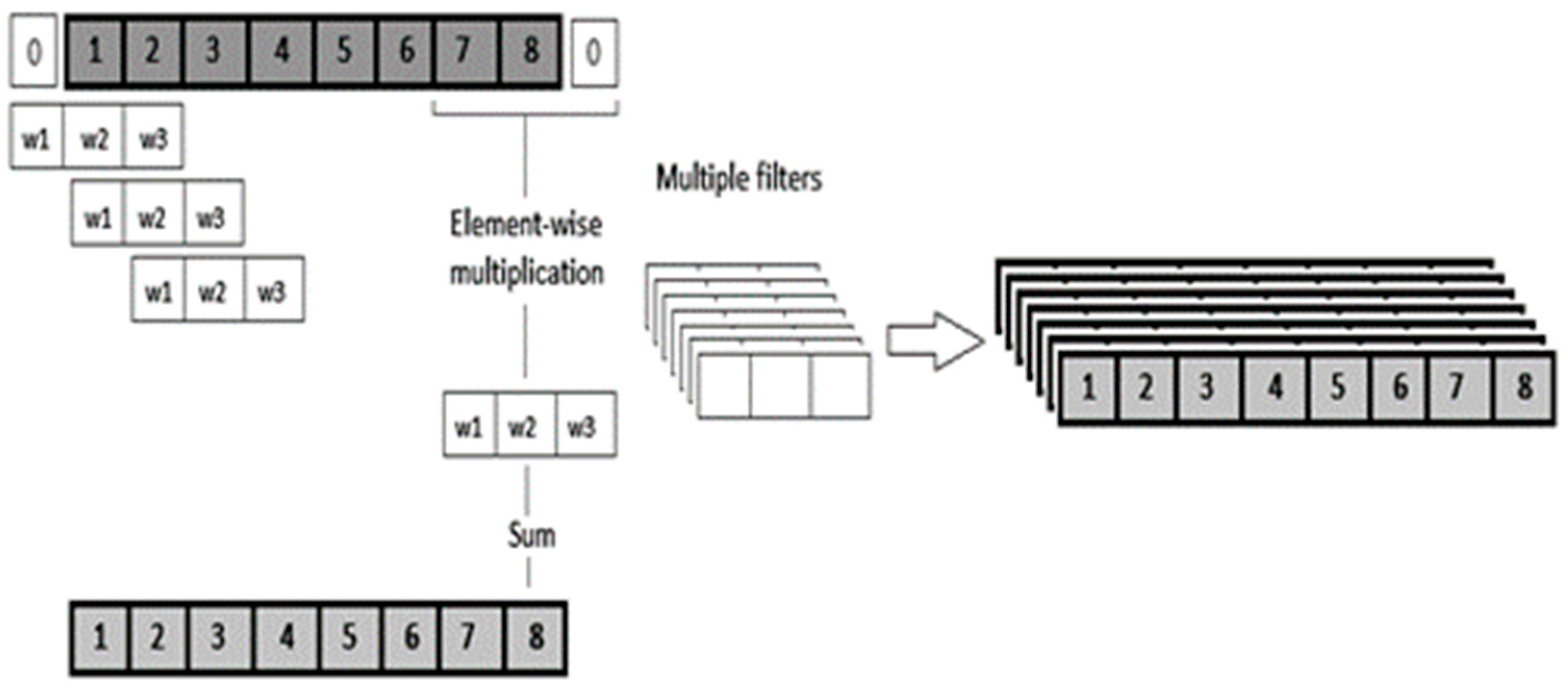
Number of Clusters	Standard Deviation	Train RMSE	Validation RMSE
100	10−5	0.0323	0.0766

. We then present the out-of-sample results for our anomaly detector in

Table 2. Test Results for Anomaly Detectors with Shallow Normal Model.

Model	TPR	FPR	Accuracy
MLP	0.947	0.366	0.791
RBF	0.918	0.085	0.912
Decision Tree	0.967	0.207	0.881
Random Forest	0.993	0.264	0.864

. As CM is essentially an alarm, we present the detector’s performance in terms of the True Positive Rate (TPR, also called sensitivity) and the False Positive Rate (FPR; also called the false alarm rate). TPR is the fraction of actual Positive (damaged) examples identified as such. FPR is the fraction of actual Negative (healthy) examples identified as Positive.

For deep learning, the normal model we designed is a 1-dimensional convolutional neural network [56] with 17 dimensions for each of the 6 inputs and a vector of 6 elements as the output, each belonging to one of the time series. Figure 9 plots the training error of the network at each epoch using the Adam optimizer in terms of Root Mean Square Error. Plainly, the CNN test error is roughly an order of magnitude less than the RBFN. The total training time for this model on our NVIDIA Titan Xp (12 GB), running on a Core i7 PC with 64 GB of RAM and Ubuntu Linux, was 6207 s.

Table 3. Test Results for Anomaly Detectors with Deep Normal Model.

Model	TPR	FPR	Accuracy
MLP (12 Inputs)	0.732	0.166	0.824
MLP (18 Inputs)	0.795	0.129	0.861
Decision Tree (12 Inputs)	0.944	0.037	0.956
Decision Tree (18 Inputs)	0.748	0.162	0.811
Random Forest (12 Inputs)	0.948	0.033	0.968
Random Forest (18 Inputs)	0.841	0.101	0.895

presents the out-of-sample results for our anomaly detector with deep learning in terms of accuracy, TPR, and FPR. According to the results, a random forest (with 100 estimators) with the original 12 inputs outperformed all other designs (TPR = 0.948, FPR = 0.033). Examining Table 2, both decision trees and random forests produce models with slightly better TPR; however, the FPR (false alarm rate) is much higher. As false alarm rates are critical considerations in a monitoring application, we believe the deep model is superior.

Table 4. Comparison between Proposed and Selected Anomaly Detectors.

Model	TPR	FPR	Accuracy
Random Forest	0.948	0.033	0.968
Soft-bound Deep SVDD [6]	0.907	0.684	0.605
One-class Deep SVDD [6]	0.919	0.635	0.637
OC-NN [7]	0.861	0.697	0.581
OCAN [8]	0.273	0.260	0.506

presents a comparison between our proposed model and selected deep anomaly detection approaches from the literature. The hyperparameters of all models were explored to find the best performance. The proposed model using random forests outperforms all other tested methods for this dataset.

6. Summary and Future Work

We have designed a condition monitoring solution for small electric motors, as might be found in an industrial site. An anomaly-detection architecture is employed, with the normal model being a time series forecasting algorithm. Both shallow and deep learning approaches for the normal model are investigated, with the deep network leading to a much lower false alarm rate (at the cost of a slightly higher false-negative rate).

In future work, we will first examine whether adding additional sensing modalities to our dataset (via, e.g., data fusion as proposed in [57]) improves fault detection. We will then apply our best design to monitoring groups of small motors connected to a common bus. This is a common layout in large industrial sites and introduces opportunities for anomalies or damage in one motor to cause further damage in other connected motors due to current or voltage surges. We envisage this monitoring problem to include three stages: the detection of a fault, the localization of that fault to a specific motor or motors, and finally, fault diagnosis or remaining life prediction as appropriate.

Beyond condition monitoring in induction motors, we intend to apply this basic architecture (deep learning for a normal model, shallow learning for the anomaly detector) to other monitoring problems and domains. We hypothesize that a hybrid deep/shallow model is an effective approach for condition monitoring of systems with a limited number of sensors in general.