A Jigsaw Puzzle Solver-Based Attack on Image Encryption Using Vision Transformer for Privacy-Preserving DNNs
Abstract
1. Introduction
2. Preparation
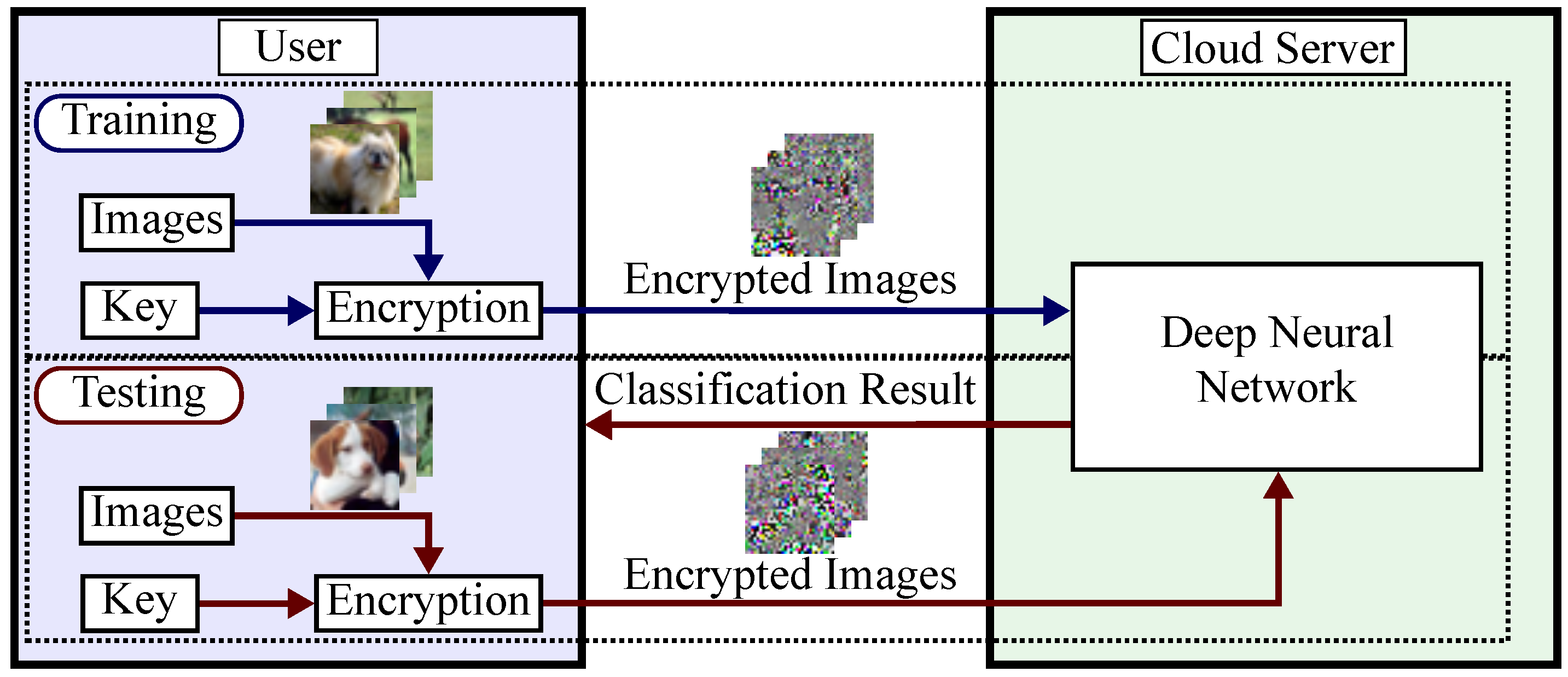
2.1. Privacy-Preserving DNNs
2.2. Image Encryption for Privacy-Preserving DNNs
- Divide the RGB color image I into blocks of pixels.
- Separate each pixel into upper and lower 4 bit pixel values to form six-channel blocks.
- Reverse the intensities of the pixel values in each block randomly by a secret key.
- Shuffle the pixel values in each block randomly by a secret key.
- Combine six channels in each block into three channel to generate an encrypted image.
- Divide RGB color image I into blocks of pixels.
- Permute randomly the divided blocks by using a secret key.
- The same procedure of LE is applied to the permuted blocks to generate an encrypted image.
- Divide RGB color image I into pixels.
- Apply negative–positive transformations to each pixel of the three color channels randomly by using a secret key. In this scheme, the secret key is independently used for all color components. In this step, a pixel q is transformed to bywhere r(i) is a random binary integer generated by the secret key. In this paper, the value of occurrence probability has been used to invert bits randomly.
- Shuffle three color components of each pixel by using a secret key.
- Combine pixels to generate an encrypted image.
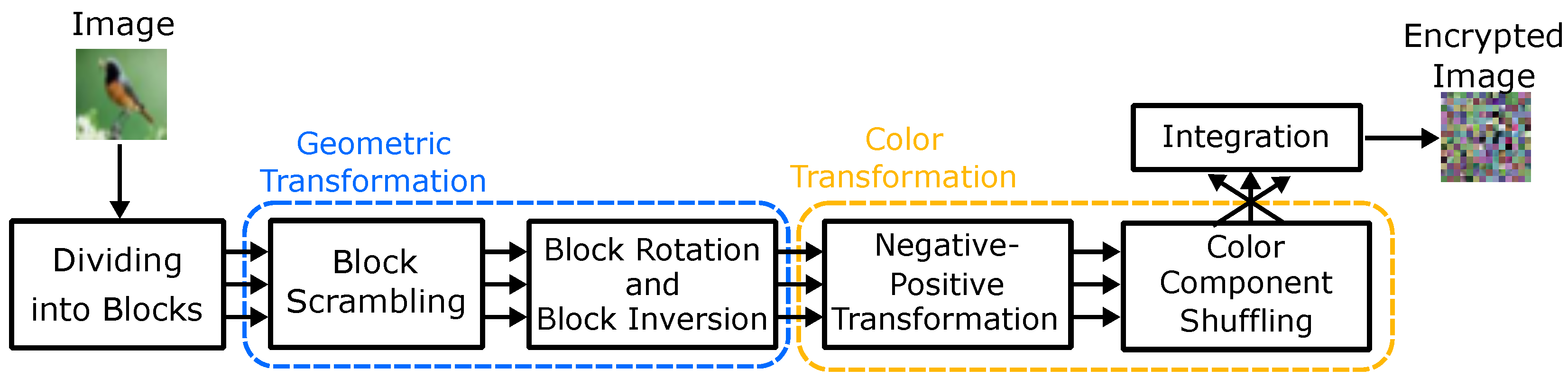
- Divide RGB color image I into blocks of pixels.
- Permute randomly the divided blocks using a secret key.
- Rotate and invert randomly each block by using a secret key.
- Apply negative–positive transformations to each block by using a secret key according to Equation (1).
- Shuffle three color components of each block by using a secret key.
- Integrate the encrypted blocks to generate an encrypted image.
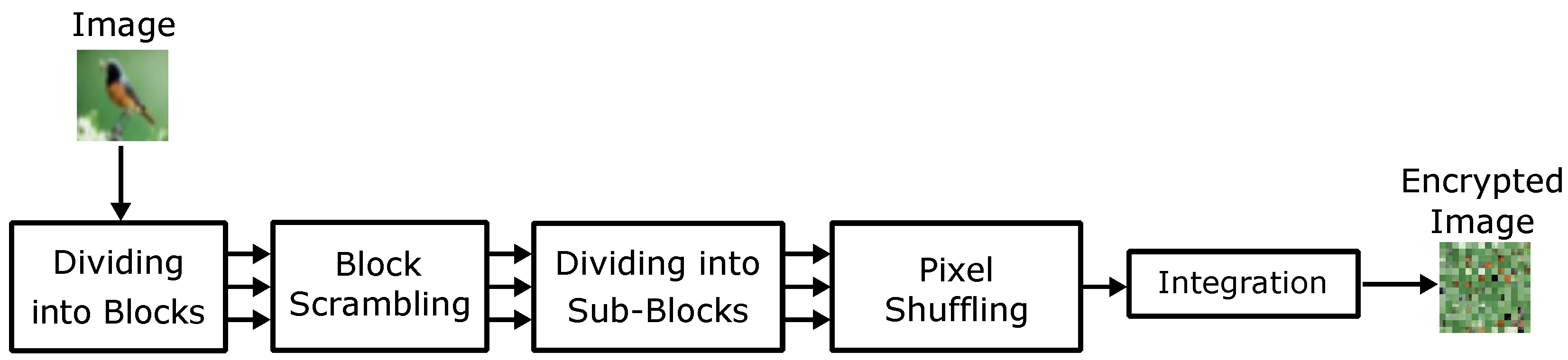
- Divide an RGB color image I into blocks , with pixels, where n is the number of divided blocks calculated by
- Permute the divided blocks by using a secret key , where is commonly used for all color components. Accordingly, the scrambled blocks are generated.
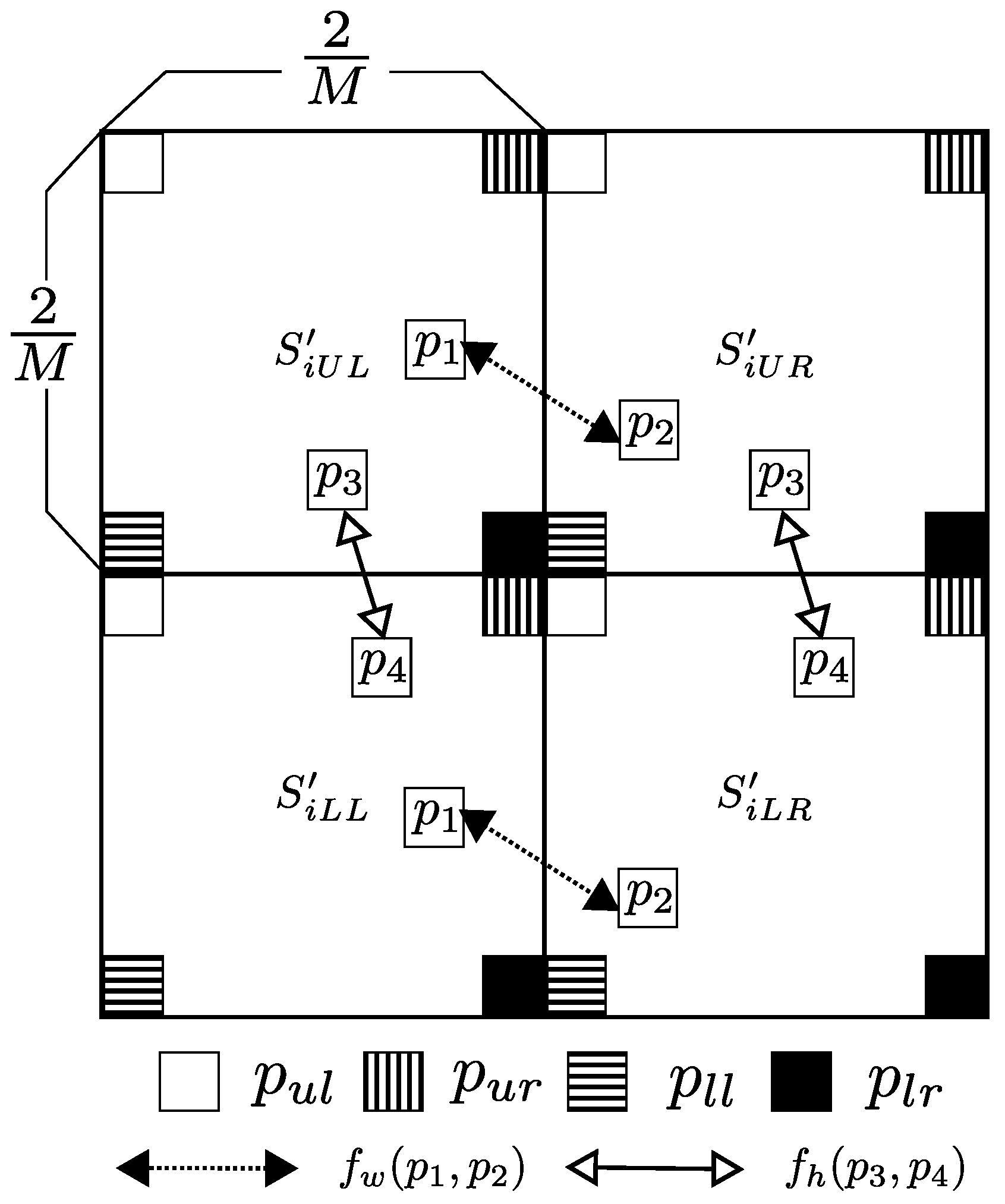
- Divide each scrambled block into four non-overlapping square sub-blocks with pixels, where is defined as the upper left position of the ith blocks, as the upper right, as the lower left, and as the lower right. Thereby, scrambled blocks divided into sub-blocks are generated. The number of sub-blocks m is described as
- Shuffle the pixel position within a sub-block by using a secret key to generate pixel shuffled sub-blocks , where is commonly used for all sub-blocks and color components. As a result, each scrambled block is divided into four encrypted sub-blocks, denoted by .
- Merge all blocks to generate an encrypted image.
3. Proposed Attacks
3.1. Threat Models
| Algorithm 1 FR-attack [14] |
|
3.2. Jigsaw Puzzle Solver-Based Attack
4. Experiments
4.1. Experimental Conditions
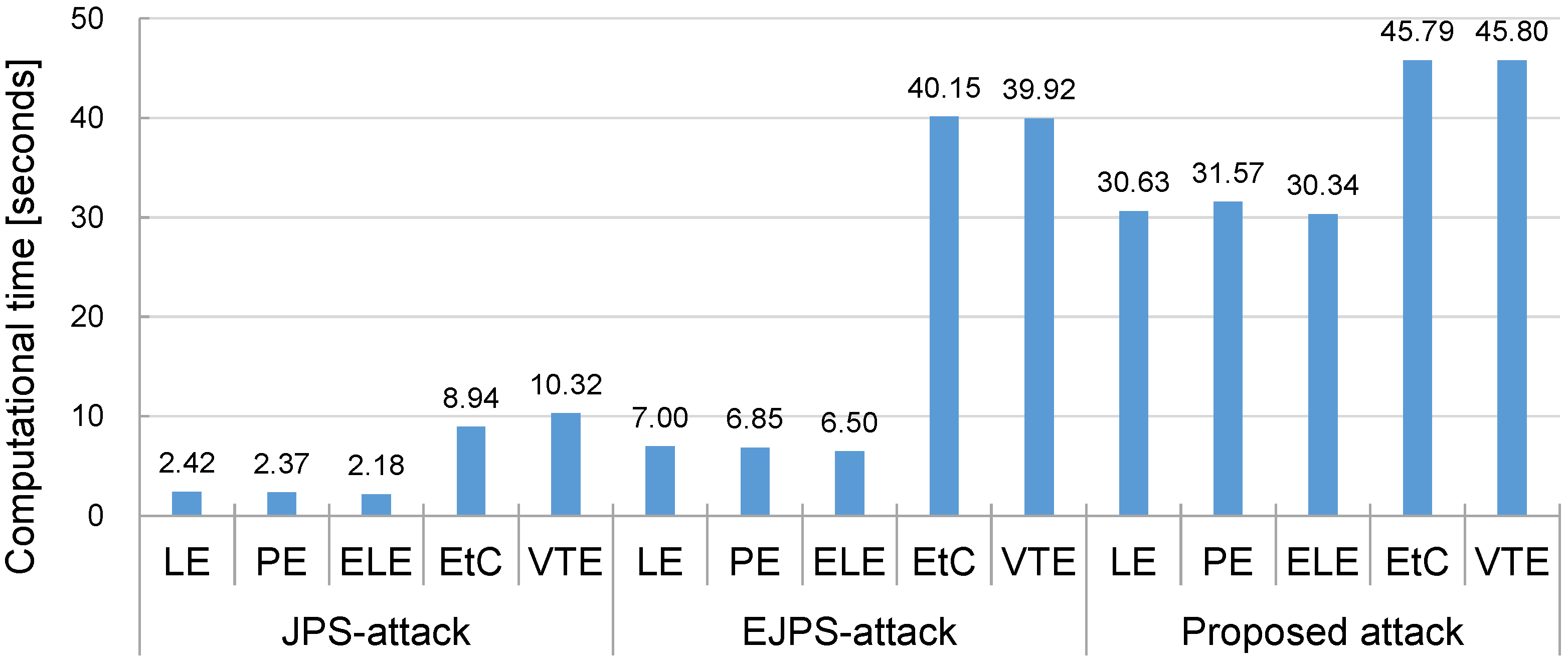
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yann, L.; Yoshua, B.; Geoffrey, H. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar]
- Huang, Q.X.; Yap, W.L.; Chiu, M.Y.; Sun, H.M. Privacy-Preserving Deep Learning With Learnable Image Encryption on Medical Images. IEEE Access 2022, 10, 66345–66355. [Google Scholar] [CrossRef]
- Zeng, W.; Lei, S. Efficient frequency domain selective scrambling of digital video. IEEE Trans. Multimed. 2003, 5, 118–129. [Google Scholar] [CrossRef]
- Ito, I.; Kiya, H. A new class of image registration for guaranteeing secure data management. In Proceedings of the IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; pp. 269–272. [Google Scholar]
- Kiya, H.; Ito, I. Image matching between scrambled images for secure data management. In Proceedings of the 16th European Signal Processing Conference, Lausanne, Switzerland, 25–29 August 2008; pp. 1–5. [Google Scholar]
- Ito, I.; Kiya, H. One-time Key Based Phase Scrambling for Phase-only Correlation Between Visually Protected Images. EURASIP J. Inf. Secur. 2009, 2009, 841045. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, X.; Lan, W. Efficient image encryption with block shuffling and chaotic map. Multimed. Tools Appl. 2015, 74, 5429–5448. [Google Scholar] [CrossRef]
- Sirichotedumrong, W.; Chuman, T.; Imaizumi, S.; Kiya, H. Grayscale-Based Block Scrambling Image Encryption for Social Networking Services. In Proceedings of the IEEE International Conference on Multimedia and Expo (ICME), San Diego, CA, USA, 23–27 July 2018; pp. 1–6. [Google Scholar]
- Kiya, H.; Nagamori, T.; Imaizumi, S.; Shiota, S. Privacy-Preserving Semantic Segmentation Using Vision Transformer. J. Imaging 2022, 8, 233. [Google Scholar] [CrossRef] [PubMed]
- Kiya, H.; Iijima, R.; AprilPyone, M.; Kinoshita, Y. Image and Model Transformation with Secret Key for Vision Transformer. IEICE Trans. Inf. Syst. 2023, 106, 2–11. [Google Scholar] [CrossRef]
- Tanaka, M. Learnable Image Encryption. In Proceedings of the IEEE International Conference on Consumer Electronics-Taiwan (ICCE-TW), Taipei, Taiwan, 6–8 July 2018; pp. 1–2. [Google Scholar]
- Sirichotedumrong, W.; Kinoshita, Y.; Kiya, H. Pixel-Based Image Encryption Without Key Management for Privacy-Preserving Deep Neural Networks. IEEE Access 2019, 7, 177844–177855. [Google Scholar] [CrossRef]
- Madono, K.; Tanaka, M.; Onishi, M.; Ogawa, T. Block-wise Scrambled Image Recognition Using Adaptation Network. In Proceedings of the Workshop on AAAI Conference Artificial Intellignece, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Chang, A.H.; Case, B.M. Attacks on Image Encryption Schemes for Privacy-Preserving Deep Neural Networks. arXiv 2020, arXiv:2004.13263. [Google Scholar] [CrossRef]
- Ito, H.; Kinoshita, Y.; Aprilpyone, M.; Kiya, H. Image to Perturbation: An Image Transformation Network for Generating Visually Protected Images for Privacy-Preserving Deep Neural Networks. IEEE Access 2021, 9, 64629–64638. [Google Scholar] [CrossRef]
- Xu, J.; Ai, B.; Chen, W.; Yang, A.; Sun, P. Image Encryption Methods in Deep Joint Source Channel Coding: A Review and Performance Evaluation. In Proceedings of the IEEE International Conference on Computer and Communications (ICCC), Xiamen, China, 28–30 July 2021; pp. 240–244. [Google Scholar]
- Kiya, H.; AprilPyone, M.; Kinoshita, Y.; Imaizumi, S.; Shiota, S. An Overview of Compressible and Learnable Image Transformation with Secret Key and Its Applications. APSIPA Trans. Signal Inf. Process. 2022, 11, e11. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- AprilPyone, M.; Kiya, H. Block-wise Image Transformation with Secret Key for Adversarially Robust Defense. IEEE Trans. Inf. Forensics Secur. 2021, 16, 2709–2723. [Google Scholar] [CrossRef]
- Qi, Z.; AprilPyone, M.; Kiya, H. Privacy-Preserving Image Classification Using ConvMixer with Adaptive Permutation Matrix. In Proceedings of the 30th European Signal Processing Conference(EUSIPCO), Belgrade, Serbia, 29 August–2 September 2022; pp. 543–547. [Google Scholar]
- Sholomon, D.; David, O.E.; Netanyahu, N.S. An automatic solver for very large jigsaw puzzles using genetic algorithms. Genet. Program. Evolvable Mach. 2016, 17, 291–313. [Google Scholar] [CrossRef]
- Son, K.; Hays, J.; Cooper, D.B. Solving Square Jigsaw Puzzle by Hierarchical Loop Constraints. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 2222–2235. [Google Scholar] [CrossRef] [PubMed]
- Chuman, T.; Kurihara, K.; Kiya, H. Security Evaluation for Block Scrambling-based ETC Systems against Extended Jigsaw Puzzle Solver Attacks. In Proceedings of the IEEE International Conference on Multimedia and Expo (ICME), Hong Kong, China, 10–14 July 2017; pp. 229–234. [Google Scholar]
- Chuman, T.; Kiya, H. A jigsaw puzzle solver-based attack on block-wise image encryption for privacy-preserving DNNs. In Proceedings of the International Workshop on Advanced Imaging Technology (IWAIT), Hong Kong, China, 4–6 January 2023; pp. 335–340. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- AprilPyone, M.; Kiya, H. Privacy-Preserving Image Classification Using an Isotropic Network. IEEE Trans. Multimed. 2022, 29, 23–33. [Google Scholar] [CrossRef]
- Chuman, T.; Sirichotedumrong, W.; Kiya, H. Encryption-then-compression systems using grayscale-based image encryption for jpeg images. IEEE Trans. Inf. Forensics Secur. 2019, 14, 1515–1525. [Google Scholar] [CrossRef]
- Chuman, T.; Kurihara, K.; Kiya, H. On the Security of Block Scrambling-Based EtC Systems against Extended Jigsaw Puzzle Solver Attacks. IEICE Trans. Inf. Syst. 2018, 101, 37–44. [Google Scholar] [CrossRef]
- Sirichotedumrong, W.; Kiya, H. Visual Security Evaluation of Learnable Image Encryption Methods against Ciphertext-only Attacks. In Proceedings of the 2020 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Auckland, New Zealand, 7–10 December 2020; pp. 1304–1309. [Google Scholar]
- Gallagher, A. Jigsaw Puzzles with Pieces of Unknown Orientation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 382–389. [Google Scholar]




| Plain | LE [11] | PE [12] | ELE [13] | EtC [28] | VTE [20] | |
|---|---|---|---|---|---|---|
| Block scrambling | √ | √ | √ | |||
| Key type | Same | Different | Different | Same | Same | |
| Key space | ||||||
| Example |  |  |  |  |  |  |
 |  |  |  |  |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chuman, T.; Kiya, H. A Jigsaw Puzzle Solver-Based Attack on Image Encryption Using Vision Transformer for Privacy-Preserving DNNs. Information 2023, 14, 311. https://doi.org/10.3390/info14060311
Chuman T, Kiya H. A Jigsaw Puzzle Solver-Based Attack on Image Encryption Using Vision Transformer for Privacy-Preserving DNNs. Information. 2023; 14(6):311. https://doi.org/10.3390/info14060311
Chicago/Turabian StyleChuman, Tatsuya, and Hitoshi Kiya. 2023. "A Jigsaw Puzzle Solver-Based Attack on Image Encryption Using Vision Transformer for Privacy-Preserving DNNs" Information 14, no. 6: 311. https://doi.org/10.3390/info14060311
APA StyleChuman, T., & Kiya, H. (2023). A Jigsaw Puzzle Solver-Based Attack on Image Encryption Using Vision Transformer for Privacy-Preserving DNNs. Information, 14(6), 311. https://doi.org/10.3390/info14060311






