An Improved Method of Heart Rate Extraction Algorithm Based on Photoplethysmography for Sports Bracelet
Abstract
1. Introduction
2. Materials and Methods
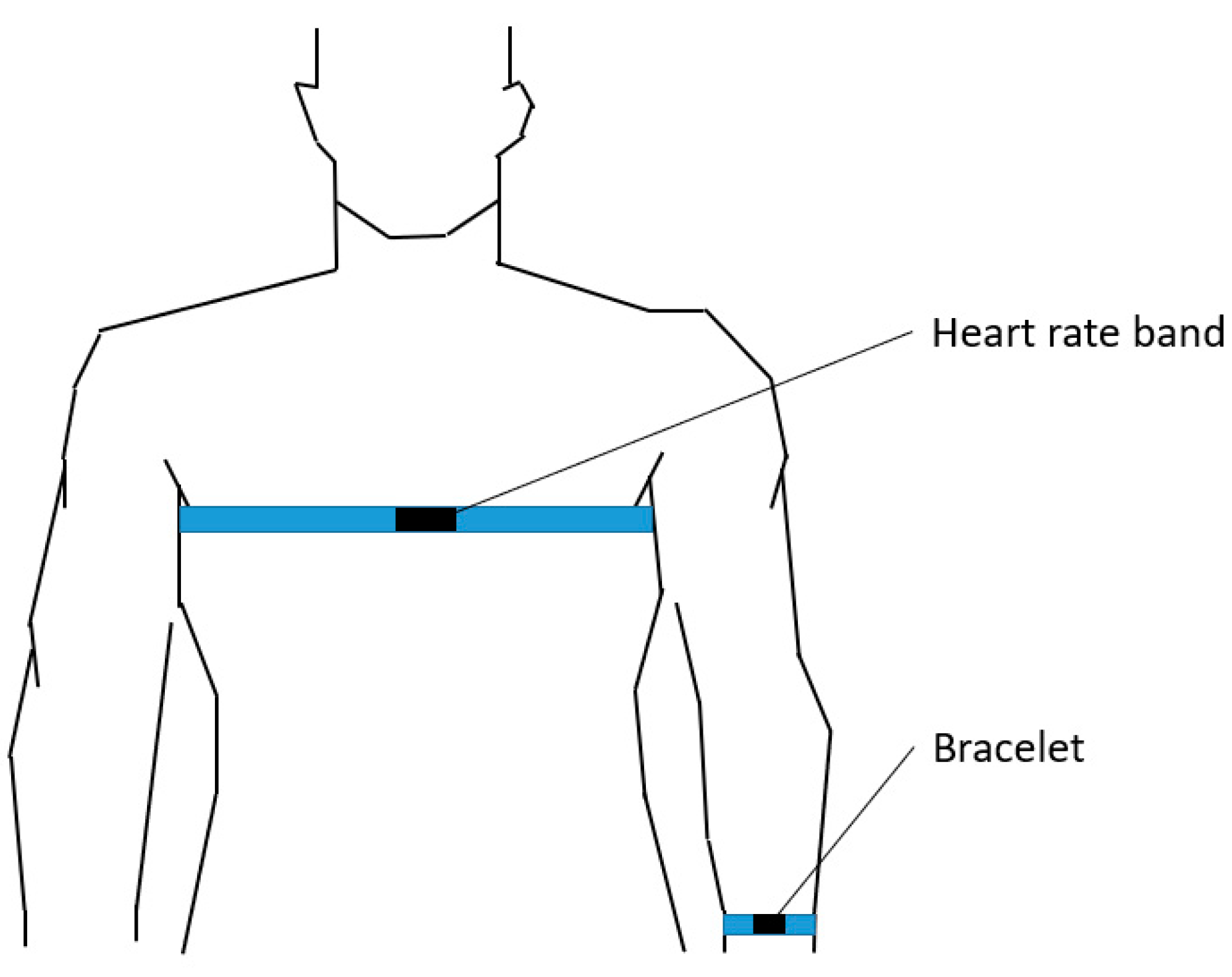
2.1. Experimental Equipment and Objects
2.2. Traditional Algorithm Architecture
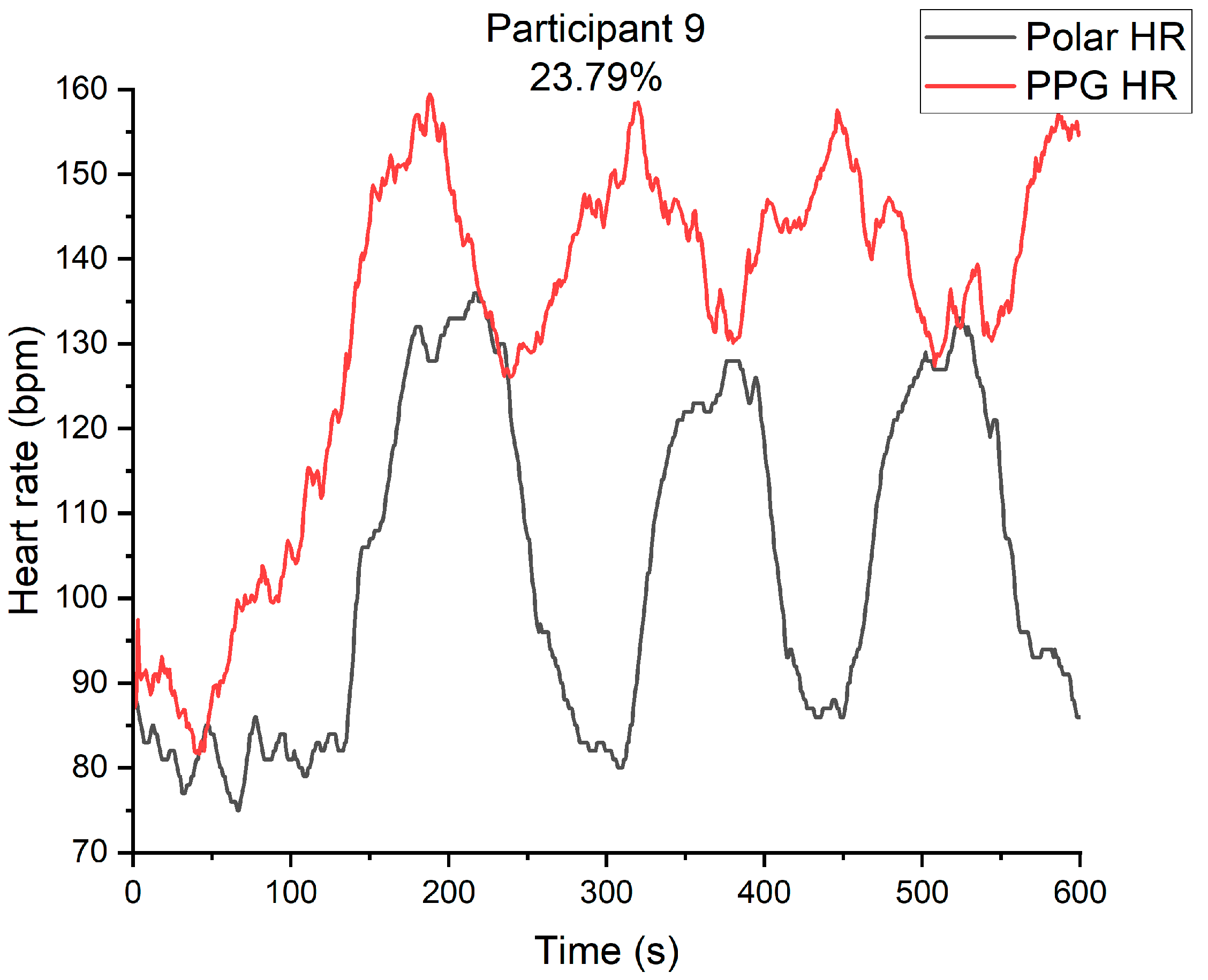
2.3. Experiment Results
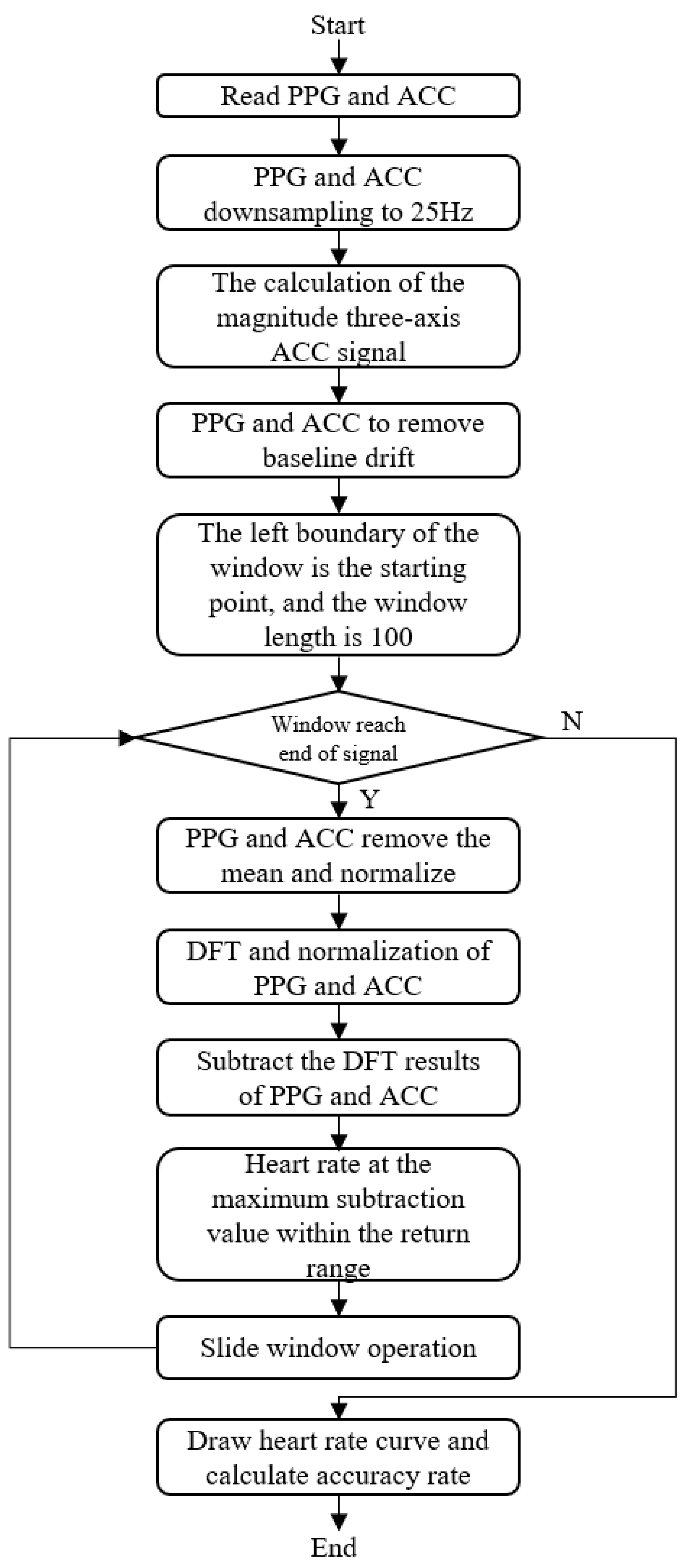
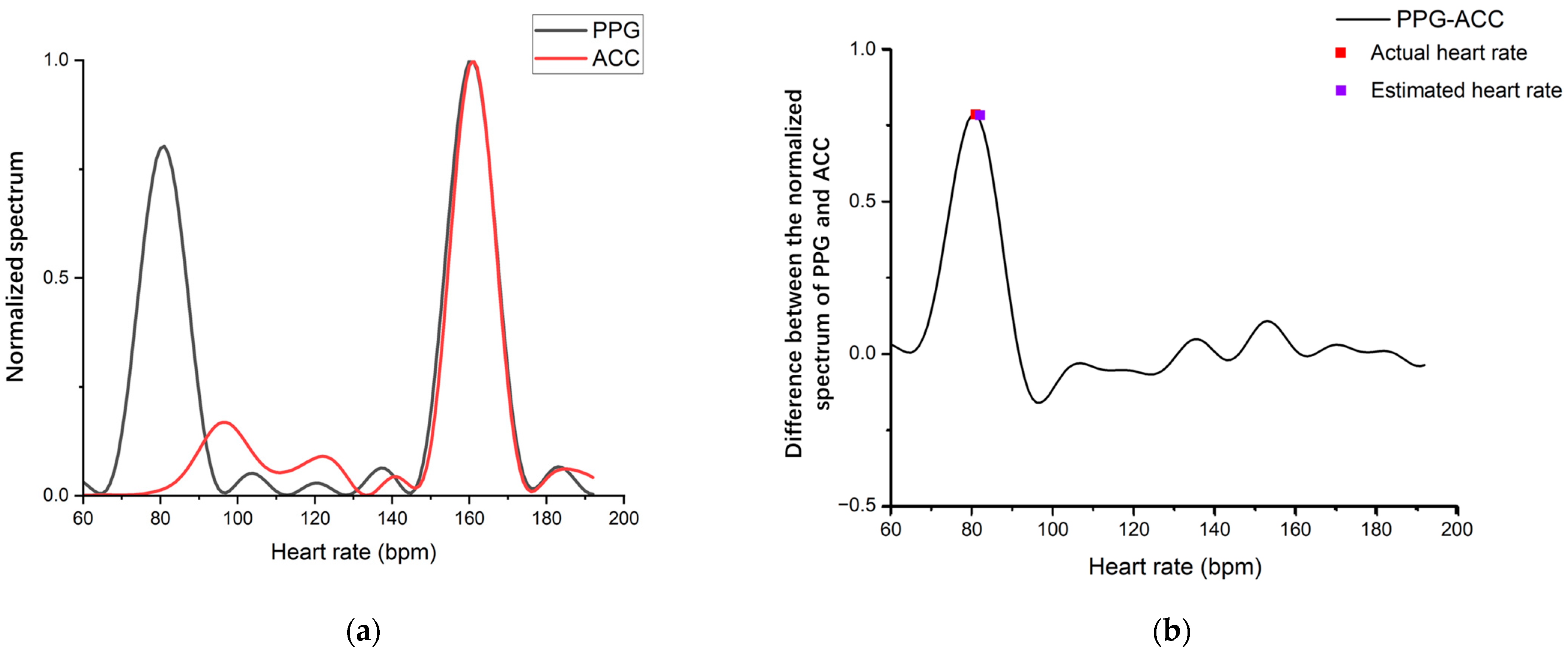
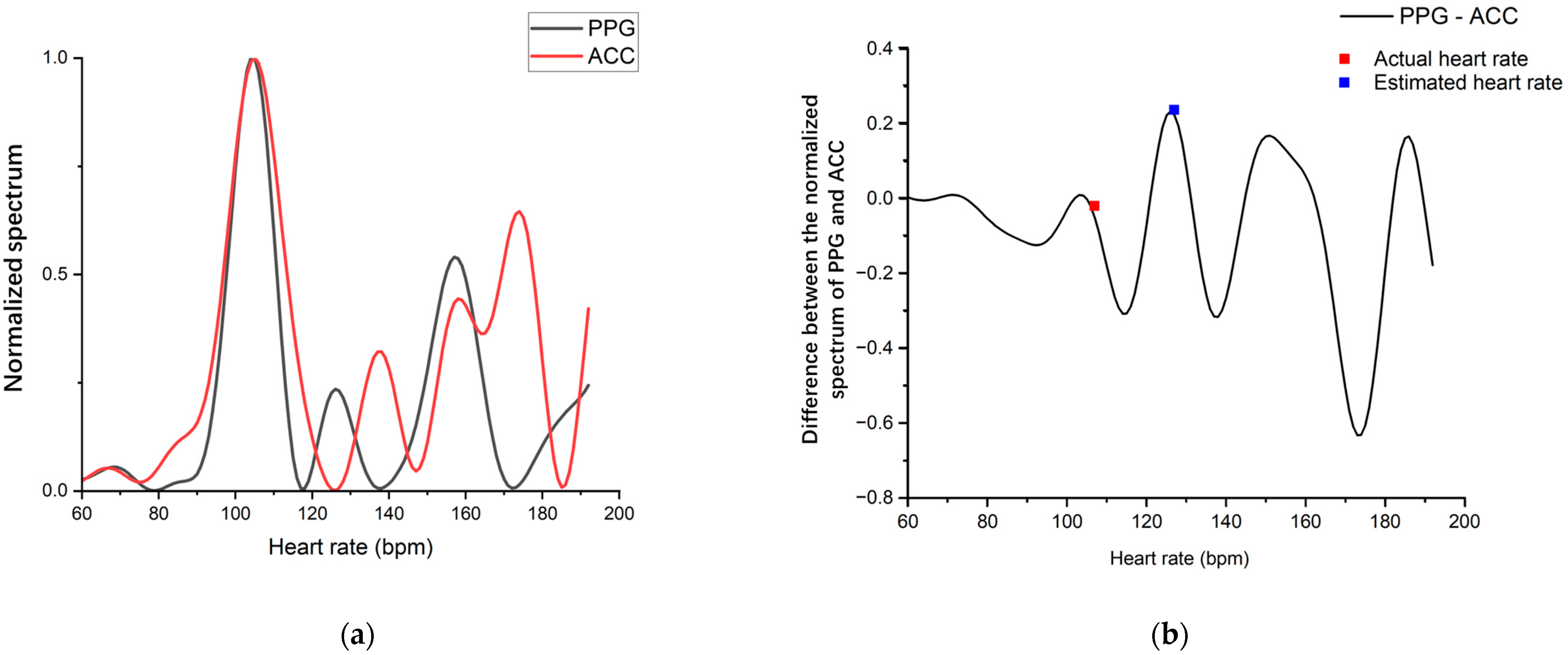
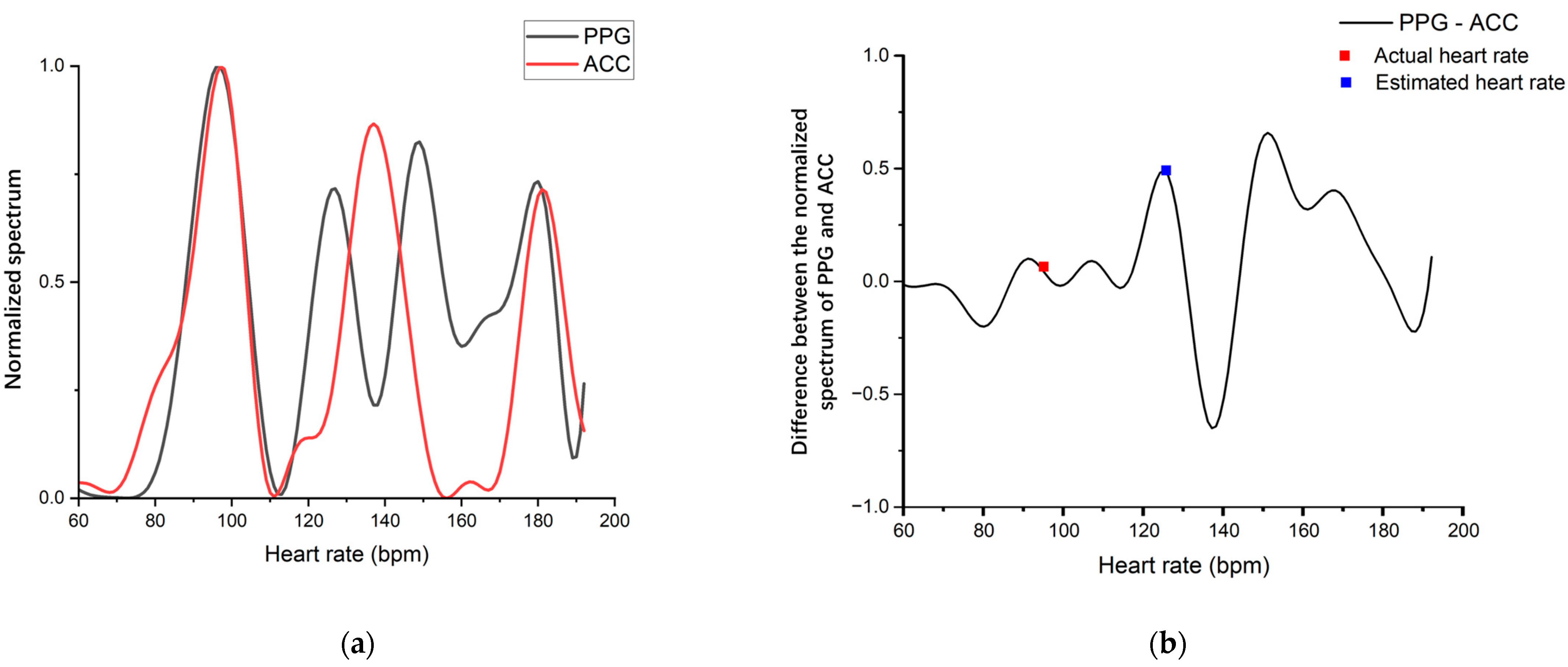
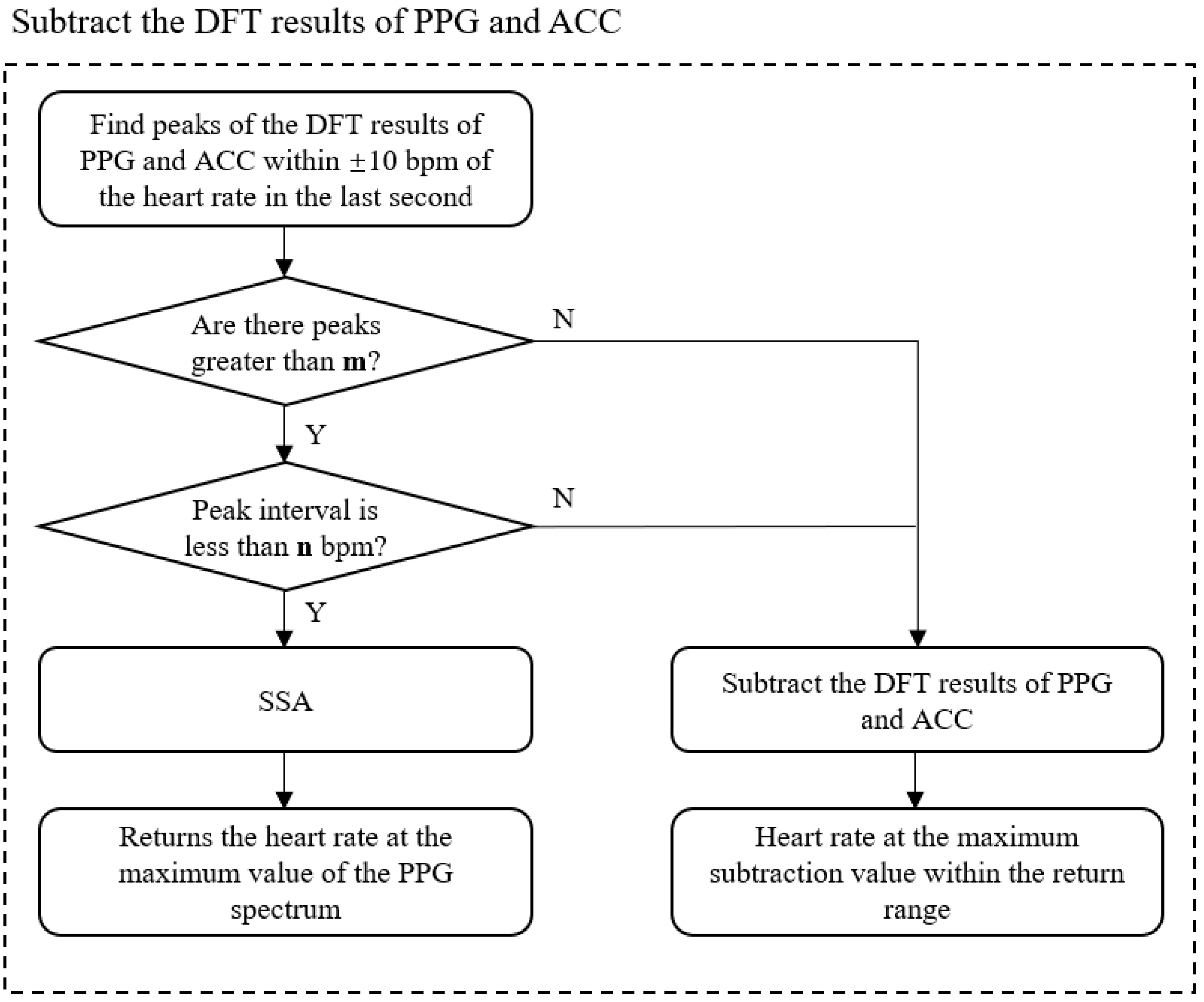
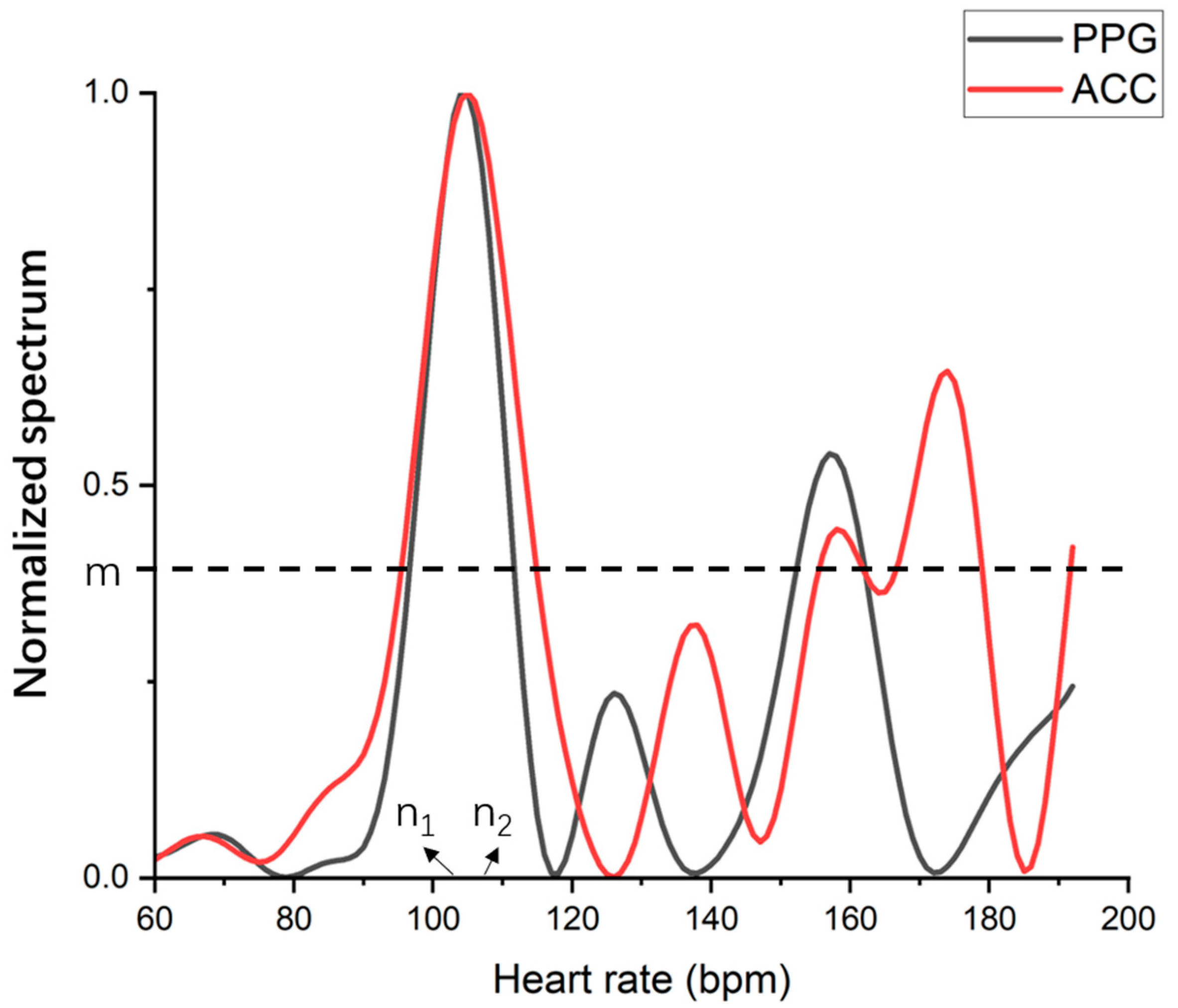
3. Algorithm Improvement
3.1. Algorithm Improvement Architecture
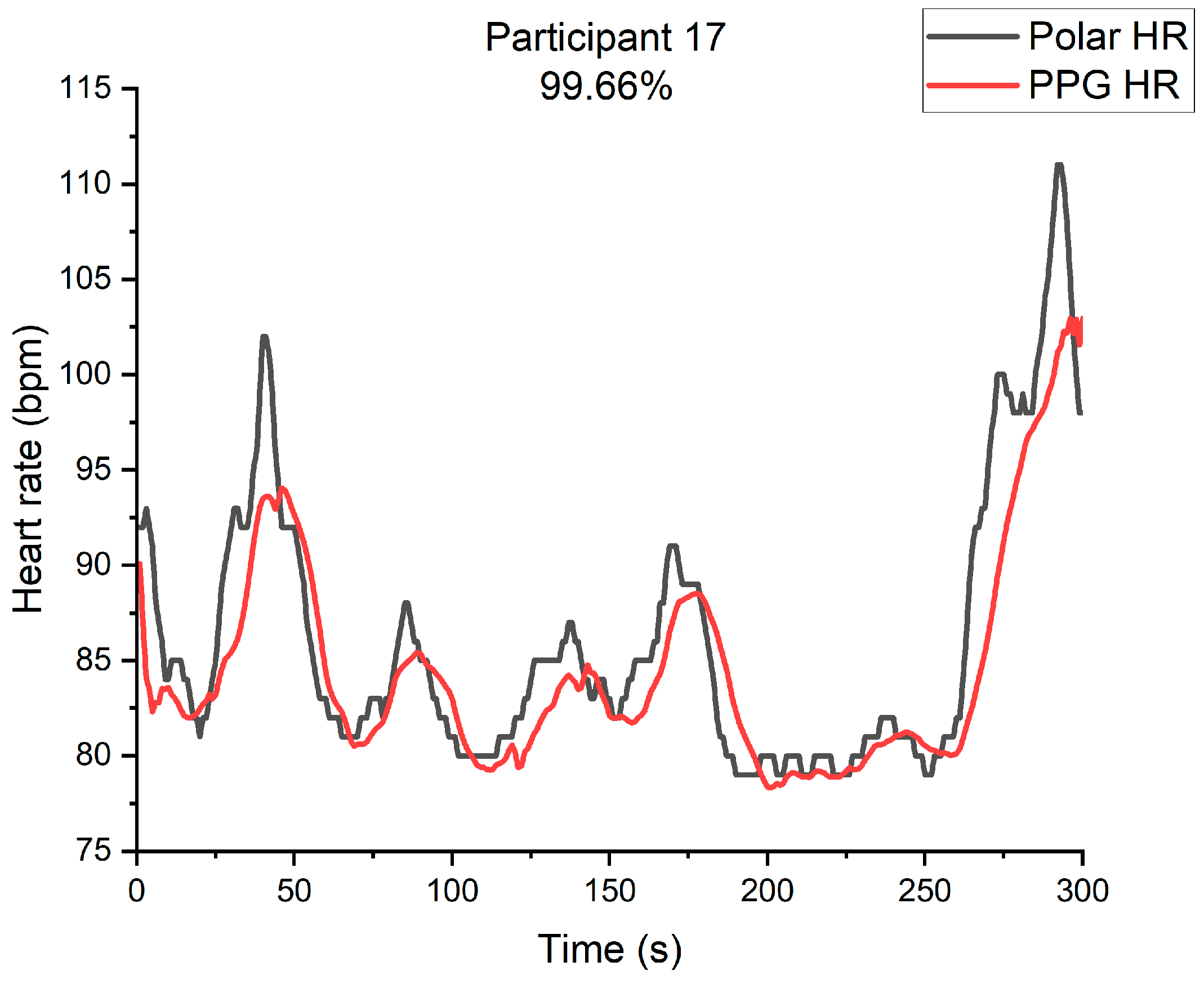
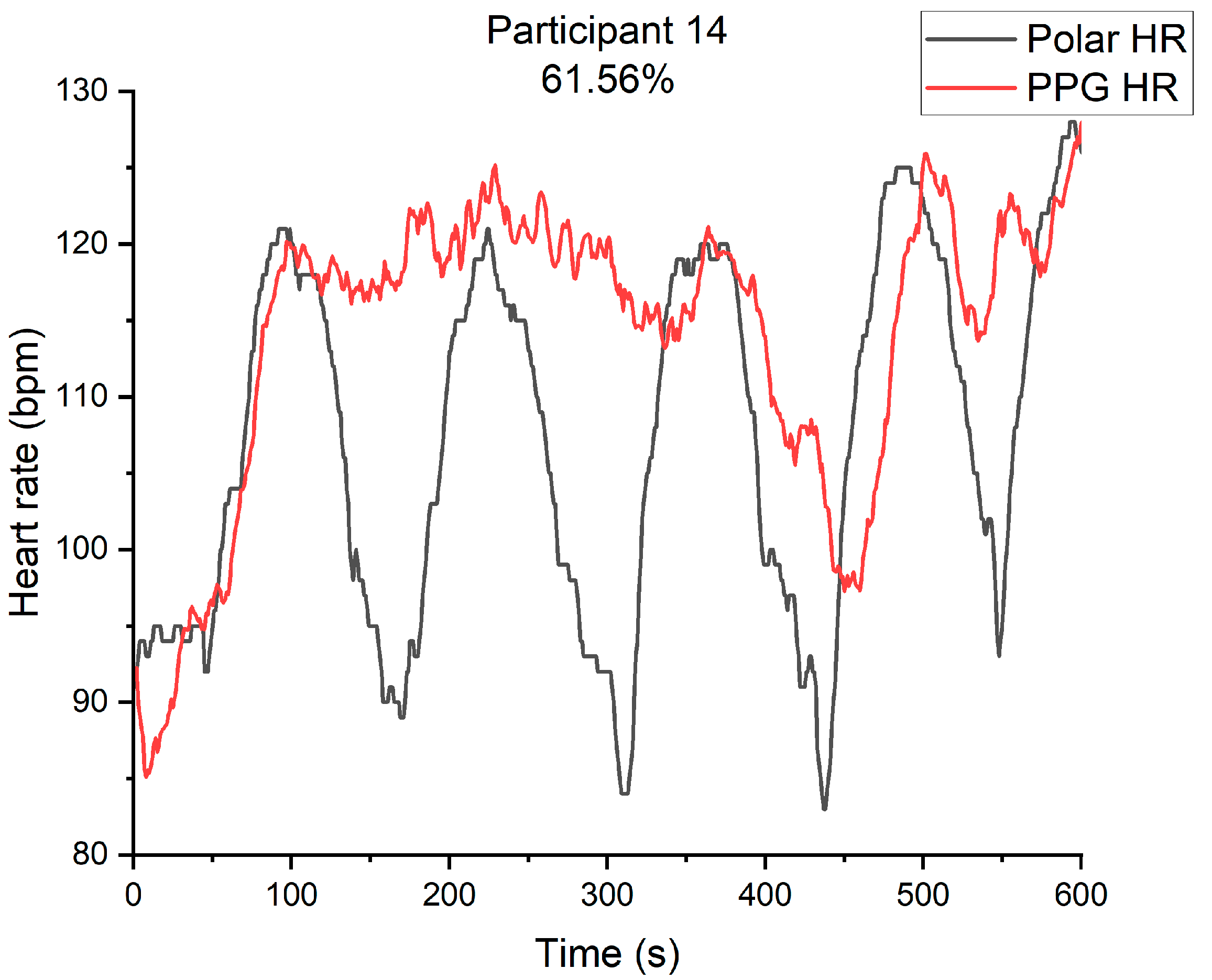
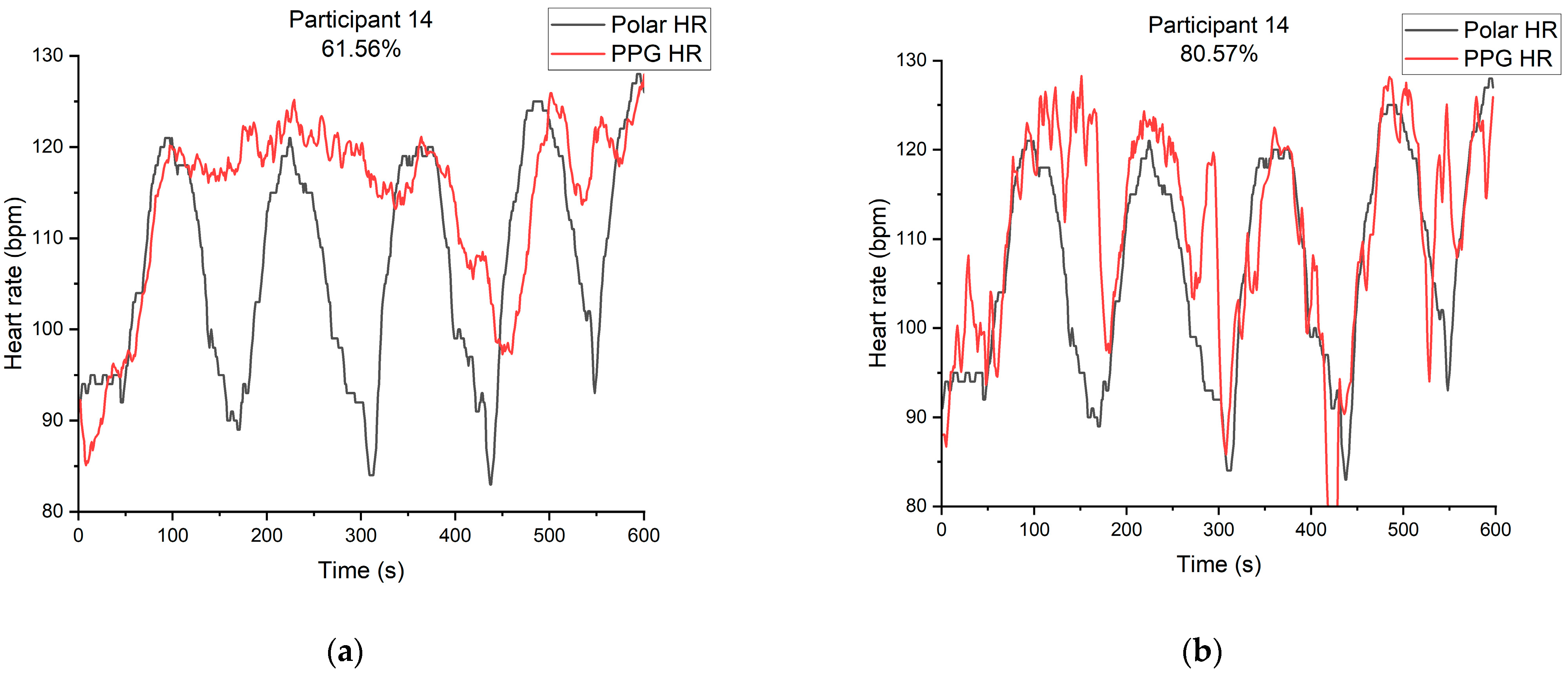
3.2. Experiment Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, Y.; Lane, D.A.; Wang, L.; Zhang, H.; Wang, H.; Zhang, W.; Wen, J.; Xing, Y.; Wu, F.; Xia, Y.; et al. Mobile Health Technology to Improve Care for Patients with Atrial Fibrillation. J. Am. Coll. Cardiol. 2020, 75, 1523–1534. [Google Scholar] [CrossRef] [PubMed]
- Pankaj; Kumar, A.; Komaragiri, R.; Kumar, M. A Review on Computation Methods Used in Photoplethysmography Signal Analysis for Heart Rate Estimation. Arch. Comput. Methods Eng. 2021, 29, 921–940. [Google Scholar] [CrossRef]
- Ray, D.; Collins, T.; Woolley, S.; Ponnapalli, P. A Review of Wearable Multi-wavelength Photoplethysmography. IEEE Rev. Biomed. Eng. 2021, 16, 136–151. [Google Scholar] [CrossRef] [PubMed]
- Fine, J.; Branan, K.L.; Rodriguez, A.J.; Boonya-Ananta, T.; Ajmal; Ramella-Roman, J.C.; McShane, M.J.; Cote, G.L. Sources of Inaccuracy in Photoplethysmography for Continuous Cardiovascular Monitoring. Biosensors 2021, 11, 126. [Google Scholar] [CrossRef]
- Salehizadeh, S.M.; Dao, D.; Bolkhovsky, J.; Cho, C.; Mendelson, Y.; Chon, K.H. A Novel Time-Varying Spectral Filtering Algorithm for Reconstruction of Motion Artifact Corrupted Heart Rate Signals during Intense Physical Activities Using a Wearable Photoplethysmogram Sensor. Sensors 2016, 16, 10. [Google Scholar] [CrossRef]
- Ismail, S.; Akram, U.; Siddiqi, I. Heart rate tracking in photoplethysmography signals affected by motion artifacts: A review. EURASIP J. Adv. Signal Process. 2021, 2021, 5. [Google Scholar] [CrossRef]
- Liu, H.; Allen, J.; Khalid, S.G.; Chen, F.; Zheng, D. Filtering-induced time shifts in photoplethysmography pulse features measured at different body sites: The importance of filter definition and standardization. Physiol. Meas. 2021, 42, 074001. [Google Scholar] [CrossRef]
- Allen, J.; Murray, A. Effects of filtering on multisite photoplethysmography pulse waveform characteristics. In Proceedings of the Computers in Cardiology, Chicago, IL, USA, 19–22 September 2004; pp. 485–488. [Google Scholar]
- Loh, H.W.; Xu, S.; Faust, O.; Ooi, C.P.; Barua, P.D.; Chakraborty, S.; Tan, R.-S.; Molinari, F.; Acharya, U.R. Application of photoplethysmography signals for healthcare systems: An in-depth review. Comput. Methods Programs Biomed. 2022, 216, 106677. [Google Scholar] [CrossRef]
- Allen, J.; Liu, H.; Iqbal, S.; Zheng, D.; Stansby, G. Deep learning-based photoplethysmography classification for peripheral arterial disease detection: A proof-of-concept study. Physiol. Meas. 2021, 42, 054002. [Google Scholar] [CrossRef]
- Kotzen, K.; Charlton, P.H.; Salabi, S.; Amar, L.; Landesberg, A.; Behar, J.A. SleepPPG-Net: A deep learning algorithm for robust sleep staging from continuous photoplethysmography. IEEE J. Biomed. Health Inform. 2022, 27, 924–932. [Google Scholar] [CrossRef]
- Khan, E.; Al Hossain, F.; Uddin, S.Z.; Alam, S.K.; Hasan, M.K. A Robust Heart Rate Monitoring Scheme Using Photoplethysmographic Signals Corrupted by Intense Motion Artifacts. IEEE Trans. Biomed. Eng. 2016, 63, 550–562. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.L.; Cheng, Y.F.; He, W.W.; Hou, M.S.; Zhang, Z.L. Combining Nonlinear Adaptive Filtering and Signal Decomposition for Motion Artifact Removal in Wearable Photoplethysmography. IEEE Sens. J. 2016, 16, 7133–7141. [Google Scholar] [CrossRef]
- Fukushima, H.; Kawanaka, H.; Bhuiyan, M.S.; Oguri, K. Estimating Heart Rate using Wrist-type Photoplethysmography and Acceleration sensor while running. In Proceedings of the 34th Annual International Conference of the IEEE Engineering-in-Medicine-and-Biology-Society (EMBS), San Diego, CA, USA, 28 August–1 September 2012; pp. 2901–2904. [Google Scholar]
- Chen, G.; Imtiaz, S.A.; Aguilar-Pelaez, E.; Rodriguez-Villegas, E. Algorithm for heart rate extraction in a novel wearable acoustic sensor. Healthc. Technol. Lett. 2015, 2, 28–33. [Google Scholar] [CrossRef] [PubMed]
- Salehizadeh, S.M.A.; Dao, D.K.; Chong, J.W.; McManus, D.; Darling, C.; Mendelson, Y.; Chon, K.H. Photoplethysmograph Signal Reconstruction based on a Novel Motion Artifact Detection-Reduction Approach. Part II: Motion and Noise Artifact Removal. Ann. Biomed. Eng. 2014, 42, 2251–2263. [Google Scholar] [CrossRef] [PubMed]
- Orphanidou, C.; Orphanidou, C. Quality Assessment for the photoplethysmogram (PPG). In Signal Quality Assessment in Physiological Monitoring: State of the Art and Practical Considerations; Springer: Cham, Switzerland, 2018; pp. 41–63. [Google Scholar]
- Khalid, S.G.; Ali, S.M.; Liu, H.; Qurashi, A.G.; Ali, U. Photoplethysmography temporal marker-based machine learning classifier for anesthesia drug detection. Med. Biol. Eng. Comput. 2022, 60, 3057–3068. [Google Scholar] [CrossRef] [PubMed]
- Karavaev, A.S.; Borovik, A.S.; Borovkova, E.I.; Orlova, E.A.; Simonyan, M.A.; Ponomarenko, V.I.; Skazkina, V.V.; Gridnev, V.I.; Bezruchko, B.P.; Prokhorov, M.D. Low-frequency component of photoplethysmogram reflects the autonomic control of blood pressure. Biophys. J. 2021, 120, 2657–2664. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Chen, F.; Hartmann, V.; Khalid, S.G.; Hughes, S.; Zheng, D. Comparison of different modulations of photoplethysmography in extracting respiratory rate: From a physiological perspective. Physiol. Meas. 2020, 41, 094001. [Google Scholar] [CrossRef] [PubMed]
- Maeda, Y.; Sekine, M.; Tamura, T. Relationship between measurement site and motion artifacts in wearable reflected photoplethysmography. J. Med. Syst. 2011, 35, 969–976. [Google Scholar] [CrossRef] [PubMed]
- Hughes, S.; Liu, H.; Zheng, D. Influences of sensor placement site and subject posture on measurement of respiratory frequency using triaxial accelerometers. Front. Physiol. 2020, 11, 823. [Google Scholar] [CrossRef]
- Saquib, N.; Papon, M.T.I.; Ahmad, I.; Rahman, A. Measurement of Heart Rate Using Photoplethysmography. In Proceedings of the Networking Systems and Security NSysS International Conference, Dhaka, Bangladesh, 5–7 January 2015; pp. 158–163. [Google Scholar]
- Robergs, R.A.; Landwehr, R. The surprising history of the “HRmax= 220-age” equation. J. Exerc. Physiol. 2002, 5, 1–10. [Google Scholar]
- Temko, A. Accurate Heart Rate Monitoring during Physical Exercises Using PPG. IEEE Trans. Biomed. Eng. 2017, 64, 2016–2024. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.L.; Pi, Z.Y.; Liu, B.Y. TROIKA: A General Framework for Heart Rate Monitoring Using Wrist-Type Photoplethysmographic Signals during Intensive Physical Exercise. IEEE Trans. Biomed. Eng. 2015, 62, 522–531. [Google Scholar] [CrossRef] [PubMed]
- Ismail, S.; Siddiqi, I.; Akram, U. Heart rate estimation in PPG signals using Convolutional-Recurrent Regressor. Comput. Biol. Med. 2022, 145, 105470. [Google Scholar] [CrossRef]
- Hnoohom, N.; Mekruksavanich, S.; Jitpattanakul, A. Physical Activity Recognition Based on Deep Learning Using Photoplethysmography and Wearable Inertial Sensors. Electronics 2023, 12, 693. [Google Scholar] [CrossRef]
- Moscato, S.; Lo Giudice, S.; Massaro, G.; Chiari, L. Wrist Photoplethysmography Signal Quality Assessment for Reliable Heart Rate Estimate and Morphological Analysis. Sensors 2022, 22, 5831. [Google Scholar] [CrossRef]


| Experimental Items | Preconditions | Experimental Procedure | Judgment Standard |
|---|---|---|---|
| Sitting | Participants were instructed to remain calm for at least 2 min prior to the experiment, commencing with a low heart rate of 100 bpm. | The participant places their hands on their thighs and sits quietly on a chair for a duration of 10 min. | When comparing with the heart rate measured by the heart rate band, sample values exhibiting an estimated heart rate deviation within ±10 bpm are considered accurate. |
| Daily activities | The same as above. | 1. The participant takes a seat on the chair in front of the computer; 2. Repeatedly types the phrase “Midsummer Night Dream” for a duration of 2 min using the keyboard; 3. Utilizes the arm wearing the bracelet to pick up and put down a pen 20 times within a 1 min timeframe; 4. Unties and ties their shoelace 10 times within a 2 min period. | The same as above. |
| Walking up and down stairs | The same as above. | The participant proceeds to walk up and down the stairs at a slow pace, ensuring that the effective experimental duration extends beyond 10 min. | The same as above. |
| Outdoor walking | The same as above. | The participant walks at a comfortable pace, typically on a flat, non-sloping surface during a sunny day, allowing both arms to swing naturally, and maintains this movement for a duration of 10 min. | The same as above. |
| Outdoor jogging | The same as above. | The participant engages in running on a flat, non-sloping surface during a sunny day, with the effective experimental duration lasting for more than 10 min. | The same as above. |
| Algorithm | Peak Detection | DFT | TROIKA | Proposed Algorithm |
|---|---|---|---|---|
| Accuracy (with spectral overlap) | 51.95% | 61.56% | 82.88% | 80.57% |
| Accuracy (without spectral overlap) | 82.70% | 96.66% | 97.17% | 96.66% |
| Algorithm complexity | ||||
| FLOPs | − 4 | )× | + |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, B.; Wang, Z.; Ma, K.; Zhou, Y.; Liu, M. An Improved Method of Heart Rate Extraction Algorithm Based on Photoplethysmography for Sports Bracelet. Information 2023, 14, 297. https://doi.org/10.3390/info14050297
Ren B, Wang Z, Ma K, Zhou Y, Liu M. An Improved Method of Heart Rate Extraction Algorithm Based on Photoplethysmography for Sports Bracelet. Information. 2023; 14(5):297. https://doi.org/10.3390/info14050297
Chicago/Turabian StyleRen, Binbin, Zhaoyuxuan Wang, Kainan Ma, Yiheng Zhou, and Ming Liu. 2023. "An Improved Method of Heart Rate Extraction Algorithm Based on Photoplethysmography for Sports Bracelet" Information 14, no. 5: 297. https://doi.org/10.3390/info14050297
APA StyleRen, B., Wang, Z., Ma, K., Zhou, Y., & Liu, M. (2023). An Improved Method of Heart Rate Extraction Algorithm Based on Photoplethysmography for Sports Bracelet. Information, 14(5), 297. https://doi.org/10.3390/info14050297





