Quantifying the Dissimilarity of Texts
Abstract
1. Introduction
2. Materials and Methods
2.1. Dissimilarity Measures
2.2. Data, Preprocessing, and Analysis
3. Analytical Results
3.1. Jaccard Distance
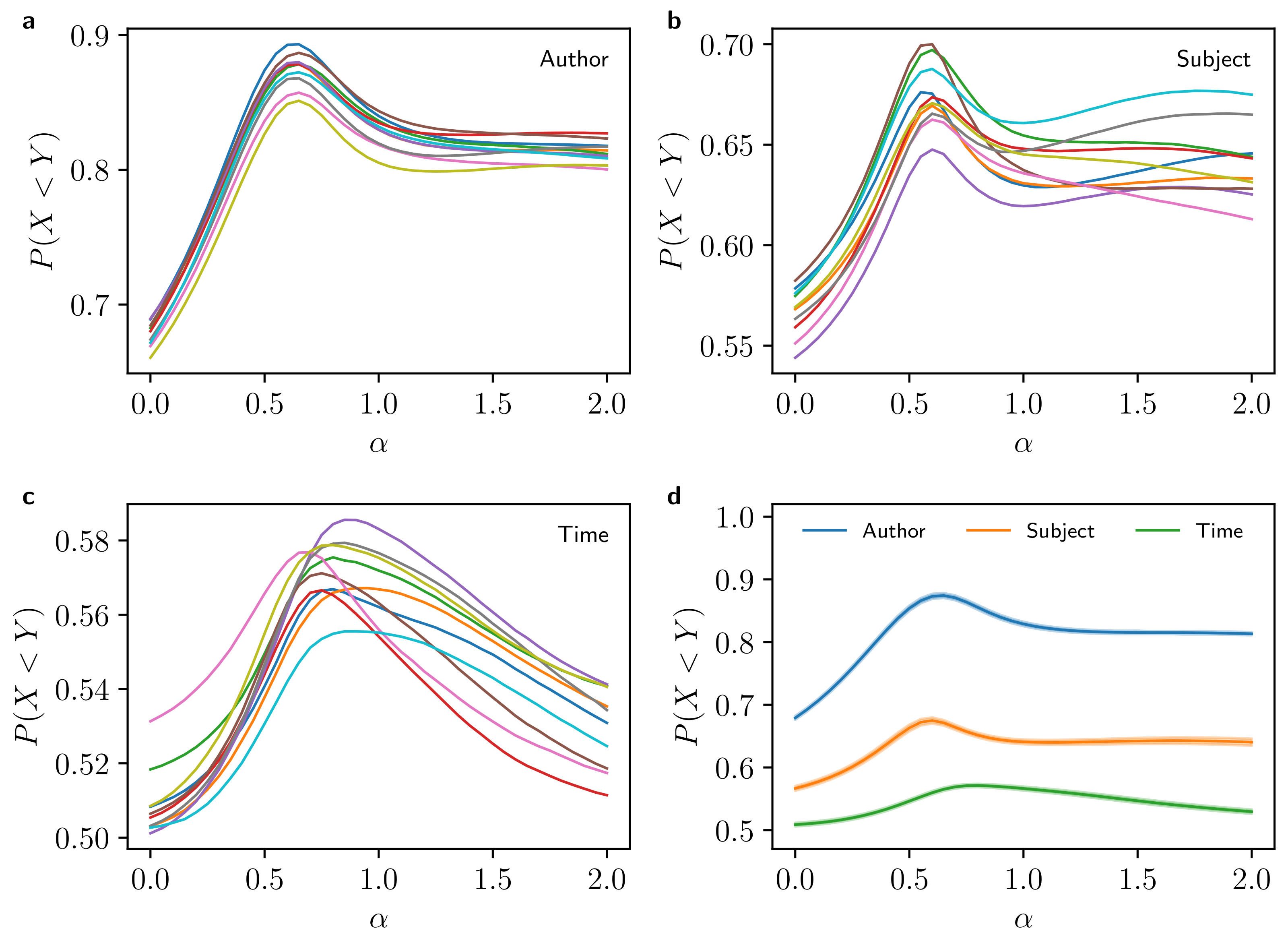
3.2. Jensen–Shannon Divergence
4. Numerical Results
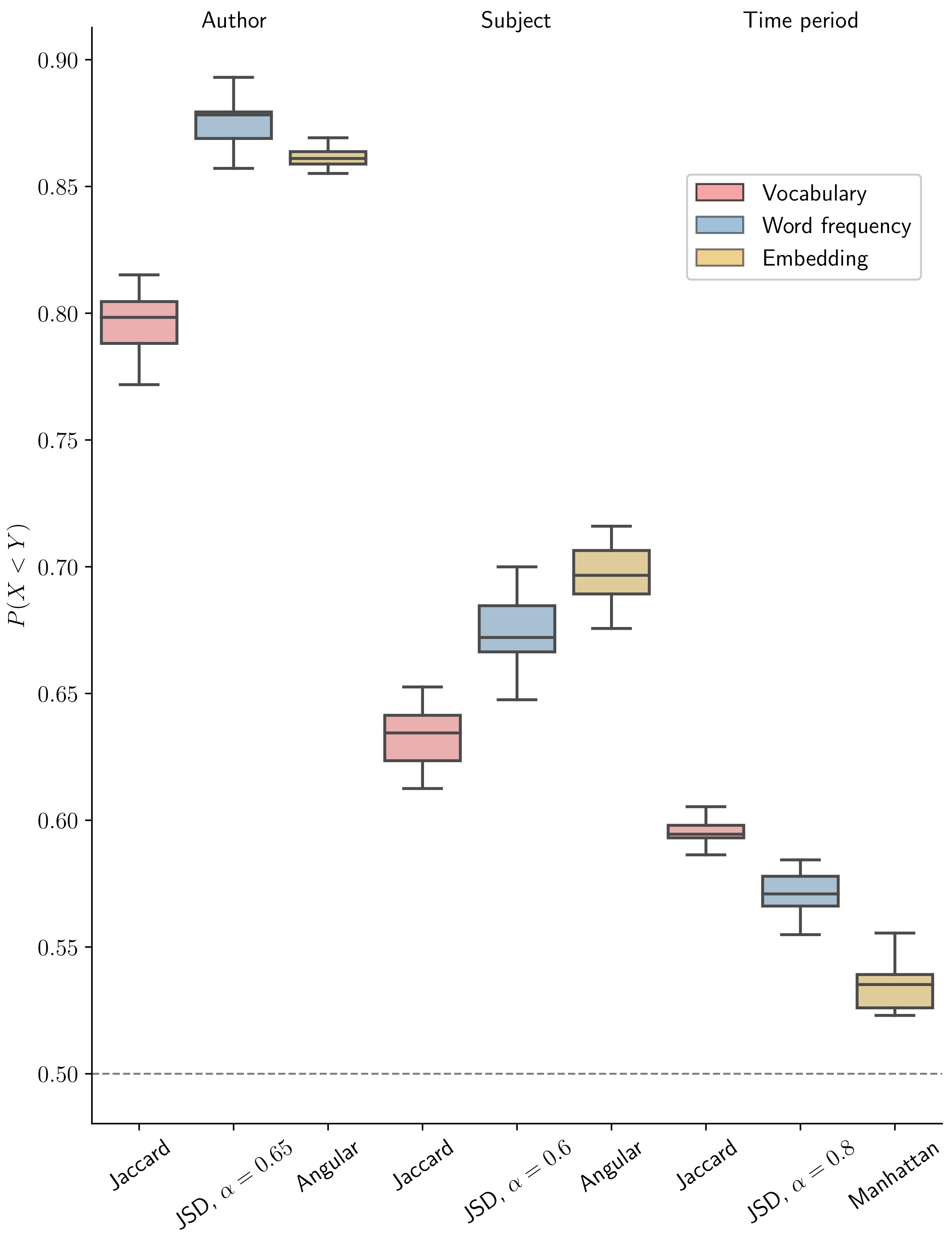
4.1. Numerical Performance Comparison
4.1.1. Vocabularies
4.1.2. Word Frequencies
4.1.3. Embeddings
4.1.4. Overall Comparison
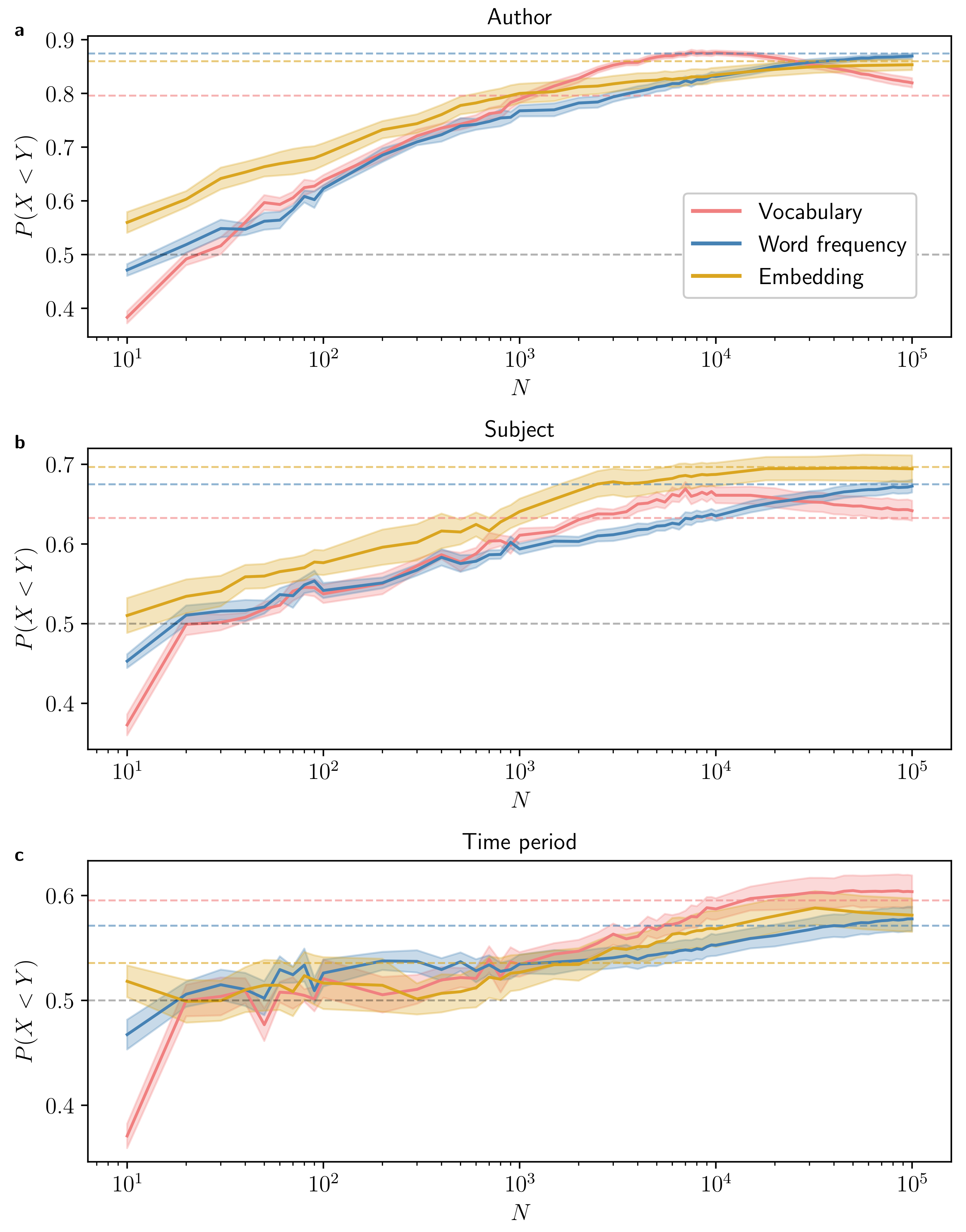
4.2. Dependence on Text Length
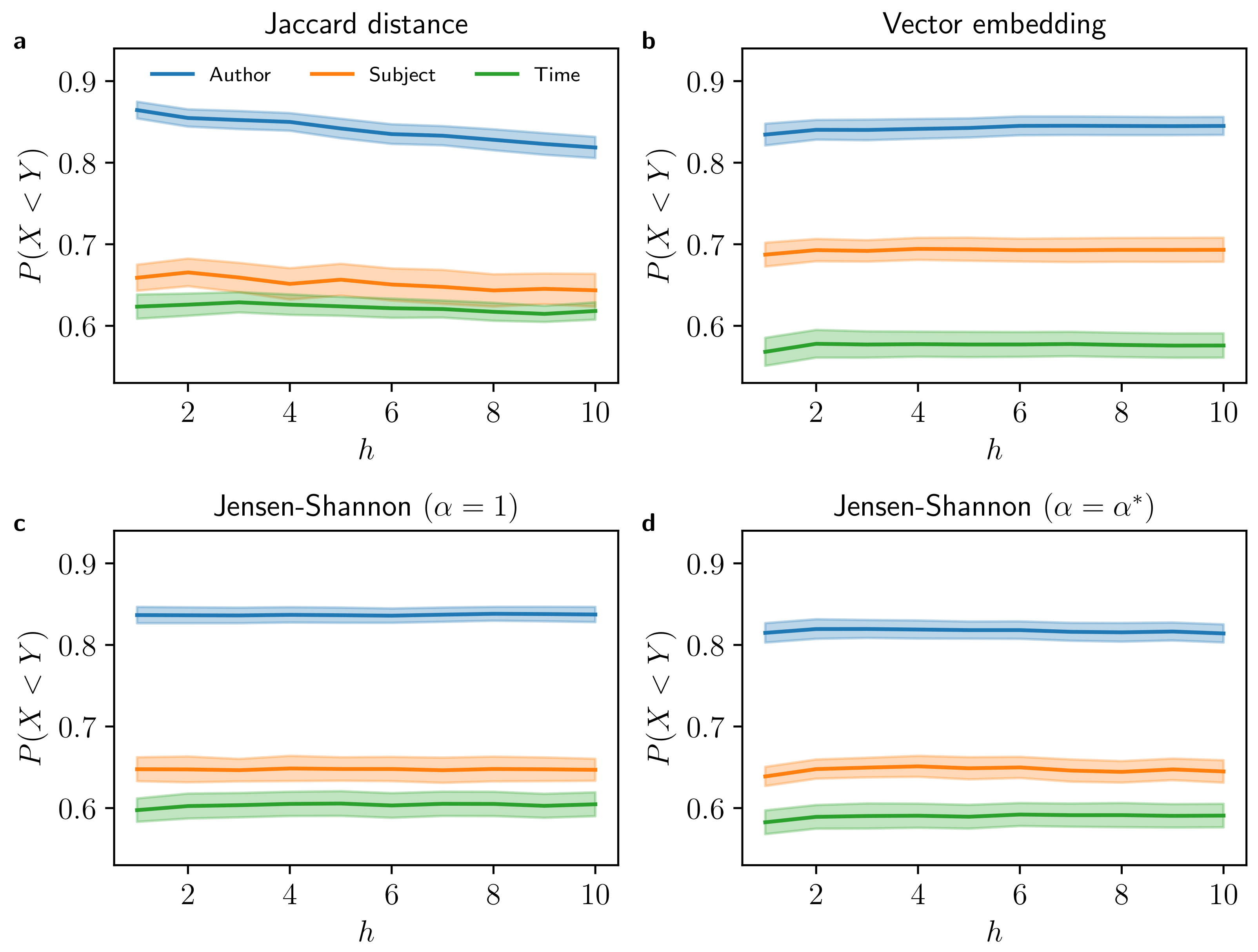
4.3. Impact of Unequal Text Length
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Metadata, Filtering and Preprocessing
Appendix B. Connecting P(X < Y) to ROC Curves
Appendix C. Derivation of the Jaccard Distance Lower Bound (Equation (9))
Appendix D. Derivation of the Bias of the Jensen–Shannon Divergence (Table 2)
- Case 1:
- Case 2:
Appendix E. Numerical Performance Results
| Task | Jaccard | Overlap | p-Value |
|---|---|---|---|
| Author | 0.796 ± 0.013 | 0.670 ± 0.007 | |
| Subject | 0.633 ± 0.013 | 0.504 ± 0.012 | |
| Time period | 0.595 ± 0.009 | 0.478 ± 0.007 |
| Task | JSD, | JSD, | p-Value |
|---|---|---|---|
| Author | 0.8288 ± 0.0035 | 0.8743 ± 0.0038 | |
| Subject | 0.6408 ± 0.0038 | 0.6749 ± 0.0048 | |
| Time period | 0.5664 ± 0.0030 | 0.5712 ± 0.0026 |
| Task | Euclidean | Manhattan | Angular |
|---|---|---|---|
| Author | 0.8448 ± 0.0026 | 0.8447 ± 0.0026 | 0.8599 ± 0.0025 |
| Subject | 0.6847 ± 0.0042 | 0.6846 ± 0.0043 | 0.6966 ± 0.004 |
| Time period | 0.5354 ± 0.0034 | 0.5357 ± 0.0034 | 0.5293 ± 0.0035 |
| Task | Metric Pair | p-Value |
|---|---|---|
| Euclidean–Manhattan | ||
| Author | Angular–Manhattan | |
| Angular–Euclidean | ||
| Euclidean–Manhattan | ||
| Subject | Angular–Manhattan | |
| Angular–Euclidean | ||
| Euclidean–Manhattan | ||
| Time period | Angular–Manhattan | |
| Angular–Euclidean |
References
- Pham, H.; Luong, M.T.; Manning, C.D. Learning distributed representations for multilingual text sequences. In Proceedings of the 1st Workshop on Vector Space Modeling for Natural Language Processing, Denver, CO, USA, 5 June 2015; pp. 88–94. [Google Scholar]
- Steyvers, M.; Griffiths, T. Probabilistic Topic Models. In Handbook of Latent Semantic Analysis; Landauer, T.K., McNamara, D.S., Dennis, S., Kintsch, W., Eds.; Psychology Press: New York, NY, USA, 2007; pp. 427–448. [Google Scholar]
- Jiang, N.; de Marneffe, M.C. Do you know that Florence is packed with visitors? Evaluating state-of-the-art models of speaker commitment. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; pp. 4208–4213. [Google Scholar]
- Wang, Q.; Li, B.; Xiao, T.; Zhu, J.; Li, C.; Wong, D.F.; Chao, L.S. Learning deep transformer models for machine translation. arXiv 2019, arXiv:1906.01787. [Google Scholar]
- Taghva, K.; Veni, R. Effects of Similarity Metrics on Document Clustering. In Proceedings of the Seventh International Conference on Information Technology: New Generations, Las Vegas, NV, USA, 12–14 April 2010; pp. 222–226. [Google Scholar]
- Zheng, L.; Jiang, Y. Combining dissimilarity measures for quantifying changes in research fields. Scientometrics 2022, 127, 3751–3765. [Google Scholar] [CrossRef]
- Dias, L.; Gerlach, M.; Scharloth, J.; Altmann, E.G. Using text analysis to quantify the similarity and evolution of scientific disciplines. R. Soc. Open Sci. 2018, 5, 171545. [Google Scholar] [CrossRef]
- Tommasel, A.; Godoy, D. Influence and performance of user similarity metrics in followee prediction. J. Inf. Sci. 2022, 48, 600–622. [Google Scholar] [CrossRef]
- Singh, K.; Shakya, H.K.; Biswas, B. Clustering of people in social network based on textual similarity. Perspect. Sci. 2016, 8, 570–573. [Google Scholar] [CrossRef]
- Tang, X.; Miao, Q.; Quan, Y.; Tang, J.; Deng, K. Predicting individual retweet behavior by user similarity: A multi-task learning approach. Know. Based Syst. 2015, 89, 681–688. [Google Scholar] [CrossRef]
- Gomaa, W.H.; Fahmy, A.A. A Survey of Text Similarity Approaches. Int. J. Comput. Appl. 2013, 68, 13–18. [Google Scholar]
- Wang, J.; Dong, Y. Measurement of Text Similarity: A Survey. Information 2020, 11, 421. [Google Scholar] [CrossRef]
- Vijaymeena, M.K.; Kavitha, K. A Survey on Similarity Measures in Text Mining. Mach. Learn. Appl. 2016, 3, 19–28. [Google Scholar]
- Prakoso, D.W.; Abdi, A.; Amrit, C. Short text similarity measurement methods: A review. Soft Comput. 2021, 25, 4699–4723. [Google Scholar] [CrossRef]
- Magalhães, D.; Pozo, A.; Santana, R. An empirical comparison of distance/similarity measures for Natural Language Processing. In Proceedings of the National Meeting of Artificial and Computational Intelligence, Salvador, Brazil, 15–18 October 2019; pp. 717–728. [Google Scholar]
- Boukhatem, N.M.; Buscaldi, D.; Liberti, L. Empirical Comparison of Semantic Similarity Measures for Technical Question Answering. In Proceedings of the European Conference on Advances in Databases and Information Systems, Turin, Italy, 5–8 September 2022; pp. 167–177. [Google Scholar]
- Upadhyay, A.; Bhatnagar, A.; Bhavsar, N.; Singh, M.; Motlicek, P. An Empirical Comparison of Semantic Similarity Methods for Analyzing down-streaming Automatic Minuting task. In Proceedings of the Pacific Asia Conference on Language, Information and Computation, Virtual, 20–22 October 2022. [Google Scholar]
- Al-Anazi, S.; AlMahmoud, H.; Al-Turaiki, I. Finding similar documents using different clustering techniques. In Proceedings of the Symposium on Data Mining Applications, Riyadh, Saudi Arabia, 30 March 2016; pp. 28–34. [Google Scholar]
- Webb, A.R. Statistical Pattern Recognition, 2nd ed.; John Wiley & Sons, Inc.: Chichester, UK, 2003; p. 419. [Google Scholar]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent Dirichlet Allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Salton, G.; Buckley, C. Term-weighting approaches in automatic text retrieval. Inf. Process. Manag. 1988, 24, 513–523. [Google Scholar] [CrossRef]
- Herdan, G. Type-Token Mathematics: A Textbook of Mathematical Linguistics, 1st ed.; Mouton & Co.: The Hague, The Netherlands, 1960. [Google Scholar]
- Bengio, Y.; Ducharme, R.; Vincent, P.; Jauvin, C. A neural probabilistic language model. J. Mach. Learn. Res. 2003, 3, 1137–1155. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representations in Vector Space. arXiv 2013, arXiv:1301.3781. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C. GloVe: Global Vectors for Word Representation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
- Le, Q.; Mikolov, T. Distributed Representations of Sentences and Documents. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 1188–1196. [Google Scholar]
- Hill, F.; Cho, K.; Horhonen, A. Learning Distributed Representations of Sentences from Unlabelled Data. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, San Diego, CA, USA, 12–17 June 2016; pp. 1367–1377. [Google Scholar]
- Wu, L.; Yen, I.E.; Xu, K.; Xu, F.; Balakrishnan, A.; Chen, P.Y.; Ravikumar, P.; Witbrock, M.J. Word Mover’s Embedding: From Word2Vec to Document Embedding. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, 31 October–4 November 2018; pp. 4524–4534. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. In Proceedings of the 31st Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), Minneapolis, MN, USA, 2–7 June 2019; pp. 4171–4186. [Google Scholar]
- Radford, A.; Narasimhan, K.; Salimans, T.; Sutskever, I. Improving Language Understanding by Generative Pre-Training; Technical Report; OpenAI: San Francisco, CA, USA, 2018. [Google Scholar]
- Shade, B. Repository with the Code Used in This Paper; Static Version in Zenodo; Dynamic Version in Github; 2023. Available online: https://doi.org/10.5281/zenodo.7861675; https://github.com/benjaminshade/quantifying-dissimilarity (accessed on 14 February 2022).
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Endres, D.M.; Schindelin, J.E. A new metric for probability distributions. IEEE Trans. Inf. Theory 2003, 49, 1858–1860. [Google Scholar] [CrossRef]
- Gerlach, M.; Font-Clos, F.; Altmann, E.G. Similarity of Symbol Frequency Distributions with Heavy Tails. Phys. Rev. X 2016, 6, 021109. [Google Scholar] [CrossRef]
- Havrda, J.; Charvát, F. Quantification Method of Classification Processes. Concept of Structural α-Entropy. Kybernetika 1967, 3, 30–35. [Google Scholar]
- Burbea, J.; Rao, C. On the convexity of some divergence measures based on entropy functions. IEEE Trans. Inf. Theory 1982, 28, 489–495. [Google Scholar] [CrossRef]
- Briët, J.; Harremoës, P. Properties of classical and quantum Jensen-Shannon divergence. Phys. Rev. A 2009, 79, 052311. [Google Scholar] [CrossRef]
- Reimers, N.; Gurevych, I. Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing, Hong Kong, China, 3–7 November 2019; pp. 3982–3992. [Google Scholar]
- Wang, W.; Wei, F.; Dong, L.; Bao, H.; Yang, N.; Zhou, M. MiniLM: Deep Self-Attention Distillation for Task-Agnostic Compression of Pre-Trained Transformers. In Proceedings of the 34th Conference on Neural Information Processing Systems, Virtual, 6–12 December 2020; pp. 5776–5788. [Google Scholar]
- Beltagy, I.; Peters, M.E.; Cohan, A. Longformer: The Long-Document Transformer. arXiv 2020, arXiv:2004.05150. [Google Scholar]
- Project Gutenberg. Available online: https://www.gutenberg.org (accessed on 8 February 2022).
- Gerlach, M.; Font-Clos, F. A Standardized Project Gutenberg Corpus for Statistical Analysis of Natural Language and Quantitative Linguistics. Entropy 2020, 22, 126. [Google Scholar] [CrossRef]
- Gerlach, M.; Font-Clos, F. Standardized Project Gutenberg Corpus, Github Repository. 2018. Available online: https://github.com/pgcorpus/gutenberg (accessed on 14 February 2022).
- Altmann, E.G.; Dias, L.; Gerlach, M. Generalized entropies and the similarity of texts. J. Stat. Mech. Theory Exp. 2017, 2017, 014002. [Google Scholar] [CrossRef]
- Gerlach, M. Universality and Variability in the Statistics of Data with Fat-Tailed Distributions: The Case of Word Frequencies in Natural Languages. Ph.D. Thesis, Max Planck Institute for the Physics of Complex Systems, Dresden, Germany, 2015. [Google Scholar]
- Gerlach, M.; Altmann, E.G. Stochastic Model for the Vocabulary Growth in Natural Languages. Phys. Rev. X 2013, 3, 021006. [Google Scholar] [CrossRef]
- Bird, S.; Klein, E.; Loper, E. Natural Language Processing with Python: Analyzing Text with the Natural Language Toolkit, 1st ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2009. [Google Scholar]
- Egloff, M.; Adamou, A.; Picca, D. Enabling Ontology-Based Data Access to Project Gutenberg. In Proceedings of the Third Workshop on Humanities in the Semantic Web, Heraklion, Crete, Greece, 2 June 2020; pp. 21–32. [Google Scholar]
- Mann, H.B.; Whitney, D.R. On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Mason, S.J.; Graham, N.E. Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: Statistical significance and interpretation. Q. J. R. Meteorol. Soc. 2002, 128, 2145–2166. [Google Scholar] [CrossRef]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef]
| Representation | Name | Expression |
|---|---|---|
| Vocabulary | Jaccard distance | |
| Overlap dissimilarity | ||
| Word frequency | Jensen–Shannon divergence of order | , |
| Embedding | Euclidean distance | |
| Manhattan distance | ||
| Angular distance |
| Range | ||
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shade, B.; Altmann, E.G. Quantifying the Dissimilarity of Texts. Information 2023, 14, 271. https://doi.org/10.3390/info14050271
Shade B, Altmann EG. Quantifying the Dissimilarity of Texts. Information. 2023; 14(5):271. https://doi.org/10.3390/info14050271
Chicago/Turabian StyleShade, Benjamin, and Eduardo G. Altmann. 2023. "Quantifying the Dissimilarity of Texts" Information 14, no. 5: 271. https://doi.org/10.3390/info14050271
APA StyleShade, B., & Altmann, E. G. (2023). Quantifying the Dissimilarity of Texts. Information, 14(5), 271. https://doi.org/10.3390/info14050271






