Abstract
Within the framework of the mathematical theory of conflicts, we consider a multi-criterial conflict situation using the example of a child–parent conflict. A general method for constructing a conflict diagram is described and possible ways of the conflicting parties influencing each other in this conflict situation are discussed. We introduce criteria that characterize the intensity of conflicts and show that the conflict resolution problem can be reduced to a multi-criterial combinatorial optimization problem. As a method for solving this problem, we consider the Monte Carlo method (Metropolis algorithm). The performed parametric calculations demonstrate the effectiveness of the proposed method.
1. Introduction
Conflicts are the driving force behind the development of society. The whole history of the development of human civilization and its individual components is a series of different conflicts (military, political, ethnolinguistic, religious, social, industrial, family, etc.); at each stage of the development of society, people have been looking for ways to resolve existing conflicts, which has led to the evolution of society, and, at the same time, given rise to new conflicts [1].
Conflicts are studied by conflictology [2,3], which arose at the junction of several scientific areas [4]: philosophy, sociology, psychology, political science [3,5,6,7], etc. Within these areas, methods have been developed for analyzing relevant conflict situations, as well as recommendations for resolving conflicts of various types [2,3,5,6,7].
There are a large number of works [1,2,3,4,5,6,7] devoted to the construction of models of various conflicts that describe the relationship between the conflicting parties and the changes caused by this. Note that most of these models are descriptive in nature (verbal models) and do not pretend to be a quantitative description of the conflict situation (its development, the quantitative prediction of its results or ways out of the situation).
From a predictive point of view, the mathematical modeling of conflicts is of the greatest interest.
Currently, various mathematical methods are used to model conflicts: game theory [8,9,10,11], dynamic systems theory [12,13,14,15], stochastic models [16,17,18], probabilistic and statistical methods [19,20,21], logical models [22,23,24,25], algebraic models [26,27], etc. We also note the approach based on the analysis of hierarchies [28]. A simple model of conflict analysis based on a three-valued rating table, in which an agent either opposes, is neutral or supports an issue was introduced in [29]. According to the interpretation of the three rating values, conflict analysis [29] is in fact a qualitative model. Two other qualitative three-part notions introduced in [30] include three relations among the set of agents, namely, allied, neutral or conflict relations and a trisection of agents into the three classes that supports, is neutral or opposes an issue, respectively. Many authors have extended and applied these notions from several different perspectives [31,32,33,34,35]. Thus, a three-way conflict analysis model and conflict degree-based decision-theoretic rough set model for conflict resolution under Pythagorean fuzzy information was proposed in [33].
It should be noted that each conflict model, in fact, uses its own definition of a conflict and even its own idea of what to call a conflict. Currently, there are several definitions of a conflict that consider this phenomenon from a philosophical or psychological point of view [3,6,36,37,38,39,40].
Very often, conflicts are considered as a clash of economic interests and the assessment of the degree of conflict and ways to resolve them is reduced to the search for economically sound solutions. However, many conflicts do not have an economic reason for existing (or the economic reason is secondary) and are associated with the cultural and psychological characteristics of the conflicting parties. In this case, an economically oriented approach to the analysis of conflicts and the search for ways to resolve them turns out to be inapplicable.
In [41], a general formal definition of conflict was proposed, which allowed us to proceed to the mathematical description of any conflict situation from a unified standpoint: a conflict is a discrepancy between a person’s desire and their capabilities, i.e., between what they want and what they have.
According to this definition, any conflict is characterized by at least two parameters: what the person wants (i.e., their desire, goal) and what they currently have .
Thus, the cause (driving force) of the conflict is the following discrepancy [41]:
where for and for .
By definition, it is considered that in the absence of a conflict, , while a conflict takes place if .
Any conflict is always associated with a specific subject of the conflict, that is, objectively existing or non-existing subjects or objects with which the discrepancy is associated.
It follows from the above definition that two persons can have a common subject of their conflict, while each of the conflicting persons has their own conflict: each of them has their own discrepancy and, therefore, their own the degree (intensity) of the conflict. Accordingly, each of them tries to resolve their own conflict in a different way, taking into account the available opportunities, circumstances and the reactions of other persons.
In this regard, it is necessary to distinguish between the concepts of a “conflict“ and “conflict situation” [41].
A conflict situation is a situation (a state of a system, a strategy) in which several persons (conflicting parties) participate who have a common subject of conflict, while different persons may have different conflict parameters and , different discrepancies and, therefore, different reasons (driving forces) for the conflict [41].
This means that any conflict situation is characterized by a full set of parameters and, accordingly, discrepancies between all participants in the conflict situation (conflicting parties).
The conflict that has arisen for the person, by definition, causes them a reaction (effort, action) aimed at resolving this conflict, i.e., to reduce the existing discrepancy.
According to Equation (1), they can achieve this either by a corresponding change in the parameter (“I want”) or by a corresponding change in the parameter (“I have”). Thus, the search for ways to resolve any conflict ultimately comes down to the search for methods, ways and means of appropriately changing the conflict parameters and .
According to [41], in a conflict situation, a person can change only those parameters that they control directly and does not have the ability to directly change those parameters that other people control. This is the fundamental difference between controlling a conflict situation (cognitive control) and controlling technical objects.
In particular, to resolve an external conflict (i.e., when parameter is controlled by an opponent) at a constant , the person must have such an impact on the opponent controlling the parameter that the opponent is forced (wants, agrees) to change in the direction necessary for the person. There is only one way to influence an opponent: to create a conflict for them, by which the opponent will be forced to change the parameter controlled by them in the direction necessary for this person.
Thus, by changing their parameters, participants in a conflict situation can influence their opponent, stimulating them to change the parameters they control.
The conflict parameters and , and with them the discrepancy , can take both continuous and discrete values.
For this reason, one can speak of conflict in terms of continuous discrepancy or discrete discrepancy. In the latter case, discrepancy is a Boolean variable and can only take two values, 0 or 1, depending on whether the person’s desire is satisfied or not.
A conflict with continuous parameters was considered in [41].
In this paper, we consider a conflict with discrete parameters.
We analyzed the existing mathematical models of conflicts and came to the conclusion that they cannot be used for a detailed description of a child–parent conflict, considered in Section 2, and similar conflicts.
The purpose of this work is to develop a general method for constructing a mathematical model of a conflict situation, regardless of its physical nature and subject area, based on the mathematical theory of conflicts formulated in [41].
This paper is organized as follows: Section 2 contains the problem description and a mathematical model of the development of a child–parent conflict and its various stages. Section 3 shows that from a mathematical point of view, child–parent conflict resolution can be considered as a combinatorial optimization problem. Section 4 describes the Monte Carlo method for finding ways to efficiently resolve conflicts and provides examples demonstrating the effectiveness of this method. Finally, our conclusions are presented in Section 5.
2. Child–Parent Conflict
In this work, we consider a model conflict situation with discrete discrepancies using the example of a child–parent conflict. Despite the fact that we are considering specific conflicts, the methods and general scheme for solving the problem are general and applicable to any conflict situation, regardless of their nature and subject area.
In the case of a conflict with discrete parameters, the discrepancy between and can be expressed both through logical functions and using ordinary arithmetic operations (functions). In this work, we use the second option. In this case, as we shall see, the function may differ from the formal Equation (1).
Note that in some cases, the parameters or may be constant (universal constants), i.e., they do not change under any circumstances. This happens, for example, when the requirements behind these parameters are fundamental to a given participant in a conflict situation. Obviously, when calculating discrepancies, universal constants can be omitted. This agreement will be used by us in the future.
Further, one side of the conflict (the child) will be denoted by the superscript “1”, while the other side of the conflict (the parent), by the superscript “2”.
Suppose a child wants to have a smartphone. From the point of view of the mathematical theory of conflicts [41], this corresponds to the parameter of the child (the parameter controlled by the child) . At the initial stage, whether the child will have a smartphone or not is determined by the parent who controls the parameter : if the child has a smartphone (the parent bought them a smartphone), if the child does not have a smartphone (the parent did not buy them a smartphone). In this case, the discrepancy that occurs for the child, associated with the absence or presence of a smartphone, can be written as .
If the child has a smartphone, then the discrepancy is , i.e., the child does not have a conflict associated with the lack of a smartphone. If the child does not have a smartphone, then they have a discrepancy and a conflict associated with it. If , then , regardless of whether the child has a smartphone or not. This means that in this case, the child does not care whether they have a smartphone or not, i.e., the lack of a smartphone in this case does not cause conflict for the child.
The question arises: why does a child want (or not want) to have a smartphone, i.e., what determines (forms) the value of the parameter ?
Obviously, the parameter only makes sense if the child does not have a smartphone (). In this case, the child themself determines the value of their parameter (i.e., whether they need a smartphone or not); however, their decision may be influenced by others (third parties). If they choose , then they will have an internal conflict: “All my friends and acquaintances have a smartphone, but I don’t!”, “Am I worse than others?”, “What about me? What will my friends and acquaintances think?”, etc. That is, this conflict is connected, among other things, with the child’s dependence on someone else’s opinion and with the desire to “be like everyone else”. To describe this, without going into the details of the causes of this conflict, we introduce the discrepancy for the child and the related conflict that occurs only when . Note that this conflict cannot simply be reduced to the conflict because it, in fact, forms the position (point of view) of the child, i.e., is an independent conflict with its own significance for the child.
Consider a situation where the presence of a smartphone with a child has a bad effect on them, for example, causing deviation in their behavior, mentality, negatively affecting their studies, social circle, interests, etc. The parent does not want the child to experience such changes; this is described by the parent parameter . In this case, the parent has a discrepancy associated with the presence of a smartphone for the child.
We assume that in the case under consideration, changes in the child’s behavior associated with the presence of a smartphone are unacceptable for the parent, and this point of view will not be changed under any circumstances: . Then, the corresponding discrepancy takes the form of .
Thus, we see that at least one conflict initially arises in the system under consideration if and (): when , the child has a conflict related to the lack of a smartphone, while when , the parent has a conflict related to the fact that the smartphone has a bad effect on the child.
We also take into account that the parent wants their child to have no conflicts, i.e., so that the child does not experience discomfort. This is described by the parent parameter . In what follows, we will also consider this condition as fundamental, i.e., . Thus, having made the decision not to buy a smartphone for the child (or having taken away an existing smartphone), i.e., having created a conflict for them, the parent will simultaneously create for themself an internal conflict associated with the discrepancy : they see that the child does not get what they want and worry about the child (the child suffers, the parent feels “guilt”, etc.). Such a conflict can be called a secondary (induced) one. Similarly, the parent experiences that the child has a conflict , which is described by a discrepancy for the parent . Note that the conflicts and , generally speaking, have a different significance for the child, i.e., are perceived by them in different ways: they consider one more significant, the other less. Therefore, these conflicts will be perceived differently by the parent: they will experience each of them differently. This means that, in general, conflicts for the parent and must be taken into account independently. However, in this paper, for simplicity, we assume that all conflicts that arise for the child cause the parent to have a single secondary conflict, which we characterize by the discrepancy . Note that it is the arithmetic sum of the discrepancies that is used here and not the disjunction; this takes into account that the presence of several conflicts at the same time for the child creates a conflict for the parent that is stronger than in the case when the child has only one conflict.
Note that the child can also worry if the parent has conflicts because of them. In this paper, we do not take this into account so as not to complicate an already ramified conflict situation.
When considering this conflict situation, we can either fix the parameters or , for example, by setting and and thus by setting the initial conflicts (corresponding to a situation where both parties will under no circumstances agree to change their positions; for example, if the significance of this conflict for the corresponding party significantly exceeds the significance of all other conflicts) or consider these parameters as variables.
In this paper, we consider the general case with variable parameters and .
Everything described above forms the initial conditions for the emergence of a conflict situation in the child–parent system under consideration.
Possible initial situations are given in Table 1.

Table 1.
Possible initial situations in a child–parent conflict.
As follows from Table 1, in the system under consideration in the initial situation, there is always at least one conflict: the parent has one conflict in all situations, while the child in situations 3 and 4 has no conflict at all, but in situations 1 and 2, there is one conflict each. In such situations, the party that has a conflict begins to look for ways to resolve this conflict.
The simplest and least expensive (but not always accessible and feasible) way to resolve a conflict situation is when the parties do not exert additional control actions on each other (i.e., do not create new conflicts for the opponent), but try to change their own parameters and in order to reduce for a common “conflict load” for themselves. That is, they try to adapt to the current situation.
Let’s consider how this method is implemented in relation to the initial situation. (Table 1).
Suppose the priority for the parent is the absence of conflict and they are ready to put up with the conflict . In this case, the parent decides not to give the child a smartphone: (situations 1 and 2, Table 1). The child, in order to adapt to the situation that has arisen, must choose what is a greater priority (more comfortable) for them: to have a smartphone () or to give it up ). That is, they must decide for themself which of the conflicts that arises in this case is less significant for them: (situation 1) or (situation 2). In this case, both the child and the parent will not make an effort to change the situation that has arisen, i.e., the system will be in forced equilibrium.
Let us now consider the case when the priority for the parent is the absence of conflict and they are ready to put up with the conflict . In this case, the parent decides to give the child a smartphone: (situations 3 and 4, Table 1). From the point of view of the child, both options are ideal, because they do not have any conflicts, and from the point of view of the parent, both options are equally acceptable. Thus, if the parent is ready to put up with the conflict , then this option is the best for both participants in the conflict situation, and the system is also in forced equilibrium.
Let us now assume that the conflicting parties failed to resolve or significantly weaken the existing conflicts by simply changing their own parameters and (i.e., by adapting to the existing situation).
In this case, each of the conflicting parties begins to look for alternative ways to resolve their conflicts or makes efforts to influence the opponent such that they change the parameters they control in the right direction. Such influences usually come down to creating new or strengthening existing conflicts with the opponent, by which they will be forced to make concessions or change their position [41].
The actions taken by a rational person are always aimed at making all or some of their discrepancies equal to zero. However, this does not mean that if the discrepancies are zero, that a rational person will not take any action to create conflicts for the other person. As practice shows, even rational persons can create (or try to create) conflicts for other persons for no apparent reason (“just like that”, for example, because they “do not like this person”, “out of stupidity”, etc.). Further, we will consider both participants in the conflict situation as rational persons in the sense that if they have any conflict, they will certainly use all the possibilities to resolve the conflict, i.e., they will try by all means available to them to influence their opponent in order to force them to change their decision (position, behavior strategy, etc.). However, in the absence of conflicts in themselves, they can, nevertheless, create conflicts for other persons “just like that”, for no visible reason to opponents. For this reason, when analyzing possible scenarios for the development of a conflict situation, it is necessary to consider all possible types of influences of the conflicting parties on each other, even if the corresponding discrepancies are equal to zero at the moment.
Let us consider various scenarios for the development of a conflict situation between a child and a parent.
A child in such a situation usually chooses the simplest and most natural (and most common) way to influence their parents: they start to act up and if this does not help, they start to behave badly, do not obey their parent, are impudent, speak badly, study poorly, etc.. In other words, this creates a conflict for the parent; the parent wants the child to be obedient and to behave well (), while the child behaves badly (). In this case, the parent has a discrepancy . Note that a child can behave badly not only because they do not have a smartphone; they can behave badly “just like that”. In other words, we can divide the child’s bad behavior into two groups: (i) “just like that” (for no reason from the parent’s point of view) and (ii) in order to influence the parent to change their decision and buy them a smartphone. Taking this into account, the discrepancy can be written as . Indeed, if a child has a conflict related to the lack of a smartphone (), then they, being a rational subject by the condition, will automatically behave badly because with their bad behavior, they will try to influence the parent to buy them a smartphone. In this case, the parent has a discrepancy and a conflict associated with it. If the child does not have a conflict associated with the lack of a smartphone (), then the child is free to choose their behavior: they can behave well () without creating a conflict with the parent () or they can behave badly () “just like that”, without a visible reason to the parent, thereby creating a conflict for the parent (). Note that the concept of “bad behavior” from the point of view of the parent (and from the point of view of the child) has gradations: different “bad behavior” of the child can be assessed differently by the parent. For example, the actions “the child is just naughty” and “the child is rude to the parent” have different meanings for the parent: the former is usually less significant for the parent than the latter. Therefore, in general, for each variant of the child’s bad behavior, one needs to enter different pairs of parameters (). In this work, for simplicity, we combined all possible types of bad behavior of a child and characterized them with only one pair of parameters and .
By creating a conflict for the parent with their bad behavior, the child realizes that they are acting badly. As a result, they may also have a secondary (induced) conflict associated with the discrepancy .
If the child could not force the parent to buy them a smartphone through bad behavior, they can take other actions aimed at resolving this conflict. In particular, they may try to solve their problem (lack of a smartphone) without the participation of a parent, i.e., get a smartphone from alternative sources. Such sources could be friends, relatives (grandparents, aunts, uncles, etc.), etc. We introduce the parameters , where is the number of alternative smartphone sources and is the number of such sources. By definition, if the child was able to get a smartphone from the k-th source and otherwise. Consider the parameter . Obviously, if , at least for one , i.e., if the child was able to get a smartphone from at least one source, including the parent, and if for all , i.e., if the child could not get a smartphone from any source, including the parent. In other words, if the child has a smartphone and if they do not have a smartphone.
Thus, in the expressions for and , it is necessary to replace with .
Consider what additional conflicts arise in this case.
First of all, the child has violated the parent’s prohibition and is afraid that the parent will find out about the presence of a smartphone. In this case, the child has an internal conflict associated with the discrepancy : , if the child got a smartphone from an alternative source (), while the parent does not allow them to have a smartphone () and if the parent themself bought the child a smartphone (). Obviously, two situations should be distinguished: (i) the parent does not know that the child obtained a smartphone from an alternative source () and (ii) the parent found out that the child obtained a smartphone from an alternative source (), where the parameter characterizes the state of the parent. However, unlike the parameter , this is not controlled by the parent (i.e., the parent cannot independently change this). Obviously, the discrepancy creates a conflict for the child only if the parent does not yet know that they got the smartphone from alternative sources. Therefore, the discrepancy should be written as .
It should be noted that the child has another conflict related to the fact that they got a smartphone from an alternative source: the feeling of guilt that the child feels towards the parent because they violated their prohibition to have a smartphone. This conflict exists both in the case when the parent does not know that the child has a smartphone and in the case when the parent found out that the child got the smartphone from an alternative source. Therefore, this conflict cannot be reduced to the discrepancy and for it, the discrepancy must be considered separately.
If a parent forbids a child from having a smartphone, then regardless of whether the child got a smartphone from alternative sources or not, the child still has a conflict (resentment against the parent), which is described by the discrepancy .
Note that the conflict for the parent, described by the discrepancy , is caused by the child’s bad behavior due to the fact that the parent does not want to buy them a smartphone. If a child obtained a smartphone from alternative sources and the parent still forbids them from having a smartphone, then the child may continue to misbehave out of resentment towards the parent. In this case, in the expression for the discrepancy , one needs to use instead of . If the child did not get a smartphone from alternative sources, then obviously and we will obtain the previous expression for .
If a child gets a smartphone from an alternative source, despite the parent’s prohibition, the parent has a conflict related to the discrepancy —the child disobeyed and deceived. Here, it is taken into account that this conflict arises only when the parent has learned about this act by the child ().
If a parent finds out that a child obtained a smartphone from an alternative source, they can take the smartphone away from the child. Let us consider what new conflicts will arise between the child and the parent. We enter the parameter : if the parent did not take away (took away) the smartphone received from an alternative source from the child.
In this case, the child has a conflict associated with the discrepancy , caused by the fact that the parent took away the smartphone (“humiliated” the child, demonstrated their power over them, etc.). It is taken into account here that this conflict occurs only if the parent found out that the child got the smartphone from an alternative source ().
In this situation, the parent also has a discrepancy and the associated conflict caused by the fact that the parent, taking away the smartphone from the child, exacerbated the existing conflict situation (“humiliates” the child, demonstrates their power over them, etc.).
If , then the child does not have a smartphone again, and this means that the parameter , which describes whether the child has a smartphone, should be equal to zero. To take this into account, we corrected the definition of the parameter as follows: .
Suppose that a parent, in addition to a smartphone, has another tool for influencing a child. This means that the child has (does not have) some other desire (for example, a new bicycle) , while the realization of this desire depends on the parent who controls the parameter : (1) if the parent does not buy (bought) the child a new bicycle. In this case, the parent can have an additional influence on the child by changing the value of the parameter . The child can also change the value of their parameter , but this may lead to new internal or external conflicts for the child. By an analogy with and we introduce the following discrepancies and conflicts associated with them: describing a conflict for a child related to the lack of a new bicycle. Meanwhile, describes a conflict for a child associated with their dependence on the opinions of others (friends, acquaintances, etc.) about the new bicycle.
In this case, new terms can be added to the discrepancy of the parent (the parent is worried that the child has new conflicts and : ).
If , then the parent does not have the opportunity to influence the child by changing the parameter ; however, when , the conflict can be used by the parent both as an instrument of influence on the child and “just like that”. In this case, by an analogy with , we introduce the parameter , and we replace with in the discrepancies and . If the child behaves badly (), then and the parent creates a conflict for the child to force the child to change their behavior, while if the child behaves well (), then and the parent may choose not to create a conflict for the child ( for ) or they can create a conflict for the child “for no reason” with .
Note that the child can also create a conflict (bad behavior) for the parent in response to the conflict . In this case, the discrepancy takes the form . That is, the child necessarily creates a conflict for the parent by their bad behavior if and/or , i.e., the child influences the parent in order to force them to change their decision (position). Otherwise, () and the child is free to choose their behavior.
At this point, we limited the scheme of development of the child–parent conflicts, although it is obvious that the chain of conflicts generated by existing conflicts, as well as the impact of the conflicting parties on each other and ways of alternative conflict resolution, can be continued further, taking into account the real situation and the possibilities of the conflicting parties. Neglecting the other conflicts, we, in fact, consider them secondary, not affecting the overall conflict situation.
All parameters and , describing the considered conflict situation and the corresponding discrepancies, were collected in Table 2. Parameters that have the sign “identically equal” are considered fundamental, i.e., unchanged under any circumstances. The remaining parameters are variable and may change over the course of the development of a conflict situation. The values of these parameters indicated in Table 2 correspond to the situations indicated in the “Comment” column (Table 2).

Table 2.
Parameters of the participants in the child–parent conflict situation (see text for explanations).
3. Combinatorial Optimization Problem
Each participant in a conflict situation decides for themself which of the possible (potential) or existing conflicts (internal or external) is more significant for them, and which is less.
This means that each conflict can be quantitatively characterized by a certain indicator of significance, showing how significant this conflict is for a given participant in the conflict situation. The higher the indicator of the significance of any conflict for a given participant, the more important it is for them to resolve this conflict.
In this case, for each participant k of the conflict situation, one can introduce a function that characterizes the level of conflict (or dissatisfaction with the current situation as a whole) [41].
In general, such a dissatisfaction function (conflict function, conflict level) can be written as
where is the coefficient (factor) of significance of the i-th conflict for the k-th person. For rational participants in the conflict situation, . Parameters are individual psychological (mental) characteristics of the k-th person. In general, these parameters are not constant even for the same person; they can change over time, as a result of which some conflicts that were previously considered insignificant for them may become significant over time (or in other circumstances), and on the contrary, other conflicts that were previously fundamental for this person may become insignificant. In any case, each subject themself explicitly or implicitly sets for themself the scale of priorities, and, hence, the values of the parameters .
For all , function (2) is non-negative and its minimum corresponds to the state when the k-th person is completely satisfied with the existing situation, i.e., does not have any significant conflicts for them. The greater the value of the function, the greater the dissatisfaction of the k-th person in this conflict situation, and, one can expect, the more they will make efforts to resolve existing conflicts.
The goal of any person is to minimize their own dissatisfaction function by changing the parameters and controlled by them.
Thus, the problem of resolving a conflict situation is reduced to the variation of all conflict parameters , taking into account the existing restrictions, and the search for such a combination of these parameters, in which the function (2) for all participants in the conflict situation will be minimal (ideally, equal to zero).
Thus, the search for ways to resolve existing and potential conflicts is reduced to a combinatorial optimization problem.
Note that, in general, the conflicting parties fail to achieve a conflict-free situation, i.e., a situation when for all . In this case, one can talk about unresolvable conflicts. Otherwise, the conflicts are resolvable.
We can write function (2) as
where
One can distinguish the following main problems of conflict resolution:
- (i)
- Search for a unilateral advantage. Find the optimal conditions for one of the participants in the conflict situation, i.e., conditions under which the function for one of the participants of the conflict situation has a minimum. In this case, the conditions for the other participant, generally speaking, will not be optimal.
- (ii)
- Find a compromise. Note that in general, there may not be conditions under which the functions and simultaneously have minimum values, i.e., when both participants can achieve optimal conditions for themselves in a given conflict situation. In this case, they may seek a compromise solution. We will call an ideal compromise such a conflict situation in which the conflict levels for both participants are the same (), and at the same time, the functions reach the minimum possible value:
This means that both participants in the conflict situation are under the same conditions, and neither of them has advantages over the other. Note that in practice, it is practically impossible to satisfy Condition (7), so it is more correct to speak of a real (not ideal) compromise that occurs when the condition
is satisfied, where parameter . For example, with , the difference in conflict levels between two participants does not exceed 10% of their minimum possible mean conflict level.
Thus, in the case of finding an ideal compromise, the problem of conflict resolution is reduced to finding a conditional minimum, for example, the function , provided . This problem can be formally solved by the method of indefinite Lagrange multipliers.
In the case of a non-ideal (real) compromise (8), the conflict resolution problem is reduced to finding the minimum of the function under Condition (8) and refers to nonlinear programming problems [42].
- (iii)
- Search for the maximum conflict level for one of the participants in the conflict situation. Find the conditions under which the function for one of the participants of the conflict situation will be maximum, regardless of what values will take the function for another participant in the conflict situation ( ). Such a problem arises when one of the participants in the conflict situation wants to create maximum discomfort for the opponent, regardless of how this will affect them.
- (iv)
- Create a maximum conflict level for the opponent with a minimum personal conflict level. That is, find the conditions corresponding to the for the or for . This problem can be formulated differently: find conditions that ensure the or .
- (v)
- Use the point of view of a third party (arbitrator, referee). Some third party interested in resolving this conflict situation as a whole can act as an arbitrator. That is, the purpose of the arbitrator in the general case is not to resolve the conflicts of a particular participant in the conflict situation (although this is also possible), but to reduce the total conflict load in general. In the event of a conflict between a child and a parent, the second parent, grandparents, etc., can act as a third party. In this case, the problem is reduced to finding conditions under which the minimum of the function is reachedwhere parameters . Without the loss of generality, one can assume
The parameters and characterize the attitude of the arbitrator (third party) towards the participants in this conflict situation: the larger the parameter , the more important it is for the arbitrator to reduce the conflict load of the participant . When , the attitude of the arbitrator to both participants in the conflict situation is equal.
Let us briefly consider how the parameters characterizing the attitude of the k-th participant of the conflict situation to the i-th conflict can be set. As already noted, the parameters are the psychological (mental) characteristics of the k-th participant in the conflict situation and characterize their point of view at a given time under these circumstances. Obviously, these parameters cannot be calculated from any models. They can be set, for example, (a) based on an analysis of the person’s previous experience of participating in similar or other conflict situations; (b) based on the psychological (mental) profile of that person; (c) based on expert judgment; or (d) based on the person’s own assessments.
In the latter case, the person is invited to assess the significance of this or that conflict for them on a certain (for example, 100-point) scale. The values given by the person in this way should be considered as . Note that when solving problem (i), the search for a unilateral advantage, the absolute values of the parameters do not matter and in this case, one can use the normalized values from Equation (5), obtained as a result of such estimates. However, when solving problems (ii) and (iv), when, in fact, there is a comparison of the conflict levels of both participants in the conflict situation, it is necessary to use the absolute values of the parameters ; moreover, for different participants in this conflict situation they should be determined on the same universal (for example, 100-point) scale. Thus, the parameters are subjective characteristics and reflect the point of view of the one who sets (defines) them. For example, the same conflict may have different significance for different persons: for one person, this conflict may be of fundamental importance and, therefore, is characterized by a large value of the corresponding parameter , while for another person, the same conflict may be insignificant and, therefore, their corresponding parameter . In this case, the first participant makes every effort to resolve this conflict, while the second one will not pay attention to this conflict. Moreover, the parameters do not remain constant even for the same person and they can change (a) over time (a person changes their views and priorities); (b) depending on the duration of the conflict (during a long conflict, a person can adapt, reconcile, reducing some of their parameters , or, on the contrary, hardening, increasing them); (c) depending on the circumstances; or (d) due to the mutual influence of some conflicts on others, etc. This issue will be discussed in future works.
The parameters and included in Expression (9) are set in a similar way.
4. Monte Carlo Method for Finding Ways to Efficiently Resolve Conflicts
As shown in the previous section, from a mathematical point of view, the problem of conflict resolution is reduced to the combinatorial optimization problem: finding the minimum of some function depending on all parameters and and characterizing the given conflict situation.
The form of the function depends on the particular problem being solved. In particular, for the problems formulated in the previous section, the following functions are used as the function .
- (i)
- For the problem of finding a unilateral advantage:where is the number of participants in the conflict situation for which optimal conditions are sought. Note that in this case, it is possible to use not the absolute values of the parameters , but their normalized values (see Equation (5)), i.e., in fact, .
- (ii)
- For the problem of finding a real compromise (see Condition (8)):where and are monotonically increasing functions of their arguments
Indeed, for (i.e., until Condition (8) is satisfied), the search for the minimum of function(12) is carried out in the direction of the decreasing parameter (13), while in the case of (i.e., when condition (8) is satisfied), the state with the minimum value is sought. In this case, the condition must hold for any and any because only in this case is the decrease in the function guaranteed when passing from the region to the region . The simplest kind of functions and are linear functions. In this case, taking into account the indicated condition, function (12) has the form:
- (iii)
- For the problem of creating the maximum conflict level for the participant :
- (iv)
- For the problem of creating the maximum conflict level for the opponent with the minimum personal conflict level:where the index corresponds to the selected participant in the conflict situation, while the index () corresponds to their opponent.
- (v)
- For the problem of finding the optimal conflict situation from the point of view of a third party (arbitrator, referee):
It should be noted that when solving all the listed problems, the parameters W and H of all participants in the conflict situation under consideration, without exception, are varied, taking into account the existing restrictions and connections.
For a small number of parameters W and H, this problem can be solved by simple enumeration; however, with a large number of these parameters and with a large number of parties involved in the conflict situation, this method of finding solutions is not optimal.
From our point of view, the Monte Carlo method (Metropolis algorithm [43]) is generally effective for solving conflict resolution problems. A general scheme for solving combinatorial optimization problems using the Monte Carlo method was described in [44].
Let us briefly describe the Metropolis algorithm [43,44] as applied to the conflict resolution problem.
At each iteration step, from the entire set of variable parameters and , one is randomly selected (using a random number generator), which we will conventionally denote as . The value of this parameter is reversed: . It is taken into account here that in the case under consideration, all parameters and can take only two values: 0 or 1. For the new value of the parameter , the change in the function is calculated as the following:
where means a set of parameters and without a parameter .
If , then the new value of the parameter is fixed; otherwise, the new value of the parameter is fixed only if the condition
is met, where is a random number uniformly distributed in the range [0, 1], and is a parameter that slowly and monotonically decreases at each iteration step.
If Condition (19) is not satisfied, then the previous value of the parameter is left. After that, the next iteration step is made. The iterative process ends when the function does not change over a given number of steps (usually a multiple of the number of all parameters and ).
For finite (non-small) values of the parameter , Condition (19) means that the parameters and can be changed even when . Thus, at the initial iteration steps, generally speaking, changes in the parameters and are admissible, leading to a temporary increase in the function . This allows for leaving the area of attraction of the local minima of the function and finding the area of attraction of the global minimum of this function. For very small values of the parameter (at the later iteration steps, when the system has already fallen into the region of attraction of the global minimum of the function ), Condition (19) will practically not be satisfied, so the changes in the parameters and will be admissible only in those cases when this leads to a decrease in the function .
As a function , one can use, for example,
where is the iteration step number, , is the parameter selected from the condition , and is the change in at the first iteration step.
A quick change in the function is undesirable, because this can lead to the fact that the system does not have time to get to the neighborhood of the global minimum of the function before the parameter becomes very small. From this point of view, it is desirable to choose the parameter close to unity.
To illustrate the method, Monte Carlo calculations of the child–parent conflict were performed for some of the problems considered in the previous sections.
In this paper, we restricted ourselves to the case when there was only one alternative source () from where the child could get a smartphone. Thus, .
It should be borne in mind that the parameter , which describes whether the parent knows that the child got the smartphone from an alternative source or not, is an independent parameter of the system, so two calculations were performed for each problem: for and .
Below are the results of calculations for a specific set of parameters (see Table 3) that characterize the child and the parent. These parameters were chosen randomly and independently using a random number generator in the range [0, 1].

Table 3.
Parameters characterizing the child and the parent used in the calculations.
For all calculation variants, the same values of the parameters and were used.
Calculation variants are presented in Table 4.

Table 4.
Calculation variants.
The calculation results are presented in Table 5 and in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7. Note that in many cases, the problem has a non-uniqueness solution: the same results and are obtained for different combinations of parameters and . In order not to clutter Table 5 with data, for each variant, we presented only one of the results obtained. The exception is variant 3, for which two different solutions are given.

Table 5.
Calculation results for the variants presented in Table 4.

Figure 1.
Calculation variants 1a (left) and 1b (right).
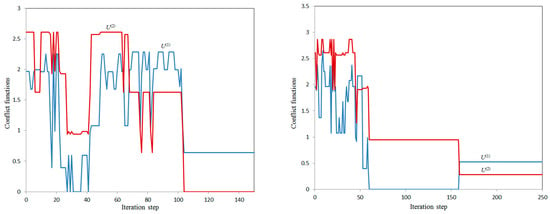
Figure 2.
Calculation variants 2a (left) and 2b (right).

Figure 3.
Calculation variant 3.
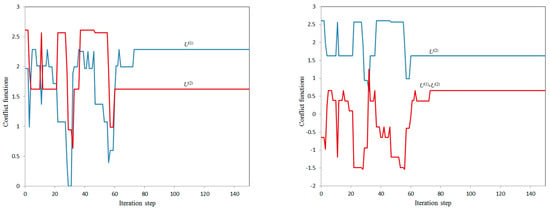
Figure 4.
Calculation variant 4a.
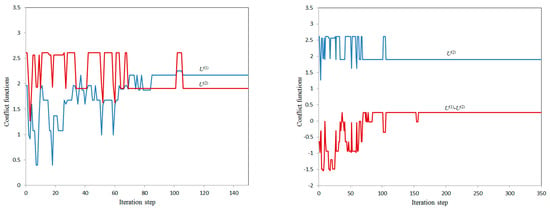
Figure 5.
Calculation variant 4b.
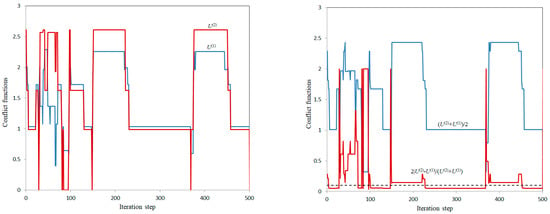
Figure 6.
Calculation variant 5a. The dashed line corresponds to the given value .
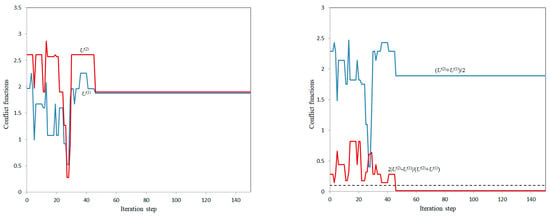
Figure 7.
Calculation variant 5b. The dashed line corresponds to the given value .
It is interesting to note that in all variants (except variant 3), the conflict level of the parent is always higher in those cases when they learned that the child got a smartphone from an alternative source (), compared to the case when the parent does not know about it (). Moreover, the calculations showed that in variant 2b, there is no solution with . That is, in this case, there is no conflict-free state for the parent. From this, we can conclude that it is better for a parent (at least for a given set of parameters ) not to know that the child got a smartphone from an alternative source (in full accordance with the saying “the less you know the better you sleep”).
For variant 3 (the child wants to create the maximum conflict situation for the parent with the minimum own conflict level), for a given set of parameters (see Table 3), the problem under consideration has the same solutions both for and , so these variants are merged into one. In this case, along with the solution having the largest difference (), there is a solution with a smaller difference , but with a higher conflict level for the parent (). In both cases, the child themself has unresolved conflicts. In addition, this problem (variant 3) has a conflict-free solution for the child (), but with an even smaller difference , which corresponds to variants 1a and 1b.
In variants 5a and 5b, the values and , respectively, were achieved with a given maximum value , which is a good compromise, but the conflict levels of participants in these cases () and (), respectively, remain quite high.
5. Conclusions
Thus, within the framework of the mathematical theory of conflicts [41], we considered a conflict with discrete discrepancies using the example of a model conflict between a child and a parent. We developed a general method for constructing a scheme of a conflict situation and analyzing it. When analyzing a specific conflict situation, several main problems can be distinguished, which, in the case of conflicts with discrete discrepancies, are reduced to a combinatorial optimization problem. Taking into account that the conflict situation is usually characterized by a large number of control parameters , the search for a solution to such problems by the simple enumeration method turns out to be inefficient. In this regard, we propose using the Monte Carlo method (Metropolis algorithm [43]) as an effective tool for solving multiple-parameter combinatorial optimization problems [44]. The above examples of solving the main problems of the mathematical theory of conflicts by this method demonstrate its effectiveness, regardless of the complexity of a particular conflict situation.
Although in this paper we considered a specific conflict situation between a child and a parent, the developed scheme for constructing a mathematical model of conflicts and methods for finding ways to resolve them can be used in relation to a variety of types of conflict situations, regardless of their physical nature and subject area.
It should be noted that the result of finding ways to effectively resolve conflicts significantly depends on the accuracy of estimating the significance parameters for each participant in the conflict situation and each existing or potentially possible conflict. In addition, to solve this problem, it is necessary to know (foresee) all possible strategies that the participants in this conflict situation can use, as well as all the opportunities that the participants have to influence each other. The success of the ongoing analysis and decision-making largely depends on this.
In this paper, we considered only the “negative” impacts of the participants in the conflict situation on each other, i.e., such influences that lead to new conflicts leading to an increase in the conflict level . However, in a real situation, along with “negative” influences, there can be “positive” influences of opponents on each other, which lead to a decrease in the conflict level . For example, a participant in a conflict situation can compensate for the conflicts they created by doing something pleasant for the opponent. So, a parent can make some nice gift, a surprise for a child (tangible or intangible), and a child can do something nice for a parent (wash the dishes, clean their room, etc.). The result of such actions can be called “negative conflict”, i.e., an action that reduces the conflict level. In this case, the dissatisfaction function can be written as the following:
where are the parameters characterizing the significance of the i-th gift (surprise) for the k-th participant, and is the index (indicator) of the i-th gift (surprise) for the k-th participant in the conflict situation , if there is no gift (surprise), or if there is a gift (surprise). At the same time, it is necessary to take into account who made this gift; if the gift to the k-th participant was made by the one who created the conflict for them, this can reduce the conflict level . However, if it was made by someone else (not the one who created the conflict), then it probably cannot affect . This issue will be considered in future papers.
In this work, we, in fact, solved a static problem: finding optimal conditions for resolving a conflict situation that has arisen. Along with this problem, of undoubted practical interest is the analysis of the development of this conflict situation in dynamics, taking into account the impacts of the conflicting parties on each other described in this paper and the opportunities they have. This issue will also be considered in future papers.
In this paper, conflicts are considered only with discrete parameters and, as a consequence, with discrete discrepancies, while in [41], only conflicts with continuous parameters } and continuous discrepancies were considered. In real conflict situations, participants can be characterized by both continuous and discrete parameters , which can be appropriately taken into account when compiling the dissatisfaction function [44]. This issue will also be considered in future papers.
In conclusion, we note that as a result of the analysis of the developed model, we came to an unexpected conclusion: the child has more conflicts than the parent, but for the chosen values of the parameters it turned out that the child is in a more advantageous situation, than the parent. It is easier for them to reduce their conflict load and it is easier to create conflicts for the parent. That is, it turned out that the child has more degrees of freedom to influence the parent than vice versa. Perhaps this result applies only to our model system, which, of course, does not take into account all possible situations and ways in which the conflicting parties influence each other; however, an analysis of real child–parent conflicts known to us shows that this conclusion is correct in many cases.
Author Contributions
Conceptualization, E.A. and S.R.; methodology, S.R.; validation, E.A. and S.R.; formal analysis, E.A.; writing—original draft preparation, E.A. and S.R.; writing—review and editing, E.A. and S.R.; supervision, S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was completed according to the theme of State Task No. AAAA-A20-120011690135-5.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Turchin, P.; Currie, T.E.; Turner, E.A.L.; Gavrilets, S. War, space, and the evolution of Old World complex societies. Proc. Natl. Acad. Sci. USA 2013, 110, 16384–16389. [Google Scholar] [CrossRef] [PubMed]
- Blank, S. Managing Organizational Conflict; McFarland: Jefferson, NC, USA, 2019. [Google Scholar]
- Omoluabi, P. Principles and Processes of Conflictology. IFE Psychol. 2001, 9, 1–13. [Google Scholar] [CrossRef]
- Vinyamata, E. Conflictology: A multidisciplinary vision. J. Confl. 2010, 1, 1. [Google Scholar]
- Clardy, A. Managing Organizational Conflict: Towards a Comprehensive Framework of Outcomes, Practices, and Competencies. Perform. Improv. 2018, 57, 10–25. [Google Scholar] [CrossRef]
- Thakore, D. Conflict and conflict management. IOSR J. Bus. Manag. 2013, 8, 7–16. [Google Scholar] [CrossRef]
- Lewicki, R.J.; Weiss, S.E.; Lewin, D. Models of conflict, negotiation and third party intervention: A review and synthesis. J. Organ. Behav. 1992, 13, 209–252. [Google Scholar] [CrossRef]
- Jones, A.J. Game Theory: Mathematical Models of Conflict; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Molinero, X.; Riquelme, F. Influence decision models: From cooperative game theory to social network analysis. Comput. Sci. Rev. 2021, 39, 100343. [Google Scholar] [CrossRef]
- Azam, N.; Zhang, Y.; Yao, J. Evaluation functions and decision conditions of three-way decisions with game-theoretic rough sets. Eur. J. Oper. Res. 2017, 261, 704–714. [Google Scholar] [CrossRef]
- Liu, J.; Yu, C.; Li, C.; Han, J. Cooperation or Conflict in Doctor-Patient Relationship? An Analysis from the Perspective of Evolutionary Game. IEEE Access 2020, 8, 42898–42908. [Google Scholar] [CrossRef]
- Cook, J.; Tyson, R.; White, J.; Rushe, R.; Gottman, J.; Murray, J. Mathematics of marital conflict: Qualitative dynamic mathematical modeling of marital interaction. J. Fam. Psychol. 1995, 9, 110. [Google Scholar] [CrossRef]
- Gottman, J.; Swanson, C.; Murray, J. The mathematics of marital conflict: Dynamic mathematical nonlinear modeling of newlywed marital interaction. J. Fam. Psychol. 1999, 13, 3. [Google Scholar] [CrossRef]
- Santonja, F.J.; Tarazona, A.C.; Villanueva, R.J. A mathematical model of the pressure of an extreme ideology on a society. Comput. Math. Appl. 2008, 56, 836–846. [Google Scholar] [CrossRef]
- Wang, Y.; Bu, F. Modeling radicalization of terrorism under the influence of multiple ideologies. AIMS Math. 2022, 7, 4833–4850. [Google Scholar] [CrossRef]
- Zammit-Mangion, A.; Dewar, M.; Kadirkamanathan, V.; Sanguinetti, G. Point process modelling of the Afghan War Diary. Proc. Natl. Acad. Sci. USA 2012, 109, 12414–12419. [Google Scholar] [CrossRef]
- Tench, S.; Fry, H.; Gill, P. Spatio-temporal patterns of IED usage by the Provisional Irish Republican Army. Eur. J. Appl. Math. 2016, 27, 377–402. [Google Scholar] [CrossRef]
- Egesdal, M.; Fathauer, C.; Louie, K.; Neuman, J. Statistical and Stochastic Modeling of Gang Rivalries in Los Angeles; SIAM Undergrad. Res. Online: Philadelphia, PA, USA, 2010; pp. 72–94. [Google Scholar] [CrossRef]
- Guo, W. Common statistical patterns in urban terrorism. R. Soc. Open Sci. 2019, 6, 190645. [Google Scholar] [CrossRef] [PubMed]
- Qadri, F. Traffic Conflict Modelling at Six Leg Unsignalized Intersection. In Proceedings of the 11th Asia Pacific Transportation and the Environment Conference (APTE 2018), Malang, Indonesia, 18–19 October 2018; Atlantis Press: Amsterdam, The Netherlands, 2018; pp. 58–61. [Google Scholar]
- Zheng, L.; Ismail, K.; Meng, X. Traffic conflict techniques for road safety analysis: Open questions and some insights. Can. J. Civ. Eng. 2014, 41, 633–641. [Google Scholar] [CrossRef]
- Deja, R. Conflict analysis. In Rough Set Methods and Applications; Physica: Heidelberg, Germany, 2000; pp. 491–519. [Google Scholar]
- Skowron, A.; Ramanna, S.; Peters, J.F. Conflict analysis and information systems: A rough set approach. In Proceedings of the International Conference on Rough Sets and Knowledge Technology, Chongquing, China, 24–26 July 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 233–240. [Google Scholar]
- Suo, L.-W.; Yang, H.-L. Three-way conflict analysis based on incomplete situation tables: A tentative study. Int. J. Approx. Reason. 2022, 145, 51–74. [Google Scholar] [CrossRef]
- He, X.; Wei, L.; She, Y. L-fuzzy concept analysis for three-way decisions: Basic definitions and fuzzy inference mechanisms. Int. J. Mach. Learn. Cybern. 2018, 9, 1857–1867. [Google Scholar] [CrossRef]
- Basile, C.; Cappadonia, A.; Lioy, A. Algebraic models to detect and solve policy conflicts. In Proceedings of the International Conference on Mathematical Methods, Models, and Architectures for Computer Network Security, St. Petersburg, Russia, 13–15 September 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 242–247. [Google Scholar]
- Ding, G.; Chen, J.; Lax, R.F.; Chen, P.P. Graph-theoretic method for merging security system specifications. Inf. Sci. 2007, 177, 2152–2166. [Google Scholar] [CrossRef]
- Saaty, T.L. Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process; RWS Publications: Pittsburgh, PA, USA, 2000; Volume 6. [Google Scholar]
- Pawlak, Z. On conflicts. Int. J. Man-Mach. Stud. 1984, 21, 127–134. [Google Scholar] [CrossRef]
- Pawlak, Z. An inquiry into anatomy of conflicts. Inf. Sci. 1998, 109, 65–78. [Google Scholar] [CrossRef]
- Pawlak, Z. Some remarks on conflict analysis. Eur. J. Oper. Res. 2005, 166, 649–654. [Google Scholar] [CrossRef]
- Xu, W.; Jia, B.; Li, X. A two-universe model of three-way decision with ranking and reference tuple. Inf. Sci. 2021, 581, 808–839. [Google Scholar] [CrossRef]
- Du, J.; Liu, S.; Liu, Y.; Yi, J. A novel approach to three-way conflict analysis and resolution with Pythagorean fuzzy information. Inf. Sci. 2022, 584, 65–88. [Google Scholar] [CrossRef]
- Lang, G.; Yao, Y. Formal concept analysis perspectives on three-way conflict analysis. Int. J. Approx. Reason. 2023, 152, 160–182. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, J. Three-hierarchical three-way decision models for conflict analysis: A qualitative improvement and a quantitative extension. Inf. Sci. 2022, 587, 485–514. [Google Scholar] [CrossRef]
- Svetlov, V.A. Introduction to Conflictology; Flinta: Moscow, Russia, 2018; p. 520. (In Russian) [Google Scholar]
- Antsupov, A.Y.; Shipilov, A.I. Conflictology; UNITI: Moscow, Russia, 1999; p. 551. (In Russian) [Google Scholar]
- Antsupov, A.Y.; Shipilov, A.I. Dictionary of Conlictologist; PITER: Sankt Petersburg, Russia, 2006; p. 528. (In Russian) [Google Scholar]
- Chaplin, J.P. Dictionary of Psychology; Dell Publishing: New York, NY, USA, 1985. [Google Scholar]
- Deutsch, M. The Resolution of Conflict; Yale University: New Haven, CT, USA, 1973. [Google Scholar]
- Antipova, E.; Rashkovskiy, S. Mathematical Theory of Conflicts as a Cognitive Control Theory. Information 2022, 14, 1. [Google Scholar] [CrossRef]
- Avriel, M. Nonlinear Programming: Analysis and Methods; Courier Corporation: Chelmsford, MA, USA, 2003. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Rashkovskiy, S.A. Monte Carlo solution of combinatorial optimization problems. Dokl. Math. 2016, 94, 720–724. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).