Energy Usage Forecasting Model Based on Long Short-Term Memory (LSTM) and eXplainable Artificial Intelligence (XAI)
Abstract
1. Introduction
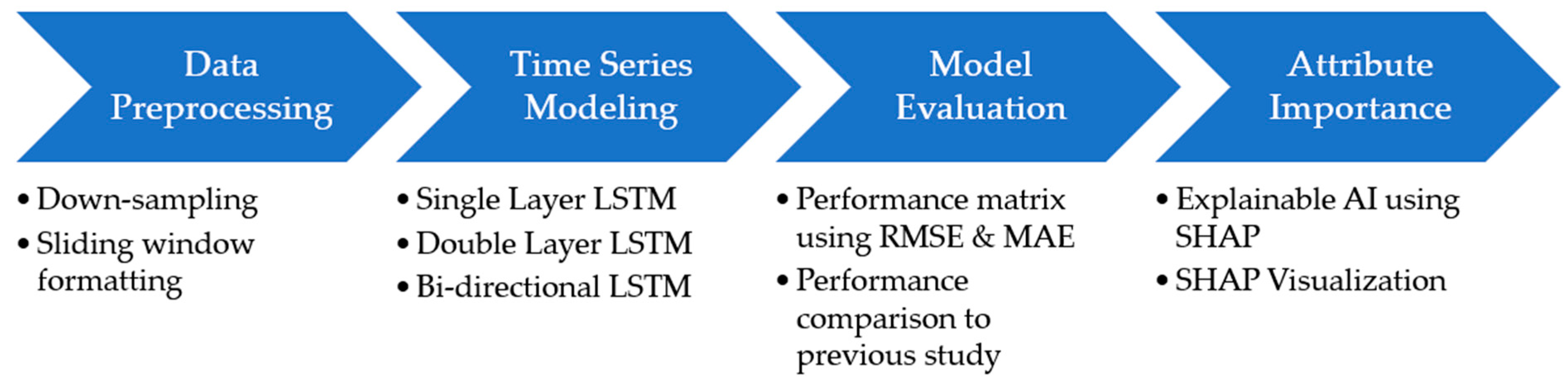
2. Materials and Methods
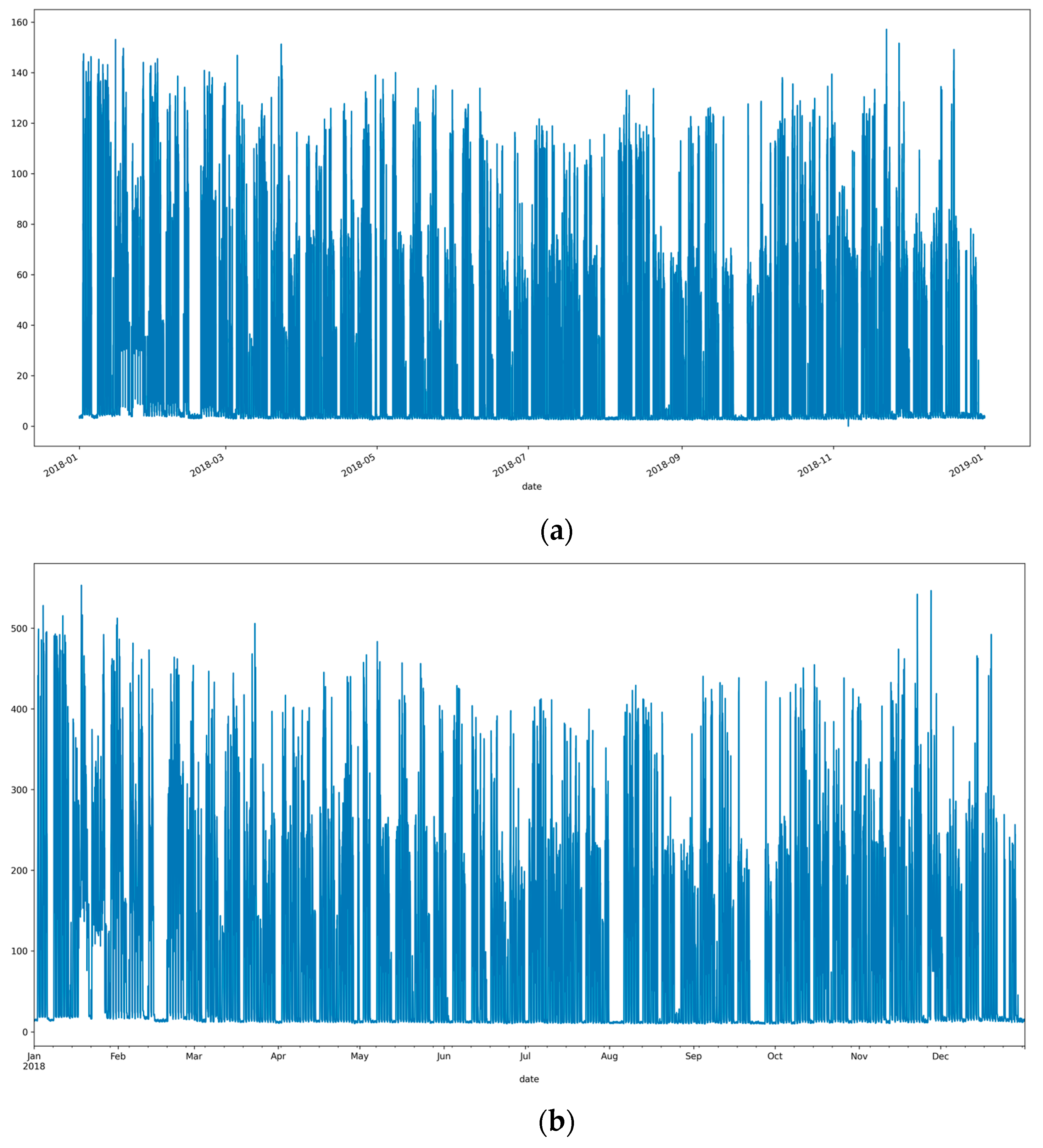
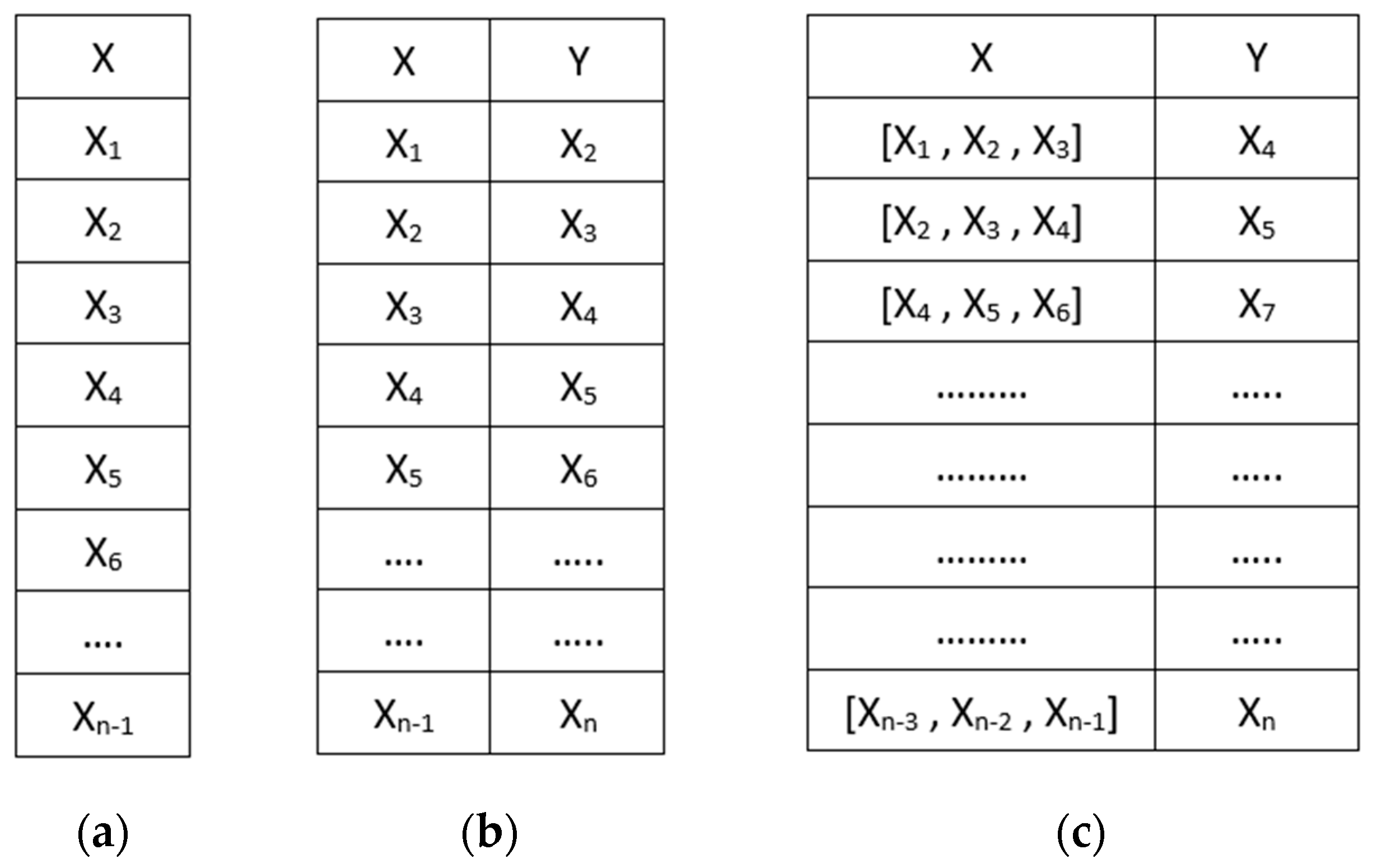
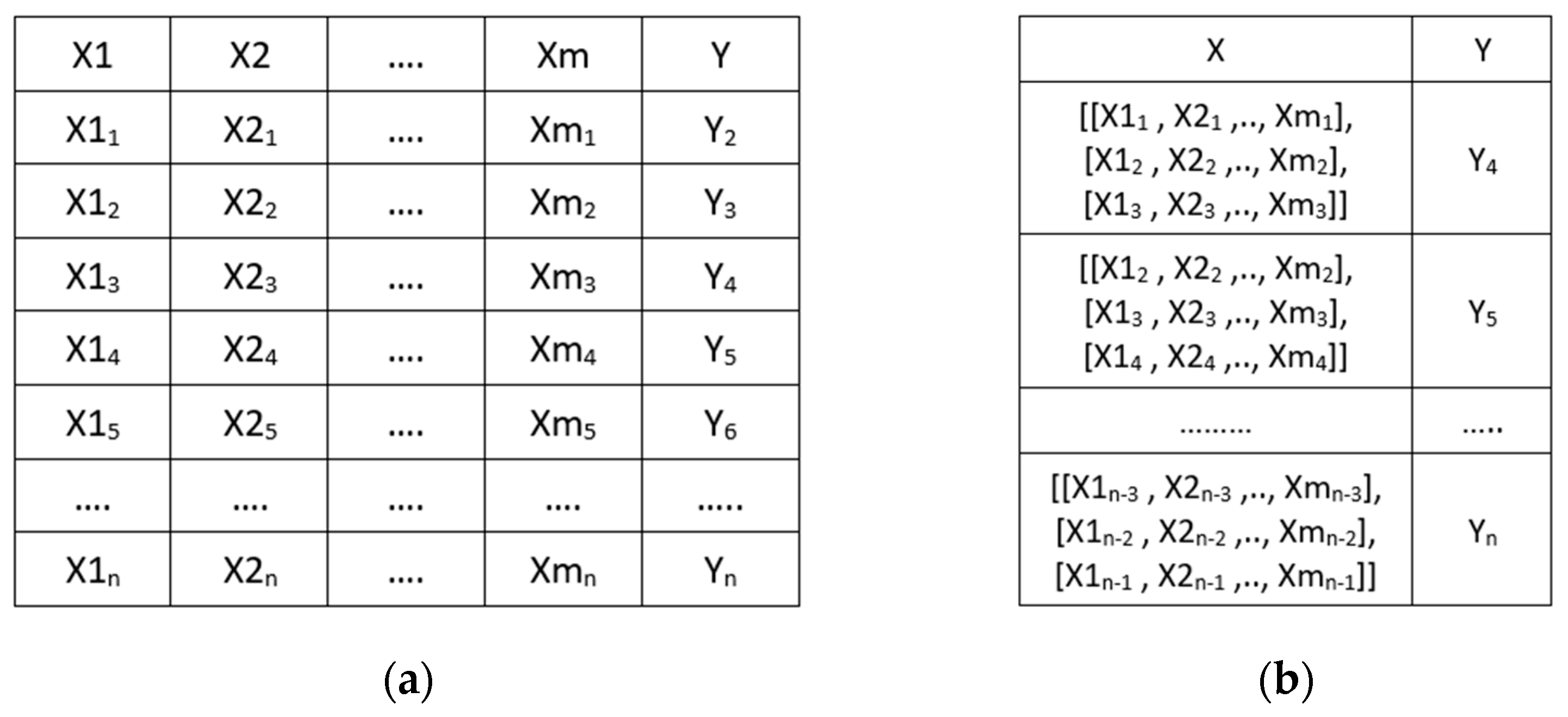
2.1. Dataset Description and Data Preprocessing
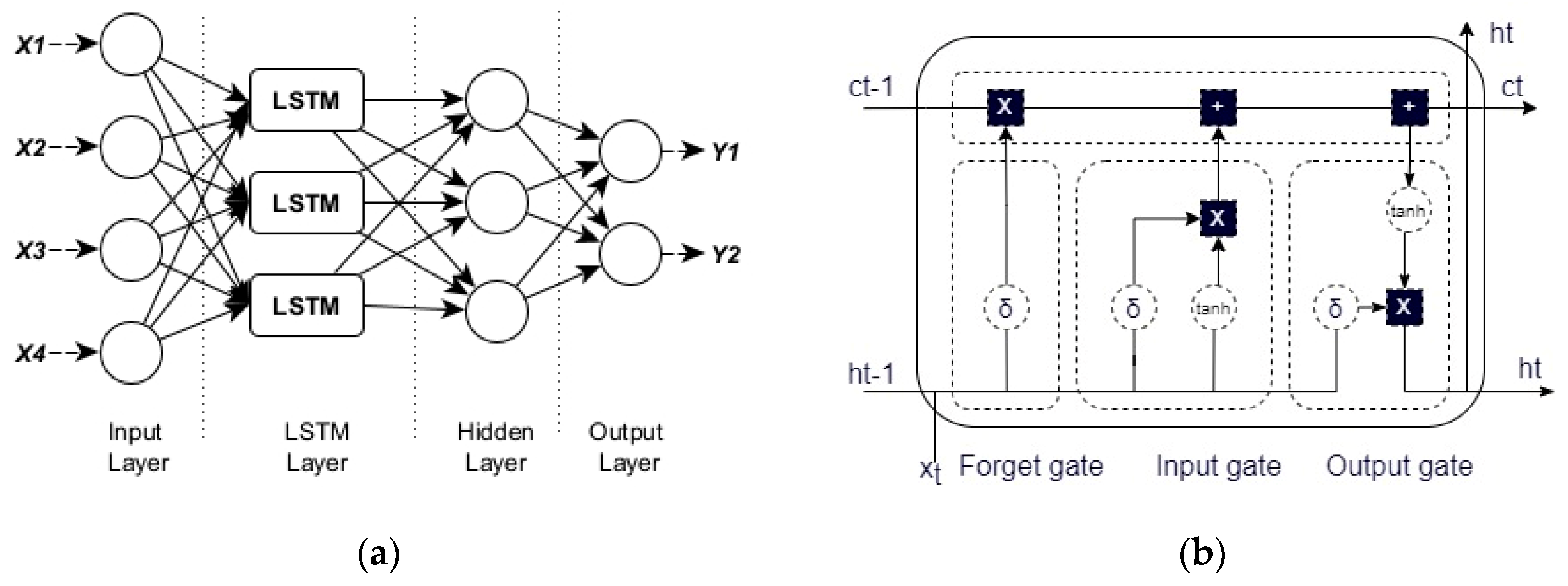
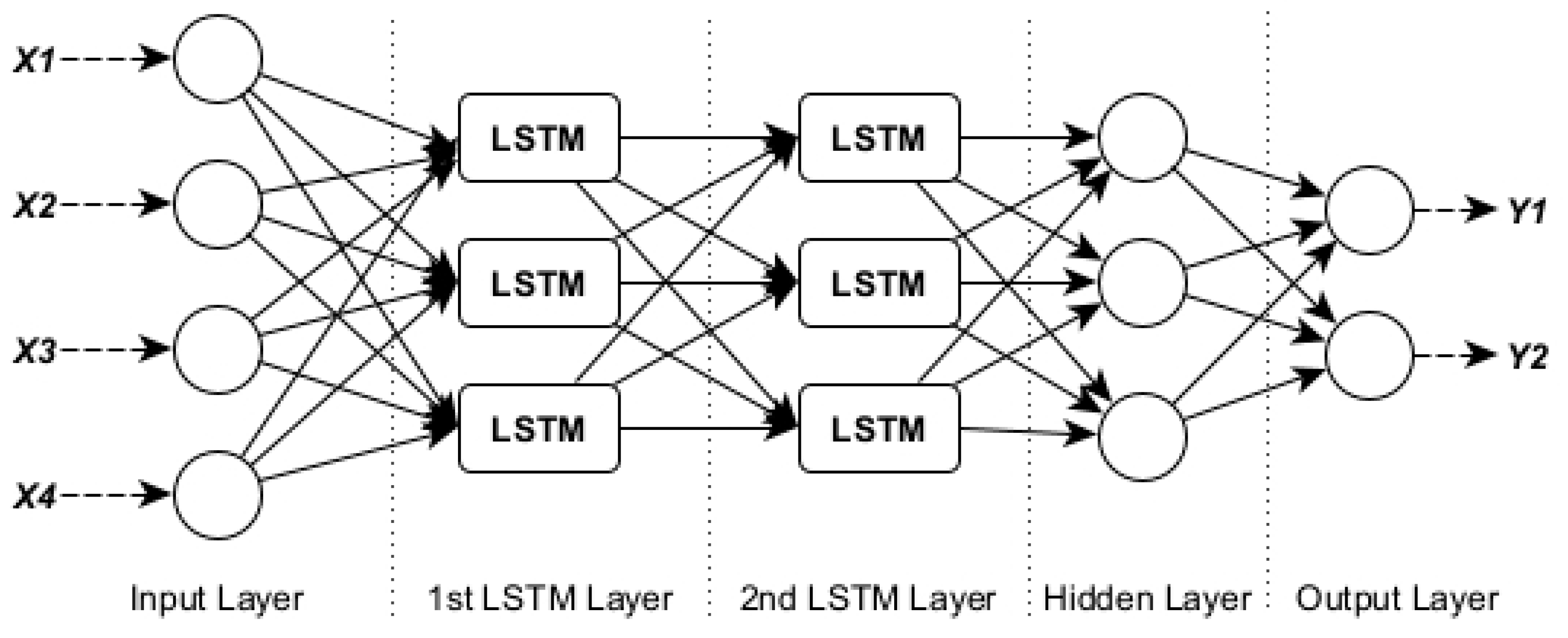
2.2. Long Short-Term Memory
2.3. Evaluation Metrics
2.4. SHapley Additive exPlanations (SHAP)
- Global interpretability: SHAP scores not only indicate the significance of a trait but also if it has a positive or negative effect on predictions.
- Local interpretability: One can calculate SHAP values for each individual prediction and understand how each feature contributes to that prediction. Other strategies merely display findings aggregated throughout the entire dataset.
- SHAP values can be used to explain a wide range of models, such as linear models (e.g., linear regression); tree-based models (e.g., XGBoost); and neural networks, but other techniques can only be used to explain a restricted number of model types.
3. Results and Discussion
3.1. Experimental Settings
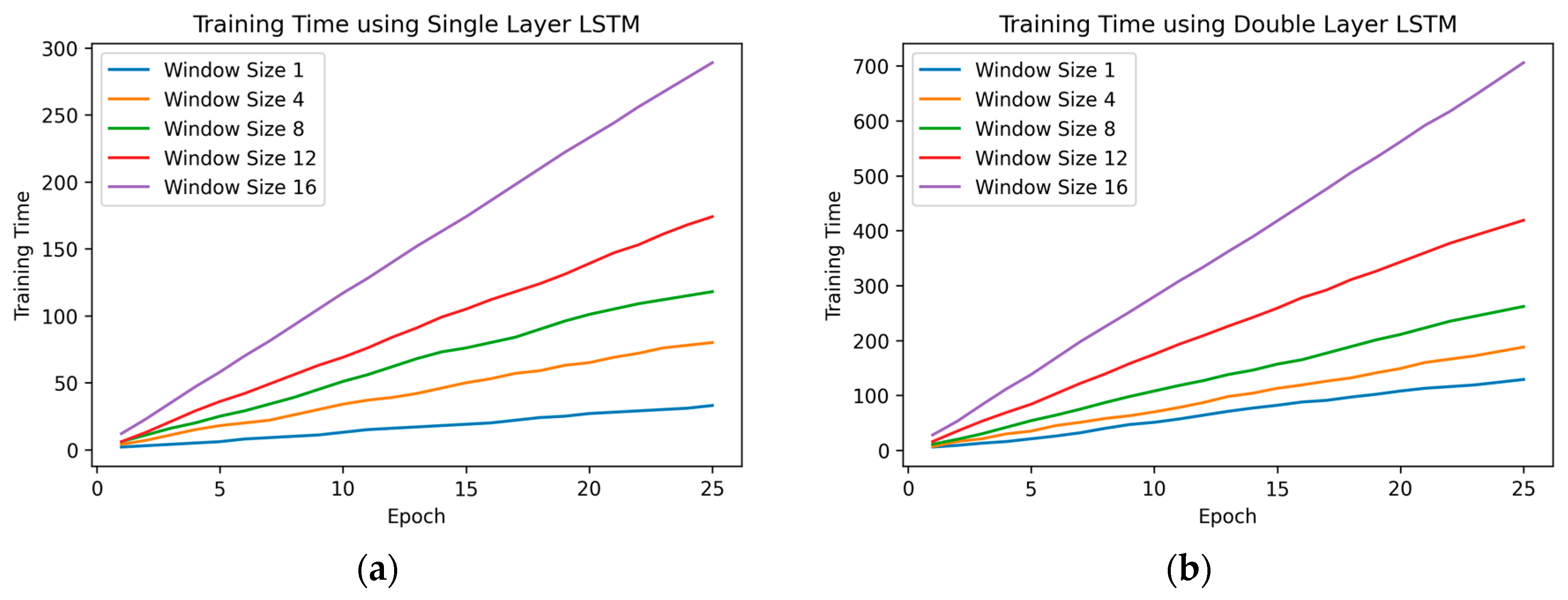
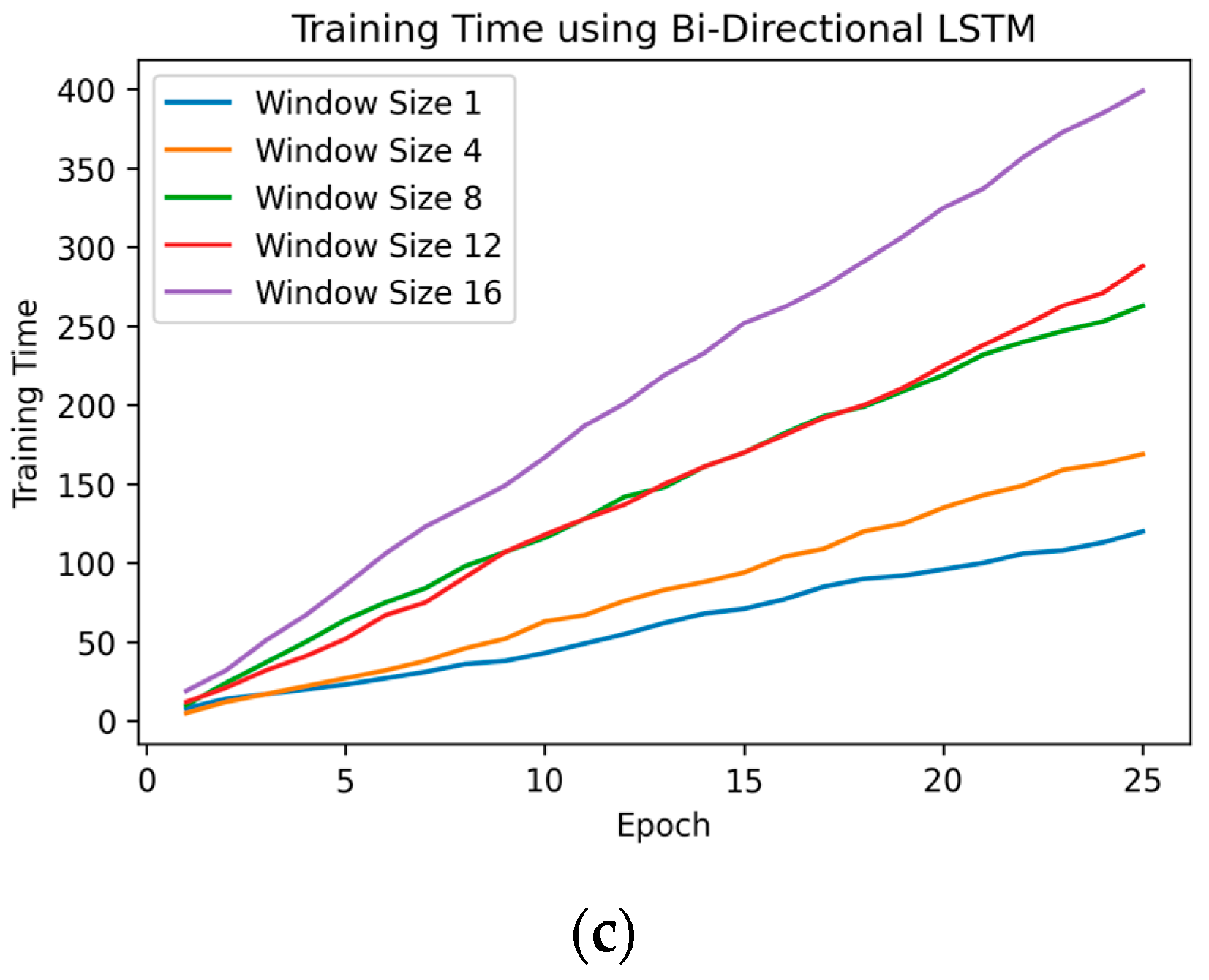
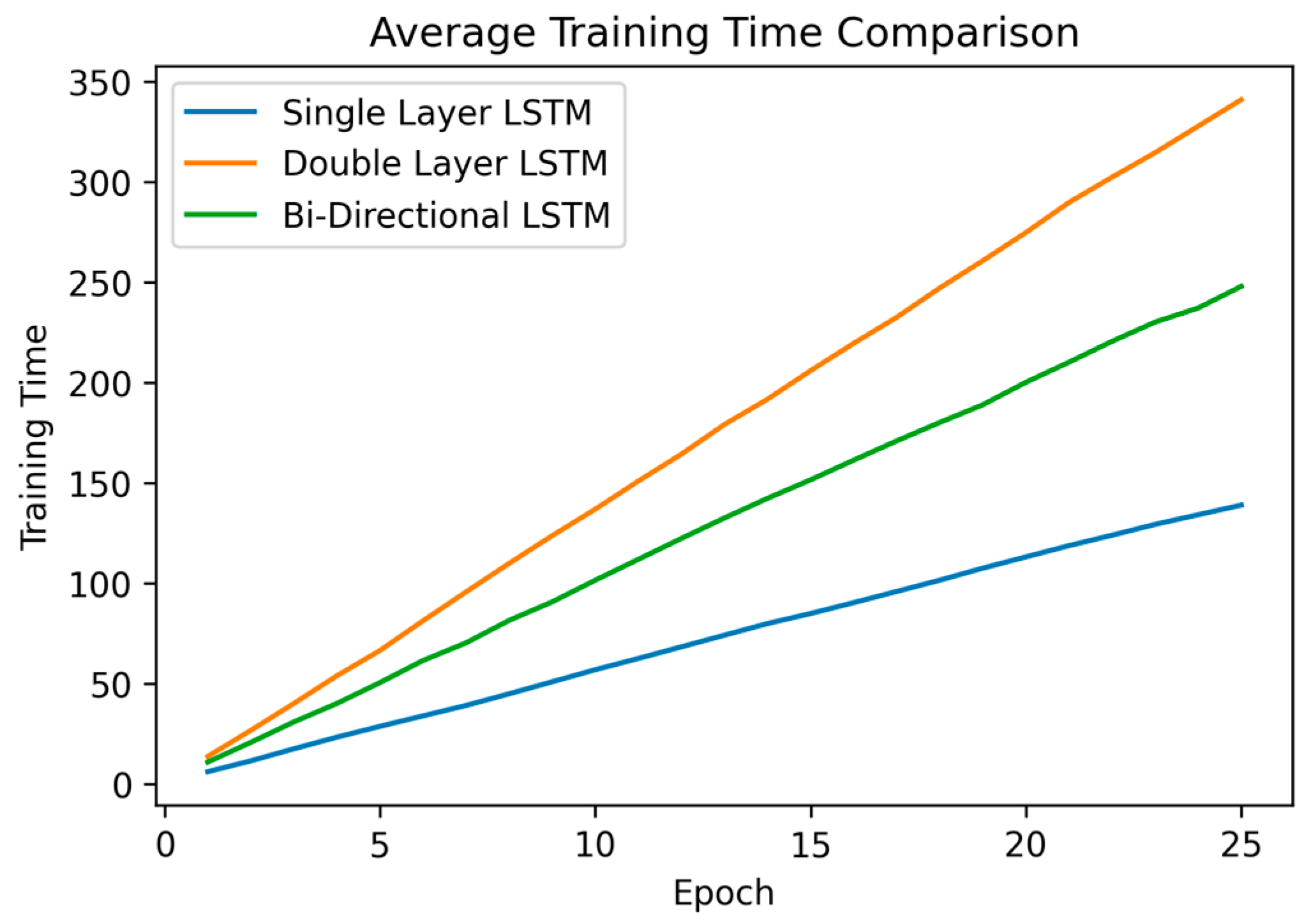
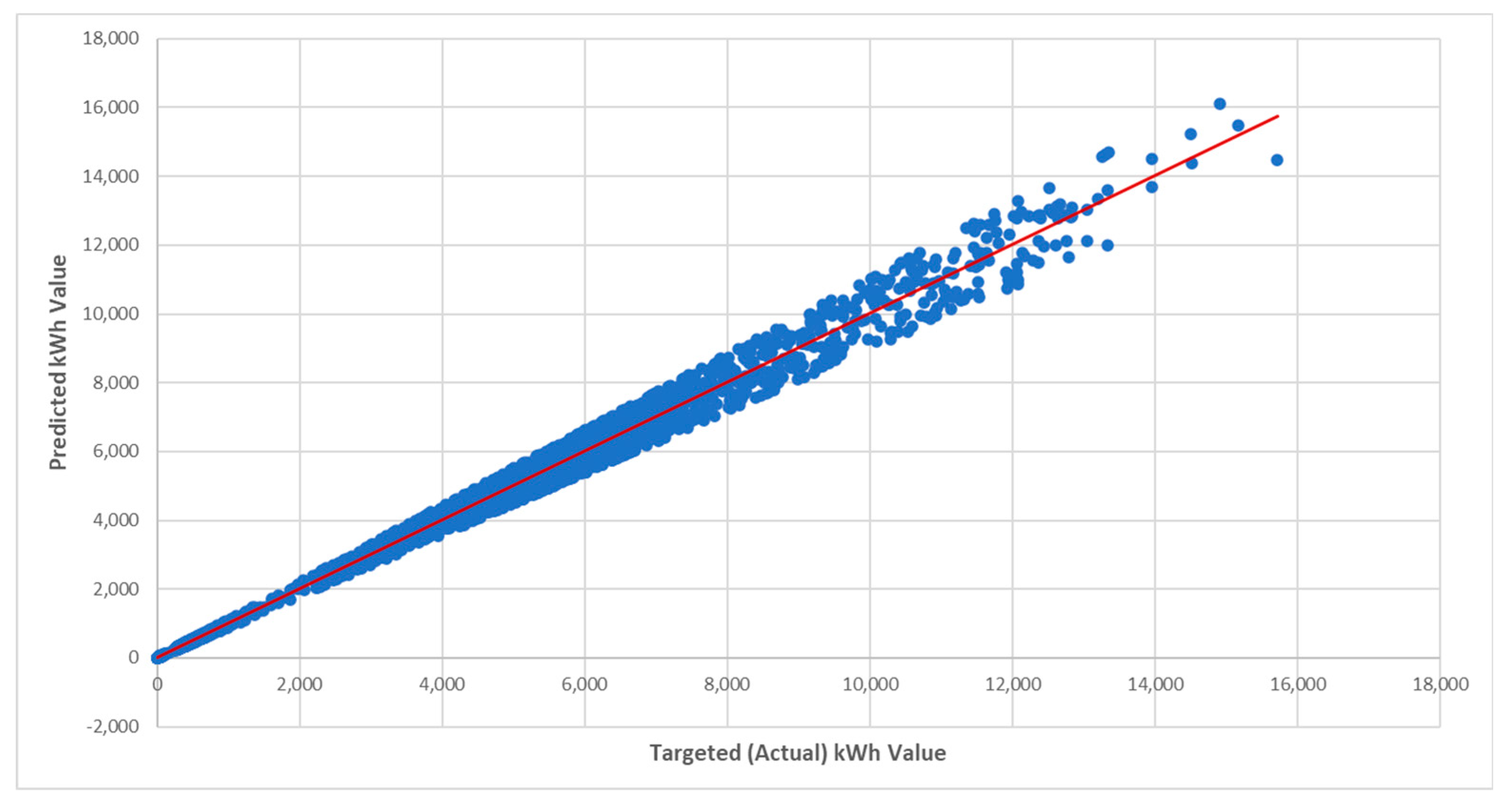
3.2. LSTM Model Evaluation Results
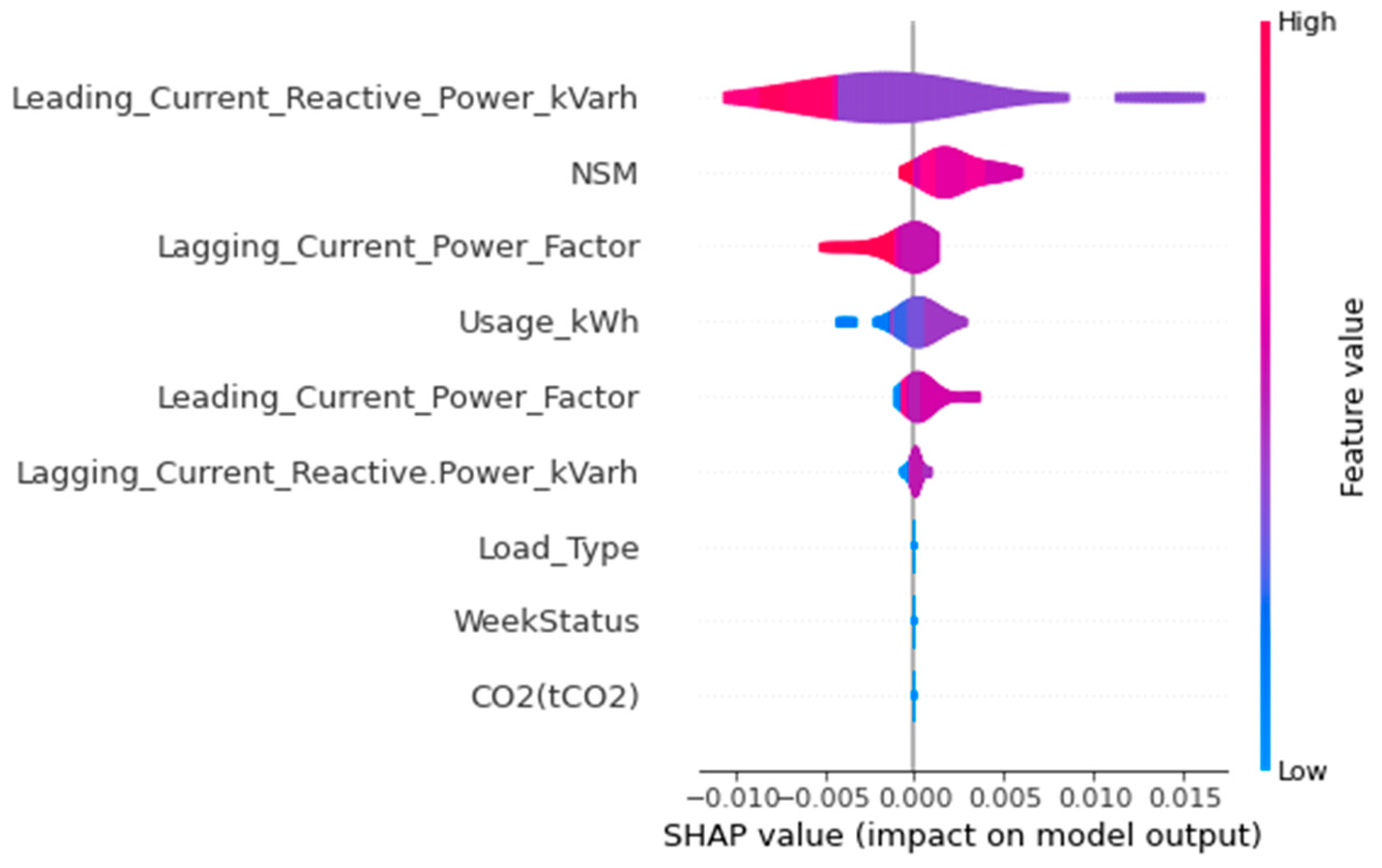
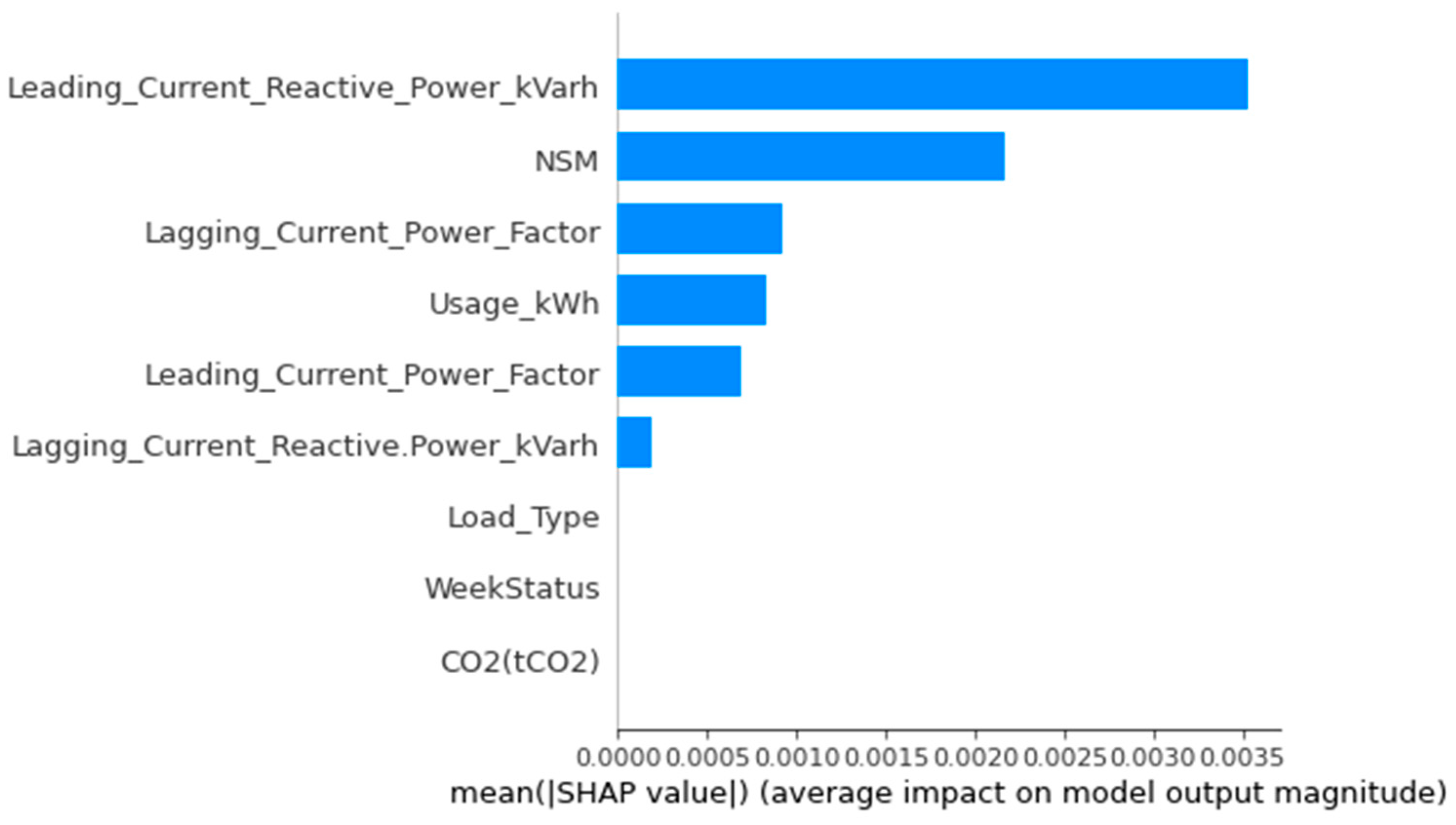
3.3. XAI Parameters Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, C.; Pinar, M.; Stengos, T. Renewable Energy Consumption and Economic Growth Nexus: Evidence from a Threshold Model. Energy Policy 2020, 139, 111295. [Google Scholar] [CrossRef]
- Chen, C.; Zuo, Y.; Ye, W.; Li, X.; Deng, Z.; Ong, S.P. A Critical Review of Machine Learning of Energy Materials. Adv. Energy Mater. 2020, 10, 1903242. [Google Scholar] [CrossRef]
- Ahmad, T.; Zhang, D.; Huang, C.; Zhang, H.; Dai, N.; Song, Y.; Chen, H. Artificial Intelligence in Sustainable Energy Industry: Status Quo, Challenges and Opportunities. J. Clean. Prod. 2021, 289, 125834. [Google Scholar] [CrossRef]
- Kandananond, K. Electricity Demand Forecasting in Buildings Based on Arima and ARX Models. In Proceedings of the 8th International Conference on Informatics, Environment, Energy and Applications—IEEA’19, Osaka, Japan, 16–19 March 2019. [Google Scholar] [CrossRef]
- Lü, X.; Lu, T.; Kibert, C.J.; Viljanen, M. Modeling and Forecasting Energy Consumption for Heterogeneous Buildings Using a Physical–Statistical Approach. Appl. Energy 2015, 144, 261–275. [Google Scholar] [CrossRef]
- Debnath, K.B.; Monjur, M. Forecasting Methods in Energy Planning Models. Renew. Sustain. Energy Rev. 2018, 88, 297–325. [Google Scholar] [CrossRef]
- Abdel-Jaber, H.; Devassy, D.; Al Salam, A.; Hidaytallah, L.; El-Amir, M. A Review of Deep Learning Algorithms and Their Applications in Healthcare. Algorithms 2022, 15, 71. [Google Scholar] [CrossRef]
- Fisher, C.K.; Smith, A.M.; Walsh, J.R. Machine Learning for Comprehensive Forecasting of Alzheimer’s Disease Progression. Sci. Rep. 2019, 9, 13622. [Google Scholar] [CrossRef]
- Scher, S.; Messori, G. Predicting Weather Forecast Uncertainty with Machine Learning. Q. J. R. Meteorol. Soc. 2018, 144, 2830–2841. [Google Scholar] [CrossRef]
- Ghoddusi, H.; Creamer, G.G.; Rafizadeh, N. Machine Learning in Energy Economics and Finance: A Review. Energy Econ. 2019, 81, 709–727. [Google Scholar] [CrossRef]
- Yang, X.; Wang, Z.; Zhang, H.; Ma, N.; Yang, N.; Liu, H.; Zhang, H.; Yang, L. A Review: Machine Learning for Combinatorial Optimization Problems in Energy Areas. Algorithms 2022, 15, 205. [Google Scholar] [CrossRef]
- Luo, B.; Wang, H.; Liu, H.; Li, B.; Peng, F. Early Fault Detection of Machine Tools Based on Deep Learning and Dynamic Identification. IEEE Trans. Ind. Electron. 2019, 66, 509–518. [Google Scholar] [CrossRef]
- Schwendemann, S.; Amjad, Z.; Sikora, A. A Survey of Machine-Learning Techniques for Condition Monitoring and Predictive Maintenance of Bearings in Grinding Machines. Comput. Ind. 2021, 125, 103380. [Google Scholar] [CrossRef]
- Loukatos, D.; Kondoyanni, M.; Alexopoulos, G.; Maraveas, C.; Arvanitis, K.G. On-Device Intelligence for Malfunction Detection of Water Pump Equipment in Agricultural Premises: Feasibility and Experimentation. Sensors 2023, 23, 839. [Google Scholar] [CrossRef]
- He, M.; He, D. Deep Learning Based Approach for Bearing Fault Diagnosis. IEEE Trans. Ind. Appl. 2017, 53, 3057–3065. [Google Scholar] [CrossRef]
- Bertolini, M.; Mezzogori, D.; Neroni, M.; Zammori, F. Machine Learning for Industrial Applications: A Comprehensive Literature Review. Expert Syst. Appl. 2021, 175, 114820. [Google Scholar] [CrossRef]
- Mosavi, A.; Salimi, M.; Ardabili, S.F.; Rabczuk, T.; Shamshirband, S.; Varkonyi-Koczy, A.R. State of the Art of Machine Learning Models in Energy Systems, a Systematic Review. Energies 2019, 12, 1301. [Google Scholar] [CrossRef]
- Fouilloy, A.; Voyant, C.; Notton, G.; Motte, F.; Paoli, C.; Nivet, M.-L.; Guillot, E.; Duchaud, J.-L. Solar Irradiation Prediction with Machine Learning: Forecasting Models Selection Method Depending on Weather Variability. Energy 2018, 165, 620–629. [Google Scholar] [CrossRef]
- Zhang, D.; Han, X.; Deng, C. Review on the Research and Practice of Deep Learning and Reinforcement Learning in Smart Grids. CSEE J. Power Energy Syst. 2018, 4, 362–370. [Google Scholar] [CrossRef]
- Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. A Review of Deep Learning for Renewable Energy Forecasting. Energy Convers. Manag. 2019, 198, 111799. [Google Scholar] [CrossRef]
- Véstias, M.P.; Duarte, R.P.; de Sousa, J.T.; Neto, H.C. Moving Deep Learning to the Edge. Algorithms 2020, 13, 125. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Z.; Liu, C.; Yu, Y.; Pang, S.; Duić, N.; Shafie-Khah, M.; Catalão, J.P. Generative Adversarial Networks and Convolutional Neural Networks Based Weather Classification Model for Day Ahead Short-Term Photovoltaic Power Forecasting. Energy Convers. Manag. 2019, 181, 443–462. [Google Scholar] [CrossRef]
- Zhang, R.; Li, G.; Ma, Z. A Deep Learning Based Hybrid Framework for Day-Ahead Electricity Price Forecasting. IEEE Access 2020, 8, 143423–143436. [Google Scholar] [CrossRef]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-Art in Artificial Neural Network Applications: A Survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef]
- Martens, J.; Sutskever, I. Training Deep and Recurrent Networks with Hessian-Free Optimization; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; pp. 479–535. [Google Scholar] [CrossRef]
- Xu, J.; Jiang, Y.; Yang, C. Landslide Displacement Prediction during the Sliding Process Using XGBoost, SVR and RNNs. Appl. Sci. 2022, 12, 6056. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) Network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Kim, T.-Y.; Cho, S.-B. Predicting Residential Energy Consumption Using CNN-LSTM Neural Networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Le, T.; Vo, M.T.; Vo, B.; Hwang, E.; Rho, S.; Baik, S.W. Improving Electric Energy Consumption Prediction Using CNN and Bi-LSTM. Appl. Sci. 2019, 9, 4237. [Google Scholar] [CrossRef]
- Angelov, P.; Soares, E. Towards Explainable Deep Neural Networks (XDNN). Neural Netw. 2020, 130, 185–194. [Google Scholar] [CrossRef] [PubMed]
- Pavone, A.; Plebe, A. How Neurons in Deep Models Relate with Neurons in the Brain. Algorithms 2021, 14, 272. [Google Scholar] [CrossRef]
- Minh, D.; Wang, H.X.; Li, Y.F.; Nguyen, T.N. Explainable Artificial Intelligence: A Comprehensive Review. Artif. Intell. Rev. 2021, 55, 3503–3568. [Google Scholar] [CrossRef]
- Angelov, P.P.; Soares, E.A.; Jiang, R.; Arnold, N.I.; Atkinson, P.M. Explainable Artificial Intelligence: An Analytical Review. WIREs Data Min. Knowl. Discov. 2021, 11, e1424. [Google Scholar] [CrossRef]
- Speith, T. A Review of Taxonomies of Explainable Artificial Intelligence (XAI) Methods. In Proceedings of the 2022 ACM Conference on Fairness, Accountability, and Transparency, Seoul, Republic of Korea, 21–24 June 2022. [Google Scholar] [CrossRef]
- Ahmed, I.; Jeon, G.; Piccialli, F. From Artificial Intelligence to Explainable Artificial Intelligence in Industry 4.0: A Survey on What, How, and Where. IEEE Trans. Ind. Inform. 2022, 18, 5031–5042. [Google Scholar] [CrossRef]
- Rehmer, A.; Kroll, A. On the Vanishing and Exploding Gradient Problem in Gated Recurrent Units. IFAC-PapersOnLine 2022, 53, 1243–1248. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, X.; Xiao, J. On Geometric Features for Skeleton-Based Action Recognition Using Multilayer LSTM Networks. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017. [Google Scholar] [CrossRef]
- Turkoglu, M.O.; D’Aronco, S.; Wegner, J.; Schindler, K. Gating Revisited: Deep Multi-Layer RNNS That Can Be Trained. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 4081–4092. [Google Scholar] [CrossRef]
- Graves, A.; Schmidhuber, J. Framewise Phoneme Classification with Bidirectional LSTM and Other Neural Network Architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Yang, S.U. Research on Network Behavior Anomaly Analysis Based on Bidirectional LSTM. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 March 2019. [Google Scholar] [CrossRef]
- Karunasingha, D.S. Root Mean Square Error or Mean Absolute Error? Use Their Ratio as Well. Inf. Sci. 2022, 585, 609–629. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 4768–4777. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018; ISBN 978-0-646-99855-8. [Google Scholar]
- Montgomery, D.C.; Jennings, C.L.; Kulahci, M. Introduction to Time Series Analysis and Forecasting; John Wiley & Sons: Hoboken, NJ, USA, 2015; ISBN 978-1-118-71283-8. [Google Scholar]
- Marcilio, W.E.; Eler, D.M. From Explanations to Feature Selection: Assessing Shap Values as Feature Selection Mechanism. In Proceedings of the 2020 33rd SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Porto de Galinhas, Brazil, 7–10 November 2020. [Google Scholar] [CrossRef]
- Van den Broeck, G.; Lykov, A.; Schleich, M.; Suciu, D. On the Tractability of Shap Explanations. J. Artif. Intell. Res. 2022, 74, 851–886. [Google Scholar] [CrossRef]
- Adadi, A.; Berrada, M. Peeking inside the Black-Box: A Survey on Explainable Artificial Intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Sathishkumar, V.E.; Shin, C.; Cho, Y. Efficient Energy Consumption Prediction Model for a Data Analytic-Enabled Industry Building in a Smart City. Build. Res. Inf. 2020, 49, 127–143. [Google Scholar] [CrossRef]
- Strumbelj, E.; Kononenko, I. Explaining Prediction Models and Individual Predictions with Feature Contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]




| Variable | Data Type | Measure |
|---|---|---|
| Industry energy consumption | Continuous | kWh |
| Lagging current reactive power | Continuous | kVarh |
| Leading current reactive power | Continuous | kVarh |
| tCO2 (CO2) | Continuous | Ppm |
| Lagging current power factor | Continuous | % |
| Leading current power factor | Continuous | % |
| Number of seconds from midnight (NSM) | Continuous | Seconds |
| Week status | Categorical | Weekday, weekend |
| Load type | Categorical | Light, medium, maximum |
| Scenario | Number of Windows | Explanation |
|---|---|---|
| 1 | 1 | Using the current hour of energy usage |
| 2 | 4 | Using the last 4 h of energy usage |
| 3 | 8 | Using the last 8 h of energy usage |
| 4 | 12 | Using the last 12 h of energy usage |
| 5 | 16 | Using the last 16 h of energy usage |
| Rank | Number of LSTM Units | Dropout Value | RMSE | Std. Dev |
|---|---|---|---|---|
| 1 | 64 | 0.1 | 0.0074 | 0.0006 |
| 2 | 128 | 0.1 | 0.0076 | 0.0005 |
| 3 | 128 | 0.2 | 0.0076 | 0.0007 |
| 4 | 32 | 0.2 | 0.0077 | 0.0007 |
| 5 | 16 | 0.1 | 0.077 | 0.0007 |
| 6 | 64 | 0.2 | 0.077 | 0.0008 |
| 7 | 32 | 0.1 | 0.078 | 0.0008 |
| 8 | 16 | 0.2 | 0.079 | 0.0007 |
| LSTM Architecture | Number of Windows | RMSE | Std. Dev. |
|---|---|---|---|
| Singe-layer | 1 | 0.13 | 0.0005 |
| 4 | 0.10 | 0.0006 | |
| 8 | 0.09 | 0.0005 | |
| 12 | 0.08 | 0.0007 | |
| 16 | 0.08 | 0.0006 | |
| Double-layer | 1 | 0.11 | 0.0007 |
| 4 | 0.09 | 0.0006 | |
| 8 | 0.08 | 0.0006 | |
| 12 | 0.08 | 0.0007 | |
| 16 | 0.07 | 0.0008 | |
| Bi-directional | 1 | 0.14 | 0.0008 |
| 4 | 0.12 | 0.0007 | |
| 8 | 0.10 | 0.0006 | |
| 12 | 0.08 | 0.0007 | |
| 16 | 0.07 | 0.0006 |
| Reference | Model | Training | Testing | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | WIA | RMSE | MAE | R2 | WIA | ||
| Satishkumar et al. [51] | SVM | 0.89 | 0.51 | - | - | 0.97 | 0.54 | - | - |
| RF | 0.51 | 0.15 | - | - | 0.62 | 0.36 | - | - | |
| Cubist | 0.11 | 0.03 | - | - | 0.24 | 0.05 | - | - | |
| Our study | Single-layer LSTM | 0.08 | 0.05 | 0.97 | 0.95 | 0.08 | 0.04 | 0.97 | 0.94 |
| Double-layer LSTM | 0.07 | 0.04 | 0.98 | 0.96 | 0.08 | 0.04 | 0.97 | 0.95 | |
| Bi-directional LSTM | 0.07 | 0.05 | 0.98 | 0.96 | 0.08 | 0.03 | 0.98 | 0.95 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maarif, M.R.; Saleh, A.R.; Habibi, M.; Fitriyani, N.L.; Syafrudin, M. Energy Usage Forecasting Model Based on Long Short-Term Memory (LSTM) and eXplainable Artificial Intelligence (XAI). Information 2023, 14, 265. https://doi.org/10.3390/info14050265
Maarif MR, Saleh AR, Habibi M, Fitriyani NL, Syafrudin M. Energy Usage Forecasting Model Based on Long Short-Term Memory (LSTM) and eXplainable Artificial Intelligence (XAI). Information. 2023; 14(5):265. https://doi.org/10.3390/info14050265
Chicago/Turabian StyleMaarif, Muhammad Rifqi, Arif Rahman Saleh, Muhammad Habibi, Norma Latif Fitriyani, and Muhammad Syafrudin. 2023. "Energy Usage Forecasting Model Based on Long Short-Term Memory (LSTM) and eXplainable Artificial Intelligence (XAI)" Information 14, no. 5: 265. https://doi.org/10.3390/info14050265
APA StyleMaarif, M. R., Saleh, A. R., Habibi, M., Fitriyani, N. L., & Syafrudin, M. (2023). Energy Usage Forecasting Model Based on Long Short-Term Memory (LSTM) and eXplainable Artificial Intelligence (XAI). Information, 14(5), 265. https://doi.org/10.3390/info14050265








