A Multi-Key with Partially Homomorphic Encryption Scheme for Low-End Devices Ensuring Data Integrity †
Abstract
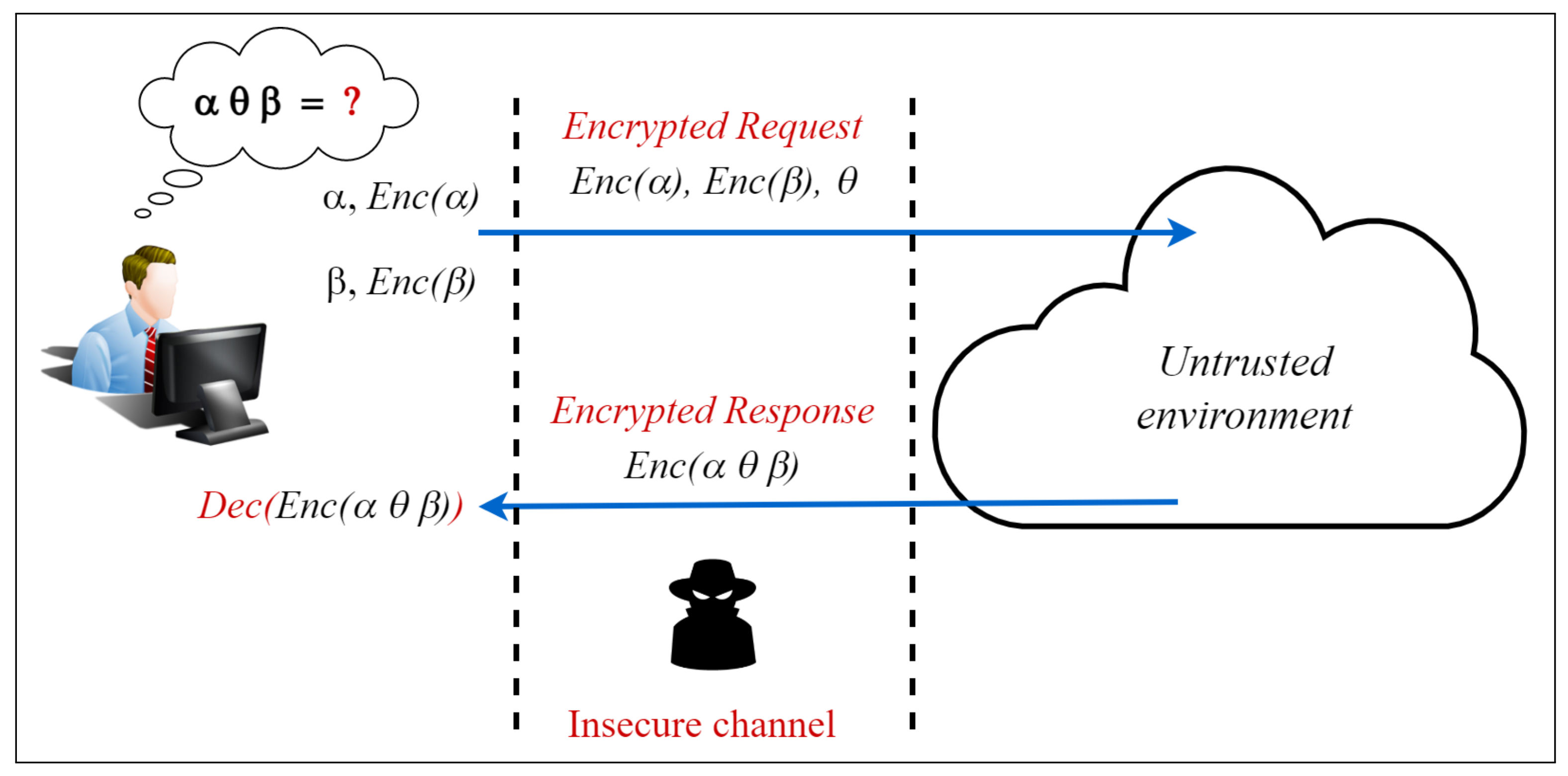
1. Introduction
- Cloud computing: Homomorphic encryption has been used to enable secure computation of sensitive data in the cloud without revealing the data to the cloud provider.
- Machine learning: Homomorphic encryption can be used to perform secure and private machine learning on encrypted data without the need for decryption.
- Blockchain: Homomorphic encryption can be used to enable secure and private transactions on a blockchain without revealing the transaction details to third parties.
- Privacy-preserving data analysis: Homomorphic encryption can be used to perform privacy-preserving data analysis on encrypted data without the need for decryption or data sharing.
- Internet of Things: Homomorphic encryption can be used to enable secure and private computation on IoT devices without the need for decryption or data sharing.
- Provide high security and privacy for the data.
- Be scalable and handle large amounts of data from various IoT devices.
- Be efficient and not add significant overhead to the computational resources required for data processing.
- Be compatible with existing support interoperability between connected low-end devices.
- Define a user-friendly mode and easy to implement for developers and end-users.
2. Related Work
2.1. Security Assumptions
2.1.1. Public Key Encryption
2.1.2. Lattice-Based Encryption
2.1.3. Code-Based Encryption
2.2. Homomorphic Operations
2.3. Computational Efficiency
3. Cryptosystem Design
- KeyGen: is equal
- : , where
- : , with presents the quotient of .
3.1. System Description
3.1.1. Keys Generation
- , d is the number of addition operations, and h denotes a small random number.
- , .
- In addition operation: , .
| Algorithm 1 KeyGen algorithm |
|
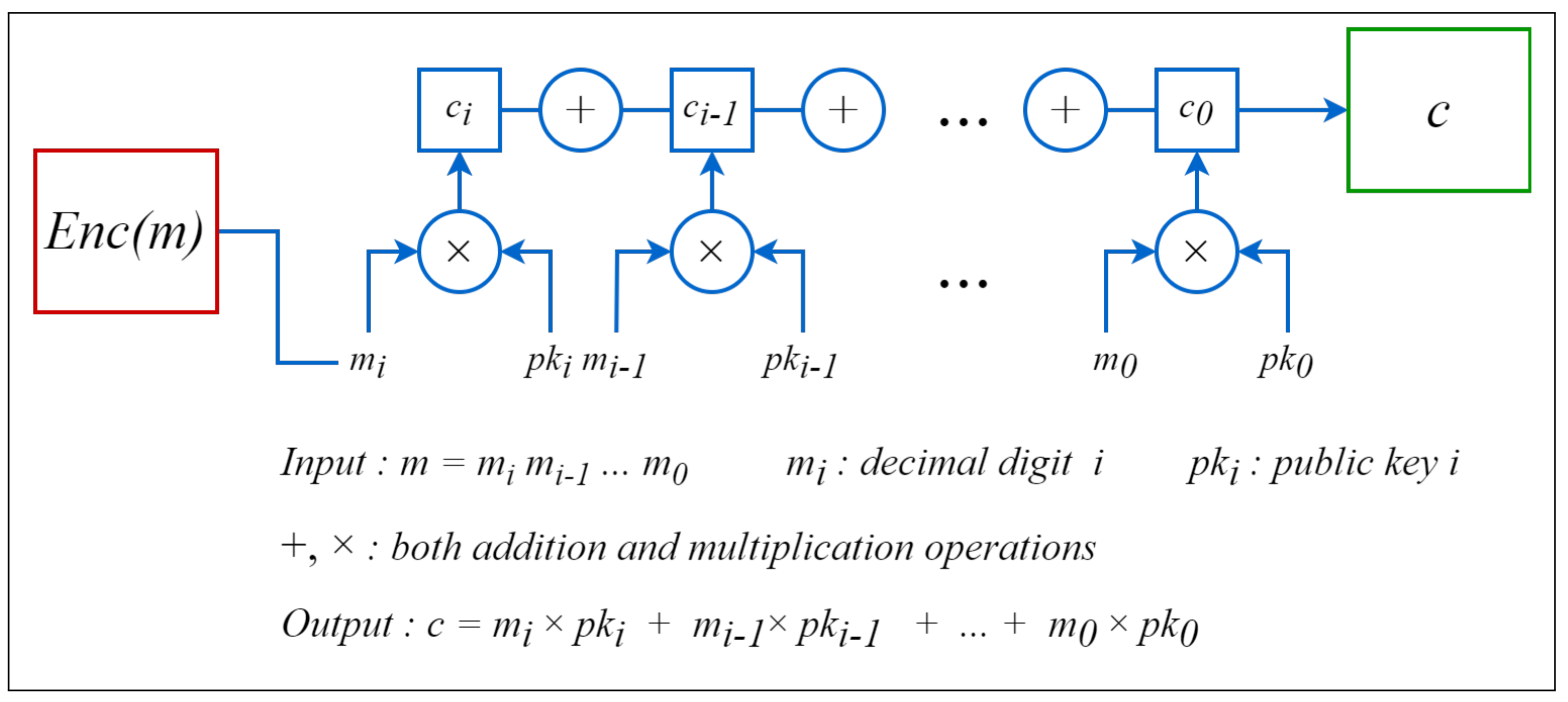
3.1.2. Encryption
| Algorithm 2 Encryption algorithm |
|
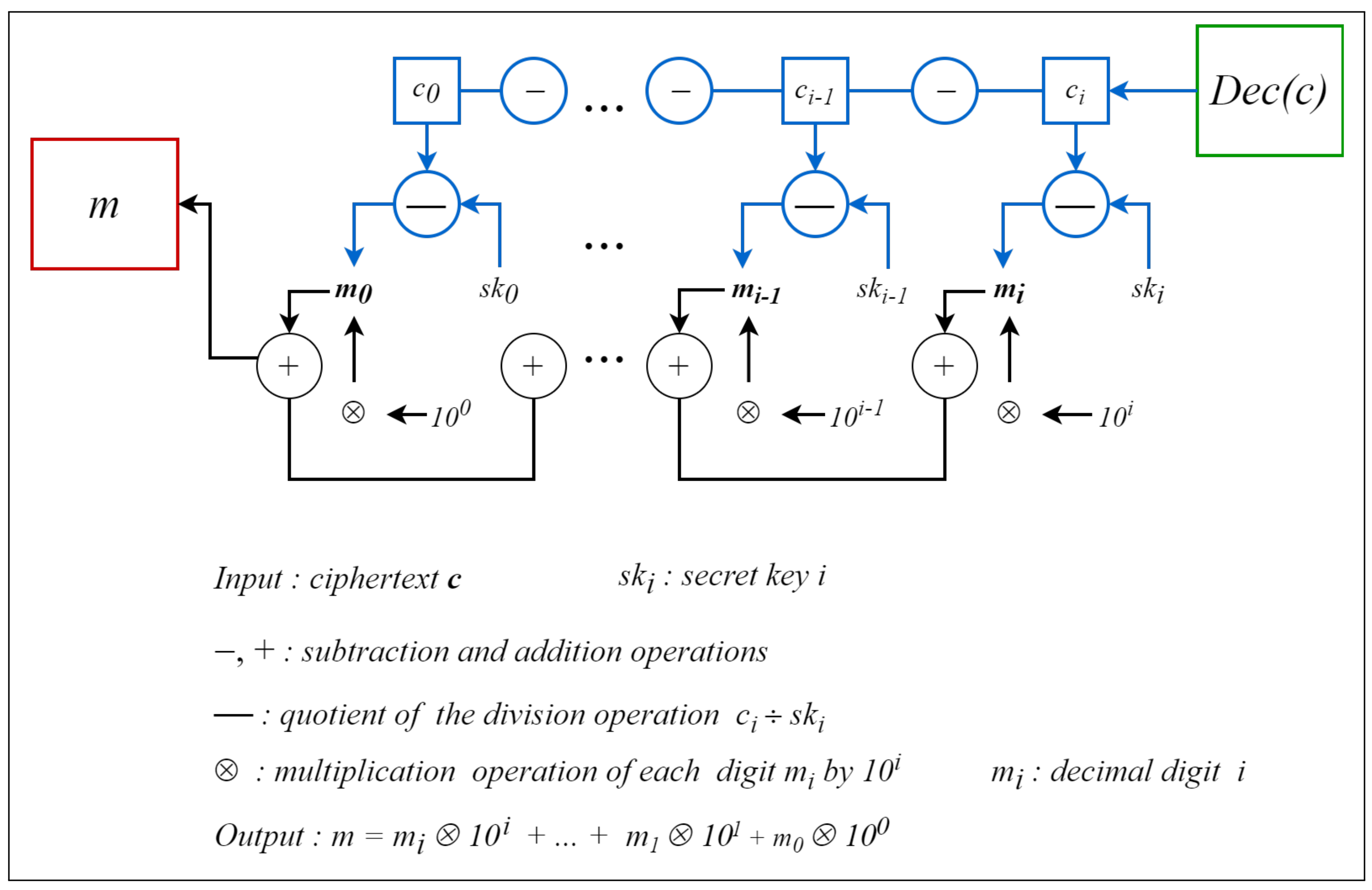
3.1.3. Decryption
3.2. Homomorphic Addition
| Algorithm 3 Addition 1 algorithm |
|
Depth Demonstration
3.3. Order-Preserving
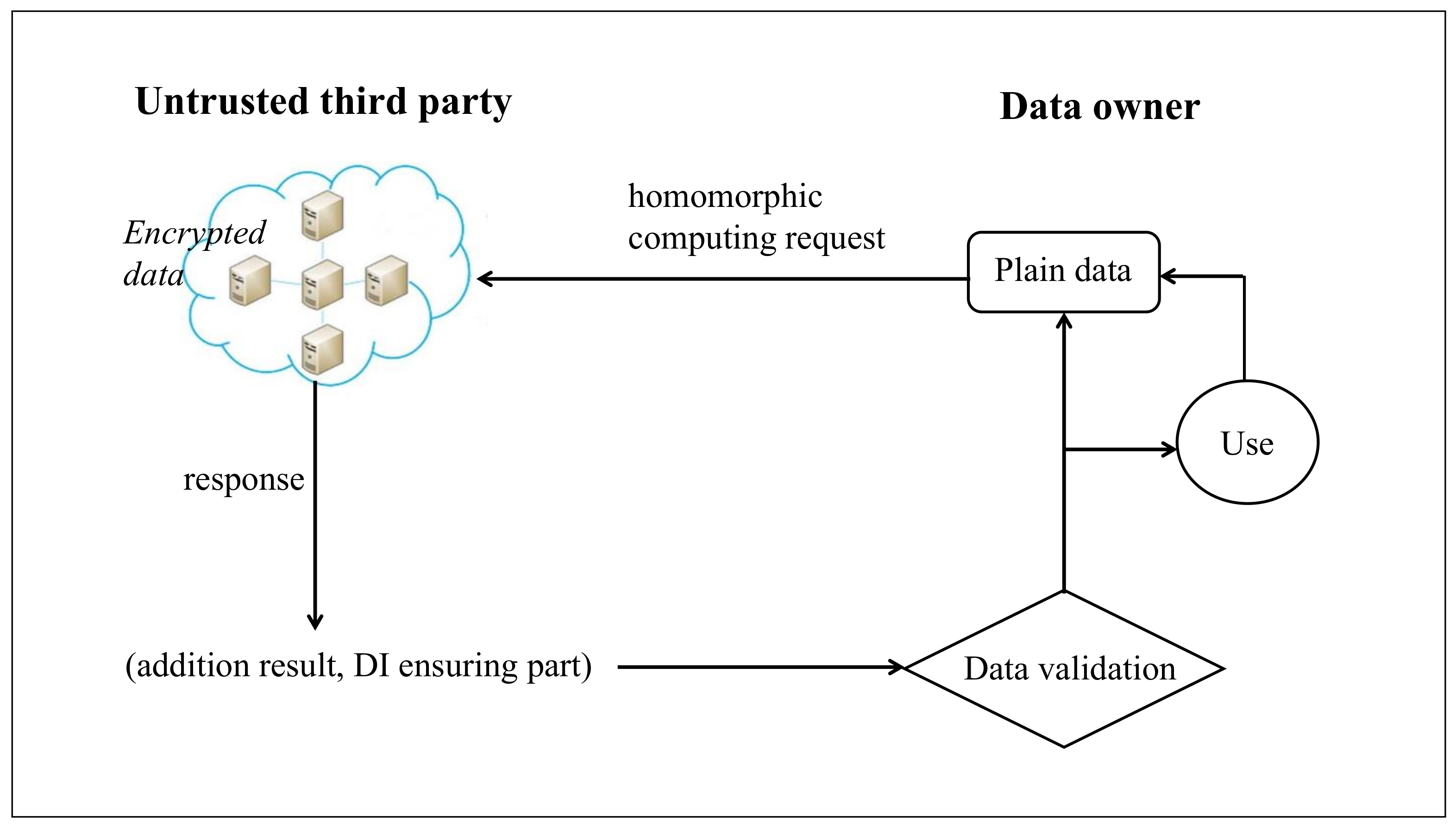
4. Data Integrity Ensuring
4.1. Scenario
| Algorithm 4 Decryption algorithm |
|
| Algorithm 5 Addition 2 algorithm |
|
4.2. Demonstration
5. Proof of Security and Performance
6. Implementation and Comparative Analysis
6.1. Comparative Study
6.2. A Comparative Study against Attacks
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alsbouí, T.; Hammoudeh, M.; Bandar, Z.; Nisbet, A. An overview and classification of approaches to information extraction in wireless sensor networks. In Proceedings of the 5th International Conference on Sensor Technologies and Applications (SENSORCOMM’11), Saint Laurent du Var, France, 21–27 August 2011; p. 255. [Google Scholar]
- Kara, M.; Laouid, A.; Bounceur, A.; Lalem, F.; AlShaikh, M.; Kebache, R.; Sayah, Z. A novel delegated proof of work consensus protocol. In Proceedings of the 2021 International Conference on Artificial Intelligence for Cyber Security Systems and Privacy (AI-CSP), El Oued, Algeria, 20–21 November 2021; pp. 1–7. [Google Scholar]
- Kara, M.; Laouid, A.; Hammoudeh, M. An Efficient Multi-Signature Scheme for Blockchain. Cryptology ePrint Archive, Paper 2023/078. 2023. Available online: https://eprint.iacr.org/2023/078 (accessed on 3 April 2023).
- Chait, K.; Laouid, A.; Laouamer, L.; Kara, M. A Multi-Key Based Lightweight Additive Homomorphic Encryption Scheme. In Proceedings of the 2021 International Conference on Artificial Intelligence for Cyber Security Systems and Privacy (AI-CSP), El Oued, Algeria, 20–21 November 2021; pp. 1–6. [Google Scholar]
- Ghafir, I.; Prenosil, V.; Hammoudeh, M.; Han, L.; Raza, U. Malicious ssl certificate detection: A step towards advanced persistent threat defence. In Proceedings of the International Conference on Future Networks and Distributed Systems, New York, NY, USA, 19–20 July 2017. [Google Scholar] [CrossRef]
- Sniatala, P.; Iyengar, S.; Ramani, S.K. Homomorphic Encryption. In Evolution of Smart Sensing Ecosystems with Tamper Evident Security; Springer: Berlin/Heidelberg, Germany, 2021; pp. 69–76. [Google Scholar] [CrossRef]
- Rivest, R.; Shamir, A.; Adleman, L. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Elgamal, T. A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theory 1985, 31, 469–472. [Google Scholar] [CrossRef]
- Naccache, D.; Stern, J. A New Public Key Cryptosystem Based on Higher Residues. In Proceedings of the 5th ACM Conference on Computer and Communications Security (CCS ’98), New York, NY, USA, 2–5 November 1998; pp. 59–66. [Google Scholar] [CrossRef]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Prague, Czech Republic, 2–6 May 1999; Springer: Berlin/Heidelberg, Germany, 1999; pp. 223–238. [Google Scholar] [CrossRef]
- Galbraith, S.D. Elliptic curve Paillier schemes. J. Cryptol. 2002, 15, 129–138. [Google Scholar] [CrossRef]
- Kawachi, A.; Tanaka, K.; Xagawa, K. Multi-bit cryptosystems based on lattice problems. In Proceedings of the International Workshop on Public Key Cryptography, Beijing, China, 16–20 April 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 315–329. [Google Scholar] [CrossRef]
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. (Leveled) fully homomorphic encryption without bootstrapping. ACM Trans. Comput. Theory TOCT 2014, 6, 1–36. [Google Scholar] [CrossRef]
- Brakerski, Z. Fundamentals of Fully Homomorphic Encryption-A Survey. Proc. Electron. Colloq. Comput. Complex. 2018, 25, 125. [Google Scholar]
- Smart, N.P.; Vercauteren, F. Fully homomorphic encryption with relatively small key and ciphertext sizes. In Proceedings of the International Workshop on Public Key Cryptography, Paris, France, 26–28 May 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 420–443. [Google Scholar] [CrossRef]
- Boneh, D.; Goh, E.J.; Nissim, K. Evaluating 2-DNF Formulas on Ciphertexts. In Proceedings of the Theory of Cryptography, Cambridge, MA, USA, 10–12 February 2005; Kilian, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 325–341. [Google Scholar] [CrossRef]
- Ishai, Y.; Paskin, A. Evaluating branching programs on encrypted data. In Proceedings of the Theory of Cryptography Conference, Amsterdam, The Netherlands, 21–24 February 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 575–594. [Google Scholar] [CrossRef]
- Gentry, C. A Fully Homomorphic Encryption Scheme; Stanford University ProQuest Dissertations Publishing: Stanford, CA, USA, 2009. [Google Scholar]
- Van Dijk, M.; Gentry, C.; Halevi, S.; Vaikuntanathan, V. Fully homomorphic encryption over the integers. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, France, 30 May–3 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 24–43. [Google Scholar]
- Brakerski, Z.; Vaikuntanathan, V. Fully homomorphic encryption from ring-LWE and security for key dependent messages. In Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 505–524. [Google Scholar]
- López-Alt, A.; Tromer, E.; Vaikuntanathan, V. On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption. In Proceedings of the Forty-Fourth Annual ACM Symposium on Theory of Computing, New York, NY, USA, 19–22 May 2012; pp. 1219–1234. [Google Scholar]
- Pang, H.; Wang, B. Privacy-preserving association rule mining using homomorphic encryption in a multikey environment. IEEE Syst. J. 2020, 15, 3131–3141. [Google Scholar] [CrossRef]
- Doröz, Y.; Shahverdi, A.; Eisenbarth, T.; Sunar, B. Toward Practical Homomorphic Evaluation of Block Ciphers Using Prince. In International Conference on Financial Cryptography and Data Security; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8438, pp. 208–220. [Google Scholar]
- Biksham, V.; Vasumathi, D. A lightweight fully homomorphic encryption scheme for cloud security. Int. J. Inf. Comput. Secur. 2020, 13, 357–371. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, S.; Yang, J.; Li, J.; Li, Z. Targeted fully homomorphic encryption based on a double decryption algorithm for polynomials. Tsinghua Sci. Technol. 2014, 19, 478–485. [Google Scholar] [CrossRef]
- Yagoub, M.A.; Abdelkader, L.; Kazar, O.; Bounceur, A.; Euler, R.; AlShaikh, M. An adaptive and efficient fully homomorphic encryption technique. In Proceedings of the 2nd International Conference on Future Networks and Distributed Systems, New York, NY, USA, 26–27 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Ding, Y.; Li, X.; Lü, H.; Li, X. A novel fully homomorphic encryption scheme bsed on LWE. Wuhan Univ. J. Nat. Sci. 2016, 21, 84–92. [Google Scholar] [CrossRef]
- Brakerski, Z.; Vaikuntanathan, V. Efficient fully homomorphic encryption from (standard) LWE. Siam J. Comput. 2014, 43, 831–871. [Google Scholar] [CrossRef]
- Zhou, T.; Zhang, Z.; Chen, L.; Che, X.; Liu, W.; Yang, X. Multi-key Fully Homomorphic Encryption Scheme with Compact Ciphertext. Cryptology ePrint Archive, Paper 2021/1131. 2021. Available online: https://eprint.iacr.org/2021/1131 (accessed on 3 April 2023).
- Kara, M.; Laouid, A.; Hammoudeh, M.; Bounceur, A. One Digit Checksum for Data Integrity Verification of Cloud-executed Homomorphic Encryption Operations. Cryptology ePrint Archive, Paper 2023/231. 2023. Available online: https://eprint.iacr.org/2023/231 (accessed on 3 April 2023).
- Gidney, C.; Ekerå, M. How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits. Quantum 2021, 5, 433. [Google Scholar] [CrossRef]
- Gai, K.; Qiu, M.; Li, Y.; Liu, X.Y. Advanced fully homomorphic encryption scheme over real numbers. In Proceedings of the 2017 IEEE 4th International Conference on Cyber Security and Cloud Computing (CSCloud), New York, NY, USA, 26–28 June 2017; pp. 64–69. [Google Scholar]
- Yang, H.M.; Xia, Q.; Wang, X.F.; Tang, D.H. A new somewhat homomorphic encryption scheme over integers. In Proceedings of the 2012 International Conference on Computer Distributed Control and Intelligent Environmental Monitoring, Zhangjiajie, China, 5–6 March 2012; pp. 61–64. [Google Scholar]
- Ramaiah, Y.G.; Kumari, G.V. Towards practical homomorphic encryption with efficient public key generation. Int. J. Netw. Secur. 2012, 3, 10. [Google Scholar]
- Cheon, J.H.; Coron, J.S.; Kim, J.; Lee, M.S.; Lepoint, T.; Tibouchi, M.; Yun, A. Batch fully homomorphic encryption over the integers. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Athens, Greece, 26–30 May 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 315–335. [Google Scholar]
- Kara, M.; Laouid, A.; Euler, R.; Yagoub, M.A.; Bounceur, A.; Hammoudeh, M.; Medileh, S. A Homomorphic Digit Fragmentation Encryption Scheme Based on the Polynomial Reconstruction Problem. In Proceedings of the 4th International Conference on Future Networks and Distributed Systems (ICFNDS), New York, NY, USA, 26–27 November 2020; pp. 1–6. [Google Scholar]
- Thangavel, M.; Varalakshmi, P. Enhanced DNA and ElGamal cryptosystem for secure data storage and retrieval in cloud. Clust. Comput. 2018, 21, 1411–1437. [Google Scholar] [CrossRef]
- Coron, J.S.; Mandal, A.; Naccache, D.; Tibouchi, M. Fully Homomorphic Encryption over the Integers with Shorter Public Keys. In Proceedings of the Advances in Cryptology—CRYPTO 2011, Santa Barbara, CA, USA, 14–18 August 2011; Rogaway, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 487–504. [Google Scholar] [CrossRef]
- Dasgupta, S.; Pal, S. Design of a Polynomial Ring based Symmetric Homomorphic Encryption Scheme. Perspect. Sci. 2016, 8, 692–695. [Google Scholar] [CrossRef]
- Boer, D.; Kramer, S. Secure Sum Outperforms Homomorphic Encryption in (Current) Collaborative Deep Learning. arXiv 2020, arXiv:2006.02894. [Google Scholar]
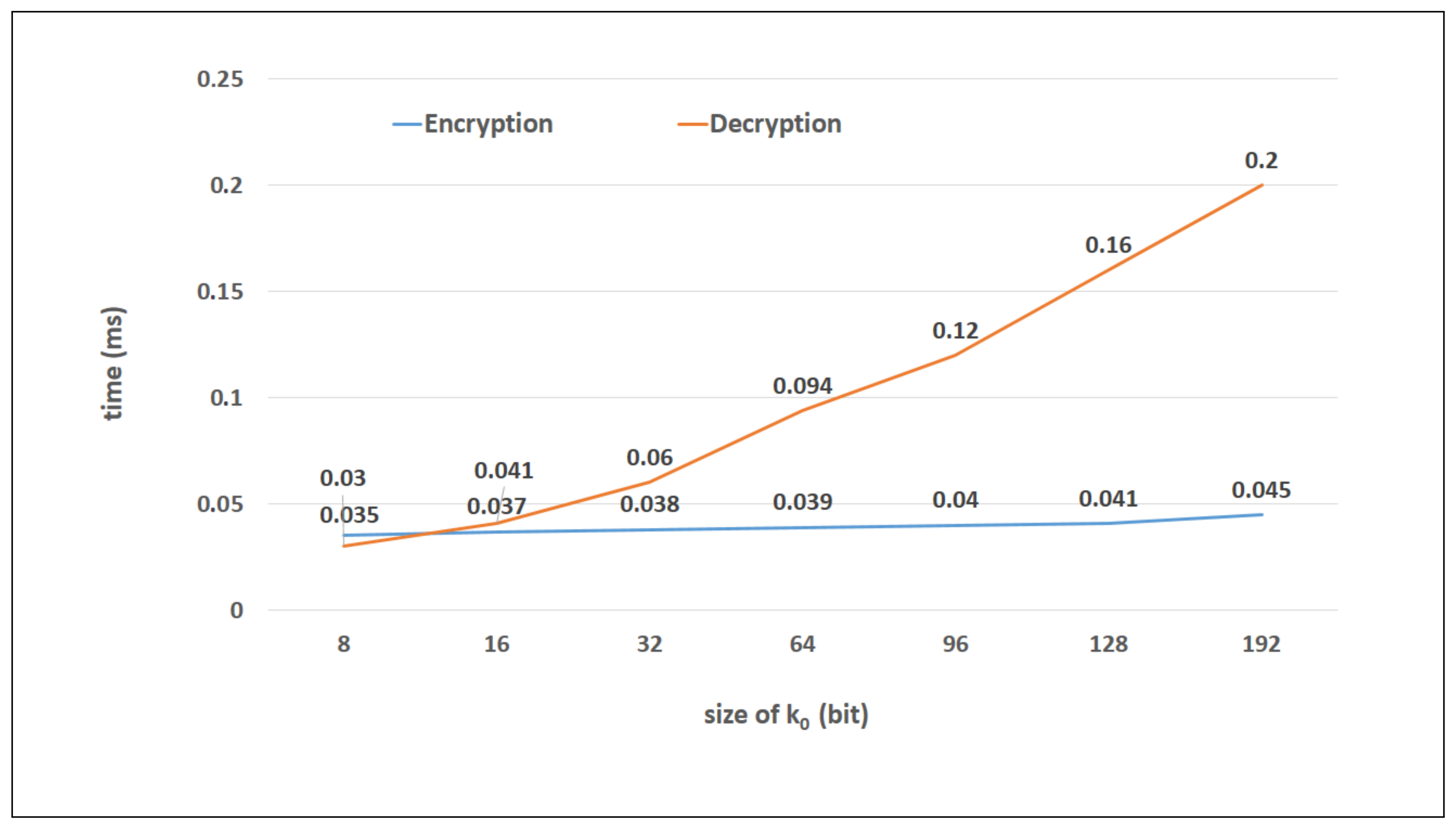
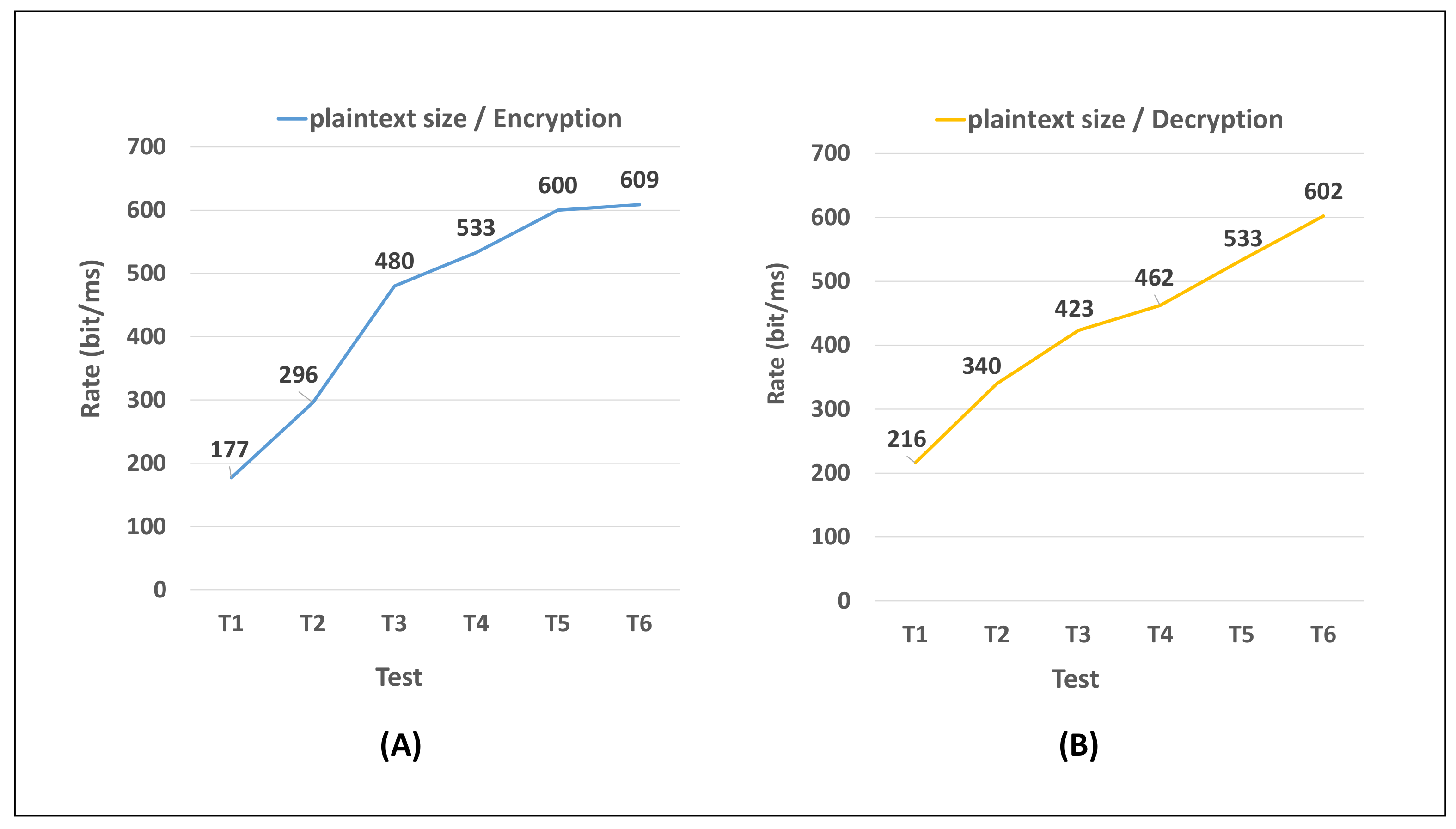

| Size (Digits) | m | k0 | p | Depth |
|---|---|---|---|---|
| 2 | 301 | 603 | ||
| 5 | 301 | 606 | ||
| 10 | 301 | 611 | ||
| 20 | 301 | 621 | ||
| 60 | 301 | 661 | ||
| 100 | 251 | 601 | ||
| 200 | 201 | 601 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medileh, S.; Laouid, A.; Hammoudeh, M.; Kara, M.; Bejaoui, T.; Eleyan, A.; Al-Khalidi, M. A Multi-Key with Partially Homomorphic Encryption Scheme for Low-End Devices Ensuring Data Integrity. Information 2023, 14, 263. https://doi.org/10.3390/info14050263
Medileh S, Laouid A, Hammoudeh M, Kara M, Bejaoui T, Eleyan A, Al-Khalidi M. A Multi-Key with Partially Homomorphic Encryption Scheme for Low-End Devices Ensuring Data Integrity. Information. 2023; 14(5):263. https://doi.org/10.3390/info14050263
Chicago/Turabian StyleMedileh, Saci, Abdelkader Laouid, Mohammad Hammoudeh, Mostefa Kara, Tarek Bejaoui, Amna Eleyan, and Mohammed Al-Khalidi. 2023. "A Multi-Key with Partially Homomorphic Encryption Scheme for Low-End Devices Ensuring Data Integrity" Information 14, no. 5: 263. https://doi.org/10.3390/info14050263
APA StyleMedileh, S., Laouid, A., Hammoudeh, M., Kara, M., Bejaoui, T., Eleyan, A., & Al-Khalidi, M. (2023). A Multi-Key with Partially Homomorphic Encryption Scheme for Low-End Devices Ensuring Data Integrity. Information, 14(5), 263. https://doi.org/10.3390/info14050263












