Power Control of Reed–Solomon-Coded OFDM Systems in Rayleigh Fading Channels

Abstract

Power control in an RS-coded orthogonal frequency division multiplex (OFDM) system with error-and-erasure correction decoding in Rayleigh fading channels was investigated. The power of each symbol within a codeword was controlled to reduce the codeword error rate (WER). Several RS-coded OFDM systems with power control are proposed. The WERs of the proposed systems as a function of the signal-to-noise ratio per bit were derived. We found that channel inversion at the transmitter in combination with the erasure generation by ordering fading amplitudes at the receiver provided the lowest WER among the considered systems. Furthermore, the erasure generation by ordering fading amplitudes was found to be better than the erasure generation by comparing fading amplitudes with a threshold.

1. Introduction

In wireless communication systems, the received signal suffers from fading due to the multipath propagation of the transmitted signal. As a fading compensation technique, coding and power control were investigated independently in [1,2,3].

Coding in combination with power control is a powerful fading compensation technique, as we can see in the following RS code example. Coding uses redundancy to correct errors in a codeword. In RS codes, unreliable symbols are erased to use redundancy more efficiently. If the number of erased symbols in a codeword is more than the minimum distance, the codeword is not correctly decoded. First, assume that a codeword is not correctly decoded because it has too many erasures. Among the erased symbols in the codeword, some symbols are in deep fades, and the other symbols are relatively not in deep fades. If many erased symbols are relatively not in deep fades, we can make these erased symbols reliable by adding a little power to these symbols and correctly decode the codeword. Now, assume that a codeword is correctly decoded. Among the unerased symbols in the codeword, some symbols may have too much power, which can be used by other symbols in another codeword. Then, we can reduce and save the transmitted power of these symbols. As we see in the example, coding is good for managing the symbols in deep fades by erasing the symbols, and power control is good for managing the symbols with excessive power. Thus, coding in combination with power control is a powerful fading compensation technique that works in a complementary fashion [4].

We considered how to combine power control with the RS-coded system and compared erasure generation schemes. One code symbol is mapped to one M-ary quadrature amplitude modulation (MQAM) symbol. A codeword is transmitted parallel in the frequency domain by OFDM. We assumed that the receiver knows the fading of code symbols in a codeword and decodes codewords with error-and-erasure correction. At the receiver, three different erasure generation schemes are used. One erasure generation scheme is ordering fading amplitudes of symbols and erasing a fixed number of symbols that have smaller fading amplitudes than the other symbols in a codeword [5]. Another erasure generation scheme is comparing the fading amplitudes of symbols with a threshold and erasing the symbols that have a smaller fading amplitude than the threshold [6]. Furthermore, the erasure generation scheme that combines ordering and comparing a threshold was considered. At the transmitter, two different power control schemes called truncated channel inversion and truncation were only considered. The transmitter with truncated channel inversion cuts off its power for the symbols to be erased and uses channel inversion for the unerased symbols so that the received power for the unerased symbols are equal. The transmitter with only truncation cuts off its power for the symbols to be erased and transmits constant power for the unerased symbols. Thus, six systems that are classified by the erasure generation scheme at the receiver and the power control scheme at the transmitter are considered. We found that the erasure generation by ordering fading amplitudes was better than the erasure generation by comparing fading amplitudes with a threshold, also for the systems with no power control. Furthermore, the truncated channel inversion in combination with the erasure generation by ordering fading amplitudes was found to provide the lowest codeword error rate (WER) among the considered systems.

This paper consists of six sections. In Section 2, the system model is shown. In Section 3, the systems that use truncated channel inversion at the transmitter are analyzed. In Section 4, the systems that use only truncation at the transmitter are analyzed. In Section 5, numerical results are shown. Finally, conclusions are made in Section 6.

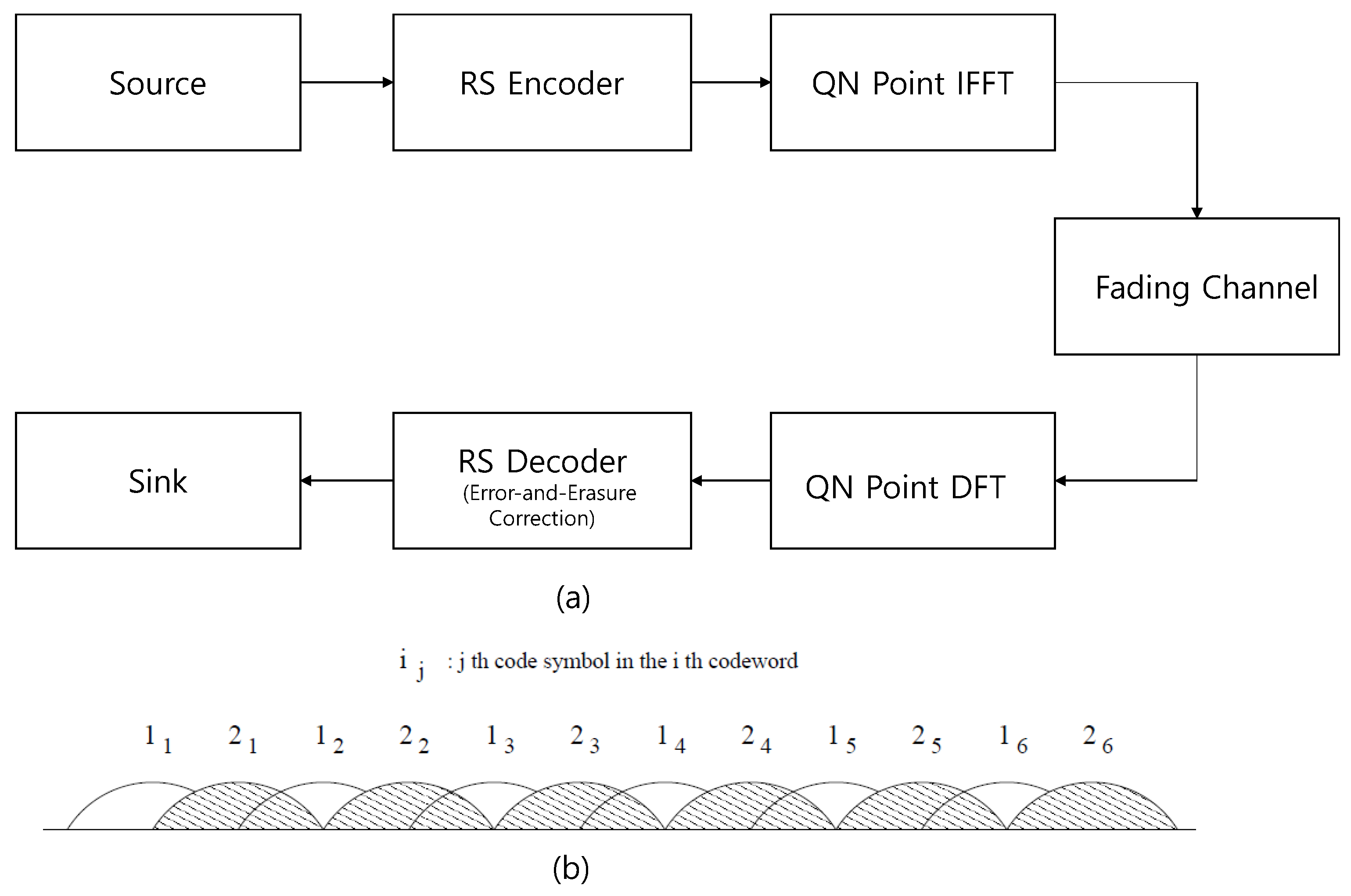
2. System Model

We considered an RS-coded OFDM system in a Rayleigh fading channel. The system model is shown in Figure 1.

The Q-ary $(N,K)$ RS codes were used, where N is the number of the code symbols and K is the number of the information symbols in a codeword. A codeword is transmitted parallel in the frequency domain by OFDM. One code symbol in the RS code is transmitted as one MQAM symbol. Thus, Q is equal to M in MQAM. We assumed that the fading amplitudes of the symbols in a codeword are independent. Thus, perfect interleaving was assumed. Furthermore, the perfect channel state information (CSI) at the transmitter was assumed. For example, this perfect CSI assumption at the transmitter is easily implemented in 5G systems that use the time division duplex (TDD). The coherence time is usually larger than the switching time of the TDD. For the OFDM system, the independence of code symbols in a codeword is hard to achieve because the frequency spectrum of each symbol overlaps. We can avoid this spectrum overlap by inserting a serial to parallel conversion block before the inverse fast Fourier transform (IFFT) block at transmitter [7]. Thus, Q frames are transmitted simultaneously. We assumed that the fading amplitudes of the symbols in a codeword that have no spectrum overlap are independent. Furthermore, we assumed that fading stays constant over at least a Q frame length so that a code symbol suffers slow fading. Thus, the received signal after phase compensation at the demodulator for the i th symbol in a codeword is

$$r_i=a_i·x_i+n_i,i=1,2,\dots ,N$$

(1)

where $a_i$ is the fading amplitude, $x_i$ is the transmitted MQAM symbol, and $n_i$ is the complex Gaussian noise of the ith symbol. Note that $x_i$ and $n_i$ are complex numbers. $a_i$ is a positive real number. We assumed that $E\left\{{a_i}^2\right\}=1$, $E\left\{{X_i}^2\right\}=E_s=\frac{K}{N}{log}_{2}M·E_b$, and $E\left\{\right|n_i{|}^2\}=N_0$, where $E_b$ is the average energy per information bit.

Error-and-erasure correction is used as the decoding scheme of RS codes. RS codes allow the correction of up to t errors and e erasures as long as [8]

$$2t+e\le N-K.$$

(2)

If we erase unreliable symbols, the performance gain over error-only decoding is achieved [5,6].

3. Truncated Channel Inversion

In this section, the truncated channel inversion as the power control scheme [9] is investigated:

$$E_i=\left\{\begin{array}{cc}{T}_2/{a_i}^2,\hfill & for unerased symbols\hfill \\ 0,\hfill & for erased symbols,\hfill \end{array}\right.$$

(3)

where $E_i$ is the transmitted energy for the ith symbol in a codeword and $T_2$ is the received energy for unerased symbols.

Finding the optimum erasure generation scheme is complex, and we analyzed three systems that use different erasure generation schemes. One erasure generation scheme is ordering fading amplitudes of symbols and erasing a fixed number of symbols in a codeword [5]. Another erasure generation scheme is comparing the fading amplitudes of symbols with a threshold and erasing the symbol that has smaller fading amplitude than the threshold [6]. Furthermore, we considered the erasure generation scheme that combines ordering and comparing a threshold.

3.1. Erasure Generation by Ordering Fading Amplitudes

In this subsection, ordering as the erasure generation scheme was assumed. The number of erased symbols within a codeword was fixed to e symbols.

After ordering the fading amplitudes, the probability density function (pdf) of ${a_i}^2$, where $a_i$ is the fading amplitude of the ith reliable symbol, is

$$f_i\left(x\right)=\frac{N!}{(N-i)!(i-1)!}{F}^{N-i}\left(x\right){\{1-F(x\left)\right\}}^{i-1}f\left(x\right)$$

(4)

where $f\left(x\right)=e^{-x}$ and $F\left(x\right)=1-e^{-x}$ in the Rayleigh fading channel. Since we assumed that the received energy of unerased symbols was set to $T_2$, the average transmitted energy per codeword is

$$\begin{array}{ccc}\hfill E_{cw}& =& \sum _{i=1}^{N-e}{\int }_0^{\infty }\frac{T_2}{x}·f_i\left(x\right)dx\hfill \\ & =& N{T}_2\sum _{i=1}^{N-e}\left\{\left(\genfrac{}{}{0pt}{}{N-1}{i-1}\right){(-1)}^{N-i+1}\sum _{j=0}^{N-i}{(-1)}^j\left(\genfrac{}{}{0pt}{}{N-i}{j}\right)ln(N-j)\right\}.\hfill \end{array}$$

(5)

See Appendix B.1 for the derivation of (5). The average transmitted energy per information bit $E_b$ is

$$E_b=\frac{E_{cw}}{K{log}_{2}M},$$

(6)

$$\frac{T_2}{N_0}=\frac{K{log}_{2}M}{N{\sum }_{i=1}^{N-e}\left\{\left(\genfrac{}{}{0pt}{}{N-1}{i-1}\right){(-1)}^{N-i+1}{\sum }_{j=0}^{N-i}{(-1)}^j\left(\genfrac{}{}{0pt}{}{N-i}{j}\right)ln(N-j)\right\}}·\frac{E_b}{N_0}.$$

(7)

The symbol error probability $P_s$ of MQAM is written as [10]

$$\begin{array}{ccc}\hfill P_s& =& 4(1-\frac{1}{\sqrt{M}})Q\left(\sqrt{\frac{3E_s}{(M-1)N_0}}\right)-4{(1-\frac{1}{\sqrt{M}})}^2{Q}^2\left(\sqrt{\frac{3E_s}{(M-1)N_0}}\right)\hfill \\ & \le & 4Q\left(\sqrt{\frac{3E_s}{(M-1)N_0}}\right)\hfill \end{array}$$

(8)

where the Q-function is defined as

$$Q\left(x\right)={\int }_x^{\infty }\frac{e^{-t^2/2}}{\sqrt{2\pi }}dt.$$

(9)

We used (8) as the tight upper bound of the symbol error probability for the analysis. Then, the symbol error probability for an unerased symbol $P_{s|\overline{E}}$ is

$$P_{s|\overline{E}}=\alpha ·Q\left(\sqrt{\beta \frac{T_2}{N_0}}\right)$$

(10)

where $\alpha =4$ and $\beta =\frac{3}{M-1}$. The WER is

$$\mathrm{WER}=\sum _{t=\lfloor \frac{N-K-e}{2}+1\rfloor }^{N-e}\left(\genfrac{}{}{0pt}{}{N-e}{t}\right){P_{s|\overline{E}}}^t{(1-P_{s|\overline{E}})}^{N-e-t}.$$

(11)

3.2. Erasure Generation by Comparing Fading Amplitudes with a Threshold

In this subsection, we erased the code symbols that have smaller fading amplitudes than threshold $T_1$.

If ${a_i}^2<T_1$, the ith symbol in a codeword is erased, where $a_i$ is the fading amplitude of the ith symbol. The pdf of ${a_i}^2$ is $f\left(x\right)=e^{-x}$. The symbol erase probability is

$$P_E={\int }_0^{T_1}{e}^{-x}dx=1-e^{-T_1}.$$

(12)

The probability that a codeword has e symbol errors is

$$P_E\left(e\right)=\left(\genfrac{}{}{0pt}{}{N}{e}\right){P_E}^e{(1-P_E)}^{N-e}.$$

(13)

The average transmitted energy of an unerased symbol is

$${\int }_{T_1}^{\infty }\frac{T_2}{x}·e^{-(x-T_1)}dx=T_2{e}^{T_1}Ei(1,T_1)$$

(14)

where $Ei(n,x)$ is an exponential integral function defined as

$$Ei(n,x)={\int }_1^{\infty }\frac{e^{-xt}}{t^n}dt.$$

(15)

The average transmitted energy per codeword is

$$E_{cw}=\sum _{e=0}^{N-K}(N-e)T_2{e}^{T_1}Ei(1,T_1)·P_E\left(e\right)$$

(16)

where $P_E\left(e\right)$ is (13). Since the average energy per information bit $E_b$ is written as (6),

$$\frac{T_2}{N_0}=\frac{K{log}_{2}M}{{\sum }_{e=0}^{N-K}(N-e)e^{T_1}Ei(1,T_1)·P_E\left(e\right)}·\frac{E_b}{N_0}.$$

(17)

The symbol error probability for an unerased symbol $P_{s|\overline{E}}$ is written as (10). The WER is

$$\mathrm{WER}=\sum _{e=0}^{N-K}\left\{P_E\left(e\right)·\sum _{t=\lfloor \frac{N-K-e}{2}\rfloor +1}^{N-e}\left(\genfrac{}{}{0pt}{}{N-e}{t}\right){P_{s|\overline{E}}}^t{(1-P_{s|\overline{E}})}^{N-e-t}\right\}+\sum _{e=N-K+1}^N{P}_E\left(e\right).$$

(18)

3.3. Erasure Generation by Ordering and Comparing Fading Amplitudes with a Threshold

Here, we considered the erasure generation scheme that includes both ordering and comparing fading amplitudes with a threshold as special cases. At least e symbols are erased in a codeword and the fading amplitudes of all unerased symbols is larger than the threshold $T_1$. In Appendix C, we verified that this erasure generation scheme is the same as ordering when $T_1=0$ and the same as comparing a threshold when $e=0$.

For the analysis, we assumed that we first erase $e^{\prime }$ symbols by comparing the threshold $T_1$. If the number of erased symbols $e^{\prime }$ is less than e, we erase $e-e^{\prime }$ symbols additionally by ordering. The average transmitted energy per codeword is

$$\begin{array}{cc}\hfill E_{cw}=& T_2\left\{{\displaystyle \sum _{e^{\prime }=0}^{e-1}}(N-e^{\prime })P_E\left(e^{\prime }\right){\displaystyle \sum _{j=1}^{N-e}}\left(\genfrac{}{}{0pt}{}{N-e^{\prime }-1}{j-1}\right){\displaystyle \sum _{k=0}^{N-e^{\prime }-j}}\left(\genfrac{}{}{0pt}{}{N-e^{\prime }-j}{k}\right){(-1)}^k{e}^{T_1(k+j)}Ei(1,T_1(k+j))\right\}\hfill \\ \hfill & +T_2{\displaystyle \sum _{e^{\prime }=e}^{N-K}}(N-e^{\prime })e^{T_1}Ei(1,T_1)P_E\left(e^{\prime }\right)\hfill \end{array}$$

(19)

where we can obtain $P_E\left(e^{\prime }\right)$ by replacing $e^{\prime }$ with e in (13). See Appendix B.2 for the derivation of (19). The symbol error probability for an unerased symbol $P_{s|\overline{E}}$ is written as (10). The WER is

$$\begin{array}{ccc}\hfill \mathrm{WER}& =& \left(\sum _{e^{\prime }=0}^e{P}_E\left(e^{\prime }\right)\right)·\sum _{t=\lfloor \frac{N-K-e}{2}\rfloor +1}^{N-e}\left(\genfrac{}{}{0pt}{}{N-e}{t}\right){P_{s|\overline{E}}}^t{(1-P_{s|\overline{E}})}^{N-e-t}\hfill \\ & & +\sum _{e^{\prime }=e+1}^{N-K}{P}_E\left(e^{\prime }\right)\sum _{t=\lfloor \frac{N-K-e^{\prime }}{2}\rfloor +1}^{N-e^{\prime }}\left(\genfrac{}{}{0pt}{}{N-e^{\prime }}{t}\right){P_{s|\overline{E}}}^t{(1-P_{s|\overline{E}})}^{N-e^{\prime }-t}\hfill \\ & & +\sum _{e^{\prime }=N-K+1}^N{P}_E\left(e^{\prime }\right).\hfill \end{array}$$

(20)

4. Truncation Only

In this section, we considered truncation as the power control scheme:

$$E_i=\left\{\begin{array}{cc}{E}_s,\hfill & for unerased symbols\hfill \\ 0,\hfill & for erased symbols,\hfill \end{array}\right.$$

(21)

where $E_i$ is the transmitted energy for the ith symbol in a codeword.

As in the previous section, we considered three different erasure generation schemes. One is ordering; another is comparing a threshold; the other is combining the form of ordering and comparing a threshold.

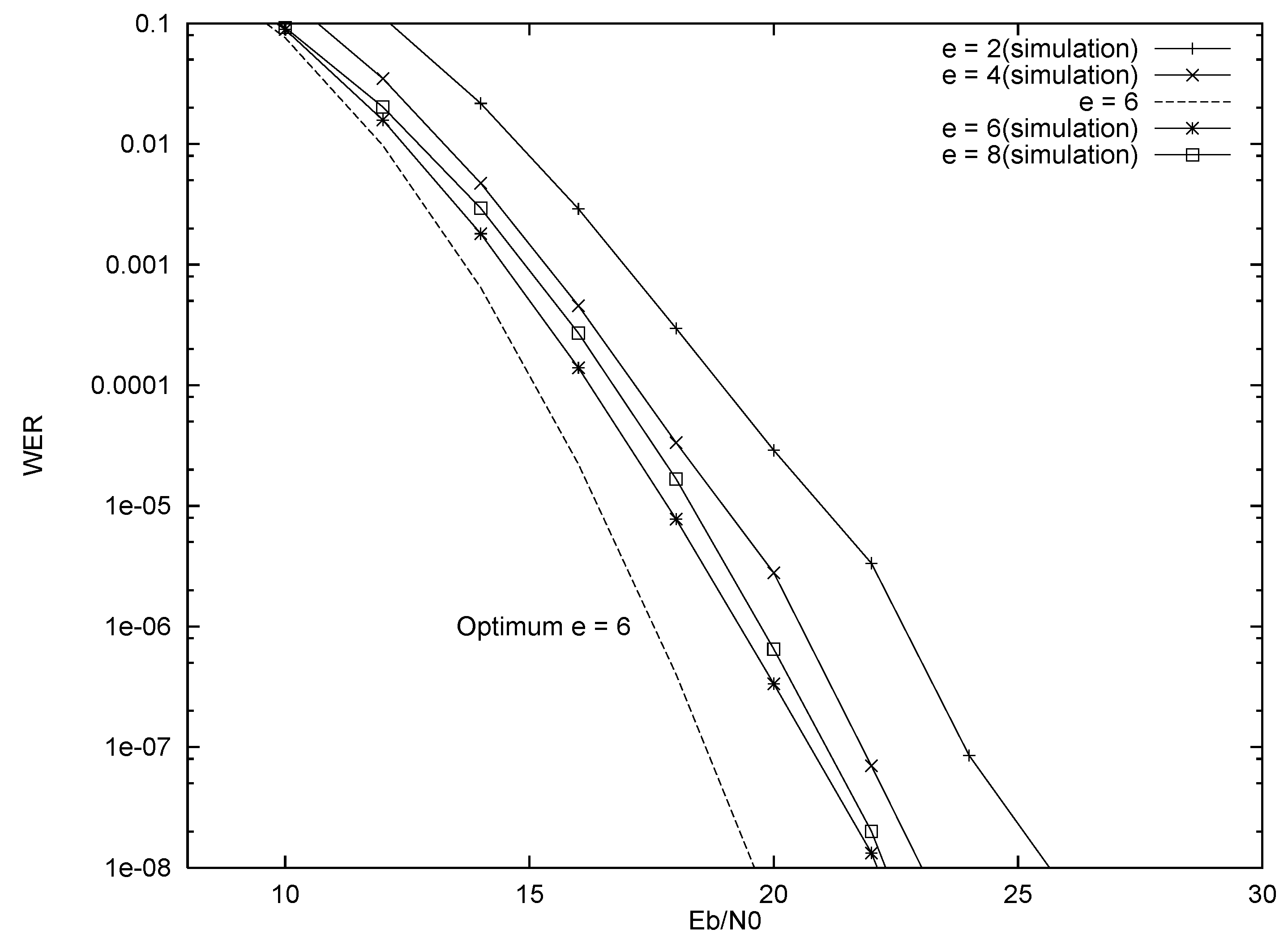
4.1. Erasure Generation by Ordering Fading Amplitudes

In this subsection, we considered ordering as the erasure generation scheme. The number of erased symbols within a codeword was fixed to e symbols.

It is hard to derive the WER exactly as a function of $E_b/N_0$ for this system because the received powers of the unerased symbols within a codeword are not independent random variables after ordering. The proof of the fact that ordering does not preserve the independence of independent and identically distributed (i.i.d.) random variables is in Appendix A.

If we assume the independence of unerased symbol powers as [5], the WER is derived as follows. After ordering the fading amplitudes, the pdf of ${a_i}^2$, where $a_i$ is the fading amplitude of the ith reliable symbol, is written as (4). The pdf of an unerased symbols is

$$\begin{array}{ccc}\hfill g\left(x\right)& =& \sum _{i=1}^{N-e}\frac{1}{N-e}·f_i\left(x\right)\hfill \\ & =& \frac{N}{N-e}\sum _{i=1}^{N-e}\left(\genfrac{}{}{0pt}{}{N-1}{i-1}\right)F^{N-i}\left(x\right){\{1-F(x\left)\right\}}^{i-1}f\left(x\right).\hfill \end{array}$$

(22)

The symbol error probability for an unerased symbol is

$$\begin{array}{ccc}\hfill P_{s|\overline{E}}& =& {\int }_0^{\infty }\alpha ·Q\left(\sqrt{\beta x}\right)·g\left(x\right)dx\hfill \\ & =& \frac{\alpha N}{2(N-e)}\sum _{i=2}^{N-e}\left(\genfrac{}{}{0pt}{}{N-1}{i-1}\right)\left\{\sum _{j=0}^{N-i}\left(\genfrac{}{}{0pt}{}{N-i}{j}\right){(-1)}^j\frac{1}{(i+j)}\left(1-\sqrt{\frac{\beta }{\beta +2i+2j}}\right)\right\}\hfill \end{array}$$

(23)

where $\beta =\frac{3}{M-1}·\frac{K}{N-e}{log}_{2}M·E_b/N_0$. The WER is written as (11). Note that (11) assumes the independence of unerased symbol powers.

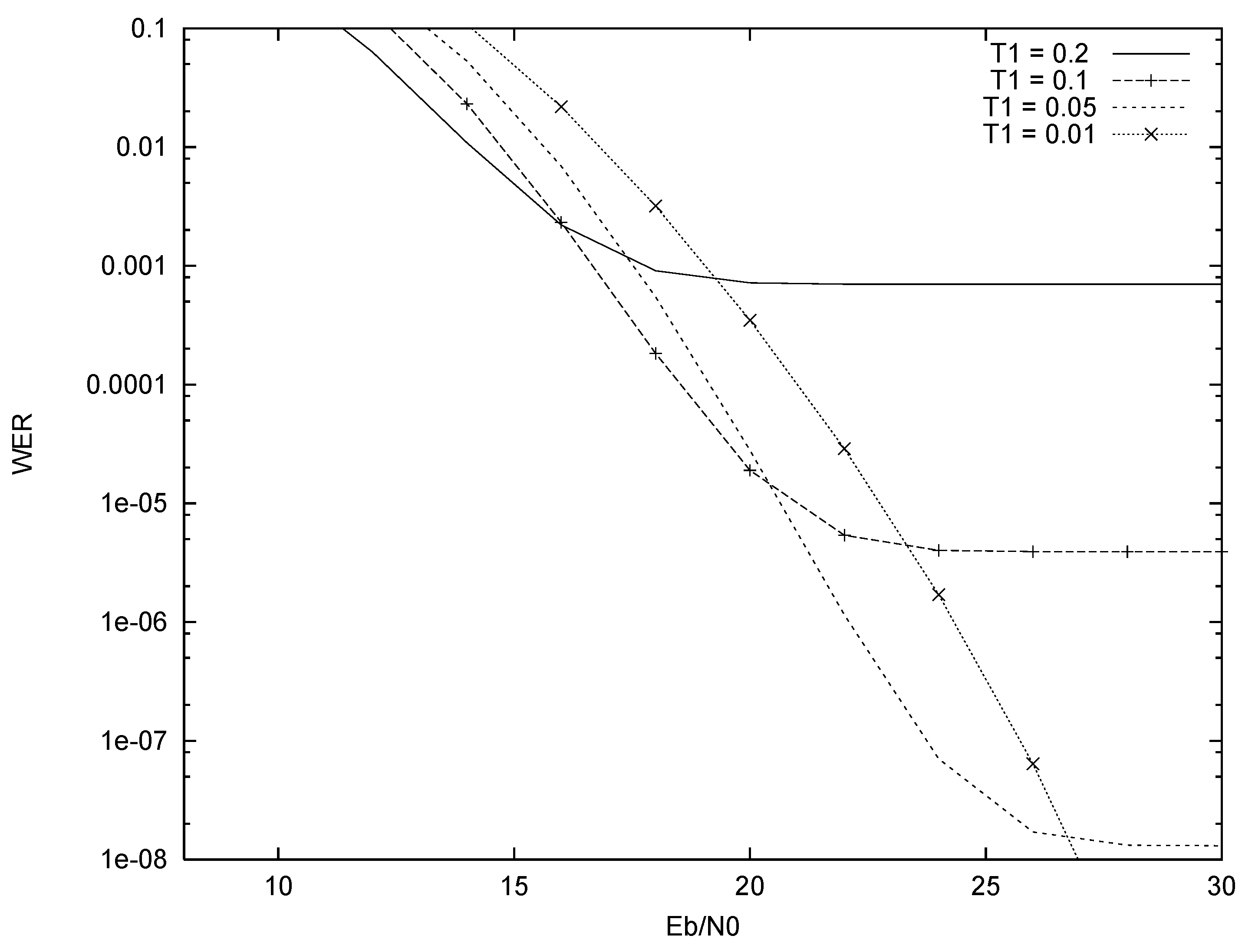
4.2. Erasure Generation by Comparing Fading Amplitudes with a Threshold

In this subsection, we erase code symbols that have smaller fading amplitudes than the threshold $T_1$.

The average energy per codeword is

$$E_{cw}=\sum _{e=0}^{N-K}{E}_s(N-e)P_E\left(e\right)$$

(24)

where $P_E\left(e\right)$ is (13). See that we do not transmit any power for the codeword that has more than $N-K$ erasures. The symbol error probability for the unerased symbol is

$$\begin{array}{ccc}\hfill P_{s|\overline{E}}& =& {\int }_{T_1}^{\infty }\alpha ·Q\left(\sqrt{\beta x}\right)·e^{-(x-T_1)}dx\hfill \\ & =& \alpha e^{T_1}\left\{e^{-T_1}Q\left(\sqrt{\beta T_1}\right)-\sqrt{\frac{\beta }{\beta +2}}·Q\left(\sqrt{(\beta +2)T_1}\right)\right\}\hfill \end{array}$$

(25)

where $\alpha =4$ and $\beta =\frac{3}{M-1}·E_s/N_0=\frac{3}{M-1}·\frac{K}{N}{log}_{2}M·E_b/N_0$. The WER is written as (18).

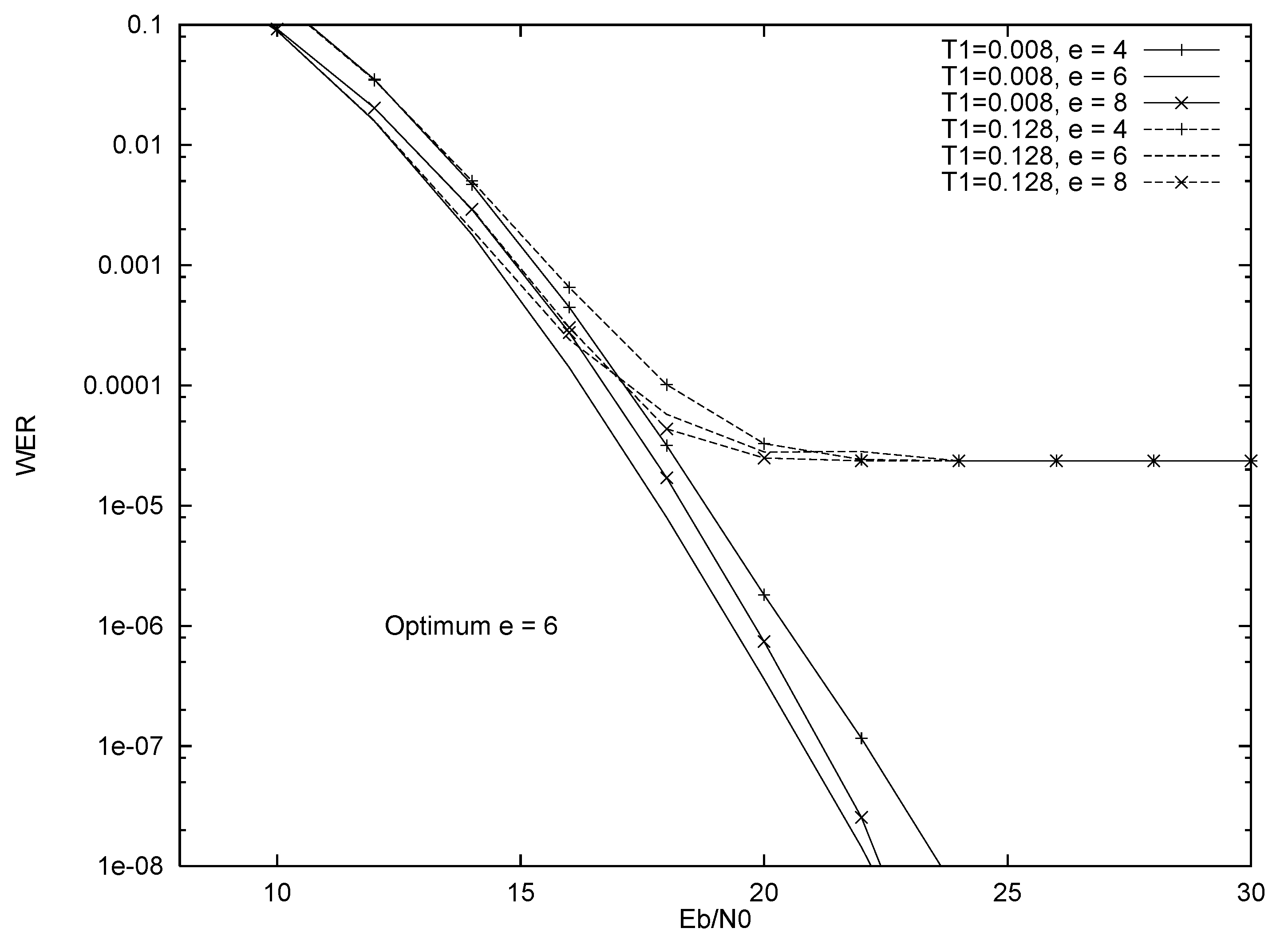
4.3. Erasure Generation by Ordering and Comparing Fading Amplitudes with a Threshold

In this subsection, we considered the erasure generation scheme that includes both ordering and comparing fading amplitudes with a threshold as special cases. At least e symbols are erased in a codeword, and the fading amplitudes of all unerased symbols are larger than the threshold $T_1$. For this system, we found the WER by computer simulation. It is hard to derive the GER since the received powers of unerased symbols are dependent after ordering.

5. Results

Throughout the numerical results, we used 16-QAM modulation for a code symbol and 16-ary (16,8) RS codes. Thus, the DFT and IFFT size was 256. As the performance measure, the WER was used.

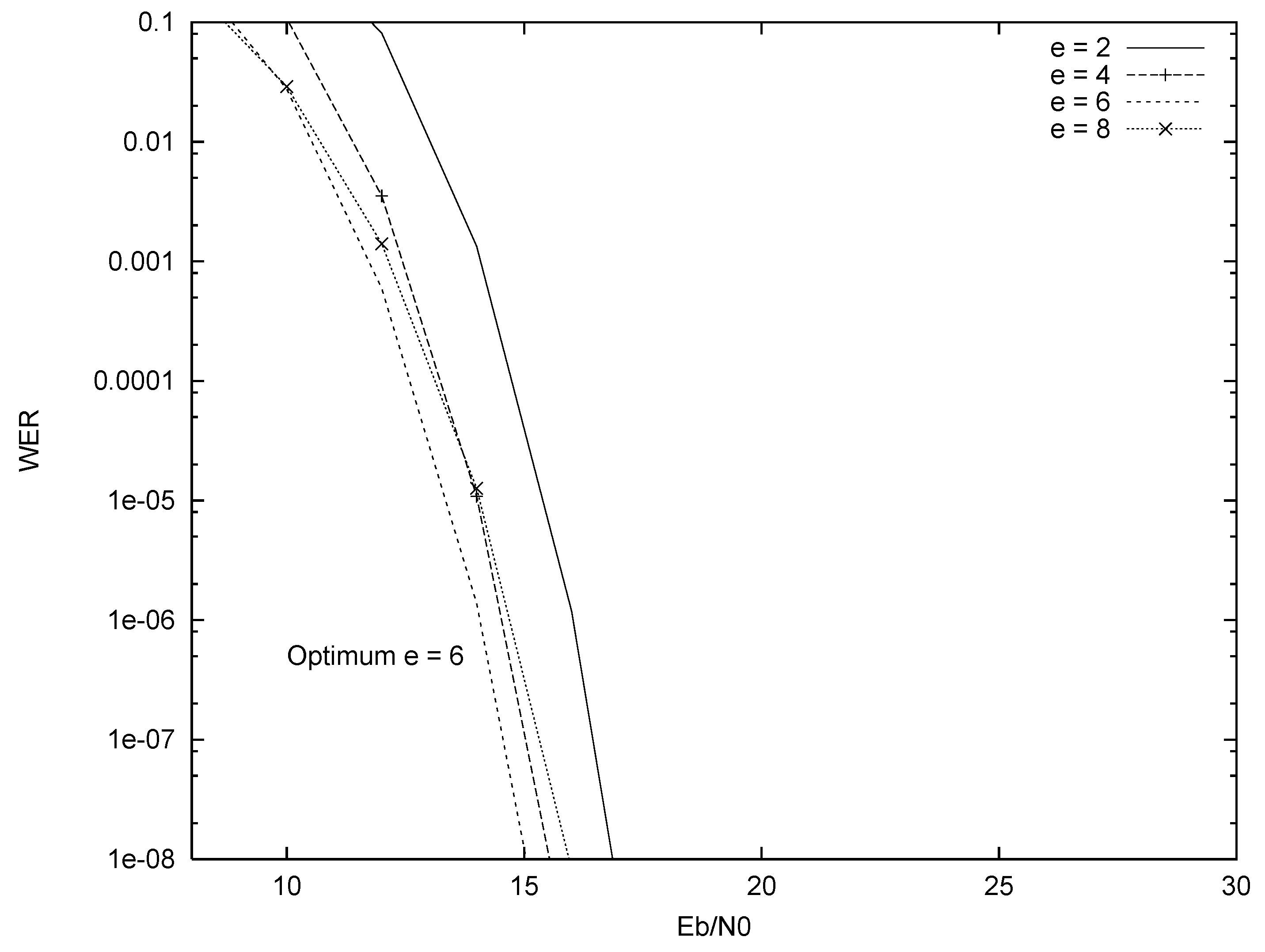
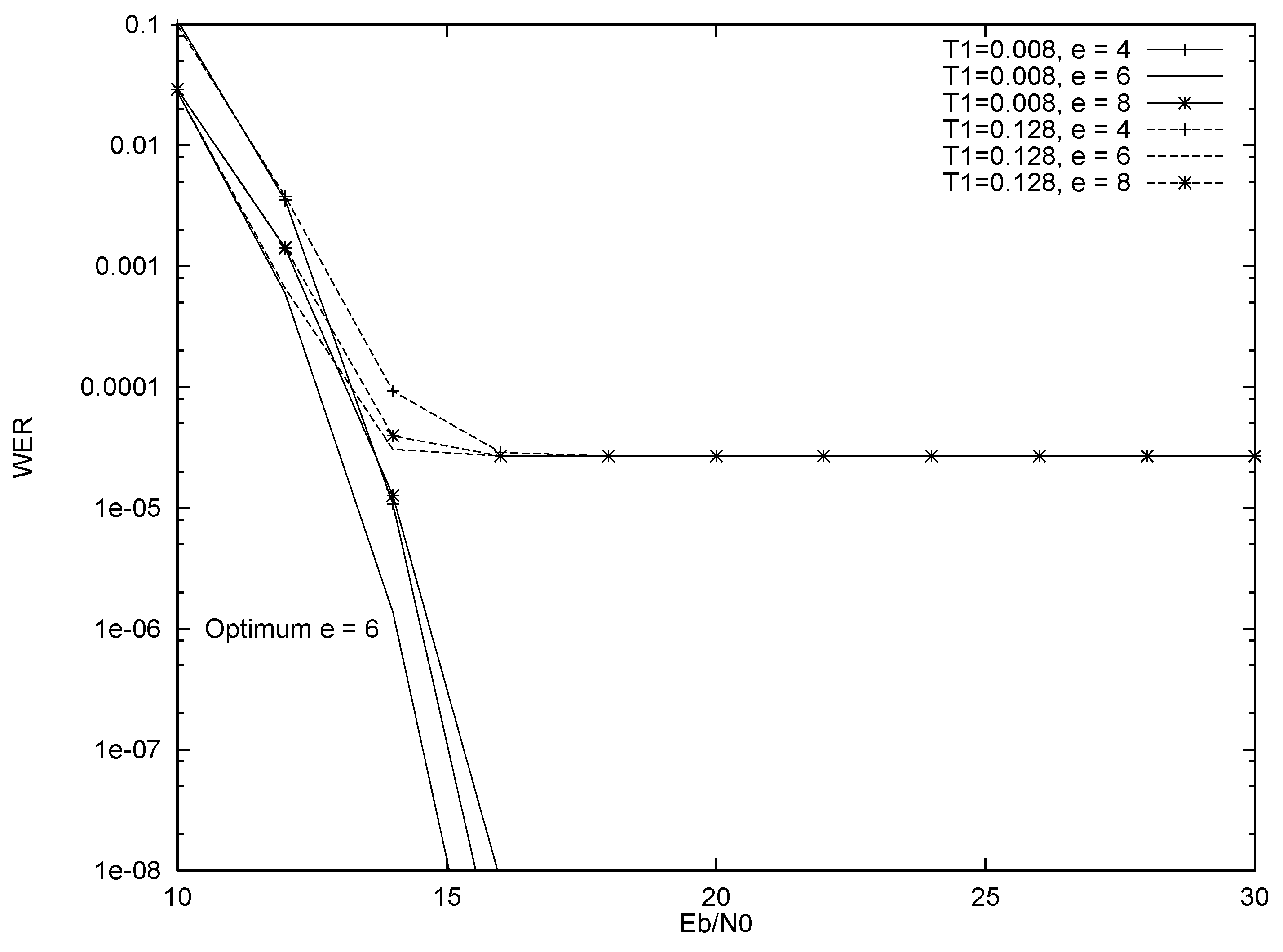
5.1. Truncated Channel Inversion

In Figure 2, Figure 3 and Figure 4, we considered the systems with truncated channel inversion.

In Figure 2, we show the WER vs. $E_b/N_0$ for the system with ordering as the erasure generation scheme. We found that that there is an optimum number of erased symbols in a codeword and that is $e=6$ when the (16,8) RS code is used.

In Figure 3, we show the WER vs. $E_b/N_0$ for the system with comparing a threshold as the erasure generation scheme. For small $E_b/N_0$, the system with the large threshold $T_1$ is better because the gain by erasing unreliable symbols is larger than the loss by erasing reliable symbols. For large $E_b/N_0$, the system with the small threshold $T_1$ is better because the loss by erasing reliable symbols is large. The optimum threshold is a decreasing function of $E_b/N_0$ since we do not have to erase symbols when we have enough power.

In Figure 4, we show the WER vs. $E_b/N_0$ for the system with ordering and comparing a threshold as the erasure generation scheme. For $T_1=0.008$, we found that the plot is the same as Figure 2. For $T_1=0.128$, we can see the error floor at large $E_b/N_0$. We can see that the combining of ordering and comparing a threshold has no power gain over the ordering only.

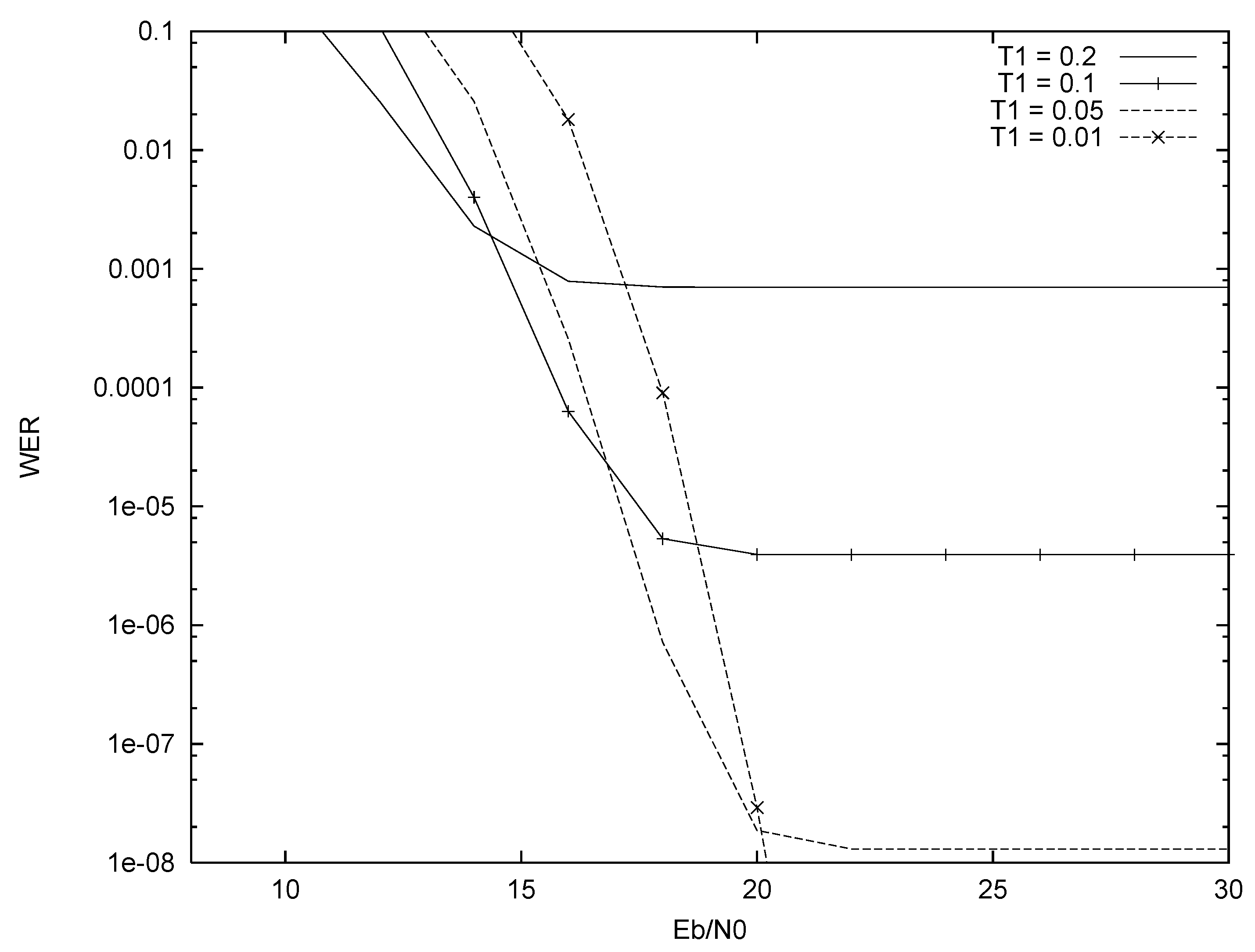
5.2. Truncation Only

In Figure 5, Figure 6 and Figure 7, we considered the systems with only truncation.

In Figure 5, we show the WER vs. $E_b/N_0$ by simulation for the system with ordering as the erasure generation scheme. We found that that there is an optimum number of erased symbols in a codeword, and that is $e=6$, as shown in Figure 2. We also show that the WER by mathematical analysis is larger than the simulation results since the WER by mathematical analysis was obtained by assuming the independence of the unerased symbols and the dependency of the unerased symbols make burst errors.

In Figure 6, we show the WER vs. $E_b/N_0$ for the system with comparing a threshold as the erasure generation scheme. Similar results were found as in Figure 3.

In Figure 7, we show the WER vs. $E_b/N_0$ for the system with ordering and comparing a threshold as the erasure generation scheme. For $T_1=0.008$, we found that the plot is the same as Figure 5. For $T_1=0.128$, we can see the error floor by the large threshold $T_1$. We can see that the combining of ordering and comparing a threshold has no power gain over the ordering only, as in Figure 4.

5.3. Performance Comparison of Systems

In Figure 8, we plot the WERs of not only power-controlled systems, but also systems with no power control. The WER comparison was based on computer simulations. All the formulae are exact except the cases with ordering. Since the ordering makes the unerased symbol powers dependent, the mathematically derived WER for the system with ordering is an upper bound. “Error-only decoding” is the system that has no fading information both at the transmitter and receiver. “Order” and “Threshold” are systems that have fading information only at the receiver. In “Error-only decoding”, “Order”, and “Threshold”, we cannot use power control since the transmitter does not have the fading information. “Order” erases e symbols in a codeword. “Threshold” erases the symbol that has a fading amplitude smaller than $T_1$. All parameters, which are $T_1$ or e in each system, were optimized as a function of $E_b/N_0$. It is shown that truncated channel inversion with ordering gave the same and lowest WER as truncated channel inversion with ordering and comparing a threshold. Truncation with ordering gave the same WER as truncation with ordering and comparing a threshold. Thus, we can see that combining ordering and comparing a threshold had no gain over ordering only. For WER = ${10}^{-3}$, truncated channel inversion with ordering provided a 4.9 dB gain over ordering and a 7.7 dB gain over error-only decoding. For WER = ${10}^{-6}$, truncated channel inversion with ordering provided a 7.4 dB gain over ordering and a 12.1 dB gain over error-only decoding. For large $E_b/N_0$, fading compensation techniques provided a larger gain than for small $E_b/N_0$, since fading, rather than Gaussian noise, was the major reason for the errors for large $E_b/N_0$. We see that ordering is a better erasure generation scheme than comparing a threshold.

In

Table 1. Required $E_b/N_0$ for WER ${10}^{-3}$ and ${10}^{-6}$.

	WER = ${10}^{-3}$	WER = ${10}^{-6}$
Error-only decoding [1]	20	26
Threshold [6]	17	22
Truncated, Threshold [9]	15.8	21.8
Order [5]	16	21
Truncated, Order	14.5	19.5
Truncated, Order, and Threshold	14.5	19.5
Channel inversion, Threshold	14.3	17.5
Channel inversion, Order	12	14
Channel inversion, Order, and Threshold	12	14

, required $E_b/N_0$ are shown when the WER’s are ${10}^{-3}$ and ${10}^{-6}$. It was shown that channel inversion with ordering provides the lowest WER. In

Table 2. $E_b/N_0$ gain for different coded OFDM schemes [11].

Coded OFDM Scheme	Gain over Uncoded OFDM Scheme
Convolutional-coded OFDM	2 dB
RS-coded OFDM	3.5 dB
RS-coded OFDM with truncated channel inversion	7 dB

, $E_b/N_0$ gains are shown for different coded OFDM schemes. It is shown that coded scheme with channel inversion power control provides the best performance.

6. Conclusions

Power control of RS-coded OFDM systems in Rayleigh fading channels were considered. The transmitter cuts off its power for for the symbols to be erased, and error-and-erasure correction was performed at the receiver. We found that the erasure generation by ordering fading amplitudes was better than the erasure generation by comparing fading amplitudes with a threshold, also for the systems with no power control. It was shown that the combining of ordering and comparing a threshold had no gain over ordering only. We found that truncated channel inversion in combination with the erasure generation scheme by ordering fading amplitudes provided the lowest codeword error rate (WER) among the considered systems. Our analysis can be generalized to other modulation schemes that have the Q-function as the symbol error rate formula.