Probabilistic Forecasting of Residential Energy Consumption Based on SWT-QRTCN-ADSC-NLSTM Model
Abstract
1. Introduction
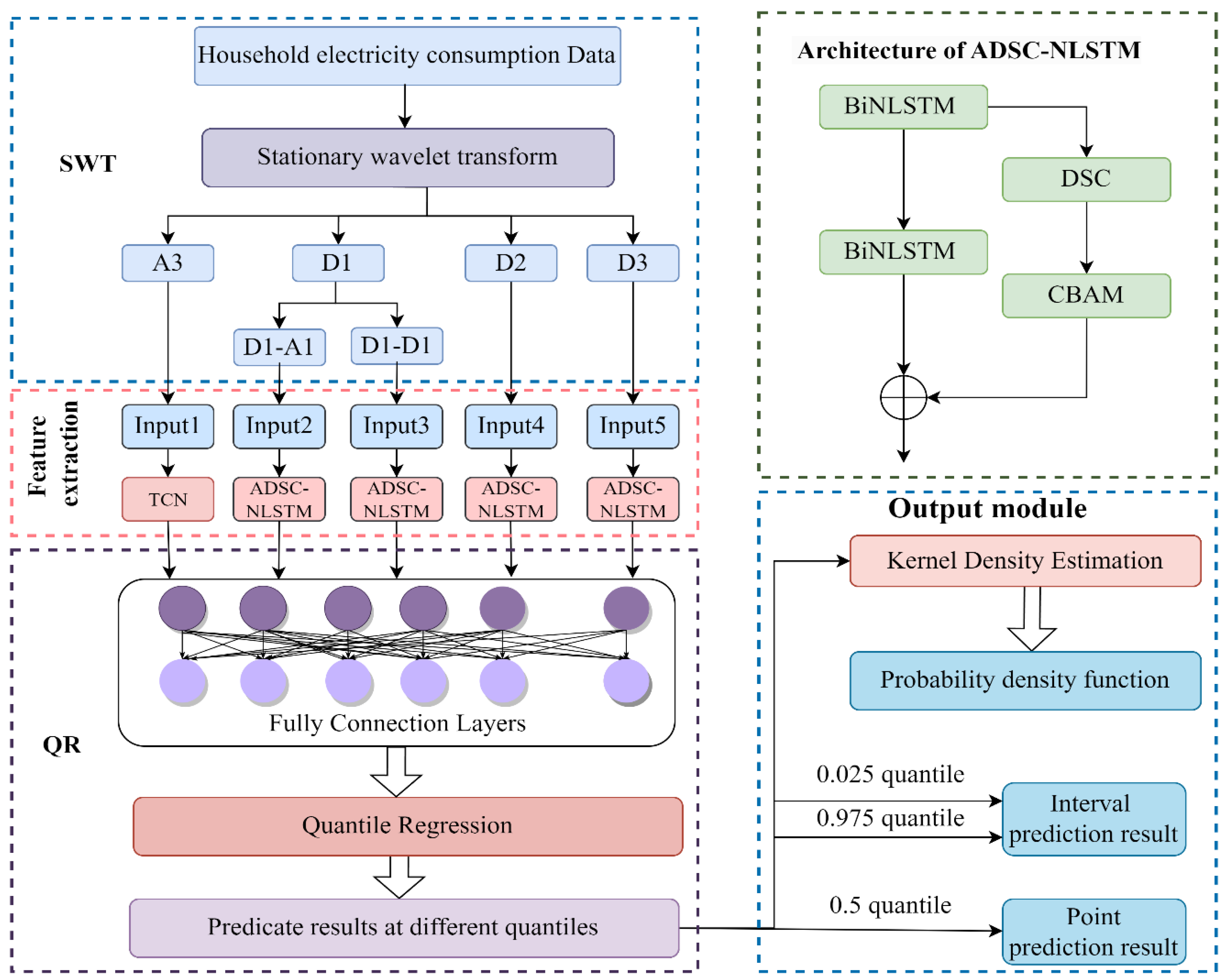
- The original data is decomposed by SWT to generate multiple sub-signals, and its high-frequency signal is decomposed twice and trained using TCN and ADSC-NLSTM for both low and high-frequency signals. This combination helps to solve the model adaptation problem for electricity consumption prediction.
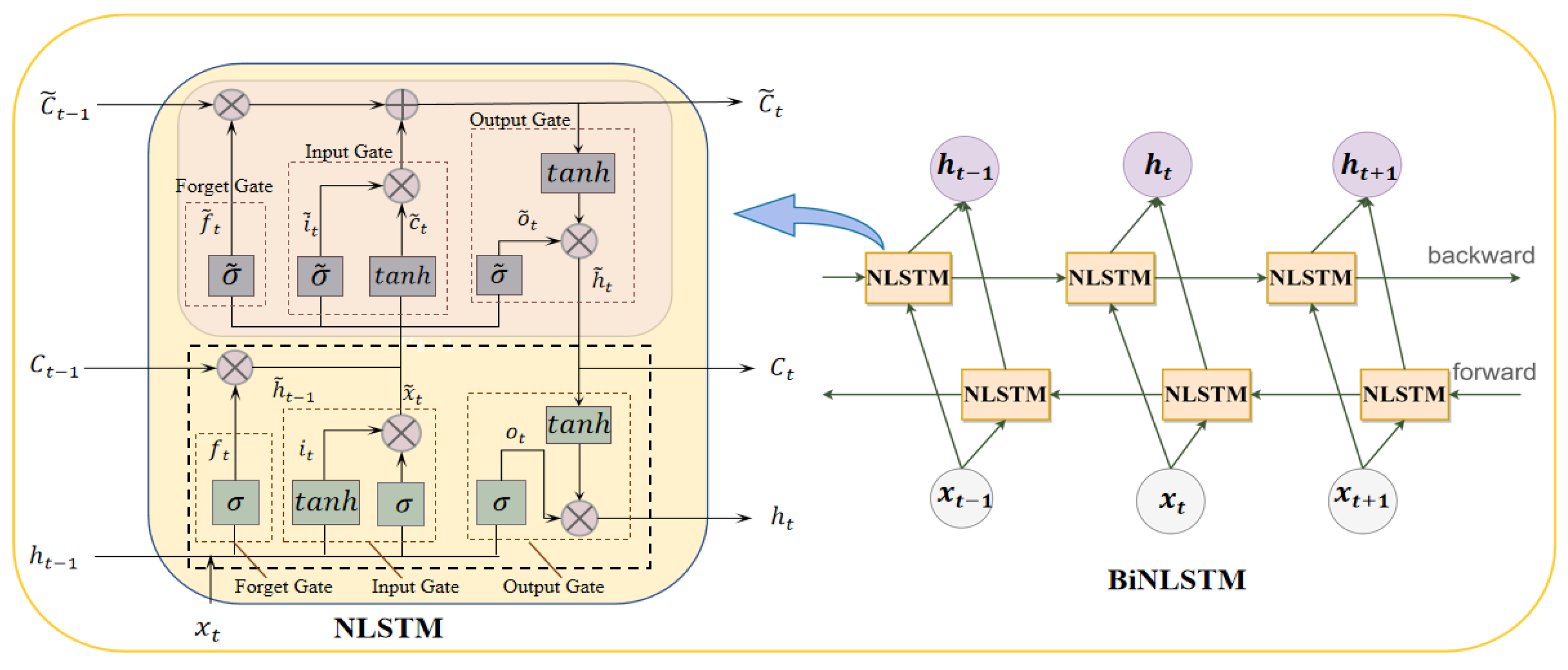
- The proposed ADSC-NLSTM network can make predictions in space and time. DSC based on the attention mechanism can preserve important information, prevent information loss and enhance feature extraction performance. The nested structure of the BiNLSTM is used to perform deep feature extraction effectively, and there are more recurrent units to obtain the dependencies of features at each time point, allowing the network to learn more adequately.
- This model is compared with existing frontier technologies, including individual models and combined models, and the experimental results show that this model achieves efficient energy consumption point prediction and probability prediction.
2. Related Works
3. Methodology
3.1. The Stationary Wavelet Transform
3.2. Deep Learning Module
3.2.1. Bidirectional Nested Long Short-Term Memory
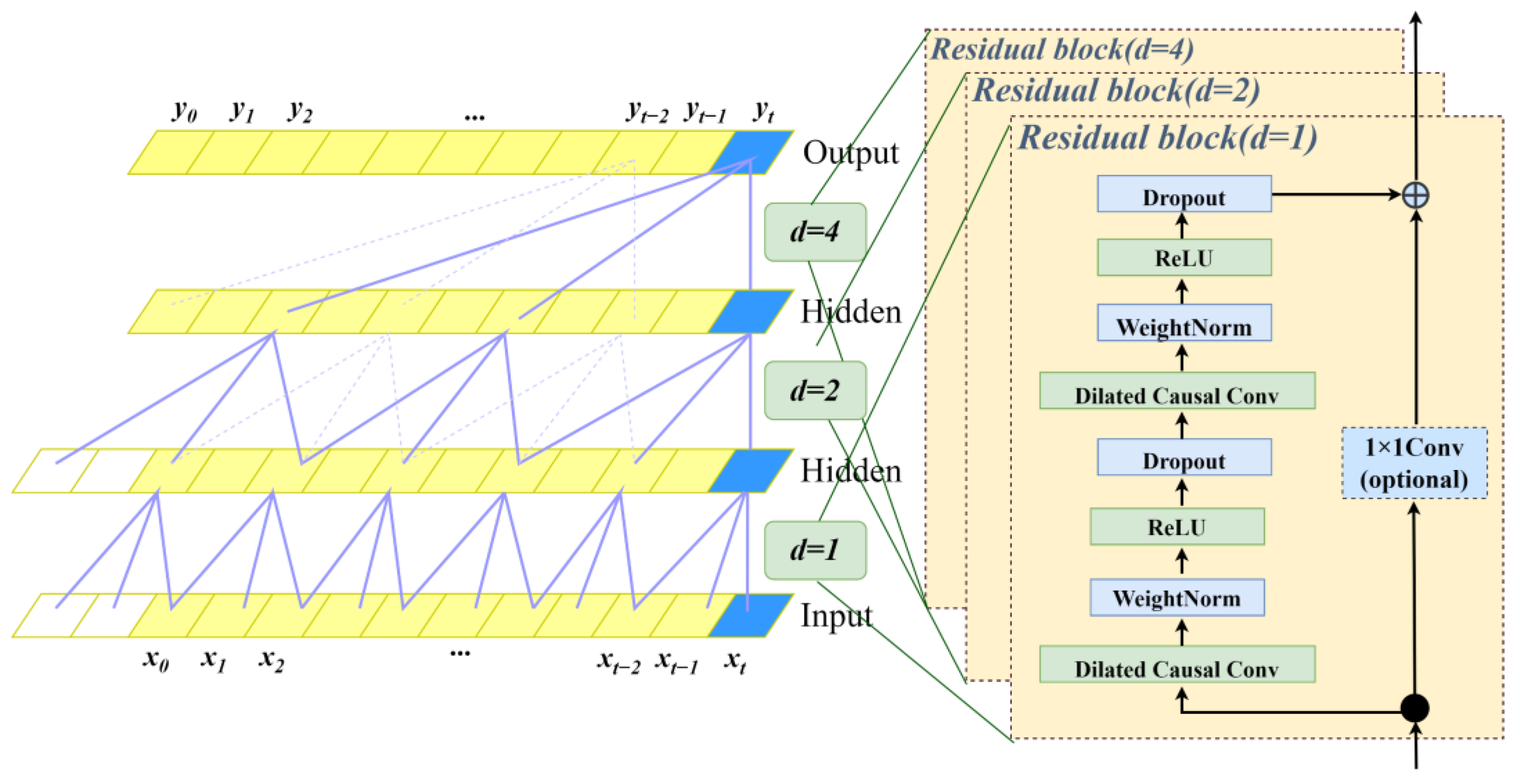
3.2.2. Temporal Convolutional Network
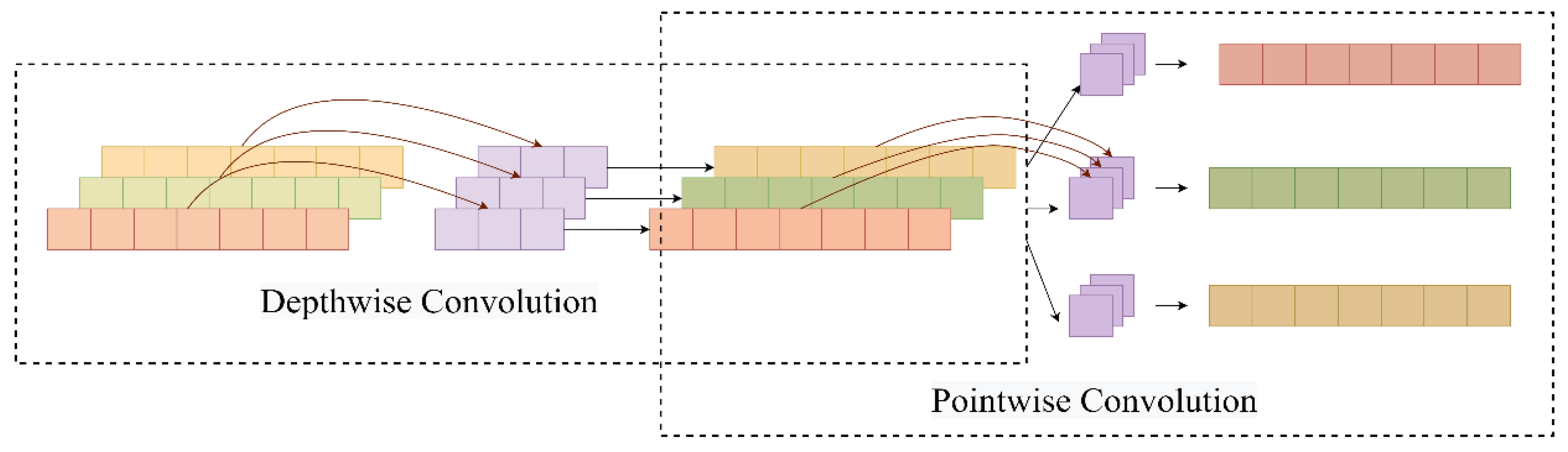
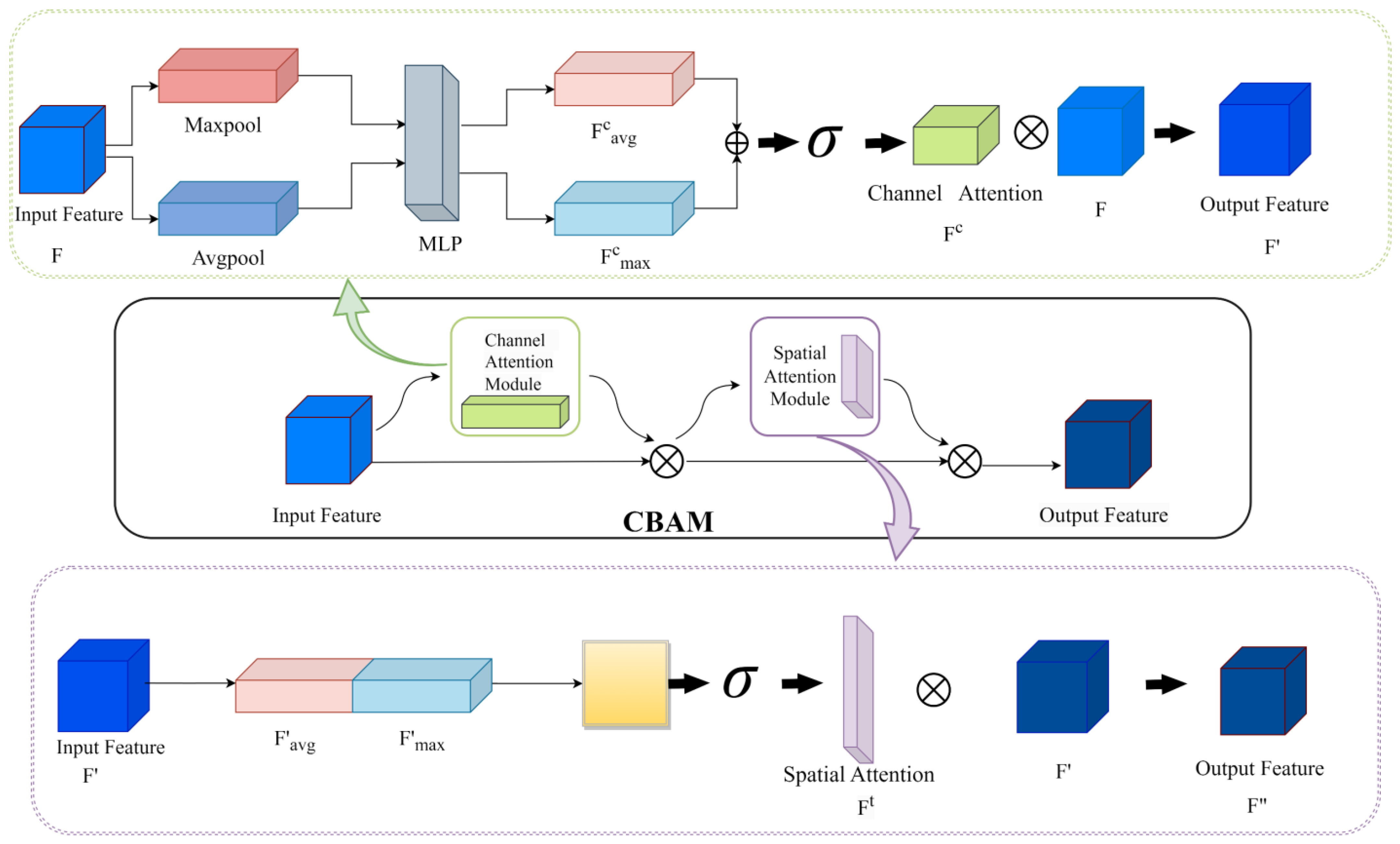
3.2.3. Depthwise Separable Convolution and Attention Mechanisms
3.3. Quantile Regression
3.4. Kernel Density Estimation
3.5. Combination Model of Electricity Consumption Probability Prediction
4. Experimental Process and Results
4.1. Dataset Description
4.2. Evaluation Metrics
4.2.1. Evaluation Metrics of Point Prediction
4.2.2. Evaluation Metrics of Interval Prediction
4.2.3. Evaluation Metrics of Probability Prediction
4.3. Prediction Results Analysis
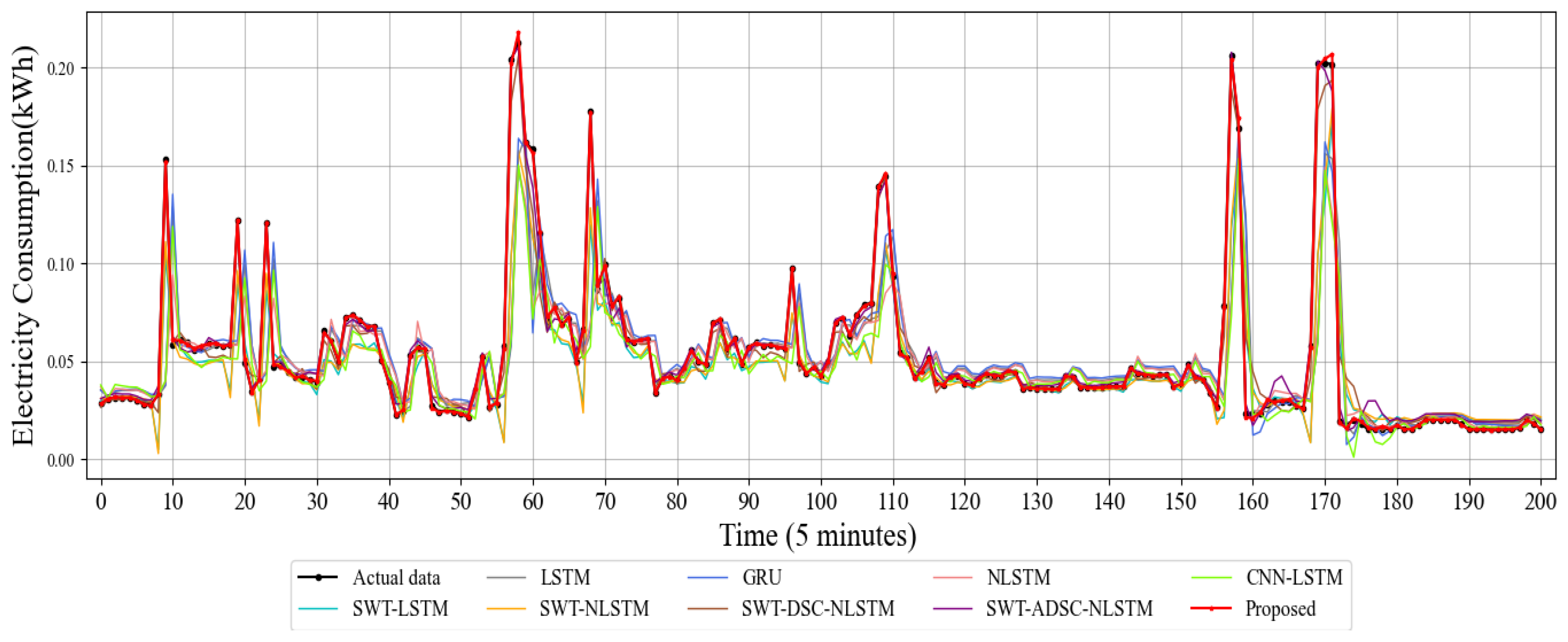
4.3.1. Point Prediction Results Analysis
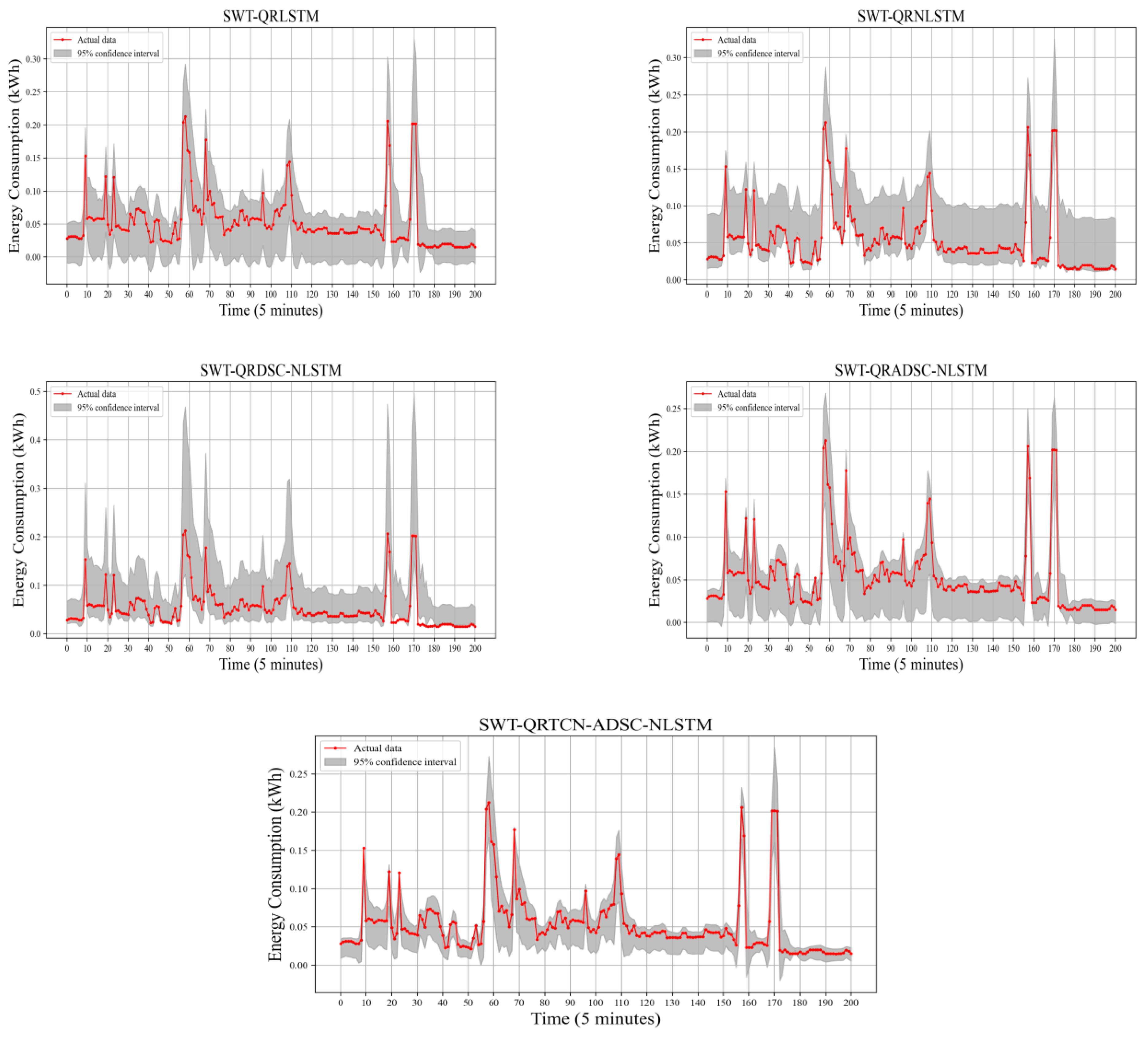
4.3.2. Interval Prediction Results Analysis
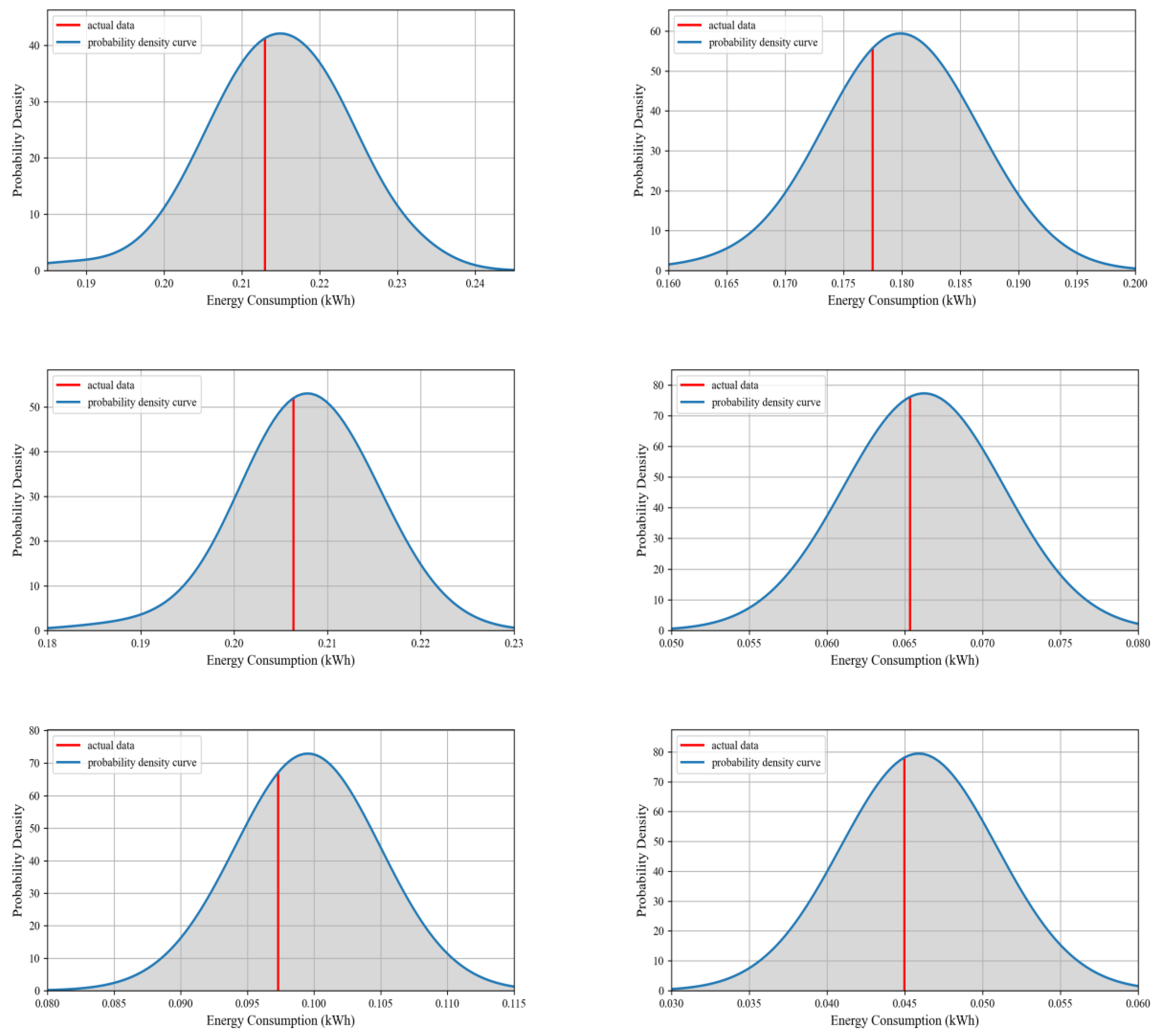
4.3.3. Probability Prediction Results Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, Y.; Liu, Z.; Zhang, C.; Ren, J.; Zhang, Y.; Shen, X. Blockchain-based Trustworthy Energy Dispatching Approach for High Renewable Energy Penetrated Power System. IEEE Internet Things J. 2022, 9, 10036–10047. [Google Scholar] [CrossRef]
- Xu, Y.; Xiao, S.; Wang, H.; Zhang, C.; Ni, Z.; Zhao, W.; Wang, G. Redactable Blockchain-based Secure and Accountable Data Management. IEEE Trans. Netw. Serv. Manag. 2023; Early Access. [Google Scholar]
- Alahakoon, D.; Yu, X. Smart electricity meter data intelligence for future energy systems: A survey. IEEE Trans. Ind. Inform. 2015, 12, 425–436. [Google Scholar] [CrossRef]
- Marzband, M.; Ghazimirsaeid, S.S.; Uppal, H.; Fernando, T. A real-time evaluation of energy management systems for smart hybrid home Microgrids. Electr. Power Syst. Res. 2017, 143, 624–633. [Google Scholar] [CrossRef]
- El-Baz, W.; Tzscheutschler, P. Short-term smart learning electrical load prediction algorithm for home energy management systems. Appl. Energy 2015, 147, 10–19. [Google Scholar] [CrossRef]
- Weber, C.; Perrels, A. Modelling lifestyle effects on energy demand and related emissions. Energy Policy 2000, 28, 549–566. [Google Scholar] [CrossRef]
- Ziekow, H.; Goebel, C.; Strüker, J.; Jacobsen, H.-A. The potential of smart home sensors in forecasting household electricity demand. In Proceedings of the 2013 IEEE International Conference on Smart Grid Communications (SmartGridComm), Vancouver, BC, Canada, 21–24 October 2013; pp. 229–234. [Google Scholar]
- Kaneko, N.; Fujimoto, Y.; Kabe, S.; Hayashida, M.; Hayashi, Y. Sparse modeling approach for identifying the dominant factors affecting situation-dependent hourly electricity demand. Appl. Energy 2020, 265, 114752. [Google Scholar] [CrossRef]
- Ye, Z.; O’Neill, Z.; Hu, F. Hardware-based emulator with deep learning model for building energy control and prediction based on occupancy sensors’ data. Information 2021, 12, 499. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Mansour-Saatloo, A.; Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Asadi, S. Introduction and literature review of the application of machine learning/deep learning to load forecasting in power system. In Application of Machine Learning and Deep Learning Methods to Power System Problems; Springer: Cham, Switzerland, 2021; pp. 119–135. [Google Scholar]
- Ervural, B.C.; Beyca, O.F.; Zaim, S. Model estimation of ARMA using genetic algorithms: A case study of forecasting natural gas consumption. Procedia-Soc. Behav. Sci. 2016, 235, 537–545. [Google Scholar] [CrossRef]
- Ediger, V.Ş.; Akar, S. ARIMA forecasting of primary energy demand by fuel in Turkey. Energy Policy 2007, 35, 1701–1708. [Google Scholar] [CrossRef]
- Hambali, A.O.J.; Akinyemi, M.; JYusuf, N. Electric power load forecast using decision tree algorithms. Comput. Inf. Syst. Dev. Inform. Allied Res. J. 2016, 7, 29–42. [Google Scholar]
- Vinagre, E.; Pinto, T.; Ramos, S.; Vale, Z.; Corchado, J.M. Electrical energy consumption forecast using support vector machines. In Proceedings of the 2016 27th International Workshop on Database and Expert Systems Applications (DEXA), Porto, Portugal, 5–8 September 2016; pp. 171–175. [Google Scholar]
- Wang, Z.; Wang, Y.; Zeng, R.; Srinivasan, R.S.; Ahrentzen, S. Random Forest based hourly building energy prediction. Energy Build. 2018, 171, 11–25. [Google Scholar] [CrossRef]
- Wei, R.R.; Wei, Z.Z.; Rong, R.; Wang, Y.; Jiang, J.D.; Yu, H. Short term load forecasting based on PCA and LS-SVM. Adv. Mater. Res. 2013, 756–759, 4193–4197. [Google Scholar] [CrossRef]
- Pinto, T.; Praça, I.; Vale, Z.; Silva, J. Ensemble learning for electricity consumption forecasting in office buildings. Neurocomputing 2021, 423, 747–755. [Google Scholar] [CrossRef]
- Sun, G.; Jiang, C.; Wang, X.; Yang, X. Short-term building load forecast based on a data-mining feature selection and LSTM-RNN method. IEEJ Trans. Electr. Electron. Eng. 2020, 15, 1002–1010. [Google Scholar] [CrossRef]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Hewage, P.; Behera, A.; Trovati, M.; Pereira, E.; Ghahremani, M.; Palmieri, F.; Liu, Y. Temporal convolutional neural (TCN) network for an effective weather forecasting using time-series data from the local weather station. Soft Comput. 2020, 24, 16453–16482. [Google Scholar] [CrossRef]
- Sun, M. Chinese text classification based on GRU-Attention. Mod. Inf. Technol. 2019, 3, 10–12. [Google Scholar]
- Yan, K.; Chen, X.; Zhou, X.; Yan, Z.; Ma, J. Physical Model Informed Fault Detection and Diagnosis of Air Handling Units Based on Transformer Generative Adversarial Network. IEEE Trans. Ind. Inform. 2022, 19, 2192–2199. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Gao, X.; Li, X.; Zhao, B.; Ji, W.; Jing, X.; He, Y. Short-term electricity load forecasting model based on EMD-GRU with feature selection. Energies 2019, 12, 1140. [Google Scholar] [CrossRef]
- Yan, K.; Wang, X.; Du, Y.; Jin, N.; Huang, H.; Zhou, H. Multi-step short-term power consumption forecasting with a hybrid deep learning strategy. Energies 2018, 11, 3089. [Google Scholar] [CrossRef]
- Li, W.; Quan, C.; Wang, X.; Zhang, S. Short-Term Power Load Forecasting Based on a Combination of VMD and ELM. Pol. J. Environ. Stud. 2018, 27, 2143–2154. [Google Scholar] [CrossRef]
- Cai, C.; Li, Y.; Su, Z.; Zhu, T.; He, Y. Short-Term Electrical Load Forecasting Based on VMD and GRU-TCN Hybrid Network. Appl. Sci. 2022, 12, 6647. [Google Scholar] [CrossRef]
- Shao, X.; Pu, C.; Zhang, Y.; Kim, C.S. Domain fusion CNN-LSTM for short-term power consumption forecasting. IEEE Access 2020, 8, 188352–188362. [Google Scholar] [CrossRef]
- Zeng, Y.; Chen, J.; Jin, N.; Jin, X.; Du, Y. Air quality forecasting with hybrid LSTM and extended stationary wavelet transform. Build. Environ. 2022, 213, 108822. [Google Scholar] [CrossRef]
- Liang, Y.; Lin, Y.; Lu, Q. Forecasting gold price using a novel hybrid model with ICEEMDAN and LSTM-CNN-CBAM. Expert Syst. Appl. 2022, 206, 117847. [Google Scholar] [CrossRef]
- Afrasiabi, M.; Mohammadi, M.; Rastegar, M.; Stankovic, L.; Afrasiabi, S.; Khazaei, M. Deep-based conditional probability density function forecasting of residential loads. IEEE Trans. Smart Grid 2020, 11, 3646–3657. [Google Scholar] [CrossRef]
- Wang, Y.; Gan, D.; Sun, M.; Zhang, N.; Lu, Z.; Kang, C. Probabilistic individual load forecasting using pinball loss guided LSTM. Appl. Energy 2019, 235, 10–20. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, H.; Liu, Y.; Yao, L.; Yu, X.; Lu, J.; Jiang, Z.; Feng, Z. Wind speed forecasting based on quantile regression minimal gated memory network and kernel density estimation. Energy Convers. Manag. 2019, 196, 1395–1409. [Google Scholar] [CrossRef]
- Nason, G.P.; Silverman, B.W. The stationary wavelet transform and some statistical applications. In Wavelets and Statistics; Springer: New York, NY, USA, 1995; pp. 281–299. [Google Scholar]
- Moniz, J.R.A.; Krueger, D. Nested LSTMs. In Proceedings of the Ninth Asian Conference on Machine Learning, PMLR, Seoul, Republic of Korea, 31 January 2018; pp. 530–544. [Google Scholar]
- Mishra, K.; Basu, S.; Maulik, U. DaNSe: A dilated causal convolutional network based model for load forecasting. In Pattern Recognition and Machine Intelligence, Proceedings of the 8th International Conference, PReMI 2019, Tezpur, India, 17–20 December 2019; Springer International Publishing: Cham, Switzerland, 2019; pp. 234–241. [Google Scholar]
- Guo, M.H.; Xu, T.X.; Liu, J.J.; Liu, Z.N.; Jiang, P.T.; Mu, T.J.; Zhang, S.H.; Martin, R.R.; Cheng, M.M.; Hu, S.M. Attention mechanisms in computer vision: A survey. Comput. Vis. Media 2022, 8, 331–368. [Google Scholar] [CrossRef]
- Koenker, R.; Hallock, K.F. Quantile regression. J. Econ. Perspect. 2001, 15, 143–156. [Google Scholar] [CrossRef]
- Węglarczyk, S. Kernel density estimation and its application. ITM Web Conf. 2018, 23, 00037. [Google Scholar] [CrossRef]
- Xu, X.; Yan, Z.; Xu, S. Estimating wind speed probability distribution by diffusion-based kernel density method. Electr. Power Syst. Res. 2015, 121, 28–37. [Google Scholar] [CrossRef]
- Kelly, J.; Knottenbelt, W. The UK-DALE dataset, domestic appliance-level electricity demand and whole-house demand from five UK homes. Sci. Data 2015, 2, 150007. [Google Scholar] [CrossRef] [PubMed]



| MAE | RMSE | MAPE (100%) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hse1 | Hse2 | Hse3 | Hse4 | Hse5 | Hse1 | Hse2 | Hse3 | Hse4 | Hse5 | Hse1 | Hse2 | Hse3 | Hse4 | Hse5 | |
| QRLSTM | 0.0103 | 0.0101 | 0.0127 | 0.0098 | 0.0081 | 0.0223 | 0.0236 | 0.0328 | 0.0211 | 0.0245 | 22.31 | 24.71 | 29.32 | 28.12 | 9.21 |
| QRGRU | 0.0108 | 0.0099 | 0.0119 | 0.0098 | 0.0085 | 0.0226 | 0.0242 | 0.0320 | 0.0214 | 0.0235 | 23.44 | 21.38 | 23.77 | 27.62 | 10.39 |
| QRNLSTM | 0.0098 | 0.0106 | 0.0137 | 0.0091 | 0.0103 | 0.0218 | 0.0231 | 0.0315 | 0.0208 | 0.0232 | 20.03 | 27.64 | 34.29 | 22.03 | 15.51 |
| QRCNN-LSTM | 0.0099 | 0.0093 | 0.0130 | 0.0098 | 0.0077 | 0.0227 | 0.0238 | 0.0317 | 0.0217 | 0.0234 | 18.55 | 19.71 | 29.14 | 25.67 | 8.65 |
| SWT-QRLSTM | 0.0073 | 0.0041 | 0.0061 | 0.0022 | 0.0035 | 0.0144 | 0.0059 | 0.0108 | 0.0028 | 0.0040 | 16.26 | 12.20 | 13.54 | 11.31 | 6.99 |
| SWT-QRNLSTM | 0.0087 | 0.0037 | 0.0033 | 0.0026 | 0.0042 | 0.0154 | 0.0054 | 0.0042 | 0.0029 | 0.0070 | 17.92 | 11.47 | 14.71 | 13.43 | 6.35 |
| SWT-QRDSC-NLSTM | 0.0018 | 0.0017 | 0.0018 | 0.0026 | 0.0026 | 0.0035 | 0.002 | 0.0020 | 0.0029 | 0.0031 | 4.57 | 6.15 | 8.95 | 9.97 | 4.48 |
| SWT-QRADSC-NLSTM | 0.0011 | 0.0009 | 0.0011 | 0.0036 | 0.0021 | 0.0027 | 0.0023 | 0.0016 | 0.0077 | 0.0058 | 2.99 | 3.29 | 4.13 | 9.57 | 2.09 |
| Proposed | 0.0003 | 0.0003 | 0.0009 | 0.0013 | 0.0007 | 0.0006 | 0.0006 | 0.0014 | 0.0025 | 0.0012 | 0.91 | 1.02 | 2.96 | 3.54 | 1.05 |
| PICP | PIAW | CRPS | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hse1 | Hse2 | Hse3 | Hse4 | Hse5 | Hse1 | Hse2 | Hse3 | Hse4 | Hse5 | Hse1 | Hse2 | Hse3 | Hse4 | Hse5 | |
| QRLSTM | 0.964 | 0.965 | 0.937 | 0.859 | 0.901 | 2.142 | 1.844 | 1.589 | 1.563 | 1.341 | 0.0074 | 0.0303 | 0.0097 | 0.0071 | 0.0058 |
| QRGRU | 0.956 | 0.974 | 0.924 | 0.947 | 0.936 | 1.965 | 2.193 | 1.566 | 1.921 | 1.292 | 0.0075 | 0.0304 | 0.0098 | 0.0071 | 0.0059 |
| QRNLSTM | 0.946 | 0.929 | 0.951 | 0.952 | 0.945 | 2.051 | 1.802 | 1.268 | 1.652 | 1.139 | 0.0069 | 0.0281 | 0.0099 | 0.0076 | 0.0056 |
| QRCNN-LSTM | 0.961 | 0.974 | 0.936 | 0.946 | 0.950 | 2.058 | 1.751 | 1.705 | 2.544 | 1.157 | 0.0064 | 0.0243 | 0.0100 | 0.0070 | 0.0057 |
| SWT-QRLSTM | 0.945 | 0.952 | 0.945 | 0.964 | 0.956 | 1.812 | 1.481 | 1.310 | 1.417 | 0.91 | 0.0049 | 0.0145 | 0.0064 | 0.0032 | 0.0027 |
| SWT-QRNLSTM | 0.981 | 0.962 | 0.955 | 0.965 | 0.951 | 1.557 | 1.590 | 1.272 | 1.526 | 0.901 | 0.0056 | 0.0143 | 0.0056 | 0.0043 | 0.0024 |
| SWT-QRDSC-NLSTM | 0.977 | 0.965 | 0.945 | 0.955 | 9.572 | 1.113 | 1.213 | 1.210 | 1.311 | 0.838 | 0.0026 | 0.0009 | 0.0018 | 0.0010 | 0.0016 |
| SWT-QRADSC-NLSTM | 0.976 | 0.968 | 0.961 | 0.972 | 9.544 | 1.32 | 1.181 | 1.219 | 1.231 | 0.456 | 0.0028 | 0.0104 | 0.0012 | 0.0008 | 0.0011 |
| Proposed | 0.985 | 0.975 | 0.967 | 0.967 | 9.645 | 0.634 | 1.091 | 1.120 | 0.977 | 0.453 | 0.0004 | 0.0005 | 0.0009 | 0.0005 | 0.0004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, N.; Song, L.; Huang, G.J.; Yan, K. Probabilistic Forecasting of Residential Energy Consumption Based on SWT-QRTCN-ADSC-NLSTM Model. Information 2023, 14, 231. https://doi.org/10.3390/info14040231
Jin N, Song L, Huang GJ, Yan K. Probabilistic Forecasting of Residential Energy Consumption Based on SWT-QRTCN-ADSC-NLSTM Model. Information. 2023; 14(4):231. https://doi.org/10.3390/info14040231
Chicago/Turabian StyleJin, Ning, Linlin Song, Gabriel Jing Huang, and Ke Yan. 2023. "Probabilistic Forecasting of Residential Energy Consumption Based on SWT-QRTCN-ADSC-NLSTM Model" Information 14, no. 4: 231. https://doi.org/10.3390/info14040231
APA StyleJin, N., Song, L., Huang, G. J., & Yan, K. (2023). Probabilistic Forecasting of Residential Energy Consumption Based on SWT-QRTCN-ADSC-NLSTM Model. Information, 14(4), 231. https://doi.org/10.3390/info14040231








