Resource Allocation in Decentralized Vehicular Edge Computing Network
Abstract
1. Introduction
- We introduce MEC to offload the computational tasks of vehicles for alleviating their computational and energy burdens. The security risks are also considered in the computational offloading process by integrating the blockchain network into the MEC network.
- In the blockchain network, the POS mechanism is used instead of the POW mechanism, avoiding the problem that POW will generate huge energy consumption.
- We analyze interactions between participants through the Stackelberg game and prove theoretically to achieve a unique Nash equilibrium. Conflicts of interest of participants are resolved by rationally allocating resource and pricing in the network.
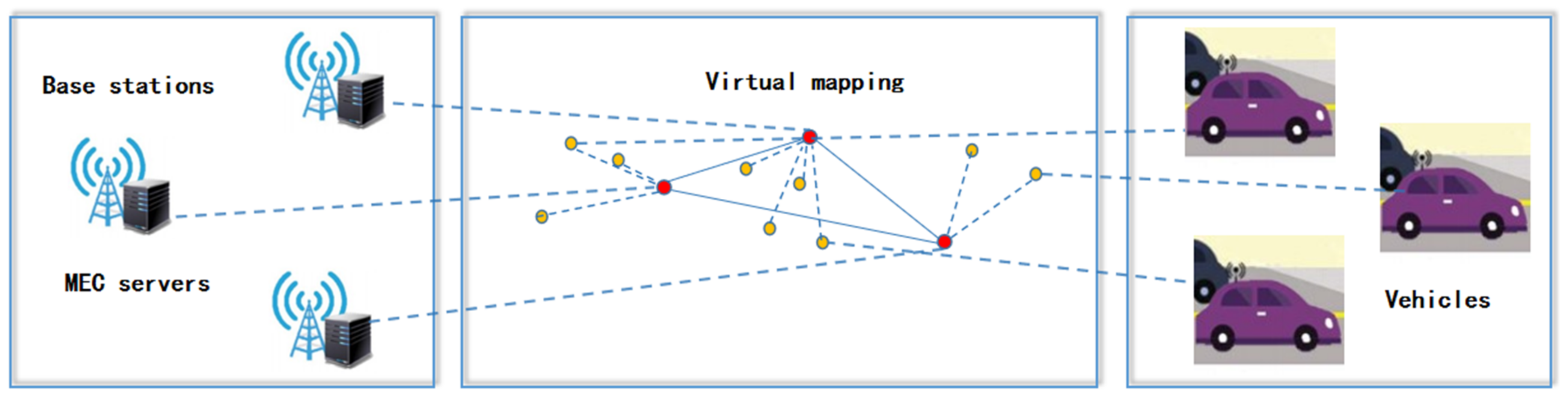
2. Blockchain-Based MEC Network Architecture
Participants in the Blockchain-Based MEC Network Architecture
3. System Model
3.1. Requesting Vehicle Model
3.1.1. Communication Model
3.1.2. Energy Consumption Model
3.1.3. Payment Model
3.1.4. Cost Function
3.2. MEC Server Model
3.2.1. Consensus Model
3.2.2. Block Reward Model
3.2.3. Energy Consumption Model
3.2.4. Utility Function
4. Stackelberg Game Analysis
4.1. Description of the Problem
4.1.1. Cost Minimization for Requesting Vehicles
4.1.2. Utility Maximization of MEC Servers
4.2. Formulation of Two-Stage Stackelberg Game
4.2.1. Vehicle-Level Game Analysis
4.2.2. Server-Level Game Analysis
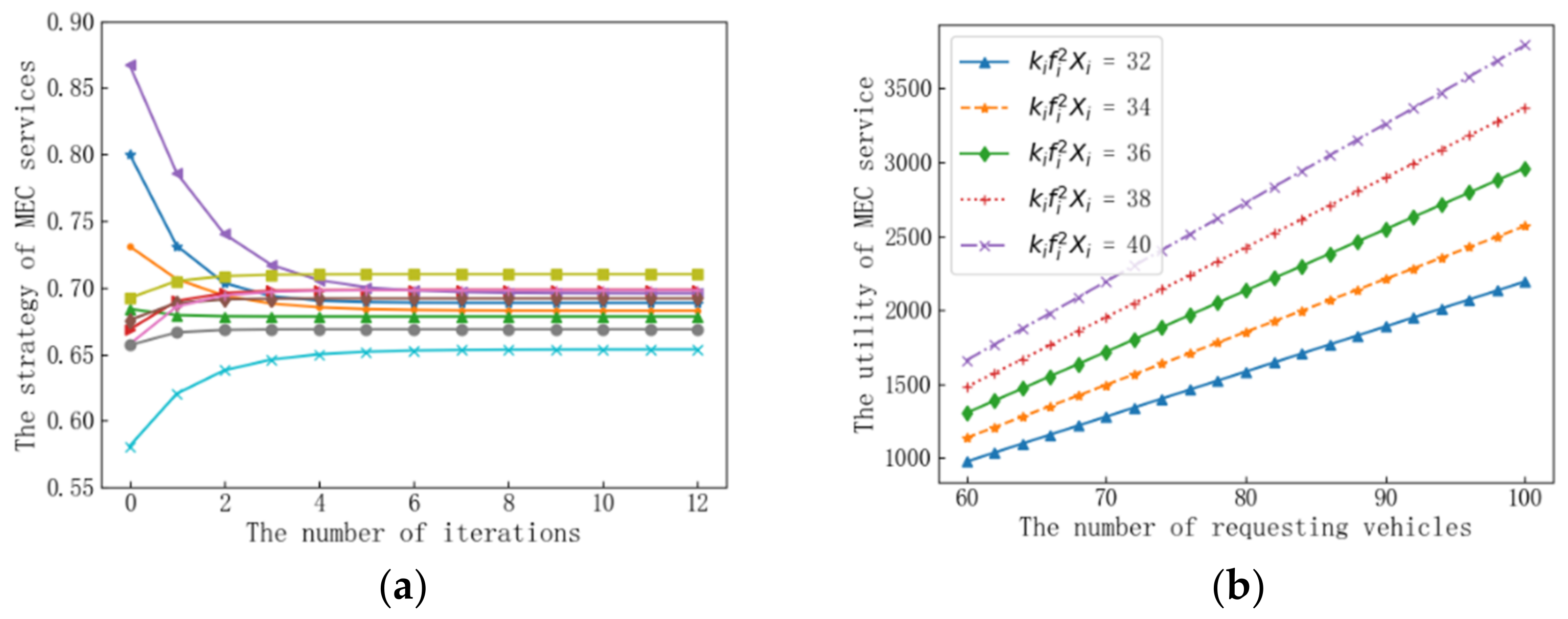
5. Simulation Experiments
5.1. Parameter Setting
5.2. Analysis of Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, A.; Li, J.; Ahmed, M. SpiderNet: A spiderweb graph neural network for multi-view gait recognition. Knowl.-Based Syst. 2020, 206, 106273. [Google Scholar] [CrossRef]
- Zhao, A.; Dong, J.; Li, J.; Qi, L.; Zhou, H. Associated spatio-temporal capsule network for gait recognition. IEEE Trans. Multimed. 2021, 24, 846–860. [Google Scholar] [CrossRef]
- Lv, Z.; Li, J.; Dong, C.; Wang, Y.; Li, H.; Xu, Z. DeepPTP: A deep pedestrian trajectory prediction model for traffic intersection. KSII Trans. Internet Inf. Syst. 2021, 15, 2321–2338. [Google Scholar]
- Xu, Z.; Li, J.; Lv, Z.; Wang, Y.; Fu, L.; Wang, X. A graph spatial-temporal model for predicting population density of key areas. Comput. Electr. Eng. 2021, 93, 107235. [Google Scholar] [CrossRef] [PubMed]
- Lv, Z.; Li, J.; Li, H.; Xu, Z.; Wang, Y. Blind travel prediction based on obstacle avoidance in indoor scene. Wirel. Commun. Mob. Comput. 2021, 2021, 5536386. [Google Scholar] [CrossRef]
- Somov, A.; Giaffreda, R. Powering IoT devices: Technologies and opportunities. IEEE IoT Newsl. 2015, 367, 368. [Google Scholar]
- Lv, Z.; Li, J.; Dong, C.; Xu, Z. DeepSTF: A deep spatial–temporal forecast model of taxi flow. Comput. J. 2023, 66, 565–580. [Google Scholar] [CrossRef]
- Xu, Z.; Li, J.; Lv, Z.; Dong, C.; Fu, L. A classification method for urban functional regions based on the transfer rate of empty cars. IET Intell. Transp. Syst. 2022, 16, 133–147. [Google Scholar] [CrossRef]
- Li, H.; Lv, Z.; Li, J.; Xu, Z.; Yue, W.; Sun, H.; Sheng, Z. Traffic Flow Forecasting in the COVID-19: A Deep Spatial-Temporal Model Based on Discrete Wavelet Transformation. ACM Trans. Knowl. Discov. Data 2022, 17, 64. [Google Scholar] [CrossRef]
- Xu, Z.; Lv, Z.; Li, J.; Sun, H.; Sheng, Z. A Novel Perspective on Travel Demand Prediction Considering Natural Environmental and Socioeconomic Factors. IEEE Intell. Transp. Syst. Mag. 2022, 15, 136–159. [Google Scholar] [CrossRef]
- Cheng, Z.; Rashidi, T.H.; Jian, S.; Maghrebi, M.; Waller, S.T.; Dixit, V. A Spatio-Temporal autocorrelation model for designing a carshare system using historical heterogeneous Data: Policy suggestion. Transp. Res. Part C Emerg. Technol. 2022, 141, 103758. [Google Scholar] [CrossRef]
- Lin, C.; Li, Y.; Ahmed, M.; Song, C. Piece-wise pricing optimization with computation resource constraints for parked vehicle edge computing. Peer-to-Peer Netw. Appl. 2023. [Google Scholar] [CrossRef]
- Shah-Mansouri, H.; Wong, V.W.; Huang, J. An incentive framework for mobile data offloading market under price competition. IEEE Trans. Mob. Comput. 2017, 16, 2983–2999. [Google Scholar] [CrossRef]
- Zeng, F.; Chen, Q.; Meng, L.; Wu, J. Volunteer assisted collaborative offloading and resource allocation in vehicular edge computing. IEEE Trans. Intell. Transp. Syst. 2020, 22, 3247–3257. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhang, Y.; Niyato, D.; Wang, P.; Han, Z. When mobile blockchain meets edge computing. IEEE Commun. Mag. 2018, 56, 33–39. [Google Scholar] [CrossRef]
- Xiong, Z.; Feng, S.; Niyato, D.; Wang, P.; Han, Z. Optimal pricing-based edge computing resource management in mobile blockchain. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), IEEE, Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Liu, Y.; Yu, F.R.; Li, X.; Ji, H.; Leung, V.C.M. Decentralized resource allocation for video transcoding and delivery in blockchain-based system with mobile edge computing. IEEE Trans. Veh. Technol. 2019, 68, 11169–11185. [Google Scholar] [CrossRef]
- Goldsmith, A. Wireless Communications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Kotobi, K.; Bilen, S.G. Secure blockchains for dynamic spectrum access: A decentralized database in moving cognitive radio networks enhances security and user access. IEEE Veh. Technol. Mag. 2018, 13, 32–39. [Google Scholar] [CrossRef]
- Tan, Z.; Yu, F.R.; Li, X.; Ji, H.; Leung, V.C.M. Virtual resource allocation for heterogeneous services in full duplex-enabled SCNs with mobile edge computing and caching. IEEE Trans. Veh. Technol. 2017, 67, 1794–1808. [Google Scholar] [CrossRef]
- Liang, C.; He, Y.; Yu, F.R.; Zhao, N. Video rate adaptation and traffic engineering in mobile edge computing and caching-enabled wireless networks. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, Canada, 24–27 September 2017; pp. 1–5. [Google Scholar]
- Wang, W.; Niyato, D.; Wang, P.; Leshem, A. Decentralized caching for content delivery based on blockchain: A game theoretic perspective. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Hao, Y.; Chen, M.; Hu, L.; Hossain, M.S.; Ghoneim, A. Energy efficient task caching and offloading for mobile edge computing. IEEE Access 2018, 6, 11365–11373. [Google Scholar] [CrossRef]
- You, C.; Huang, K.; Chae, H.; Kim, B.-H. Energy-efficient resource allocation for mobile-edge computation offloading. IEEE Trans. Wirel. Commun. 2016, 16, 1397–1411. [Google Scholar] [CrossRef]
- Zhang, W.; Wen, Y.; Guan, K.; Kilper, D.; Luo, H.; Wu, D.O. Energy-optimal mobile cloud computing under stochastic wireless channel. IEEE Trans. Wirel. Commun. 2013, 12, 4569–4581. [Google Scholar] [CrossRef]
- Liang, Y.; Li, Y.; Guo, J.; Li, Y. Resource Competition in Blockchain Networks under Cloud and Device Enabled Participation. IEEE Access 2022, 10, 11979–11993. [Google Scholar] [CrossRef]
- Kiayias, A.; Russell, A.; David, B.; Oliynykov, R. Ouroboros: A provably secure proof-of-stake blockchain protocol. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 20–24 August 2017; pp. 357–388. [Google Scholar]
- Li, Y.; Li, J.; Ahmed, M. A three-stage incentive formation for optimally pricing social data offloading. J. Netw. Comput. Appl. 2020, 172, 102816. [Google Scholar] [CrossRef]
- Qiao, Y.; Li, Y.; Li, J. An economic incentive for D2D assisted offloading using stackelberg game. IEEE Access 2020, 8, 136684–136696. [Google Scholar] [CrossRef]
- Zhao, A.; Wang, Y.; Li, J. Transferable Self-Supervised Instance Learning for Sleep Recognition. IEEE Trans. Multimed. 2022. [Google Scholar] [CrossRef]
- Xu, Z.; Lv, Z.; Li, J.; Shi, A. A Novel Approach for Predicting Water Demand with Complex Patterns Based on Ensemble Learning. Water Resour. Manag. 2022, 36, 4293–4312. [Google Scholar] [CrossRef]
- Lv, Z.; Li, J.; Dong, C.; Li, H.; Xu, Z. Deep learning in the COVID-19 epidemic: A deep model for urban traffic revitalization index. Data Knowl. Eng. 2021, 135, 101912. [Google Scholar] [CrossRef]
- Cheng, Z.; Jian, S.; Rashidi, T.H.; Maghrebi, M.; Waller, S.T. Integrating household travel survey and social media data to improve the quality of od matrix: A comparative case study. IEEE Trans. Intell. Transp. Syst. 2020, 21, 2628–2636. [Google Scholar] [CrossRef]

| Parameter | Meaning |
|---|---|
| The MEC server indexed by in the proposed model | |
| The requesting vehicle connected to MEC server | |
| The bandwidth between vehicle and MEC server | |
| The channel gain vehicle between vehicle and MEC server | |
| The noise variances of vehicle to MEC server | |
| The total computational workload required for the task of vehicle | |
| The uplink transmission time of the task submitted by vehicle | |
| The computational workload required per unit of task data | |
| The transmit power between vehicle and MEC server | |
| The computation resource pricing of MEC server | |
| The probability of selecting server as a block producer | |
| The energy coefficient of vehicle and MEC server | |
| The CPU computing capability of of vehicle and MEC server | |
| The transmission rate between vehicle and MEC server | |
| The block generation reward and block consensus reward | |
| The total energy consumed by vehicle | |
| The total energy consumed by MEC server |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 10 | 0.7–0.9 ms | ||
| 60–100 | 0.5–0.65 | ||
| 5 MHz | 0.35–0.5 | ||
| 54–57 dBm | 0.02 | ||
| 60 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Li, Y. Resource Allocation in Decentralized Vehicular Edge Computing Network. Information 2023, 14, 206. https://doi.org/10.3390/info14040206
Zhang H, Li Y. Resource Allocation in Decentralized Vehicular Edge Computing Network. Information. 2023; 14(4):206. https://doi.org/10.3390/info14040206
Chicago/Turabian StyleZhang, Hongli, and Ying Li. 2023. "Resource Allocation in Decentralized Vehicular Edge Computing Network" Information 14, no. 4: 206. https://doi.org/10.3390/info14040206
APA StyleZhang, H., & Li, Y. (2023). Resource Allocation in Decentralized Vehicular Edge Computing Network. Information, 14(4), 206. https://doi.org/10.3390/info14040206






