Enhanced Learning and Forgetting Behavior for Contextual Knowledge Tracing

Abstract

Knowledge tracing (KT) is based on modeling students’ behavior sequences to obtain students’ knowledge state and predict students’ future performance. The KT task aims to model students’ knowledge state in real-time according to their historical learning behavior, so as to predict their future learning performance. Online education has become more critical in recent years due to the impact of COVID-19, and KT has also attracted much attention due to its importance in the education field. However, previous KT models generally have the following three problems. Firstly, students’ learning and forgetting behaviors affect their knowledge state, and past KT models have yet to exploit this fully. Secondly, the input of traditional KT models is mainly limited to students’ exercise sequence and answers. In the learning process, students’ answering performance can reflect their knowledge level. Finally, the context of students’ learning sequence also affects their judgment of the knowledge state. In this paper, we combined educational psychology theories to propose enhanced learning and forgetting behavior for contextual knowledge tracing (LFEKT). LFEKT enriches the features of exercises by introducing difficulty information and considers the influence of students’ answering behavior on the knowledge state. In order to model students’ learning and forgetting behavior, LFEKT integrates multiple influencing factors to build a knowledge acquisition module and a knowledge retention module. Furthermore, LFEKT introduces a long short-term memory (LSTM) network to capture the contextual relations of learned sequences. From the experimental results, it can be seen that LFEKT had better prediction performance than existing models on four public datasets, which indicates that LFEKT can better trace students’ knowledge state and has better prediction performance.

1. Introduction

In recent years, online education platforms have become increasingly popular among students because of their convenience and freedom, and the online education market has further expanded [1]. Online education methods such as online education and online courses are not limited by time and space. Students can flexibly arrange their study time and study freely. They can also share high-quality educational resources remotely. These advantages make online education a valuable form of learning. Coupled with the threat of COVID-19, many schools have been forced to adopt strict epidemic prevention policies, which has resulted in many students who were originally studying at school being forced to stay at home [2]. Against this backdrop, online education, which plays an integral role in minimizing disruption to education, is growing on an unprecedented scale and is gradually becoming a fashionable way of learning. It is foreseeable that, with the change in people’s educational concepts, online education will play an increasingly important role.

Online education systems such as massive open online courses (MOOCs) offer millions of online courses and exercises, attracting the public’s attention [3,4]. Students can study according to their plans in these online systems [5]. However, students’ blind study is not conducive to their improvement, so KT is needed to help students understand their mastery of various knowledge, and they can strengthen themselves according to their weaknesses. KT is inherently complex, necessitating the modeling of students’ learning sequences to obtain their knowledge state [6]. How to use KT and other technologies to diagnose and analyze students’ knowledge mastery state in real-time to provide targeted and personalized learning guidance has become a hot topic in intelligent education and educational data mining [7].

The KT task can be formally expressed as a supervised sequence learning task [8]. As shown in Figure 1, $e_i$ is an exercise, and its color represents the knowledge concept (KC) that the exercise contains. In the online learning process, the student interacts with exercises containing different KCs and generates an exercise–answering interactive record. The student answers five exercises in sequence ($e_1$–$e_5$); $e_1$, $e_2$, $e_3$, and $e_4$ were correct, and $e_5$ was wrong, indicating that he/she may be proficient in “Absolute value”, but not familiar with “Linear Equations”. Through learning, the student’s knowledge state $S_i$ would change, and the color of the radar chart represents the student’s mastery of different KCs. With the current mastery of each KC, how will the student perform in the following exercise $e_6$, which examines “Absolute value”? KT is a very effective technique for solving this problem.

Traditional KT models mainly include Bayesian knowledge tracing (BKT) [5] based on hidden Markov models (HMMs) [9], and early KT models mainly focused on probabilistic modeling. Although these models have made much excellent progress, they mostly rely on simplifying assumptions, such as the assumption that knowledge forgetting does not occur during learning [5], which limits their application in real-world scenarios. In recent years, deep learning technology has played a significant role in various fields, and many KT models based on deep learning have also appeared in the field of KT. Deep knowledge tracing (DKT) [6] uses a recurrent neural network (RNN) [10] or LSTM [11] to model students’ learning sequences and uses the hidden vectors of the RNN or LSTM to represent students’ knowledge state to predict students’ answering performance. Inspired by the memory networks [12], dynamic key–value memory networks for knowledge tracing (DKVMNs) [13] utilize the relationship between basic KCs to directly output students’ knowledge state. DKVMNs use a key matrix to store KCs and a value matrix to store and update students’ knowledge state.

The above research introduced deep learning into KT models to improve the prediction performance, but there are still three problems.

Firstly, the impact of student learning and forgetting behavior is underappreciated. Most KT models were based on the simple assumption that students’ correctly answering exercises will increase their knowledge state and incorrectly answering exercises will reduce their knowledge state [14]. However, such a simple assumption is inconsistent with neurological theory. From the perspective of neurological theory, it is inevitable for students to make mistakes in learning. Making mistakes is normal and is a kind of information that can make students grow [15]. The process of students making mistakes and correcting mistakes is also the process of growing myelin and gaining knowledge [16]. Students’ learning behavior determines the degree of knowledge growth obtained in the learning process. Students’ forgetting behavior determines the degree of knowledge forgetting. Many forgetting theories in educational psychology delved into various factors that affect human forgetting. The Ebbinghaus forgetting curve theory explained in detail why people forget [17]. The trace decay theory revealed that forgetting is induced by the gradual disappearance of memory traces [18], and the deeper the original trace, the lower the degree of forgetting. Memories are stored in engram cells, and forgetting occurs when engram cells cannot be reactivated [19]. KT is a prediction based on previous performance, but the real application is personalized learning. However, many KT models frequently disregard students’ psychological and physiological aspects. Therefore, how to connect KT with educational psychology theory and neurological theory to model learning and forgetting behavior is a pressing issue that needs to be addressed.

Secondly, the input of KT models is mainly limited to KCs involved in students’ exercises and answers. Existing KT models directly use KCs to index exercises [7], which ignores differences between exercises covering the same KC, resulting in the limited flexibility and personalization potential of KT models. For students’ answering performance, existing KT models usually summarize their performance with answers. In fact, in the learning process, much answering behavior of students can reflect their ability level.

Finally, the context of students’ learning sequences also affects the judgment of their knowledge state. Sequence context is often used in the field of natural language processing to mine the latent information of text and has achieved remarkable results in previous work [20]. Students’ answering performance is related to their historical performance in answering related exercises, and their performance on similar exercises will have a certain similarity [21].

Therefore, we focused on the following three questions:

• Can exercise embeddings and students’ answering performance be enriched to increase the learnable information of models?
• Can contextual information for exercises be derived by considering students’ historical learning sequences?
• Can the learning and forgetting behavior of students be modeled more accurately by incorporating pedagogical theory?

The Ebbinghaus forgetting curve theory describes the phenomena of progressive memory deterioration over time. In the early exploration of forgetting behavior, models such as augmenting knowledge tracing by considering forgetting behavior (DKT-Forgetting) [22] simulated forgetting by adding a time-related factor, and models such as context-aware attentive knowledge tracing (AKT) [23] controlled forgetting behavior by designing a time-based decay function. In terms of exercise embeddings and students’ answering performance, AKT was combined the Rasch model to enrich exercise features, and learning process consistent knowledge tracing (LPKT) [14] enriched the answering performance by adding answering time. However, integrating various educational psychology theories into the KT models is a topic that requires more study. For example, the trace decay theory [24] revealed that information not recalled or utilized infrequently is usually erased from memory. If students do not review what they have learned, their mastery of knowledge will continue to deteriorate. In the Methodology Section, we examine various pedagogical theories in depth.

We have published a short paper to discuss briefly how to model students’ learning and forgetting behavior by combining educational psychology theory [25], but it is not enough to answer all the above questions. To answer these questions, we propose a new KT model, enhanced learning and forgetting behavior for contextual knowledge tracing (LFEKT). The main contributions of this paper are as follows:

• To distinguish exercises involving the same KC, we incorporated item response theory (IRT) [26] to enrich the exercise embeddings with difficulty information. In addition, we present an expanded Q matrix and an exercise–KC relation layer to address the issue of subjective bias in the human-calibrated Q matrix. Then, we incorporated students’ response time and hint times into the embeddings for their answer performance. Students’ answering time and hint times reflect their proficiency in using the corresponding KC. That is, the higher the proficiency of the corresponding KC, the less the required answer time and hint times are.
• Inspired by self-attention KT models such as AKT, we modeled the contextual information of learned sequences using the LSTM network to represent the impact of historically learned sequences.
• Combining our KT model with educational psychology theories, we split the students’ learning process into two parts: knowledge acquisition and knowledge retention. Knowledge acquisition simulates the expansion of knowledge gained by students’ learning behavior, and knowledge retention simulates students’ knowledge absorption and forgetting to determine the degree of knowledge retention. Furthermore, we modeled three factors affecting knowledge acquisition and retention: students’ repeated learning times, sequential learning time intervals, and current knowledge state.

2. Related Works

2.1. Knowledge Tracing

The KT task can be formally represented as a supervised sequence learning task. In the online learning process, users interact with exercises containing different KCs to generate an interactive record of answering exercises [8]. The goal of KT is to model user’s answering performance, evaluate their knowledge state, and predict their future answering performance. According to the research direction of our paper, we divided the main research directions of mainstream KT models, as shown in

Table 1. Main research directions of different KT models.

Model	Deep Learning	Forgetting	Context	Exercise Embedding	Answering Performance
BKT
DKT	✓
DKT+	✓
DKVMN	✓
PDKT-C	✓	✓
SKVMN	✓	✓	✓
SAKT	✓		✓
DKVMN-DT	✓				✓
RKT	✓	✓	✓	✓
AKT	✓	✓	✓	✓
SSAKT	✓	✓	✓	✓
CKT	✓
GameDKT	✓
KPT	✓	✓
DKT-Forgetting	✓	✓
LPKT	✓	✓			✓
HawkesKT	✓	✓
iAKT	✓		✓
ERAKT	✓		✓
EKT	✓	✓	✓
SAINT	✓	✓	✓
SAINT+	✓	✓	✓
DKT-IRT	✓			✓
Deep-IRT	✓			✓
DIMKT	✓			✓
PEBG	✓			✓
LFEKT	✓	✓	✓	✓	✓

.

BKT [5] is one of the most-representative models [7], which uses the hidden Markov model to update their knowledge state based on students’ exercise performance. In recent years, as deep learning has been widely used in various fields, researchers have also tried to apply deep learning techniques to KT tasks [8]. DKT was the first attempt of using the RNN and LSTM in the KT task [6]. It took students’ learning history as the input and used the hidden state vector of the RNN or LSTM to represent their knowledge state, so as to predict their future learning performance. The DKT model cannot represent students’ knowledge state for each KC, but only their overall knowledge state. Although the DKT model can automatically adjust the learning parameters of students without much human intervention, it requires much computing power when the time series is too long, and the hidden knowledge state is not smooth in time. Yeung et al. proposed DKT+ [27] to solve the problem that the knowledge state generated by DKT is not smooth in time. Chen et al. improved the prediction performance of DKT by considering the prior relationship between KCs [28]. The DKVMN drew on the idea of a memory network, used a value matrix to model students’ knowledge state of each KC, examined the relationship between exercises and each KC, and traced students’ mastery of each KC. Abdelrahman et al. proposed DKVMN-based knowledge tracing with sequential key–value memory networks (SKVMNs) [29], which uses an improved LSTM to capture long-term dependencies between exercises. The study of Sun et al. extended the behavioral characteristics of students when answering exercises to the DKVMN so as to achieve better prediction results [30]. The self-attention model for knowledge tracing (SAKT) [31] was the first to introduce transformers directly into the KT domain and was also the first model to use a self-attention mechanism in the KT field. Relation-aware self-attention for knowledge tracing (RKT) [32] was extended based on SAKT and improved that model by introducing the exercise relation coefficient matrix. AKT [23] used context-aware attention to model students’ forgetting behavior and combined attention mechanisms with cognitive and psychometric models, such as using IRT to model exercise difficulty. The sequential self-attentive model for knowledge tracing (SSAKT) [33] also introduced a self-attention mechanism and used LSTM to perform positional encoding in the self-attention layer. Convolutional knowledge tracing (CKT) [34] introduced the hierarchical convolutional layer to trace students’ knowledge state. GameDKT [35] applied KT to the field of educational games and used a CNN to trace students’ mastery of the skills required for educational games.

2.2. Learning and Forgetting

During the learning process, students accumulate knowledge through learning, and their knowledge state declines due to inevitable forgetting. Classic theories of forgetting, such as the Ebbinghaus forgetting curve, assumed that memory retention declines over time. A forgetting curve can be modeled as a power-law function, where memory declines rapidly at first and then decays slowly over a longer time. In the field of KT, many models also used time as an influencing factor to model forgetting.

Knowledge proficiency tracing (KPT) simulated students’ knowledge state through learning and forgetting theory and dynamically captured changes in students’ knowledge state over time [36]. DKT-forgetting tried to improve DKT by considering students’ repeated learning times, the time interval from the last learning of the same KC, and the time interval from previous learning [22]. RKT [32] assumed that students’ knowledge state decays over time and involved an exponentially decaying kernel function in simulating the forgetting effect. Qiu et al. considered the time interval from the last learning of the same KC and added a new day’s mark to BKT to model the forgetting behavior of one day after the previous learning [37]. Khajah et al. used students’ repeated learning times to estimate the probability of forgetting to improve the prediction accuracy of BKT [38]. LPKT [14] monitored changes in students’ knowledge state during their learning process by taking into account their learning and forgetting. Wang et al. proposed HawkesKT, which assumed that a student’s mastery of the KC is not only affected by previous interactions on the same KC, but also by previous interactions with other problems [39]. Furthermore, the effects of interactions decay over time with different efficiencies, and some KCs may be more forgettable than others.

2.3. The Context of Learning Sequence

Sequence context has often been used in the field of natural language processing to mine the latent information of text, and has achieved remarkable results in previous work [20]. Bert [40] utilized a bidirectional function to combine the context of a sentence to determine specific semantics, addressing the semantic representation problem in previous methods. Since LSTMs can capture aspects and semantic relationships between contextual content in a flexible way, Tang et al. proposed aspect-dependent LSTM (TD-LSTM) and aspect-connected LSTM (TC-LSTM) to extend LSTM by considering aspects [41], and they combined a given aspect with contextual content for aspect-level sentiment classification.

Due to the serialization characteristics of students’ historical learning, the KT problem can be regarded as a supervised learning sequence prediction problem in the field of machine learning [42], so the method of learning sequence context is also applicable to the field of KT. AKT [23] obtained the learning sequence context by considering students’ entire historical learning sequences to measure the impact of past exercises and answers. Subsequently, incremental context-aware attentive knowledge tracing (iAKT) [43] made further improvements to the AKT model. iAKT first demonstrated an evolving knowledge tracing (eKT) scene through experience and continued to learn incrementally from this scene. Context-aware knowledge tracing integrated with the exercise representation and association in mathematics (ERAKT) [42] considered both the textual semantics and conceptual representation of exercises in the exercise embedding stage and proposed a bidirectional-neural-network-based sequential exercise mining method to obtain the associated content. Exercise-aware knowledge tracing (EKT) [21] captured contextual information through the attention mechanism. SAINT+ [44], the successor of SAINT [45], was a transformer-based KT model that processed exercise information and students’ response information separately. Following the architecture of SAINT, SAINT+ had an encoder–decoder structure, where the encoder applied self-attention layers to the motion embedding stream and the decoder applied self-attention layers and encoder–decoder attention layers alternately to the response embedding stream and encoder output stream. Furthermore, SAINT+ embedded two temporal features into the response embedding: elapsed time and latency.

2.4. Item Response Theory

In traditional KT models, students’ knowledge state and correct answer rate were usually predicted based on their learning sequences. The information used is the KCs involved in exercises and students’ answers. If exercise is only represented by KCs, the information about these exercises themselves will be ignored. The classic IRT in educational psychology was a commonly used theory for cognitive diagnosis [46], which was used to evaluate the quality of an item’s response. The theory usually used a probabilistic form to describe how item response is affected by factors such as item difficulty or a combination of factors. Items are affected by two dimensions: item difficulty and discrimination [26]. Through the research of [47], it was found that the difficulty of exercises plays a crucial role in enriching the characteristics of exercises. In traditional KT models, Yudelson et al. integrated the exercise difficulty to enhance the interpretability of BKT [48]. Inspired by the above models, the DKT-IRT model [49] was proposed, incorporating IRT with KT. While predicting students’ answers, it comprehensively analyzes the difficulty of exercises to improve prediction accuracy. Reference [50] also made a similar attempt. They combined IRT with the DKVMN model, used the DKMVN to model students’ learning path, and used IRT to analyze the difficulty of exercises to improve the prediction efficiency. Difficulty matching knowledge tracing (DIMKT) [51] simulated and analyzed the impact of exercise difficulty on student learning to measure the difference of exercises on learning. In DIMKT, an adaptive sequential neural network (ASNN) is carefully designed to establish the relationship between students’ knowledge state and the level of exercise ambiguity during learning. Pre-training embeddings via bipartite graphs (PEBGs) [52] pre-trained each exercise embedding to extract exercises’ high-level information, then trained the KT model on the obtained embeddings to improve the prediction performance.

3. Problem Definition

We define $C=\left\{c_1,c_2,\dots ,c_i,\dots ,c_I\right\}$ as the set of KCs and $E=\left\{e_1,e_2,\dots ,e_j,\dots ,e_J\right\}$ as the set of exercises, each of which is related to a specific KC. The Q matrix consists of 0 and 1, $c_i$, then $Q_{ji}$ = 1, otherwise $Q_{ji}$ = 0. Each student learns independently and does not affect the other. The student will use what he/she has learned to answer the exercises, and the answering process will take a certain amount of time. In the learning process, the above answering behavior will be repeated continuously, and there is an interval between adjacent answering actions, so the student’s answering history h is expressed as $\left\{\left({eu}_1,{pu}_1\right),{it}_1,\left({eu}_2,{pu}_2\right),{it}_2,\dots ,\left({eu}_t,{pu}_t\right),{it}_t,\dots \right\}$, where ${eu}_t$ represents the exercise unit, including $c_t$, $e_t$, and ${df}_t$. ${df}_t$ indicates the difficulty of $e_t$. ${pu}_t$ indicates the performance of answering exercises, including ${at}_t$, $a_t$, and ${ht}_t$. ${at}_t$ indicates the time spent answering $e_t$. $a_t$ indicates the answer to the exercise; 1 means the correct answer, and 0 means the wrong answer. ${ht}_t$ indicates the hint times, and ${it}_t$ indicates the time interval between two answers. $\left({eu}_1,{pu}_1\right)$ constitute a basic unit in the learning process ${epu}_t$. After a student completes an exercise, his/her knowledge state $S_t$ will be updated, and $S_t$ contains his/her knowledge mastery involved in all KCs. The student will forget part of the knowledge in the learning process, resulting in the decay of the corresponding knowledge state. Given a student’s answering history h, the purpose of KT is to monitor the student’s change in knowledge state and predict his/her performance on the next candidate exercise $e_{t+1}$.

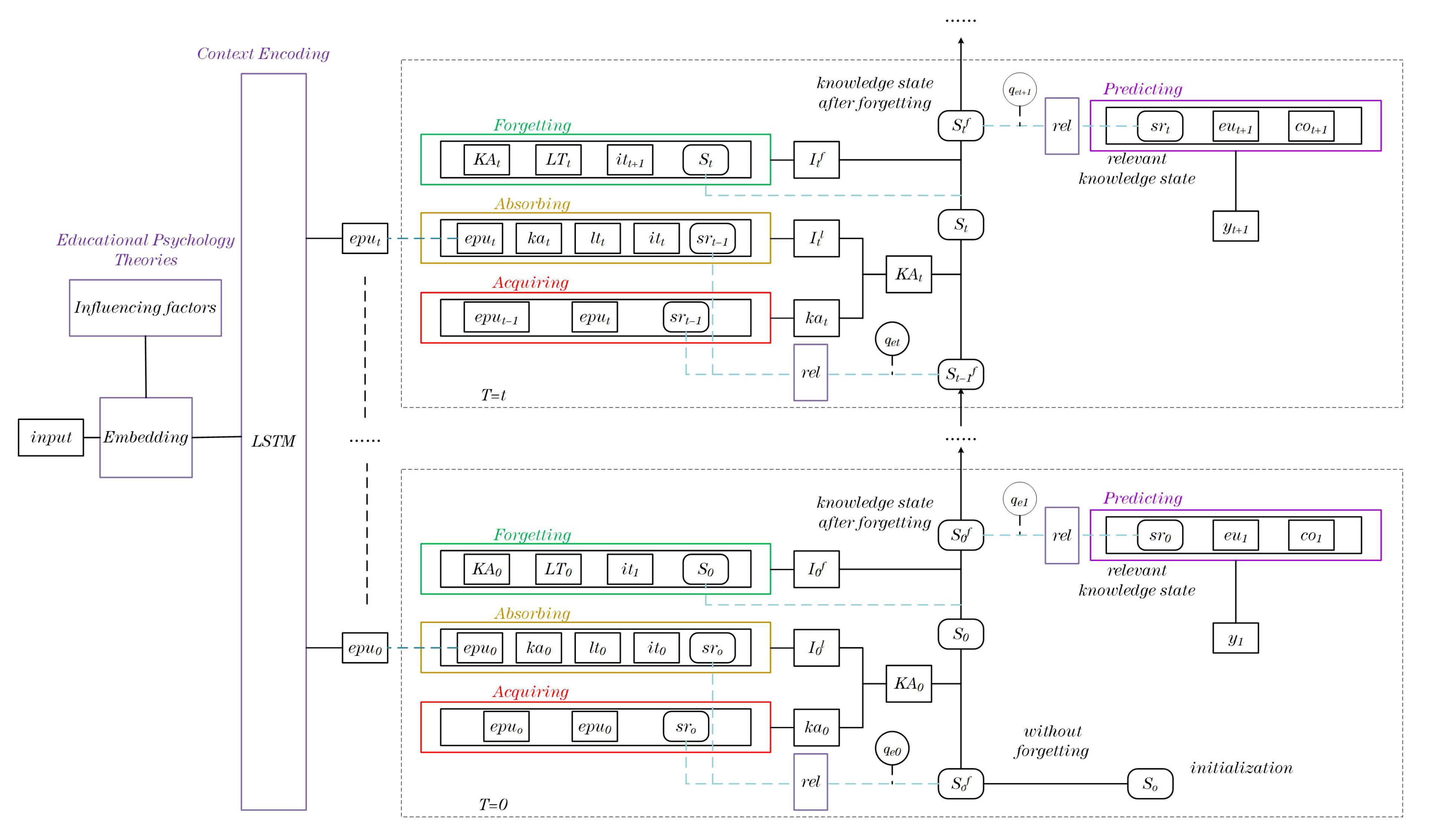
4. Methodology

4.1. Embedding Module

Before introducing the model’s overall structure (Figure 2), we briefly introduce the embedding of elements from the following five categories.

4.1.1. Exercise Embedding

The mainstream way of exercise embedding is to use the corresponding KC to represent exercises, which will ignore the information of exercises themselves, resulting in no distinction between exercises. EKT [21] extracted information from exercise text and used a convolutional neural network (CNN) [53] to extract text features to obtain exercise embeddings, but the number of datasets containing exercise text information is relatively limited. In the field of educational psychology, IRT estimates students’ answers based on their ability and the difficulty of the exercises. Therefore, we introduced difficulty information to enrich the exercise embeddings. The difficulty is defined as follows:

$$diff=1-\frac{{\displaystyle \sum _{i=1}^N}{G}_i}{N}$$

(1)

As shown in Formula (1), we calculated the proportion of each exercise being answered correctly. $G_i$ is the total score obtained by students who responded correctly on this exercise; 1 point is awarded if students answer this exercise correctly; no score is awarded for a wrong answer; N is the total number of students. We mapped the correct rate to an interval in the range of 0–10 by a normalization method. Then, the difficulty of each exercise is represented as an embedding vector as ${df}_t\in {\mathbb{R}}^{d_k}$, where $d_k$ is the dimension of the vector. The exercise embeddings can be enriched through the difficulty of exercises so that the model can learn more helpful information.

We deeply integrated the exercise information $e_t$, the KC information $c_t$, and the difficulty information $d{f}_t$ into the exercise unit $e{u}_t$. The formula is expressed as

$${eu}_t=W_1^T\left[e_t\oplus c_t\oplus {df}_t\right]+b_1$$

(2)

where ⊕ is the connection operation, $e_t,c_t\in {\mathbb{R}}^{d_k}$. In this paper, $W_i$ is the weight matrix of the neural network layer and its output dimension is $d_k$, and $b_i$ is the bias term.

4.1.2. Answering Performance Embedding

Some KT models [14,23] will directly express the answering performance as students’ answers. Students’ proficiency in KCs can be seen from many responses in the learning process, such as the answering time and the hint times when answering exercises. For the same exercise, the less time a student spends answering the exercise, the better his/her mastery of the corresponding KC. Therefore, we considered the above factors to construct the answering performance unit $p{u}_t$. $p{u}_t$ includes the answer $a_t$, the answering time $a{t}_t$, and the hint times $h{t}_t$, and the formula is expressed as

$${pu}_t=W_2^T\left[a_t\oplus {at}_t\oplus {ht}_t\right]+b_2$$

(3)

where $a_t\in {\mathbb{R}}^{d_k}$. For an answer of 0 or 1, we expanded it into a vector of 0 or 1. ${at}_t\in {\mathbb{R}}^{d_k}$. We discretized ${at}_t$ by seconds. ${ht}_t\in {\mathbb{R}}^{d_k}$.

4.1.3. Exercise Performance Embedding

We divided the learning sequence into basic exercise performance units ${epu}_t$, which are the main components of students’ learning and can be used to measure students’ knowledge acquisition via exercise answering. ${epu}_t$ includes exercise information and students’ performance. Our original design was to capture ${epu}_t$ with a fully connected layer, connecting ${eu}_t$ and ${pu}_t$ together and deeply fused, as shown below:

$${epu}_t=W_3^T\left[{eu}_t\oplus {pu}_t\right]+b_3$$

(4)

This approach will cause the model to focus only on the current exercise, ignoring some useful contextual information and the correlation between exercises. Students may receive similar scores on similar exercises. For example, student ${stu}_1$ is correct in answering exercises $e_1$ and $e_3$ because these two exercises may be similar and have the same KCs. If only the current interactive exercise information and students’ answering performance are used as the input, the context information of the learning sequences will be ignored. Moreover, HawkesKT explained that students’ mastery of KCs is not only affected by previous interactions with exercises examining the same KCs, but also by previous interactions with other exercises, and this effect will decay over time. Inspired by the contextual encoding in [54,55], we used LSTM to encode useful contextual information. In the field of natural language processing, LSTM has often been used to capture context features. LSTM is an excellent variant model of the RNN [56], which can be used to deal with problems and tasks sensitive to time series and solves the long-term dependence problem of RNNs. Due to its gating mechanism, LSTM can mitigate the effects of distant past exercises. Our $LSTM$ takes an exercise performance sequence $\left({eu}_t,{pu}_t\right)$ as the input and outputs a context sequence. Due to its recurrent structure, $LSTM$ can encode contextual features into embeddings. Therefore, ${epu}_t$ can be expressed as

$${epu}_t=LSTM\left({eu}_t\oplus {pu}_t\right)$$

(5)

where the output dimension of $LSTM$ is $d_k$.

4.1.4. Historical Behavior Embedding

Students’ historical learning behavior can be used to model learning and forgetting behavior. According to Ebbinghaus curve theory [17], the retention rate of students’ KCs is affected by historical behavior records, such as the lag time of interaction and students’ repeated learning times. The lag time can be calculated as the time interval for repeated learning of the same KC and the time interval for sequential learning. The time interval for repeated learning of the same KC was commonly used in previous studies [57,58]. We used the sequential learning interval because the time interval for repeated learning of the same KC is already reflected in the sequential learning interval. Furthermore, if the KC of a student’s current answering exercise and other KCs of the previous exercises are correlated, the time interval between these interactions may affect answering performance. Incorporating sequential learning intervals into the model can capture this effect. Students’ repeated learning times refer to the total number of previous studies for the same KC. In addition, for a specific KC, we introduced the historical accuracy rate of students’ answers to exercises $co\in {\mathbb{R}}^{d_k}$ as a reference for predicting students’ answering performance. The time interval embedding vector is $it\in {\mathbb{R}}^{d_k}$, and the repeated learning times embedding vector is $lt\in {\mathbb{R}}^{d_k}$.

4.1.5. Knowledge Embedding

We used a knowledge embedding matrix to represent students’ knowledge state. In LFEKT, the knowledge embedding matrix $s\in {\mathbb{R}}^{d_s\times d_k}$ is initially initialized to 0 at the beginning, where $d_s$ is the number of KCs. Each row represents the mastery state of each KC. During the learning process, LFEKT will change students’ knowledge state according to each learning interaction. The Q matrix represents the relationship between exercises and KCs and is used to control the updated rows in the knowledge embedding matrix after answering relevant exercises. Traditionally, if $c_i$ is not included in $e_j$, $Q_{ji}$ will be set to 0, indicating that the student’s answering performance on $e_j$ has nothing to do with the student’s mastery of $c_i$. However, the human-calibrated Q matrix may be invalid due to unavoidable errors and subjective biases [46]. Referring to [14], this paper defines an enhanced Q matrix, where $Q_{ji}$ will be set to a small fixed value to correct possible errors. Furthermore, a relationship coefficient layer is introduced to measure the matching degree between the current exercise and the KC, which is expressed as

$$\left.{rel}_t={sigmoid\left(W\right.}_4^T\left[e_t\oplus c_t\right]+b_4\right)$$

(6)

where $sigmoid$ is a nonlinear activation function.

4.2. Knowledge Acquisition Module

During the interval between two learning interactions, students will forget knowledge due to the unavoidable forgetting behavior. Therefore, when the learning interaction starts at time t, students’ knowledge mastery state decreases from $S_{t-1}$ to $S_{t-1}^f$. Then, we first multiply $S_{t-1}^f$ and the KC vector $q_{e_t}$ of the current exercise to obtain the knowledge mastery of the KC related to the currently answered exercise $s_{t-1}^f$:

$$s_{t-1}^f=q_{e_t}{S}_{t-1}^f$$

(7)

where $q_{e_t}\in {\mathbb{R}}^{d_s}$ is obtained through the Q matrix and $q_{e_t}$ is the KC involved in the exercise. $S_{t-1}^f\in {\mathbb{R}}^{{d_s\times d}_k}$ is the students’ overall knowledge state, so $s_{t-1}^f\in {\mathbb{R}}^{d_k}$, which represents the knowledge mastery of the KC related to the currently answered exercise.

Exercises may involve multiple KCs, and there are also correlations between KCs. Therefore, the matching degree between the exercise and the KC is measured by the relation layer in Equation (6), so as to know how much knowledge is required to correctly answer the exercise. The relevant knowledge state ${sr}_{t-1}$ to answer the current exercise can be expressed as

$${sr}_{t-1}=s_{t-1}^f\circ {rel}_t$$

(8)

What students gain in the learning process can be expressed as how much knowledge is acquired. Traditionally, the amount of knowledge acquisition can be viewed as the “travel distance” [59], which represents the difference in students’ performance between two learning interactions. Not all students have the same knowledge acquisition, and knowledge acquisition is directly related to exercises students perform. The KCs examined by different exercises are different, and what students gain is the knowledge growth of different KCs. Exercises of different difficulty bring different degrees of knowledge growth to students. Then, the current knowledge state of students reflects the room for their improvement to a certain extent and affects their knowledge acquisition. Students with lower mastery have more room to improve, and students with higher mastery may encounter bottlenecks. Therefore, we introduce $ep{u}_t$ and ${sr}_{t-1}$ to build the knowledge acquisition layer to model the evolution of students’ knowledge acquisition. Besides, no one is perfect, and failure is the mother of success. Making mistakes is an essential factor in the learning process of students, and people will grow by making mistakes [60]. Even if students answer an exercise incorrectly, they can still learn from it and gain knowledge. Therefore, we always set students’ knowledge acquisition $k{a}_t$ to a positive value through the tanh activation function:

$${ka}_t=\left(tanh\left(W_5^T\left[{epu}_{t-1}\oplus {epu}_t\oplus {sr}_{t-1}\right]+b_5\right)\right)/2$$

(9)

4.3. Knowledge Retention Module

While there are some studies that considered forgetting when modeling students’ knowledge state, some models only consider part of the information affecting forgetting, and others consider multiple factors that influence forgetting, ignoring students’ learning sequences. Students’ knowledge retention mainly consists of two parts: the proportion of knowledge absorption they have learned and the natural forgetting over time.

4.3.1. Knowledge Absorption Module

The absorption of knowledge emphasizes that the knowledge learned is effectively interpreted and understood by students. Students need to effectively integrate new knowledge with existing knowledge, because the knowledge that cannot be understood is difficult to reuse and develop. Therefore, we designed a knowledge absorption layer to evaluate students’ knowledge absorption rate.

Trace decay theory [24] revealed that the forgetting of memory content gradually declines because it is not strengthened. Repeated learning can consolidate previously learned knowledge and strengthen students’ understanding of knowledge. The theory of extinction interference inhibition believes that different learning contents will interfere with each other and affect students’ learning, including both proactive and backward inhibition [61]. Proactive inhibition means that the previously learned content interferes with the later learned content, and backward inhibition means that the later learned content interferes with the previously learned content, indicating that the time interval will affect the learning behavior of students, which means efficient learning processes tend to be compact and continuous. Our answering behavior, such as hint times and answering time, reflects students’ proficiency in using the corresponding KC to a certain extent. Moreover, answering exercises through a large number of requests for hints will also lead to a reduction in students’ thinking processes and affect their knowledge absorption rate. $ep{u}_t$ contains exercise information and students’ answer information. The human brain is indeed complex, and the factors that affect students’ forgetting are far more than these. However, limited by real public datasets, we combined the above-mentioned classic forgetting theory to extract common factors affecting forgetting and designed a knowledge absorption layer to simulate the absorption rate of learned knowledge $I_t^l$:

$$I_t^l=sigmoid\left(W_6^T\left[{epu}_t\oplus {sr}_{t-1}\oplus {ka}_t\oplus {lt}_t\oplus {it}_t\right]+b_6\right)$$

(10)

We needed to obtain the knowledge absorption that students really absorb, so we multiplied the knowledge absorption rate $I_t^l$ by ${ka}_t$:

$${ka}_t^n=I_t^l\circ {ka}_t$$

(11)

Then, the overall knowledge absorption amount ${KA}_t$ can be obtained by multiplying $q_{e_t}^T$ by ${ka}_t^n$:

$${KA}_t=q_{e_t}^T{ka}_t^n$$

(12)

where $q_{e_t}\in {\mathbb{R}}^{d_s}$ and ${ka}_t^n\in {\mathbb{R}}^{d_k}$, so ${KA}_t\in {\mathbb{R}}^{d_s\times d_k}$ represents the overall knowledge absorption amount at each KC.

Therefore, the current overall knowledge state $S_t$ is the overall knowledge state at time t−1 $S_{t-1}^f$ plus the overall knowledge absorption amount ${KA}_t$:

$$S_t=S_{t-1}^f+{KA}_t$$

(13)

4.3.2. Knowledge Forgetting Module

Forgetting is an integral part of the brain’s regular operations. Due to the limitation of the brain’s working mechanism, it is impossible for people to reproduce all they have seen and heard. Models such as AKT simulated the exponential decay of memory over time by designing a time-based kernel function without considering other potentially influencing factors. According to the trace decay theory [24], students’ mastery of KCs affects their forgetting degree, and the amount of memorized learning materials decays exponentially with time. Memory is a function of the human brain in accumulating knowledge and experience, and memory traces in the brain decline over time. Learning alters the central nervous system, and unless the information is used or repeated regularly, it will gradually decay and disappear completely. Therefore, information not recalled or used infrequently is often easily lost from memory. If students have not reviewed the knowledge they have learned, their mastery of knowledge will continue to decline. Ebbinghaus forgetting curve theory [17] revealed that active repetition and recall of learned knowledge can enhance memory. It can be seen that time and students’ repeated learning times are common factors affecting students’ forgetting. On the other hand, knowledge acquisition from the last learning time also has an impact. The more knowledge acquired in single learning, the greater the probability of forgetting, and cramming education is often counterproductive. In order to model the complex forgetting behavior, based on the theories above, we designed the knowledge forgetting layer to measure the overall forgetting degree of students’ knowledge state. The knowledge forgetting layer can decide which knowledge to keep and which to ignore.

The knowledge forgetting rate $I_t^f$ can be expressed as

$$I_t^f=sigmoid\left(W_7^T\left[{KA}_{t-1}\oplus S_{t-1}\oplus {it}_t\oplus {LT}_t\right]+b_7\right)$$

(14)

where ${LT}_t$ is the number of historical learning times for each KC. We eliminated the effects of forgotten knowledge by multiplying $I_t^f$ by $S_{t-1}$. Knowledge $S_{t-1}^f$ is updated to

$$S_{t-1}^f=I_t^f\circ S_{t-1}$$

(15)

4.4. Predicting Module

After obtaining students’ knowledge state at time t, we can make predictions about the performance of students’ interaction at time t + 1. For the candidate exercise $e_{t+1}$, students will use relevant knowledge to answer this exercise. Whether or not students answer the exercises correctly is closely related to the exercises and students’ relevant knowledge state. The historical accuracy of students on the corresponding KC can also be used as a reference. Therefore, we connected $e{u}_t$, $s{r}_t$, and $c{o}_t$ and then projected them to the output layer through a fully connected network. The predicted performance of students $y_{t+1}$ can be expressed as

$$y_{t+1}=sigmoid\left(W_8^T\left[{eu}_{t+1}\oplus {sr}_t\oplus {co}_t\right]+b_8\right)$$

(16)

where $y_{t+1}$ is the range of (0, 1), representing the predicted performance of students in the next exercise $e_{t+1}$. According to the relationship between $y_{t+1}$ and the threshold, students’ performance is judged. If $y_{t+1}$ is greater than the threshold, it is predicted that students’ answers are correct. Otherwise, it is incorrect. We set the threshold to 0.5.

5. Experiments

5.1. Training Details

To train the LFEKT model, we chose the cross-entropy loss function between the real result of the answer $a_t$ and the predicted value $y_t$ as the objective function and used the Adam optimizer [62] to minimize the objective function:

$$\mathbb{L}\left(\theta \right)=-\sum _{t=1}^T\left(a_{t}log{y}_t+\left(1-a_t\right)log\left(1-y_t\right)\right)+{\lambda }_{\theta }{∥\theta ∥}^2$$

(17)

We conducted experiments on four popular public datasets. Their statistics are shown in

Table 2. Details of all datasets.

Model	ASSISTChall	ASSIST2012	ASSIST2009	Statics2011
Students	1709	29,018	4151	333
Exercises	3162	50,803	17,751	278
Concepts	102	198	123	1178
Answer Time	1326	26,747	140	2031
Interval Time	2839	29,538	25,290	4241
Learning Times	745	335	290	24
Hint Times	41	11	10	50

. For all datasets, 70% of the students were used as the training set, and the rest were used as the test set. Ten-fold cross-validation is the standard for machine learning. Still, the effects of 5-fold, 20-fold, and 10-fold cross-validation are similar. Referring to the experimental settings of AKT [23], RKT [32], and other articles, we performed 5-fold cross-validation to evaluate all models, and each fold was split randomly.

We first sorted the learning records of all students according to their interaction order. For processing the input sequences, we set the input sequence length according to the average length of every dataset. If the length of the sequences was greater than the input sequence length, we sliced them into several unique subsequences based on the input sequence length. If the length of sequence was less than the input sequence length, we padded with a zero vector to the input sequence length. For the dataset ASSIST2009, since there was no start time for answering the exercises, the time interval cannot be calculated. We used the difference of the interaction sequence numbers as the interval time.

Our proposed model was implemented with PyTorch, and to establish the training process, we randomly and uniformly initialized all parameters in the distribution [63]. In LFEKT, a dropout layer was set to prevent overfitting, and its dropout was 0.2. In our implementation, the parameter $d_k$ was set to 256. The $\gamma$ of the enhanced Q matrix was set to 0.03. For all the comparison models, we referred to the settings in the original paper to debug them to the best level. For example, the implementation of AKT on the ASSIST2009 dataset was based on the Rasch model, while on the Statics dataset, due to the lack of corresponding parameters, the implementation of AKT was not based on the Rasch model. All model training was performed on an A100-SXM4 server.

5.2. Datasets

To evaluate our model, we conducted controlled experiments on four real-world public datasets. A brief description of all the datasets is listed as follows:

• ASSISTments 2009 (ASSIST2009) (https://sites.google.com/site/assistmentsdata/home (accessed on 1 March 2022)) was collected by the online intelligent tutoring system ASSISTment [64] and has been widely used in the evaluation of KT models in several papers.
• ASSISTments 2012 (ASSIST2012) (https://sites.google.com/site/assistmentsdata/home (accessed on 1 March 2022)) was also collected from ASSISTments, which contains data and impact forecasts for the 2012–2013 school year.
• ASSISTments Challenge (ASSISTChall) (https://sites.google.com/site/assistmentsdata/home (accessed on 1 March 2022)) belongs to the same source as ASSISTments2009 and ASSISTments2012. The researchers gathered these data from a study that traced secondary school students’ use of teaching assistant blended learning platforms between 2004–2007. The average learning sequence length of students in this dataset is the longest.
• Statics2011 (https://pslcdatashop.web.cmu.edu/DatasetInfo?datasetId=507 (accessed on 1 April 2022)) was provided by the university-level Engineering Statics course and has the most KCs in the four datasets.

5.3. Baseline Models

To illustrate the advantages of LFEKT, we compared LFEKT with several other advanced KT models. We grouped these control models into the following categories.

Classic KT models without deep learning:

• BKT [5] is a classic KT model using the HMM. BKT uses the HMM to trace and represent students’ mastery of KCs.

Classic KT models with deep learning:

• DKT [6] was the first to apply the RNN and LSTM to KT. We used LSTM to simulate students’ changing knowledge state.
• The DKVMN [13] borrowed the idea of a memory network to obtain interpretable students’ knowledge state. When updating students knowledge state, the forgetting mechanism is also considered.
• CKT [34] proposed a student-personalized KT task called convolutional knowledge tracing model, which uses hierarchical convolutional layers to extract personalized learning rates based on continuous learning interactions.

Classic KT models using context encoding:

• SAKT [31] introduced a self-attention mechanism to the KT task and used a transformer model to capture the relationship between students’ learning interactions over time.
• AKT [23] adopted two self-attention encoders that are used to learn the contextual software representations of exercises and answers and combined self-attention and monotonic attention mechanisms to capture long-term temporal information. Besides, AKT also generated an embedding for exercises based on the Rasch model.

Classic KT models that simulate learning and forgetting behavior:

• LPKT [14] recorded the changes after each learning interaction of students, taking into account the impact of students’ learning and forgetting.

5.4. Evaluation Methodology

We used the area under the curve (AUC) and the accuracy (ACC) as the metrics to evaluate the prediction performance. The AUC is defined as the area enclosed by the ROC curve and the lower coordinate axis. The four public datasets are balanced, so an AUC value of 50% represents the prediction performance obtained by random guessing. A high AUC value indicates that the model has a higher prediction performance. The ACC is the accuracy rate, that is the percentage of the correct prediction results in the total results. A high ACC value indicates that the model has a high prediction performance.

5.5. Experimental Results and Analysis

From

Table 3. Results of the comparison methods on performance prediction. We denote by “*” and “**” that LFEKT is significantly better than the corresponding baseline by p < 0.05 and p < 0.01, respectively.

Model	ASSISTChall		ASSIST2012		ASSIST2009		Statics2011
	AUC	ACC	AUC	ACC	AUC	ACC	AUC	ACC
BKT	$0.562{}^{**}$	$0.555{}^{**}$	$0.613{}^{**}$	$0.601{}^{**}$	$0.678{}^{**}$	$0.661{}^{**}$	$0.719{}^{**}$	$0.698{}^{**}$
DKT	$0.724{}^{**}$	$0.693{}^{**}$	$0.730{}^{**}$	$0.737{}^{**}$	$0.741{}^{**}$	$0.708{}^{**}$	$0.815{}^{**}$	$0.723{}^{**}$
DKVMN	$0.711{}^{**}$	$0.684{}^{**}$	$0.725{}^{**}$	$0.735{}^{**}$	$0.739{}^{**}$	$0.618{}^{**}$	$0.814{}^{**}$	$0.722{}^{**}$
CKT	$0.726{}^{**}$	$0.692{}^{**}$	$0.731{}^{**}$	$0.737{}^{**}$	$0.707{}^{**}$	$0.654{}^{**}$	$0.829$	$0.805$
SAKT	$0.661{}^{**}$	$0.679{}^{**}$	$0.725{}^{**}$	$0.736{}^{**}$	$0.735{}^{**}$	$0.679{}^{**}$	$0.803{}^{**}$	$0.797{}^{*}$
AKT	$0.756{}^{**}$	$0.712{}^{**}$	$0.774{}^{**}$	$0.755{}^{*}$	$0.835{}^{*}$	$0.785{}^{**}$	$0.827{}^{*}$	$0.777{}^{**}$
LPKT	$0.799{}^{**}$	$0.741{}^{**}$	$0.777{}^{**}$	$0.758{}^{*}$	$0.760{}^{**}$	$0.729{}^{**}$	$0.771{}^{**}$	$0.763{}^{**}$
LFEKT	$0.853$	$0.771$	$0.795$	$0.766$	$0.841$	$0.809$	$0.835$	$0.807$

, it can be seen that LFEKT had different degrees of improvement for the four datasets compared with the other models, indicating that LFEKT is more effective at predicting students’ performance on exercises.

The advantages of LFEKT are mainly reflected in the following three aspects:

• The KT models based on deep learning outperformed the traditional methods. For all four datasets, DKT, the DKVMN, SAKT, AKT, LPKT, and LFEKT had significant improvements over BKT, which can be seen as the effectiveness of the deep-learning-based KT models.
• Students’ learning and forgetting behavior cannot be ignored. Compared to the traditional KT model, the LSTM-based DKT exhibited excellent performance. However, DKT represents the overall knowledge state of students through the latent vector of LSTM, and it is impossible to obtain students’ mastery of each KC. The DKVMN can represent students’ knowledge mastery on each KC through a value matrix, but it does not consider the forgetting behavior in the learning process. The DKVMN defaults to the students’ mastery of KCs remains unchanged over time and is somewhat straightforward in modeling learning behavior, so the prediction performance of the DKVMN was not as good as that of LFEKT. Both SAKT and AKT use a self-attention mechanism to optimize their performance. AKT combines the Rasch model to enhance exercises’ information, so AKT’s prediction performance was better than that of SAKT. However, AKT only uses a decaying kernel function to simulate the forgetting behavior of students, and LFEKT, which comprehensively models students’ learning and forgetting behavior, performed better and could more accurately predict students’ future performance. Both CKT and LFEKT performed well on the Statics2011 dataset; however, LFEKT performed significantly better than CKT on the other datasets, demonstrating that generality is an advantage of our model.
• The setting of the exercise performance units containing exercise information and students’ answering performance was valid. Compared with LPKT, which also models learning and forgetting effects, LFEKT showed certain advantages on the four datasets. It can be seen that the enhancement of the exercise unit and the performance unit was effective, and encoding the learned sequence context was helpful for improving the prediction performance.

5.6. Ablation Experiments

To investigate how each module and each parameter in LFEKT affects the final result, we designed six variants to conduct ablation experiments on the ASSISTChall dataset:

• LFEKT-NF refers to the LFEKT that does not consider knowledge forgetting, that is the knowledge forgetting layer was removed.
• LFEKT-NL refers to the LFEKT without considering knowledge retention, that is the knowledge absorption layer was removed.
• LFEKT-NCT refers to the LFEKT that does not use LSTM to capture contextual information as set by Equation (5).
• LFEKT-NQ refers to the LFEKT without using an enhanced Q matrix and the rel layer.
• LFEKT-ND refers to the LFEKT that does not introduce difficulty information to enhance the information of the exercise itself.
• LFEKT-NP refers to the LFEKT that does not introduce other answering performances, that is it does not include the answering time and the hint time.

From the results in Figure 3, we can draw some conclusions. First, students’ answering performance is indispensable because it is an important reference for students’ knowledge state in our KT model. Compared to LFEKT, the prediction performance of LFEKT-NP showed the largest prediction performance loss because it simply defines answering performance as answers. Secondly, it can be seen from LFEKT-NL that the role of the knowledge absorption rate cannot be ignored, and ignoring knowledge absorption will lead to a significant loss in prediction performance. Then, the performance of LFEKT-NF decreased to a certain extent, which showed that the forgetting behavior also plays an indispensable role in simulating students’ knowledge state. We set up a knowledge acquisition layer that is always positive to simulate the knowledge growth of students and then controlled the natural decline of students’ knowledge state over time through the knowledge forgetting layer. From LFEKT-NQ, it can be seen that the degree of matching between exercises and KCs also affected the model’s prediction performance, that is the Q matrix described by humans may have some errors. Students’ answering performance is related to their historical learning records. Compared with LFEKT-NCT, LFEKT had a certain degree of improvement, indicating that modeling the learning sequence context can also improve the model’s performance. Finally, it can be seen from LFEKT-ND that simply using the KC as the exercise embedding is not enough to describe the complex information of exercises, and introducing the difficulty of exercises can effectively enrich the input of our model and improve the model’s performance.

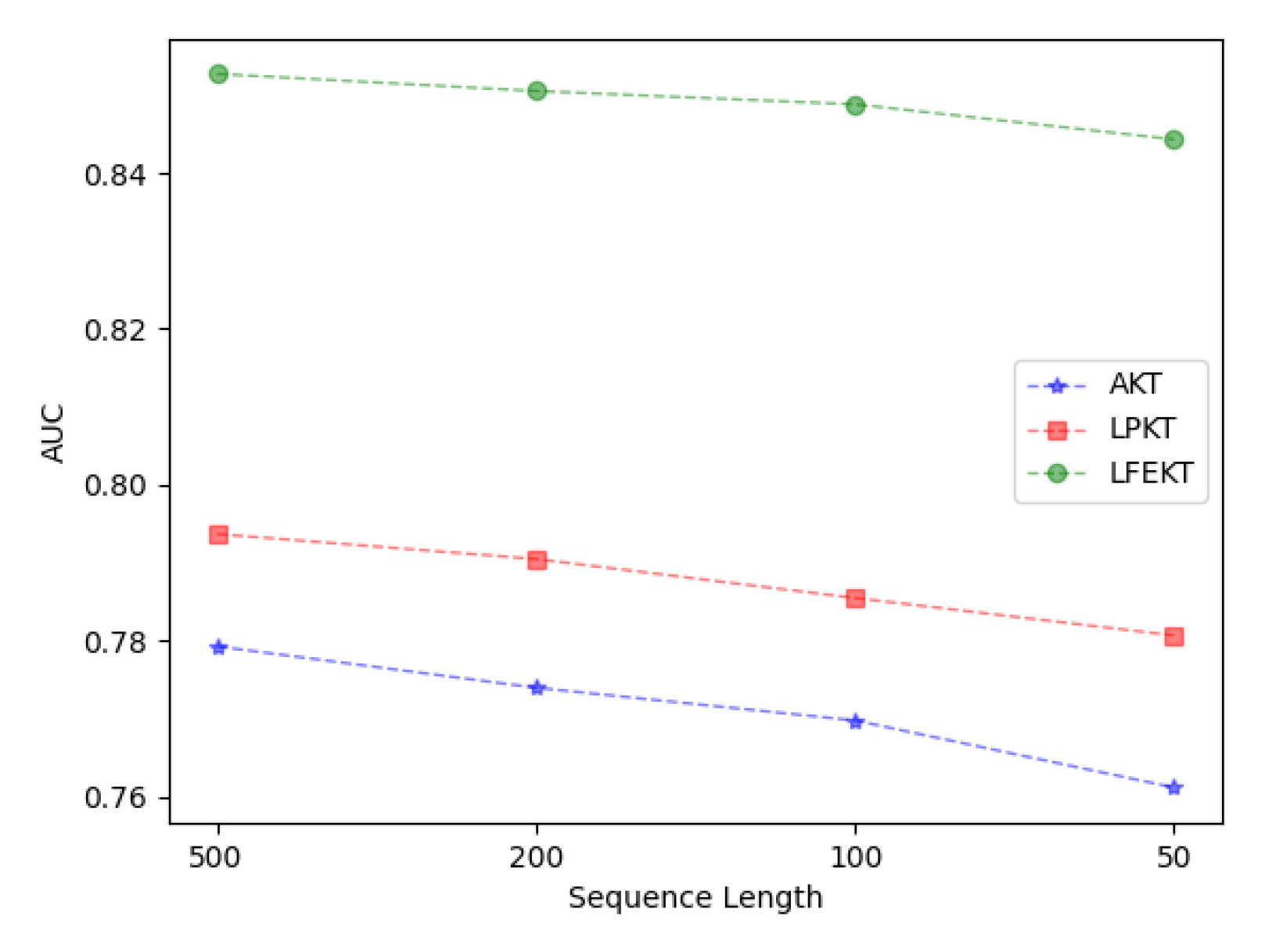
5.7. The Effect of the Length of the Learned Sequence

We also conducted experiments to evaluate how LFEKT is affected by the length of learned sequences.

We compared the student performance prediction results of LFEKT, LPKT, and AKT under different learning sequence lengths. We set four lengths: 50, 100, 200, and 500. Generally speaking, the length of learning sequences represents the completeness of student’s learning process, and the more complete the learning sequence, the more conducive to KT modeling it is. It can also be seen from Figure 4 and Figure 5 that the prediction performance of all models decreased as the sequence length decreased. However, the decrease of LFEKT was smaller than that of the other two comparison models, and finally, a gap can be seen between LFEKT and the other two comparison models. It can be seen that LFEKT can better model student learning, as it was least affected by incomplete learning sequences. In real learning environments, students’ learning sequences are usually incomplete, and LFEKT’s robustness to incomplete sequences is also one of its advantages.

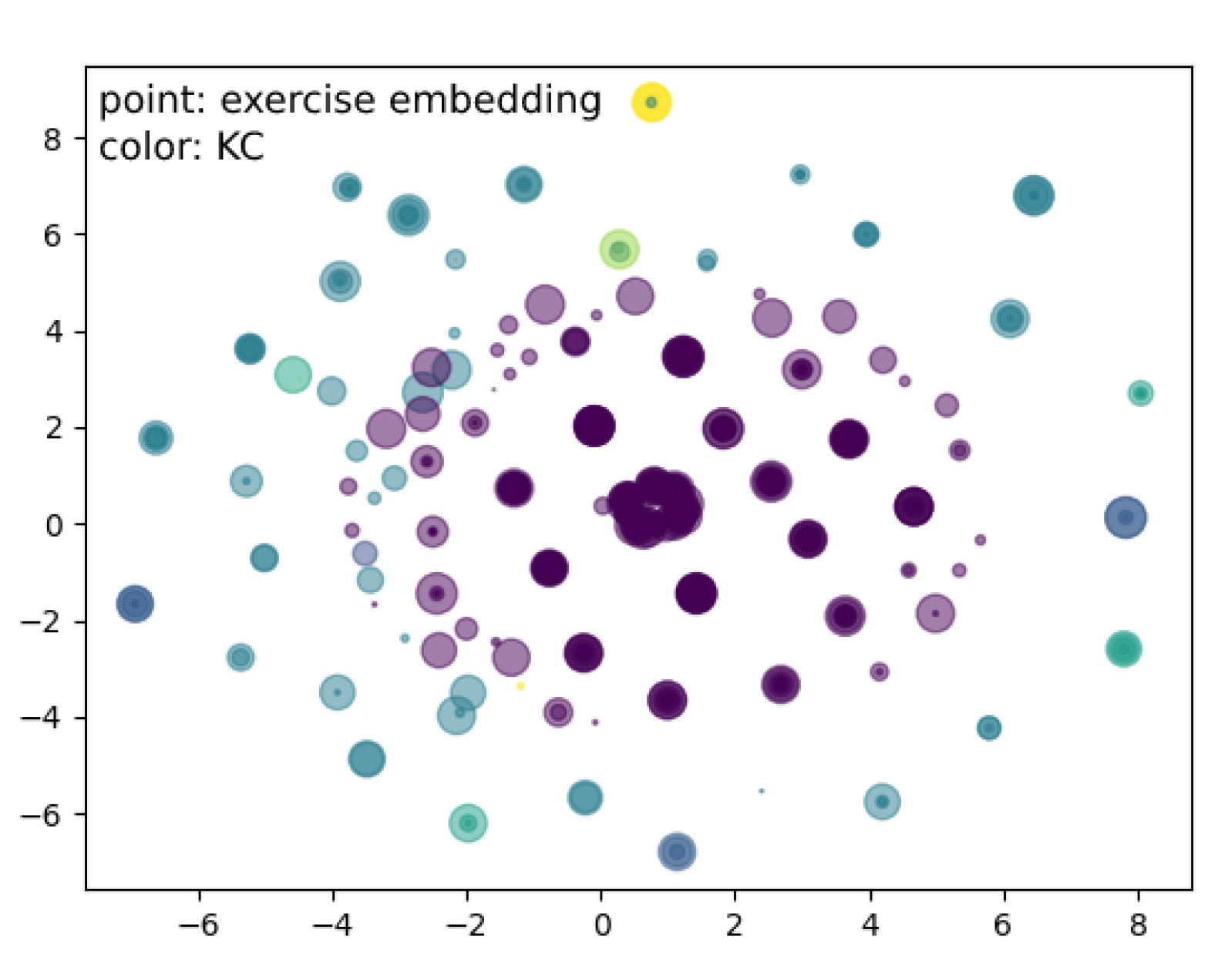
5.8. Knowledge State Visualization

We selected the learning sequences of the same student of length 20 for visualization. Figure 6 shows that LFEKT traced the changing knowledge state over the course of the same student’s learning.

At the beginning, the student’s knowledge state at each KC was set to 0 and was updated through learning. It can be seen that if the student answered correctly, the knowledge state corresponding to the KC increased accordingly. For example, when the student correctly answered the seventh exercise with $K{C}_3$, the knowledge state displayed in the third row increased accordingly. Moreover, we set a constant positive knowledge acquisition. If the student answered incorrectly, the corresponding knowledge state may also improve, but if he/she continuously gives the wrong answers, LFEKT will dynamically adjust his/her knowledge state to an appropriate level. Furthermore, even if the student answers correctly, he/she does not necessarily gain much knowledge, which is related to the difficulty of the exercise and the time to answer the exercise. During the learning process, we can observe that the mastery of a certain KC will be affected by other KCs. For example, the student only learned $K{C}_2$ in Step 8, but the knowledge state of $K{C}_2$ also changed at other times, except for Step 8, mainly because there are potential connections between different KCs, so they may affect the updating of each other’s mastery during learning. Eventually, we can obtain the student’s final knowledge state of each KC, and it can be seen that the student’s knowledge state improved to varying degrees compared with the beginning.

5.9. Effectiveness of Exercise Embedding

To understand how exercises are related to each other, we used t-SNE [65] to visualize them. Figure 7 and Figure 8 present t-SNE visualizations of exercise embeddings $e_t$ and exercise embedding units $e{u}_t$ in the ASSISTChall dataset. Each point in Figure 7 represents the exercise embedding, and each point in Figure 8 represents the exercise embedding unit. The color of points in the figure represents the KCs of the exercises. Points with the same color mean they contain the same KC.

Figure 7 shows that the distribution of exercise embeddings was relatively discrete, and the items of the same KC were not clustered together. Figure 8 shows a clear pattern. The exercise embedding units of the same KC were clustered, and different exercises were differentiated due to their different difficulty levels, which showed that simple exercise embedding cannot capture complex exercise information, while exercise embedding unit vectors can capture the KC and the difficulty of exercises to enrich the differentiated features of exercises. Although not all clustering results were correct, exercise embedding units can expand the information of exercises and improve the prediction performance.

6. Conclusions

In this work, we proposed a new KT model, LFEKT, incorporating pedagogical theory. Our learning process was divided into basic learning units. The basic unit included exercise information, students’ answering performance, and the time interval. We introduced difficulty information to enrich exercise information and introduced the answering times and hint times to enrich the answering performance. To capture the dependencies between exercises, we used LSTM to encode the learned sequence context, and we introduced an augmented Q matrix and added a layer of exercise–KC relations. Then, we combined pedagogical theory to focus on the factors that affect students’ learning behavior and forgetting behavior, measure their knowledge acquisition through the knowledge acquisition layer, and then, obtain students’ real knowledge absorption through the knowledge absorption layer. The forgetting layer simulates the process of knowledge forgetting caused by various forgetting factors and traces the changing process of the knowledge state caused by students’ forgetting behavior in real-time. Experiments on four benchmark datasets in KT research demonstrated the effectiveness and robustness of LFEKT. We also used LFEKT to visualize the change in each student’s knowledge state during the learning process, proving that LFEKT can obtain an interpretable knowledge state.

However, our model also has some limitations, which we will optimize in the future:

• The definition of exercise difficulty is relatively simple and may not be applicable in all educational scenarios. Currently, the Bloom taxonomy [66] is a popular method for determining difficulty. In addition, difficulty may be determined by performing a semantic extraction of the question text. For programming questions with less text information, it is feasible to extract information from suggested answers (i.e., the codes).
• Although our model is robust to changes in sequence length, the prediction performance will still decrease if the length of sequences becomes shorter. In a real learning environment, it is difficult to obtain the complete learning sequences of students. Therefore, achieving better results in short-sequence KT scenarios will also be a very challenging topic.
• In this paper, we integrated educational psychology theory and some neurological theories into our KT model. However, several other learning-related theories should be explored. Bruner learning theory highlighted the significance of learning motivation [67]. The learning process of students is motivated by their high cognitive requirements. Integrating students’ learning motivation into the KT model is a direction that may be explored. Furthermore, students’ learning behavior is a kind of physiological activity, so we can also try something more biologically inspired.
• Most of the public datasets used in current research are balanced, but real-world data are likely to be unbalanced. How to deal with unbalanced data and perform the corresponding preprocessing are questions to be studied.