Research on Optimization of Public Opinion Supervision Model of Social Network Platform Based on Evolutionary Game

Abstract

Network environments have recently emerged as a considerable research area. In addition to government supervision, platform supervision is also critical to improve network environments. So, we should improve the social network platform’s single regulatory model. Against this background, we described public opinion supervision as a game between marketing accounts, netizens, and the platform. Unlike previous studies, we considered the influence of marketing accounts on online public opinion. Because of the players’ bounded rationality, we built an evolutionary game model, and by solving it, we obtained the evolutionarily stable strategy (ESS). Then, we analyzed the influence of relevant parameters on the evolutionary stable state. Our research results show that if the authenticity of the information is not high, to not publish is the best choice for the marketing account, and to not participate is the best choice for the netizen. The platform penalty for the marketing account is also directly related to the marketing account’s decision making. The platform penalty for the government, as well as the increase in the penalty risk coefficient, considerably affected the choice of platform. Finally, we put forward the “pre-event–in-the-event–post-event” three-stage supervision model, which provides countermeasures and suggestions for all parties to jointly maintain the network environment.

1. Introduction

According to the China Mobile Internet Development report (2022), by the end of 2021, there will be an online population of 4.9 billion, accounting for about 63% of the global population [1]. The blue book cites International Telecommunication Union (ITU) data to show that the global online population increased by 19.5% during 2019 (4.1 billion) after the start of the global COVID-19 pandemic. Under the influence of COVID-19, humanity has further accelerated the process of entering digital life. Surfing the Internet has become necessary for people to work, live, and study. With the rapid development of the Internet, the popularity of online media has also considerably increased, becoming a considerable channel for the public to obtain information and express opinions [2]. However, the increase in the number of netizens and continued growth of Internet penetration have brought considerable challenges for the governance of network environments. At the same time, there are also a series of governance problems regarding online public opinion, resulting in the network environments of social platforms becoming the focus of national public attention.

At present, it is difficult to distinguish between true and false information on the Internet, with content credibility often being mixed [3]. Some groups even publish special opinions to gain attention, spreading rumors about hot spots and emergencies. An example is the “marketing account”. Generally, negative marketing accounts often appear for political purposes and commercial interest, in addition to being used to vent personal anger and spread habitual rumors, among other types of marketing accounts. When netizens face explosive network information, they are subject to information noise and the limitations of self-judgment. They often become disseminators of unknown information, which gradually evolves into cyber language violence or group irrational dilemmas. Negative energy and extreme public opinion communication will not only interfere with network life but also affect real life, bringing great harm to economic and social development. The effective governance of the Internet environment is an urgent problem for all sectors of society [4]. Therefore, how to strengthen the supervision of network media, such as marketing accounts, is a considerable research direction for network environment governance.

However, due to the government’s information asymmetry, high regulatory costs, and the diversity of participants, problems such as the low efficiency of government regulation and imperfect information mechanisms still exist. This has led to inadequate network environment governance. Therefore, social platforms are needed to assist the government to supervise and govern the network environment. In fact, the network information environment is the result of the interests of the relevant subjects, and the root cause of confusion is the imbalance of interests. Each participant focuses on economic benefits while ignoring the negative social effects generated by their own behavior.

In view of the above analysis, based on the bounded rationality assumption, we introduce the marketing account into the dynamic game system to build an evolutionary game model, which consists of the marketing account, netizens, and the platform. We use the evolutionary game method to analyze the behavior choices and strategy interactions of the three actors in the process of network environment governance. Using MATLAB for numerical simulation, we build an environmental governance mechanism for the Internet, in which multiple subjects, such as the marketing account, netizens, and platforms, participate in coordination. We also analyze the influence of various factors on system stability to identify the considerable links in the network’s environmental governance mechanism and clarify the direction and focus of future policy formulation.

This paper is organized as follows: Section 2 provides a literature review. Section 3 provides the problem description and notations. Section 4 shows the evolutionary game model of public opinion supervision, as well as our analysis of evolutionary stable strategies. Section 5 gives an impact analysis of some of the parameters for the game’s evolutionary stable strategies. Finally, our conclusions are presented in Section 6.

2. Literature Review

Information dissemination is a social network platform’s basic function. When it brings freedom of speech to every netizen, there are also many hidden dangers. The anonymity of information gives many unscrupulous people the opportunity to recklessly publish false and radical statements [5]. Once the passive voice spreads, public opinion will surge and become the focus of netizens’ attention and discussion [6]. However, supervision of online media, such as marketing accounts, is not in place due to a lack of supervision in the Internet industry. The government has constantly been improving relevant laws and regulations regarding network environment governance, and the implementation of relevant public opinion policies has also greatly improved the network environment. However, most of the current policies and regulations are measures taken after the outbreak of public opinion, and supervision has a certain lag. Therefore, optimizing a social network platform’s supervision model is necessary for purifying the network environment.

Many scholars have conducted research on the dissemination and governance of public opinion. Chen et al. (2013) [7] analyzed the relevant literature on the evolution of online public opinion in China and summarized the main views of various scholars. Huang et al. (2017) [8] summarized the influencing factors of changes in the popularity of online public opinion to better control guidance for decision makers. Chen (2020) [9] constructed a multi-layer coupling network of public opinion communication, including the “WeChat layer–microblog layer–control layer”, in addition to a public opinion control model. They also studied media guidance and government intervention strategies regarding multi-platform interactive communication. Zhang et al. (2018) [10] used the improved SIR model to analyze news-event data collected from Weibo and WeChat, visualizing the cross-network information dissemination process. Song et al. (2021) [11] also improved the SIR model, constructed the car model of simultaneous transmission of positive and negative information, and simulated the transmission process of public opinion.

In addition, many scholars have also used the game theory method to study the spread of public opinion in networks. Jiang et al. (2106) [3] simulated the public opinion information game process between the government and netizen and determined the best time for the government to intervene regarding public opinion on the Internet. Guo et al. (2019) [12] proposed an information dissemination model based on evolutionary game theory, which simulates the strategic choice of individuals when facing two competitive messages in social networks. Wang et al. (2020) [13] constructed a three-party evolutionary game model and proposed public opinion communication management strategies and critical intervention points. In addition, Wen et al. (2020) [14] constructed a tripartite game between the media, college students, and managers, and discussed the evolution mechanism of college network public opinion events. Xie et al. (2020) [15] built a tripartite game between doctors, the government, and netizens based on the network public opinion of the doctor–patient relationship, and they found the main factors affecting participants’ behavior. Deng (2021) [16] also used game theory to analyze the profits and losses of relevant subjects in public opinion information dissemination on public health emergencies. Li et al. (2017) [17] constructed a tripartite game of government, online media, and the public to analyze the action-strategy mechanisms of various subjects on the restoration of social trust in response to the public crisis caused by animal epidemics.

Based on the evolutionary game, some scholars also introduced mechanisms and models to conduct in-depth research on the dissemination and supervision of network public opinion. Hou et al. (2021) [18] combined traditional evolutionary game theory and complex network theory to put forward the network communication game model of competitive public opinion information. Then, they theoretically analyzed the profit conditions and group sizes of positive public opinion information communication. Qi et al. (2020) [19] introduced the central-government penalty mechanism and compared the game between online media and the government. Meanwhile, they provided new methods for the central government to solve the problem of public opinion governance during emergencies by using multi-scenario evolution. Chen et al. (2017) [20] introduced the BA scale-free network into game theory, and they put forward policy suggestions from the perspective of the government by building a multi-agent network model. Based on the “situation response” model, Yang and Qi (2018) [21] used evolutionary game theory to study the evolutionary process of the group strategy selection of network public opinion communicators and network public opinion guides in sudden network public opinion events. Chen et al. (2017) [22] introduced prospect theory based on the evolutionary game and explored the model of political media cooperation to govern network public opinion.

From our above analysis, we discerned that scholars have performed much research on the dissemination and supervision of online public opinion. However, there is less research on the impact of marketing accounts on disseminating online public opinion. Marketing accounts are an essential participant in online public opinion communication and they can promote the spread of public opinion. Therefore, the platform and various regulatory departments must supervise the marketing account. In addition, the game subjects are characterized by bounded rationality, and evolutionary game theory is considered to participate in the subjects of bounded rationality and time consistency so that the equilibrium result is a repeated, constantly revised, and improved process. Based on this, we built a three-party “marketing account–netizen–platform” evolutionary game model to discuss the stability strategies of the network public opinion supervision system under different circumstances, and we analyzed the influence of relevant parameters on the equilibrium state of the system. Then, we put forward the supervision countermeasures for transforming from a single “post-event” supervision model to a diversified “pre-event–in-the-event–post-event” three-stage supervision model. We also provide suggestions for optimizing the network environment.

3. Problem Description and Notations

3.1. Problem Description

Most of the online media that can affect the direction of public opinion are marketing accounts. Because the marketing account has too many negative colors, it will carry out a secondary processing of information or publish information obtained from informal channels. Therefore, the authenticity and comprehensiveness of its content need to be verified because popular marketing accounts can easily affect the direction of public opinion. Assuming that the platform does not supervise and review information, marketing accounts will take the opportunity to publish harmful, fabricated, or offensive information, which can quickly spread among netizens and potentially foment unrest. Therefore, to avoid potential chaos resulting from the dissemination of information on major social platforms, government regulators are also gradually improving the corresponding laws and supervisions. However, to better purify the network environment, the platform is also required to play a crucial role in actively supervising the marketing account to ensure that it can correctly guide public opinion. Therefore, the choice of behavior strategies of marketing accounts, netizens and social platforms is crucial to whether the public opinion crisis will break out and whether it will further ferment after the outbreak. Figure 1 shows the relationship between the relevant subjects of public opinion dissemination and supervision on social networking platforms.

3.2. Assumptions

Based on the above problem description, we put forward the following basic assumptions:

Assumption 1.

Regarding the evolution of network public opinion, multiple interests are involved. The main stakeholders investigated in our study are marketing accounts, netizens, and social network platforms. All stakeholders are characterized by bounded rationality. We use evolutionary game theory to build a three-party “marketing account–netizen–platform” game model and analyze the evolutionary stability of the game subjects in different cases, as well as the impact of changes in relevant parameters on the strategy choices of the game subject.

Assumption 2.

For the sake of social responsibility or traffic benefits, the marketing account may choose to publish or not publish, and the publish strategy is recorded as$h_1$, the not-publish strategy is recorded as$h_2$, and the strategy is set as$S_1=\left\{h_1,\left.h_2\right\}\right.$. Affected by their own factors and the external environment, a netizen may choose to participate or not participate. The participate strategy is recorded as$l_1$the not-participate strategy is recorded as$l_2$, and the strategy is set as$S_2=\left\{l_1,\left.l_2\right\}\right.$. The social network platform may utilize positive supervision measures toward marketing accounts in consideration of reputation and government regulation or take negative supervision measures against marketing accounts in consideration of public opinion supervision costs or marketing advertising revenue. The strategy of adopting positive supervision is recorded as$r_1$, the strategy of adopting negative supervision is recorded as$r_2$, and the strategy is set as$S_3=\{r_1,r_2\}$.

Assumption 3.

The probability of the marketing account adopting the publish behavior strategy is$x$, and the probability of adopting the not-publish behavior strategy is$1-x$. The probability of the netizen adopting the participating strategy is$y$, and the probability of adopting the not-participate strategy is$1-y$. The probability of the platform adopting the positive supervision strategy is$z$, and the probability of adopting the negative supervision strategy is $1-z$. $x$, $y$and$z$are both shown as a function of time, where$x=x\left(t\right),y=y\left(t\right),z=z(t)$,$0\le x\le 1$,$0\le y\le 1$,$0\le z\le 1$.

3.3. Notations

To express the income matrix of each subject and ensure the objectivity of parameter setting as much as possible, we set the parameters considering the three perspectives of cost, loss, and income based on a large number of references and in combination with the actual network marketing scenarios (

Table 1. Parameters and implications.

	Parameters	Implications
Marketing account	$C_{11}$	The marketing cost.
	$P_{11}$	Losses of public message delay, such as less traffic.
	$\beta$	Publish the delay degree, and the range of values is $(0,1)$.
	$P_{12}$	In the case of negative marketing, the penalty of the platform to the marketing account.
	$\alpha$	The degree-of-truthfulness of information, and the range of values is $(0,1)$.
	$P_{13}$	Losses of not publishing, such as the decline in Internet attention or the departure of advertisers.
	$R_{11}$	Under the positive supervision of the platform, the marketing account obtains a large amount of traffic and advertising revenue.
	$R_{12}$	Under the negative supervision of the platform, the marketing account obtains excellent attention and traffic ($R_{12}>R_{11}$).
Netizen	$C_{21}$	The cost of netizen participation.
	$P_{21}$	Netizen could be punished for participating in the spread of the topic, including platform penalty and government penalty.
	$R_{21}$	Benefits gained by netizen through participating in topics, such as psychological satisfaction and identity.
	$R_{22}$	When the platform positively supervises, netizens enjoy the benefits brought by social stability.
Platform	$C_{31}$	The cost of positive supervision, such as workforce, time, and energy.
	$C_{32}$	The cost of negative supervision, such as workforce, time, and energy $(C_{31}>C_{32})$.
	$P_{31}$	Losses caused by positive supervision, such as excessive pursuit of traffic causing marketing account withdrawal.
	$P_{32}$	Losses of negative supervision, such as netizens quitting because of the platform’s public opinion atmosphere.
	$P_{33}$	The penalty intensity of the government to the platform.
	$\gamma$	The penalty risk coefficient of the government to the platform. The range of values is $(0,1)$.
	$R_{31}$	The benefits of the platform include improving the credibility of the platform and gaining a good reputation.
	$R_{32}$	Revenue under positive supervision of the platform when the marketing account publishes information.
	$R_{33}$	Revenue under negative supervision of the platform when the marketing account publishes information and netizens participate.
	$R_{34}$	Revenue under negative supervision of the platform when the marketing account publishes information.

).

4. Model

According to the above model assumptions, we can obtain the tripartite game income matrix of marketing accounts, netizen, and platforms, as shown in

Table 2. Pay-off matrix of three-party evolution game.

Game Participants	Marketing Account	Netizen	Platform
(Publish, Participate, Positive Supervision)	$R_{11}-C_{11}-\beta P_{11}-(1-\alpha )P_{12}$	$R_{21}+R_{22}-C_{21}-P_{21}$	$R_{31}+R_{32}-C_{31}-P_{31}$
(Publish, Not Participate, Positive Supervision)	$-C_{11}-(1-\alpha )P_{12}$	$0$	$R_{32}-C_{31}$
(Not Publish, Participate, Positive Supervision)	$-P_{13}$	$R_{22}-C_{21}$	$R_{31}-C_{31}$
(Not Publish, Not Participate, Positive Supervision)	$0$	$0$	$-C_{31}$
(Publish, Participate, Negative Supervision)	$R_{12}-C_{11}-\beta P_{11}$	$R_{21}-C_{21}-P_{21}$	$R_{33}+R_{34}-C_{32}-P_{32}-\gamma P_{33}$
(Publish, Not Participate, Negative Supervision)	$-C_{11}$	$0$	$R_{34}-C_{32}-\gamma P_{33}$
(Not Publish, Participate, Negative Supervision)	$-P_{13}$	$-C_{21}$	$-C_{32}-P_{32}-\gamma P_{33}$
(Not Publish, Not Participate, Negative Supervision)	$0$	$0$	$-C_{32}-\gamma P_{33}$

.

In the governance of online public opinion marketing events, the selection strategies of the three parties toward the game are characterized as bounded rationally. By the stability of duplicate dynamic equations, we can obtain the game equilibrium point. According to the above assumptions, we built a three-party evolutionary game model of marketing accounts, netizens, and platforms and described its evolution process. The strategic expectations and average income of all parties are as follows:

$U_{11}$ represents the expectation when the marketing account adopts the publish strategy, $U_{12}$ represents the expectation when the marketing account adopts the not-publish strategy, and $\overline{U_1}$ represents the average income of the marketing account:

$$U_{11}=yz{R}_{11}+y\left(1-z\right)R_{12}-C_{11}-y\beta P_{11}-z(1-\alpha )P_{12}$$

(1)

$$U_{12}=-y{P}_{13}$$

(2)

$$\overline{U_1}=x{U}_{11}+(1-x)U_{12}=xyz{R}_{11}+xy\left(1-z\right)R_{12}-x{C}_{11}-xy\beta P_{11}-xz(1-\alpha )P_{12}-(1-x)y{P}_{13}$$

(3)

$U_{21}$ represents the expectation of netizens when they adopt the participate strategy, $U_{22}$ represents the expectation of netizens when they adopt the not-participate strategy, and $\overline{U_2}$ represents the average income of a netizen:

$$U_{21}=x{R}_{21}+z{R}_{22}-C_{21}-x{P}_{21}$$

(4)

$$U_{22}=0$$

(5)

$$\overline{U_2}=y{U}_{21}+(1-y)U_{22}=xy{R}_{21}+yz{R}_{22}-y{C}_{21}-xy{P}_{21}$$

(6)

$U_{31}$ represents the expectation of the platform when it adopts a positive supervision strategy, $U_{32}$ represents the expectation of the platform when it adopts a negative supervision strategy, and $\overline{U_3}$ represents the average income of the platform:

$$U_{31}=y{R}_{31}+x{R}_{32}-C_{31}-xy{P}_{31}$$

(7)

$$U_{32}=xy{R}_{33}+x{R}_{34}-C_{32}-y{P}_{32}-\gamma P_{33}$$

(8)

$$\overline{U_3}=z{U}_{31}+(1-z)U_{32}=yz{R}_{31}+xz{R}_{32}+xy(1-z)R_{33}+x(1-z)R_{34}-z{C}_{31}-(1-z)C_{32}-xyz{P}_{31}-y(1-z)P_{32}-(1-z)\gamma P_{33}$$

(9)

According to the above strategic expectations and average returns of all parties, we can further obtain the replication dynamic equation of all parties and analyze the stability of the game strategy.

The replication dynamic equation of the marketing account is

$$f(x)=\frac{dx}{dt}=x(U_{11}-\overline{U_1})=x(1-x)[yz{R}_{11}+y(1-z)R_{12}-C_{11}-y\beta P_{11}-z(1-\alpha )P_{12}+y{P}_{13}]$$

(10)

If $y*=\frac{C_{11}+z(1-\alpha )P_{12}}{z{R}_{11}+(1-z)R_{12}-\beta P_{11}+P_{13}}$, $f(x)=\frac{dx}{dt}=0$. No matter how much the value of $x$ is, both marketing account strategies can achieve a stable state.

If $y>\frac{C_{11}+z(1-\alpha )P_{12}}{z{R}_{11}+(1-z)R_{12}-\beta P_{11}+P_{13}}$, $x=0$ or $x=1$, and $f(x)=\frac{dx}{dt}=0$, this is a steady state, while if $\frac{df(x)}{dx}\left|{}_{x=1}\right.<0$, $\frac{df(x)}{dx}\left|{}_{x=0}\right.>0$, and $x=1$ is the equilibrium solution, publish is the marketing account’s stable strategy. Otherwise, $x=0$ is the equilibrium solution and not publish is the marketing account’s stable strategy.

The replication dynamic equation of the netizen is:

$$f(y)=\frac{dy}{dt}=y(U_{21}-\overline{U_2})=y(1-y)[x{R}_{21}+z{R}_{22}-C_{21}-x{P}_{21}]$$

(11)

If $z*=\frac{C_{21}+x{P}_{21}-x{R}_{21}}{R_{22}}$, $f(y)=\frac{dy}{dt}=0$, and no matter how much the value of $y$ is, both netizen strategies can achieve a stable state.

If $z>\frac{C_{21}+x{P}_{21}-x{R}_{21}}{R_{22}}$, $y=0$ or $y=1$, and $f(y)=\frac{dy}{dt}=0$, this is a steady state and if $\frac{df(y)}{dy}\left|{}_{y=1}\right.<0$, $\frac{df(y)}{dy}\left|{}_{y=0}\right.>0$, and $y=1$ is the equilibrium solution, participate is the netizen’s stable strategy. Otherwise, $y=0$ is the equilibrium solution and not participate is the netizen’s stable strategy.

The replication dynamic equation of the platform is:

$$f(z)=\frac{dz}{dt}=z(U_{31}-\overline{U_3})=z(1-z)[y{R}_{31}+x{R}_{32}-C_{31}-xy{P}_{31}-xy{R}_{33}-x{R}_{34}+C_{32}+y{P}_{32}+\gamma P_{33}]$$

(12)

If $x*=\frac{C_{31}-C_{32}-\gamma P_{33}-y{P}_{32}-y{R}_{31}}{R_{32}-R_{34}-y{R}_{33}-y{P}_{31}}$, $f(z)=\frac{dz}{dt}=0$. No matter how much the value of $z$ is, both strategies of the platform can achieve a stable state.

If $x>\frac{C_{31}-C_{32}-\gamma P_{33}-y{P}_{32}-y{R}_{31}}{R_{32}-R_{34}-y{R}_{33}-y{P}_{31}}$, $z=0$ or $z=1$, and $f(z)=\frac{dz}{dt}=0$, this is a steady state, while if $\frac{df(z)}{dz}\left|{}_{z=1}\right.<0$, $\frac{df(z)}{dz}\left|{}_{z=0}\right.>0$, and $z=1$ is the equilibrium solution, positive supervision is the platform’s stable strategy. Otherwise, $z=0$ is the equilibrium solution and negative supervision is the platform’s stable strategy.

Based on the above analysis, we can obtain the following nine equilibrium points: $(0,0,0)$, $(1,0,0)$, $(0,1,0)$, $(0,0,1)$, $(1,1,0)$, $(1,0,1)$, $(0,1,1)$, $(1,1,1)$, $(x*,y*,z*)$. Then, the Jacobian matrix is as follows:

$$J1=\left[\begin{array}{ccc}\frac{\partial f(x)}{\partial x}& \frac{\partial f(x)}{\partial y}& \frac{\partial f(x)}{\partial z}\\ \frac{\partial f(y)}{\partial x}& \frac{\partial f(y)}{\partial y}& \frac{\partial f(y)}{\partial z}\\ \frac{\partial f(z)}{\partial x}& \frac{\partial f(z)}{\partial y}& \frac{\partial f(z)}{\partial z}\end{array}\right]=\left[\begin{array}{ccc}{K}_{11}& K_{12}& K_{13}\\ K_{21}& K_{22}& K_{23}\\ K_{31}& K_{32}& K_{33}\end{array}\right]$$

where:

$$\begin{array}{}{K}_{11}=(1-2x)[yz{R}_{11}+y(1-z)R_{12}-C_{11}-y\beta P_{11}-z(1-\alpha )P_{12}+y{P}_{13}]\\ K_{12}=x(1-x)[z{R}_{11}+(1-z)R_{12}-\beta P_{11}+P_{13}]\\ K_{13}=x(1-x)[y{R}_{11}-y{R}_{12}-(1-\alpha )P_{12}]\\ K_{21}=y(1-y)[R_{12}-P_{21}]\\ K_{22}=(1-2y)[x{R}_{21}+z{R}_{22}-C_{21}-x{P}_{21}]\\ K_{23}=y(1-y)R_{22}\\ K_{31}=z(1-z)(R_{32}-y{P}_{31}-y{R}_{33}-R_{34})\\ K_{32}=z(1-z)[R_{31}-x{R}_{33}-x{P}_{31}+P_{32}]\\ K_{33}=(1-2z)[y{R}_{31}+x{R}_{32}-C_{31}-xy{P}_{31}-xy{R}_{33}-x{R}_{34}+C_{32}+y{P}_{32}+\gamma P_{33}]\end{array}$$

Friedman believes that the stability of the equilibrium point can be analyzed by a Jacobian matrix. According to Lyapunov stability theory, the asymptotic stability at the equilibrium point can be judged by analyzing the eigenvalues of the Jacobian matrix. If and only if all eigenvalues are less than zero, that is, ${\lambda }_i<0$, the equilibrium point is the stable point of the evolutionary game. The system’s stability conditions are shown in

Table 3. Stability conditions.

Equilibrium Point	Stability Conditions	No.
$(0,0,0)$	$-C_{11}<0$, $-C_{21}<0$, $\gamma P_{33}+C_{32}<C_{31}$	1
$(0,0,1)$	$-C_{11}-(1-\alpha )P_{12}<0$, $R_{22}<C_{21}$, $C_{31}<C_{32}+\gamma P_{33}$	2
$(0,1,0)$	$R_{12}+P_{13}<C_{11}+\beta P_{11}$, $C_{21}<0$, $R_{31}+P_{32}+\gamma P_{33}+C_{32}<C_{31}$	3
$(1,0,0)$	$C_{11}<0$, $R_{21}<C_{21}+P_{21}$, $R_{32}+\gamma P_{33}+C_{32}<R_{34}+C_{31}$	4
$(1,1,0)$	$\beta P_{11}+C_{11}<R_{12}+P_{13}$, $C_{21}+P_{21}<R_{21}$, $R_{31}+R_{32}+P_{32}+\gamma P_{33}+C_{32}<R_{33}+R_{34}+P_{31}+C_{31}$	5
$(1,0,1)$	$C_{11}+(1-\alpha )P_{12}<0$, $R_{21}+R_{22}<C_{21}+P_{21}$, $R_{34}+C_{31}<R_{32}+\gamma P_{33}+C_{32}$	6
$(0,1,1)$	$R_{11}+P_{13}<\beta P_{11}+(1-\alpha )P_{12}+C_{11}$, $C_{21}<R_{22}$, $C_{31}<R_{31}+P_{32}+\gamma P_{33}+C_{32}$	7
$(1,1,1)$	$\beta P_{11}+(1-\alpha )P_{12}+C_{11}<R_{11}+P_{13}$, $C_{21}+P_{21}<R_{21}+R_{22}$, $R_{33}+R_{34}+P_{31}+C_{31}<R_{31}+R_{32}+P_{32}+\gamma P_{33}+C_{32}$	8

.

According to the above-related parameters, $C_{ij}>0,P_{ij}>0,R_{ij}>0$, conditions 3, 4, and 6 are not tenable, that is, equilibrium points $(0,1,0)$, $(1,0,0)$, $(1,0,1)$ are unstable. This means that the three situations are unstable. The three parties to the game will undoubtedly continue to play according to the current situation. However, the remaining five equilibrium points cannot be directly judged as stable game points according to the conditions. Therefore, this paper gives the system’s evolutionary stability strategy under different conditions, as shown in Proposition 1.

Proposition 1.

case a: If$\gamma P_{33}+C_{32}<C_{31}$, the ESS of the system is$(0,0,0)$.

case b: If$R_{22}<C_{21}$,$\gamma P_{33}+C_{32}>C_{31}$, the ESS of the system is$(0,0,1)$.

case c: If$C_{11}+\beta P_{11}<R_{12}+P_{13}$,$R_{21}>C_{21}+P_{21}$,$R_{31}+R_{32}+P_{32}+\gamma P_{33}+C_{32}<R_{33}+R_{34}+P_{31}+C_{31}$, the ESS of the system is$(1,1,0)$.

case d: If$\beta P_{11}+(1-\alpha )P_{12}+C_{11}>R_{11}+P_{13}$,$R_{22}>C_{21}$,$R_{31}+P_{32}+\gamma P_{33}+C_{32}>C_{31}$, the ESS of the system is$(0,1,1)$.

case e: If$\beta P_{11}+(1-\alpha )P_{12}+C_{11}<R_{11}+P_{13}$,$R_{21}+R_{22}>C_{21}+P_{21}$,$R_{33}+R_{34}+P_{31}+C_{31}<R_{31}+R_{32}+P_{32}+\gamma P_{33}+C_{32}$, the ESS of the system is$(1,1,1)$.

According to the evolutionary game model constructed above, we used MATLAB to analyze the evolutionary process. We set the parameters shown in

Table 4. Initial parameter values.

${\mathit{C}}_{11}$	${\mathit{P}}_{11}$	${\mathit{P}}_{12}$	${\mathit{P}}_{13}$	${\mathit{R}}_{11}$	${\mathit{R}}_{12}$	${\mathit{C}}_{21}$	${\mathit{P}}_{21}$	${\mathit{R}}_{21}$	${\mathit{R}}_{22}$	${\mathit{C}}_{31}$	${\mathit{C}}_{32}$	${\mathit{P}}_{31}$	${\mathit{P}}_{32}$	${\mathit{P}}_{33}$	${\mathit{R}}_{31}$	${\mathit{R}}_{32}$	${\mathit{R}}_{33}$	${\mathit{R}}_{34}$
20	10	10	10	15	25	23	15	40	20	20	10	8	8	8	20	30	25	20

. By setting parameters, we provide the evolution trend of the above five propositions in Figure 2. We set the parameter values as $\alpha =\beta =\gamma =0.5$, and we set the other baseline parameter values as follows:

The above five propositions give the system’s evolution- and stability-trend chart in these five cases. Under changing circumstances, increasing the government’s penalty to the platform can promote positive supervision, that is, enact a strategic change from case (a) to (b). With the positive supervision of the platform, increasing the benefits of netizen participation can encourage netizens to engage in topical discussions, that is, enact a strategic change from case (b) to (c). On this basis, reducing the marketing account’s publishing cost can encourage it to choose the publishing strategy, that is, enact a strategic change from case (c) to (d). In case (d), if the cost of the positive supervision of the platform increases, the platform will turn to negative supervision, that is, enact a strategic change from case (d) to (e). Furthermore, except for the parameters given in the figure, the other parameters are the initial values.

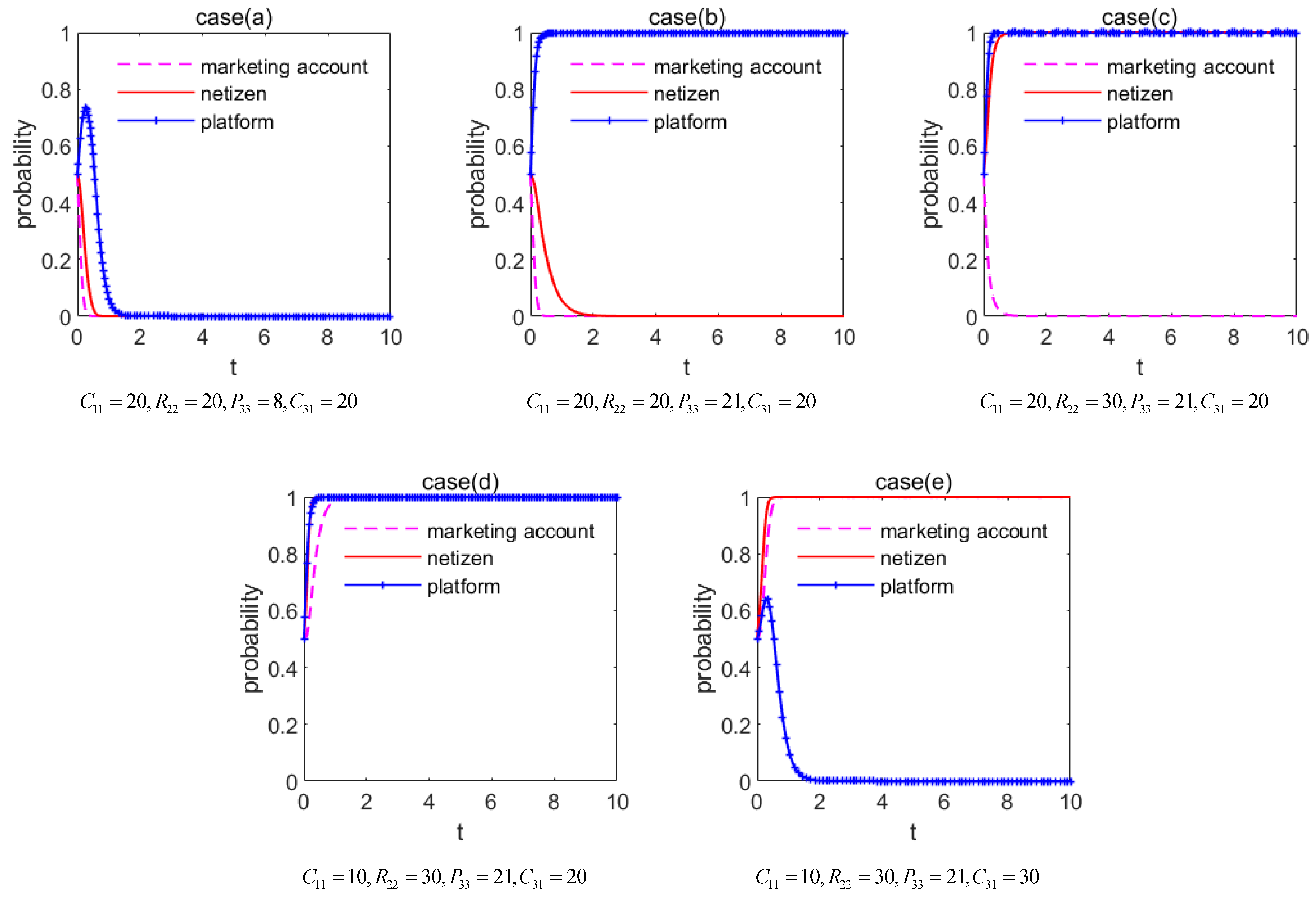
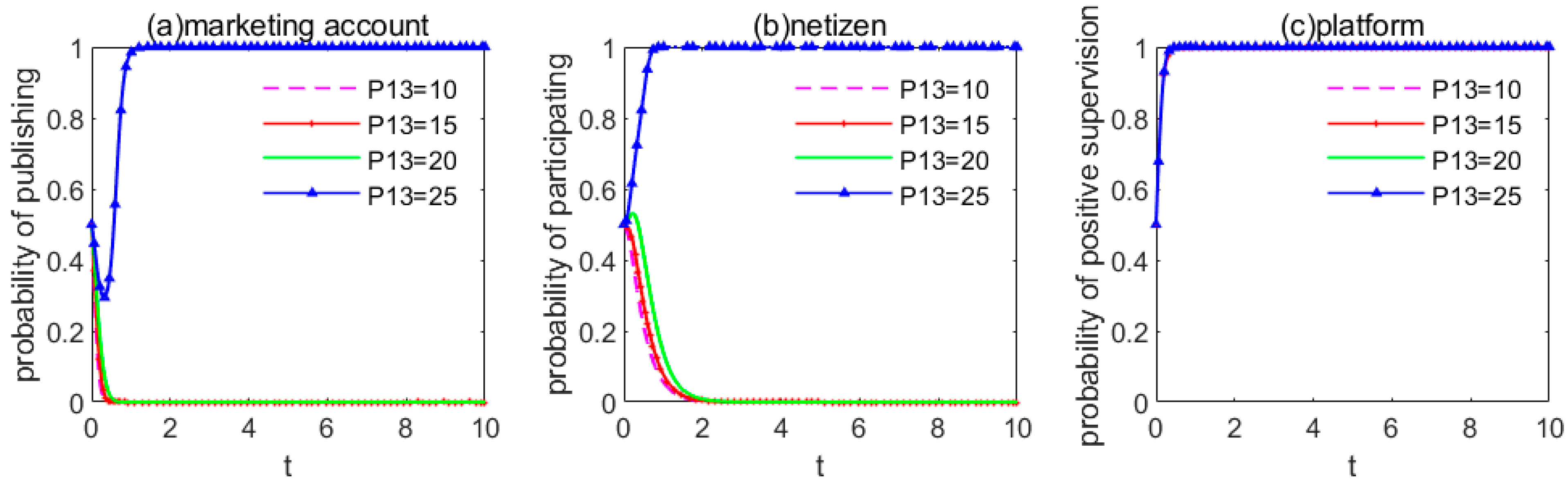
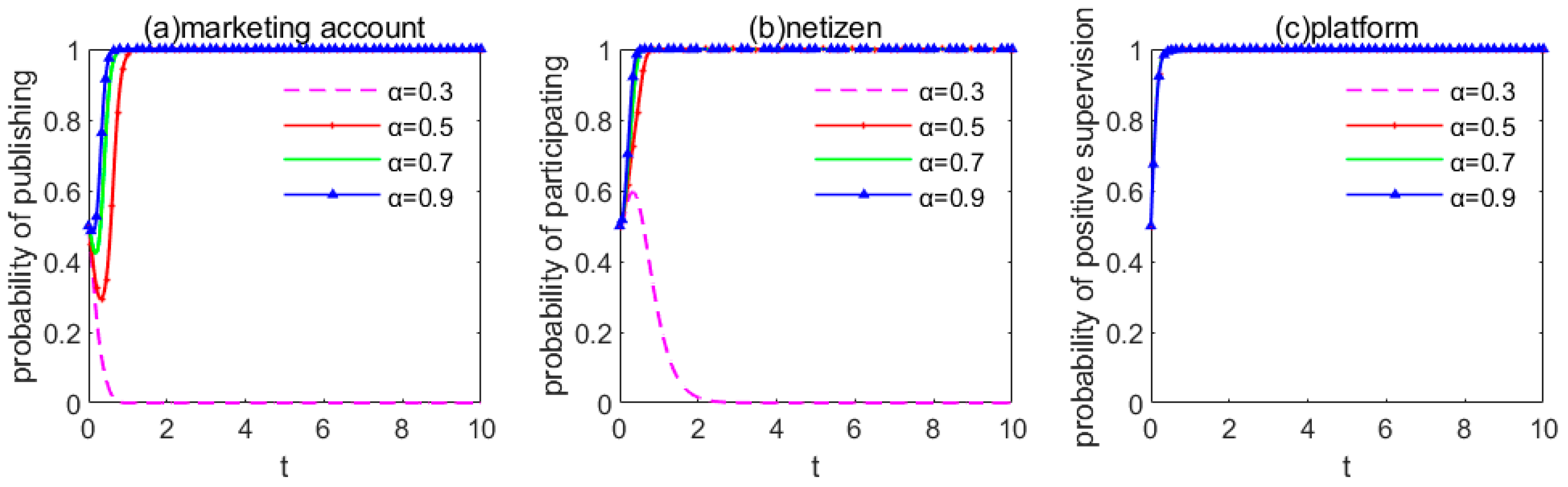
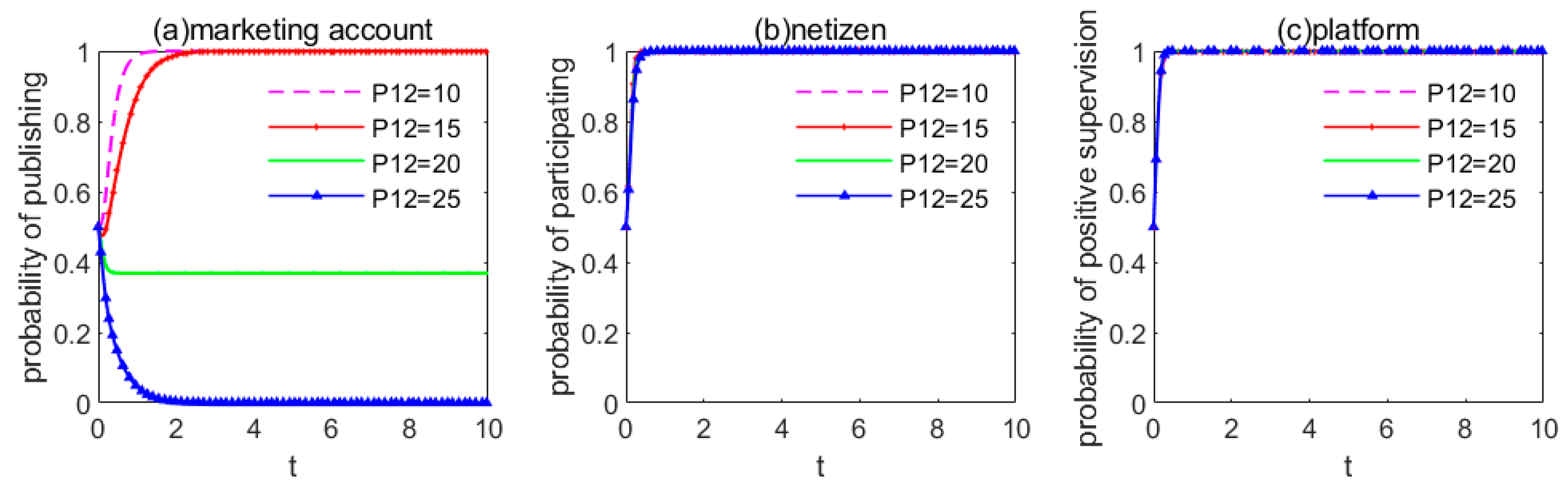
5. Impact Analysis of Supervisory Relevant Parameters on ESS

According to the above analysis, the strategy choice of either party will change according to the change in relevant parameters. Different parameter values will affect the system’s evolutionary stability strategy. The next part mainly analyzes the impact of relevant parameters on the choice of the primary strategy.

5.1. Impact Analysis of Losses of Not Publish $P_{13}$ and Degree-of-Truthfulness of Information $\alpha$

Except for the losses of not publish $P_{13}$, the values of the other parameters are the same as those in case (b) of Figure 2—that is, the value of $(0,0,1)$. According to Proposition 1, if $P_{13}>C_{11}-R_{11}+\beta P_{11}+(1-\alpha )P_{12}$, then the ESS of the system would be $(1,1,1)$. The marketing account’s losses resulting from not publishing information have an obvious influence on the marketing account and netizen strategy choices. When $P_{13}$ exceeds a certain value, the strategic choice of the three parties will change from $(0,0,1)$ to $(1,1,1)$, as shown in Figure 3. When the non-publish losses increase, the marketing account will tend to publish, while the netizen will choose to participate.

In this case, when increasing the degree-of-truthfulness value of the information $\alpha$, the three-party strategy remains unchanged. However, when the degree-of-truthfulness value of information $\alpha$ becomes smaller, the marketing account choosing not to publish is the stable strategy, as is the netizen choosing not to participate. Therefore, if the authenticity of the information is not high, not publish is the best choice for the marketing account, while not participate is the best choice for a netizen. Figure 4 shows the impact of the degree-of-truthfulness value of information $\alpha$ on the strategy of the three-party game players.

However, some scholars believe that unreliable information only accounts for a small part of people’s lives, and that people will not fully believe the information they see online [23]. False information has little effect on people‘s behavior. This is because the network environment is so bad that people have seen too much false information, so they question the authenticity of the network. If the network environment does not change for a long time, the network may only have entertainment, losing the essence of information transmission. Some scholars believe that netizens can continue to forge their true views, but as long as they have a social hierarchy similar space, they can state their true views [24]. For individuals, the authenticity of the information they publish depends partly on their social status, so the authenticity of information is difficult to guarantee. However, the marketing account is different from the individual in the interest goal. The marketing account needs traffic. In order to obtain more benefits in the future, they need to establish their own credibility. If they often publish false information, it will always be found by netizens, and then there will be less attention and less traffic. Therefore, marketing accounts should carefully judge the authenticity of information in order to achieve a better equilibrium.

5.2. Impact Analysis of Penalty Intensity of Platform $P_{12}$ to Marketing Accounts

Except for the penalty intensity $P_{12}$ of the platform, the values of the other parameters are the same as those in case (d) of Figure 2, that is, the value of $(1,1,1)$. According to Proposition 1, if $P_{12}<(R_{11}+P_{13}-C_{11}-\beta P_{11})/(1-\alpha )$, then the ESS of the system would be $(1,1,1)$, and if $P_{12}>(R_{11}+P_{13}-C_{11}-\beta P_{11})/(1-\alpha )$ then the ESS of the system would be $(0,1,1)$. The change in the penalty intensity of the platform has a considerable impact on the marketing account’s strategic choice, and there is a critical value. When the penalty intensity reaches this value, the strategic choice of the three parties will change from case (d) to (e). When the penalty of the platform to the marketing account increases, the marketing account’s strategic choice gradually tends toward the not-publishing option over time. Therefore, to improve the network environment, the platform should increase the penalties incurred by marketing accounts that publish negative information to reduce the probability of its publication. The impacts of penalties on netizens and platform strategy selection are not apparent. Figure 5 shows the impact of the change in the penalty of the platform to the marketing account on the strategy of the three-party game players.

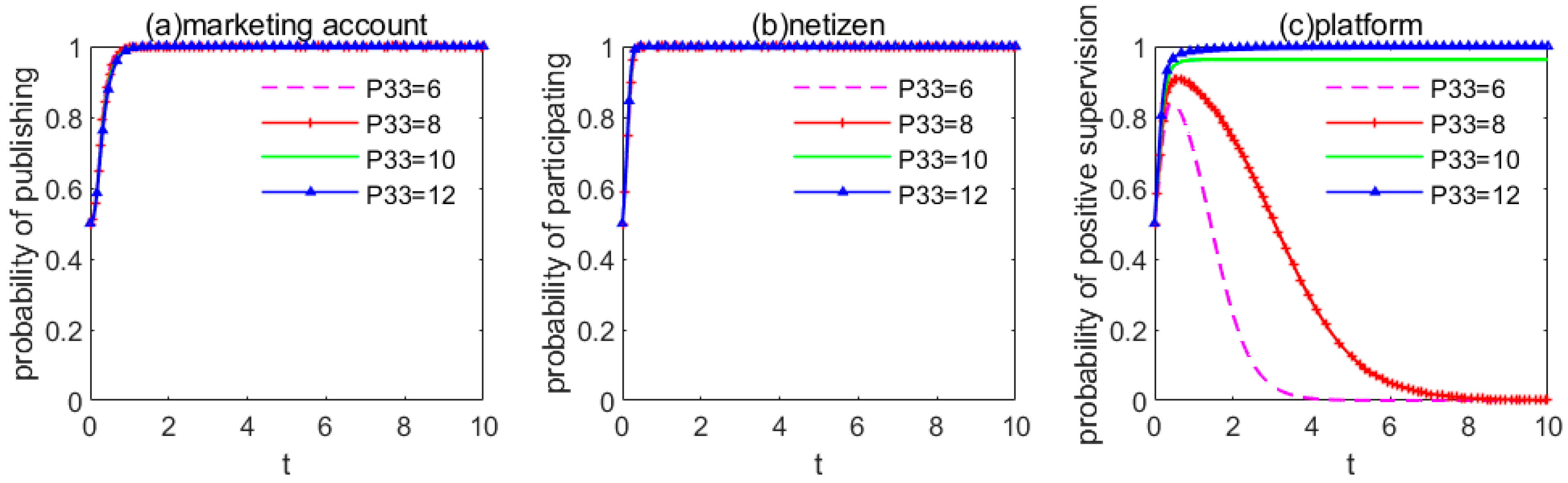
5.3. Impact Analysis of Penalty Intensity of Government $P_{33}$

Figure 2 shows that, except for the penalty intensity $P_{33}$ of the government, the values of the other parameters are the same as in case (d)—that is, the value of $(1,1,1)$. According to proposition 1, if $P_{33}>(R_{33}+R_{34}+P_{31}+C_{31}-R_{31}-R_{32}-P_{32}-C_{32})/\gamma$, then the ESS of the system would be $(1,1,1)$ and if $P_{33}<(R_{33}+R_{34}+P_{31}+C_{31}-R_{31}-R_{32}-P_{32}-C_{32})/\gamma$, then the ESS of the system would be $(1,1,0)$. The government penalty has no considerable impact on the strategic choices of marketing accounts and netizens; however, the change in government penalty considerably impacts the strategic choice of the platform, and there is a critical value. When the government penalty reaches this value, the strategic choice of the three parties will first change from case (d) to (e). When the government increasingly punishes the platform, the platform’s strategic choice gradually tends toward being actively supervised over time. This shows that the government should increase the penalty for the negative supervision of the platform. If the penalty is too small, the benefits brought by the negative supervision may be far greater than the government penalty. Driven by interests, the platform will choose negative supervision, which gives the marketing account the opportunity of negative marketing. Figure 6 shows the impact of the change in the government’s penalty to the platform on the strategy of the three-party game players.

5.4. Optimization of Online Public Opinion Supervision Model

• Based on the above analysis, we put forward some countermeasures and suggestions that can improve the efficiency of network supervision and the previous single “post-event” supervision that the regulatory authorities used to directly punish the information publisher.
• Before publishing information, the marketing account should consciously and strictly screen and confirm the information to achieve the supervision of the “pre-event”. It could avoid creating topics driven by interests to obtain traffic and publish false information. For example, if the “Detective Zhao Wuer” repeatedly confirms the authenticity of the information before publishing the information, it can reduce the spread of false information. It will not be blocked by major platforms for publishing falsehoods, hype, and other information.
• The platform should establish a review mechanism for marketing accounts or other media and strictly review the information published by marketing accounts. At the same time, the platform should fully mobilize the monitoring power of netizens and adopt a reward mechanism to encourage netizens to complain about marketing accounts that publish false or vulgar information. For example, marketing accounts in the process of live-streaming vulgar speech or conveying false information to fans, could be reported in real time by users, reducing the emergence of such marketing accounts. This could ensure the authenticity of information and promptly suppress the vulgar content and false statements published by marketing accounts to achieve “in-the-event” supervision.
• The government regulatory authorities can implement a reward and penalty mechanism to the platform encourage supervision. The government and the platform should effectively punish the marketing accounts that caused negative public opinion to achieve “post-event” supervision, thus forming a diversified “pre-event–in-the-event–post-event” three-stage supervision model based on a single “post-event” supervision model.

6. Conclusions

Marketing accounts, netizens, and platforms are the promoters, disseminators, and carriers of network public opinion communication, respectively, in addition to being stakeholders. Therefore, a game relationship exists between marketing accounts, netizens, and a platform. Considering the influence of network stakeholders on the governance of the network environment, we constructed an evolutionary game model of “marketing account– netizen–platform” among network stakeholders to give the evolutionary stability strategy of the three parties in different cases. Then, we performed a simulation analysis and studied the influence of relevant parameters on the stability of the game. At the same time, to improve the network environment and the supervision efficiency of network public opinion, we provided countermeasures and suggestions for transforming network public opinion supervision from a single “post-event” supervision to a “pre-event–in-the-event–post-event” three-stage supervision model.

The different values of relevant parameters would affect the system’s evolutionary stability strategy. When the authenticity of the information is not high, not publishing is the best choice for the marketing account, while the best choice for the netizen is to not participate. By increasing the platform’s penalty intensity toward the marketing account, the marketing account will choose not to publish information. By increasing the government’s penalty toward the platform, the censorship of content published by the platform will be stricter.

Our paper also has some limitations. The setting of relevant parameters is subjective, and there are many other factors that affect the network’s public opinion environment and subject’s behavior strategies. Therefore, our future research direction should combine the actual case study with a consideration of the influence of other factors to improve the existing model.