Abstract
Code readability and software complexity are considered essential components of software quality. They significantly impact software metrics, such as reusability and maintenance. The maintainability process consumes a high percentage of the software lifecycle cost, which is considered a very costly phase and should be given more focus and attention. For this reason, the importance of code readability and software complexity is addressed by considering the most time-consuming component in all software maintenance activities. This paper empirically studies the relationship between code readability and software complexity using various readability and complexity metrics and machine learning algorithms. The results are derived from an analysis dataset containing roughly 12,180 Java files, 25 readability features, and several complexity metric variables. Our study empirically shows how these two attributes affect each other. The code readability affects software complexity with 90.15% effectiveness using a decision tree classifier. In addition, the impact of software complexity on the readability of code using the decision tree classifier has a 90.01% prediction accuracy.
1. Introduction
Code readability is considered a critical component of software quality. It is defined as a human judgment on how much the source code is understandable and easy to read. Recently, it has become an increasingly important development feature in software engineering due to the increasing number of software projects and their significantly growing size and complexity.
Code readability is strongly related to the maintainability process as it greatly influences software maintenance. According to [1], maintainability consumes 40% to 80% of the software life-cycle cost; it is considered a very costly phase. Thus, this phase requires consistent monitoring to gain better control of it. Ref. [2] claimed that both source code and documentation readability were critical factors for maintainability, and they should be considered when measuring it. Furthermore, some researchers found that the most time-consuming component in all maintenance activities is reading the code, and they illustrated its importance as a key activity in this process [3,4,5].
The researchers have established the importance of code readability and complexity to software quality. Software complexity is considered an “essential” property of software since it reflects the problem statement [6]. On the other hand, code readability is considered an “accidental property”, not an essential one, as it is not determined by the problem space and can be controlled by software engineers. While code readability considers the local and line-by-line factors such as indentations and spaces, software complexity measures the size of classes, methods, and interdependencies between code modules.
However, there have been few investigations of the relationship between software readability and complexity [7,8]. In the first paper, Buse and Weimer proposed an approach for constructing an automatic readability tool using local code features. They claimed that readability was weakly correlated with complexity in the absolute sense and was effectively uncorrelated with complexity in a relative sense. In [8], the investigation was based on component-based software engineering (CBSE). It used a complexity metric that measured interface complexity for software components and showed how it was strongly correlated to readability for software components. The results indicated a negative correlation between readability and complexity with −0.974, which confirmed that the highly complex component was much harder to maintain and understand.
In this paper, we address the previous shortcomings and study the relationships between code readability and software complexity. We examine the relationships between these two attributes using various readability and complexity metrics. In particular, we aimed to find the answers to the following research questions: What are the code block sizes that affect readability? What type of relationship exists between code readability and software complexity?
To answer these questions, this study analyzed 12,180 Java files covering various programming constructs such as blank lines, loops, nested loops, etc. Applying machine learning algorithms with readability features and complexity metrics identified code constructs that had a high effect on code readability and confirmed that code complexity and readability were strongly correlated. Machine learning algorithms were preferred since it is known that a correlation analysis indicates only whether there is a linear relationship between two data sets or not. In contrast, some machine learning algorithms can model a nonlinear relationship between two data sets, as in the case of neural networks (NN), support vector machines (SVM), and decision trees. In this work, we applied five classifier algorithms to the dataset. All these algorithms implementations were used from the WEKA tool.
The major contributions to this work are as follows:
- Investigate the relationship between code readability and software complexity and use an approach for constructing automatic tools using machine learning and various readability features.
- Provide a comprehensive analysis of various classifiers, including decision tree, naïve Bayes, Bayesian network, neural network, and SVM classifiers, with several measures to provide the flexibility to select the classifier whose accuracy specifications are most relevant to users.
- Investigate the effectiveness of 24 readability features on classifier performance.
- Apply a variety of complexity metrics to gain a better inspection of the software complexity, including Chidamber and Kemerer’s metrics (WMC, RFC, DIT, and LCOM), which are considered as object-oriented metrics, Lorenz and Kidd’s metric (OSavg) for operation-oriented metrics, lines-of-code metric (LOC), and Halstead’s metric.
The scope of this research focused on applying machine learning to key topics in software engineering including code readability and software complexity and studying the relationship between both of them.
The rest of this paper is organized as follows: Section 2 reviews existing literature related to the application classification. Section 3 describes the methodology and provides further details on feature extraction and machine learning classifiers. Section 4 discusses the experiments and results. Section 5 presents the comparison studies. Lastly, Section 5 shows the conclusion of this work.
2. Literature Review
Software engineering has gained much research attention in the past years. To gain control of the software development, there must be some measurements and metrics that provide a broad insight into the software characteristics and features. Thus, many researchers focus on software metrics to extract important features from software to provide insight into software and the software development processes. This section discusses many related works and focuses on readability and complexity metrics as a field of study.
2.1. Readability Metrics
For several decades, researchers have investigated software quality and which attributes influence it. Code readability is a very important topic in software engineering, where readable code leads to consistent code that has few errors and can be maintained and reused easily. Thus, many researchers study code readability and the factors that affect it.
Ref. [9] proposed a new test for readability based on sentence length, word length, and word form. This test is very popular and well-known, and it claims that short sentences and words make the text more readable as the reader can understand them much easier than long ones.
Ref. [7] investigated the relationship between code readability and software quality and proposed an approach for constructing an automatic readability tool using local code features. A survey was applied to 120 human annotators with 100 code snippets, which gave a total of 12,000 human judgments. They used snippets through a web interface to collect participants’ judgments by scoring each code snippet based on their readability estimation and setting some policies regarding snippet selection. They extracted 25 local code features that were correlated with readability from these human judgments, such as average arithmetic operators, the average and the maximum number of line lengths (characters), the average number of spaces, the average number of blank lines, and other features. However, some of these features had a positive impact, and others had a negative impact on readability. They used these features to map from the code snippets to vectors of real numbers and then to apply them to machine learning algorithms using WEKA.
Their readability tool was trained based on human judgments, where they produced an automatic readability tool with 80% effectiveness. The study also showed how readability was strongly correlated to some software quality attributes, including code changes, defect log messages, and automated defect reports. They investigated the relationship between code readability and software complexity as they showed that code readability was weakly correlated to complexity in an absolute sense using a Pearson correlation analysis to investigate the relationship between their readability values obtained by the proposed tool and the cyclomatic complexity metric.
Ref. [10] explored the identifier name’s quality and how they affect the software quality. They showed how poor identifiers’ quality could affect the code leading to less readable, more complex, and less maintainable source code. Moreover, they explained how the identifier length, including the number of characters and components, could be used as a lightweight approach for both the maintenance and complexity of software.
Ref. [11] investigated the impact of programming features on code readability and developed an approach called IPFCR (impact of programming features on code readability). The proposed tool calculated the exact readability value as an indicator of software quality. It included twenty-two coding features, such as comments, indentations, meaningful identifier names, and other features. Odat investigated the relationship between coding features and software readability, where a questionnaire was handed out to programmers. Based on the questionnaire feedback, a formula for each feature was proposed using the ANOVA test, and a numerical value of the code readability overall was produced.
Ref. [12] provided a novel approach to detect the readability of software game code which are built in C++ or Java for mobile and desktop environments. Depending on machine learning techniques, an approach for predicting game type was introduced according to readability and some other software metrics. Their classifiers were built using data mining algorithms (J48 decision tree, support vector machine, SVM, and naive Bayes, NB) that are available in the WEKA data mining tool.
In [13], the authors mentioned the importance of software code readability in the context of agile software development for software maintenance. They indicated that several approaches that were interested in evaluating software code readability depended on experts who were responsible for providing an assessment methodology. That led to outcomes that were subjective. In their research, they applied a huge group of static analysis metrics besides several coding breaches in order to explain readability as perceptible by software developers. That was for the purpose of supplying a fully automated approach that did not depend on experts. The authors built a dataset that involved more than one million ways that covered various development cases. After doing clustering depending on the size of the source code, they implemented a support vector regression to demonstrate the range to which a software part was readable on three bases: complexity, documentation, and coupling.
In [14], the authors provided a new approach that presented how radiofrequency identification (RFID) technology could be employed in several conditions, such as unreliability in chain management to produce different warehouses. Moreover, they investigated how the optimal number of readers could affect warehouse shapes. Ref. [15] used a variety of max-flow algorithms, including Edmond Karp, Ford Fulkerson, and Dinic’s, to find the optimal algorithm that optimized the flow of goods between the outbound dock and inbound port and presented a logical explanation to reduce the waiting time of the cross-dock that carried the goods. The result concluded that Dinic’s algorithm had a better performance than the other algorithm in addressing the problem of finding the maximum flow at the cross-dock based on a numerical approach.
2.2. Complexity Metrics
Many metrics have been proposed to measure code complexity as another indicator of software quality. The importance of these metrics is in helping developers to evaluate their workload and cost and estimating the cost and effort needed for software maintenance. In this subsection, several complexity metrics are presented.
Ref. [16] proposed a metrics suite in 1994 as complexity metrics for object-oriented languages. This metrics suite has been one of the most referenced sets; it measures the complexity based on six metrics:
- Weighted methods per classWeighted methods per class (WMC) is the summation of all method’s complexities for a single class; the complexity of the method is computed using the cyclomatic complexity. Thus, the complexity of the class increases when the number of methods and their complexity are increased; hence, the WMC measure should be kept as low as possible.
- Depth of inheritance treeThe depth of the inheritance tree (DIT) is the max length from the root to the lowest class. When the value of the DIT increases, this indicates that the lower classes will inherit many methods and properties, so the class behavior will be difficult to predict, leading to design complexity. On the other hand, the DIT refers to the reusability of code which has a positive impact on the code. However, there is no standard range that can be used as an accepted value for the DIT.
- Number of direct childrenThe number of direct children (NOC) indicates the number of subclasses that are immediately inherited from the class. When the NOC increases, the reusability of the code increases, but the amount of testing will also increase [17].
- Coupling between objectsThe coupling between objects (CBO) refers to the number of couplings between objects in the same class. A high CBO value indicates complicated modifications and testing for the class, so the CBO value should be as low as possible.
- Response for a classThe response for a class (RFC) metric is the set of methods that will be executed when responding to an object message. When the RFC value is high, the testing effort will increase because of the test sequence [17], thus increasing the design complexity for the class.
- Lack of cohesion in object methodsThe lack of cohesion in object methods (LCOM) metric indicates methods in one class that access the same attributes, so if the LCOM is high, this indicates a higher complexity of the class design. Therefore, it is better to keep the LCOM value low.
Ref. [18] mentioned in his research that the advancement of software was important for the success of application systems. One of the essential terms of software improvement is that the internal quality of a software system decreases when it evolves. In his research paper, the way to improve the interior quality of object-oriented open-source software systems was tested by implementing a software measure approach. The author resolved how application systems improved over releases regarding size and the connection between size and distinct interior quality measures. The findings and observations of his research were: (1) there was an important distinction between several systems regarding the LOC variable, (2) there was a considerable relationship between all pairwise differentiation of inner quality measures, and (3) the impact of complexity and legacy on the LOC was affirmative and important, while the influence of the coupling and cohesion was not worthy.
Ref. [19] discussed the theoretical graph complexity, which is considered one of the most significant complexity metrics for software. The author applied graph theory concepts to complexity. The cyclomatic complexity is defined by the number of all possible linear paths that may be executed in the program. The graph consists of nodes and edges. Nodes represent lines of source code of software, and the directed edges represent the next node (line of code) to be executed. The conditional statements, such as if, switch case, for, and while, lead to many branches and are considered test cases. The cyclomatic complexity metric is computed by the following formula:
where:
CC: cyclomatic complexity.
E: number of directed edges.
N: number of nodes.
P: number of connected components.
McCabe illustrated that the program component complexity must be less than 10 to have a good component that is easy to be tested and maintained.
Ref. [20] introduced the Halstead complexity model (HCM). It uses primitive measures to compute many metrics including code complexity. Halstead metrics used four primitive measures:
n1: number of unique operators which appear in the program;
n2: number of unique operands which appear in the program;
N1: total number of all operators appearing in the program with repetition;
N2: total number of all operands appearing in the program with repetition.
The HCM divides the source code into tokens using a lexical analyzer, where these tokens are classified into two factors: operator and operand. The operators includes mathematical operations, logical expressions, and programming language keywords (+, *, =, <, if, double, class). The operands include identifiers’ name, numbers, and string literal such as (class_A, “Hello”, 23, 0xfc).
Halstead used the primitive measure to compute many metrics including program volume, program length, potential program volume, program level, and program effort.
where:
V: program volume;
Ln: program length;
V*: potential program volume;
N*: total number of input and output parameters;
L: program level;
E: program effort.
Ref. [21] proposed three simple metrics for operation-oriented metrics. These metrics measured the complexity and size of operations within a class:
- Average operation size (OSavg).
- Operation complexity (OC).
- Average number of parameters per operation (NPavg).
Ref. [22] described in their paper that software complexity metrics are considered an important component of software engineering. These metrics can be utilized to predict significant information associated with the reliability, testability, and manageability of application systems from the study of the source code. Their paper introduced the outcomes of three different software complexity measures that were implemented in two searching techniques (linear and binary search algorithms). The aim was to contrast the complexity of linear and binary search techniques applied in Java, Python, and C++ languages and measure the sample algorithms by utilizing a line of code and McCabe and Halstead’s measures.
2.3. Software Complexity and Readability
Some researchers have investigated the relation between software complexity and code readability as in [7,8,23].
In [8], a new complexity metric was proposed to measure the interface complexity for software components, then a correlation study was conducted between the proposed complexity metric and readability using Karl Pearson’s correlation coefficient. They used the following readability formula to measure the readability of components.
The results showed a negative correlation of −0.974 between the readability and complexity of interfaces, which confirmed that a highly complex component was much harder to maintain and understand.
As mentioned earlier, Ref. [7] proposed an approach for constructing a readability tool. They used the proposed readability tool to investigate whether code readability was correlated with the cyclomatic complexity metric by applying Pearson’s product-moment correlation. They found that readability was weakly correlated with complexity in the absolute sense, and it was effectively uncorrelated to complexity in a relative sense.
Ref. [23] stated in their paper that reactive programming was considered a programming model introduced to simplify the construction of event-driven reactive software. It was assumed by its supporters to improve the quality of code, but little research had been conducted to confirm these claims experimentally, so the goal of the authors’ research work was to discover the distinction in the complexity and readability of code between classical mandatory programming and reactive programming. The authors performed a case study where the presented open-source project code was restructured, yielding a compulsory release and a reactive release of the same code. In order to examine if any changes in code readability and code complexity could be discovered, static analysis tools were used. The results of their study indicated that the readability was influenced by reactive programming negatively when measured with state-of-the-art readability metrics, while code complexity was reduced in a huge manner.
3. Study Methodology
In the previous sections, the importance of software readability and complexity was briefly discussed, with the most important software metrics that were proposed to measure these attributes. In this section, we introduce our research methodology for investigating the relationship between readability and complexity.
Figure 1 presents the research methodology flowchart. First, we downloaded Java source code files by utilizing Eclipse, which is a well-known software development environment and open-source software. We then extracted various software metrics from these source code files, which were related to software readability and complexity. After that, we built our data set. In the next step, we applied some statistical techniques proposed in this paper to combine the readability metrics or complexity metrics into a single variable for further analysis. Then, we used analysis methods and data mining techniques, including machine learning algorithms, to test several research hypotheses. Finally, we discussed the results and presented our contribution. The later sections briefly explain the processes for the research work.
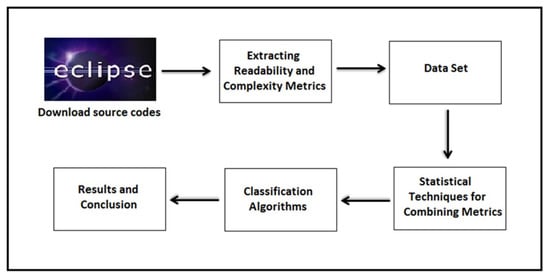
Figure 1.
Research methodology flowchart.
3.1. Source Code Projects
In this section, we present the process of source code collection. We chose Eclipse to be our main source code for the investigation since it is an extensible, large, well-known, open-source, integrated development environment (IDE). It is written in the Java language, widely used for development, and includes several add-ons for the different software development tasks. It runs under different operating systems, including Windows, Linux, Solaris, and Mac OS X [24].
3.2. Software Metrics and Tools Selection
In this subsection, we discuss the metrics that were selected for our work, including readability and complexity metrics, and the process of extracting these metrics from java source code. In addition, we present the tools used in the extraction process.
3.2.1. Readability Metrics Selection
Considering the readability metrics, we used a metric proposed by [7], which was discussed earlier in the literature review (see Section 2.1). In their paper, Buse and Weimer developed a tool for readability. This tool was designed for Java code. They assembled a set of 25 features that may affect the readability; these features were related to the density, structure, and other code attributes. According to the paper, each feature was independent of the size block, where they assumed that the size of the code should not affect the readability value. The values of these features were divided into two categories: average value per line and maximum value for all lines. These features were:
- Average line length (number of characters);
- Maximum line length (number of characters);
- Average number of identifiers;
- Maximum number of identifiers;
- Average identifier length;
- Maximum identifier length;
- Average indentation (preceding whitespace);
- Maximum indentation (preceding whitespace);
- Average number of keywords;
- Maximum number of keywords;
- Average number of numbers;
- Maximum number of numbers;
- Average number of comments;
- Average number of periods;
- Average number of commas (,);
- Average number of spaces;
- Average number of parentheses and braces;
- Average number of arithmetic operators (+, −, *, /, %);
- Average number of comparison operators (<, >, ==);
- Average number of assignments (=);
- Average number of branches (if);
- Average number of loops (for, while);
- Average number of blank lines;
- Maximum number of occurrences of any single character;
- Maximum number of occurrences of any single identifier.
These features were correlated to form software readability metrics or attributes. However, some of these features have positive impacts, and others have negative impacts. The average number of arithmetic operators, the average number of comments, and an average number of blank lines are attributes with a positive impact where the readability value increases as their value increases. The rest of the features have a negative impact, where the readability decreases when their value increases.
We utilized the readability model from [7]. The model gives the readability value as a numeric value. However, for our investigation, we wanted to use the features themselves; therefore, since the model was open source, we adjusted the source code to parse the values of these 25 features to study their relation and behavior with the complexity metrics. Thus, at this point, for readability, we used these 25 features and not only the readability value from the author’s developed model.
3.2.2. Complexity Metrics Selection
Considering the complexity metrics and the many metrics proposed over the past decades, we chose different metrics:
- Chidamber and Kemerer’s metrics suite:This is one of the most referenced metrics suites for object-oriented metrics [25]. It was proposed by Chidamber and Kemerer in 1994 and contains six metrics: WMC, DIT, NOC, CBO, RFC, and LCOM. From these metrics we chose the ones that were the most related to complexity; consequently, we chose:
- (a)
- WMC;
- (b)
- DIT;
- (c)
- LCOM;
- (d)
- RFC.
The selection was based on the metrics measurement, since they were the metrics most related to software complexity and measured it. The WMC metric measures the complexities for all the methods within a class, and the DIT, LCOM, and RFC metrics measure the design complexity of the class. - Lorenz and Kidd’s metrics:In 1999, Lorenz and Kidd proposed three simple metrics for operation-oriented metrics. These metrics were concerned with the complexity and size of operations. We selected the average operation size (OSavg) to be one of our complexity metrics. It computes the average complexity of operations using the following formula:where:WMC*: summation of all methods’ complexity for a given class.N: number of methods per class.It is better to keep the OSavg low, and classes with an OSavg value greater than 10 should be redesigned.
- Lines of code (LOC):The size of code is correlated to software complexity. The LOC metric is one of the easiest measures that are used to measure the productivity of the programmer and complexity of software [26]. This metric basically counts the lines of code of software including source code, whitespaces, and comments.
- Halstead’s complexity measure:This is a very common code complexity measure that was proposed by Halstead in 1977. It uses primitive measures to compute many metrics. We selected program volume to use in our investigation since it focuses on the program’s physical size, whereas the code complexity increases as the program volume increases.
All the complexity metrics discussed above were extracted using the Krakatau metrics professional tool [27]. This tool extracts broad metrics for software with different languages: C, C++, and Java. Since our source code files were written in Java, we used this tool in order to build our data set. It is implemented at the file level so that both values of readability and complexity metrics are at the file level. Some metrics such as Chidamber and Kemerer’s metrics (WMC, RFC, DIT, LCOM) and Lorenz and Kidd’s metric (OSavg) are computed at the class level since they are metrics designed for class measurements. However, the file may contain several classes per file. Therefore, we obtained the value of these metrics by aggregating the values of the classes obtained in that file, so all the metrics would be at the file level. For example, if we had Class_A, Class_B, and Class_C in File 1, the metrics were computed as follows:
In addition, there were some files that did not contain any classes, as these files contained other software components (e.g., interfaces). We decided to exclude these files from the dataset since all the class measurements were not available for them and it produced many missing values. The data set in our research contained roughly 12,180 Java files.
3.2.3. Classification Algorithms
Classification algorithms are used to capture the relation between input and output, where the input variables refer to the independent variables and can be more than one variable, and the output variable refers to the dependent variable, which is one variable, unlike the independent variables. The classifier tries mapping the independent variables to the dependent variable. In our work, we used several algorithms, which were a decision tree (J48), a naïve Bayes classifier, a Bayesian network, an artificial neural network, and a support vector machine (SVM).
3.2.4. Statistical Techniques for Combining Metrics
In this subsection, we present the statistical techniques used for combining both the complexity and readability metrics into a single variable for further analysis. Since the dependent variable should be only one variable, unlike the independent variables, which could be many variables, when using classification algorithms for further analysis, we must first transform the dependent variables into one variable using statistical techniques, namely, clustering analysis, summation division, PCA dimension reduction, and quartile analysis. We briefly discuss each approach and consequently use the results obtained for the classification algorithms.
- Clustering analysis:In this technique, we decided to group the metrics based on the clustering method. Clustering is an unsupervised learning approach that is used to group similar objects into the same cluster. Unlike supervised learning, the number of clusters or names is unknown. Thus, the clustering algorithm determines the best number of clusters to obtain based on some measures. To determine whether two objects are in the same cluster or not, it uses a distance measure such as the Euclidean distance, Manhattan distance, or others. The K-means algorithm works as follows:
- (a)
- Randomly select K points as centroid values for the classes.
- (b)
- Assign each object to the most similar (closet) centroid.
- (c)
- For each cluster, calculate the mean value, which is the new centroid value of the class.
- (d)
- Reassign each object to the closest centroid.
- (e)
- Repeat the last two steps (3 and 4) until no change.
- (f)
- Assign the class labels for the objects.
- Summation division:For this approach, we decided to combine the metrics into one variable based on the summation division. Let us assume that we have N metrics that we want to combine into one variable; in this approach, we follow these steps:
- (a)
- For each metric:
- Compute the mean.
- If the metric value is greater than the mean, set it to 1; if the value is equal to the mean, set it to 0; and if it is less than the mean, set it to −1. This step produces N columns. Each column represents a metric with only three possible values (1, 0, −1).
- (b)
- Add a new variable (i.e., called Metrics_Sum) that represents the summation of the N columns produced by the previous step, the Metrics_Sum column’s value ranges from N to −N.
- (c)
- Compute the median for the Metrics_Sum column.
- (d)
- If the Metrics_Sum is greater than the median, give it a class label of “High”, and if it is less than the median give it a class label of “Low”
This approach produces two class labels: “High” and “Low”. In step 4, when dividing the data into two intervals, we can use two statistical measures depending on the data distribution: median or mean. The mean is used when the data have a normal distribution, and the median is used if our data are not normally distributed. - PCA dimension reduction:In this approach, we combined the metrics into one variable using a principal component analysis as a dimension reduction technique. It is used for a linear transformation of the data to a lower dimension space as the variance of the lower data is maximized. For this technique, we applied the PCA for dimension reduction on the metrics, specifying only to produce one component which was the strongest one.
- Quartile analysis:Quartiles are used to divide the data into equal groups; they have three values: first quartile (Q1), second quartile (Q2), and third quartile (Q3). Q1 splits the lowest 25% of the data; Q2, known as the median, splits the data in half; and Q3 splits the lowest 75% of the data. We chose this method in order to combine the metrics into one variable. The steps for this approach were as follows (assuming N metrics):
- (a)
- For each metric:
- Compute the mean.
- If the metric value is greater than the mean, set it to 1; if the value equal the mean, set it to 0; and if it is less than the mean, set it to −1. This step produces N columns. Each column represents a complexity metric with only three values (1, 0, −1).
- (b)
- Add a new variable (e.g., called Metrics_Sum) that represents the summation of the N columns produced by the previous step, the Metrics_Sum column’s value ranges from N to −N.
- (c)
- Compute Q1, Q2, and Q3 for the Metrics_Sum column.
- (d)
- If the Metrics_Sum is greater than Q3, give it a class label of “High”; if it is between Q1 and Q3, give it a class label of “Medium”; and if it less than Q1, give it a class label “Low”.
This method produces three class labels: “High”, “Medium”, and “Low”.
4. Experiments and Results
In this section, we examine the hypothesis that software readability and complexity are correlated. Several experiments were conducted to answer this hypothesis. We introduced three case studies. In the first case study, we tested whether code readability had an influence on the software complexity. In other words, can we consider readability as an independent variable and complexity to be a dependent variable that is affected by the readability and influenced by it? In the second case study, we tested if software complexity had an influence on the readability of code, assuming complexity as an independent variable and readability as the dependent variable. In the third case study, we investigated if code size had an influence on code readability features or not.
All the experiments in this chapter were conducted on Java source code files, which included roughly 2,900,970 lines of code after we excluded some files which did not contain any classes in order to avoid producing missing values.
4.1. Principal Component Analysis
A principal component analysis (PCA) is one of the most known multivariate statistical techniques [28]; it is used to measure orthogonal dimensions and extract important information. It generates several components that carry the same class property and can be used as a dimension-reduction technique.
We applied the PCA on all the metrics to gain a better insight into the data’s orthogonal dimensionalities. Eight principal components were extracted, which captured 73.315% of the variance of the data; metrics with significant coefficients were highlighted in bold (i.e., more than 0.50 for a positive correlation and less than −0.50 for a negative correlation). A threshold was set for retaining eigenvalues with more than one value; this threshold is known as the Kaiser criterion, and the varimax rotation was used for a better interpretation as it provided better results. The eight components extracted from the PCA were:
- PC1: Max character occurrences, Max word, LOC, LCOM, RFC, WMC, and Program Volume.
- PC2: average parenthesis, average arithmetic, average assignment, average if, average comments, average indent, and max indent.
- PC3: average spaces, average comparisons, average blank lines, average comments, and average identifier length.
- PC4: max indents, max line length, and max numbers.
- PC5: average periods, average indents, and average line length.
- PC6: DIT, OSavg, RFC, and WMC.
- PC7: average keywords, and max keywords.
- PC8: average identifier length, average numbers, and max word length.
Results explanation:
The PCA results indicated how some readability features and complexity metrics were correlated with each other and showed the same class property as with PC1.
- PC2, PC3, PC4, PC5, PC7, and PC8 showed how the readability features captured the same orthogonal measure.
- PC6 contained some software complexity measures which were correlated with each other.
4.2. Case Study 1: Mapping from Readability to Complexity
The general purpose of this case study was to investigate the relation between readability and complexity and investigate the impact of software readability to complexity. In this case study, we considered readability as an independent variable and complexity as a dependent variable to examine if code readability influenced software complexity or not and whether software complexity was dependent on code readability and influenced by it.
Hypothesis:
H 0.
Code readability has an influence on software complexity.
H 1.
Code readability has no influence on software complexity.
For our investigation of these hypotheses, we ran several experiments with different statistical techniques used for grouping the complexity metrics, where the complexity metrics were grouped into one independent variable using the four techniques discussed earlier. After grouping the complexity metrics, we applied several classification algorithms and discussed the results obtained by these techniques.
4.2.1. Statistical Techniques
In this subsection, we present the statistical techniques used for combining the complexity metrics into one variable for further analysis since the dependent variable should be only one variable, unlike the independent variable, which could be many variables. These techniques were clustering analysis, summation division, PCA dimension reduction, and quartile analysis. We performed these experiments and used the results obtained for the classification algorithms. SPSS Statistics version 17.0 tool [29] was used for the following experiments.
- Clustering analysis:In this technique, we decided to group the complexity metrics based on the clustering method. We used the K-means clustering algorithm and chose the Euclidean distance as the distance measure. Table 1 illustrates the experimental results obtained by applying the K-means clustering algorithm with different k values from two up to five. After looking at the values of the LOC, DIT, LCOM, OSavg, RFC, WMC, and program volume complexity metrics, we managed to give each class a complexity degree. However, when looking at the class distribution, we noticed that the data were not well distributed in both classes.
 Table 1. Clustering technique results.From the previous experiments, we concluded that clustering was not a good technique to apply on our dataset, since the classes produced were not well distributed, even when selecting different K values.
Table 1. Clustering technique results.From the previous experiments, we concluded that clustering was not a good technique to apply on our dataset, since the classes produced were not well distributed, even when selecting different K values. - Summation division:For this approach, we decided to combine the seven complexity metrics into one variable that represented the overall complexity based on the summation division. In step 4, when dividing the data into two intervals, the median was used rather than other statistical measures since the data were not normally distributed and had a positively skewed distribution, where the mean was greater than the mode, and the skewness value was equal to 1.098.This approach produced two class labels, “High”, representing a high complexity, and “Low”, referring to a low complexity. From the class distribution for this approach, we noticed the data had an accepted distribution with 66% for the low complexity and 34% for the high complexity.
- PCA dimension reduction:In this approach, we combined the seven complexity metrics into one variable based on the PCA dimension reduction. For this experiment, we applied the PCA for dimension reduction on the seven complexity metrics specifying only to produce one component, which was the strongest one. The component produced had an eigenvalue equal to 4.165, which described the total variance explained. As shown in Table 2, all the complexity metrics in this component had values greater than 0.50, and the WMC had the highest value of 0.963. The varimax rotation matrix was used to get cleaner and better results.
 Table 2. Complexity component matrix for PCA dimension reduction approach.The component result was stored as a variable named Comp1. Then, for this variable, the median value was calculated. We selected the median rather than any other statistical measure since the data were not normally distributed and had a positively skewed distribution where the skewness value was equal to 9.130.The data were given two class labels: “High” for a variable “Comp1” that was above the median and “Low” if it was below the median. In this approach, the data were equally distributed into the two classes, 50% for the class “High” and 50% for the class “Low”.
Table 2. Complexity component matrix for PCA dimension reduction approach.The component result was stored as a variable named Comp1. Then, for this variable, the median value was calculated. We selected the median rather than any other statistical measure since the data were not normally distributed and had a positively skewed distribution where the skewness value was equal to 9.130.The data were given two class labels: “High” for a variable “Comp1” that was above the median and “Low” if it was below the median. In this approach, the data were equally distributed into the two classes, 50% for the class “High” and 50% for the class “Low”. - Quartile analysis:Quartiles were used to divide the data into three groups. They had three values: first quartile (Q1), second quartile (Q2), and third quartile (Q3). The classes’ distributions were class “High” with 26.66%, class “Medium” with 38.37%, and class “Low” with 34.98% after applying the quartile approach. Looking at the results, the classes were well distributed.
4.2.2. Statistical Techniques Selection
From the above experiments, we introduced four statistical techniques that could be used for combining the complexity metrics into a single variable. However, we wanted to use these techniques in our case study and decided which one to further conduct the analysis with. By looking at the distribution of the classes produced from the previous techniques, we noticed that all the statistical techniques gave an accepted class distribution except the clustering technique, where most of the data were concentrated in one class. Thus, it was not considered an appropriate technique in our dataset and was eliminated.
We applied five classification algorithms on our dataset, to observe which technique from the remaining three techniques could produce good results for testing and evaluation. We used a percentage split test, where the data were divided into 66% for training and 34% for testing.
From the results obtained from applying the classification algorithms, the best accuracy was obtained from the percentage split validation with the summation division technique, followed by the PCA dimension reduction technique, and the least accuracy for the quartile technique. The quartile technique gave us poor results so it was excluded. Thus, for our further analysis, we used two techniques, summation division and PCA dimension reduction, as they provided us with the most significant results.
4.2.3. Results
For this case study, we applied several machine learning algorithms to investigate these hypotheses:
H 2.
Code readability has an influence on software complexity.
H 3.
Code readability has no influence on software complexity.
The classifications algorithms used were a decision tree, a naïve Bayes classifier, a Bayesian network, a neural network, and a support vector machine. In this case study, we tried mapping from readability features to complexity metrics considering readability features as independent variables and complexity metrics as dependent variables. In order to achieve this, the dependent variables should be only one variable. Therefore, the previous subsection discussed several approaches used to combine the seven complexity metrics into one variable to be used for further analysis.
We applied the results obtained from the four approaches to the classification algorithms. All the experiments confirmed the hypothesis H0 which indicated that code readability had an influence on software complexity. However, only the two most significant results are presented in this subsection: summation division and PCA dimension reduction. The WEKA tool was used for this analysis [30].
- Summation division results:We used the complexity metric variable produced by the summation division approach as a dependent variable, and the 25 readability features as independent variables. We applied the five classifiers on the dataset. All these algorithms were implemented using the WEKA tool.For testing and evaluation, two techniques were used, namely, the percentage split and a cross-validation. In the percentage split test, the data were divided into 66% for training and 34% for testing, and for the cross-validation test 10 folds were used.The results are listed in Table 3 and Table 4 for the two testing techniques. The best accuracy was obtained for the percentage split validation was with the decision tree classifier with an accuracy of 90.07%, and the mean absolute error and F-measure values were 0.13 and 0.90, respectively. On the other hand, the best result obtained from the 10-fold cross validation was also with the decision tree with a 90.15% accuracy and mean absolute error and F-measure values of 0.12 and 0.90, respectively.
 Table 3. Case study 1 results for summation division approach using percentage split.
Table 3. Case study 1 results for summation division approach using percentage split. Table 4. Case study 1 results for summation division approach using cross-validation.
Table 4. Case study 1 results for summation division approach using cross-validation. - PCA dimension reduction results:In this experiment, we used the five classifiers and applied them to our dataset. We used the complexity variable produced by the PCA dimension reduction approach as the dependent variable and the 25 readability features as independent variables. For testing and evaluation, two techniques were used, namely, the percentage split and cross-validation.The results are listed in Table 5 and Table 6. The best accuracy was obtained for the percentage split validation with the neural network classifier with an accuracy of 89.54% and a mean absolute error and F-measure of 0.16 and 0.90, respectively. On the other hand, the best result obtained from the 10-fold cross-validation was also with a neural network with a 89.23% accuracy and mean absolute error and F-measure values of 0.15 and 0.89, respectively.
 Table 5. Case study 1 results for PCA dimension reduction approach using percentage split.
Table 5. Case study 1 results for PCA dimension reduction approach using percentage split. Table 6. Case study 1 results for PCA dimension reduction approach using cross validation.From this case study, we found that code readability had a great influence and impact on software complexity, which addressed the essential role that code readability plays on the maintainability process and on overall software quality. The experimental results confirmed the H0 hypothesis which claimed that code readability had an influence on software complexity and proved the invalidity of hypothesis H1 which claimed that code readability had no influence on software complexity. Moreover, the results indicated that code readability affected software complexity with a 90.15% accuracy using a decision tree classifier. Therefore, it was considered as a strong influence. Figure 2 presents the first three levels of the tree model. Due to the tree’s large size, we only show the first three levels; these levels show the most effective readability features in this relation which are: max character occurrences, average arithmetic, average parenthesis, max indents, and max indent (preceding white space).
Table 6. Case study 1 results for PCA dimension reduction approach using cross validation.From this case study, we found that code readability had a great influence and impact on software complexity, which addressed the essential role that code readability plays on the maintainability process and on overall software quality. The experimental results confirmed the H0 hypothesis which claimed that code readability had an influence on software complexity and proved the invalidity of hypothesis H1 which claimed that code readability had no influence on software complexity. Moreover, the results indicated that code readability affected software complexity with a 90.15% accuracy using a decision tree classifier. Therefore, it was considered as a strong influence. Figure 2 presents the first three levels of the tree model. Due to the tree’s large size, we only show the first three levels; these levels show the most effective readability features in this relation which are: max character occurrences, average arithmetic, average parenthesis, max indents, and max indent (preceding white space).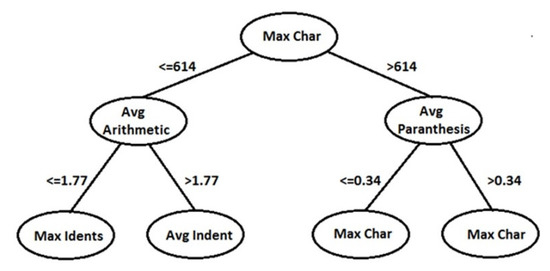 Figure 2. First three levels of the model for case study 1.Consequently, readability is not a simple attribute that can be measured directly or can be reflected on one attribute. However, software developers must pay more attention and focus on this attribute in the development phase, as it affects other software quality attributes and the maintainability process.
Figure 2. First three levels of the model for case study 1.Consequently, readability is not a simple attribute that can be measured directly or can be reflected on one attribute. However, software developers must pay more attention and focus on this attribute in the development phase, as it affects other software quality attributes and the maintainability process.
4.3. Case Study 2: Mapping from Complexity to Readability
The general purpose of this case study was to investigate the relation between complexity and readability, considering complexity as an independent variable and readability as a dependent variable, to show whether complexity influenced the readability or not and whether the readability was dependent on software complexity.
Hypothesis:
H 4.
Software complexity has an influence on the readability of code.
H 5.
Software complexity has no influence on the readability of code.
Several experiments were conducted to investigate these hypotheses with different statistical techniques. According to the previous case study, we decided to use the same statistical analysis approaches that were previously selected as they gave the best results, namely, summation division and PCA dimension reduction. These statistical analysis techniques were used in order to group the 25 readability features into one variable; this was because, as mentioned earlier, the dependent variable had to be only one variable, unlike the independent variable, which could be many variables. After applying these techniques and having the readability combined as one variable, we used several classification algorithms and discuss the techniques proposed and results obtained.
4.3.1. Statistical Techniques
- Summation division:For this approach, we decided to combine the 25 readability features into one variable that represented the overall readability, based on the summation division. Keeping in mind that there were some readability features with positive impact and others with negative impact, some steps from this approach were modified as follows:
- (a)
- For each readability metric:
- Compute the mean.
- If the feature has a positive impact then: if the readability value is greater than the mean, set it to 1; if the value is equal to the mean, set it to 0; and if it is less than the mean, set it to a value of −1
- Otherwise, if the feature has a negative impact, do the following step: if the readability value is greater than the mean, set it to −1; if the value is equal to the mean, set it to 0; and if it less than the mean, set it to 1
- (b)
- At the end of the previous step, 25 columns are produced, where each column represents a readability feature with only one of three possible values (1, 0, or −1).
- (c)
- Add a new variable (called Readability_Sum) that represents the summation of all 25 columns produced by the previous step, the Readability_Sum column’s value ranges from 25 to −25.
- (d)
- Compute the median for the Readability _Sum column.
- (e)
- If the Readability_Sum is greater than the median, give it a class label of “High”, and if it less than the median, give it a class label of “Low”.
This approach produced two class labels, “High” representing a high readability, and “Low” referring to a low readability. The median was used to divide the data into two intervals. It was used rather than any other statistical measure since the data were not normally distributed, where the skewness value equaled −0.265.Considering the class distribution for this approach, the data had an accepted distribution with 46.53% for the low readability and 53.47% for the high readability. - PCA dimension reduction:In this approach, we combined the 25 readability features into one variable that represented the overall readability based on the PCA dimension reduction. For this experiment, we applied the PCA on the 25 readability features, specifying only one component to be produced, which was the strongest component. The component produced had an eigenvalue equal to 5.578. The component contained all the readability features, and the highest feature value was the average indent with 0.797. The varimax rotation matrix was used to get cleaner and better results.When looking at the readability features, we noticed that there were some features that had negative values, which indicated that they were correlated with the component in a negative way. In contrast, the positive values referred to a positive correlation. The negatively correlated features were average spaces, average arithmetic, average blank lines, and average comments. These features had a positive impact on the readability, except for average spaces, which could be excluded since it was almost not correlated to the extracted component (a very low value close to zero). The other features were considered positive features.The component result was stored as a variable named Component_1. Then, for this variable, the median value was calculated. We selected the median rather than another statistical measure since the data were not normally distributed, and the skewness value equaled 1.117. The data were given two class labels: “Low” for the variable Component_1 value above the median and “High” if it was below the median, since the coefficient metrics in the component with positive values had a negative impact on the readability, while the coefficients with negative values had a positive impact. Considering the class distribution for this approach, the data were equally distributed into the two classes, 50% for class “High” and 50% for class “Low”.
4.3.2. Results
In this section, we applied several machine learning algorithms to investigate these hypotheses:
H 6.
Software complexity has an influence on the readability of code.
H 7.
Software complexity has no influence on the readability of code.
The classification algorithms used were decision tree, naïve Bayes, Bayesian network, neural network, and support vector machine. We tried to establish a mapping from complexity metrics to readability metrics, considering complexity metrics as independent variable and readability as a dependent variable. In order to achieve this, the dependent variable was combined into one variable. Therefore, as discussed earlier, two approaches were used to combine the 25 readability features into one variable to use for further analysis. We applied the results obtained from the two approaches, the summation division and PCA dimension reduction, to the classification algorithms and the WEKA tool was used for this analysis [30].
- Summation division results:We used the readability variable produced by the summation division approach as the dependent variable and the seven complexity metrics as independent variables. We applied the five classification algorithms on the dataset. All these algorithms were implemented in the WEKA tool.For testing and evaluation, two techniques were used, namely, percentage split and cross-validation. In the percentage split test, the data were divided into 66% for training and 34% for testing, and for the cross-validation test 10 folds were used. The results are listed in Table 7 and Table 8. The best accuracy was obtained for the percentage split validation with the decision tree classifier with an accuracy of 85.15% and mean absolute error and F-measure values of 0.20 and 0.85, respectively. On the other hand, the best result obtained from the 10-fold cross-validation was also with the decision tree with a 85.54% accuracy and mean absolute error and F-measure the values of 0.19 and 0.86, respectively.
 Table 7. Case study 2 results for summation division approach using percentage split.
Table 7. Case study 2 results for summation division approach using percentage split. Table 8. Case study 2 results for summation division approach using cross-validation.
Table 8. Case study 2 results for summation division approach using cross-validation. - PCA dimension reduction results:In this experiment, we used the five classifiers and applied them on our dataset. We used the readability variable produced by the PCA dimension reduction approach as the dependent variable and the seven complexity metrics as independent variables. For testing and evaluation, two techniques were used, namely, percentage split and cross-validation.
The results are listed in Table 9 and Table 10. The best accuracy was obtained for the percentage split validation with the decision tree classifier with an accuracy of 89.54% and mean absolute error and F-measure values of 0.14 and 0.90, respectively. On the other hand, the best result obtained from the 10-fold cross-validation was with the decision tree with a 90.01% accuracy and mean absolute error and F-measure values of 0.13 and 0.90, respectively.

Table 9.
Case study 2 results for PCA dimension reduction approach using percentage split.

Table 10.
Case study 2 results for PCA dimension reduction approach using cross-validation.
From this case study, we captured the software complexity’s influence on the readability of code. It is intuitive as the readability reflects many attributes, including code structure and density. Thus, there must be an overlap between those attributes. The experiment confirmed the H0 hypothesis, which claimed that software complexity had an influence on the readability of code, and proved the invalidity of hypothesis H1, which claimed that software complexity had no influence on the readability of code. Moreover, the results indicated that software complexity affected code readability with 90.01% accuracy using a decision tree classifier. Therefore, it was considered a strong influence. Figure 3 presents the first three levels of the tree model. We used only the first three levels due to the large tree size; these levels showed the most effective complexity metrics in this relation, which were Halstead volume and OSavg.
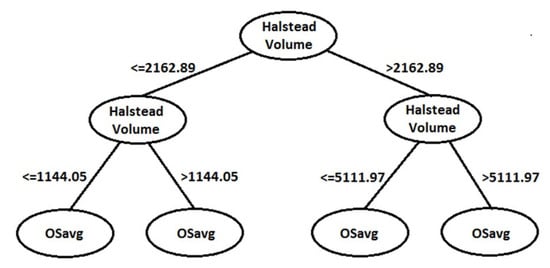
Figure 3.
First three levels of the model for case study 2.
Thus, the code complexity must be monitored as it affects two parts of the software life cycle: in the development phase, where it affects the effort of testing and debugging components, and in the maintenance phase, where the less complex the software is, the more readable the code will be. Further, maintainability activities are expected to cost less.
4.4. Case Study 3: Investigating the Size Independence Claim
The paper [7] assumed in their readability notion that the readability features were independent from the block size. We investigated this claim. Thus, several experiments were conducted to examine the following hypotheses for this case study:
H 8.
Code size has an influence on code readability features.
H 9.
Code size has no influence on code readability features.
In order to examine both hypotheses, we used two approaches, correlation analysis and classification algorithms, to verify whether readability features were independent from the code size, and in both experiments, we used the LOC metric as a measure for code size.
- Correlation analysis:We applied the correlation analysis to examine the correlation between the lines of code (LOC) and the 25 readability features using Spearman and Kendall’s tau-b correlation coefficients. The correlation tests confirmed that size was correlated with readability features. Some of them were strongly correlated, such as average arithmetic, average if, max word and max character occurrences. On the other hand, others were weakly correlated such as the average spaces and average commas.We then defined three relations between the LOC metric and readability features, which were a weak relation, a strong positive relation, and a strong negative relation. A weak relation referred to the readability features which were weakly correlated with the LOC metric, where the correlation was between 0.50 and −0.50. Therefore, we considered that these features had a weak relation with the LOC metric. A strong positive relation indicated that the readability metrics had a strong and positive correlation with the LOC metric, where the correlation was between 1.0 and 0.50. A strong negative relation referred to the readability metrics having a strong but negative correlation to the LOC metric and the correlation was between −0.50 and −1.0.Table 11 shows the relation between the LOC and readability metrics, where 14 features had a weak relation with the LOC metric, 10 features had a strong positive relation, and only one feature had a strong negative relation. The results indicated that many features had a relation with the LOC metric which could be either a positive or negative relation.
 Table 11. LOC and readability metrics relation.
Table 11. LOC and readability metrics relation. - Classification AlgorithmsSeveral experiments were held to investigate the previous hypotheses using two techniques, namely, summation division and PCA dimension reduction. We used the results obtained from Section 4.3.2, where these statistical analysis techniques were used to group the 25 readability features into one variable, because as mentioned earlier, the dependent variable should be only one variable. Then, we applied several classification algorithms.We applied the results obtained from the two approaches, summation division and PCA dimension reduction, on the classification algorithms. All the experiments confirmed the hypothesis H0, which indicated that code size had an influence on code readability features.
4.4.1. Summation Division Results
We used the readability variable produced by the summation division approach as a dependent variable and the LOC metric as an independent variable. We applied the five classification algorithms on the dataset. All these algorithms were implemented in the WEKA data mining tool.
For testing and evaluation, two techniques were used, namely, percentage split and cross-validation. In the percentage split test, the data were divided into 66% for training and 34% for testing, and for the cross-validation test 10 folds were used. The results are listed in Table 12 and Table 13. The best result obtained for the percentage split validation was with a Bayesian network classifier with an accuracy of 79.16% and mean absolute error and F-measure values of 0.27 and 0.79, respectively. On the other hand, the best result obtained from the 10-fold cross-validation was with a decision tree with a 79.66% accuracy and mean absolute error and F-measure values of 0.32 and 0.80, respectively.

Table 12.
LOC and readability metrics results for summation division approach using percentage split.

Table 13.
LOC and readability metrics results for summation division approach using cross-validation.
4.4.2. PCA Dimension Reduction Results
In this experiment, we used the five classifiers and applied them on our dataset. We used the readability variable produced by the PCA dimension reduction approach as a dependent variable and the LOC metric as an independent variable. For testing and evaluation, two techniques were used, namely, percentage split and cross-validation.
The results are listed in Table 14 and Table 15. The best accuracy obtained for the percentage split validation was with the decision tree classifier with an accuracy of 79.98% and mean absolute error and F-measure values of 0.32 and 0.80, respectively. On the other hand, the best result obtained from the 10-fold cross-validation was also with a decision tree with a 80.07% accuracy and mean absolute error and F-measure values of 0.32 and 0.80, respectively.

Table 14.
LOC and readability metrics results for PCA dimension reduction approach using percentage split.

Table 15.
LOC and readability metrics results for PCA dimension reduction approach using cross-validation.
Based on our experiments and results, we found that readability features were dependent on the code size, where the code size had an influence on code readability features. The accuracy results illustrated the strong influence and relationship that the readability features have on the code size, which confirmed the H0 hypothesis and consequently proved the invalidity of hypothesis H1. Therefore, we illustrated in this case study that readability was affected by the attribute size directly and indirectly.
5. Comparison Studies
In this section, we introduce comparison studies between our research approach and the results of previous research studies. The literature review established the importance of code readability and software complexity to the quality of software. There have been few investigations on the relationship between software readability and complexity [7,8]. Thus, two comparison studies are conducted regarding code readability.
(1) First Study:
Buse and Weimer investigated whether code readability was correlated with the cyclomatic Complexity metric by applying a correlation analysis. They developed a readability tool using local code features and conducted a survey on 120 human annotators with 100 source code snippets, with a total of 12,000 human judgments, where the participants scored each snippet based on their readability assessment. Twenty-five code features were extracted from these snippets and used for mapping from snippet codes to snippet vectors of real numbers. Then, the authors applied machine language algorithms using the WEKA mining tool and trained the model using human judgments. Then, they used this tool to investigate whether it was correlated with the cyclomatic complexity metric by applying Pearson’s product-moment correlation, where they used the cyclomatic complexity as their complexity measure.
In our approach, we used their tool, which gave the readability value as a numeric value. However, for our investigation, we wanted to use the features themselves. Therefore, since their tool was open source, we adjusted the source code to parse the values of these 25 features to study their relationship and behavior with the complexity metrics. We used four proposed approaches, namely, clustering analysis, summation division, PCA dimension reduction, and quartile analysis.
These techniques were used to combine the readability features into one variable representing the overall readability. Our methodology judged only the code with “High” and “Low” class labels. We used this measure since we were concerned with the relative judgment, not with the absolute value of the readability. Unlike Buse and Weimer’s investigation, we preferred using machine learning algorithms in our research instead of a correlation analysis since it is known that a correlation analysis only indicates whether there is a linear relationship between two variables. However, some machine learning algorithms have the ability to discover and model nonlinear relationships between two variables, e.g., the neural network (NN), support vector machine (SVM), and decision tree algorithms.
Regarding the complexity metrics, we used seven different complexity metrics, including Chidamber and Kemerer’s metrics (WMC, RFC, DIT, and LCOM), Lorenz and Kidd’s metric (OSavg), the LOC metric, and Halstead’s metric (program volume). Both studies were performed on the Java programming language, which is an object-oriented language. Consequently, we thought to use object-oriented metrics where the selected metrics provided some class measurements that captured the essence of object-oriented design; this was unlike the cyclomatic complexity metric, which was used in the previous work, as it did not measure that essence.
Buse and Weimer found that readability was weakly correlated with complexity in the absolute sense, and it was effectively uncorrelated with complexity in a relative sense. While in our investigation and based on our results and experiments, we managed to find a relation between code readability and software complexity with an almost 90% accuracy.
To examine the reliability of the approaches we used for the readability assessment, we conducted a correlation analysis between the readability values obtained by the two approaches using a summation division and PCA dimension reduction. We also evaluated their correlation with the original value of the readability tool [7] since our investigation was at the file level, and the readability tool was designed for class readability. For each file, we calculated the readability value of the file by computing the average readabilities of classes.
We considered two correlation tests, where we used nonparametric correlation using Spearman and Kendall’s tau-b correlation coefficients. We used these tests since our focus was not on the absolute readability values as much as their relative values and their ranks. Moreover, our data were not normally distributed, so other correlation tests (e.g., Pearson’s correlation coefficient) were not applicable [31].
The statistical results were conducted using 12,180 files. The Spearman correlation test between the readability tool (Buse and Weimer’s tool) and both division and PCA approaches (our approaches) showed a strong correlation with 0.81 and −0.85, respectively. Kendall’s tau-b test also showed a strong correlation with the readability tool and both division and PCA approaches with 0.62 and −0.66, respectively. We noticed that the PCA readability was negatively correlated with others since all the positive readability metrics correlated to it had a negative impact on readability (this issue was discussed briefly in the PCA dimension reduction approach). However, the results showed that our readability value was strongly correlated with those of the Buse and Weimer’s tool.
We also conducted another correlation test but at the class level. As we used the readability tool, the value for each class was calculated once at a time, and to do this for the whole project classes would have been a very time-consuming process. We hence decided to use a sample of code that involved 26 classes obtained from the (org.Eclipse.ant.core, accessed on 6 January 2022) plugin from Eclipse.
The correlation results were conducted using the 26 classes. The Spearman correlation test between the readability tool and our approaches showed a strong correlation of 0.60 and −0.80, respectively. Kendall’s tau-b test also showed a strong correlation with the readability tool and both division and PCA approaches with values of 0.46 and −0.64, respectively. PCA readability was negatively correlated with others since all the positive readability metrics correlated with it had a negative impact on readability, as we explained earlier.
(2) Second Study:
Another study was conducted on component-based software engineering (CBSE) by Goswami to investigate the relationship between readability and complexity [8]. A new complexity metric was proposed to measure interface complexity for software components based on different constituents, where it used interface methods and properties. Then, a correlation study was conducted between the proposed complexity metric and readability using Karl Pearson’s correlation coefficient. They used the readability Formula (7) to measure the readability of components.
The results showed a negative correlation between readability and complexity, with a value of −0.974. This confirmed that a highly complex component was much harder to maintain and understand.
Both studies managed to find a relationship between the two attributes. However, while Goswami studied the relation between readability and complexity for the interfaces of the components, our study investigated the relation for the software project overall by using different complexity measures. Those measures reflected many aspects of the project, including object-oriented metrics, operation-oriented metrics, the volume of the code, and others. Thus, we managed to capture different aspects of the complexity, such as inheritance, cohesion, class response, size, and volume.
6. Threats to the Validity and Assumptions
There are some factors that may potentially affect the validity of our work. First, the metrics values were used from different tools; with the complexity, we used Krakatau Metrics Professional tool to extract them, and for the readability features, we used the source code obtained by Buse and Weimer’s tool and extracted the readability features values. However, we did not validate these metrics manually or by using other tools, as we assumed they were correctly gathered. The second threat is that we built our study on code readability and software complexity assumptions based only on one software project, Eclipse, and using one programming language. However, this threat can be mitigated since Eclipse is well-known software that is widely used for development and includes several add-ons for the different software development tasks. For our investigation, we roughly examined 2,900,970 lines of code, which was considered a significant volume.
7. Conclusions
In this research, an empirical investigation was conducted to evaluate code readability and study its impact on software and its relationship with other software quality attributes, namely, software complexity. This quality attribute was taken since it had an impact on software maintainability in particular. Several experiments were held to study the code readability and software complexity impact and influence on each other using Eclipse, a known open-source project, which is implemented using the Java programming language.
Different data analysis methods and data mining techniques, including machine learning algorithms, were applied to test several research hypotheses raised for the study. In a study including over 2,900,970 lines of source code and based on our results and experiments, we proved that code readability had a significant influence on software complexity with 90.15% effectiveness using a decision tree classifier. On the other hand, naïve Bayes obtained the lowest value with 74.23% effectiveness using a percentage split approach. In addition, we showed the impact of software complexity on the readability of code using a decision tree classifier with a 90.01% prediction accuracy. Thus, the results indicated the strong relation between code readability and software complexity and proved that these attributes had a great influence and impact on each other. One of the limitations of this study was the dependence on only one programming language, the Java programming language.
Furthermore, we validated that readability features were dependent on block size using a PCA, and we managed to find a relation between readability features and block size using a decision tree with a 80.07% accuracy. Finally, a comparison study was conducted to compare our results with other papers and the approaches used in each one.
8. Future Work
Future work can involve extending our approach to different programming languages, as our study was mainly on the Java programming language. Thus, using other object-oriented languages, such as Python, C++, and C#, we can gain a better viewpoint on the relationship between code readability and software complexity and whether the relationship can change or be dependent on the programming language. In addition, we can investigate whether code readability is language-dependent or not, and whether using different programming languages can affect our judgment of the readability of the code or not.
Author Contributions
Conceptualization, Y.T., N.A.-E.-R. and O.D.; methodology, Y.T., N.A.-E.-R. and O.D.; software, Y.T., N.A.-E.-R., O.D., S.A.-E. and D.D.; validation, N.A.-E.-R., O.D. and S.A.-E.; formal analysis, Y.T., N.A.-E.-R., O.D. and S.A.-E.; investigation, Y.T., N.A.-E.-R., O.D., D.D. and O.K.; resources, Y.T., O.D., S.A.-E. and D.D.; data curation, Y.T. and N.A.-E.-R.; writing—original draft, N.A.-E.-R.; writing—review and editing, N.A.-E.-R., O.D., S.A.-E., D.D. and O.K.; visualization, N.A.-E.-R.; supervision, Y.T. and O.D.; project administration, Y.T. and O.D.; funding acquisition, Y.T., N.A.-E.-R., O.D. and O.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The readability model and Krakatau metrics professional tool utilized in our research project can be found in [7,27], respectively, while the dataset for our research was collected manually from the Web.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Dubey, S.; Rana, A. Assessment of Maintainability Metrics of Object-Oriented Software System. ACM Sigsoft Softw. Eng. Notes 2011, 36, 1–7. [Google Scholar] [CrossRef]
- Aggarwal, K.K.; Singh, Y.; Chhabra, J.K. An Integrated Measure of Software Maintainability; Reliability and Maintainability Symposium: Seattle, WA, USA, 2002; pp. 235–241. [Google Scholar] [CrossRef]
- Raymond, D. Reading Source Code. In Proceedings of the 1991 Conference of the Centre for Advanced Studies on Collaborative Research, Toronto, ON, Canada, 28–30 October 1991; pp. 3–16. [Google Scholar] [CrossRef]
- Deimel, L. The Uses of Program Reading. ACM Sigcse Bull. 1985, 17, 5–14. [Google Scholar] [CrossRef]
- Rugaber, S. The Use of Domain Knowledge in Program Understanding. Ann. Softw. Eng. 2000, 9, 143–192. [Google Scholar] [CrossRef]
- Brooks, F. No Silver Bullet Essence and Accidents of Software Engineering. IEEE Comput. 1987, 20, 10–19. [Google Scholar] [CrossRef]
- Buse, R.; Weimer, W. Learning a Metric for Code Readability. IEEE Trans. Softw. Eng. 2010, 36, 546–558. [Google Scholar] [CrossRef]
- Goswami, P.; Kumar, P.; Nand, K. Evaluation of Complexity for Components in Component Based Software Engineering. Int. J. Res. Eng. Appl. Sci. 2012, 2, 902. [Google Scholar]
- Rudolph, F. A New Readability Yardstick. J. Appl. Psychol. 1948, 32, 221–233. [Google Scholar]
- Butler, S.; Wermelinger, M.; Yu, Y.; Sharp, H. Exploring the Influence of Identifier Names on Code Quality: An Empirical Study. In Proceedings of the 14th European Conference on Software Maintenance and Reengineering (CSMR), Madrid, Spain, 15–18 March 2010; IEEE Computer Society: Washington, DC, USA, 2010; pp. 156–165. [Google Scholar] [CrossRef]
- Tashtoush, Y.; Odat, z.; Alsmadi, I.; Yatim, Y. Impact of Programming Features on Code Readability. Int. J. Softw. Eng. Its Appl. 2013, 7, 441–458. [Google Scholar] [CrossRef]
- Tashtoush, Y.; Darweesh, D.; Albdarneh, M.; Alsmadi, I.; Alkhatib, K. A Business Classifier to Detect Readability Metrics on Software Games and Their Types. Int. J. Entrep. Innov. 2015, 4, 47–57. [Google Scholar] [CrossRef]
- Karanikiotis, T.; Papamichail, M.D.; Gonidelis, L.; Karatza, D.; Symeonidis, A.L. A Data-driven Methodology towards Interpreting Readability against Software Properties. In Proceedings of the 15th International Conference on Software Technologies, Paris, France, 7–9 January 2020; pp. 61–72. [Google Scholar] [CrossRef]
- Sarkar, B.; Takeyeva, D.; Guchhait, R.; Sarkar, M. Optimized radio-frequency identification system for different warehouse shapes. Knowl.-Based Syst. 2022, 258, 109811. [Google Scholar] [CrossRef]
- Sarkar, B.; Takeyeva, D.; Guchhait, R.; Sarkar, M. Mathematical estimation for maximum flow of goods within a cross-dock to reduce inventory. Math. Biosci. Eng. 2022, 19, 13710–13731. [Google Scholar]
- Chidamber, S.; Kemerer, C. A Metrics Suite for Object Oriented Design. IEEE Trans. Softw. Eng. 1994, 20, 476–493. [Google Scholar] [CrossRef]
- Pressman, R. Software Engineering: A Practitioner’s Approach, 6th ed.; McGraw-Hill Science: Irvine, CA, USA, 2005; ISBN 9780071238403. [Google Scholar]
- Alenezi, M. Internal Quality Evolution of Open-Source Software Systems. Appl. Sci. 2021, 11, 5690. [Google Scholar] [CrossRef]
- McCabe, T. A Complexity Measure. IEEE Trans. Softw. Eng. 1976, 2, 308–320. [Google Scholar] [CrossRef]
- Halstead, M. Elements of Software Science; Elsevier: New York, NY, USA, 1977; ISBN 978-0444002051. [Google Scholar]
- Lorenz, M.; Kidd, J. Object-Oriented Software Metrics, 1st ed.; Prentice Hal: St. Kent, OH, USA, 1994; ISBN 013179292X. [Google Scholar]
- Muriana, B.; Onuh, O. Comparison of software complexity of search algorithm using code based complexity metrics. Int. J. Eng. Appl. Sci. Technol. 2021, 6, 24–29. [Google Scholar] [CrossRef]
- Gillberg, A.; Holst, G. The Impact of Reactive Programming on Code Complexity and Readability: A Case Study. Bachelor’s Thesis, Mid Sweden University, Sundsvall, Sweden, 2020. [Google Scholar]
- International Business Machines Corp. Eclipse Platform Technical Overview. 2006. Available online: https://www.eclipse.org/articles/Whitepaper-Platform-3.1/eclipse-platform-whitepaper.pdf (accessed on 6 January 2022).
- Shaik, A.; Reddy, C.; Manda, B.; Prakashini, C.; Deepthi, K. Metrics for Object Oriented Design Software Systems: A Survey. J. Emerg. Trends Eng. Appl. Sci. (JETEAS) 2010, 2, 190–198. [Google Scholar]
- Najadat, H.; Alsmadi, I.; Shboul, Y. Predicting Software Projects Cost Estimation Based on Mining Historical Data. ISRN Softw. Eng. 2012, 2012, 823437. [Google Scholar] [CrossRef]
- Powersoftware. Krakatau Metrics. 2021. Available online: http://www.powersoftware.com/ (accessed on 5 January 2022).
- Hervé, A.; Williams, L. Principal Component Analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- IBM. IBM SPSS Statistics. 2021. Available online: https://www.ibm.com/products/spss-statistics (accessed on 2 January 2022).
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I. The WEKA Data Mining Software: An Update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Stemler, S. A Comparison of Consensus, Consistency, and Measurement Approaches to Estimating Interrater Reliability. Pract. Assessment, Res. Eval. 2004, 9, 66–78. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).