Abstract
Radial pulse signals are produced by the periodic ejection of blood from the heart, and physiological and pathological information of the human body can be analyzed by extracting the time-domain characteristics of pulse waves. However, since pulse signals are weak physiological signals on the body surface and complex, the acquisition of pulse characteristics using the traditional curvature method will produce a large error, which cannot meet the needs of pulse wave analysis in current clinical practice. To solve this problem, a multi-morphological pulse signal feature recognition algorithm based on the one-dimensional deep convolutional neural network (1D-DCNN) model is proposed. We used the multi-channel pulse diagnosis instrument independently developed by the team to collect radial pulse signals under continuous pressure of the test subjects and collected 115 subjects and extracted a total of 1300 single-cycle pulse signals and then divided these pulse signals into 6 different forms. Five types of pulse signal time-domain feature points were labeled, and five independent feature point datasets were labeled and formed five customized neural network models that were generated to train and identify the pulse feature point datasets independently. The results show that the correction coefficient () of the multi-class pulse signal processing algorithm proposed in this paper for each type of feature point recognition reaches more than 0.92. The performance is significantly better than that of the traditional curvature method, which shows the accuracy and superiority of the proposed method. Therefore, the multi-class pulse signal characteristic parameter recognition model based on the 1D-DCNN model proposed in this paper can efficiently and accurately identify pulse time-domain characteristic parameters, which can be applied to discriminate time-domain pulse information in clinical practice and assist doctors in diagnosis.
1. Introduction
Radial pulse signals contain a wealth of physiological pathological information on humans, and this pressure signal at the surface of the body is formed via the coupling of periodic ejections of the heart to the arterial canal and its surrounding tissues [1,2,3,4]. In traditional Chinese medicine, doctors analyze pulse wave characteristics based on parameters such as the intensity, depth, width, and frequency of the pulse wave and then make a diagnosis of the subject’s physical condition [5,6,7]. Among these features, the pulse waveform is a key factor in analyzing a subject’s pulse signature, which is also an important task for pulse measurement devices. As a result, pulse wave characteristics have been extensively studied in recent years [8,9,10].
At present, there are mainly the following feature extraction methods for pulse waves, namely, the frequency domain method, modeling method, and time domain method. With the frequency domain method, Chang, C.W. [11,12] used the Fourier transform method to extract the amplitude of the first 11 harmonics of a subject’s pulse wave and analyzed the relationship between harmonic characteristics and the health status of the subject. Liao, K.M. [13] analyzed the relationship between the fourth harmonic amplitude in the spectrum and patients with type 2 diabetes. However, the physiological significance of the pulse characteristic parameters extracted using the frequency domain method is not intuitive and difficult to interpret. With the modeling method, Cornet, A. [14] simulated the pressure wave waveform of irregular arteries (such as bifurcations, stiff arteries, stenoses, or aneurysms) using mathematical modeling methods, and then predicted the pulse waveforms of different pathological scenarios. Charlton, P.H. [15] designed a model that can simulate hemodynamic characteristics and pulse wave characteristics in different age groups by extracting the pulse wave index of people aged 25–75 years. However, the disadvantage of the above model-fitting method is that the model complexity is high, and it is easy to ignore the details of the original pulse wave features, thereby losing the features associated with a disease. With the time-domain method, Elgendi, M. [16] extracted the time-domain characteristic parameters of a pulse signal using the second-order difference method and evaluated the heat stress effect during the subject’s exercise. Hou, J. [17] defines a new characteristic parameter of pulse wave angle value using the curvature method and realizes the extraction of time-domain pulse wave features. However, the parameter extraction accuracy of the above method, which is greatly affected by the complexity of pulse waveforms, resulted in poor robustness. Therefore, how to accurately extract the characteristic parameters of pulse waves from the perspective of the time domain, so as to improve the physiological interpretability of pulse waves, is the focus of this study.
With the rapid development of machine learning, there is more and more research that has been conducted in the field of pulse waves. Wang, K. [18] used the support vector machine (SVM) method to classify cardiovascular disease patients and non-cardiovascular disease control groups, indicating the characteristic differences in pulse waveforms between the two groups. Li, G. [19,20] used convolutional neural networks to classify pulse waves in patterns, achieving an accuracy of about 90%. Ding, X. [21] used a variety of machine learning models such as k-nearest neighbor, logistic regression, and SVM to classify the normal and abnormal pulse cycles of pulse waves in 390 outpatients. The above machine learning methods focus on the pulse wave signal itself to achieve the pattern classification of a pulse wave and analyze the relationship between pulse waves and disease. Few researchers have extracted the characteristic parameters of pulse waves from the perspective of the time domain so as to achieve an explanation of the physiological significance of pulse waves.
To solve this problem, a feature point recognition model based on the 1D-DCNN model is proposed. Time-domain feature extraction of six common pulse waveforms was carried out, and the value of each feature point reached more than 0.92. The method was as follows: First of all, the pulse diagnosis equipment independently developed by our laboratory, which can collect pulse signals under a continuous pressure sequence at multiple positions of the radial artery to ensure the integrity of data collection, was used to obtain the radial pulse signals of 115 subjects. Secondly, according to morphology, after signal preprocessing, 1300 single-cycle pulse waveforms were extracted and divided into 6 categories. Based on the hemodynamic theory of pulse waves, five feature points with physiological significance on the waveform were marked, and five independent datasets were generated. Finally, using the 1D-DCNN method, five datasets were independently trained, and five customized feature point neural network models were generated by adjusting their respective network structures. Compared with the traditional curvature method, the results show that the values of the customized 1D-DCNN models reached more than 0.92, which improves the robustness of the time-domain feature point recognition of complex waveforms. The accuracy and applicability of this method are illustrated and provide strong support for traditional Chinese medicine from the perspective of pulse wave waveform interpretation of human physiological and pathological information.
2. Materials and Methods
This section mainly elaborates on the following four aspects: The first part contains details of the data acquisition equipment used in the research process, as well as the equipment acquisition process and results. The second part contains an explanation of the traditional method of typical pulse wave time-domain feature point extraction and an explanation of the physiological significance of feature points. The third part covers the construction and training process of the one-dimensional convolutional neural network model. The fourth part contains the evaluation methods for model training results.
2.1. Data Acquisition
The data acquisition equipment used in this institute is a pulse diagnostic instrument independently developed by the laboratory [22], as shown in Figure 1a. The device contains 3 sensor channels, and each sensor probe adopts a composite structure, as shown in Figure 1b. It can simultaneously record pulse strength and pressure applied to the corresponding position, recorded as dynamic pressure and static pressure, respectively. The device enables the simultaneous acquisition of pulse data from multiple locations of the human radial artery. The wristband balloon pressurization method was used to realize the data acquisition under the continuous pressure sequence of the radial artery, the total number of pressurizations was 14 times, the time of each compression was maintained for 10 s, and the sampling frequency of the device was 225 Hz. The raw data obtained are shown in Figure 1c, where the abscissa represents the sampling time, the left ordinate represents the dynamic pressure, and the right ordinate represents the static pressure. After preprocessing such as filtering and periodic division, a single-cycle pulse waveform under a continuous pressure sequence can be obtained, as shown in Figure 1d, where the abscissa represents the static pressure, and the abscissa represents the pulse strength.
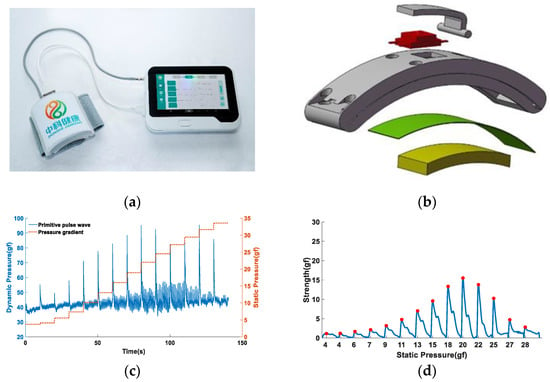
Figure 1.
Pulse data acquisition equipment and signal acquisition diagram: (a) multi-channel pulse diagnosis equipment, including a wristband data collector and a display storage device; (b) composite sensor construction; and (c) raw pulse signal. The solid blue line represents the pulse signal, where the spike is due to the pressure pulse at the beginning of pressurization, and the signal we use is the signal when the pressure is flat, so it has no effect on the result. The orange dashed line indicates the pressure gradient. (d) Single-cycle pulse signal under continuous stress sequence.
2.2. Typical Pulse Wave Time-Domain Feature Points
A pressure pulse wave signal is produced due to periodic ejection of the heart, so the pulse waveform characteristics are closely related to the ejection mechanism of the heart. The typical single-cycle pulse waveform is shown in Figure 2a. According to traditional Chinese medicine theory and related references [23], the time-domain feature points of single-cycle pulse waves can be explained by the following 7 feature points, as shown in A, B, C, D, E, F, and G in Figure 2a. A–G represents a complete ejection cycle of the heart, A–E is the systolic process, and E–G is the diastolic process. A complete single-cycle pulse wave can be broken down into the following steps:
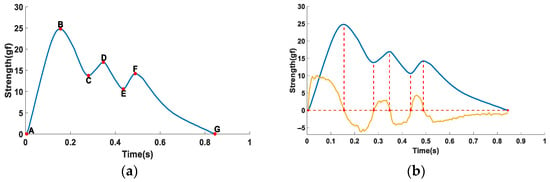
Figure 2.
Typical single-cycle pulse wave: (a) single-cycle pulse waveform and physiological characteristic points; (b) feature point identification using traditional curvature methods.
- Point A is the starting point of the periodic pulse wave, which indicates the beginning of the cardiac ejection cycle;
- The process of A–B occurs during ventricular rapid ejection. At this time, due to the contraction of the ventricles compressing blood into the aorta, the blood in the arteries accumulates rapidly, and the arterial wall expands sharply, forming a relatively steep ascending branch. When point B is reached, the arterial wall is at its most dilated. The amplitude of the B spot can reflect the ejection function of the ventricles and the elasticity of the arterial canal;
- The process of B–C occurs in the late stage of ventricular ejection. At this time, the blood flow into the root of the artery is less than the blood flow out of the root of the artery, resulting in a decrease in pressure in the arterial canal and elastic contraction of the arterial wall and forming the branch of B–C;
- The process of C–E occurs when ventricular ejection stops, and the initial wave of the aorta propagates outward. This process is mainly related to the tension and peripheral resistance of the arterial canal. When arterial canal resistance becomes greater, blood flow slows, and aortic pressure increases, resulting in an increase in the local peak point D between C–E, which may be larger in amplitude than point B. When the arterial canal tension becomes greater, the elasticity of the arterial wall becomes worse, at which point the blood flow velocity increases, and the D point appears earlier and may coincide with the B point;
- The process of E–G occurs during the diastolic phase of the heart. Point E is the cut-off point of cardiac systolic relaxation. At this time, the aortic valve closes, and blood circulation back to the aorta increases the volume of the aorta. Because the aortic valve closes, the blood cannot flow back, and the rebound blood flow produces a shock to form the ascending branch of E–F, after which the pressure of the arterial canal gradually decreases because the ventricles have stopped ejection. The function of the aortic valve and arterial resistance are the main factors affecting this process;
- The G spot is the end point of the cycle pulse wave, which indicates the completion of a complete cardiac ejection cycle.
The existing pulse wave time-domain feature parameter extraction methods often revolve around the curvature method. The feature recognition is carried out by setting a certain curvature threshold or custom curvature parameters. The basic idea is to obtain the curvature value by calculating the first-order differential of the single-cycle pulse wave signal and to find the zero-crossing position of the pulse signal so as to determine the extreme value point present in the original waveform, that is, the pulse wave time-domain characteristic point. To facilitate the observation of feature point positions, we set the scale factor of the first-order difference curve to 10, as shown in Figure 2b. However, a pulse wave is a weak physiological signal on the body surface, and its formation reasons are complex and easily disturbed by the external environment. As such, the actual pulse waveform collected is complex and diverse, and use of the curvature method to extract feature values will produce large errors, resulting in poor robustness of feature recognition. Therefore, machine learning methods were used to identify the pulse wave time-domain features of complex polymorphic recognition.
2.3. 1D-DCNN Model Construction
The design process of the 1D-CNN model in this study consists of two parts. The first part was the preparation of the dataset, and the second part was the design of the algorithm model. The model flow chart is shown in Figure 3.
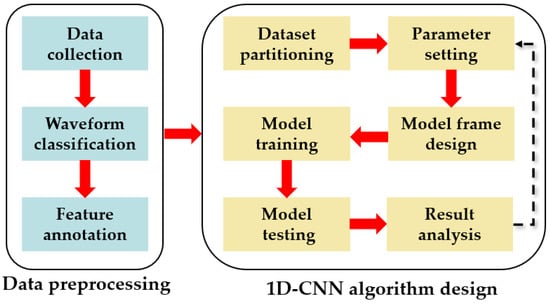
Figure 3.
Model building flowchart.
2.3.1. Data Preprocessing
Before designing a machine learning feature extraction model algorithm, we need to prepare the dataset.
Firstly, a single-cycle pulse wave at the radial artery of a subject’s sample was acquired according to the device and method shown in Figure 1.
Secondly, due to the diversity of pulse morphology across different physiological individuals, the collected pulse waves were divided into 6 categories according to morphology so as to facilitate the unified labeling of feature points, and the specific morphological characteristics of the 6 types of waveforms are shown in Figure 4. Among them, the morphological characteristics of the first type of pulse wave are shown in Figure 4a, which has the morphological characteristics closest to the typical single-cycle pulse wave and manifests as three clear characteristic peaks. The morphological characteristics of the second type of pulse wave are shown in Figure 4b, which has two peaks and a curved inflection point, and the curved inflection point is located between the two peaks. The morphology of the third type of waveform is shown in Figure 4c, which has only one peak and two more obvious curve inflection points after the peak appears. The morphological characteristics of the fourth type of waveform are shown in Figure 4d, which has two peaks, and the height of the second peak is greater than the height of the first. The morphology of the fifth type of waveform is shown in Figure 4e, which has only two peaks and no other significant feature points. The morphological characteristics of the sixth type of waveform are shown in Figure 4f, which has a peak and a curved inflection point and no other significant feature points.
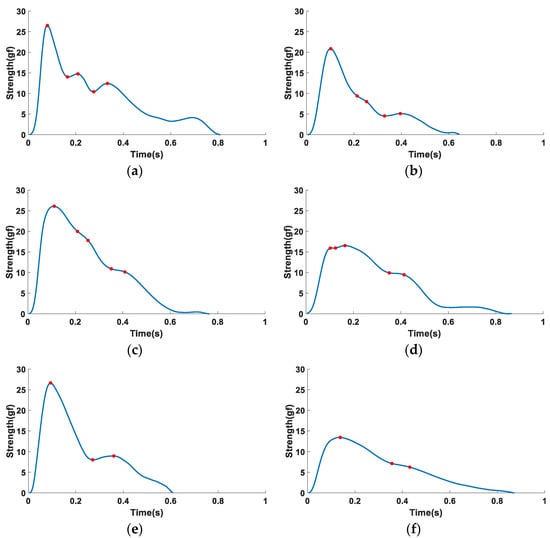
Figure 4.
Six types of pulse waveforms: (a) three peak packets; (b) two peak packets and one curve inflection point, and the inflection point is between the two peak packets; (c) one peak packet and two curve inflection points; (d) two peak packets and one curve inflection point, and the inflection point is located after the two peak packets; (e) two peak packets; and (f) one peak packet and one curve inflection point.
Finally, the time-domain feature points of the six types of pulse waveforms were labeled, as shown by the red solid dots in Figure 4, in which no additional feature recognition is carried out because the start point A and the end point G of the pulse wave have been determined during the periodic segmentation. Therefore, this study focused on identifying the five time-domain feature points of B–F. Among them, the four types of waveforms in Figure 4a–d have a common feature of three obvious peak packets or curve inflection points. The annotation method of this type of waveform feature point is: if the waveform has a peak packet, the peak point and trough point are used as the pulse wave time-domain feature points. If the waveform has no peak packet, the curve inflection point is used as the pulse wave time-domain feature point, and then corresponds to the five feature points of B–F, respectively. The common feature of the two types of waveforms in Figure 4e,f is that there are only two more obvious peak packets or curve inflection points. According to the formation of the pulse wave, the second peak packet of this type of waveform may be submerged in the first peak packet. Therefore, it was considered that the B, C, and D points of such waveforms coincide and that the E and F points correspond to the peak point or curve inflection point after the first characteristic peak packet.
2.3.2. 1D-DCNN Algorithm Design
Pulse signals are time-series signals, so pulse signal feature recognition processes one-dimensional signals. In supervised neural network models, recurrent neural networks (RNNs) and long short-term memory (LSTM) are often used to predict the output signal at the next moment based on previous time series signals. However, when it comes to signal feature recognition that is independent of prior temporal features, they do not perform better than convolutional neural networks (CNNs). CNNs are good at global feature extraction and have strong adaptability to one-dimensional pulse signals, so CNNs were selected as the basic framework for pulse waveform feature recognition. Figure 5 shows the 1D-DCNN model framework of this study, which mainly consists of the following three parts.
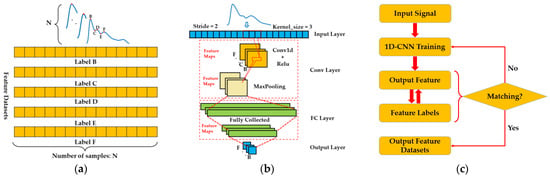
Figure 5.
1D-CNN algorithm design process: (a) generation of feature datasets; (b) 1D-DCNN model training; and (c) 1D-CNN model testing.
The first part is the generation of the feature dataset, as shown in Figure 5a. Firstly, according to morphology, 1300 single-cycle pulse waves divided into 6 categories are labeled with feature points. Each waveform will generate a total of 5 feature points, B, C, D, E, and F, and combine all feature points with the same label to generate the corresponding feature point collection. That is, a dataset of 5 types of feature points can be obtained. These 5 types of feature point datasets will be used as labels for model training.
The second part is the design of the 1D-DCNN framework flow, as shown in Figure 5b. The model framework is mainly divided into the following 4 layers, namely: the input layer, convolutional (Conv) layer, fully connected (FC) layer, and output layer. Among them, the hyperparameters of the model are mainly set in the input layer, including parameters such as training times, convolution kernel size, and step size. In this study, the empirical value of setting the convolution kernel size is 3 and the empirical value of the step size is 2. The training core of this part is the Conv layer and the FC layer. In the operation of the Conv layer, it is mainly divided into three operation steps: one-dimensional convolution, Relu function activating, and maximum pooling. In the convolution operation, the pulse one-dimensional time-series signal is first convolved through the set convolution kernel parameters. The main function of this step is to extract features and obtain the convoluted feature layer. Then, the feature layer is activated with the Relu function, which is used to increase the nonlinear relationship between the layers of the neural network and enable the neural network to complete complex learning tasks. Finally, the features activated with the Relu function are maximally pooled according to the established step size and size. The main function of this step is to downsample the features to obtain the pooled feature layer. After the above steps, the weight parameters and bias of the network are obtained. The process of network training is a process of continuously updating and . To obtain the final output features, it is also necessary to perform a fully connected operation of flattening the pooled feature layer into a feature tensor, using the linear fully connected layer, and calculating the weight of each network node trained to obtain the final output feature, as shown in Equation (1). Because our purpose was to extract 5 time-domain feature parameters such as pulse waves B, C, D, E, and F, 5 parallel trainings were required, which resulted in 5 specific 1D-DCNN networks for the identification and prediction of each time-domain feature point.
where represents the output tensor, represents the input tensor, represents the weight, and represents the bias.
The third part is the testing of the model. After 1D-DCNN training, the feature output of each network is obtained, the output feature points are continuous vectors, and 5 feature vector sets can be obtained. By calculating the degree of matching between each output feature set and feature set labels, it is decided whether to perform a new round of training and update of network training parameters. In this study, the loss function was used as a marker to test whether the network training was complete. When the loss function value is trained for 30 consecutive times and no longer decreases, the network is considered to have been trained. Otherwise, the loss function value is propagated forward to continue training the network. The loss function is shown in Equation (2):
2.4. Model Evaluation
The purpose of this study was to predict specific feature values, so it belongs to the regression problem in supervised learning. The training accuracy of a model is usually evaluated using the following method: The adjusted R square () parameter represents the ratio of the sum of squares of regression to the sum of squares of the residuals and is a measure of the goodness-of-fit of regression. The closer this statistic is to 1, the better the fit of the model, which is an important indicator of accurate measurement in regression problems. The average absolute error () parameter represents the sum of the absolute values of the difference between the predicted value and the actual value, which can better reflect the actual situation of the predicted value error. The root-mean-square error () parameter is the square of the mean squared error. The smaller the values of and , the higher the prediction accuracy of a model, and the calculation method is shown in Equation (3):
where represents the predicted value, represents the actual value, represents the average of the actual values, and represents the sample size.
3. Results and Discussion
This section is mainly elaborated from the following parts. The first part contains the sources of the data. The second part covers the training process and results of the 1D-DCNN model. The third part covers the evaluation and comparison of the results of the model. The fourth part is a discussion of the results obtained.
3.1. Data Sources
In this study, a total of 115 volunteers participated in the data collection process, and the volunteers came from the laboratory team. During the experiment, each participant fully understood the research content of the project and volunteered to participate in the data collection. The specific inclusion criteria for the subjects are shown below:
- In good physical condition and no cold symptoms;
- Good heart condition without cardiac surgery;
- There are no malformations or injuries in the radial artery.
Using the data acquisition equipment in Section 2.1 and the pulse wave signal acquisition method, a total of 1300 single-cycle pulse waves were collected. The basic physiological parameters of the subjects are shown in Table 1.

Table 1.
Table of basic physiological parameters of the subjects.
3.2. 1D-DCNN Training Results
Since there was no correlation between the identification of five types of feature points in the pulse wave time domain, five independent neural network models were trained. According to our analysis, the main factors affecting the recognition accuracy and training time of the 1D-DCNN model are sample size and model structure. Because the number of samples used in this experiment was limited, the identification of pulse feature points was achieved by changing the model structure. In general, the model can be optimized by varying the number of Conv layers and the number of input and output channels.
Table 2 shows the influence of 1D-DCNN models with different numbers of Conv layers on the of feature point recognition. It can be seen from Table 2 that when the number of Conv layers is five and six, the values of the five types of feature points are close to one. However, on the whole, the values of the six Conv layers are closer to one, which means that the predicted value of the model is closest to the actual value at this time. For feature point B, the values obtained for the 7 Conv layers reach the local maximum, but the difference from the 6 Conv layers is only 0.01. After comprehensive consideration, the number of Conv layers was set to six in this study.

Table 2.
Influence of Conv layer number on of model.
To design a 1D-DCNN model with higher accuracy and fewer training times, on the basis of determining the number of Conv layers, this study optimized the model by changing the number of input and output channels of each Conv layer. Based on a Python 3.8.8 and Pytorch 1.12.0 development environment, eight network model structures as shown in Table 3 were designed.

Table 3.
Different structures of 1D-DCNN models.
As shown in Table 3, we designed eight 1D-DCNN model structures. Among them, the Conv layer has six layers, and the structure of each layer is (a–b), where (a) represents the input channel, and (b) represents the output channel. The FC layer has two layers, and the structure of each layer is (c–d), where (c) represents the number of input features, and (d) represents the number of output features. The number of network training times is determined by setting the loss function threshold. When the loss function threshold condition is reached, fewer training times means less network training time. The loss function threshold condition set in this study was as follows: when the loss function output value of the network does not decrease for 30 consecutive times, the network is considered to have been trained. The training is stopped, and the final network model is output. Table 4 describes the model parameters.

Table 4.
Model parameter settings for 1D-DCNN.
To prevent the model from falling into local optimum, we randomly shuffled 1300 one-dimensional pulse wave signals, and 70% of them were used as the training set (a total of 910 single-cycle pulse signals), and 30% of the samples were used as the test set (a total of 390 single-cycle pulse signals). Taking the five feature points corresponding to the pulse signal as the training label, eight different network structures were applied to the training of the five feature point training sets. The model training results obtained are shown in Figure 6.
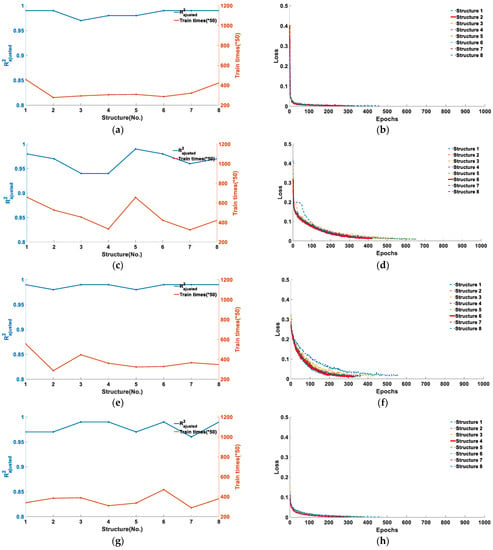
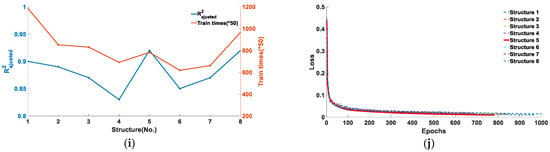
Figure 6.
Training results for five types of feature points under eight network structure models: (a) and training number of feature point B; (b) the loss function of feature point B; (c) and training number of feature point C; (d) the loss function of feature point C; (e) and training number of feature point D; (f) the loss function of feature point D; (g) and training number of feature point E; (h) the loss function of feature point E; (i) and training number of feature point F; and (j) the loss function of feature point F.
As can be seen from Figure 6, the five types of feature points were adapted to different model structures. Figure 6a,b corresponds to the training results of feature point B. It can be seen from Figure 6a that when the model structure is 2, the obtained by training is 0.99, and the number of training cycles at this time is 277 training cycles. Figure 6b shows the loss function curves of the eight model structures reaching the loss function threshold, and it can be seen that the loss function of the second model structure converges the fastest and the training times are the least. Considering the training accuracy and training period, structure 2 is the model structure most suitable for feature point B recognition. Similarly, the training results corresponding to feature points C and D are Figure 6c–f. It can be determined that when the model structure is 6, the of feature point C is 0.98, the training period is 422, the of feature point D is 0.99, and the training period is 328, respectively, and that it is the optimal model for corresponding feature point recognition. From Figure 6f,g, it can be determined that when the model structure is 4, the of feature point E is 0.99, the training period is 310, and the loss function converges the fastest, and that it is the optimal model structure of feature point E. From Figure 6i,j, it can be determined that when the model structure is 5, the of feature point F is 0.92, and the training period is 782, and that it is the optimal model of feature point F.
In summary, the optimal model structure corresponding to the five types of feature points is shown in Figure 7, in which each Conv layer contains three parts, namely, the one-dimensional convolutional layer, the activation layer, and the pooling layer. The input signal of each network is a one-dimensional pulse signal (a total of 256 data). Including a total of six Conv layers and two FC layers, the input and output of each layer are determined by the network structure. The specific parameter amount is shown in Figure 7, and the final output is the value of one specific feature point.
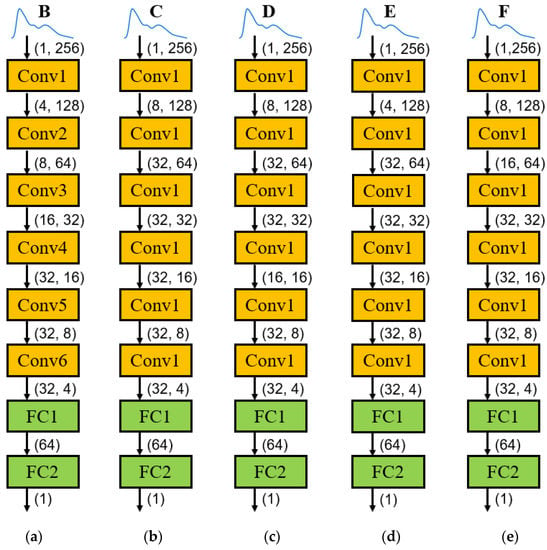
Figure 7.
Optimal model structure of 5 types of feature points: (a) model structure of feature point B; (b) model structure of feature point C; (c) model structure of feature point D; (d) model structure of feature point E; and (e) model structure of feature point F.
3.3. Model Testing and Evaluation
The test set data of the five types of feature points were substituted into the trained model structure in Figure 6, and the sample size of each type of feature point test set was 390. We also compared the results of the training set with the results obtained using traditional methods and obtained the test results shown in Table 5.

Table 5.
Model test results.
It can be seen from the results in Table 5 that after the training of the 1D-DCNN model in this study, the values of the training set of pulse wave time-domain feature points B–F reach more than 0.92, and the values of feature points B, D, and E reach 0.99. The statistical parameters such as and corresponding to each feature point dataset are below five, indicating that the trained model has achieved high feature point recognition accuracy.
The trained model was tested using the test set data, and it was found that the values of feature points B–F was equal to or slightly lower than the values of the training set. However, the overall value reached more than 0.92, and the values of and were also below 6, indicating that the 5 independent feature point recognition models could achieve high recognition accuracy.
The same test set data were identified using the traditional curvature method, and it was found that only the value of feature point B reached 0.92, and the statistical parameters were below 5. However, the values of the other feature points were all negative, and the statistical parameter values were large. The values of feature points C–F reached 17.83, 24.14, 26.49, and 26.71, respectively, indicating that the predicted feature point position was quite different from the actual feature point position.
After our analysis, the reason for the low recognition accuracy of the traditional curvature method is that when the pulse waveform is more complex, the waveform features of the feature points C–F are not obvious, leading to a decrease in recognition accuracy, so the robustness of the curvature method to identify the feature points is poor. The feature point B is the main peak of the pulse wave, which is easy to identify, so the recognition accuracy of both the traditional curvature method and the 1D-DCNN method is high. However, the recognition accuracy of the curvature method is still lower than that of the 1D-DCNN model.
3.4. Discussion
In this study, a 1D-DCNN model was designed by using the deep learning framework to accurately identify five time-domain feature points of pulse waves. Through the separate training of five types of feature points, an independent model corresponding to each feature point was obtained. The results show that the regression values of the five types of feature points reached more than 0.92, and the recognition accuracy of the feature points in the test set was also great, and the value reached more than 0.92. Compared with the traditional curvature method, the accuracy and robustness are greatly improved.
However, due to the limited sample size we obtained, we cannot include all morphological pulse waves, which will lead to some morphologically complex pulse waves not being able to be identified using deep learning models with accurate time-domain feature points, resulting in a lower accuracy of model recognition. However, this problem can be gradually solved with an increase in sample size and pulse wave morphology, and more complex deep learning network structures can be designed through larger samples so as to realize more morphological pulse wave feature recognition and improve the universality and robustness of the feature point recognition model. In the future, on the basis of the above research, we will collect more pulse data, gradually update and optimize the network model, improve the robustness of the model, and achieve better feature point recognition accuracy.
4. Conclusions
A pulse signal contains rich physiological and pathological information on the human body, and the time-domain characteristics of pulse waves are closely related to heart beat and cardiovascular state. However, due to the complex and diverse pulse morphology, the traditional curvature method has low accuracy and robustness for pulse time-domain feature point recognition. Therefore, this study proposed a pulse signal time-domain feature recognition method based on the 1D-DCNN model. We extracted 1300 single-cycle pulse signals by collecting pulse data from 115 volunteers. All single-period signals were divided into six categories according to morphology, and then the time-domain feature labeling of each type of pulse signal and the dataset of five time-domain feature points were obtained. We used 70% of these data as a training set and 30% as a test set. By designing 1D-DCNN models with different structures, five independent feature point recognition models were trained. The results show that each model obtains good prediction results in the corresponding feature point training set and test set, and their values reached more than 0.92. This is significantly better than the accuracy of the traditional curvature method for pulse time-domain feature recognition. It was explained that the 1D-DCNN model designed in this study can accurately identify the time-domain characteristics of polymorphic pulse waves, which proves the superiority and universality of the method. This indicates that this method can also assist doctors in the diagnosis of pulse characteristic information in traditional Chinese medicine clinics.
Author Contributions
Conceptualization, G.W., X.G. and Y.Z.; methodology, G.W.; software, G.W., L.H. and X.G.; data collection, G.W., X.G. and X.K.; data analysis, G.W.; writing—original draft preparation; writing—review and editing, G.W., X.G. and X.K.; final approval, G.W., X.G., X.K., Y.Z., J.Z. and H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Sichuan Science and Technology Major Project (No.2022ZDZX0033) and the Key Research Program of the Chinese Academy of Sciences (No. ZDRW-ZS-2021-1).
Data Availability Statement
The raw/processed data required to reproduce these findings cannot be shared at this time as the data also form part of an ongoing study.
Conflicts of Interest
There are no conflicts of interest among the authors.
References
- Korpas, D.; Halek, J.; Dolezal, L. Parameters describing the pulse wave. Physiol. Res. 2009, 58, 473–479. [Google Scholar] [CrossRef]
- Korpas, D. [Arterial hemodynamics and pulse wave propagation]. Cesk. Fysiol. 2003, 52, 153–159. [Google Scholar] [PubMed]
- Yang, T.H.; Kim, J.U.; Kim, Y.M.; Koo, J.H.; Woo, S.Y. A New Blood Pulsation Simulator Platform Incorporating Cardiovascular Physiology for Evaluating Radial Pulse Waveform. J. Healthc. Eng. 2019, 2019, 4938063. [Google Scholar] [CrossRef]
- Obata, Y.; Ruzankin, P.; Gottschalk, A.; Nyhan, D.; Berkowitz, D.E.; Steppan, J.; Barodka, V. Pulse wave travel distance as a novel marker of ventricular-arterial coupling. Heart Vessels 2018, 33, 279–290. [Google Scholar] [CrossRef] [PubMed]
- Fei, Z.F. Contemporary Sphygmology in Traditional Chinese Medicine (in Chinese); People’s Medical Publishing House: Beijing, China, 2003. [Google Scholar]
- Chen, C.L.; Li, Z.Q.; Zhang, Y.T.; Zhang, S.L.; Hou, J.N.; Zhang, H.Y. A 3D Wrist Pulse Signal Acquisition System for Width Information of Pulse Wave. Sensors 2020, 20, 11. [Google Scholar] [CrossRef]
- Yoo, S.K.; Shin, K.Y.; Lee, T.B.; Jin, S.O. New pulse wave measurement method using different hold-down wrist pressures according to individual patient characteristics. Springerplus 2013, 2, 406. [Google Scholar] [CrossRef]
- Moura, N.G.; Cordovil, I.; Ferreira Ade, S. Traditional Chinese medicine wrist pulse-taking is associated with pulse waveform analysis and hemodynamics in hypertension. J. Integr. Med. 2016, 14, 100–113. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.; Balmer, J.; Pretty, C.G.; Mehta-Wilson, T.; Desaive, T.; Shaw, G.M.; Chase, J.G. Incorporating pulse wave velocity into model-based pulse contour analysis method for estimation of cardiac stroke volume. Comput. Methods Programs Biomed. 2020, 195, 105553. [Google Scholar] [CrossRef] [PubMed]
- Kotecha, D.; New, G.; Collins, P.; Eccleston, D.; Krum, H.; Pepper, J.; Flather, M.D. Radial artery pulse wave analysis for non-invasive assessment of coronary artery disease. Int. J. Cardiol. 2013, 167, 917–924. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.W.; Chen, J.M.; Wang, W.K. Development of a Standard Protocol for the Harmonic Analysis of Radial Pulse Wave and Assessing Its Reliability in Healthy Humans. IEEE J. Transl. Eng. Health Med. 2015, 3, 2900206. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.W.; Wang, W.K. Reliability assessment for pulse wave measurement using artificial pulse generator. J. Med. Eng. Technol. 2015, 39, 177–184. [Google Scholar] [CrossRef]
- Liao, K.M.; Chang, C.W.; Wang, S.H.; Chang, Y.T.; Chen, Y.C.; Wang, G.C. Risk assessment of macrovascular and microvascular events in patients with type 2 diabetes by analyzing the amplitude variation of the fourth harmonic component of radial pulse wave. Physiol. Rep. 2019, 7, e14252. [Google Scholar] [CrossRef] [PubMed]
- Cornet, A. Mathematical modelling of cardiac pulse wave reflections due to arterial irregularities. Math. Biosci. Eng. 2018, 15, 1055–1076. [Google Scholar] [CrossRef] [PubMed]
- Charlton, P.H.; Mariscal Harana, J.; Vennin, S.; Li, Y.; Chowienczyk, P.; Alastruey, J. Modeling arterial pulse waves in healthy aging: A database for in silico evaluation of hemodynamics and pulse wave indexes. Am. J. Physiol. Heart Circ. Physiol. 2019, 317, H1062–H1085. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M.; Fletcher, R.; Norton, I.; Brearley, M.; Abbott, D.; Lovell, N.H.; Schuurmans, D. On Time Domain Analysis of Photoplethysmogram Signals for Monitoring Heat Stress. Sensors 2015, 15, 24716–24734. [Google Scholar] [CrossRef]
- Hou, J.; Zhang, Y.; Zhang, S.; Geng, X.; Zhang, J.; Chen, C.; Zhang, H. A novel angle extremum maximum method for recognition of pulse wave feature points. Comput. Methods Programs Biomed. 2020, 189, 105321. [Google Scholar] [CrossRef]
- Wang, K.; Wang, L.; Wang, D.; Xu, L. SVM classification for discriminating cardiovascular disease patients from non-cardiovascular disease controls using pulse waveform variability analysis. In AI 2004: Advances in Artificial Intelligence, Proceedings of the 17th Australian Joint Conference on Artificial Intelligence, Cairns, Australia, 4–6 December 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 109–119. [Google Scholar]
- Li, G.; Watanabe, K.; Anzai, H.; Song, X.; Qiao, A.; Ohta, M. Pulse-Wave-Pattern Classification with a Convolutional Neural Network. Sci. Rep. 2019, 9, 14930. [Google Scholar] [CrossRef]
- Chen, C.; Li, Z.; Zhang, Y.; Zhang, S.; Hou, J.; Zhang, H.J.A. Low-Power FPGA Implementation of Convolution Neural Network Accelerator for Pulse Waveform Classification. Algorithms 2020, 13, 213. [Google Scholar] [CrossRef]
- Ding, X.; Cheng, F.; Morris, R.; Chen, C.; Wang, Y. Machine Learning-Based Signal Quality Evaluation of Single-Period Radial Artery Pulse Waves: Model Development and Validation. JMIR Med. Inform. 2020, 8, e18134. [Google Scholar] [CrossRef]
- Geng, X.; Liu, S.; Zhang, Y.; Zhang, S.; Hou, J.; Zhang, J.; Asif, M.; Zhang, H.-Y. Adjacent Channel Interference Modeling of Single Vibration Point on Multichannel Dynamic Pressure Sensors. J. Sens. 2020, 2020, 1953506. [Google Scholar] [CrossRef]
- Luo, Z.Y.; Cui, J.; Hu, X.J.; Tu, L.P.; Liu, H.D.; Jiao, W.; Zeng, L.Z.; Jing, C.C.; Qiao, L.J.; Ma, X.X.; et al. A Study of Machine-Learning Classifiers for Hypertension Based on Radial Pulse Wave. BioMed Res. Int. 2018, 2018, 2964816. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).