Research on Traffic Congestion Forecast Based on Deep Learning
Abstract
1. Introduction
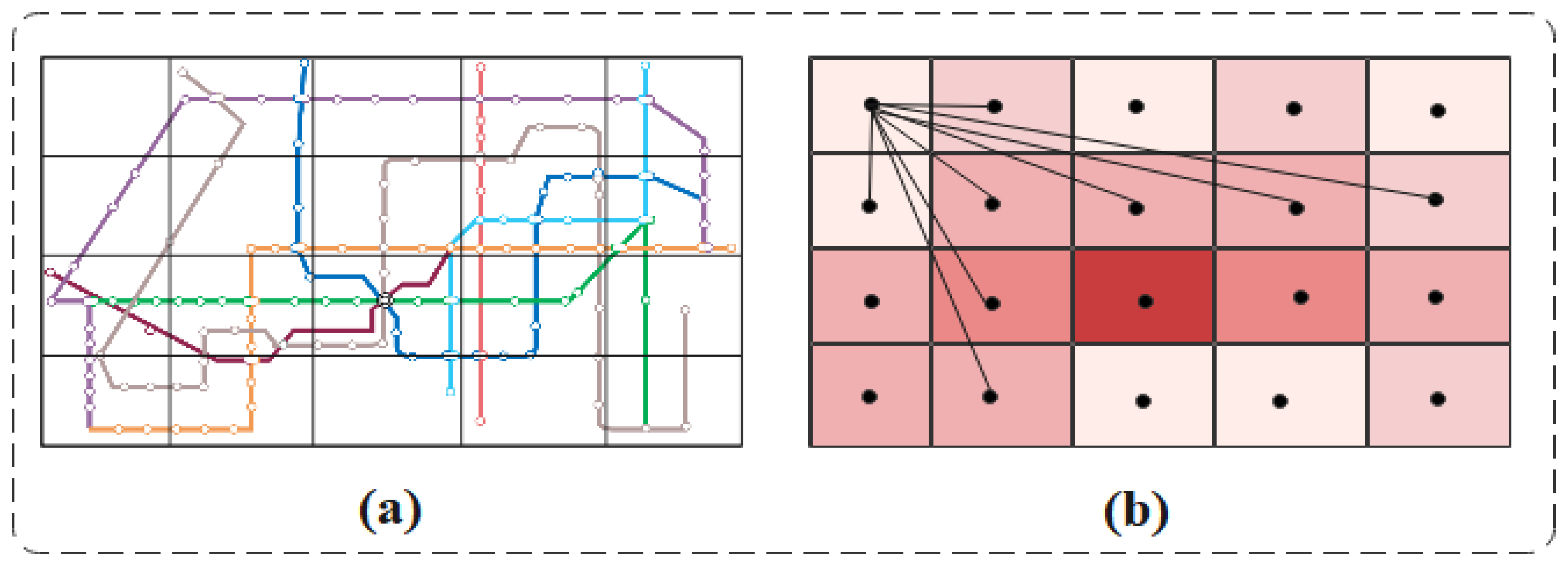
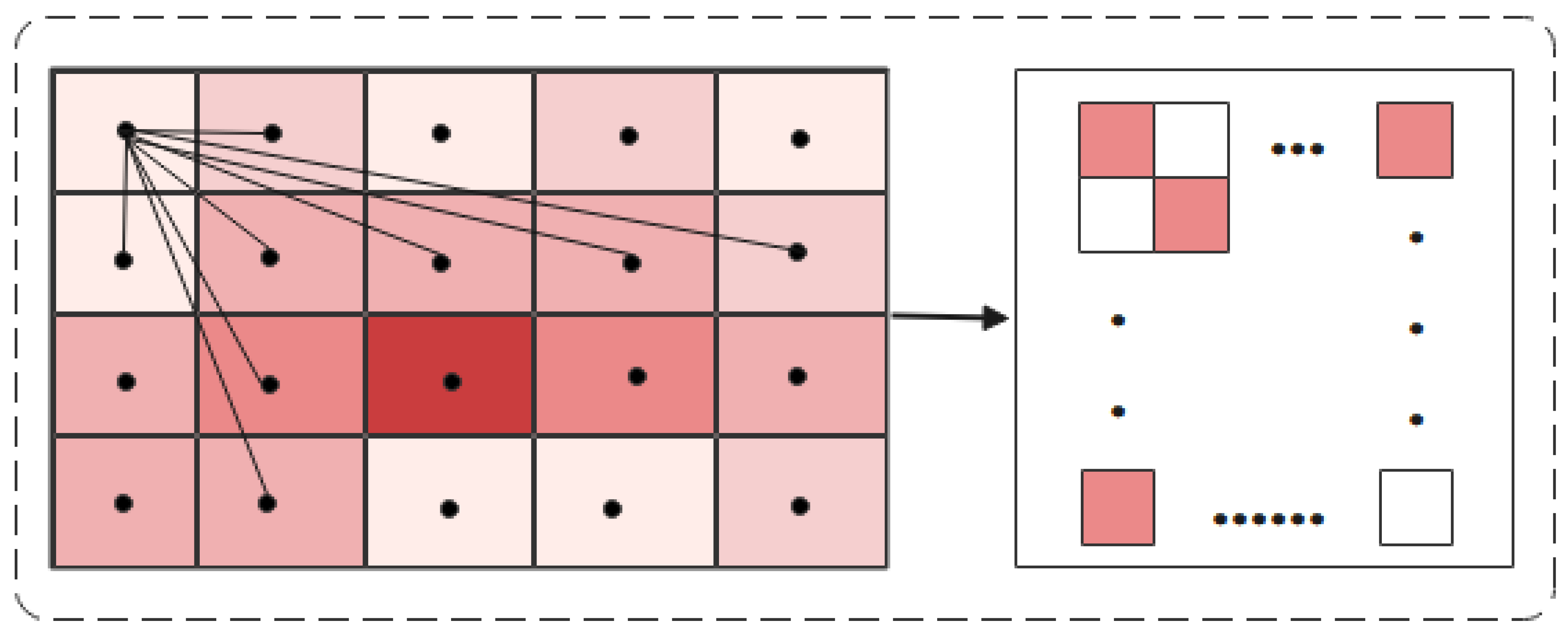
- Unlike the previous division of cities into equal-sized grids, we divide the transportation network into grids based on the attributes to which urban area belongs. Each grid represents an independent region. In this paper, the centroids of the grid are abstracted as nodes and the adjacency matrix is used to represent the spatial correlation between the nodes.
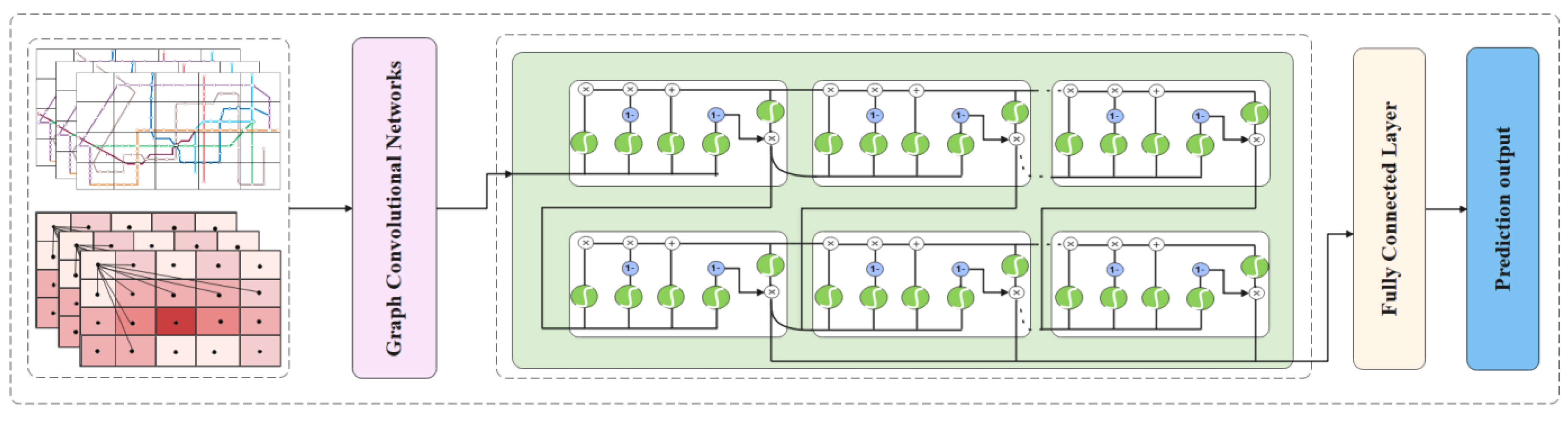
- In this study, a DSGCN model is designed to accomplish the traffic congestion prediction task. DSGCN consists of two important parts. The first part is an optimized graph convolutional neural network module that can obtain better spatial features. The second part is a two-layer DSTM unit, which allows better sequential learning of long-term and short-term temporal features.
- In this paper, experimental validation is performed on the PeMS dataset. The results show that DSGCN cannot only adequately calculate the time dependence, but can also enhance the spatial correlation of nodes in the traffic network. Meanwhile, the prediction effect of the DSGCN model proposed in this study is better than the existing baseline.
2. Related Work
3. Methodology
3.1. Data Definition
3.1.1. Problem Definition
3.1.2. Grid Division Method
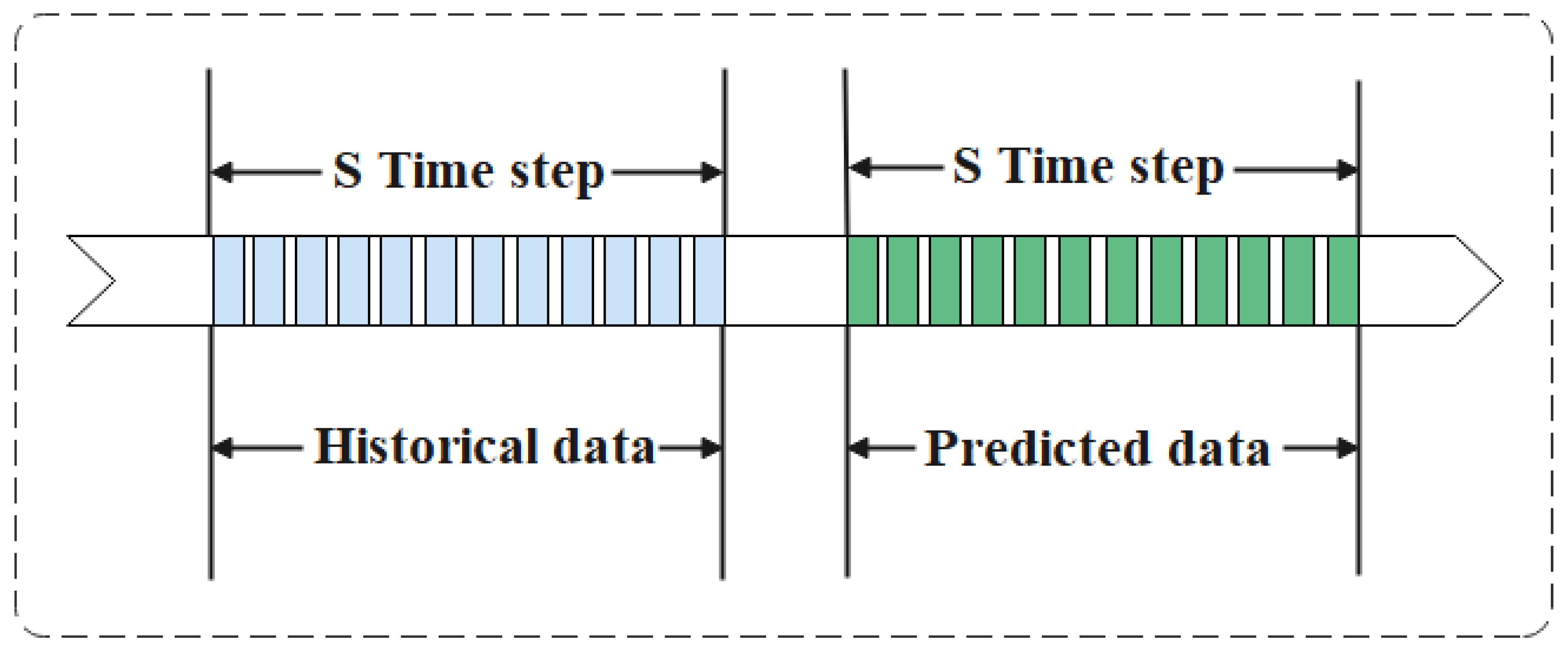
3.2. Input and Output Definitions
3.3. Spatial Feature Extraction
3.4. Time Feature Extraction
4. Experimental Section
4.1. Data Preparation
4.2. Experimental Setup
- CNN: One convolutional layer can describe the short distance dependence of spatial regions well, while two convolutional layers can further describe the long-distance dependence.
- LSTM: A special type of RNN model. By adding input gates, forgetting gates, and output gates to control the transmission state of data, long-time memory is preserved, and unimportant information is forgotten compared with RNN.
- ConvLSTM: With the time-series modeling function of LSTM, it can also capture local features by CNN, so it can learn the spatio-temporal features of spatio-temporal data.
- T-GCN: This model combines a GCN and a gated recursive unit GRU. the GCN is used to learn complex topologies to capture spatial dependencies and the GRU is used to learn dynamic changes in traffic data to capture temporal features.
- STGCN: STGCN consists of two temporal graph convolution blocks (ST-Conv Block) and one output fully connected layer (Output Layer). The spatio-temporal convolution block consists of two temporal gated convolutions and a spatial graph convolution. The spatio-temporal dependence is modeled by graph convolution and gated convolution.
4.3. Quantitative Experimental Analysis
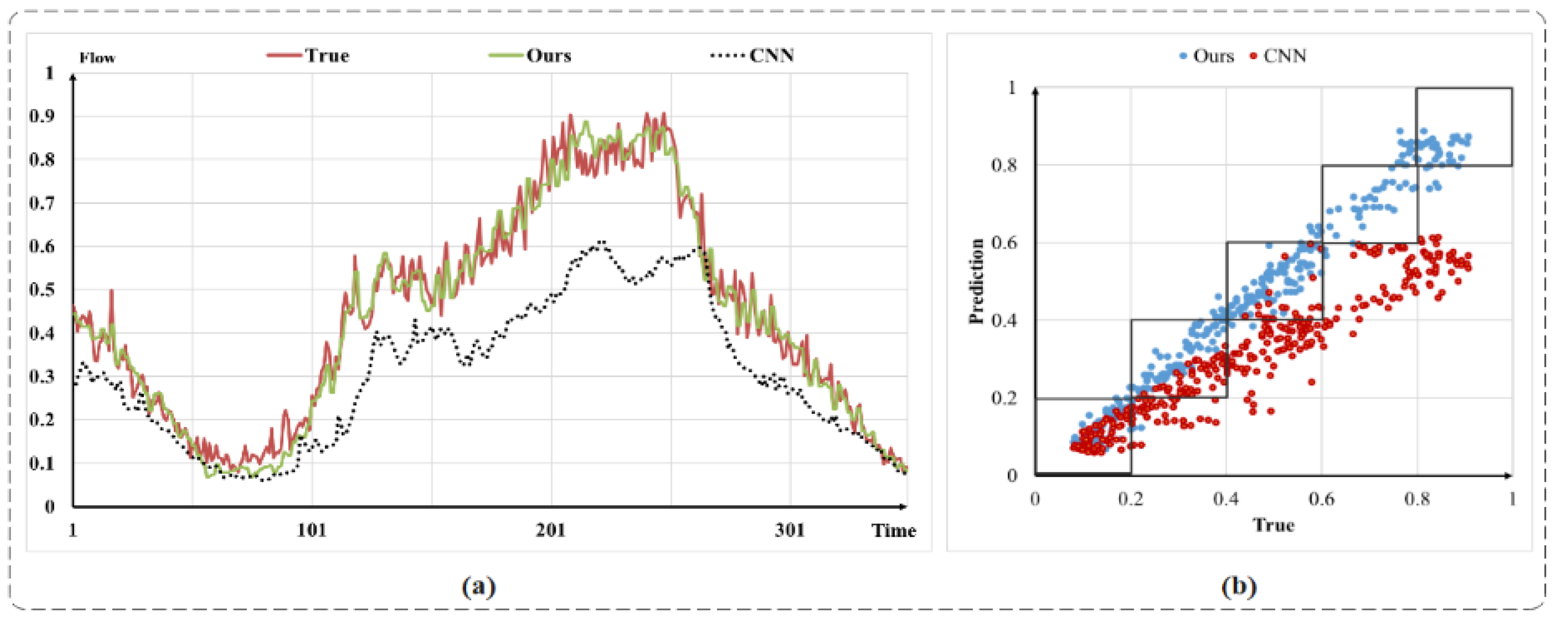
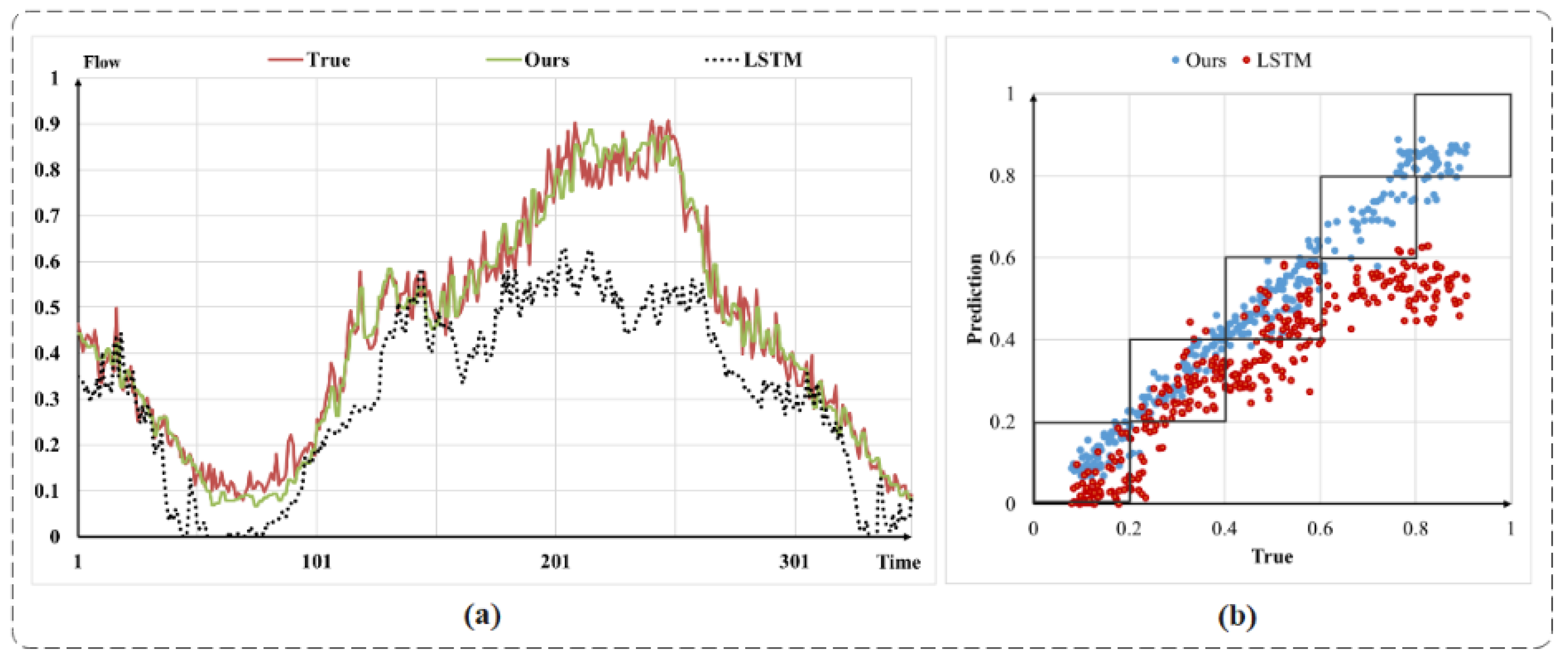
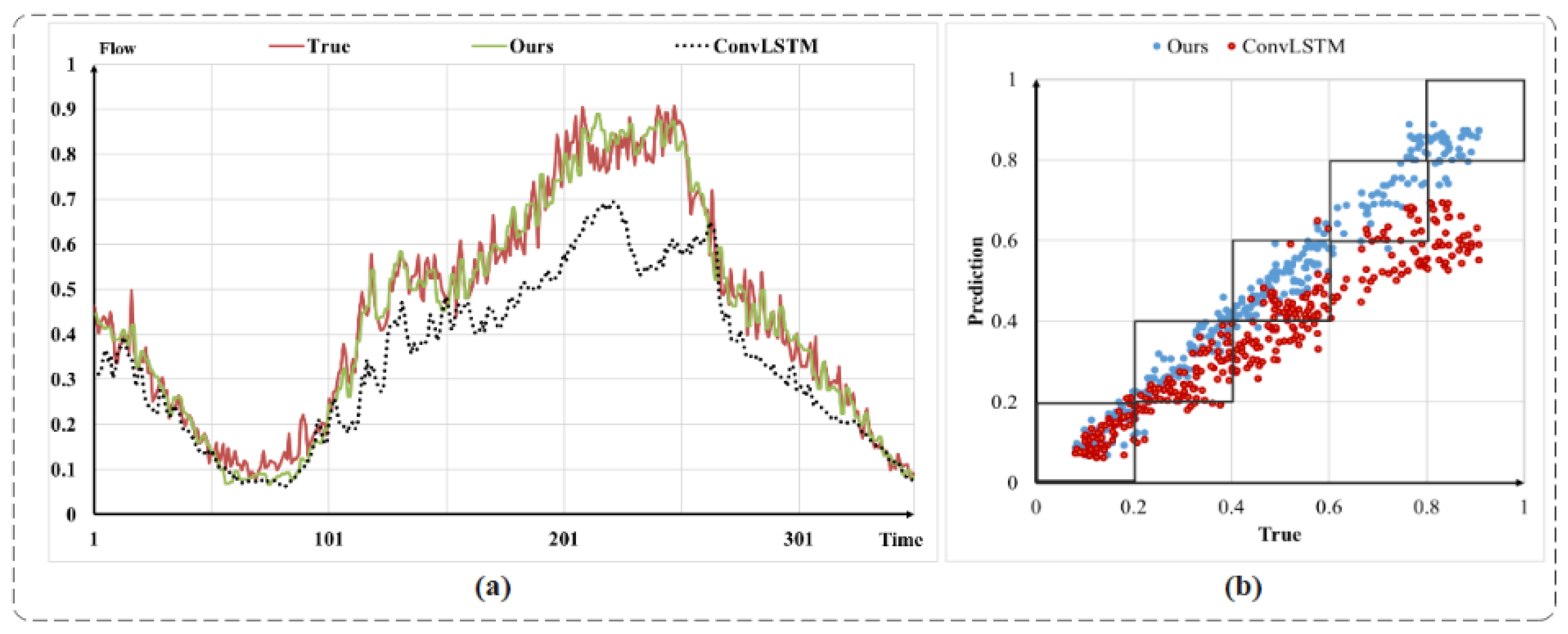
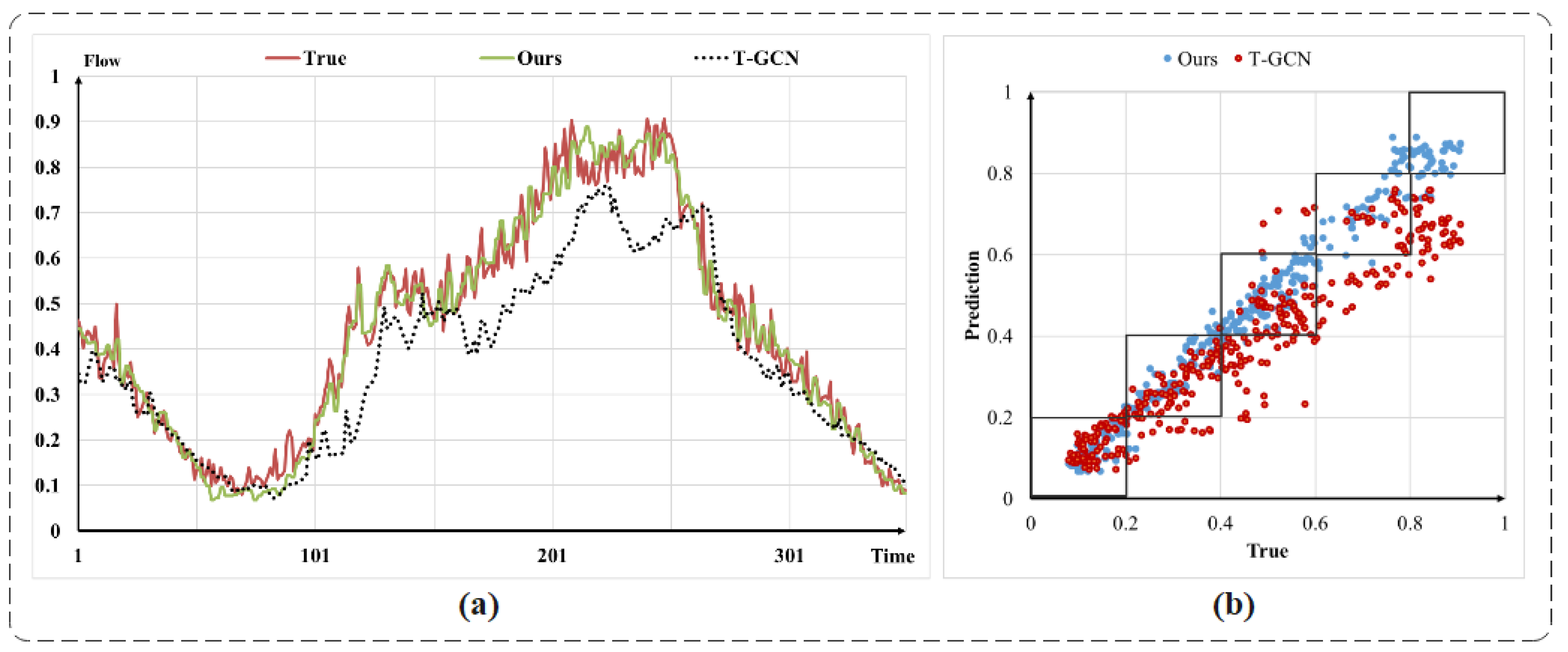
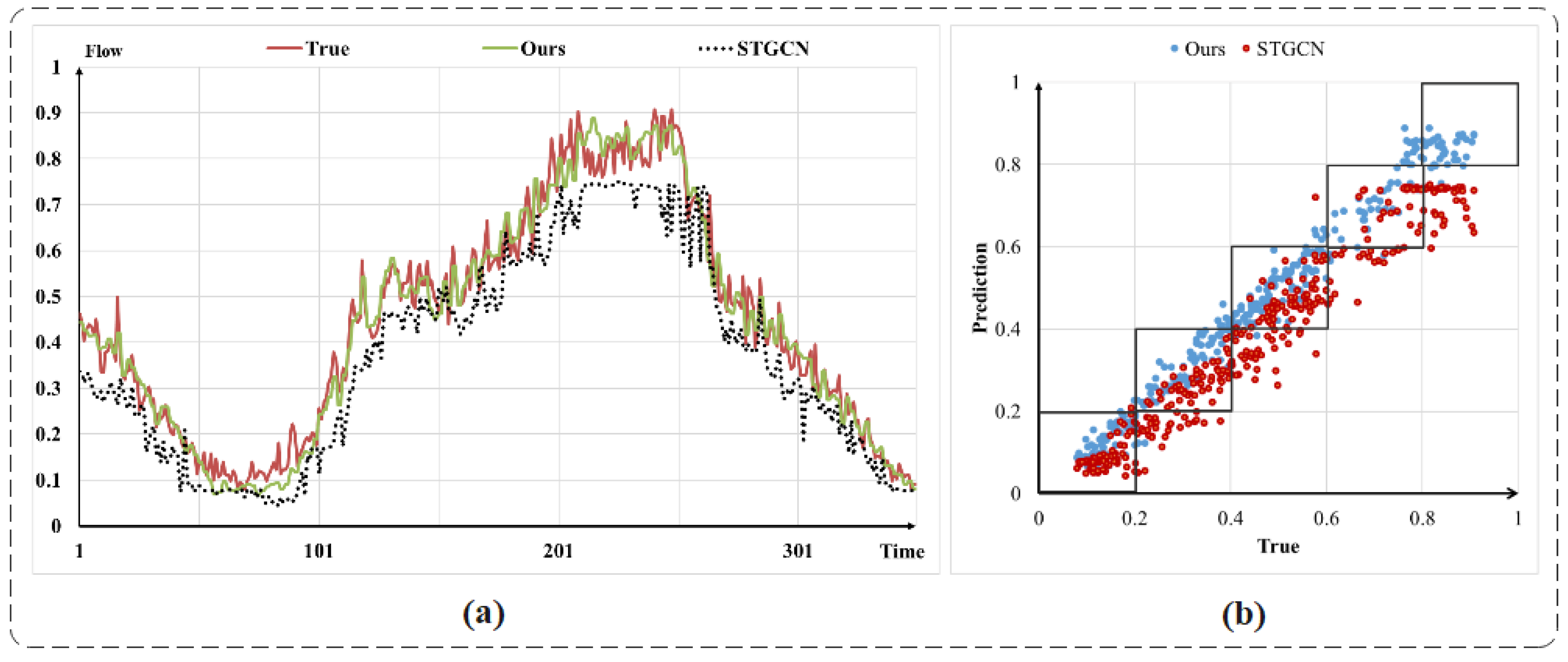
4.4. Qualitative Experimental Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects. In IEEE Transactions on Neural Networks and Learning Systems; IEEE: Piscataway, NJ, USA, 2021; pp. 1–21. [Google Scholar]
- Katz, G.; Huang, D.A.; Ibeling, D.; Julian, K.; Lazarus, C.; Lim, R.; Shah, P.; Thakoor, S.; Wu, H.; Zeljić, A.; et al. The Marabou Framework for Verification and Analysis of Deep Neural Networks. In Computer Aided Verification; Springer International Publishing: Cham, Switzerland, 2019; pp. 443–452. [Google Scholar]
- Samek, W.; Montavon, G.; Lapuschkin, S.; Anders, C.J.; Müller, K.R. Explaining Deep Neural Networks and Beyond: A Review of Methods and Applications. Proc. IEEE 2021, 109, 247–278. [Google Scholar] [CrossRef]
- Fang, W.; Zhuo, W.; Yan, J.; Song, Y.; Jiang, D.; Zhou, T. Attention meets long short-term memory: A deep learning network for traffic flow forecasting. Phys. A Stat. Mech. Its Appl. 2022, 587, 126485. [Google Scholar] [CrossRef]
- Sahoo, K.S.; Tripathy, B.K.; Naik, K.; Ramasubbareddy, S.; Balusamy, B.; Khari, M.; Burgos, D. An Evolutionary SVM Model for DDOS Attack Detection in Software Defined Networks. IEEE Access 2020, 8, 132502–132513. [Google Scholar]
- Al-Qatf, M.; Lasheng, Y.; Al-Habib, M.; Al-Sabahi, K. Deep Learning Approach Combining Sparse Autoencoder with SVM for Network Intrusion Detection. IEEE Access 2018, 6, 52843–52856. [Google Scholar] [CrossRef]
- Lv, Z.; Li, J.; Dong, C.; Li, H.; Xu, Z. Deep learning in the COVID-19 epidemic: A deep model for urban traffic revitalization index. Data Knowl. Eng. 2021, 135, 101912. [Google Scholar] [CrossRef]
- Tian, C.; Fei, L.; Zheng, W.; Xu, Y.; Zuo, W.; Lin, C.W. Deep learning on image denoising: An overview. Neural Netw. 2020, 131, 251–275. [Google Scholar]
- Lv, Z.; Li, J.; Dong, C.; Wang, Y.; Li, H.; Xu, Z. DeepPTP: A Deep Pedestrian Trajectory Prediction Model for Traffic Intersection. KSII Trans. Internet Inf. Syst. 2021, 15, 2321–2338. [Google Scholar]
- Huang, B.; Ge, L.; Chen, G.; Radenkovic, M.; Wang, X.; Duan, J.; Pan, Z. Nonlocal graph theory based transductive learning for hyperspectral image classification. Pattern Recognit. 2021, 116, 107967. [Google Scholar]
- Vlahogianni, E.I.; Karlaftis, M.; Golias, J. Optimized and meta-optimized neural networks for short-term traffic flow prediction: A genetic approach. Transp. Res. Part C Emerg. Technol. 2005, 13, 211–234. [Google Scholar]
- Lu, J.; Chen, S.; Wang, W.; Van Zuylen, H. A hybrid model of partial least squares and neural network for traffic incident detection. Expert Syst. Appl. 2012, 39, 4775–4784. [Google Scholar] [CrossRef]
- Xu, Z.; Lv, Z.; Li, J.; Shi, A. A Novel Approach for Predicting Water Demand with Complex Patterns Based on Ensemble Learning. Water Resour. Manag. 2022, 36, 4293–4312. [Google Scholar]
- Xu, Z.; Lv, Z.; Li, J.; Sun, H.; Sheng, Z. A Novel Perspective on Travel Demand Prediction Considering Natural Environmental and Socioeconomic Factors. IEEE Intell. Transp. Syst. Mag. 2022, 15, 2–25. [Google Scholar] [CrossRef]
- Lv, Z.; Li, J.; Li, H.; Xu, Z.; Wang, Y. Blind Travel Prediction Based on Obstacle Avoidance in Indoor Scene. Wirel. Commun. Mob. Comput. 2021, 2021, 5536386. [Google Scholar]
- Liang, Y.; Li, Y.; Guo, J.; Li, Y. Resource Competition in Blockchain Networks Under Cloud and Device Enabled Participation. IEEE Access 2022, 10, 11979–11993. [Google Scholar] [CrossRef]
- Zhao, A.; Dong, J.; Li, J.; Qi, L.; Zhou, H. Associated Spatio-Temporal Capsule Network for Gait Recognition. IEEE Trans. Multimed. 2022, 24, 846–860. [Google Scholar]
- Zhao, A.; Li, J.; Ahmed, M. SpiderNet: A spiderweb graph neural network for multi-view gait recognition. Knowl. Based Syst. 2020, 206, 106273. [Google Scholar] [CrossRef]
- Zhao, A.; Wang, Y.; Li, J. Transferable Self-Supervised Instance Learning for Sleep Recognition. IEEE Trans. Multimed. 2022, 1. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, W.; Waller, S.T.; Yin, Y. Modelling and managing the integrated morning-evening commuting and parking patterns under the fully autonomous vehicle environment. Transp. Res. Part B Methodol. 2019, 128, 380–407. [Google Scholar] [CrossRef]
- Wang, H.; Liu, L.; Dong, S.; Qian, Z.; Wei, H. A novel work zone short-term vehicle-type specific traffic speed prediction model through the hybrid EMD–ARIMA framework. Transp. B Transp. Dyn. 2015, 4, 159–186. [Google Scholar] [CrossRef]
- Ding, Q.Y.; Wang, X.F.; Zhang, X.Y.; Sun, Z.Q. Forecasting Traffic Volume with Space-Time ARIMA Model. Adv. Mater. Res. 2010, 156–157, 979–983. [Google Scholar]
- Tseng, F.H.; Hsueh, J.H.; Tseng, C.W.; Yang, Y.T.; Chao, H.C.; Chou, L.D. Congestion Prediction with Big Data for Real-Time Highway Traffic. IEEE Access 2018, 6, 57311–57323. [Google Scholar]
- Zhang, T.; Liu, Y.; Cui, Z.; Leng, J.; Xie, W.; Zhang, L. Short-Term Traffic Congestion Forecasting Using Attention-Based Long Short-Term Memory Recurrent Neural Network. In Computational Science—ICCS; Springer: Cham, Switzerland, 2019; pp. 304–314. [Google Scholar]
- Di, X.; Xiao, Y.; Zhu, C.; Deng, Y.; Zhao, Q.; Rao, W. Traffic Congestion Prediction by Spatiotemporal Propagation Patterns. In Proceedings of the 2019 20th IEEE International Conference on Mobile Data Management (MDM), Hong Kong, China, 10–13 June 2019; pp. 298–303. [Google Scholar]
- Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Deng, M.; Li, H. T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3848–3858. [Google Scholar] [CrossRef]
- Guo, S.; Lin, Y.; Feng, N.; Song, C.; Wan, H. Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting. Proc. AAAI Conf. Artif. Intell. 2019, 33, 922–929. [Google Scholar] [CrossRef]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting. In Proceedings of the IJCAI’18: Proceedings of the 27th International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018. [Google Scholar]

| Model | MAE | RMSE | MAPE |
|---|---|---|---|
| CNN | 44.35 | 55.24 | 36.89% |
| LSTM | 36.44 | 50.23 | 28.56% |
| ConvLSTM | 20.26 | 27.85 | 16.93% |
| T-GCN | 17.53 | 26.97 | 13.87% |
| STGCN | 11.81 | 19.87 | 12.49% |
| DSGCN | 9.98 | 16.63 | 9.35% |
| Model | MAE | RMSE | MAPE |
|---|---|---|---|
| CNN | 44.52 | 55.49 | 37.24% |
| LSTM | 35.86 | 49.91 | 28.25% |
| ConvLSTM | 20.78 | 28.34 | 17.19% |
| T-GCN | 18.26 | 27.13 | 14.13% |
| STGCN | 12.16 | 20.03 | 12.67% |
| DSGCN | 11.39 | 17.39 | 10.11% |
| Model | MAE | RMSE | MAPE |
|---|---|---|---|
| CNN | 44.84 | 55.68 | 37.41% |
| LSTM | 34.98 | 49.32 | 27.91% |
| ConvLSTM | 21.03 | 28.53 | 17.63% |
| T-GCN | 19.23 | 27.65 | 14.30% |
| STGCN | 13.08 | 20.25 | 13.12% |
| DSGCN | 10.76 | 17.16 | 9.82% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Y.; Cheng, Z. Research on Traffic Congestion Forecast Based on Deep Learning. Information 2023, 14, 108. https://doi.org/10.3390/info14020108
Qi Y, Cheng Z. Research on Traffic Congestion Forecast Based on Deep Learning. Information. 2023; 14(2):108. https://doi.org/10.3390/info14020108
Chicago/Turabian StyleQi, Yangyang, and Zesheng Cheng. 2023. "Research on Traffic Congestion Forecast Based on Deep Learning" Information 14, no. 2: 108. https://doi.org/10.3390/info14020108
APA StyleQi, Y., & Cheng, Z. (2023). Research on Traffic Congestion Forecast Based on Deep Learning. Information, 14(2), 108. https://doi.org/10.3390/info14020108





