Temporal Convolutional Networks and BERT-Based Multi-Label Emotion Analysis for Financial Forecasting
Abstract
:1. Introduction
2. Related Work
3. Experimental & Evaluation Framework
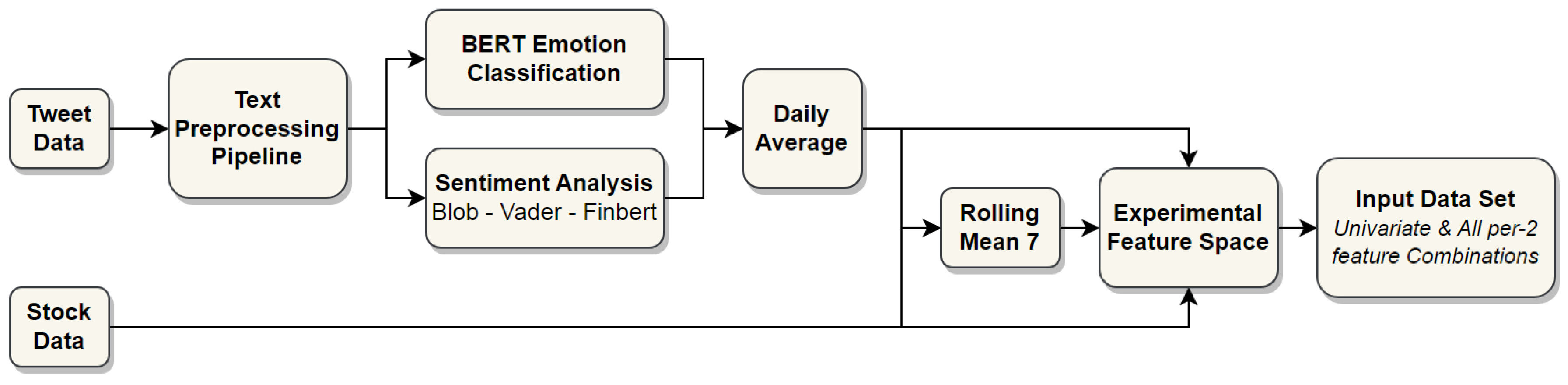
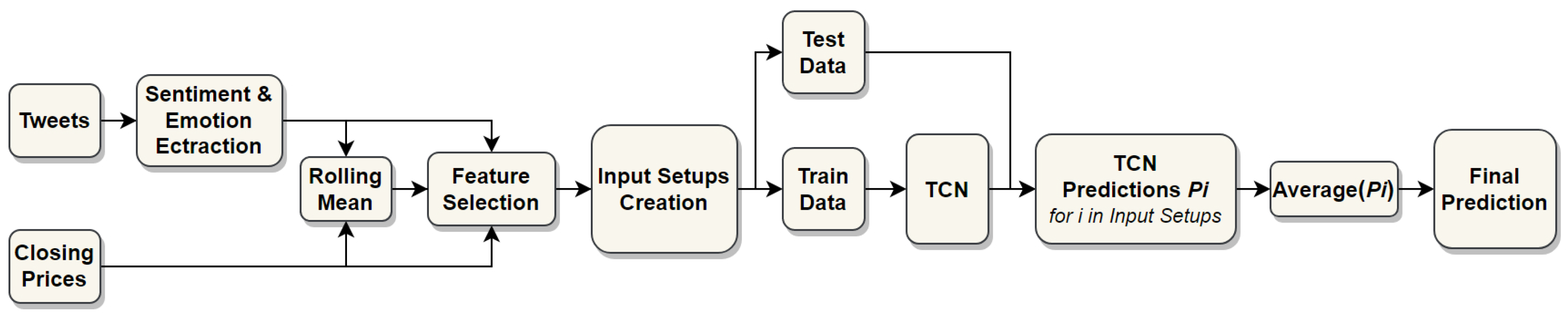
3.1. Framework Outline
3.2. Algorithms
3.3. Data
3.3.1. Stock Data
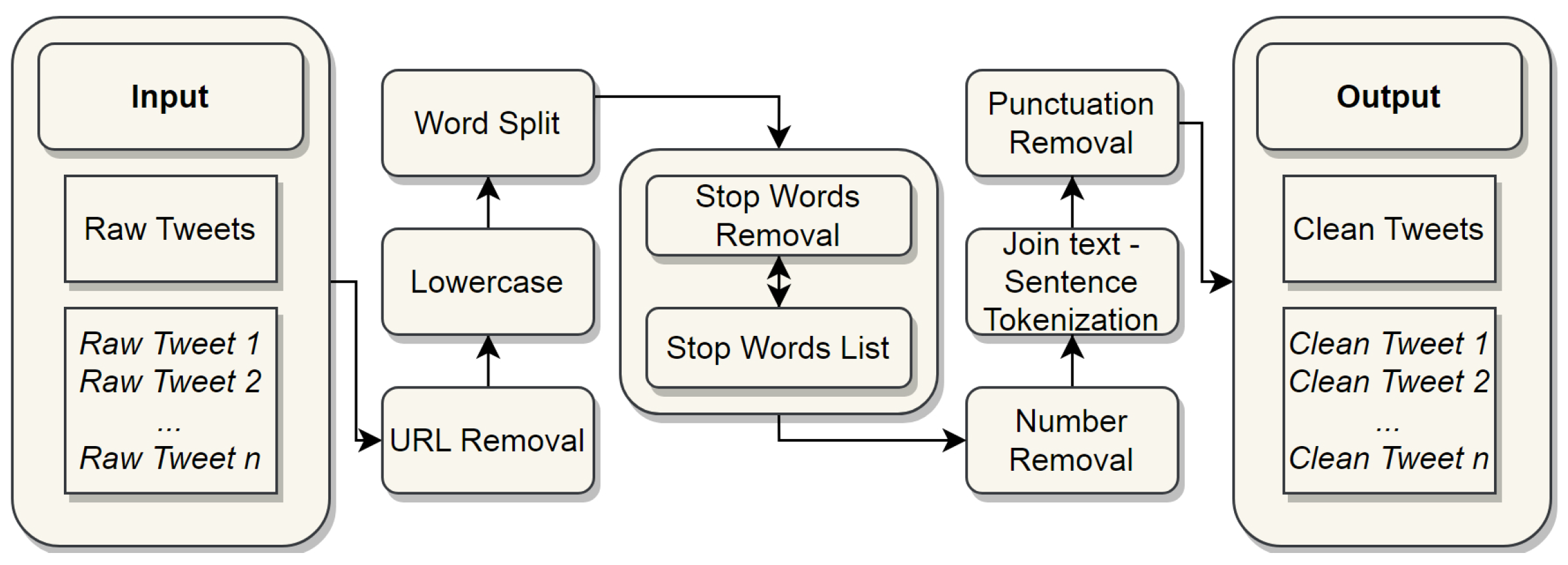
3.3.2. Twitter Data
3.4. Sentiment Analysis and Multi-Label Emotion Classification
3.5. Metrics
4. Proposed Methodology
4.1. Emotion Classification and Feature Selection
4.2. Temporal Convolutional Network Predictions
4.3. Averaging
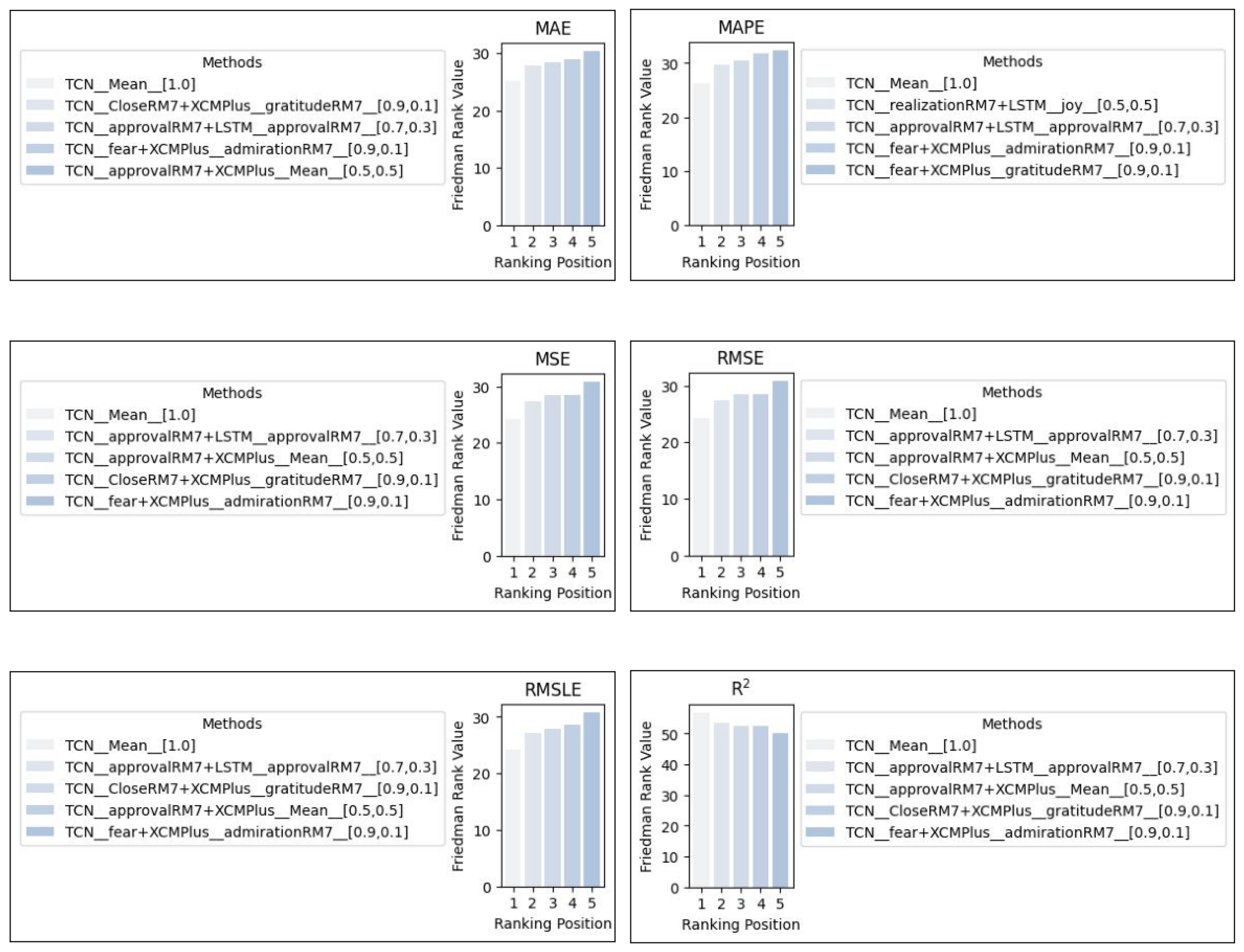
5. Results
| № | Method | MAE | № | Method | MAPE |
|---|---|---|---|---|---|
| 1 | TCN Mean | 4.158 | 1 | TCN Mean | 0.171 |
| 2 | TCN fear & XCMPlus admiration RM7 | 4.309 | 2 | TCN fear & XCMPlus admiration RM7 | 0.174 |
| 3 | TCN disgust RM7 | 4.502 | 3 | TCN fear & XCMPlus gratitude RM7 | 0.175 |
| № | Method | MSE | № | Method | RMSE |
| 1 | TCN Mean | 74.057 | 1 | TCN Mean | 5.120 |
| 2 | TCN fear & XCMPlus admiration RM7 | 75.891 | 2 | TCN fear & XCMPlus admiration RM7 | 5.321 |
| 3 | TCN disgust RM7 | 79.539 | 3 | TCN disgust RM7 | 5.430 |
| № | Method | RMSLE | № | Method | R2 |
| 1 | TCN Mean | 0.093 | 1 | TCN Mean | 0.400 |
| 2 | TCN Close RM7 & XCMPlus gratitude RM7 | 0.098 | 2 | TCN fear & XCMPlus admiration RM7 | 0.209 |
| 3 | TCN fear & XCMPlus admiration RM7 | 0.101 | 3 | TCN nervousness RM7 | 0.185 |


6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Initial Set of All Examined Algorithms
| No. | Abbreviation | Algorithm |
|---|---|---|
| 1 | FCN | Fully Convolutional Network [50] |
| 2 | FCNPlus | Fully Convolutional Network Plus [51] |
| 3 | IT | Inception Time [52] |
| 4 | ITPlus | Inception Time Plus [53] |
| 5 | MLP | Multilayer Perceptron [50] |
| 6 | RNN | Recurrent Neural Network [37] |
| 7 | LSTM | Long Short-Term Memory [36] |
| 8 | GRU | Gated Recurrent Unit [54] |
| 9 | RNNPlus | Recurrent Neural Network Plus [37] |
| 10 | LSTMPus | Long Short-Term Memory Plus [37] |
| 11 | GRUPlus | Gated Recurrent Unit Plus [37] |
| 12 | RNN_FCN | Recurrent Neural—Fully Convolutional Network [55] |
| 13 | LSTM_FCN | Long Short-Term Memory—Fully Convolutional Network [56] |
| 14 | GRU_FCN | Gated Recurrent Unit—Fully Convolutional Network [57] |
| 15 | RNN_FCNPlus | Recurrent Neural—Fully Convolutional Network Plus [58] |
| 16 | LSTM_FCNPlus | Long Short-Term Memory—Fully Convolutional Network Plus [58] |
| 17 | GRU_FCNPlus | Gated Recurrent Unit—Fully Convolutional Network Plus [58] |
| 18 | ResCNN | Residual—Convolutional Neural Network [59] |
| 19 | ResNet | Residual Network [50] |
| 20 | RestNetPlus | Residual Network Plus [60] |
| 21 | TCN | Temporal Convolutional Network [34] |
| 22 | TST | Time Series Transformer [61] |
| 23 | TSTPlus | Time Series Transformer Plus [38] |
| 24 | TSiTPlus | Time Series Vision Transformer Plus [62] |
| 25 | Transformer | Transformer Model [63] |
| 26 | XCM | Explainable Convolutional Neural Network [64] |
| 27 | XCMPlus | Explainable Convolutional Neural Network Plus [35] |
| 28 | XceptionTime | Xception Time Model [65] |
| 29 | XceptionTimePlus | Xception Time Plus [66] |
| 30 | OmniScaleCNN | Omni-Scale 1D-Convolutional Neural Network [67] |
References
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv 2019, arXiv:1810.04805. [Google Scholar]
- Liapis, C.M.; Karanikola, A.; Kotsiantis, S.B. Investigating Deep Stock Market Forecasting with Sentiment Analysis. Entropy 2023, 25, 219. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.; Li, F.; Li, J.; Fei, H.; Ji, D. Effective Token Graph Modeling using a Novel Labeling Strategy for Structured Sentiment Analysis. In Proceedings of the Annual Meeting of the Association for Computational Linguistics, Dublin, Ireland, 22–27 May 2022. [Google Scholar]
- Fei, H.; Li, F.; Li, C.; Wu, S.; Li, J.; Ji, D. Inheriting the Wisdom of Predecessors: A Multiplex Cascade Framework for Unified Aspect-based Sentiment Analysis. In Proceedings of the International Joint Conference on Artificial Intelligence, Vienna, Austria, 23–29 July 2022. [Google Scholar]
- Fei, H.; Ren, Y.; Wu, S.; Li, B.; Ji, D. Latent Target-Opinion as Prior for Document-Level Sentiment Classification: A Variational Approach from Fine-Grained Perspective. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021. [Google Scholar]
- Fei, H.; Li, B.; Liu, Q.; Bing, L.; Li, F.; Chua, T.S. Reasoning Implicit Sentiment with Chain-of-Thought Prompting. In Proceedings of the Annual Meeting of the Association for Computational Linguistics, Toronto, ON, Canada, 9–14 July 2023. [Google Scholar]
- Araci, D. FinBERT: Financial Sentiment Analysis with Pre-trained Language Models. arXiv 2019, arXiv:1908.10063. [Google Scholar]
- Hájek, P.; Munk, M. Speech emotion recognition and text sentiment analysis for financial distress prediction. Neural Comput. Appl. 2023, 35, 21463–21477. [Google Scholar] [CrossRef]
- Kratzwald, B.; Ilić, S.; Kraus, M.; Feuerriegel, S.; Prendinger, H. Deep learning for affective computing: Text-based emotion recognition in decision support. Decis. Support Syst. 2018, 115, 24–35. [Google Scholar] [CrossRef]
- Valle-Cruz, D.; Fernandez-Cortez, V.; Chau, A.L.; Sandoval-Almazán, R. Does Twitter Affect Stock Market Decisions? Financial Sentiment Analysis During Pandemics: A Comparative Study of the H1N1 and the COVID-19 Periods. Cogn. Comput. 2021, 14, 372–387. [Google Scholar] [CrossRef]
- Agarwal, B. Financial sentiment analysis model utilizing knowledge-base and domain-specific representation. Multimed. Tools Appl. 2022, 82, 8899–8920. [Google Scholar] [CrossRef]
- Sohangir, S.; Wang, D.; Pomeranets, A.; Khoshgoftaar, T.M. Big Data: Deep Learning for financial sentiment analysis. J. Big Data 2018, 5, 1–25. [Google Scholar] [CrossRef]
- Lengkeek, M.; van der Knaap, F.; Frasincar, F. Leveraging hierarchical language models for aspect-based sentiment analysis on financial data. Inf. Process. Manag. 2023, 60, 103435. [Google Scholar] [CrossRef]
- Xiang, C.; Zhang, J.; Li, F.; Fei, H.; Ji, D. A semantic and syntactic enhanced neural model for financial sentiment analysis. Inf. Process. Manag. 2022, 59, 102943. [Google Scholar] [CrossRef]
- Chai, Y.; Teng, C.; Fei, H.; Wu, S.; Li, J.; Cheng, M.; Ji, D.H.; Li, F. Prompt-Based Generative Multi-label Emotion Prediction with Label Contrastive Learning. In Proceedings of the Natural Language Processing and Chinese Computing, Guilin, China, 24–25 September 2022. [Google Scholar]
- Alhuzali, H.; Ananiadou, S. SpanEmo: Casting Multi-label Emotion Classification as Span-prediction. arXiv 2021, arXiv:2101.10038. [Google Scholar]
- Fei, H.; Ji, D.; Zhang, Y.; Ren, Y. Topic-Enhanced Capsule Network for Multi-Label Emotion Classification. IEEE/ACM Trans. Audio, Speech Lang. Process. 2020, 28, 1839–1848. [Google Scholar] [CrossRef]
- Fei, H.; Zhang, Y.; Ren, Y.; Ji, D. Latent Emotion Memory for Multi-Label Emotion Classification. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Ma, H.; Ma, J.; Wang, H.; Li, P.; Du, W.C. A Comprehensive Review of Investor Sentiment Analysis in Stock Price Forecasting. In Proceedings of the 2021 IEEE/ACIS 20th International Fall Conference on Computer and Information Science (ICIS Fall), Xi’an, China, 13–15 October 2021; pp. 264–268. [Google Scholar]
- Janková, Z. Critical Review Of Text Mining And Sentiment Analysis For Stock Market Prediction. J. Bus. Econ. Manag. 2023, 24, 177–198. [Google Scholar] [CrossRef]
- Ashtiani, M.N.; Raahemi, B. News-based intelligent prediction of financial markets using text mining and machine learning: A systematic literature review. Expert Syst. Appl. 2023, 217, 119509. [Google Scholar] [CrossRef]
- Seroyizhko, P.; Zhexenova, Z.; Shafiq, M.; Merizzi, F.; Galassi, A.; Ruggeri, F. A Sentiment and Emotion Annotated Dataset for Bitcoin Price Forecasting Based on Reddit Posts. In Proceedings of the FINNLP, Abu Dhabi, United Arab Emirates (Hybrid), 8 December 2022; pp. 203–210. [Google Scholar]
- Velu, S.R.; Ravi, V.; Tabianan, K. Multi-Lexicon Classification and Valence-Based Sentiment Analysis as Features for Deep Neural Stock Price Prediction. Sci 2023, 5, 8. [Google Scholar] [CrossRef]
- Ider, D.; Lessmann, S. Forecasting Cryptocurrency Returns from Sentiment Signals: An Analysis of BERT Classifiers and Weak Supervision. arXiv 2022, arXiv:2204.05781. [Google Scholar]
- Ko, C.R.; Chang, H.T. LSTM-based sentiment analysis for stock price forecast. PeerJ Comput. Sci. 2021, 7, e408. [Google Scholar] [CrossRef]
- Lee, J.; Youn, H.L.; Poon, J.; Han, S.C. StockEmotions: Discover Investor Emotions for Financial Sentiment Analysis and Multivariate Time Series. arXiv 2023, arXiv:2301.09279. [Google Scholar]
- Wan, R.; Mei, S.; Wang, J.; Liu, M.; Yang, F. Multivariate Temporal Convolutional Network: A Deep Neural Networks Approach for Multivariate Time Series Forecasting. Electronics 2019, 8, 876. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Chen, X.; Zeng, X.; Kong, Y.; Sun, S.; Guo, Y.; Liu, Y. Short-Term Load Forecasting for Industrial Customers Based on TCN-LightGBM. IEEE Trans. Power Syst. 2020, 36, 1984–1997. [Google Scholar] [CrossRef]
- Hewage, P.R.P.G.; Behera, A.; Trovati, M.; Pereira, E.G.; Ghahremani, M.; Palmieri, F.; Liu, Y. Temporal convolutional neural (TCN) network for an effective weather forecasting using time-series data from the local weather station. Soft Comput. 2020, 24, 16453–16482. [Google Scholar] [CrossRef]
- Lei, B.; Zhang, B.; Song, Y. Volatility Forecasting for High-Frequency Financial Data Based on Web Search Index and Deep Learning Model. Mathematics 2021, 9, 320. [Google Scholar] [CrossRef]
- Gong, L.; Yu, M.; Jiang, S.; Cutsuridis, V.; Pearson, S. Deep Learning Based Prediction on Greenhouse Crop Yield Combined TCN and RNN. Sensors 2021, 21, 4537. [Google Scholar] [CrossRef] [PubMed]
- Friedman, M. The Use of Ranks to Avoid the Assumption of Normality Implicit in the Analysis of Variance. J. Am. Stat. Assoc. 1937, 32, 675–701. [Google Scholar] [CrossRef]
- Dunn, O.J. Multiple Comparisons among Means. J. Am. Stat. Assoc. 1961, 56, 52–64. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Oguiza, I. tsAI Models: XCMPlus. Available online: https://timeseriesai.github.io/tsai/models.xcmplus.html (accessed on 7 November 2022).
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Oguiza, I. tsAI Models: RNNS. Available online: https://timeseriesai.github.io/tsai/models.rnn.html (accessed on 7 November 2022).
- Oguiza, I. tsAI Models: TSTPlus. Available online: https://timeseriesai.github.io/tsai/models.tstplus.html (accessed on 7 November 2022).
- timeseriesAI. Timeseriesai/Tsai: Time Series Timeseries Deep Learning Machine Learning Pytorch FASTAI: State-of-the-Art Deep Learning Library for Time Series and Sequences in Pytorch/Fastai. Available online: https://github.com/timeseriesAI/tsai (accessed on 9 September 2023).
- Liapis, C.M.; Karanikola, A.; Kotsiantis, S.B. A Multi-Method Survey on the Use of Sentiment Analysis in Multivariate Financial Time Series Forecasting. Entropy 2021, 23, 1603. [Google Scholar] [CrossRef]
- TextBlob: Simplified Text Processing. Available online: https://textblob.readthedocs.io/en/dev/ (accessed on 9 September 2023).
- Hutto, C.J.; Gilbert, E. VADER: A Parsimonious Rule-Based Model for Sentiment Analysis of Social Media Text. In Proceedings of the International AAAI Conference on Web and Social Media, Ann Arbor, Michigan USA, 1–4 June 2014. [Google Scholar]
- Demszky, D.; Movshovitz-Attias, D.; Ko, J.; Cowen, A.; Nemade, G.; Ravi, S. GoEmotions: A Dataset of Fine-Grained Emotions. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics (ACL), Online, 5–10 July 2020. [Google Scholar]
- Iandola, F.N.; Shaw, A.E.; Krishna, R.; Keutzer, K.W. SqueezeBERT: What can computer vision teach NLP about efficient neural networks? arXiv 2020, arXiv:2006.11316. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- van den Oord, A.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.W.; Kavukcuoglu, K. WaveNet: A Generative Model for Raw Audio. arXiv 2016, arXiv:1609.03499. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Oguiza, I. tsAI Models: TCN. Available online: https://timeseriesai.github.io/tsai/models.tcn.html (accessed on 7 November 2022).
- Ross, B.C. Mutual Information between Discrete and Continuous Data Sets. PLoS ONE 2014, 9, e87357. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yan, W.; Oates, T. Time series classification from scratch with deep neural networks: A strong baseline. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1578–1585. [Google Scholar]
- Oguiza, I. tsAI Models: FCNPlus. Available online: https://timeseriesai.github.io/tsai/models.fcnplus.html (accessed on 7 October 2021).
- Fawaz, H.I.; Lucas, B.; Forestier, G.; Pelletier, C.; Schmidt, D.F.; Weber, J.; Webb, G.I.; Idoumghar, L.; Muller, P.A.; Petitjean, F. InceptionTime: Finding AlexNet for Time Series Classification. arXiv 2020, arXiv:1909.04939. [Google Scholar]
- Oguiza, I. tsAI Models: InceptionTimePlus. Available online: https://timeseriesai.github.io/tsai/models.inceptiontimeplus.html (accessed on 7 October 2021).
- Chung, J.; Çaglar, G.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Oguiza, I. tsAI Models: RNN_FCN. Available online: https://timeseriesai.github.io/tsai/models.rnn_fcn.html (accessed on 7 October 2021).
- Karim, F.; Majumdar, S.; Darabi, H.; Chen, S. LSTM Fully Convolutional Networks for Time Series Classification. IEEE Access 2018, 6, 1662–1669. [Google Scholar] [CrossRef]
- Elsayed, N.; Maida, A.; Bayoumi, M.A. Deep Gated Recurrent and Convolutional Network Hybrid Model for Univariate Time Series Classification. arXiv 2019, arXiv:1812.07683. [Google Scholar] [CrossRef]
- Oguiza, I. tsAI Models: RNN_FCNPlus. Available online: https://timeseriesai.github.io/tsai/models.rnn_fcnplus.html (accessed on 7 October 2021).
- Zou, X.; Wang, Z.; Li, Q.; Sheng, W. Integration of residual network and convolutional neural network along with various activation functions and global pooling for time series classification. Neurocomputing 2019, 367, 39–45. [Google Scholar] [CrossRef]
- Oguiza, I. tsAI Models: ResNetPlus. Available online: https://timeseriesai.github.io/tsai/models.resnetplus.html (accessed on 7 October 2021).
- Zerveas, G.; Jayaraman, S.; Patel, D.; Bhamidipaty, A.; Eickhoff, C. A Transformer-based Framework for Multivariate Time Series Representation Learning. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021. [Google Scholar]
- Oguiza, I. tsAI Models: TSIT. Available online: https://timeseriesai.github.io/tsai/models.tsitplus.html (accessed on 7 October 2021).
- Oguiza, I. tsAI Models: Transformermodel. Available online: https://timeseriesai.github.io/tsai/models.transformermodel.html (accessed on 7 October 2021).
- Fauvel, K.; Lin, T.; Masson, V.; Fromont, E.; Termier, A. XCM: An Explainable Convolutional Neural Network for Multivariate Time Series Classification. arXiv 2021, arXiv:2009.04796. [Google Scholar] [CrossRef]
- Rahimian, E.; Zabihi, S.; Atashzar, S.F.; Asif, A.; Mohammadi, A. XceptionTime: A Novel Deep Architecture based on Depthwise Separable Convolutions for Hand Gesture Classification. arXiv 2019, arXiv:1911.03803. [Google Scholar]
- Oguiza, I. tsAI Models: XceptionTimePlus. Available online: https://timeseriesai.github.io/tsai/models.xceptiontimeplus.html (accessed on 7 October 2021).
- Tang, W.; Long, G.; Liu, L.; Zhou, T.; Blumenstein, M.; Jiang, J. Omni-Scale CNNs: A simple and effective kernel size configuration for time series classification. In Proceedings of the ICLR, Online, 25–29 April 2022. [Google Scholar]
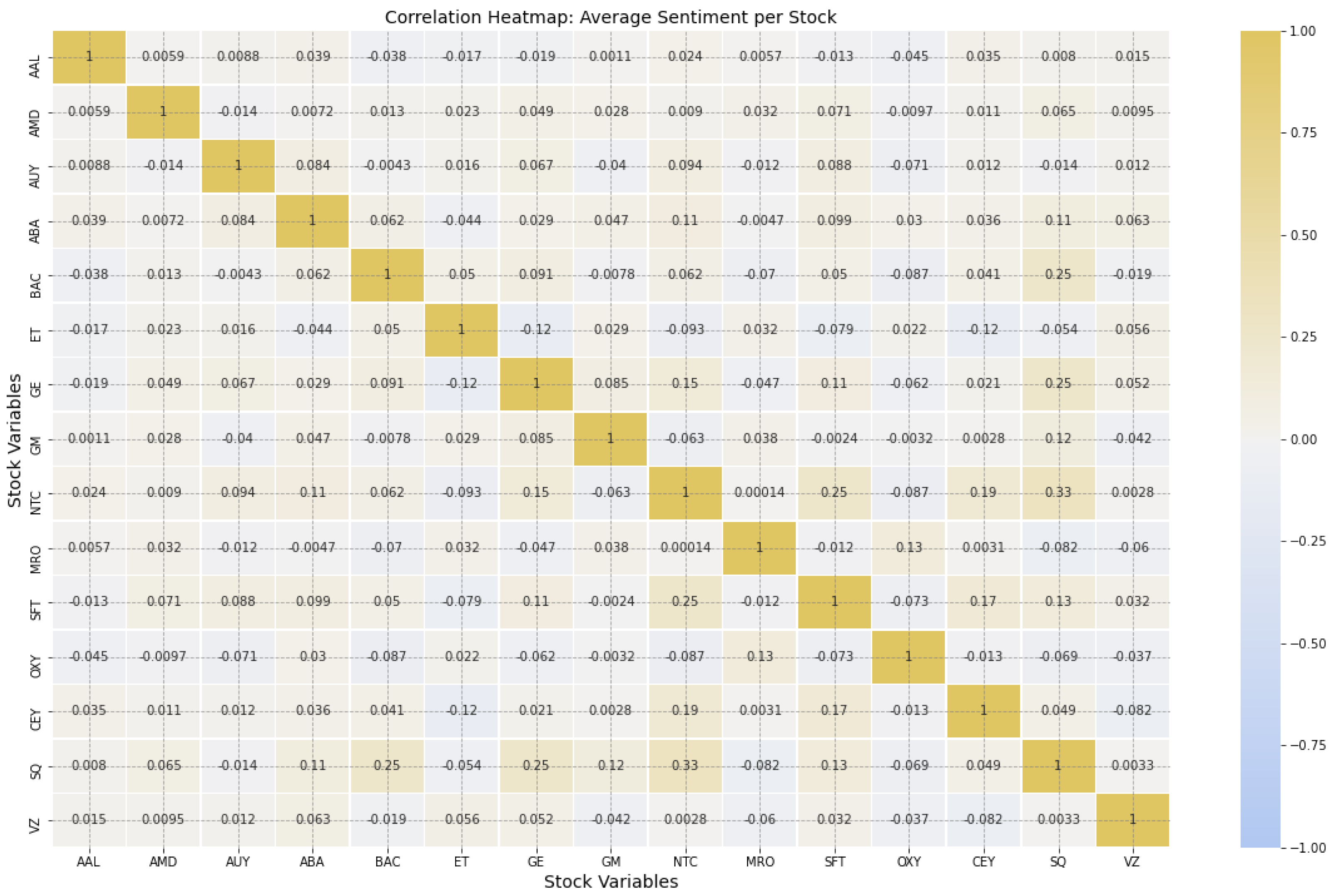
| № | Dataset | Stocks |
|---|---|---|
| 1 | AAL | American Airlines Group |
| 2 | AMD | Advanced Micro Devices |
| 3 | AUY | Yamana Gold Inc. |
| 4 | BABA | Alibaba Group |
| 5 | BAC | Bank of America Corp. |
| 6 | ET | Energy Transfer L.P. |
| 7 | GE | General Electric |
| 8 | GM | General Motors |
| 9 | INTC | Intel Corporation |
| 10 | MRO | Marathon Oil Corp. |
| 11 | MSFT | Microsoft |
| 12 | OXY | Occidental Petroleum Corp. |
| 13 | RYCEY | Rolls-Royce Holdings |
| 14 | SQ | Square |
| 15 | VZ | Verizon Communications |
| № | Statistic | Value |
|---|---|---|
| 1 | Average number of tweets | 15,497 |
| 2 | Average tweets per day | 15 |
| 3 | Average minimum tweets per day | 2 |
| 4 | Average maximum tweets per day | 90 |
| 5 | Average total tokens per day | 496,739 |
| 6 | Average vocabulary per day (unique tokens) | 52,004 |
| № | Emo | № | Emo | № | Emo | № | Emo |
|---|---|---|---|---|---|---|---|
| 1 | admiration | 8 | curiosity | 15 | fear | 22 | pride |
| 2 | amusement | 9 | desire | 16 | gratitude | 23 | realization |
| 3 | anger | 10 | disappointment | 17 | grief | 24 | relief |
| 4 | annoyance | 11 | disapproval | 18 | joy | 25 | remorse |
| 5 | approval | 12 | disgust | 19 | love | 26 | sadness |
| 6 | caring | 13 | embarrassment | 20 | nervousness | 27 | surprise |
| 7 | confusion | 14 | excitement | 21 | optimism | 28 | neutral |
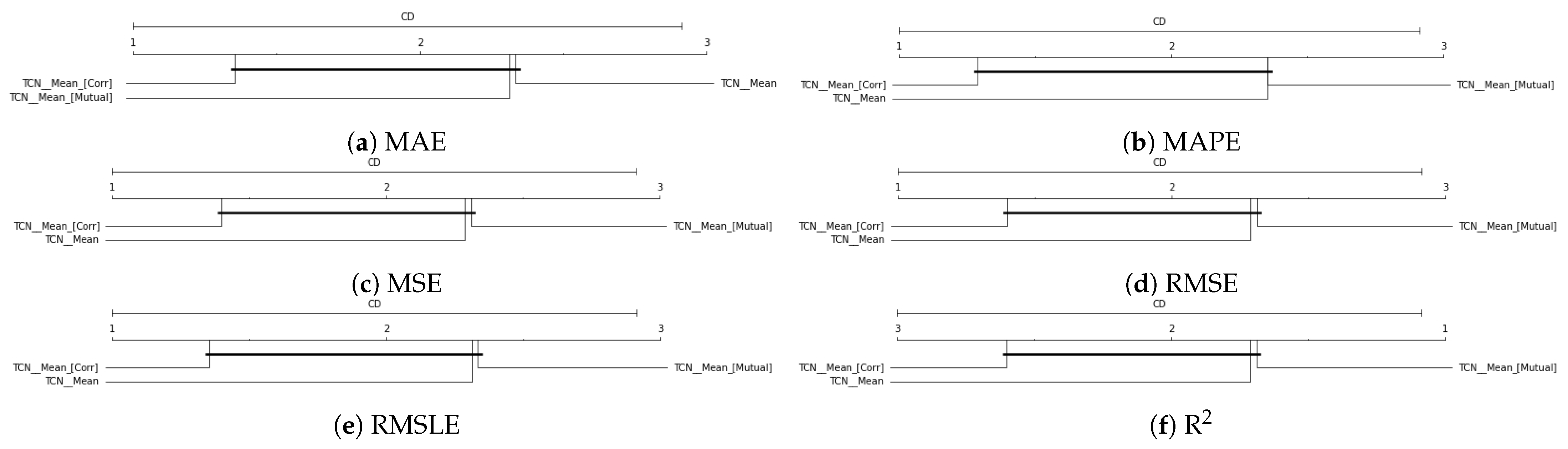
| TCN Mean | TCN Cor | TCN Mut | Best | |
|---|---|---|---|---|
| MAE | 4.158 | 3.804 | 3.866 | TCN Cor |
| MAPE | 0.082 | 0.074 | 0.078 | TCN Cor |
| MSE | 74.057 | 68.764 | 68.622 | TCN Mut |
| RMSE | 5.120 | 4.798 | 4.865 | TCN Cor |
| RMSLE | 0.093 | 0.087 | 0.090 | TCN Cor |
| R2 | 0.400 | 0.471 | 0.437 | TCN Cor |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liapis, C.M.; Kotsiantis, S. Temporal Convolutional Networks and BERT-Based Multi-Label Emotion Analysis for Financial Forecasting. Information 2023, 14, 596. https://doi.org/10.3390/info14110596
Liapis CM, Kotsiantis S. Temporal Convolutional Networks and BERT-Based Multi-Label Emotion Analysis for Financial Forecasting. Information. 2023; 14(11):596. https://doi.org/10.3390/info14110596
Chicago/Turabian StyleLiapis, Charalampos M., and Sotiris Kotsiantis. 2023. "Temporal Convolutional Networks and BERT-Based Multi-Label Emotion Analysis for Financial Forecasting" Information 14, no. 11: 596. https://doi.org/10.3390/info14110596
APA StyleLiapis, C. M., & Kotsiantis, S. (2023). Temporal Convolutional Networks and BERT-Based Multi-Label Emotion Analysis for Financial Forecasting. Information, 14(11), 596. https://doi.org/10.3390/info14110596







