Range-Free Localization Approaches Based on Intelligent Swarm Optimization for Internet of Things
Abstract
:1. Introduction
- Three new algorithms to increase localization accuracy, denoted as DV-HopCSO, W-DV-HopCSO, and HW-DV-HopCSO.
- New and enhanced steps to increase localization accuracy.
- Evaluation of the presented algorithms considering four distinct types of complex topology.
- Verification of the reliability of the proposed localization approaches regarding their accuracy and error considering four distinct types of complex topology through comparisons with existing algorithms (DV-Hop, PSODV-Hop, MDV-Hop, W-DV-Hop, and HW-DV-Hop) involving the communication range, number of anchor nodes, total number of nodes, and maximum number of iterations.
2. Related Works and Background
2.1. Weight-Based Enhancements to DV-Hop
2.1.1. Basic DV-HOP Algorithm
2.1.2. W-DV-Hop Localization Algorithm
2.1.3. HW-DV-Hop Localization Algorithm
3. Proposed Localization Algorithms
3.1. Motivation behind Using Intelligent Swarm Optimization
3.2. CSO Optimization Approach
3.3. CSO-Based Enhanced DV-Hop Algorithm
| Algorithm 1: Pseudocode of the Proposed Algorithms |
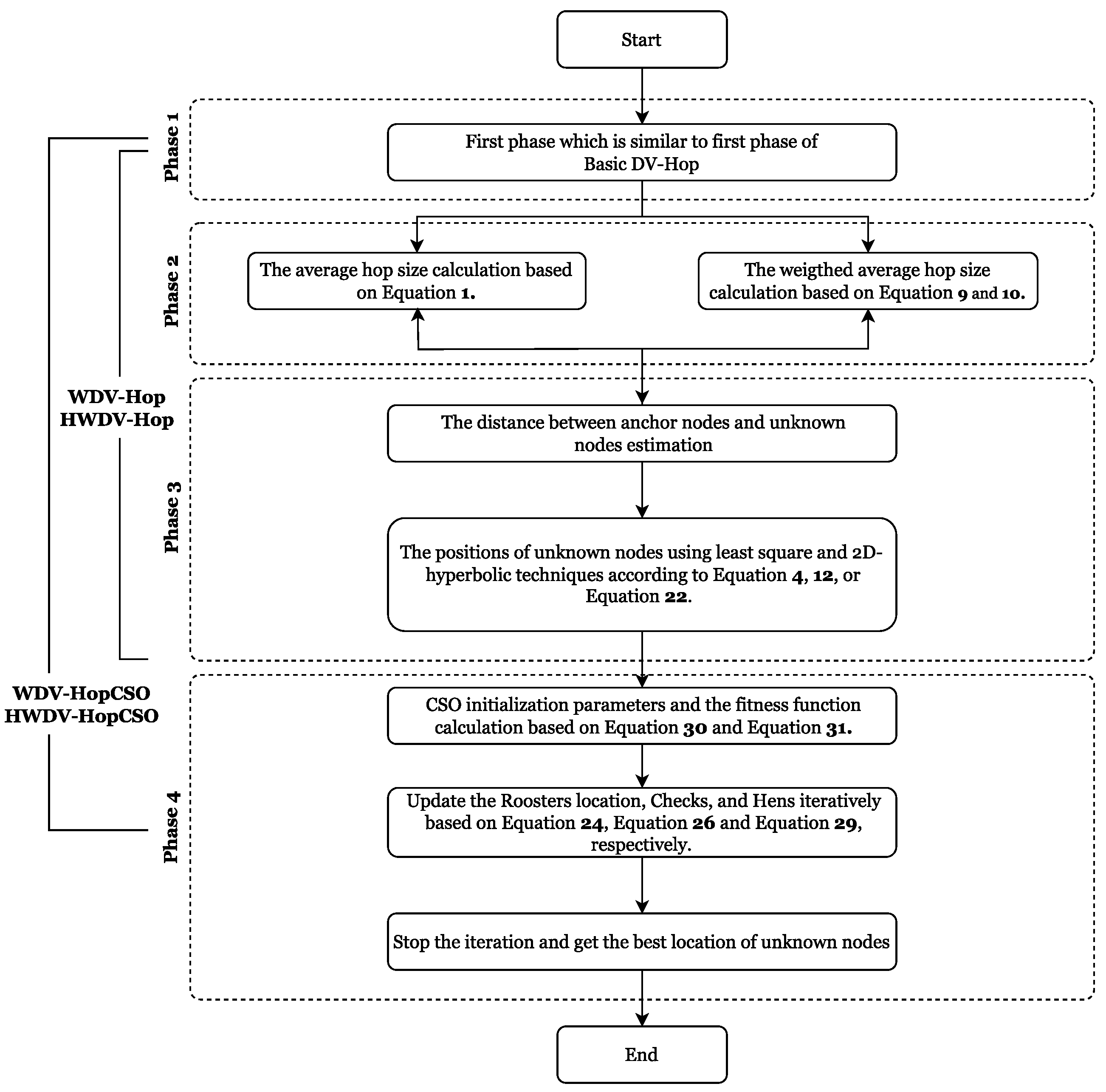
1: Input: n nodes; k anchors; communication range R 2: 3: Network topology distribution: square random; H-shaped; O-shaped; W-shaped 4: for i = 1 to n do 5: for j = 1 to n do 6: Distance calculation 7: 8: and initialize hop-count ; 9: if then 10: ; 11: else if then 12: ; 13: else 14: ; 15: end if 16: end for 17: end for 18: 19: Creation of the Matrix of hop count between anchors based on the path algorithm; 20: Creation of distance matrix between anchors based on the path algorithm; 21: 22: for i = 1 to k do 23: Average hop size distance calculation per anchor node based on Equation (1); 24: end for 25: 26: for i = 1 to k do 27: weighted values calculation per anchor nodes based on Equation (18); 28: end for 29: 30: New corrected average hop size distance according to Equation (17); 31: for i = 1 to k do 32: from i-th anchor to k-th unknown node; 33: end for 34: 35: Determine the position of the unknown node using a 2D-hyperbolic based on Equation (23); 36: 37: CSO parameters initialization and using the coordinate of nodes calculated according to 38: 2D-hyperbolic; 39: Evaluate the chickens’ fitness values; 40: Made iteratively an update of the positions according to Equations (24), (26), and (29); 41: Stop the iteration when the goals are reached; 42: Output: the best locations of unknown nodes. |
4. Simulation Results and Discussions
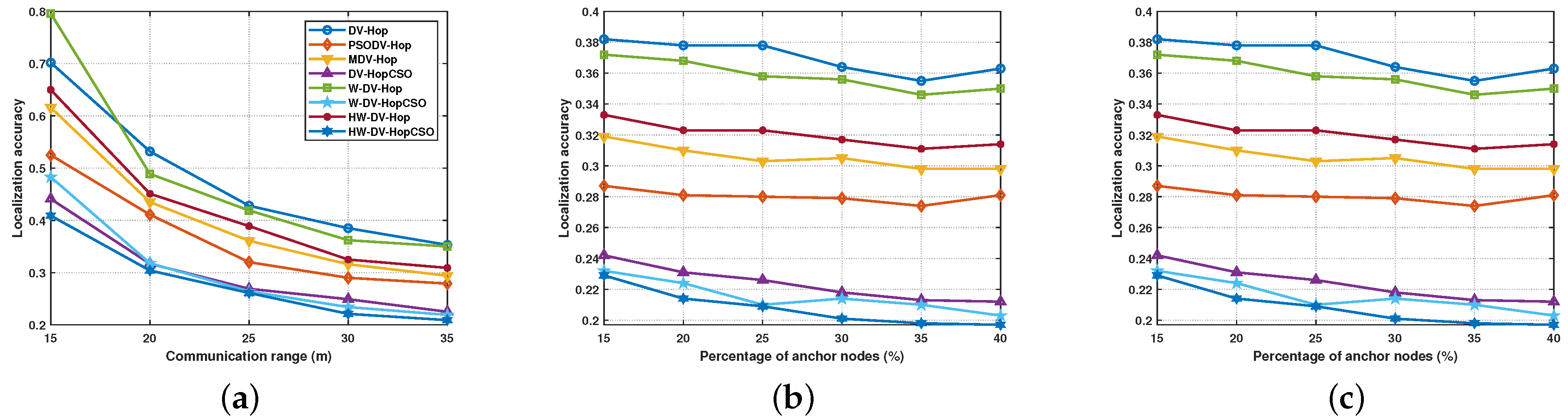
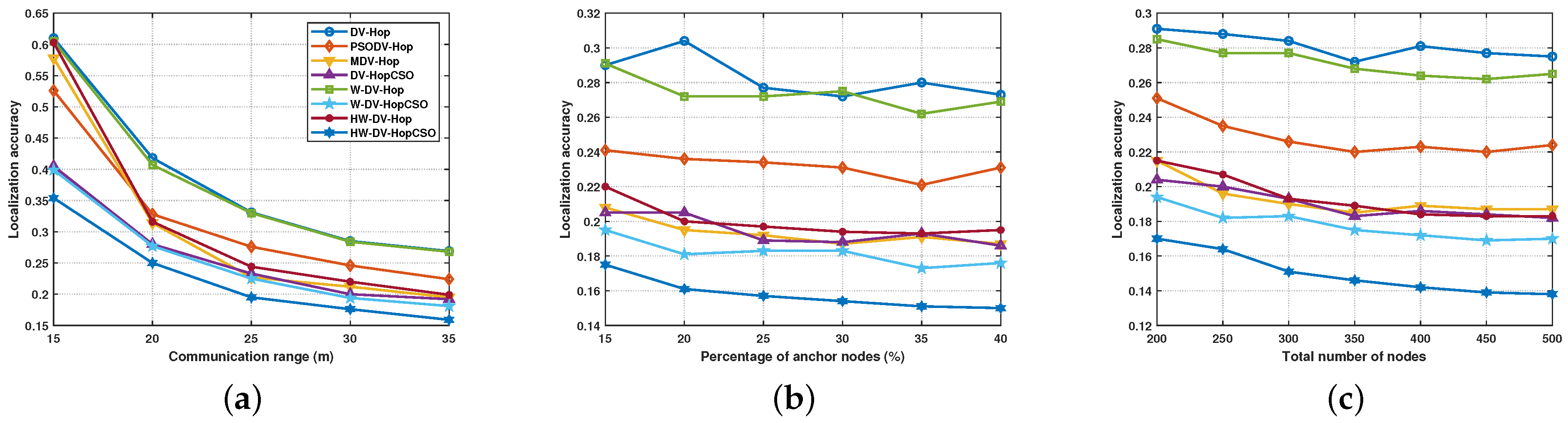
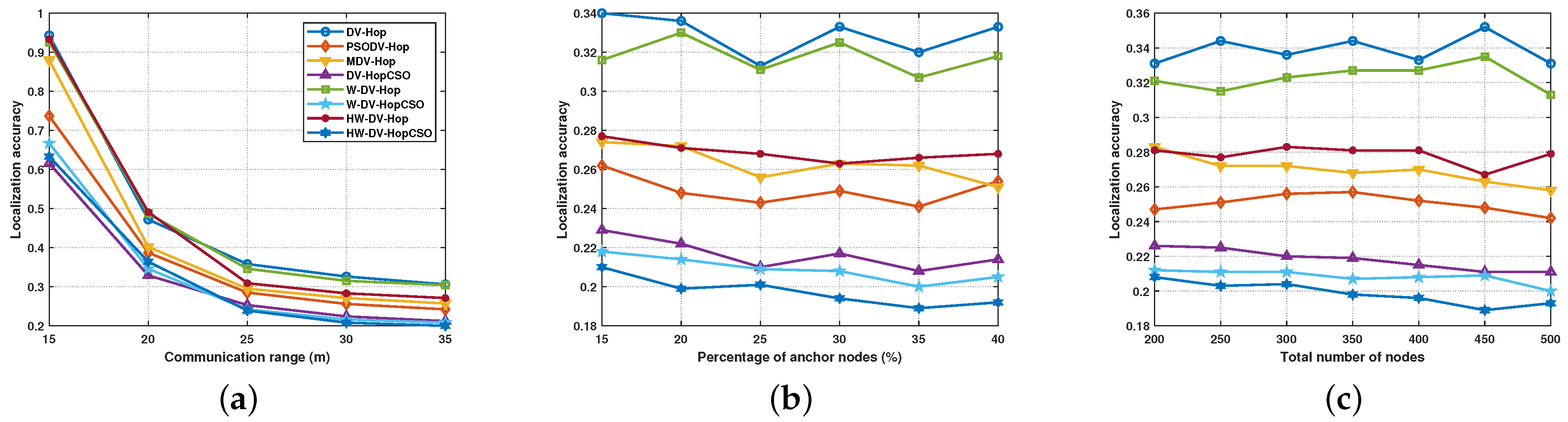
4.1. Impact of Communication Range
4.2. Impact of the Percentage of Anchor Nodes
4.3. Impact of the Total Number of Nodes
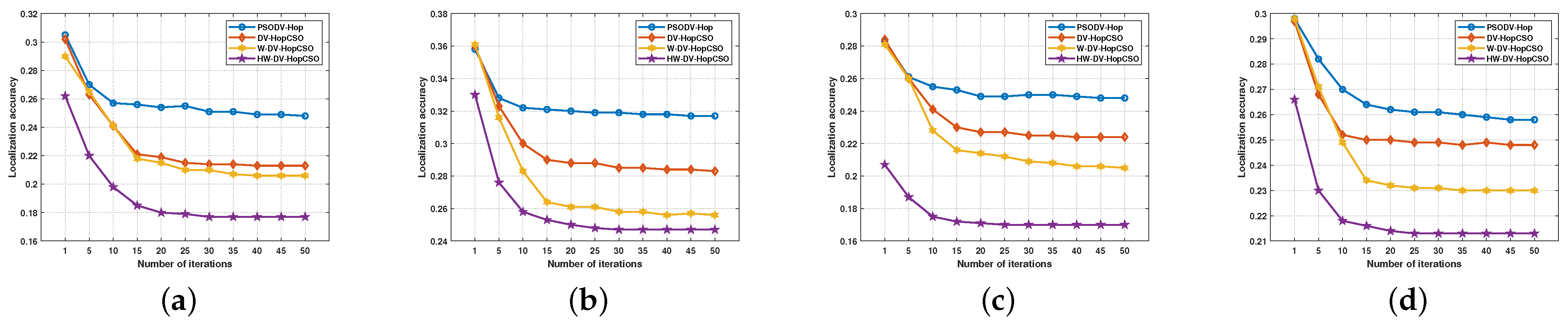
4.4. Number of Iterations Analysis
4.5. Analysis of Time Complexity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zrelli, A. Hardware, software platforms, operating systems and routing protocols for Internet of Things applications. Wirel. Pers. Commun. 2022, 122, 3889–3912. [Google Scholar] [CrossRef]
- Soldatos, J.; Gusmeroli, S.; Malo, P.; Di Orio, G. Internet of things applications in future manufacturing. In Digitising the Industry Internet of Things Connecting the Physical, Digital and Virtual Worlds; River Publishers: Nordjylland, Denmark, 2022; pp. 153–183. [Google Scholar]
- Suresh, S.; Chakaravarthi, G. RFID technology and its diverse applications: A brief exposition with a proposed Machine Learning approach. Measurement 2022, 195, 111197. [Google Scholar] [CrossRef]
- Nourildean, S.W.; Hassib, M.D.; Mohammed, Y. Internet of things based wireless sensor network: A review. Indones. J. Electr. Eng. Comput. Sci. 2022, 27, 246–261. [Google Scholar] [CrossRef]
- Gliga, L.I.; Khemmar, R.; Chafouk, H.; Popescu, D. A Survey of Wireless Communication Technologies for an IoT-connected Wind Farm. Wirel. Pers. Commun. 2022, 122, 2253–2272. [Google Scholar] [CrossRef]
- Jin, Y.; Cui, L. Discovering Influential Positions in RFID-Based Indoor Tracking Data. Information 2020, 11, 330. [Google Scholar] [CrossRef]
- Alhayani, B.; Kwekha-Rashid, A.S.; Mahajan, H.B.; Ilhan, H.; Uke, N.; Alkhayyat, A.; Mohammed, H.J. 5G standards for the Industry 4.0 enabled communication systems using artificial intelligence: Perspective of smart healthcare system. Appl. Nanosci. 2023, 13, 1807–1817. [Google Scholar] [CrossRef]
- Kabashkin, I. Availability of Services in Wireless Sensor Network with Aerial Base Station Placement. J. Sens. Actuator Netw. 2023, 12, 39. [Google Scholar] [CrossRef]
- Asha, A.; Arunachalam, R.; Poonguzhali, I.; Urooj, S.; Alelyani, S. Optimized RNN-based performance prediction of IoT and WSN-oriented smart city application using improved honey badger algorithm. Measurement 2023, 210, 112505. [Google Scholar] [CrossRef]
- Ghazal, T.M.; Hasan, M.K.; Alshurideh, M.T.; Alzoubi, H.M.; Ahmad, M.; Akbar, S.S.; Al Kurdi, B.; Akour, I.A. IoT for Smart Cities: Machine Learning Approaches in Smart Healthcare—A Review. Future Internet 2021, 13, 218. [Google Scholar] [CrossRef]
- Oğur, N.B.; Al-Hubaishi, M.; Çeken, C. IoT data analytics architecture for smart healthcare using RFID and WSN. ETRI J. 2022, 44, 135–146. [Google Scholar] [CrossRef]
- Khalifeh, A.; Gupta, M.; Almomani, O.; Khasawneh, A.M.; Darabkh, K.A. Smart remote sensing network for early warning of disaster risks. In Nanotechnology-Based Smart Remote Sensing Networks for Disaster Prevention; Elsevier: Amsterdam, The Netherlands, 2022; pp. 303–324. [Google Scholar]
- Hadir, A.; Zine-Dine, K.; Bakhouya, M.; El Kafi, J.; El Ouadghiri, D. Towards an integrated geographic routing approach using estimated sensors position in WSNs. In Proceedings of the 2018 International Conference on High Performance Computing & Simulation (HPCS), Orleans, France, 16–20 July 2018; pp. 943–948. [Google Scholar]
- Naghibi, M.; Barati, H. EGRPM: Energy efficient geographic routing protocol based on mobile sink in wireless sensor networks. Sustain. Comput. Inform. Syst. 2020, 25, 100377. [Google Scholar] [CrossRef]
- Prasanth, A.; Jayachitra, S. A novel multi-objective optimization strategy for enhancing quality of service in IoT-enabled WSN applications. Peer-Netw. Appl. 2020, 13, 1905–1920. [Google Scholar] [CrossRef]
- Arafat, M.Y.; Alam, M.M.; Moh, S. Vision-based navigation techniques for unmanned aerial vehicles: Review and challenges. Drones 2023, 7, 89. [Google Scholar] [CrossRef]
- Singh, P.; Mittal, N.; Salgotra, R. Comparison of range-based versus range-free WSNs localization using adaptive SSA algorithm. Wirel. Netw. 2022, 28, 1625–1647. [Google Scholar] [CrossRef]
- Rizk, H.; Elmogy, A.; Yamaguchi, H. A robust and accurate indoor localization using learning-based fusion of Wi-Fi RTT and RSSI. Sensors 2022, 22, 2700. [Google Scholar] [CrossRef] [PubMed]
- Aubry, A.; Babu, P.; De Maio, A.; Fatima, G.; Sahu, N. A Robust Framework to Design Optimal Sensor Locations for TOA or RSS Source Localization Techniques. IEEE Trans. Signal Process. 2023, 71, 1293–1306. [Google Scholar] [CrossRef]
- Wang, W.; Wang, G.; Ho, K.; Huang, L. Robust TDOA localization based on maximum correntropy criterion with variable center. Signal Process. 2023, 205, 108860. [Google Scholar] [CrossRef]
- Chen, H.; Cao, L.; Yue, Y. TDOA/AOA Hybrid Localization Based on Improved Dandelion Optimization Algorithm for Mobile Location Estimation Under NLOS Simulation Environment. Wirel. Pers. Commun. 2023, 131, 2747–2772. [Google Scholar] [CrossRef]
- Dou, Z.; Yao, Z.; Zhang, Z.; Lu, M. A Lidar-assisted Self-localization Technology for Indoor Wireless Sensor Networks. IEEE Internet Things J. 2023, 10, 17515–17529. [Google Scholar] [CrossRef]
- Niculescu, D.; Nath, B. DV based positioning in ad hoc networks. Telecommun. Syst. 2003, 22, 267–280. [Google Scholar] [CrossRef]
- Latha, T.S.; Rekha, K.B.; Ferede, A.W. Lightweight APIT with Bat Optimization with Simulated Annealing Localization for Resource-Constrained Sensor Networks. Wirel. Commun. Mob. Comput. 2023, 2023, 7982038. [Google Scholar] [CrossRef]
- Qu, S.; Bao, Z.; Yin, Y.; Yang, X. MineBL: A Battery-Free Localization Scheme with Binocular Camera for Coal Mine. Sensors 2022, 22, 6511. [Google Scholar] [CrossRef] [PubMed]
- Tripathy, P.; Khilar, P. An ensemble approach for improving localization accuracy in wireless sensor network. Comput. Netw. 2022, 219, 109427. [Google Scholar] [CrossRef]
- Liu, J.; Liu, M.; Du, X.; Stanimirovi, P.S.; Jin, L. An improved DV-Hop algorithm for wireless sensor networks based on neural dynamics. Neurocomputing 2022, 491, 172–185. [Google Scholar] [CrossRef]
- Meng, X.; Liu, Y.; Gao, X.; Zhang, H. A new bio-inspired algorithm: Chicken swarm optimization. In Proceedings of the Advances in Swarm Intelligence: 5th International Conference, ICSI 2014, Hefei, China, 17–20 October 2014; Proceedings, Part I 5. Springer: Berlin/Heidelberg, Germany, 2014; pp. 86–94. [Google Scholar]
- Chen, T.; Hou, S.; Sun, L.; Sun, K. An Enhanced DV-Hop Localization Scheme Based on Weighted Iteration and Optimal Beacon Set. Electronics 2022, 11, 1774. [Google Scholar] [CrossRef]
- Yanfei, J.; Kexin, Z.; Liquan, Z. Improved DV-hop location algorithm based on mobile anchor node and modified hop count for wireless sensor network. J. Electr. Comput. Eng. 2020, 2020, 9275603. [Google Scholar] [CrossRef]
- Shi, Q.; Wu, C.; Xu, Q.; Zhang, J. Optimization for DV-Hop type of localization scheme in wireless sensor networks. J. Supercomput. 2021, 77, 13629–13652. [Google Scholar] [CrossRef]
- Han, D.; Yu, Y.; Li, K.C.; de Mello, R.F. Enhancing the sensor node localization algorithm based on improved DV-hop and DE algorithms in wireless sensor networks. Sensors 2020, 20, 343. [Google Scholar] [CrossRef]
- Zhang, S.; Li, J.; He, B.; Chen, J. LSDV-Hop: Least Squares Based DV-Hop Localization Algorithm for Wireless Sensor Networks. J. Commun. 2016, 11, 243–248. [Google Scholar] [CrossRef]
- Messous, S.; Liouane, H. Online sequential DV-hop localization algorithm for wireless sensor networks. Mob. Inf. Syst. 2020, 2020, 8195309. [Google Scholar] [CrossRef]
- Song, G.; Tam, D. Two novel DV-Hop localization algorithms for randomly deployed wireless sensor networks. Int. J. Distrib. Sens. Netw. 2015, 11, 187670. [Google Scholar] [CrossRef]
- Tomic, S.; Mezei, I. Improvements of DV-Hop localization algorithm for wireless sensor networks. Telecommun. Syst. 2016, 61, 93–106. [Google Scholar] [CrossRef]
- Singh, S.P.; Sharma, S.C. A PSO based improved localization algorithm for wireless sensor network. Wirel. Pers. Commun. 2018, 98, 487–503. [Google Scholar] [CrossRef]
- Rabhi, S.; Ouahab, A.; Baddou, S.; Chetouah, K. An Improved Algorithm Based on Chicken Swarm Optimization for Localization in Wireless Sensor Networks. Adv. Model. Anal. B 2021, 64, 34–39. [Google Scholar] [CrossRef]
- Hadir, A.; Zine-Dine, K.; Bakhouya, M.; El Kafi, J. An optimized DV-hop localization algorithm using average hop weighted mean in WSNs. In Proceedings of the 2014 5th Workshop on Codes, Cryptography and Communication Systems (WCCCS), El Jadida, Morocco, 27–28 November 2014; pp. 25–29. [Google Scholar]
- Hadir, A.; Zine-Dine, K.; Bakhouya, M.; Kafi, J.E. Novel localisation algorithms in wireless sensor networks. Int. J. Wirel. Mob. Comput. 2019, 16, 80–96. [Google Scholar] [CrossRef]
- Hadir, A.; Regragui, Y.; Garcia, N.M. Accurate range-free localization algorithms based on PSO for wireless sensor networks. IEEE Access 2021, 9, 149906–149924. [Google Scholar] [CrossRef]
- Nagpal, R.; Shrobe, H.; Bachrach, J. Organizing a global coordinate system from local information on an ad hoc sensor network. In Proceedings of the Information Processing in Sensor Networks, Palo Alto, CA, USA, 22–23 April 2003; pp. 333–348. [Google Scholar]
- Rockmore, D.N.; Healy, D.M., Jr. Modern Signal Processing; Cambridge University Press: Cambridge, UK, 2004; Volume 46. [Google Scholar]
- Chan, Y.T.; Ho, K.C. A simple and efficient estimator for hyperbolic location. IEEE Trans. Signal Process. 1994, 42, 1905–1915. [Google Scholar] [CrossRef]
- Gad, A.G. Particle swarm optimization algorithm and its applications: A systematic review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Xie, X.; Tang, Z.; Cai, J. The multi-objective inspection path-planning in radioactive environment based on an improved ant colony optimization algorithm. Prog. Nucl. Energy 2022, 144, 104076. [Google Scholar] [CrossRef]
- Kaya, E.; Gorkemli, B.; Akay, B.; Karaboga, D. A review on the studies employing artificial bee colony algorithm to solve combinatorial optimization problems. Eng. Appl. Artif. Intell. 2022, 115, 105311. [Google Scholar] [CrossRef]
- Singh, S.P.; Sharma, S.C. Implementation of a PSO based improved localization algorithm for wireless sensor networks. IETE J. Res. 2019, 65, 502–514. [Google Scholar] [CrossRef]


| Authors | Summary | Strength of Approach | Anchors Based | Node Density | Localization Error | Approaches of Localization | Complexity | Accuracy |
|---|---|---|---|---|---|---|---|---|
| Chen et al. in [29] | A novel method that integrates redundancy, optimized beacons, and iterative techniques using hop error-based signal weighting and an optimal average hop size to improve localization. | Weighted redundancy and optimized beacons are used. | Yes | High | Medium | Iterative | Medium | Medium |
| Yanfei et al. in [30] | An approach that involves modifying the hop count technique and incorporating a mobile anchor node. The hop count computation is modified. | Both static and mobile anchor nodes are used. | Yes | High | Medium | Distributed | Medium | Medium |
| Shi et al. in [31] | A modified approach that combines Particle Swarm Optimization (PSO) and Simulated Annealing (SA) to handle nonlinear equations. | Uses the PSO and SA methods to address nonlinear equations. The anisotropic networks. | Yes | High | Lower | Iterative | High | High |
| Han et al. in [32] | DEIDV-Hop combines an enhanced DV-Hop algorithm with Differential Evolution (DE) to correct inaccuracies caused by the average hop size in the network. | Uses PSO with four distinct network topologies. | Yes | High | Lower | Iterative | High | High |
| Zhang et al. in [33] | A localization approach called LSDV-Hop that leverages the least squares theory to enhance the precision of node localization. | Transformation vector using the least-squares method. | Yes | High | Medium | Distributed | Medium | Medium |
| Messous et al. in [34] | An online sequential localization algorithm based on the DV-Hop technique. | Modifies DV-Hop into an online sequential localization algorithm | Yes | High | Medium | Distributed | High | Medium |
| Song et al. [35] | An approach based on a novel method for hop size distance calculation with 2D hyperbolic techniques. | Uses a new average hop size and 2D hyperbolic techniques | Yes | High | Medium | Iterative | Medium | Medium |
| Tomic et al. in [36] | Three enhanced algorithms (iDV-Hop1, iDV-Hop2, and Quad DV-Hop) based on the DV-Hop technique. | New approaches based on geometry. | Yes | High | Medium | Distributed | High | Medium |
| Singh et al. in [37] | A new DV-Hop-based scheme that incorporates PSO to minimize the localization error. | Combines DV-Hop and PSO | Yes | High | High | Iterative | High | High |
| Rabhi et al. in [38] | An optimized algorithm based on the chicken swarm optimization approach. | Uses chicken swarm optimization to achieve superior results in comparison with the PSO method. | Yes | High | High | Iterative | High | High |
| Parameter | Value |
|---|---|
| Network | |
| Network topology | Square random, H-shaped, O-shaped, and W-shaped |
| Total runs | 30 |
| Length of area | 100 m × 100 m |
| Number of nodes | 200, 250, 300, 350, 400, 450, and 500 |
| Number of anchor nodes | 15%, 20%, 25%, 30%, 35%, and 40% |
| Communication range R | 15 m, 20 m, 25 m, 30 m, and 35 m |
| PSO | |
| Number of iterations | 50 |
| particle sizes | 20 |
| Random values and | [0, 1] |
| Learning coefficient , | 1.5 and 2 |
| Particle’s velocity | 10 |
| CSO | |
| Number of iterations | 50 |
| Size of chicken swarm | 20 |
| Number of roosters | 8 |
| Number of chicks | 1 |
| Number of hens | 15 |
| Network Topology | Random Square | H-Shaped | O-Shaped | W-Shaped | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | MIN | MAX | AVG | MIN | MAX | AVG | MIN | MAX | AVG | MIN | MAX | AVG |
| DV-Hop | 0.032 | 0.693 | 0.282 | 0.021 | 1.065 | 0.379 | 0.053 | 0.806 | 0.282 | 0.017 | 0.772 | 0.274 |
| DV-HopPSO | 0.039 | 1.11 | 0.272 | 0.013 | 1.148 | 0.288 | 0.007 | 0.892 | 0.236 | 0.009 | 0.854 | 0.225 |
| MDV-Hop | 0.025 | 0.647 | 0.258 | 0.022 | 0.974 | 0.327 | 0.025 | 0.522 | 0.208 | 0.031 | 0.79 | 0.299 |
| DV-HopCSO | 0.017 | 0.595 | 0.201 | 0.021 | 0.804 | 0.233 | 0.019 | 0.564 | 0.191 | 0.017 | 0.772 | 0.212 |
| W-DV-Hop | 0.012 | 0.976 | 0.278 | 0.012 | 1.595 | 0.38 | 0.017 | 0.713 | 0.267 | 0.013 | 1.09 | 0.278 |
| W-DV-HopCSO | 0.012 | 0.708 | 0.182 | 0.012 | 0.969 | 0.252 | 0.017 | 0.61 | 0.186 | 0.013 | 0.752 | 0.187 |
| HW-DV-Hop | 0.034 | 0.816 | 0.243 | 0.009 | 0.821 | 0.269 | 0.024 | 0.785 | 0.244 | 0.006 | 0.71 | 0.286 |
| HW-DV-HopCSO | 0.016 | 0.646 | 0.174 | 0.009 | 0.729 | 0.200 | 0.008 | 0.456 | 0.194 | 0.006 | 0.538 | 0.201 |
| Network Topology | Random Square | H-Shaped | O-Shaped | W-Shaped | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | 30 | 80 | 100 | 30 | 80 | 100 | 30 | 80 | 100 | 30 | 80 | 100 |
| DV-Hop | 0.282 | 0.303 | 0.316 | 0.379 | 0.374 | 0.370 | 0.282 | 0.305 | 0.300 | 0.274 | 0.324 | 0.322 |
| PSODV-Hop | 0.272 | 0.243 | 0.247 | 0.288 | 0.286 | 0.287 | 0.236 | 0.257 | 0.256 | 0.225 | 0.243 | 0.245 |
| MDV-Hop | 0.258 | 0.225 | 0.230 | 0.327 | 0.288 | 0.286 | 0.208 | 0.199 | 0.197 | 0.299 | 0.255 | 0.265 |
| DV-HopCSO | 0.201 | 0.200 | 0.204 | 0.233 | 0.233 | 0.233 | 0.191 | 0.211 | 0.208 | 0.212 | 0.225 | 0.222 |
| W-DV-Hop | 0.278 | 0.288 | 0.298 | 0.38 | 0.367 | 0.365 | 0.267 | 0.289 | 0.281 | 0.278 | 0.310 | 0.312 |
| W-DV-HopCSO | 0.182 | 0.190 | 0.194 | 0.252 | 0.232 | 0.234 | 0.186 | 0.197 | 0.192 | 0.187 | 0.215 | 0.221 |
| HW-DV-Hop | 0.243 | 0.248 | 0.243 | 0.269 | 0.329 | 0.327 | 0.244 | 0.212 | 0.214 | 0.286 | 0.276 | 0.276 |
| HW-DV-HopCSO | 0.174 | 0.177 | 0.176 | 0.200 | 0.226 | 0.222 | 0.194 | 0.186 | 0.171 | 0.201 | 0.208 | 0.211 |
| Algorithm | Time Complexity | Space Complexity |
|---|---|---|
| DV-Hop | ||
| PSODV-Hop | ||
| MDV-Hop | ||
| DV-HopCSO | ||
| W-DV-Hop | ||
| W-DV-HopCSO | ||
| HW-DV-Hop | ||
| HW-DV-HopCSO |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hadir, A.; Kaabouch, N.; El Houssaini, M.-A.; El Kafi, J. Range-Free Localization Approaches Based on Intelligent Swarm Optimization for Internet of Things. Information 2023, 14, 592. https://doi.org/10.3390/info14110592
Hadir A, Kaabouch N, El Houssaini M-A, El Kafi J. Range-Free Localization Approaches Based on Intelligent Swarm Optimization for Internet of Things. Information. 2023; 14(11):592. https://doi.org/10.3390/info14110592
Chicago/Turabian StyleHadir, Abdelali, Naima Kaabouch, Mohammed-Alamine El Houssaini, and Jamal El Kafi. 2023. "Range-Free Localization Approaches Based on Intelligent Swarm Optimization for Internet of Things" Information 14, no. 11: 592. https://doi.org/10.3390/info14110592
APA StyleHadir, A., Kaabouch, N., El Houssaini, M.-A., & El Kafi, J. (2023). Range-Free Localization Approaches Based on Intelligent Swarm Optimization for Internet of Things. Information, 14(11), 592. https://doi.org/10.3390/info14110592






