1. Introduction
Generative modeling, as produced by
Variational AutoEncoders (VAEs) [
1] or
Generative Adversarial Networks (GANs), is used to solve the problem of learning a joint distribution over all the variables. As a result, these models can simulate how data are created, contrary to discriminative modeling, which learns a predictor given the observations [
2]. Hence, multiple applications have been developed using generative modeling, while GANs and VAEs are usually employed for image analysis [
3,
4].
VAE is a deep generative model [
5] that can be viewed as a combination of coupled encoder and decoder Bayesian networks that were independently parameterized. The first network (encoder) is the recognition model responsible for mapping the input data to a latent vector, delivering an estimate of its posterior over latent random variables. The result is a model capable of providing an amortized inference procedure for the computation of latent representations. In contrast, the second network (decoder) is the generative model that reverses the process. At the same time, the decoder can estimate an implicit density model given the data. Therefore, according to the Bayes rule, the recognition model is the approximate inverse of the generative model [
2,
6].
Conversely, VAEs [
2,
6] are associated with several prominent challenges. These encompass the susceptibility of the models to suffer from the curse of dimensionality and the inherent absence of interpretable meaning in their latent representations. This work primarily concentrates on mitigating these problems, focusing principally on the latter issue.
Particularly, the main goal of this work is to provide an interpretable model that can then be used in feature creation for probabilistic models. The rationale behind the proposed solution is to provide a methodology capable of filtering uninformative features. To address this challenge, the proposed solution uses Convolutional Neural Networks (CNNs) for both recognition and generative models, producing an individual representation for each kernel of the last convolution layer of the recognition model. As a result, a different set of latent random variables was assessed for each of these kernels. The VAE was trained using the standard unsupervised learning methodology. Afterward, the encoder was employed as a feature creation layer (with frozen weights) for the probabilistic model, trained using supervised learning.
Two approaches were examined to select which latent variables are more relevant for the probabilistic classifier. It is worth noting that each latent variable was sampled from a distribution associated with a kernel of the last convolution layer of the encoder. A distribution was created for each kernel; hence, each latent variable represents one of the kernels, and these variables were used as features for the classification procedure. As a result, using feature selection on the sampled latent variables leads to the kernel selection of the last convolution layer of the encoder.
The first feature selection approach used a wrapper method, employing Sequential Forward Selection (SFS) to choose the most important kernels. In contrast, the second used a filter method to determine the relevance of each kernel, ranked according to which are the most dissimilar kernels. This second proposed method follows the main hypothesis of this work that an interpretation of the latent representation can be performed by examining the shape of the created distributions, suggesting that the least relevant distributions can be identified by how similar they are to the other distributions. As a result, it is possible to filter the uninformative features (when the encoder is used for feature creation) by removing the irrelevant distributions. In this view, SFS was used as a benchmark for the proposed second method, which has the main advantage of only requiring a number of examinations that is equal to the number of kernels k to be selected (while SFS will produce k (k + 1)/2 sets to be examined), thus being a much faster algorithm (especially for larger k) that is also classifier independent (filter method).
Therefore, the main contributions of the work are:
The proposal of a technique for assessing the distribution created by each kernel of the VAE last convolution layer.
The proposal of a methodology for feature selection in VAEs based on the filter method that examines the shape of the created distributions for assessing the uninformative features.
The proposed technique follows the rationale of model pruning, which is essential for building applications for resource-constrained devices frequently used in the
Internet of Things (IoT) [
7,
8]. The phenomenon of variational pruning in VAEs occurs when latent variables are unused in the model, resulting in the posterior matching the prior distribution (posterior collapse) [
9]. However, our proposed approach diverges from this concept as we propose selecting a subset of latent variables from a pre-trained model with fixed weights without addressing the posterior collapse problem, which was already studied in state-of-the-art models. For example, Yeung et al. [
10] introduced the concept of epitomic variational autoencoders, which generate sets of mutually exclusive latent factors that compete to explain the data. Another approach was proposed by Razavi et al. [
11] using the
δ-VAE, which, instead of going for the standard approach for preventing the posterior collapse (that either requires altering the training objective or weakening the capacity of the decoder), imposes a constraint on the variational family for the posterior, ensuring it maintains a minimum distance from the prior. On the other hand, Tomczak and Welling [
12] used a type of prior named variational mixture of posteriors.
Our proposal focuses on post-training pruning to fed features for a subsequent model. Although several works have previously used VAEs for classification and regressions tasks [
13,
14,
15], to the best of the authors’ knowledge, no prior state-of-the-art research has introduced the concept presented in this work, which involves combining the proposed feature pruning for selecting the kernels of a VAE and, subsequently, utilizing the derived features to feed a machine-learning model.
The following sections present the developed methods, followed by the results and discussion. This paper is then concluded by presenting the main conclusions.
2. Developed Methods
The developed methodology is composed of two main steps: The first refers to producing a VAE that can create an individual representation for each kernel of the last convolution layer of the recognition model. This model maps
x to posterior distributions Q(
|
x) in the encoder while the likelihood P(
x|
) is parametrized by the decoder. The second step involved using the encoder model as feature creation (with frozen weights), employing a feature selection procedure to filter features from uninformative kernels. This produced a subset
u that fed the probabilistic classifier to make a forecast of the labels
y.
Figure 1 presents a simplified overview of the proposed methodology. All of the code was developed in Python 3 using TensorFlow.
2.3. Kernel Selection Methods
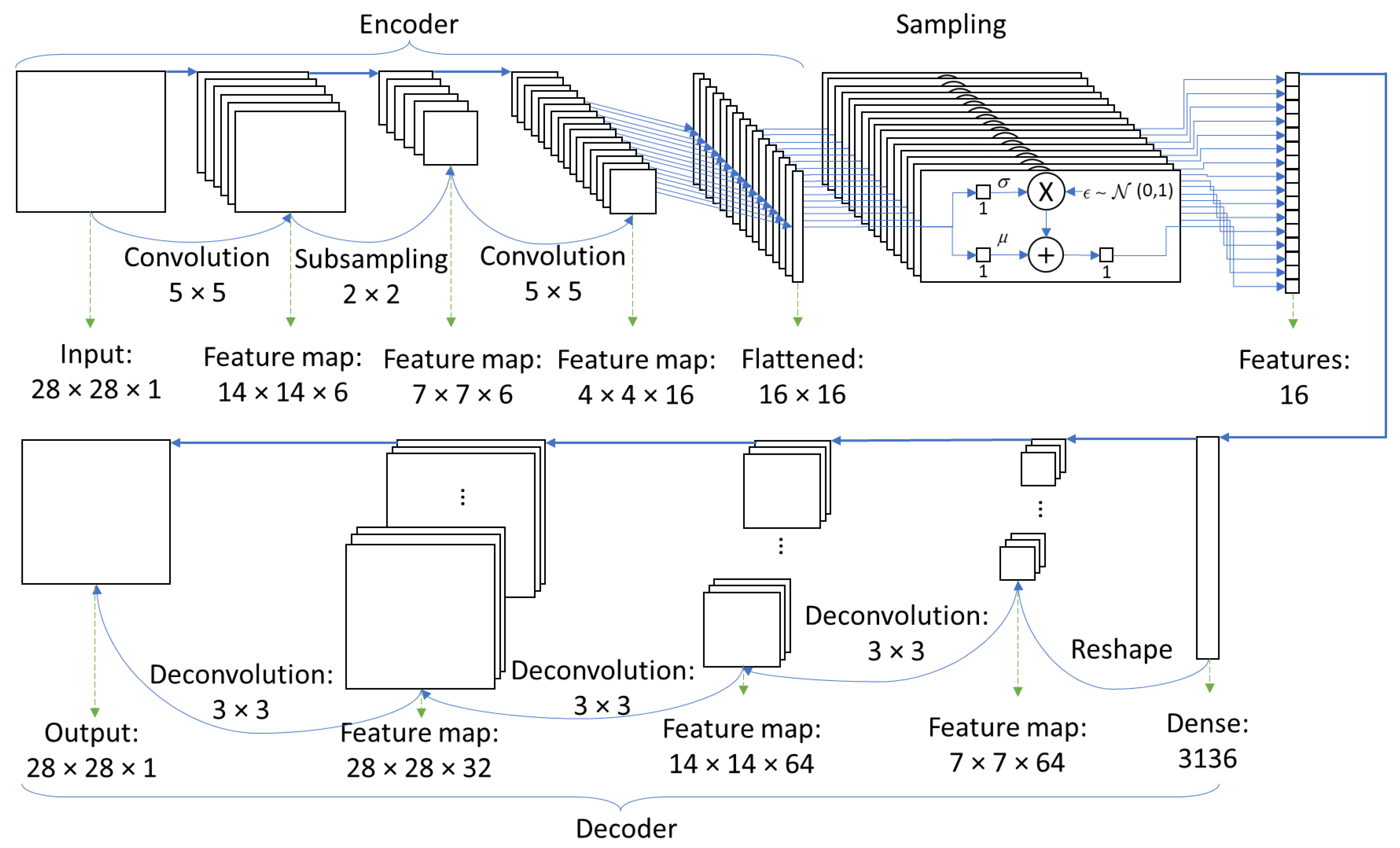
The standard VAE implementation uses one dense layer to learn each parameter of the employed distribution. Hence, two dense layers are usually used since two parameters define the Gaussian distribution. The number of neurons on these layers is the same and defines the latent space. All neurons of the two dense layers are connected to all kernels of the previous convolutional layer, so they all learn distributions from the same feature data.
The proposed approach of this work goes in the opposite direction, using two dense layers (with just one output neuron in each) connected to each kernel from the convolutional layer that provides the features to the distributions. This way, each distribution learns from a single kernel (instead of learning from all kernels), allowing the possibility of assessing which are the most relevant kernels (latent space interpretation) for classification. This can confirm the basic assumption of this work that the sampled features (from each individual kernel) produce dissimilar output distributions (by the sampling layer) for input data from different classes.
Two methodologies were studied to select the most relevant set of latent variables. The first was the benchmark and depended on the classifier, using the standard wrapper SFS method. Particularly, two vectors were produced, one containing all latent variables and a second that was empty. The goal was to create a feature vector to provide the maximum Accuracy (Acc) for the intended classification. In the first iteration, all features of the first vector were used one by one alone, and the most relevant feature (the one that, when used alone, led to the highest Acc) was identified, being moved to the second vector. In the subsequent iterations, the algorithm looked for the features in the first vector that, when combined with the features in the second vector, provide the highest Acc, being sequentially moved to the second vector. This iterative process was repeated until the first vector was empty.
The first methodology is usable when the number of latent variables (denoting the number of kernels) to be evaluated is considerably small since it requires numerous simulations. This problem is addressed by the second methodology proposed in this work, which uses a filter method to assess the relevance of the features. The second method was named KLD selection (KLDS), and its pseudocode is presented in Algorithm 1.
The premise was that a kernel with a lower relevance was more similar to all other kernels; hence, it was less relevant as it conveyed less unique information. Therefore, the created features could be ranked according to the kernel relevance measure, sorting them in a vector from more to less dissimilar (i.e., first was the feature with the highest kernel relevance, then the feature with the second highest kernel relevance, and successively until we reach the feature with the lowest kernel relevance).
The second methodology’s algorithm is composed of three parts: In detail, in the first part of KLDS, several Monte Carlo samples were performed. For each class, the training dataset samples fed the encoder, and the latent space features were stored. As each feature represents one of the kernels in a known sequence, it was then possible to produce the distribution of that kernel for each dataset class. Therefore, number_of_kernels defines the number of distributions (one for each kernel) to be assessed for each dataset class (number_of_classes).
Afterward, for the second part, the distributions assessed for all kernels of one class were examined, calculating for each kernel distribution the KLD between their distribution and the distribution of all other kernels (in pairs). These calculations were then used to determine the mean value of all KLD estimations of each kernel. This process was repeated for all dataset classes, leading to
number_of_kernels average KLD estimations (one per kernel), indicated by
KLD_measures, for each class. Finally, each kernel’s assessed
KLD_measures were averaged (resulting in
KLD_kernels) for all classes in the third. The resulting value (for each kernel) was named kernel relevance.
| Algorithm 1: Pseudocode for the KLDS algorithm, presenting the required inputs, the produced outputs, and the procedures. |
inputs: number_of_classes, number_of_kernels, train_data, train_labels, encoder
output: kernel_relevance |
| for class ← 1 to number_of_classes do |
| | samples ← encoder(train_data(train_labels equal to class)) |
| | kernels_distributions ← distribution(samples) |
| | for testing_kernel ← 1 to number_of_kernels do |
| | | for comparing_kernel ← 1 to number_of_kernels do |
| | | | KLD_measures(testing_kernel, comparing_kernel) ← KLD(testing_kernel, comparing_kernel) |
| | | KLD_kernels(testing_kernel, class) ← mean(KLD_measures(testing_kernel, all)) |
| for testing_kernel ← 1 to number_of_kernels do |
| | kernel_relevance(testing_kernel) ← mean(KLD_kernels(testing_kernel, all)) |
| kernel_relevance(testing_kernel) ← sort_descending(kernel_relevance) |
The rationale for checking these two methodologies is to verify if a classifier-independent method (the second proposed methodology) can perform similarly to a classifier-dependent method (the first proposed methodology).
Frequently, a classifier-dependent method can produce a better performance but require the selection to be redone when the classifier changes and takes much more time to perform the selection [
20]. Hence, when the number of kernels is too high, the classifier-dependent methods become unfeasible, leading to the need for the proposed classifier-independent approach.
Author Contributions
Conceptualization, F.M., S.S.M., F.M.-D. and A.G.R.-G.; methodology, F.M., S.S.M., F.M.-D. and A.G.R.-G.; software, F.M. and S.S.M.; validation, F.M. and S.S.M.; formal analysis, F.M.; investigation, F.M., S.S.M., F.M.-D. and A.G.R.-G.; resources, F.M., S.S.M., F.M.-D. and A.G.R.-G.; data curation, F.M.; writing—original draft preparation, F.M.; writing—review and editing, S.S.M., F.M.-D. and A.G.R.-G.; visualization, F.M.; supervision, F.M.-D. and A.G.R.-G.; project administration, F.M.-D. and A.G.R.-G.; funding acquisition, F.M.-D. and A.G.R.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by LARSyS (Project—UIDB/50009/2020). The authors acknowledge the Portuguese Foundation for Science and Technology (FCT) for their support through Projeto Estratégico LA 9—UID/EEA/50009/2019, and ARDITI (Agência Regional para o Desenvolvimento da Investigação, Tecnologia e Inovação) under the scope of the project M1420-09-5369-FSE-000002—Post-Doctoral Fellowship, co-financed by the Madeira 14–20 Program—European Social Fund.
Data Availability Statement
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kingma, D.; Welling, M. Auto-encoding variational bayes. In Proceedings of the 2nd International Conference on Learning Representations, ICLR 2014, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Kingma, D.; Welling, M. An Introduction to Variational Autoencoders. Found. Trends® Mach. Learn. 2019, 12, 307–392. [Google Scholar] [CrossRef]
- Ternes, L.; Dane, M.; Gross, S.; Labrie, M.; Mills, G.; Gray, J.; Heiser, L.; Chang, Y. A multi-encoder variational autoencoder controls multiple transformational features in single-cell image analysis. Commun. Biol. 2022, 5, 255. [Google Scholar] [CrossRef] [PubMed]
- Kazeminia, S.; Baur, C.; Kuijper, A.; Ginneken, B.; Navab, N.; Albarqouni, S.; Mukhopadhyay, A. GANs for medical image analysis. Artif. Intell. Med. 2020, 109, 101938. [Google Scholar] [CrossRef] [PubMed]
- Rezende, D.; Mohamed, S.; Wierstra, D. Stochastic backpropagation and approximate inference in deep generative models. In Proceedings of the 31st International Conference on Machine Learning, Bejing, China, 21–26 June 2014. [Google Scholar]
- Wei, R.; Garcia, C.; El-Sayed, A.; Peterson, V.; Mahmood, A. Variations in Variational Autoencoders—A Comparative Evaluation. IEEE Access 2020, 8, 153651–153670. [Google Scholar] [CrossRef]
- Ashiquzzaman, A.; Kim, S.; Lee, D.; Um, T.; Kim, J. Compacting Deep Neural Networks for Light Weight IoT & SCADA Based Applications with Node Pruning. In Proceedings of the 2019 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Okinawa, Japan, 11–13 January 2019. [Google Scholar]
- Qi, C.; Shen, S.; Li, R.; Zhao, Z.; Liu, Q.; Liang, J.; Zhang, H. An efficient pruning scheme of deep neural networks for Internet of Things applications. EURASIP J. Adv. Signal Process. 2021, 2021, 31. [Google Scholar] [CrossRef]
- Singh, A.; Ogunfunmi, T. An Overview of Variational Autoencoders for Source Separation, Finance, and Bio-Signal Applications. Entropy 2022, 24, 55. [Google Scholar] [CrossRef] [PubMed]
- Yeung, S.; Kannan, A.; Dauphin, Y.; Fei-Fei, L. Tackling Over-pruning in Variational Autoencoders. arXiv 2017. [Google Scholar] [CrossRef]
- Razavi, A.; Oord, A.v.d.; Poole, B.; Vinyals, O. Preventing Posterior Collapse with delta-VAEs. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Tomczak, J.; Welling, M. VAE with a VampPrior. In Proceedings of the Twenty-First International Conference on Artificial Intelligence and Statistics, Playa Blanca, Spain, 9–11 April 2018. [Google Scholar]
- Xu, W.; Tan, Y. Semisupervised Text Classification by Variational Autoencoder. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 295–308. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Adeli, E.; Honnorat, N.; Leng, T.; Pohl, K.M. Variational AutoEncoder for Regression: Application to Brain Aging Analysis. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2019, Shenzhen, China, 13–17 October 2019; Shen, D., Liu, T., Peters, T.M., Staib, L.H., Essert, C., Zhou, S., Yap, P.-T., Khan, A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 823–831. [Google Scholar]
- Feiyang Cai, A.I.O.; Koutsoukos, X. Variational Autoencoder for Classification and Regression for Out-of-Distribution Detection in Learning-Enabled Cyber-Physical Systems. Appl. Artif. Intell. 2022, 36, 2131056. [Google Scholar] [CrossRef]
- Lee, S.; Park, S.; Choi, B. Application of domain-adaptive convolutional variational autoencoder for stress-state prediction. Knowl.-Based Syst. 2022, 248, 108827. [Google Scholar] [CrossRef]
- Blei, D.; Kucukelbir, A.; McAuliffe, J. Variational Inference: A Review for Statisticians. J. Am. Stat. Assoc. 2016, 112, 859–877. [Google Scholar] [CrossRef]
- Nagi, J.; Ducatelle, F.; Caro, G.; Cireşan, D.; Meier, U.; Giusti, A.; Nagi, F.; Schmidhuber, J.; Gambardella, L. Max-pooling convolutional neural networks for vision-based hand gesture recognition. In Proceedings of the 2011 IEEE International Conference on Signal and Image Processing Applications (ICSIPA), Kuala Lumpur, Malaysia, 16–18 November 2011. [Google Scholar]
- Noh, H.; Hong, S.; Han, B. Learning deconvolution network for semantic segmentation. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Mostafa, S.; Morgado-Dias, F.; Ravelo-García, A. Comparison of SFS and mRMR for oximetry feature selection in obstructive sleep apnea detection. Neural Comput. Appl. 2020, 32, 15711–15731. [Google Scholar] [CrossRef]
- Ryu, S.; Kwon, Y.; Kim, W. A Bayesian graph convolutional network for reliable prediction of molecular properties with uncertainty quantification. Chem. Sci. 2019, 36, 8438–8446. [Google Scholar] [CrossRef] [PubMed]
- Wen, Y.; Vicol, P.; Ba, J.; Tran, D.; Grosse, R. Flipout: Efficient Pseudo-Independent Weight Perturbations on Mini-Batches. In Proceedings of the Sixth International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A Feature Similarity Index for Image Quality Assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed]
- Ozdemir, O.; Russell, R.; Berlin, A. A 3D Probabilistic Deep Learning System for Detection and Diagnosis of Lung Cancer Using Low-Dose CT Scans. IEEE Trans. Med. Imaging 2019, 39, 1419–1429. [Google Scholar] [CrossRef] [PubMed]
- Amroun, H.; Temkit, M.; Ammi, M. Best Feature for CNN Classification of Human Activity Using IOT Network. In Proceedings of the IEEE/ACM International Conference on and International Conference on Cyber, Physical and Social Computing (CPSCom) Green Computing and Communications (GreenCom) Exeter, Devon, UK, 21–23 June 2017. [Google Scholar]
- Know, J.; Park, D. Hardware/Software Co-Design for TinyML Voice-Recognition Application on Resource Frugal Edge Devices. Appl. Sci. 2021, 11, 11073. [Google Scholar]
Figure 1.
Simplified overview of the proposed methodology, composed of two main steps: The first step develops the VAE, whose encoder was then used for feature creation that fed the classifier created in the second step.
Figure 2.
Implemented VAE architecture for the two-dimensional input. The layer operations and their produced output shape are also presented.
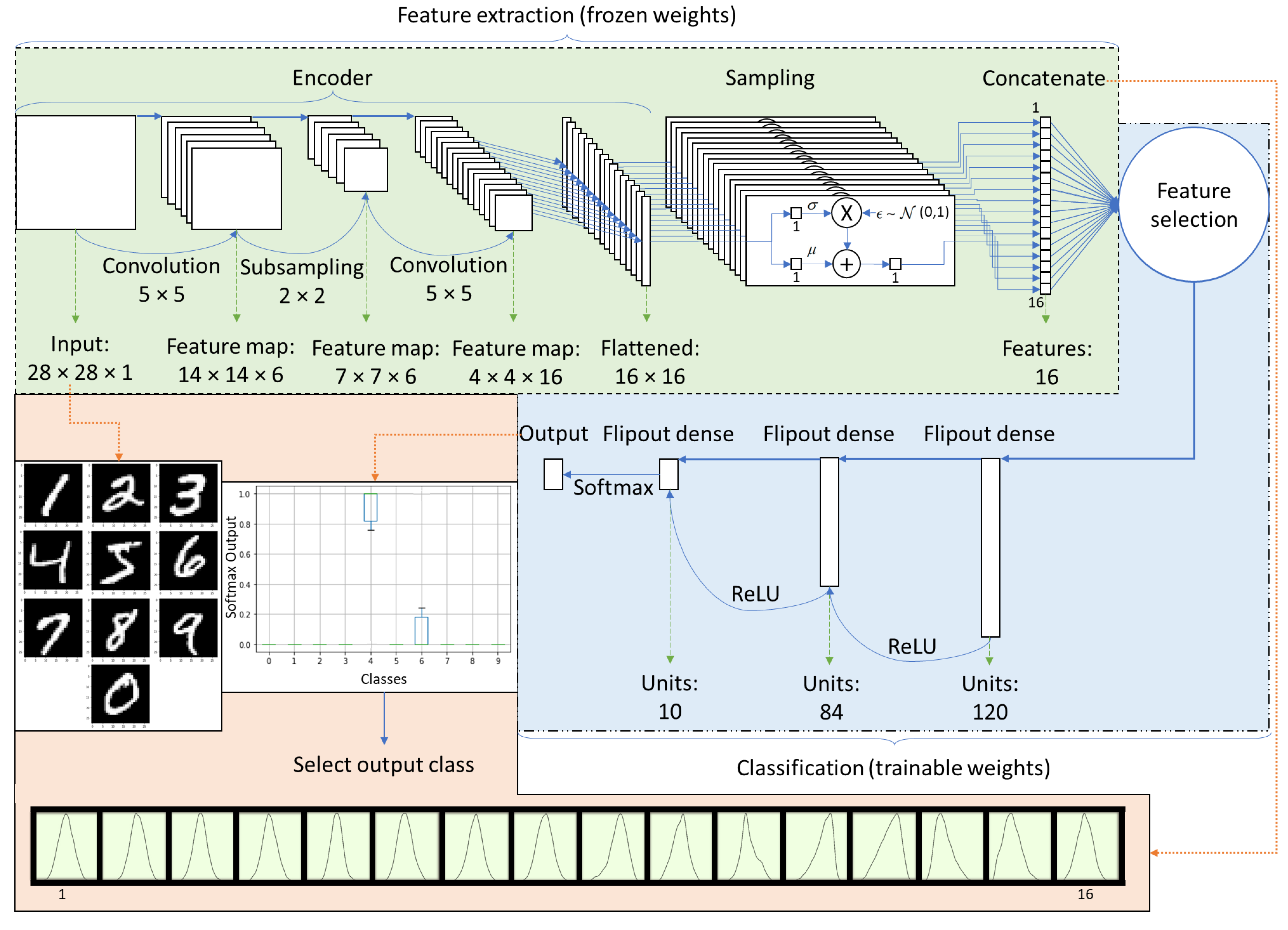
Figure 3.
Structure of the classifier used for the classification analysis. The feature extraction part comprises the encoder developed by the VAE, and the weights of this part were frozen (non-trainable). A feature selection procedure was employed for the classification, and the classifier’s weights were optimized using supervised learning.
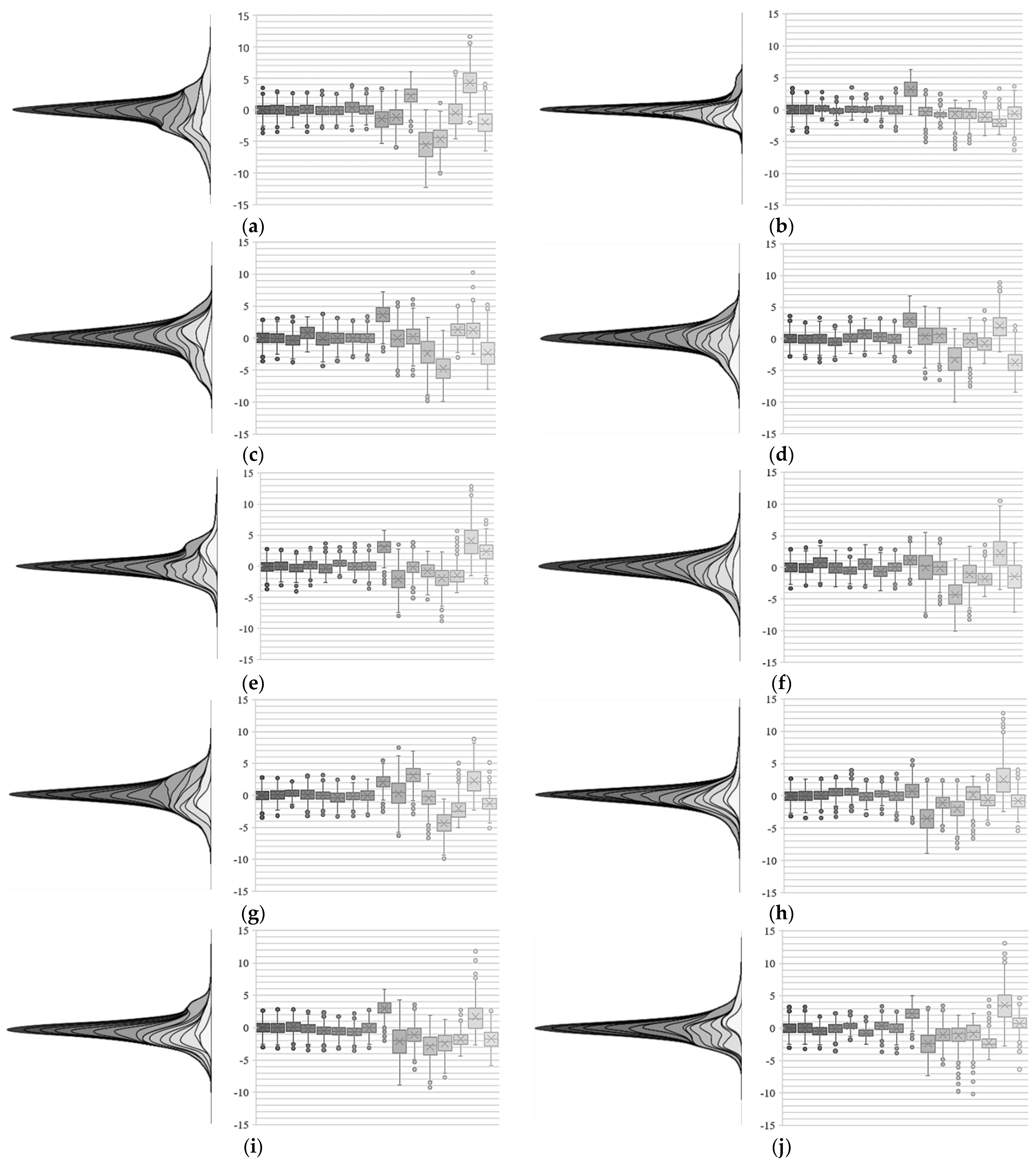
Figure 4.
Distributions produced by the samples of the kernel of the last convolution layer of the encoder, for classes (a) 1, (b) 2, (c) 3, (d) 4, (e) 5, (f) 6, (g) 7, (h) 8, (i) 9, and (j) 10, showing the 16 kernels in sequence, from left (kernel 1) to the right (kernel 16). The left figure shows the shape of each distribution produced from the samples, whose amplitude was gradually reduced (from the first to the last kernel) to allow the visualization of all distributions. In contrast, the right figure shows the box plot of the samples.
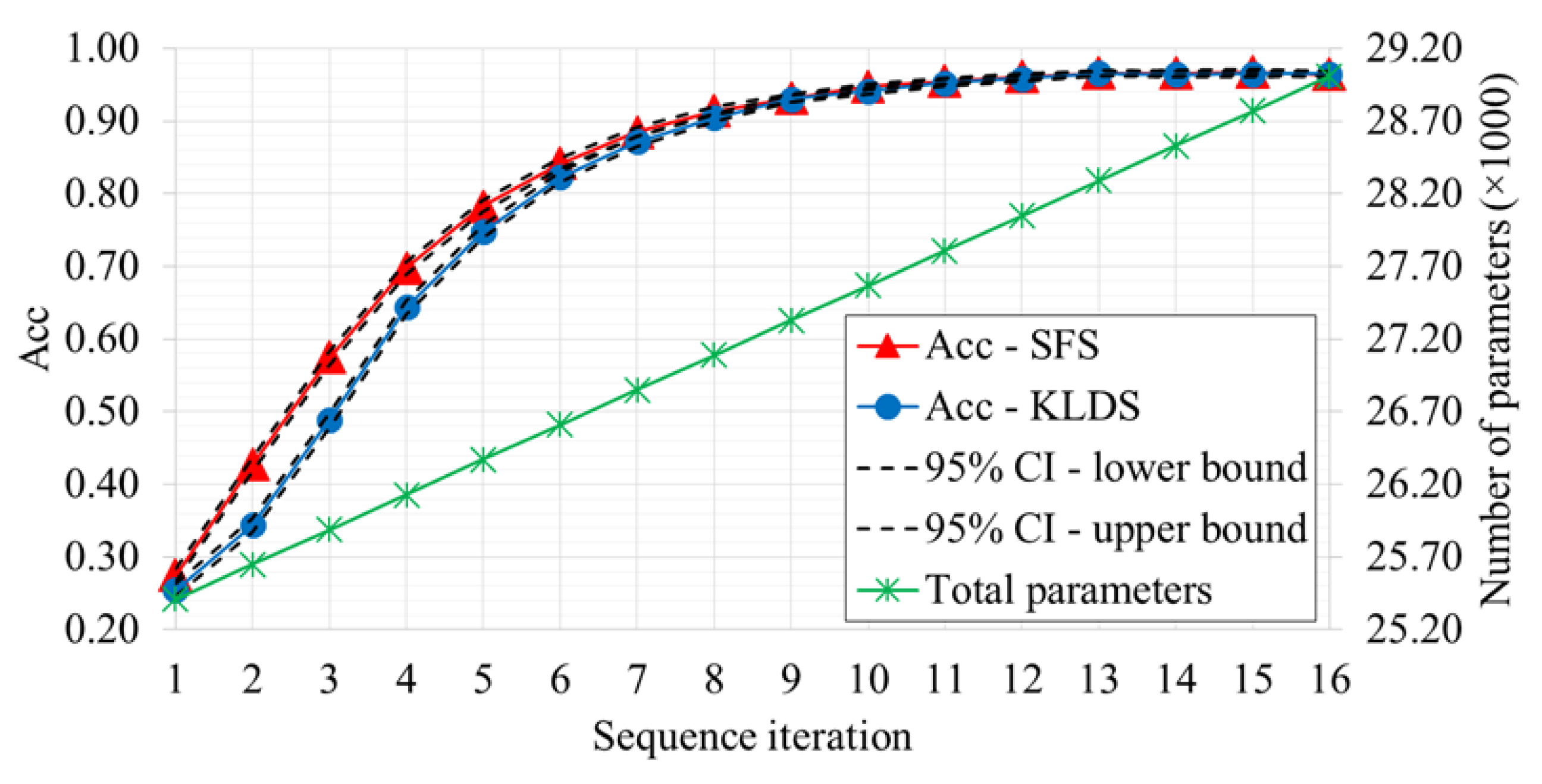
Figure 5.
Variation of the Acc through the sequence iteration of the evaluated feature selection algorithms. The total number of parameters of the model, as the number of kernels varies, is also presented.
Figure 6.
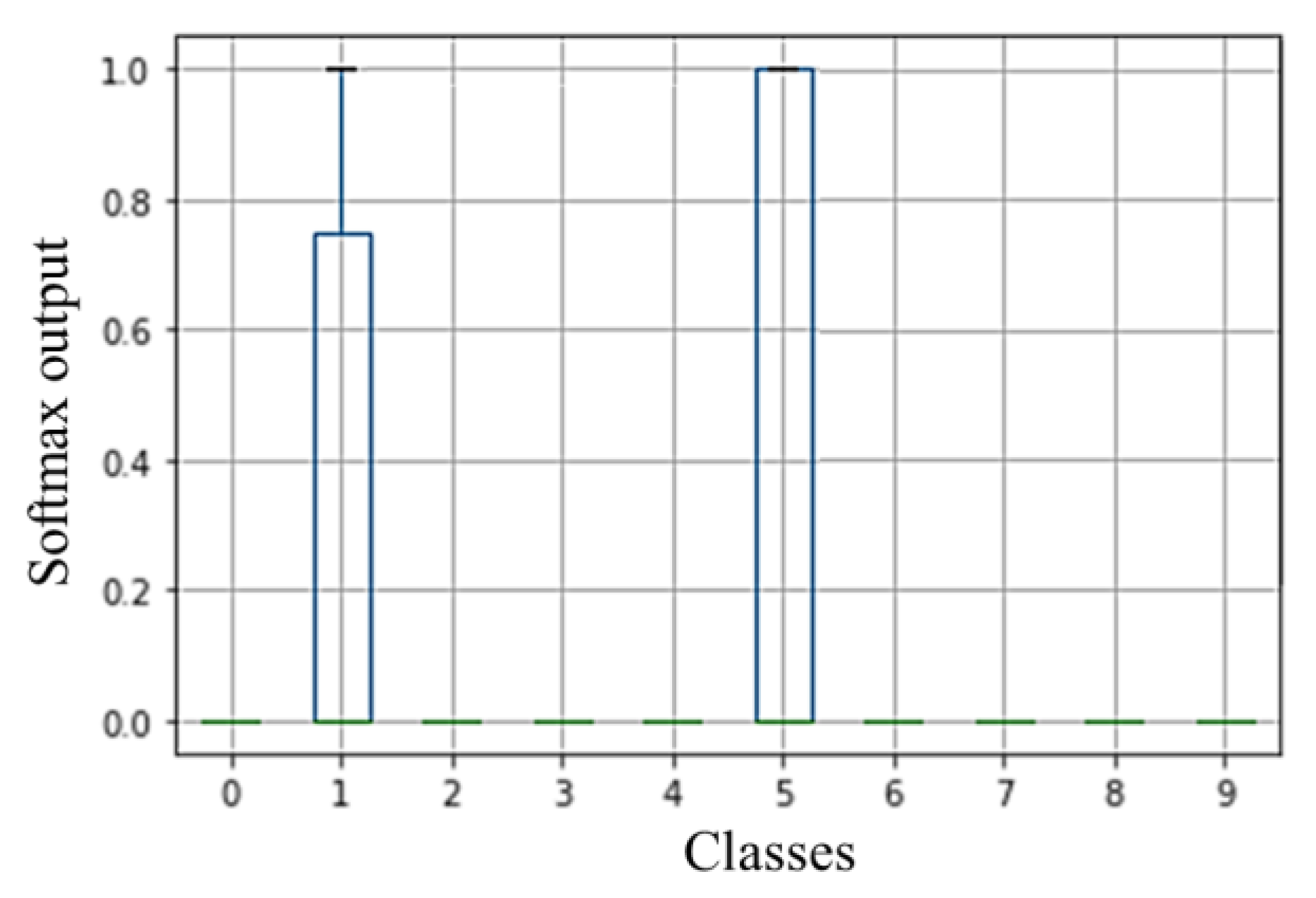
Example of the variation in the models’ forecast (the softmax output) from a specific misclassified sample with high epistemic uncertainty.
Figure 7.
Variation of the FSIM as the kernels selected by KLDS is progressively used (one by one), from more to less relevant. The image also displays the FSIM variation for a specific example (original image) and the progression in the reconstructed images as the number of used kernels increases.
Figure 8.
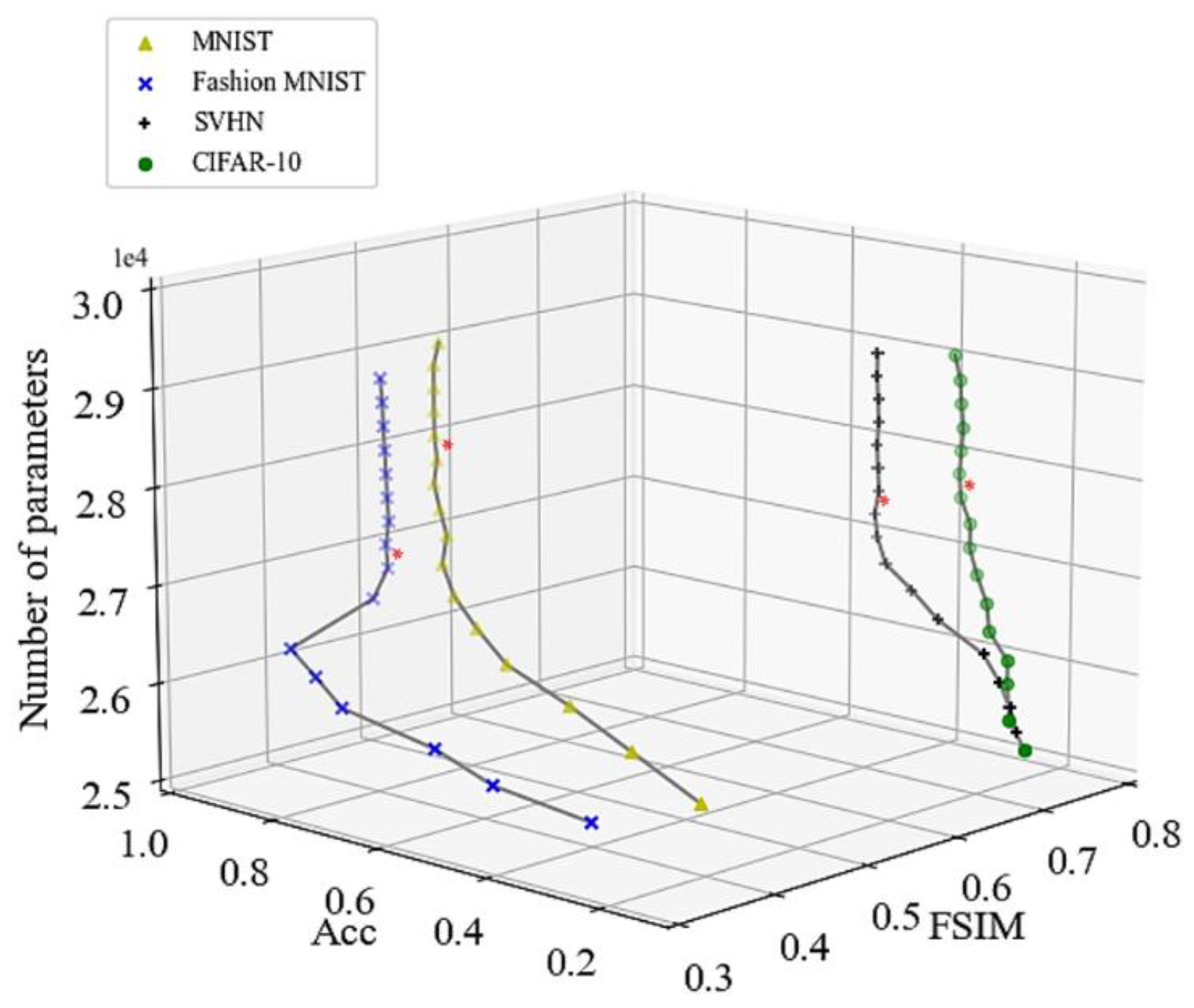
Variation of the Acc and FSIM as the used kernels, whose sequence was selected by KLDS, is progressively increased (leading to an increase in the number of parameters of the model) for the four examined datasets. The asterisk indicates when variation in both metrics is lower than 1%.
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).