Abstract
One of the WHO’s strategies to reduce road traffic injuries and fatalities is to enhance vehicle safety. Driving fatigue detection can be used to increase vehicle safety. Our previous study developed an ECG-based driving fatigue detection framework with AdaBoost, producing a high cross-validated accuracy of 98.82% and a testing accuracy of 81.82%; however, the study did not consider the driver’s cognitive state related to fatigue and redundant features in the classification model. In this paper, we propose developments in the feature extraction and feature selection phases in the driving fatigue detection framework. For feature extraction, we employ heart rate fragmentation to extract non-linear features to analyze the driver’s cognitive status. These features are combined with features obtained from heart rate variability analysis in the time, frequency, and non-linear domains. In feature selection, we employ mutual information to filter redundant features. To find the number of selected features with the best model performance, we carried out 28 combination experiments consisting of 7 possible selected features out of 58 features and 4 ensemble learnings. The results of the experiments show that the random forest algorithm with 44 selected features produced the best model performance testing accuracy of 95.45%, with cross-validated accuracy of 98.65%.
1. Introduction
One of the goals of SDG 3 focuses on reducing road traffic injuries and fatalities. The goal is to halve the number of deaths and injuries caused by road traffic accidents worldwide by 2030. To achieve SDG 3.6, the WHO suggests a comprehensive strategy that includes enhancing road safety management, enhancing road regulation and enforcement, promoting safer road infrastructure and mobility, increasing vehicle safety standards, enhancing emergency trauma care, and increasing public awareness [1]. In this paper, we focus on vehicle safety by developing a framework for detecting driver fatigue. Driving fatigue detection aims to detect fatigue or drowsiness while driving by monitoring a driver’s physiological state with various types of fatigue measurement methods [2]. For example, an electrocardiogram or an encephalogram are examples of objective measurements.
In our previous study [3], we developed a driving fatigue detection framework. Developments were carried out at three phases in the driving fatigue detection framework using ECG. In the data preprocessing phase, we applied the resampling method with an overlapping window to increase the diversity of the dataset. In the data processing phase, we applied heart rate variability (HRV) analysis methods with two non-linear approaches, a Poincare plot analysis and a multi-fractal detrended fluctuation analysis. Thus, five HRV analysis feature extraction methods were used: statistical analysis, geometrical analysis, spectral analysis, Poincare plot analysis, and multi-fractal detrended fluctuation analysis. These methods were utilized to extract features from the NN intervals in the time domain, frequency domain, and non-linear approach. The number of total extracted features was 54. In the classification phase, the ensemble method was applied to classify two fatigue states: alert and fatigue. With all of these developments in three phases, the random forest classification model produced a cross-validated accuracy of 97.98% and a testing accuracy of 86.36%. The AdaBoost classification model produced a cross-validated accuracy of 98.82% and a testing accuracy of 81.82%. This study shows significant results; however, our previous study uncovered the following problems.
- The study did not consider the cognitive fatigue status experienced by drivers when they were fatigued. Several studies [4,5,6] stated that there is an association between driver cognitive fatigue and the causal factor of driving fatigue. Therefore, it is necessary to consider extracting information from interval NN data related to cognitive status.
- The study did not consider the redundant feature factors that can affect the performance of the classification model. It was demonstrated that the Poincare plot analysis and multifractal detrended fluctuation analysis methods only improved in the random forest and AdaBoost models but not in the bagging and gradient boosting models. This is due to the total of 54 features extracted, which makes the model too complex and reduces the model’s interpretability. Therefore, a feature selection method is needed to reduce the number of redundant features.
To address all of these issues and improve the performance of the classification model, we propose two developments for feature extraction and feature selection within the proposed driving fatigue detection framework (Figure 1). In this paper, our main contributions are explained as follows:
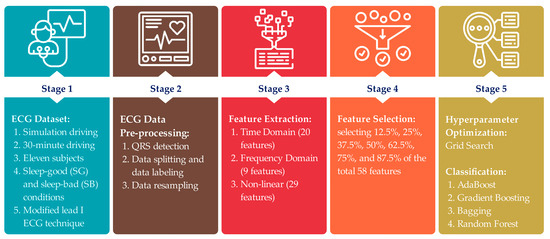
Figure 1.
Proposed five-phase driving fatigue detection framework.
- In the feature extraction phase, we applied heart rate fragmentation. It was first proposed by Costa et al. [7] and has never been used or further investigated in previous driving fatigue studies (Table 1). Costa et al. [8] reported that heart rate fragmentation can be useful to monitor cognitive status. We hypothesized that heart rate fragmentation can be used to monitor driver cognitive status, which represents the fatigue state of the driver. Heart rate fragmentation is used to extract non-linear features from NN interval data.
- Our previous study [3] had no feature selection applied in the driving fatigue detection framework; therefore, we added the feature selection phase to the driving fatigue detection framework proposed here (Figure 1). In the feature selection phase, we chose mutual information over other feature selection methods because we applied both linear and non-linear feature extraction methods, and mutual information can capture both linear and non-linear relationships between variables. Additionally, mutual information can be used to measure the relevance of features to the target variable [9].
This study is organized as follows: the second section, “Related Works”, discusses previous driving fatigue detection studies that used ECG fatigue measurement. The third section, “Materials and Methods”, describes the dataset used in this study, data preprocessing, feature extraction, feature selection, and the classification model. The fourth section, “Results and Discussion”, presents the various experiments applied to the proposed driving fatigue detection method, the experimental results, and discussion. The last section, “Conclusions”, concludes the study.
2. Related Works
May and Baldwin [10] presented a study showing that it is important to first identify the causal factors of fatigue before deciding what measurement methods to use to detect driving fatigue. They presented two types of causal factors for driving fatigue: sleep-related fatigue and task-related fatigue. Sleep-related fatigue is caused by the circadian rhythm effect, prolonged wakefulness, and sleep deprivation. Task-related fatigue is a type of fatigue that results from the length and task demands of driving and is unrelated to any sleep-related causes. The type of fatigue presented in this paper is sleep-related fatigue, specifically caused by sleep deprivation.
Bier et al. [11] presented two fatigue measurement methods: performance-based fatigue measurement and condition-based fatigue measurement. In surveys of driving fatigue studies [12,13], most researchers applied fatigue measurements based on condition data. For example, Khunpisuth et al. [14] used fatigue measurement based on aspects of the physical condition (such as facial features, eye features, or a combination of physical features), which resulted in a very high accuracy of up to 99.59%. Another study [15] applied fatigue measurement based on physiological conditions using EEG, which resulted in a high accuracy of 97.19%. Due to its high accuracy in fatigue detection, fatigue measurement based on condition data is more popular than fatigue measurement based on performance data among driving fatigue detection studies.
There are several important points to consider when choosing a fatigue measurement method: accuracy, non-intrusiveness, suitability for any driving conditions, adaptability to any driver condition, and practicality [12,16,17]. The most popular fatigue measurement method is measuring fatigue based on the driver’s physical state [16,18], for example. This method is practical, non-intrusive, and generally produces very high accuracy, but it is not suitable for all driving conditions with regard to daytime or nighttime driving, and it cannot adapt to any driver condition related to skin color, eye color, or cloth. Another popular fatigue measurement method is measuring fatigue through physiological signals using EEG, for example [15]. This method has adaptability to any driver condition, is suitable for any driving conditions, and generally has high accuracy because it measures brain activity directly; however, it is not practical since it needs at least six electrodes placed on the scalp to measure brain signals [19].
In this paper, we chose ECG as a fatigue measurement method because it can adapt to the driver’s condition, is suitable in any driving condition, and has high accuracy if it is combined with the right processing and classification methods. The use of an ECG while driving can be intrusive if the ECG recording method uses the standard 3, 6, or 12 lead placements; however, the ECG can be non-intrusive if the driver uses a single-lead ECG device, a textile-based ECG, or a wearable ECG device, such as a smart watch. Our previous study [3] proposed a framework for driving fatigue detection using an ECG with two electrodes. With the right preprocessing of ECG data using the proposed resampling method, the AdaBoost model achieved an accuracy of 98.82% for validation and 81.81% for testing (Table 1); thus, its model performance can be increased by using the feature engineering method or extracting more features from RR interval data. As a comparison, considering the development of a driving fatigue detection framework, we reviewed a list of driving fatigue detection methods with ECG in the literature from 2018 to 2023, as shown in Table 1. Generally, recent studies over the past five years, as shown in Table 1, have predominantly utilized a binary classification approach, distinguishing between “alert” and “fatigue” states. Researchers are still actively exploring various combinations of preprocessing, feature extraction, feature selection, and classification methods to improve the accuracy of driver fatigue detection.
In Table 1, most driving fatigue detection studies applied feature selection with a filter approach to select relevant features to improve the model’s performance. For example, Kim and Shin [20] extracted 104 features using HRV analysis, weighted standard deviation, weighted mean, and dominant respiration, and applied the greedy feed forward to select 12 features out of 104 features. It filtered out the number of features by 88.46%. Its model performance resulted in an area under the curve of 95% for validation and an unknown area for testing. The majority of these studies (Table 1) that applied feature selection did not specify the method used to determine the optimal number of features and did not explore the effect of the selected features on the performance of the model. On the other hand, a study by Babeian et al. [21] extracted 52 features using the wavelet transform and proposed a feature selection algorithm along with ensemble learning. It selected 24 features, or 46.15% of the total number of features, based on a balanced classification rate. Their feature selection algorithm chose the number of selected features—24 features—with the highest balanced classification rate. Its model performance resulted in an accuracy of 92.5% for training and an unknown accuracy for testing. Babeian et al.’s approach inspired us to explore the effect of a number of selected features on the model’s performance.
Another factor that should be considered in developing a driving fatigue detection framework is the feature extraction method. Feature extraction also plays an important role in detecting driving fatigue, as it can reduce dimensionality, improve the interpretability of data, and improve the model’s performance [22]. The majority of studies (Table 1) used HRV analysis to extract data from the time domain, frequency domain, and non-linear approach. HRV analysis is still an effective feature extraction method to increase the model’s performance. For example, a study by Kundinger et al. [23] extracted 26 features from RR interval data using HRV analysis and resulted in a cross-validated accuracy of 97.37% with the random forest model, and our previous study [3] extracted 54 features from RR interval data using HRV analysis and resulted in a cross-validated accuracy of 98.82% with the AdaBoost model. Furthermore, our previous study [3] also proved that the use of HRV analysis combined with time, frequency, and a non-linear approach results in improvement in model performance than using HRV analysis with time and frequency domains alone. In short, this paper proposes an improvement in the driving fatigue framework compared to our previous study [3]. We focus on the development of the feature extraction phase using the HRV analysis method, and of the feature selection phase using the mutual information method.

Table 1.
A detailed review of studies on fatigue or drowsy driving detection using ECG from 2018 to 2023. An asterisk (*) denotes the cross-validated accuracy; a double asterisk (**) denotes the testing accuracy; and a triple asterisk (***) denotes the training accuracy.
Table 1.
A detailed review of studies on fatigue or drowsy driving detection using ECG from 2018 to 2023. An asterisk (*) denotes the cross-validated accuracy; a double asterisk (**) denotes the testing accuracy; and a triple asterisk (***) denotes the training accuracy.
| Source (Year) | Number of Subjects | Feature Extraction Method (Number of Features) | Feature Selection | Classification | Class | Accuracy |
|---|---|---|---|---|---|---|
| [24] (2018) | Simulated driving 29 subjects | HRV analysis; time domain (5), freq. domain (5), total: 10 features | Mean decrease accuracy + mean decrease Gini; 6 features selected | KNN | 2 | 75.5% * |
| [20] (2019) | Simulated driving 6 subjects | HRV analysis; weighted standard deviation, weighted mean, dominant respiration, total: 104 features | Greedy feed-forward; 12 features selected | Support Vector Machine | 2 | AUC: 95% * |
| [25] (2019) | Simulated driving 6 subjects | Recurrence plot; non-linear (3) | Convolutional neural network (CNN) | 2 | 70% ** | |
| [21] (2019) | Simulated driving 25 subjects | Wavelet transform; freq. domain (52) | Ensemble logistic regression based on a balanced classification rate value; 24 features selected | 2 | 92.5% *** | |
| [26] (2020) | Simulated driving 10 subjects | HRV analysis; time domain (14), freq. domain (3), non-linear (3), total: 20 features | One-way ANOVA; 15 features selected | Ensemble Learning | 2 | 96.6% *** |
| [23] (2020) | Simulated Driving 27 subjects | HRV analysis; time domain (13), freq. domain (10), non-linear (3), total: 26 features | Correlation-based feature subset selection; 2 features selected | Random Forest | 2 | 97.37% * |
| [27] (2020) | Simulated driving 16 subjects | Cross-correlation and convolution techniques | None | DMKL -SVM | 2 | AUC: 97.1% * |
| [28] (2021) | Real driving 86 subjects | HRV analysis; time domain (8), freq. domain (10), entropy (6), total: 24 features | Sequential forward floating selection (SFFS); 5 features selected | Random Forest | 2 | 85.4% ** |
| [3] (2023) | Simulated driving 11 subjects | HRV analysis; time domain (20), freq. domain (9), non-linear: (25), total: 54 features | None | AdaBoost | 2 | 98.82% * 81.81% ** |
| Random Forest | 2 | 97.98% * 86.36% ** | ||||
3. Materials and Methods
3.1. ECG Dataset
In this study, an electrocardiogram was utilized as the objective method for measuring driver fatigue. The dataset utilized for testing the proposed driving fatigue detection framework is taken from [29], the same dataset utilized in our previous study [3]. The dataset was created based on a sleep-related fatigue induction approach. Eleven healthy subjects (ten men and one woman) between the ages of 24 and 28 participated in the driving simulation. Each of them held a driver’s license and simulated driving for at least 30 min under the two specified driving states: alert and fatigued. Each driving state was tested on two separate days. In order to achieve the state of alert driving, drivers were given directions to sleep for at least seven hours prior to the driving simulation. In order to induce driver fatigue, the drivers were given directions to go to bed late and sleep for less than seven hours prior to the driving simulation.
Before the experiment, the subjects completed a subjective questionnaire to assess their levels of fatigue, and the results demonstrate that the sleep-deprived subjects were significantly more fatigued than the well-rested subjects. The average sleepiness scores for all subjects were 1.4 for the well-rested state and 4.1 for the sleep-deprived state (1: rarely sleepy to 5: very sleepy). All the subjects were compensated approximately $10 per hour for their participation in the simulated driving. The Institutional Review Board of the Gwangju Institute of Science and Technology approved the experiment [29].
There are three types of recorded physiological signals contained in the dataset [29]: EEG, EOG, and ECG. However, we only used the ECG data that was recorded using BioSemi ActiveTwo with a sampling rate of 512 Hz in this study. The ECG data were labeled sleep-good (SG), representing the alert state, and sleep-bad (SB), representing the fatigued state. The ECG signals were acquired using a modified lead-I with two electrodes placed in the second intercostal position, as shown in Figure 2.
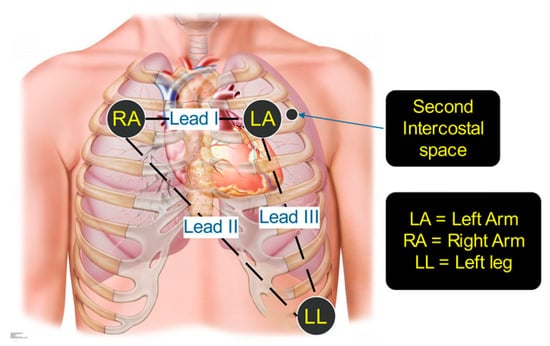
Figure 2.
Modified lead-I ECG electrode placement.
The dataset used in this study exhibits variations among the subjects, primarily encompassing age, gender, and ECG recording time; however, specific information regarding the age and gender of the individual subjects is unavailable. Figure 3 illustrates the ECG recording time (measured in minutes) for each subject in two different driving fatigue states: alert and fatigued.
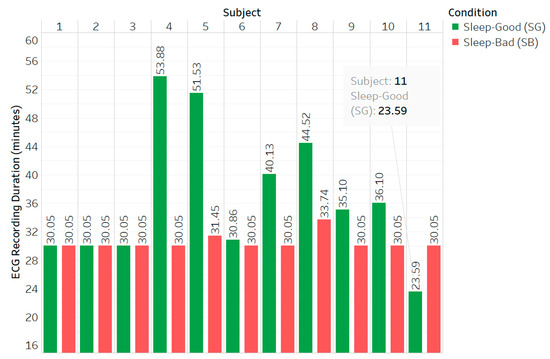
Figure 3.
ECG recording durations for each subject in two different driving conditions: sleep-good, denoting the alert state, and sleep-bad, denoting the fatigued state.
3.2. ECG Data Preprocessing
3.2.1. QRS Detection
The next phase was QRS wave detection from the ECG signals (Figure 1). Afterwards, the peak of the R wave was detected for each QRS wave. The accuracy of the detection of the QRS wave is important because it relates to the detection of the R wave and can indirectly affect the analysis of heart rate variability [30]. In this study, we chose the same QRS detection algorithm as that used in our previous study, the Pan–Tompkins algorithm [3]. The minimum sampling frequency needed for performing the Pan–Tompkins approach is 200 Hz [31], and the dataset utilized for the study fulfills this requirement. After detecting the R wave of a QRS wave, the next step was to measure the RR interval, which is the distance between two consecutive R waves in two adjacent QRS complex waves. This study uses the term NN interval instead of RR interval.
3.2.2. Data Splitting and Labeling
Figure 3 shows the different ECG recording durations for each subject under two different states. Before splitting the data, the dataset should first be balanced to prevent bias towards one class and improve model performance [32]. This study used an undersampling approach instead of a data augmentation or oversampling approach to obtain a balanced dataset, considering the originality of the data and the risk of overfitting in the classification of fatigue [33]. In Figure 3, the shortest ECG recording duration is 23.59 min, taken from the 11th subject in a sleep-good or alert state. Thus, the ECG recording durations for each subject under two different states were taken for up to 23.59 min and used as a duration reference for the balanced dataset.
In machine learning applications, data splitting is generally needed to evaluate the performance of a model. The most prevalent method of data splitting is to divide a dataset into two separate parts. The first part of the dataset used to train the model is known as the training dataset. The rest of the data, also known as the testing dataset or new data, is used to assess the predictive ability of the model. There is no standardization of the data splitting ratio between the training and testing datasets because it can vary between studies of machine learning applications. However, when splitting data, two conditions must be met: the training dataset must be sufficiently large to represent the entire dataset, and the testing dataset must be adequate to evaluate the performance of a model [34]. Most machine learning application studies use a ratio of 80% for training data and 20% for testing dataset [35].
The dataset used in this study consisted of 11 subjects under two different states. Therefore, there are two possible ways to divide the dataset into training and testing datasets: subject-dependent test and subject-independent test approaches. A subject-dependent test means that a small amount of data is taken from the dataset of each subject and labeled as the testing dataset, while a subject-independent test means that one subject is left out from all the subjects and labeled as the testing dataset. In this study, we preferred to use a subject-dependent test approach, as shown in Figure 4. There are two considerations when choosing a subject-dependent test approach. First, there have been some driving fatigue detection studies [23,28] reporting that a subject-independent test approach produces lower model performance than a subject-independent approach because the trained model does not learn the characteristics of the subject test data. Secondly, a subject-independent test approach will produce a different classification model each time the subject test is changed.
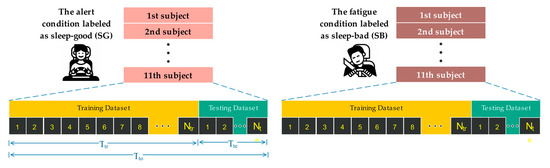
Figure 4.
The illustration of data splitting with a subject-dependent test approach and data labeling with sleep-good and sleep-bad.
Before determining the ratio of the training and testing datasets, there is something that needs to be considered: the use of the HRV analysis method at the feature extraction phase in the driving fatigue detection framework (Figure 1). The HRV analysis method [36], used to extract features from NN interval data, suggests a 5 min window of observation to analyze heart rate variability in the short-term. The duration of 5 min is the reference duration of the window for analyzing heart rate variability in this study. Thus, the duration of 5 min within the total duration of the ECG recording of each subject is the shortest duration needed for the testing dataset. The remaining ECG recording duration for each subject is determined to be training data. The ratio of the testing dataset as a percentage can be calculated as follows [3]:
where is the total ECG recording duration of each subject and is the ECG recording duration of each subject for the testing dataset. Both variables are measured in minutes. Since the total ECG recording duration reference for the balanced dataset is 23.59 min, the total ECG recording duration for each subject () was set to 23.59 min. In addition, the minimum ECG recording duration needed for a window of HRV analysis is 5 min, so the ECG recording duration of each subject for the testing dataset () is set to 5 min. By using Equation (1), the ratio of the testing dataset was found to be approximately 22%. The remaining ECG recording duration was 18.59 min for the training data, resulting in an approximate ratio of 78%. In short, the ratio of the training and testing dataset is 78% to 22% for each subject. Afterwards, all the ECG data were labeled according to the type of dataset along with subject conditions: the sleep-good label as the alert state, and the sleep-bad label as the fatigued state.
3.2.3. Data Resampling
A number of studies on driving fatigue detection (Table 1) used the resampling method with a sample called a window or epoch: for example, a 5 min window [3,23,24,28], 1 min epoch [20], a 3 min window [2], and a thirty-five-second window [21].
According to previous studies [37,38], the diversity of datasets used in the learning model impacts the model’s performance in ensemble learning. The diversity of a dataset can be increased by dividing it into smaller subsets. The resampling method can increase diversity by dividing the dataset into smaller data subsets. Our previous study [3] tested three types of resampling methods with five resampling scenarios on the driving fatigue detection framework. We concluded that resampling with the overlapping window method, specifically a resampling window duration of 300 s and an overlap window of 270 s, had the greatest impact on increasing the accuracy of the model’s performance. This study uses the same resampling method as in [3] by dividing the entire NN interval dataset into several windows, with two adjacent windows overlapping, as illustrated in Figure 5.
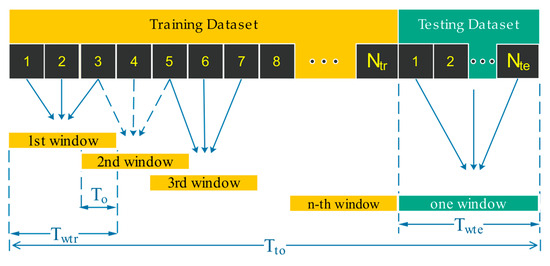
Figure 5.
The illustration of resampling with the overlapping windows method.
The number of windows in the training dataset using resampling with the overlapping window method can be calculated as follows [3]:
where is the total ECG recording duration of each subject, is the window duration for each subject for the testing dataset, is the window duration for each subject for the training dataset, and is the duration between two adjacent and overlapping windows. All the variables are measured in seconds. The total ECG recording duration of each subject () was determined to be 23.59 min, or approximately 1415 s. According to [36], the minimum ECG recording duration needed for a window of HRV analysis is 5 min, so the window duration for each subject for the training and testing datasets ( was set to 5 min, or 300 s. The overlap window duration () was set to 270 s. Referring to Equation (2), the number of windows in the training dataset () was 27, and the number of windows in the testing dataset () was 1 for each subject and each state.
3.3. Feature Extraction
There are many methods to extract features from ECG data, as stated in a previous review [39], such as HRV analysis in the time domain, the frequency domain, and non-linear approaches [36,40]; statistical features with feature-based information retrieval with a self-similarity matrix [41]; and wavelet features with the wavelet transform [42]. However, the majority of driving fatigue detection studies (Table 1) extracted features from NN interval data using HRV analysis. These studies were carried out by Huang et al. [24], Kim and Shin [20], Murugan et al. [26], Kundinger et al. [23], Persson et al. [28], and Halomoan et al. [3]. These studies showed that HRV analysis was proven to produce high-accuracy fatigue detection. In this study, we applied HRV analysis in the time domain, the frequency domain, and the non-linear approaches for feature extraction. These methods extracted 20 features in the time domain, 9 features in the frequency domain, and 29 features from the non-linear approach. The total number of features extracted was 58. All the feature extraction methods are described in detail in the following sub-sections.
3.3.1. Time Domain Approach
The use of HRV analysis in the time domain has been used in many driving fatigue detection studies, including those by Huang et al. [24], Murugan et al. [26], Kundinger et al. [23], Persson et al. [28], and Halomoan et al. [3]. Moreover, one study [43] showed that the features of SDNN, RMSSD, SDSD, pNN50, MeanNN, heart rate (HR), and CVNN are useful to analyze fatigue states. Another study [44] reported that the logarithm of RMSSD was the most useful feature for identifying fatigue. In this study, we applied statistical analysis and geometrical analysis to extract 20 features, as shown in Table 2. These twenty features were extracted using the same method as in our previous study [3].

Table 2.
Extracted features using HRV analysis in the time domain.
3.3.2. Frequency Domain Approach
There are several fatigue studies reporting that HRV analysis in the frequency domain can be used to measure fatigue. One such study [43] shows that the ratio of spectral power in the low-frequency band to spectral power in the high-frequency band, the normalized spectral power in the low-frequency band, and the normalized spectral power in the high-frequency band all change when the subject is fatigued. Another study [44] reported that HRV spectral analysis is more sensitive and informative than time domain HRV indices for monitoring fatigue status. Furthermore, the study presented in [46] reported that at least 10 features extracted from HRV analysis in the frequency domain can be used to distinguish alert and fatigued states. For these reasons, HRV analysis in the frequency domain is needed for measuring driver fatigue. In this study, we applied spectral analysis with the Welch method. We extracted nine features from the NN interval data, as shown in Table 3, using the same method as in our previous study [3].

Table 3.
Extracted features using HRV analysis in the frequency domain.
3.3.3. Non-Linear Approach
One study [47] reported that the combination of HRV analysis in the frequency domain and the non-linear approach can distinguish a person’s psychological state better than HRV analysis in the frequency domain alone. Our previous study [3] showed that using HRV analysis on non-linear approaches with Poincare plot analysis and multifractal detrended fluctuation analysis methods improved the performance of specific classification models like random forest and AdaBoost. With these methods of non-linear feature extraction added to the driving fatigue detection framework, random forest produced an increase in cross-validated accuracy of 0.33% and testing accuracy of 9.09%. AdaBoost produced an increase in cross-validated accuracy of 0.84% and testing accuracy of 9.09%. These results motivated us to extract more non-linear features from NN interval data.
In this study, we applied the Poincare plot analysis method and multifractal detrended fluctuation as in our previous study [3]. These methods extracted 25 non-linear features from NN interval data, as shown in Table 4. In addition, we proposed a method for extracting non-linear features from NN interval data that can be used to analyze the cognitive status and, thus, classify driving fatigue states. This paper proposes the use of heart rate fragmentation to extract non-linear features. It was proposed by Costa et al. [7] and has never been used or further investigated in previous driving fatigue studies (Table 1).

Table 4.
Extracted features using HRV analysis in a non-linear approach: Poincare plot analysis and multifractal detrended fluctuation.
Heart rate fragmentation is a biomarker of a form of sinoatrial instability characterized by the appearance of inflection in the RR intervals, despite the electrocardiogram showing sinus rhythm [52]. It can be used to analyze cardiac interbeat intervals in the autonomic nervous system [53]. Costa et al. [8] reported that heart rate fragmentation can be useful to monitor cognitive status. We hypothesized that heart rate fragmentation can be used to monitor driver cognitive status because previous studies [4,5,6] showed that there is an association between driver cognition, sleep loss, and driving fatigue. In addition, the dataset utilized in the proposed driving fatigue detection framework was created in a sleep-related fatigue scenario [29]. Every subject was instructed to have sleep restrictions on two separate days. To achieve an alert state prior to simulated driving, the subjects were instructed to get at least seven hours of sleep. Another day prior to the simulated driving, to induce a fatigued driving condition, the subjects were instructed to sleep less than seven hours per day. Therefore, the subjects who had had good sleep had better cognition than the subjects who had experienced sleep deprivation. This method extracted four non-linear features from the NN interval data, as shown in Table 5.

Table 5.
Extracted features using HRV analysis in a non-linear approach: heart rate fragmentation.
The total number of features extracted from the non-linear approach is 29, consisting of 7 features from the Poincare plot analysis, 18 features from the multifractal detrended fluctuation, and 4 features from the heart rate segmentation.
3.4. Feature Selection
Our previous study [3] showed that the use of non-linear feature extraction only improved the performance of certain classification models like random forest and AdaBoost, but not bagging and gradient boosting. This means one or more non-linear features were not relevant to the gradient boosting and bagging models. Such irrelevant features are referred to as redundant features, and they may represent more noise than valuable data [54]. This motivated us to use the feature selection method in the proposed driver fatigue detection (Figure 1). In Table 1, most studies applied feature selection to select the relevant features to improve the model’s performance. Each study offers the advantages of its feature selection method; however, we chose mutual information over other feature selection methods because our study used linear and non-linear feature extraction methods, and mutual information can capture both linear and non-linear relationships between variables. In addition, mutual information can measure the relevance of features to the target variable [9].
Mutual information (MI) is a measure of the dependence between two random variables and is interpreted as the amount of information that is gained about one random variable by observing the other [55]. Mutual information can be used to measure the similarity between two random variables. Two random variables with high mutual information means that they are similar, indicating a large reduction in uncertainty. Two random variables with low mutual information means that they are dissimilar, indicating a small reduction in uncertainty. Two random variables with zero mutual information are independent of each other [56]. The formula for the mutual information of two random variables, X and Y, whose joint probability distribution is defined by , can be calculated as follows [57]:
where and are the marginal probability distribution of X and Y. Mutual information is used to assess the relevance of features and targets in a dataset by calculating the mutual information between each feature and the target variable.
3.5. Hyperparameter Optimization and Classification Model
3.5.1. Hyperparameter Optimization
Before optimizing the hyperparameters, the cross-validation method needs to be applied in the proposed driving fatigue detection to reduce the possibility of high variance or bias in the performance of the learning models [58]. The k-fold cross-validation method was used on the training data after the feature extraction was completed. In this study, we chose 10-fold cross-validation by dividing the dataset into 10 parts of the same size. One part out of a total of ten parts is represented as a subset of data for validation, while the other nine parts are represented as a subset of data for training the model. As the dataset is divided into 10 parts, there are 10 possible validation iterations, resulting in 10 validation accuracy results. The average of all the validation accuracy results is called the cross-validation accuracy.
In machine learning applications, hyperparameter optimization is crucial for constructing the most effective model architecture with optimal hyperparameter configurations. Optimized hyperparameters can substantially boost model performance [59]. In this study, we chose the hyperparameter optimization algorithm with a grid search strategy, which is easy to implement and can be run in parallel. The grid search strategy is carried out by manually setting up a grid of possible values and trying out all possible combinations of the hyperparameter values during model training [59]. The hyperparameter grid values used for hyperparameter optimization are shown in Table 6.

Table 6.
The hyperparameter values for the grid search strategy.
The best model with optimized hyperparameter values yields the highest validation accuracy. The final model is later evaluated with the testing dataset.
3.5.2. Classification Model
In our previous study [3], as shown in Table 1, AdaBoost produced a high cross-validated accuracy of 98.82%, and random forest produced a high cross-validated accuracy of 97.98%. The proposed driving fatigue detection framework shown in Figure 1 uses the ensemble learning method as in our previous study [3] to classify two fatigue states. To evaluate the proposed framework, there are four ensemble learning models applied: AdaBoost, bagging, gradient boosting, and random forest. Further details regarding these four ensemble learning models can be found in [60].
4. Results and Discussion
In this paper, we propose improvements to the feature extraction phase by adding heart rate fragmentation and the feature selection phase using mutual information in the driving fatigue detection framework (Figure 1). All the results and effects of the proposed improvements to model performance are presented and discussed in this section. There are two types of lists of experiments presented: lists of experiments without feature selection and lists of experiments with feature selection. The first list consists of two experiments applied in the proposed driving fatigue detection framework (Figure 1) without feature selection: an experiment using 58 features in the proposed study and an experiment using 54 features in the previous study. Table 7 describes these experiments, which are used to evaluate the effect of 58 features with heart rate fragmentation included in the proposed study without feature selection on model performance. To conduct a more comprehensive feature analysis, we provide a description of the distribution of 58 features extracted from the training dataset in Appendix A.

Table 7.
The summary of all experiments applied on the proposed driving fatigue detection in comparison to our previous study without feature selection.
The second list of experiments is used to analyze the effect of a number of selected features using feature selection on the model’s performance. Since there is no ideal method to select the best number of features, we used Chen et al.’s approach [61] of finding the optimal number of features based on mutual information to determine the ideal number of features. The method is based on the observation of model performance and the number of selected features. The more relevant features added to the model, the higher the model’s performance. The more irrelevant features added to the model, the lower the model’s performance.
The optimal number of features will be found at a turning point. With the number of selected features denoted as , all the features denoted as , and the optimal number of features denoted as , the procedures to select a subset of features from the full feature space are described as follows:
- 1.
- Conduct a feature ranking of based on the mutual information score between the feature and the target variables. The results of all the mutual information between the feature and the target are ranked from the highest mutual information score to the lowest mutual information score. A higher mutual information score for a feature means that the feature and target variables have a dependency. Thus, the feature represents more useful information for classification [56]. The result of feature ranking is the sequence of features denoted as
- 2.
- Train the model with the number of selected features, from the biggest number of selected features to the smallest number of selected features, and assess the model with the testing dataset. In this paper, we suggest seven experiments, selecting 87.5%, 75%, 62.5%, 50%, 37.5%, 25%, and 12.5% out of all the ranked features ()
- 3.
- Plot the model performance (accuracy) against the number of selected features ( and observe the results. The optimal number of features will be found at the turning point where the highest testing accuracy of a classification model is plotted.
The seven experiments selecting 87.5%, 75%, 62.5%, 50%, 37.5%, 25%, and 12.5% of all the ranked features applied in the proposed driving fatigue detection framework (Figure 1) are further described in Table 8.

Table 8.
The summary of all experiments applied to the proposed driving fatigue detection framework with feature selection.
This section is organized into three subsections that present and discuss the results. The first subsection analyzes the effect of feature selection on model performance. The second subsection analyzes the necessity of non-linear features in the proposed driving fatigue framework. The last subsection discusses comparisons of the model’s performance in the proposed study and the previous study.
4.1. The Effect of Feature Selection on Model Performance
4.1.1. The Performance of Each Classification Model without Feature Selection
Figure 6 shows the results of the experiments in Table 7, which compares the performance of each classification model in the proposed study and the previous study without using feature selection. The difference between the proposed study and the previous study [3] is that heart rate fragmentation is one of the non-linear extraction methods applied in the proposed driving fatigue detection (Figure 1).
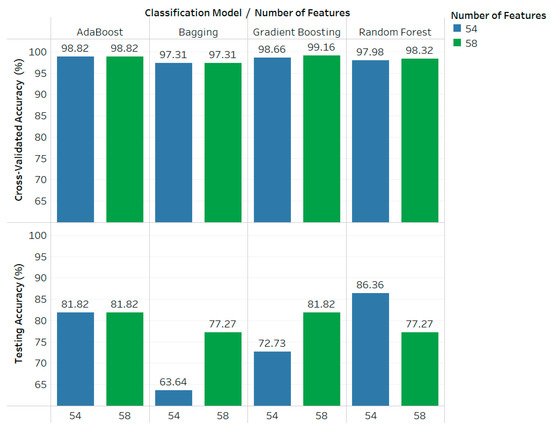
Figure 6.
The cross-validated accuracy and testing accuracy of each classification model without feature selection.
The 58 features with heart rate fragmentation included have the effect of increasing the cross-validated accuracy and testing accuracy on the gradient boosting model. The gradient boosting model resulted in an increase in cross-validated accuracy of 0.5%, from 98.66% with 54 features to 99.16% with 58 features. In addition, the gradient boosting model resulted in an increase in the testing accuracy of 9.09%, from 72.73% with 54 features to 81.82% with 58 features. The 58 features with heart rate fragmentation included do not have any effect on the AdaBoost model’s performance.
The 58 features with heart rate fragmentation included have an effect on the random forest model, resulting in an increase in cross-validated accuracy of 0.44%, from 97.88% with 54 features to 98.32% with 58 features; however, there was a decrease in testing accuracy of 9.13%, from 86.36% with 54 features to 77.27% with 58 features. This indicates that the random forest model with 58 features is prone to overfitting due to the model being too complex. The complexity of the random forest depends on the number of trees, the depth of the trees, the number of samples, and the number of features [62]. The random forest with 58 features may have higher accuracy, but it makes the model more complex, which consequently requires higher processing costs and increases the risk of overfitting.
The 58 features with heart rate fragmentation included have no effect on the performance of the bagging model in terms of cross-validated accuracy; however, it resulted in an increase in testing accuracy of 13.63%, from 63.64% with 54 features to 77.27% with 58 features.
In short, the 58 features with heart rate fragmentation included have a significant effect only on the gradient boosting model’s performance. This is possible because the gradient boosting model has the ability to capture complex variable interactions in data and perform implicit feature selection. It assigns higher importance to features that contribute more by minimizing the loss function during the boosting iterations. Consequentially, with many trees added to the model, the training error of the fitted model may be arbitrarily small, which can lead to poor generalization [63,64].
Since there are 58 features extracted from the NN interval data, the classification model becomes more complex. This increases the dimensionality. This could lead to less accurate predictions from the model [65]. This is why the feature selection method is needed in the driving fatigue detection framework.
4.1.2. The Performance of Each Classification Model with Feature Selection
The results of the feature selection experiments in Table 8 are shown in Figure 7 to find the optimal number of features using Chen et al.’s approach [61]. It shows the cross-validated accuracy and testing accuracy of each classification model with various numbers of selected feature comparisons. Table 9 provides detailed information on each classification model’s performance with various selected features.
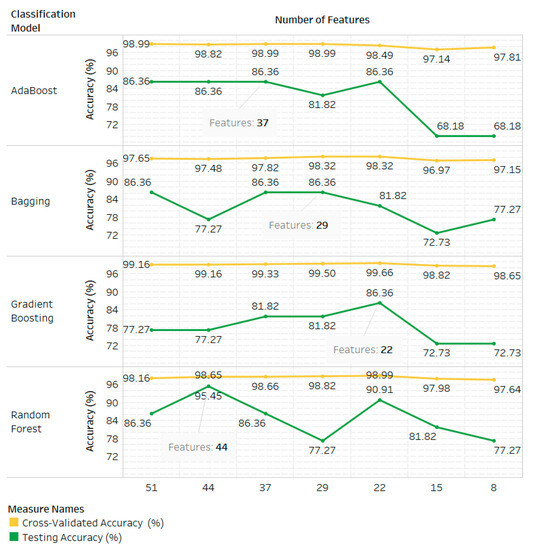
Figure 7.
The cross-validated accuracy and testing accuracy of each classification model with various numbers of selected feature comparisons.

Table 9.
Detailed information on the cross-validated accuracy and testing accuracy of each classification model without feature selection and with feature selection.
The number of selected features has a major influence on the performance of the classification model. For example, the AdaBoost model results in a testing accuracy of 68.18% and cross-validated accuracy of 97.81% for eight selected features (Table 9). Its deviation between the cross-validated accuracy and testing accuracy of 29.63% indicates that the model has high variance and fails to generalize accurately to testing data or unseen data. This happens because of insufficient information or because the selected features represent redundant features rather than useful features. This condition makes the model prone to overfitting.
In Figure 7, it is found that the highest testing accuracy of the AdaBoost model is 86.36%, plotted with four peak points of different cross-validated accuracy, so it is difficult to find the optimal number of features. We consider using the cross-validated accuracy and model complexity factors to determine the optimal number of selected features for AdaBoost. The highest cross-validated accuracy of AdaBoost is 98.99%, so the optimal number of features is 37 for AdaBoost.
The highest testing accuracy of the bagging model is 86.36%, plotted with three peak points of different cross-validated accuracy (Figure 7). With the same approach as we used for AdaBoost, the highest cross-validated accuracy of the bagging model is 98.32%, so the optimal number of features is 29.
The highest testing accuracy of the gradient boosting model is 86.36%, plotted for the number of features of 22 in Figure 7. The highest cross-validated accuracy of gradient boosting is 99.66%, plotted for the number of features of 22. The optimal number of features is therefore 22 for gradient boosting.
Of the four ensemble models, the random forest model gave the most accurate testing results of 95.45% and cross-validated accuracy of 98.65%, with an optimal number of features of 44. This shows that the combination of the heart rate fragmentation method at the feature extraction phase and the mutual information method at the feature selection phase makes a very significant contribution to the performance of the random forest model.
4.2. The Necessity of Non-Linear Features in the Proposed Driving Fatigue Framework
In Figure 7, it is clear that the random forest model results in the highest testing accuracy of 95.45% and cross-validated accuracy of 98.65% with an optimal number of features of 44. In this section, we analyze the importance of non-linear features among the 44 selected features in the proposed driving fatigue detection framework (Appendix B). Figure 8 shows the top 44 ranked features out of 58 ranked features, visualized as packed bubbles. A larger bubble represents a higher mutual information score.
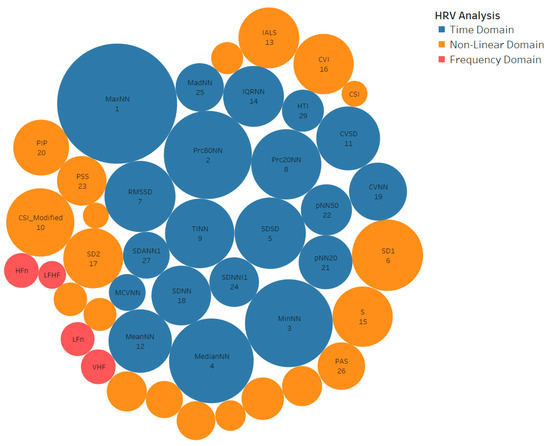
Figure 8.
The top 44 ranked features visualized as packed bubbles.
The features obtained from the HRV analysis in the time domain dominate the majority of the large bubbles in Figure 8. This means that the features extracted by the HRV analysis in the time domain dominate the high scores of mutual information. Non-linear features dominate the second-largest majority of large bubbles. This means that features extracted in the time domain have higher dependencies and are more relevant than non-linear features on the target variable; however, the non-linear features have higher dependencies than the features extracted in the frequency domain, as it can be proved that the ranks occupied by features extracted in the frequency domain are from 35 to 42, which are lower ranks (Figure 9).
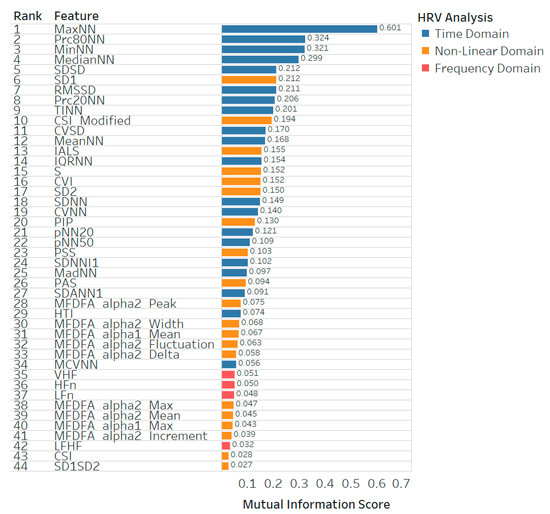
Figure 9.
The top 44 ranked features with the mutual information scores.
Based on the categorization of the HRV analysis approach shown in Table 10, 20 features extracted in the time domain are all used for classification. The number of features extracted in the non-linear approach was 20 out of 29 features. The number of features extracted in the frequency domain was 4 out of 9 features. This suggests that the features extracted in the time domain have an important role as more useful features compared to the features extracted in the non-linear and frequency domains. This also aligned with the study presented in [23], which produced a high cross-validated accuracy of 97.37% (Table 1). The study extracted 26 features, consisting of 13 features in the time domain, 10 features in the frequency domain, and 3 non-linear features. With the correlation-based feature subset selection method, the study selected two features out of 26, namely, MaxHR and MinHR. MaxHR represents MinNN, ranked no. 3, and MinHR represents MaxNN, ranked no. 1 in our proposed study (Figure 9).

Table 10.
The categorization of 58 features (without feature selection) and 44 features (with feature selection) based on the HRV analysis approach.
The performance of a classification model depends on the model complexity. The complexity of the random forest depends on the number of trees, the depth of the trees, the number of samples, and the number of features [62]. With 44 selected features, both features extracted from the non-linear approach and the time domain play the same role in the complexity of the random forest model. This is because the selected features extracted in the time domain and from the non-linear approach are the same (20 out of 44 features).
The feature rankings for the non-linear features extracted by heart rate fragmentation are as follows (Figure 9): IALS at rank 13, PIP at rank 20, PSS at rank 23, and PAS at rank 26. This suggests that the features extracted using heart rate fragmentation occupied the top 26 features in terms of importance, meaning these features are relevant to the target variable and are useful information for classification. In addition, the heart rate fragmentation method can be effectively used to classify fatigue based on cognitive status.
4.3. Comparison of the Performance of Each Classification Model in the Proposed Study and the Previous Study and Model Selection
Figure 10 shows a comparison of the performance of the four classification models in our proposed study and our previous study [3]. Overall, our proposed study can improve the performance of all classification models compared to our previous study [3] by adding a non-linear feature extraction of heart rate fragmentation in the feature extraction stage and mutual information for feature selection in the driving fatigue detection framework. For example, in our previous study [3], we reported that the AdaBoost model with 54 features produced the most optimal cross-validated accuracy of 98.82% and testing accuracy of 81.82%. In our proposed study, the AdaBoost model with 37 selected features produced a cross-validated accuracy of 98.99% and testing accuracy of 86.36%.
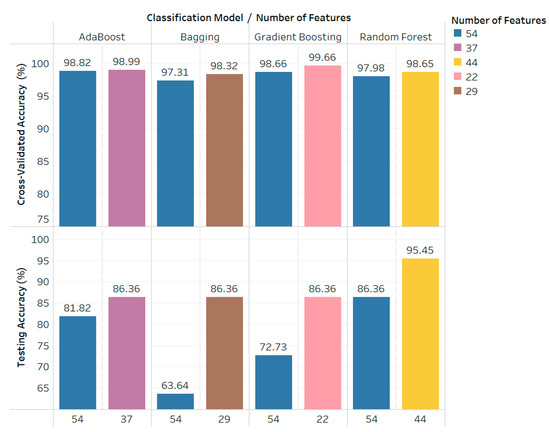
Figure 10.
Comparison of cross-validated accuracy and testing accuracy of AdaBoost, bagging, gradient boosting, and random forest in the previous study with 54 features and the proposed study.
In our previous study [3], we used cross-validation as the main parameter for model selection to estimate generalization errors in the training dataset. As a result, AdaBoost was chosen as the most optimal model of four ensemble learning models because it had the highest cross-validated accuracy at 98.82%; however, the study presented in [66] reported that cross-validation is no longer an effective estimate of generalization to select a model because the study shows empirically that the risk of overfitting increases as the model becomes larger. This is why we consider the testing accuracy along with the confusion matrix metric, which represents the true model performance, for model selection.
Figure 10 shows that the random forest model with 44 extracted features gave the highest testing accuracy of 95.45% with a cross-validated accuracy of 98.65%. In addition, the confusion matrix of the random forest model (Figure 11d) shows that it can correctly classify all of the fatigued state data and misclassify one alert state data as the fatigued state. In summary, the random forest model has the best generalization among the four ensemble learning models and was chosen as the best classification model in this proposed study.
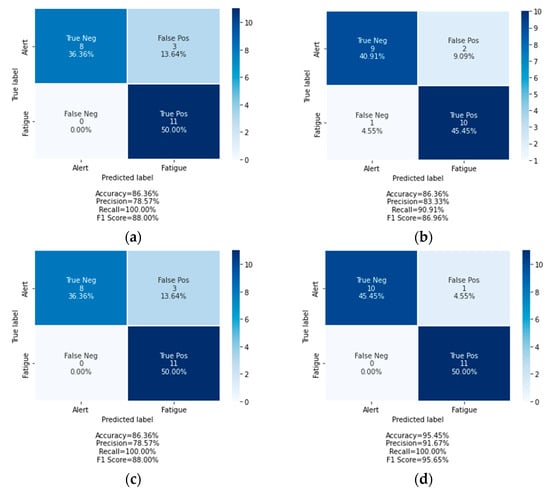
Figure 11.
Confusion matrix of the testing dataset for all classification models with selected features: (a) Adaboost with 37 selected features; (b) bagging with 29 selected features; (c) gradient boosting with 22 selected features; (d) random forest with 44 selected features.
4.4. Future Directions
The proposed driving fatigue detection framework has shown remarkable accuracy when compared to prior studies in driving fatigue detection (Table 1); however, the proposed method was tested using a simulated driving dataset with a sleep-related fatigue scenario. The performance of our proposed method requires further evaluation with a larger number of subjects in real-world driving scenarios.
When conducting real-world driving with sleep-related fatigue scenarios, driver safety must be considered carefully, as sleep deprivation can lead to microsleep episodes in drivers [67], potentially resulting in accidents. Following are some considerations that can be taken into account in real-world driving scenarios:
- Utilizing a co-driver: having a co-driver accompany the main driver during real-world driving can enhance safety by providing assistance and monitoring, thereby minimizing the risk of accidents.
- Driving in monitored and controlled environments: conducting real-world driving scenarios in a controlled and monitored environment can help mitigate accident risks.
- Objective and periodic fatigue assessment: implementing objective and periodic fatigue assessments, overseen by experts in the scientific study of sleep, is crucial to monitoring drivers’ conditions during the experiments.
Our study utilized a dataset [29] specifically designed to distinguish between two states: alertness and fatigue. The dataset focuses on fatigue related to sleep deprivation. Sleep-deprived individuals tend to be more susceptible to attention lapses, microsleep episodes, and slower reaction times [67]. These indications show decreased alertness, which substantially elevates the risk of accidents and traffic incidents. Consequently, future work needs to consider the driver’s level of alertness, which can be evaluated in a periodic fatigue assessment using subjective and/or objective measures. Subjective fatigue measurement can be conducted using questionnaires, such as the Chalder Fatigue Scale [68], while objective fatigue measurement can be assessed by specialists in the field of sleep medicine or sleep specialists. These measurements should be performed at specific intervals and periodically during driving experiments. The results of these measurements represent the driver’s degree of alertness and can serve as ground-truth data for training or validating the model. Therefore, the system can detect a driver’s fatigue at a certain level and issue warnings accordingly.
5. Conclusions
Most of the features extracted in the time domain have high mutual information scores. This means that, compared to non-linear features, time domain features are more dependent on the target variable and have more relevance to it. Nevertheless, the inclusion of non-linear features contributes to the model’s complexity and subsequently impacts the performance of a classification model. It has been demonstrated that the inclusion of four non-linear features of heart rate fragmentation in the feature extraction stage leads to improved model performance. For instance, in the bagging model without feature selection, there was a notable increase in testing accuracy of 13.63%, rising from 63.64% with 54 features to 77.27% with 58 features. Similarly, the gradient boosting model without feature selection exhibited an increase in testing accuracy of 9.09%, rising from 72.73% with 54 features to 81.82% with 58 features.
The number of selected features has a major influence on the performance of the classification model. Fewer selected features caused the model to fail to accurately generalize to testing data or unseen data because of insufficient information. More selected features made the model more complex, which can lead to overfitting. A method for finding the optimal number of features is needed to find the best model performance.
Our proposed study found that the random forest model, with an optimally selected number of 44 features, produced the most accurate results in testing at 95.45%, along with a cross-validated accuracy of 98.65%. This outcome surpasses the findings of our previous study [3], in which the AdaBoost model, employing 54 features, achieved a testing accuracy of 81.82% along with a cross-validated accuracy of 98.82%. The results from our proposed study demonstrate that the inclusion of the heart rate fragmentation method for feature extraction and the mutual information method for feature selection significantly enhances the performance of the random forest model.
Author Contributions
Conceptualization, J.H. and K.R.; methodology, J.H.; software, J.H.; validation, K.R., D.S., and T.S.G.; formal analysis, J.H.; investigation, J.H., K.R., D.S. and T.S.G.; resources, K.R. and D.S.; data curation, J.H.; writing—original draft preparation, J.H.; writing—review and editing, J.H., K.R., D.S. and T.S.G.; visualization, J.H.; supervision, K.R.; project administration, M.S.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Universitas Indonesia through the Hibah Publikasi Terindeks Internasional (PUTI) Q2 Scheme (Grant no. NKB-701/UN2.RST/HKP.05.00/2022).
Informed Consent Statement
Informed consent was obtained from all the subjects involved in the study.
Data Availability Statement
Restrictions apply to the availability of the dataset. The dataset used in this work was obtained from Deep BCI, Korea, to whom any request for data should be addressed (kyunghowon0712@gist.ac.kr).
Acknowledgments
The authors would like to thank Deep BCI, Institute of Information & Communications Technology Planning & Evaluation (IITP), Korea, for providing the dataset.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Distribution of 58 Features Extracted from the Training Dataset
This section presents the distribution of 58 features extracted from the training dataset, which comprised approximately 78% of the total NN interval data. All the NN interval data in the training dataset was resampled using the overlapping window method. As a result, there are a total of 27 windows for each subject and each state. Thus, with 11 subjects, there are 297 records for the alert state and 297 records for the fatigued state.
Figure A1, Figure A2 and Figure A3 visualize the distribution of features that are extracted using a time-domain approach. Figure A4 visualizes the distribution of features that are extracted using a frequency domain approach. Figure A5 visualizes the distribution of features that are extracted using a non-linear approach called Poincare plot analysis. Figure A6, Figure A7 and Figure A8 visualize the distribution of features that are extracted using a non-linear approach: multifractal detrended analysis. Figure A9 visualizes the distribution of features that are extracted using a non-linear approach: heart rate fragmentation. All the feature distributions are presented in a histogram plot. It consists of a series of bins (intervals) on the horizontal axis and the frequency of data points falling into each bin with bars on the vertical axis.
Figure A1.
The distribution of MeanNN, SDNN, SDSD, SDANN, SDNNI, RMSSD, and CVNN features that are extracted using a time-domain approach. The horizontal axis represents the range of feature values, while the vertical axis illustrates the number of records, providing insight into the distribution of feature values across both alert and fatigued states. Each feature has a number of records: 297 for the alert state and 297 for the fatigued state.
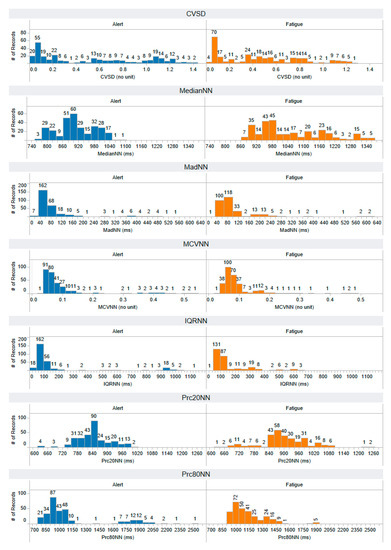
Figure A2.
The distribution of CVSD, MedianNN, MadNN, MCVNN, IQRNN, Prc20NN, and Prc80NN features that are extracted using a time-domain approach. The horizontal axis represents the range of feature values, while the vertical axis illustrates the number of records, providing insight into the distribution of feature values across both alert and fatigued states. Each feature has a number of records: 297 for the alert state and 297 for the fatigued state.
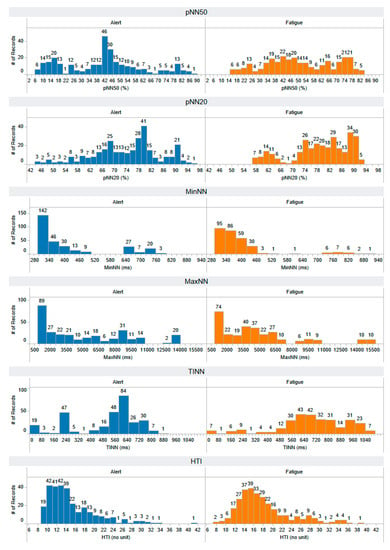
Figure A3.
The distribution of pNN50, pNN20, MinNN, MaxNN, TINN, and HTI features that are extracted using a time-domain approach. The horizontal axis represents the range of feature values, while the vertical axis illustrates the number of records, providing insight into the distribution of feature values across both alert and fatigued states. Each feature has a number of records: 297 for the alert state and 297 for the fatigued state.
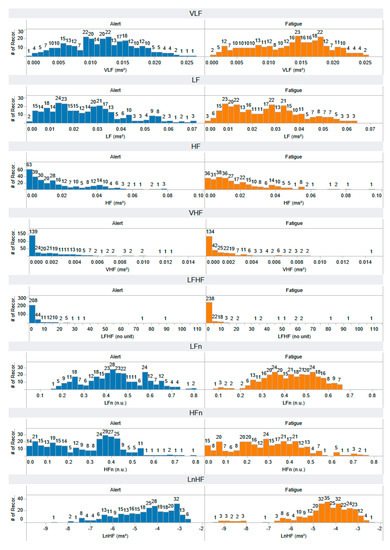
Figure A4.
The distribution of VLF, LF, HF, VHF, LFHF, LFn, HFn, and LnHF features that are extracted using a frequency-domain approach. The horizontal axis represents the range of feature values, while the vertical axis illustrates the number of records, providing insight into the distribution of feature values across both alert and fatigued states. Each feature has a number of records: 297 for the alert state and 297 for the fatigued state.
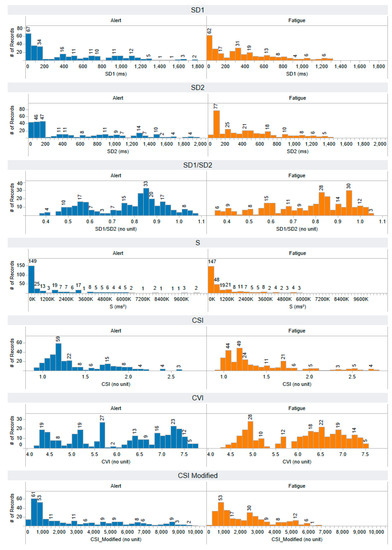
Figure A5.
The distribution of SD1, SD2, SD1/SD2, S, CSI, CVI, and modified CSI features that are extracted using a non-linear approach: Poincare plot analysis. The horizontal axis represents the range of feature values, while the vertical axis illustrates the number of records, providing insight into the distribution of feature values across both alert and fatigued states. Each feature has a number of records: 297 for the alert state and 297 for the fatigued state.
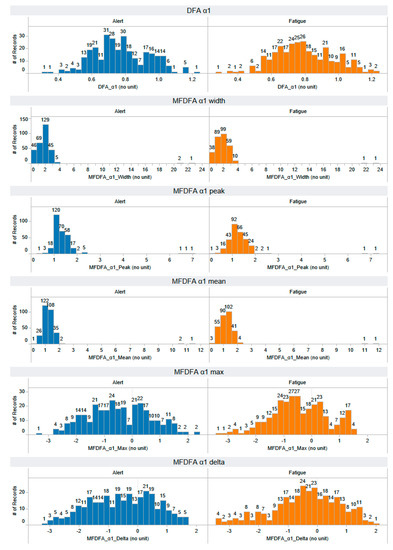
Figure A6.
The distribution of DFA α1, MDFA α1-width, MDFA α1-peak, MDFA α1-mean, MDFA α1-max, and MDFA α1-delta features that are extracted using a non-linear approach: multifractal detrended fluctuation analysis (MFDFA). The horizontal axis represents the range of feature values, while the vertical axis illustrates the number of records, providing insight into the distribution of feature values across both alert and fatigued states. Each feature has a number of records: 297 for the alert state and 297 for the fatigued state.
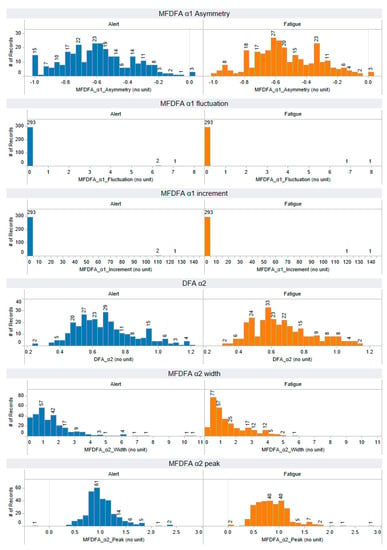
Figure A7.
The distribution of MDFA α1-asymmetry, MDFA α1-fluctuation, MDFA α1-increment, DFA α2, MDFA α2-width, and MDFA α2-peak features that are extracted using a non-linear approach: multifractal detrended fluctuation analysis (MFDFA). The horizontal axis represents the range of feature values, while the vertical axis illustrates the number of records, providing insight into the distribution of feature values across both alert and fatigues states. Each feature has a number of records: 297 for the alert state and 297 for the fatigues state.
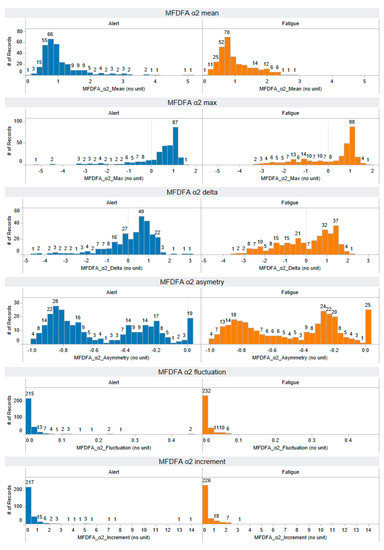
Figure A8.
The distribution of MDFA α2-mean, MDFA α2-max, MDFA α2-asymmetry, MDFA α2-fluctuation, and MDFA α2-increment features that are extracted using a non-linear approach: multifractal detrended fluctuation analysis (MFDFA). The horizontal axis represents the range of feature values, while the vertical axis illustrates the number of records, providing insight into the distribution of feature values across both alert and fatigued states. Each feature has a number of records: 297 for the alert state and 297 for the fatigued state.
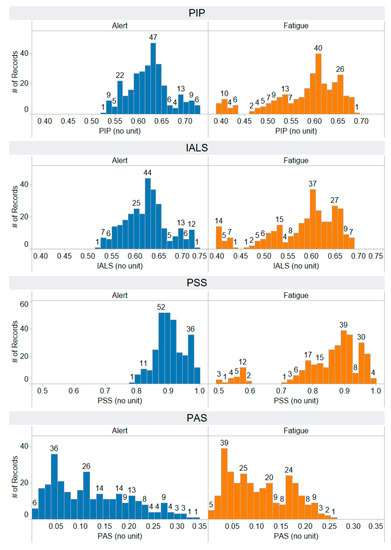
Figure A9.
The distribution of PIP, IALS, PSS, and PAS features that are extracted using a non-linear approach: heart rate fragmentation. The horizontal axis represents the range of feature values, while the vertical axis illustrates the number of records, providing insight into the distribution of feature values across both alert and fatigued states. Each feature has a number of records: 297 for the alert state and 297 for the fatigued state.
Appendix B. The Distribution of 44 Selected Features Extracted from the Testing Dataset
This section presents the distribution of 44 selected features extracted from the testing dataset, which comprised approximately 22% of the total NN interval data. The testing dataset was not resampled because there is only one window of NN interval data for each subject and each state. Thus, with 11 subjects, there are 11 records for the alert state and 11 records for the fatigued state.
Figure A10 and Figure A11 visualize the distribution of features that are extracted using a time-domain approach. Figure A12 visualizes the distribution of features that are extracted using a frequency domain approach. Figure A13 visualizes the distribution of features that are extracted using a non-linear approach called Poincare plot analysis. Figure A14 visualizes the distribution of features that are extracted using a non-linear approach: multifractal detrended analysis. Figure A15 visualizes the distribution of features that are extracted using a non-linear approach: heart rate fragmentation. All the feature distributions are presented in a histogram plot. It consists of a series of bins (intervals) on the horizontal axis and the frequency of data points falling into each bin with bars on the vertical axis.
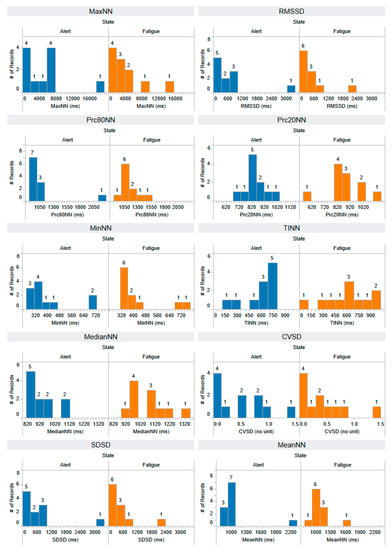
Figure A10.
The distribution of MaxNN, Prc80NN, MinNN, MedianNN, SDSD, RMSSD, Prc20NN, TINN, CVSD, and MeanNN features that are extracted using a time domain approach. The horizontal axis represents the range of feature values, while the vertical axis illustrates the number of records, providing insight into the distribution of feature values across both alert and fatigued states. Each feature has a number of records: 11 for the alert state and 11 for the fatigued state.
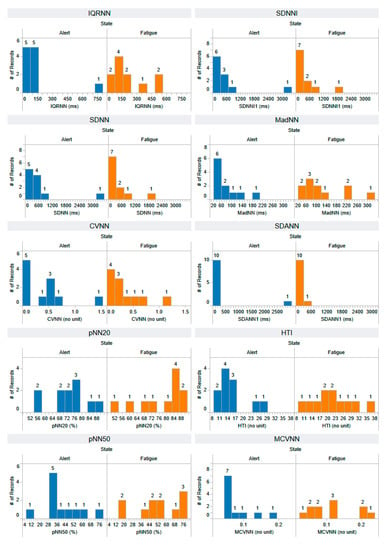
Figure A11.
The distribution of IQRNN, SDNN, CVNN, pNN20, pNN50, SDNNI, MadNN, SDANN, HTI, and MCVNN features that are extracted using a time domain approach. The horizontal axis represents the range of feature values, while the vertical axis illustrates the number of records, providing insight into the distribution of feature values across both alert and fatigued states. Each feature has a number of records: 11 for the alert state and 11 for the fatigued state.
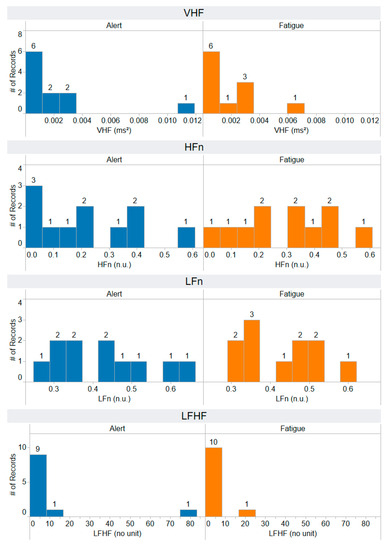
Figure A12.
The distribution of VHF, HFn, LFn, and LFHF features that are extracted using a frequency domain approach. The horizontal axis represents the range of feature values, while the vertical axis illustrates the number of records, providing insight into the distribution of feature values across both alert and fatigued states. Each feature has a number of records: 11 for the alert state and 11 for the fatigued state.
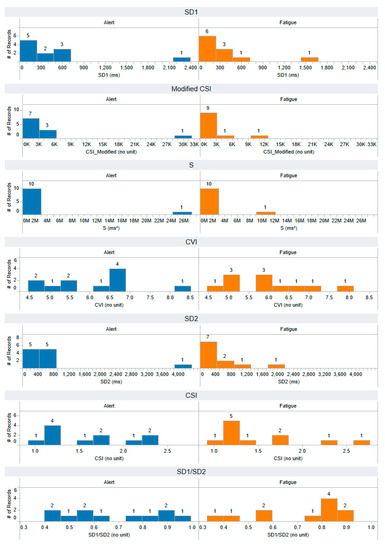
Figure A13.
The distribution of SD1, modified CSI, S, CVI, SD2, CSI, and SD1/SD2 features that are extracted using a non-linear approach: Poincare plot analysis. The horizontal axis represents the range of feature values, while the vertical axis illustrates the number of records, providing insight into the distribution of feature values across both alert and fatigued states. Each feature has a number of records: 11 for the alert state and 11 for the fatigued state.
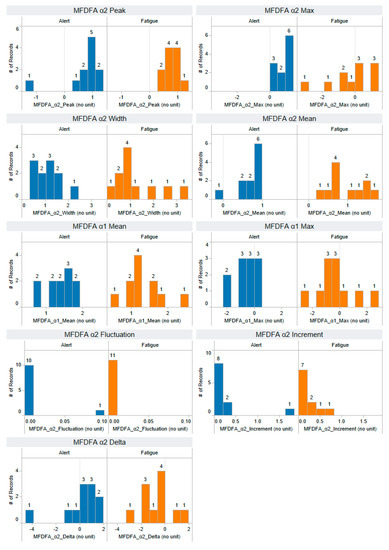
Figure A14.
The distribution of MDFA α2-peak, MDFA α2-width, MDFA α1-mean, MDFA α2-fluctuation, MDFA α2-delta, MDFA α2-max, MDFA α2-mean, MDFA α1-max, and MDFA α2-increment features that are extracted using a non-linear approach: multifractal detrended fluctuation analysis (MFDFA). The horizontal axis represents the range of feature values, while the vertical axis illustrates the number of records, providing insight into the distribution of feature values across both alert and fatigued states. Each feature has a number of records: 11 for the alert state and 11 for the fatigued state.
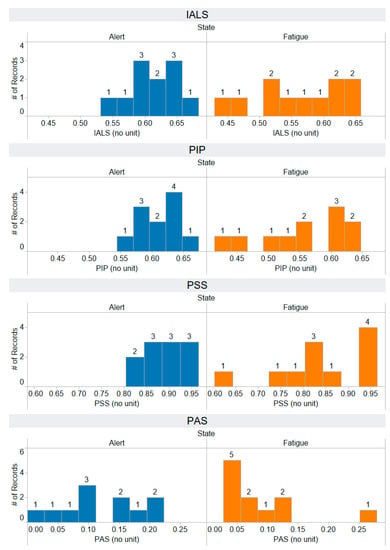
Figure A15.
The distribution of IALS, PIP, PSS, and PAS features that are extracted using a non-linear approach: heart rate fragmentation. The horizontal axis represents the range of feature values, while the vertical axis illustrates the number of records, providing insight into the distribution of feature values across both alert and fatigued states. Each feature has a number of records: 11 for the alert state and 11 for the fatigued state.
References
- Mohan, D.; Jha, A.; Chauhan, S.S. Future of road safety and SDG 3.6 goals in six Indian cities. IATSS Res. 2021, 45, 12–18. [Google Scholar] [CrossRef]
- Ani, M.F.; Kamat, S.R.; Fukumi, M.F.; Noh, N.A. A critical review on driver fatigue detection and monitoring system. Int. J. Road Saf. 2020, 1, 53–58. [Google Scholar]
- Halomoan, J.; Ramli, K.; Sudiana, D.; Gunawan, T.S.; Salman, M. A New ECG Data Processing Approach to Developing an Accurate Driving Fatigue Detection Framework with Heart Rate Variability Analysis and Ensemble Learning. Information 2023, 14, 210. [Google Scholar] [CrossRef]
- Ma, J.; Gu, J.; Jia, H.; Yao, Z.; Chang, R. The relationship between drivers’ cognitive fatigue and speed variability during monotonous daytime driving. Front. Psychol. 2018, 9, 459. [Google Scholar] [CrossRef] [PubMed]
- Ansari, S.; Du, H.; Naghdy, F.; Stirling, D. Automatic driver cognitive fatigue detection based on upper body posture variations. Expert Syst. Appl. 2022, 203, 117568. [Google Scholar] [CrossRef]
- Jackson, M.L.; Croft, R.J.; Kennedy, G.; Owens, K.; Howard, M.E. Cognitive components of simulated driving performance: Sleep loss effects and predictors. Accid. Anal. Prev. 2013, 50, 438–444. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.D.; Davis, R.B.; Goldberger, A.L. Heart rate fragmentation: A new approach to the analysis of cardiac interbeat interval dynamics. Front. Physiol. 2017, 8, 255. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.D.; Redline, S.; Hughes, T.M.; Heckbert, S.R.; Goldberger, A.L. Prediction of cognitive decline using heart rate fragmentation analysis: The multi-ethnic study of atherosclerosis. Front. Aging Neurosci. 2021, 13, 708130. [Google Scholar] [CrossRef]
- Song, L.; Langfelder, P.; Horvath, S. Comparison of co-expression measures: Mutual information, correlation, and model based indices. BMC Bioinform. 2012, 13, 328. [Google Scholar] [CrossRef]
- May, J.F.; Baldwin, C.L. Driver fatigue: The importance of identifying causal factors of fatigue when considering detection and countermeasure technologies. Transp. Res. Part F Traffic Psychol. Behav. 2009, 12, 218–224. [Google Scholar] [CrossRef]
- Bier, L.; Wolf, P.; Hilsenbek, H.; Abendroth, B. How to measure monotony-related fatigue? A systematic review of fatigue measurement methods for use on driving tests. Theor. Issues Ergon. Sci. 2020, 21, 22–55. [Google Scholar] [CrossRef]
- Rather, A.A.; Sofi, T.A.; Mukhtar, N. A Survey on Fatigue and Drowsiness Detection Techniques in Driving. In Proceedings of the 2021 International Conference on Computing, Communication, and Intelligent Systems (ICCCIS), Greater Noida, India, 19–20 February 2021; pp. 239–244. [Google Scholar]
- Ramzan, M.; Khan, H.U.; Awan, S.M.; Ismail, A.; Ilyas, M.; Mahmood, A. A survey on state-of-the-art drowsiness detection techniques. IEEE Access 2019, 7, 61904–61919. [Google Scholar] [CrossRef]
- Khunpisuth, O.; Chotchinasri, T.; Koschakosai, V.; Hnoohom, N. Driver drowsiness detection using eye-closeness detection. In Proceedings of the 2016 12th International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), Naples, Italy, 28 November–1 December 2016; pp. 661–668. [Google Scholar]
- Khare, S.K.; Bajaj, V. Entropy-Based Drowsiness Detection Using Adaptive Variational Mode Decomposition. IEEE Sens. J. 2021, 21, 6421–6428. [Google Scholar] [CrossRef]
- Albadawi, Y.; Takruri, M.; Awad, M. A review of recent developments in driver drowsiness detection systems. Sensors 2022, 22, 2069. [Google Scholar] [CrossRef] [PubMed]
- Sikander, G.; Anwar, S. Driver fatigue detection systems: A review. IEEE Trans. Intell. Transp. Syst. 2018, 20, 2339–2352. [Google Scholar] [CrossRef]
- Gao, X.-Y.; Zhang, Y.-F.; Zheng, W.-L.; Lu, B.-L. Evaluating driving fatigue detection algorithms using eye tracking glasses. In Proceedings of the 2015 7th International IEEE/EMBS Conference on Neural Engineering (NER), Montpellier, France, 22–24 April 2015; pp. 767–770. [Google Scholar]
- Soler, A.; Moctezuma, L.A.; Giraldo, E.; Molinas, M. Automated methodology for optimal selection of minimum electrode subsets for accurate EEG source estimation based on Genetic Algorithm optimization. Sci. Rep. 2022, 12, 11221. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Shin, M. Utilizing HRV-derived respiration measures for driver drowsiness detection. Electronics 2019, 8, 669. [Google Scholar] [CrossRef]
- Babaeian, M.; Amal Francis, K.; Dajani, K.; Mozumdar, M. Real-time driver drowsiness detection using wavelet transform and ensemble logistic regression. Int. J. Intell. Transp. Syst. Res. 2019, 17, 212–222. [Google Scholar] [CrossRef]
- Khalid, S.; Khalil, T.; Nasreen, S. A survey of feature selection and feature extraction techniques in machine learning. In Proceedings of the 2014 Science and Information Conference, London, UK, 27–29 August 2014; pp. 372–378. [Google Scholar]
- Kundinger, T.; Sofra, N.; Riener, A. Assessment of the potential of wrist-worn wearable sensors for driver drowsiness detection. Sensors 2020, 20, 1029. [Google Scholar] [CrossRef]
- Huang, S.; Li, J.; Zhang, P.; Zhang, W. Detection of mental fatigue state with wearable ECG devices. Int. J. Med. Inform. 2018, 119, 39–46. [Google Scholar] [CrossRef]
- Lee, H.; Lee, J.; Shin, M. Using wearable ECG/PPG sensors for driver drowsiness detection based on distinguishable pattern of recurrence plots. Electronics 2019, 8, 192. [Google Scholar] [CrossRef]
- Murugan, S.; Selvaraj, J.; Sahayadhas, A. Detection and analysis: Driver state with electrocardiogram (ECG). Phys. Eng. Sci. Med. 2020, 43, 525–537. [Google Scholar] [CrossRef] [PubMed]
- Chui, K.T.; Lytras, M.D.; Liu, R.W. A generic design of driver drowsiness and stress recognition using MOGA optimized deep MKL-SVM. Sensors 2020, 20, 1474. [Google Scholar] [CrossRef] [PubMed]
- Persson, A.; Jonasson, H.; Fredriksson, I.; Wiklund, U.; Ahlström, C. Heart rate variability for classification of alert versus sleep deprived drivers in real road driving conditions. IEEE Trans. Intell. Transp. Syst. 2020, 22, 3316–3325. [Google Scholar] [CrossRef]
- Ahn, S.; Nguyen, T.; Jang, H.; Kim, J.G.; Jun, S.C. Exploring neuro-physiological correlates of drivers’ mental fatigue caused by sleep deprivation using simultaneous EEG, ECG, and fNIRS data. Front. Hum. Neurosci. 2016, 10, 219. [Google Scholar] [CrossRef] [PubMed]
- Oweis, R.J.; Al-Tabbaa, B.O. QRS detection and heart rate variability analysis: A survey. Biomed. Sci. Eng. 2014, 2, 13–34. [Google Scholar]
- Pan, J.; Tompkins, W.J. A real-time QRS detection algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Jia, M.; Lin, T.-Y.; Song, Y.; Belongie, S. Class-balanced loss based on effective number of samples. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9268–9277. [Google Scholar]
- Ng, W.W.; Xu, S.; Zhang, J.; Tian, X.; Rong, T.; Kwong, S. Hashing-based undersampling ensemble for imbalanced pattern classification problems. IEEE Trans. Cybern. 2020, 52, 1269–1279. [Google Scholar] [CrossRef]
- Vilette, C.; Bonnell, T.; Henzi, P.; Barrett, L. Comparing dominance hierarchy methods using a data-splitting approach with real-world data. Behav. Ecol. 2020, 31, 1379–1390. [Google Scholar] [CrossRef]
- Meng, Z.; McCreadie, R.; Macdonald, C.; Ounis, I. Exploring data splitting strategies for the evaluation of recommendation models. In Proceedings of the Fourteenth ACM Conference on Recommender Systems, Virtual Event, Brazil, 22–26 September 2020; pp. 681–686. [Google Scholar]
- Malik, M. Heart rate variability: Standards of measurement, physiological interpretation, and clinical use: Task force of the European Society of Cardiology and the North American Society for Pacing and Electrophysiology. Ann. Noninvasive Electrocardiol. 1996, 1, 151–181. [Google Scholar] [CrossRef]
- Zhou, Z.-H. Ensemble learning. In Machine Learning; Springer: Berlin/Heidelberg, Germany, 2021; pp. 181–210. [Google Scholar]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wires Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Gupta, V.; Mittal, M.; Mittal, V.; Saxena, N.K. A critical review of feature extraction techniques for ECG signal analysis. J. Inst. Eng. Ser. B 2021, 102, 1049–1060. [Google Scholar] [CrossRef]
- Shaffer, F.; Ginsberg, J.P. An overview of heart rate variability metrics and norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, J.; Liu, H.; Folgado, D.; Belo, D.; Schultz, T.; Gamboa, H. Feature-based information retrieval of multimodal biosignals with a self-similarity matrix: Focus on automatic segmentation. Biosensors 2022, 12, 1182. [Google Scholar] [CrossRef] [PubMed]
- Khan, T.T.; Sultana, N.; Reza, R.B.; Mostafa, R. ECG feature extraction in temporal domain and detection of various heart conditions. In Proceedings of the 2015 International Conference on Electrical Engineering and Information Communication Technology (ICEEICT), Savar, Bangladesh, 21–23 May 2015; pp. 1–6. [Google Scholar]
- Chen, S.; Xu, K.; Zheng, X.; Li, J.; Fan, B.; Yao, X.; Li, Z. Linear and nonlinear analyses of normal and fatigue heart rate variability signals for miners in high-altitude and cold areas. Comput. Methods Programs Biomed. 2020, 196, 105667. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, L.; Regnard, J.; Millet, G.P. Monitoring fatigue status with HRV measures in elite athletes: An avenue beyond RMSSD? Front. Physiol. 2015, 6, 343. [Google Scholar] [CrossRef] [PubMed]
- Makowski, D.; Pham, T.; Lau, Z.J.; Brammer, J.C.; Lespinasse, F.; Pham, H.; Schölzel, C.; Chen, S. NeuroKit2: A Python toolbox for neurophysiological signal processing. Behav. Res. Methods 2021, 53, 1689–1696. [Google Scholar] [CrossRef] [PubMed]
- Zeng, C.; Wang, W.; Chen, C.; Zhang, C.; Cheng, B. Sex differences in time-domain and frequency-domain heart rate variability measures of fatigued drivers. Int. J. Environ. Res. Public Health 2020, 17, 8499. [Google Scholar] [CrossRef]
- Fell, J.; Röschke, J.; Mann, K.; Schäffner, C. Discrimination of sleep stages: A comparison between spectral and nonlinear EEG measures. Electroencephalogr. Clin. Neurophysiol. 1996, 98, 401–410. [Google Scholar] [CrossRef]
- Tulppo, M.P.; Makikallio, T.H.; Takala, T.; Seppanen, T.; Huikuri, H.V. Quantitative beat-to-beat analysis of heart rate dynamics during exercise. Am. J. Physiol. Heart Circ. Physiol. 1996, 271, H244–H252. [Google Scholar] [CrossRef]
- Jeppesen, J.; Beniczky, S.; Johansen, P.; Sidenius, P.; Fuglsang-Frederiksen, A. Detection of epileptic seizures with a modified heart rate variability algorithm based on Lorenz plot. Seizure 2015, 24, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Ihlen, E.A. Introduction to multifractal detrended fluctuation analysis in Matlab. Front. Physiol. 2012, 3, 141. [Google Scholar] [CrossRef] [PubMed]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Hayano, J.; Kisohara, M.; Ueda, N.; Yuda, E. Impact of heart rate fragmentation on the assessment of heart rate variability. Appl. Sci. 2020, 10, 3314. [Google Scholar] [CrossRef]
- da Silva, T.M.; Silva, C.A.A.; Salgado, H.C.; Fazan, R., Jr.; Silva, L.E.V. The role of the autonomic nervous system in the patterns of heart rate fragmentation. Biomed. Signal Process. Control 2021, 67, 102526. [Google Scholar] [CrossRef]
- Kotsiantis, S. Feature selection for machine learning classification problems: A recent overview. Artif. Intell. Rev. 2011, 42, 157–176. [Google Scholar] [CrossRef]
- Learned-Miller, E.G. Entropy and Mutual Information; Department of Computer Science, University of Massachusetts: Amherst, MA, USA, 2013; Volume 4. [Google Scholar]
- Latham, P.E.; Roudi, Y. Mutual information. Scholarpedia 2009, 4, 1658. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Xu, Y.; Goodacre, R. On splitting training and validation set: A comparative study of cross-validation, bootstrap and systematic sampling for estimating the generalization performance of supervised learning. J. Anal. Test. 2018, 2, 249–262. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- González, S.; García, S.; Del Ser, J.; Rokach, L.; Herrera, F. A practical tutorial on bagging and boosting based ensembles for machine learning: Algorithms, software tools, performance study, practical perspectives and opportunities. Inf. Fusion 2020, 64, 205–237. [Google Scholar] [CrossRef]
- Chen, P.; Wilbik, A.; Van Loon, S.; Boer, A.-K.; Kaymak, U. Finding the optimal number of features based on mutual information. In Proceedings of the Advances in Fuzzy Logic and Technology 2017, EUSFLAT-2017–The 10th Conference of the European Society for Fuzzy Logic and Technology, Warsaw, Poland, 11–15 September 2017; Volume 1, pp. 477–486. [Google Scholar]
- Verikas, A.; Gelzinis, A.; Bacauskiene, M. Mining data with random forests: A survey and results of new tests. Pattern Recognit. 2011, 44, 330–349. [Google Scholar] [CrossRef]
- Zhang, Y.; Haghani, A. A gradient boosting method to improve travel time prediction. Transp. Res. Part C Emerg. Technol. 2015, 58, 308–324. [Google Scholar] [CrossRef]
- Upadhyay, D.; Manero, J.; Zaman, M.; Sampalli, S. Gradient boosting feature selection with machine learning classifiers for intrusion detection on power grids. IEEE Trans. Netw. Serv. Manag. 2020, 18, 1104–1116. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to feature extraction. In Feature Extraction: Foundations and Applications; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–25. [Google Scholar]
- Rao, R.B.; Fung, G.; Rosales, R. On the dangers of cross-validation. An experimental evaluation. In Proceedings of the 2008 SIAM International Conference on Data Mining, Atlanta, GA, USA, 24–26 April 2008; pp. 588–596. [Google Scholar]
- Eoh, H.J.; Chung, M.K.; Kim, S.-H. Electroencephalographic study of drowsiness in simulated driving with sleep deprivation. Int. J. Ind. Ergon. 2005, 35, 307–320. [Google Scholar] [CrossRef]
- Jackson, C. The Chalder fatigue scale (CFQ 11). Occup. Med. 2015, 65, 86. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).