Can Triplet Loss Be Used for Multi-Label Few-Shot Classification? A Case Study
Abstract
:1. Introduction
2. Relevant Works
3. Dataset
3.1. Multi-Labeled Dataset
3.2. Binary Dataset: Accounting Cases
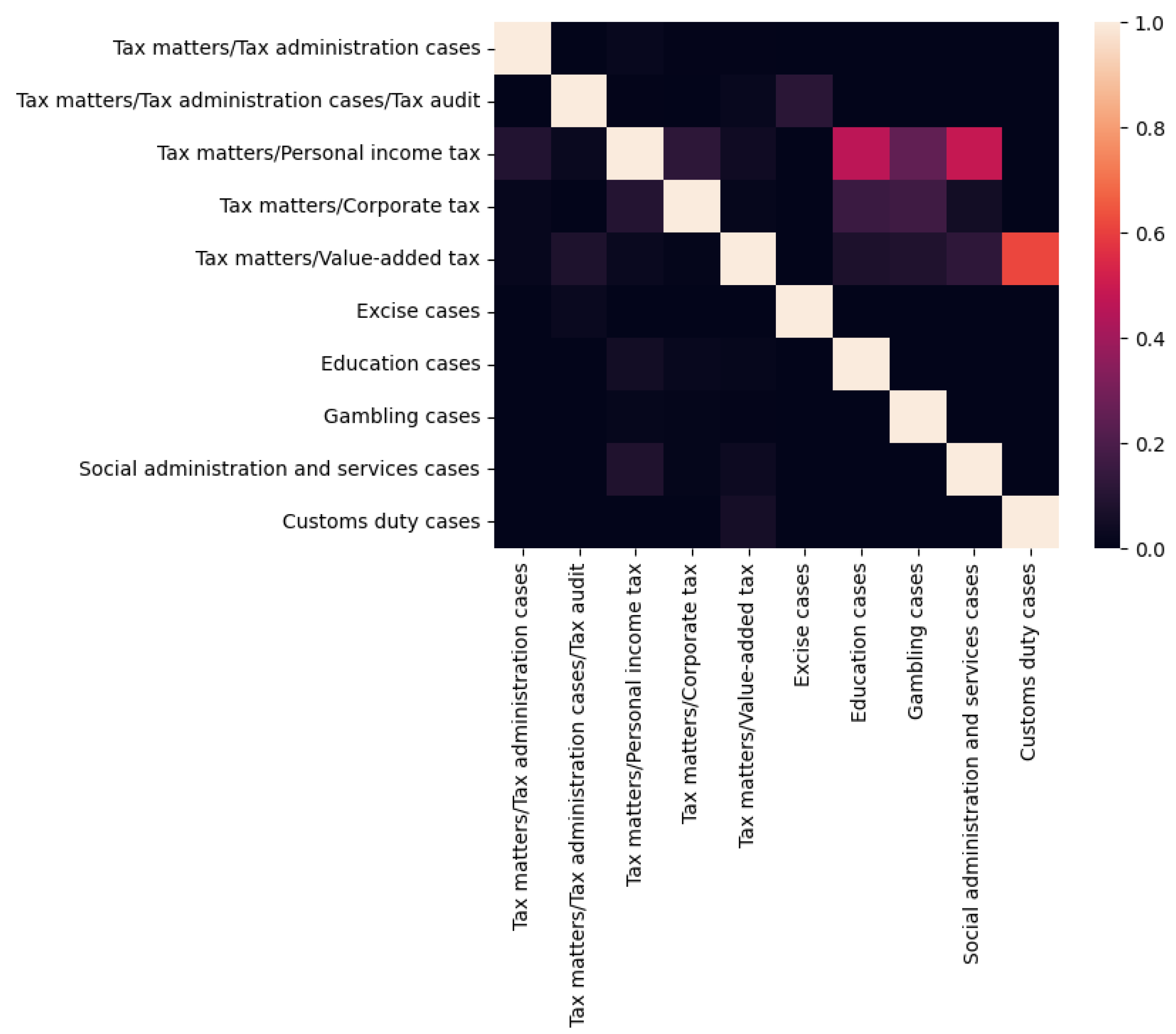
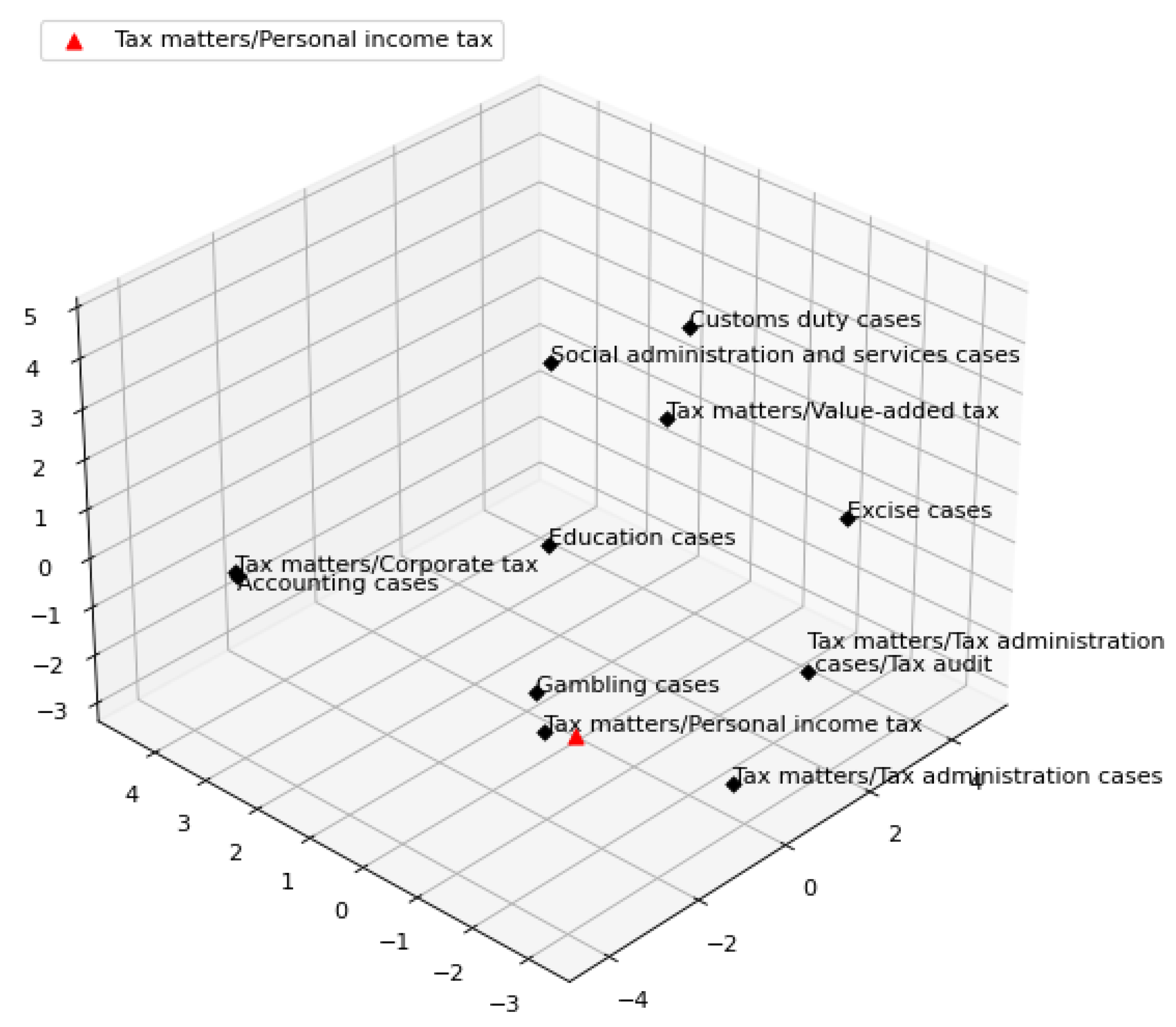
3.3. Overlapping of Different Categories
4. Categorization Approaches
4.1. Classical Approach
4.2. Few-Shot Learning
4.2.1. Siamese Architectures
4.2.2. Triplet Loss
4.2.3. Triplet Sampling
4.2.4. Training
5. Experiments
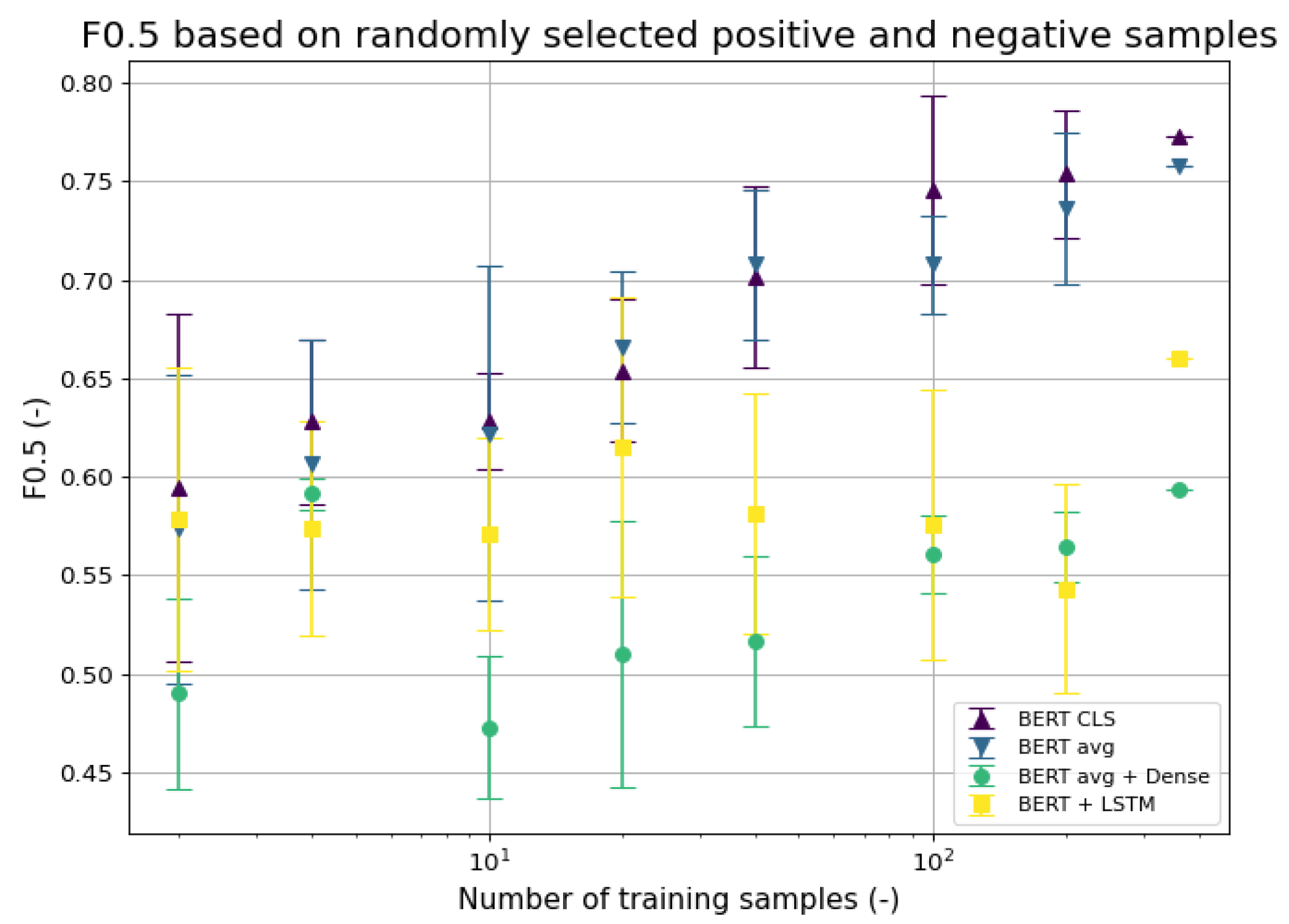
5.1. Few-Shot Binary Classification
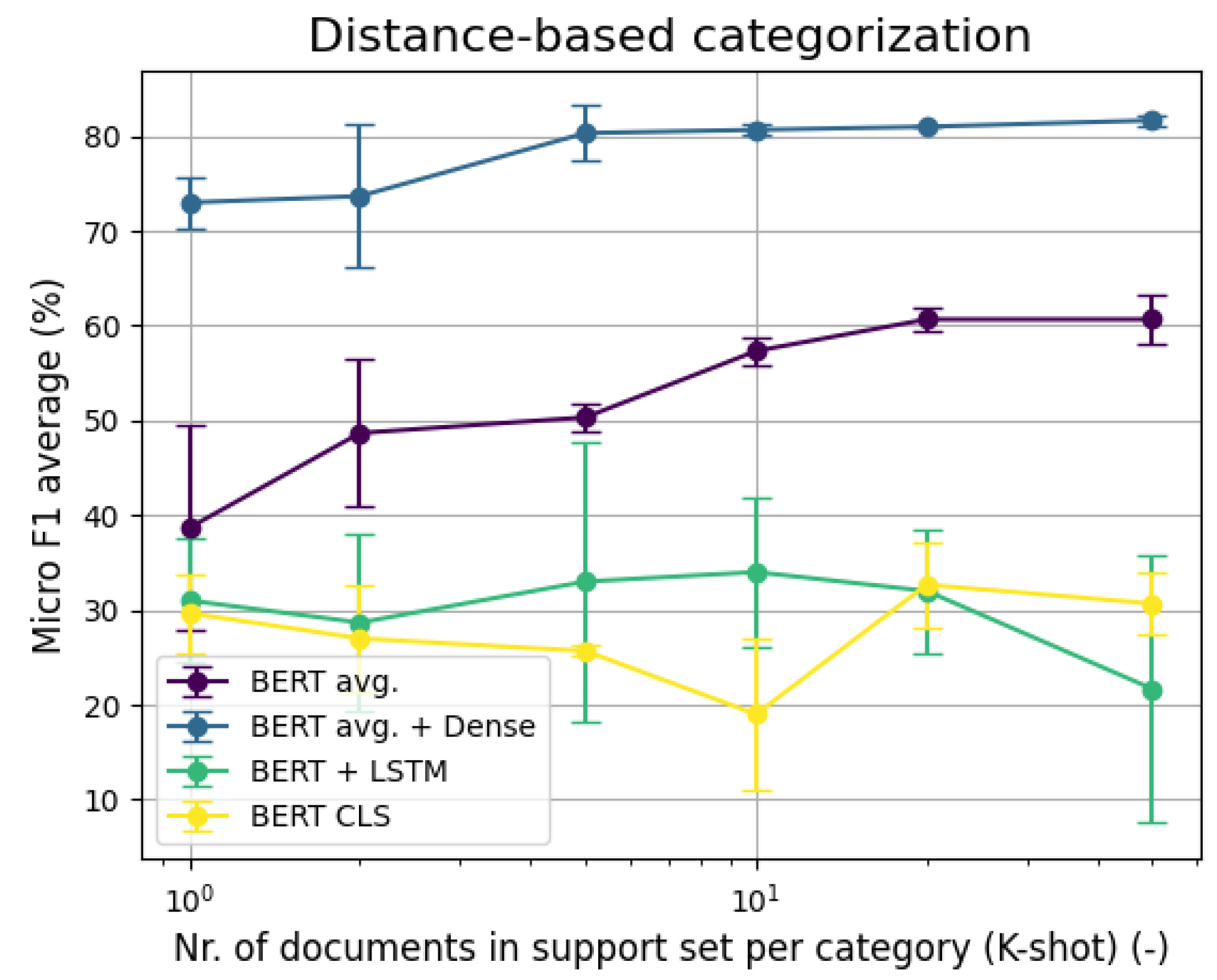
5.2. Few Shot Multi-Label Classification
6. Results and Discussion
6.1. Few-Shot Binary Classification
6.2. Few-Shot Multi-Label Classification
6.3. Comparison with Classical Classifiers
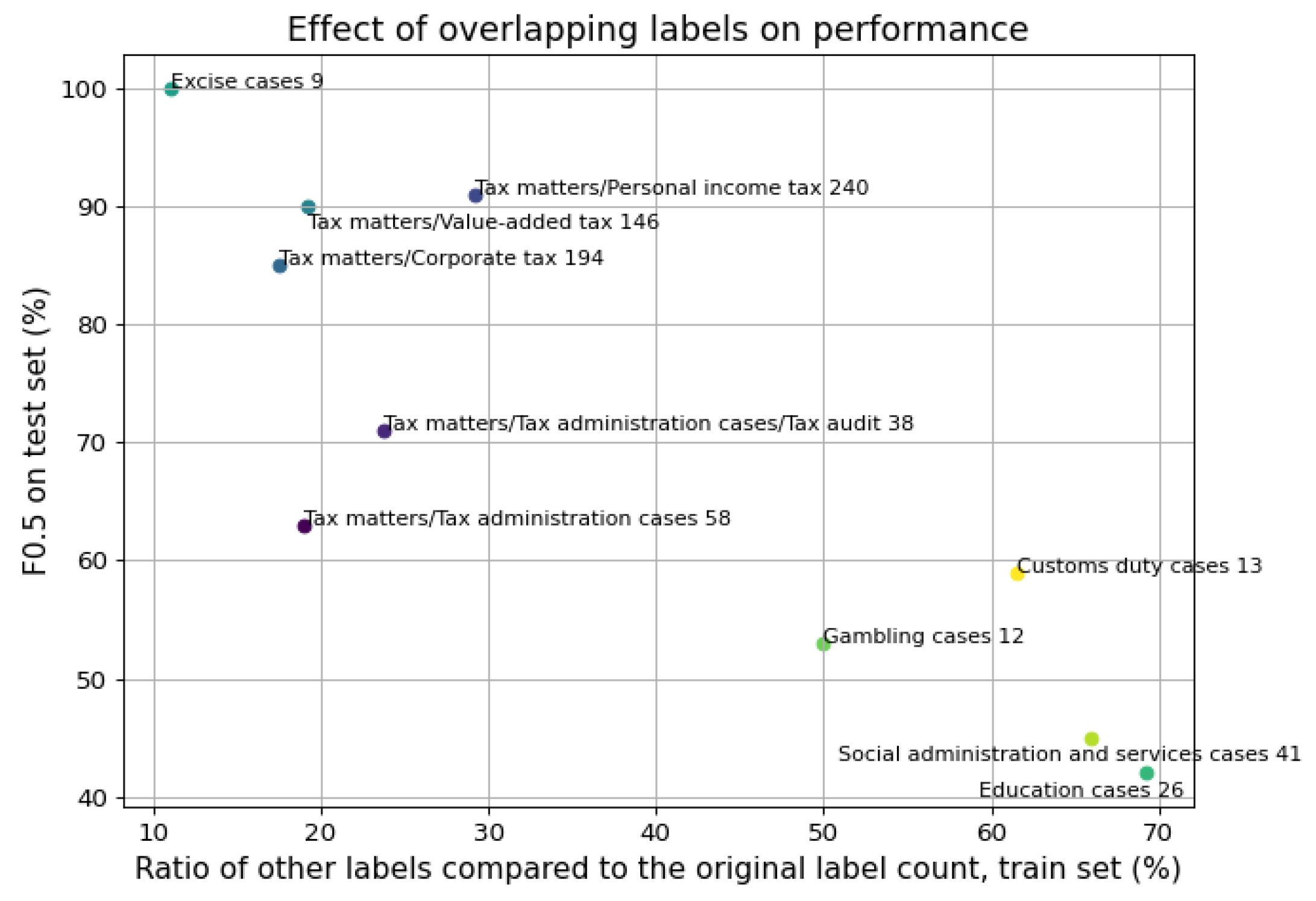
6.4. Effect of Overlapping Labels on Triplet-Trained Siamese Networks for Multi-Label Classification
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Benyus, J.M. Biomimicry: Innovation Inspired by Nature; Morrow: New York, NY, USA, 1997. [Google Scholar]
- Müller, B.; Reinhardt, J.; Strickland, M.T. Neural Networks: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Fei-Fei, L.; Fergus, R.; Perona, P. One-shot learning of object categories. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 594–611. [Google Scholar] [CrossRef]
- Fink, M. Object classification from a single example utilizing class relevance metrics. Adv. Neural Inf. Process. Syst. 2004, 17, 449–456. [Google Scholar]
- Wang, Y.; Yao, Q.; Kwok, J.T.; Ni, L.M. Generalizing from a few examples: A survey on few-shot learning. Acm Comput. Surv. 2020, 53, 1–34. [Google Scholar] [CrossRef]
- Wang, H.; Xu, C.; McAuley, J. Automatic multi-label prompting: Simple and interpretable few-shot classification. arXiv 2022, arXiv:2204.06305. [Google Scholar]
- Sung, F.; Yang, Y.; Zhang, L.; Xiang, T.; Torr, P.H.; Hospedales, T.M. Learning to compare: Relation network for few-shot learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1199–1208. [Google Scholar]
- Garcia, V.; Bruna, J. Few-shot learning with graph neural networks. arXiv 2017, arXiv:1711.04043. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. Adv. Neural Inf. Process. Syst. 2017, 30, 4077–4087. [Google Scholar]
- Yan, G.; Li, Y.; Zhang, S.; Chen, Z. Data augmentation for deep learning of judgment documents. In Proceedings of the Intelligence Science and Big Data Engineering, Big Data and Machine Learning: 9th International Conference, IScIDE 2019, Nanjing, China, 17–20 October 2019; Proceedings, Part II 9. Springer: Berlin/Heidelberg, Germany, 2019; pp. 232–242. [Google Scholar]
- Csányi, G.; Orosz, T. Comparison of data augmentation methods for legal document classification. Acta Tech. Jaurinensis 2022, 15, 15–21. [Google Scholar] [CrossRef]
- OpenAI. GPT-4 Technical Report. arXiv 2023, arXiv:2303.08774.
- Chowdhery, A.; Narang, S.; Devlin, J.; Bosma, M.; Mishra, G.; Roberts, A.; Barham, P.; Chung, H.W.; Sutton, C.; Gehrmann, S.; et al. Palm: Scaling language modeling with pathways. arXiv 2022, arXiv:2204.02311. [Google Scholar]
- Touvron, H.; Lavril, T.; Izacard, G.; Martinet, X.; Lachaux, M.A.; Lacroix, T.; Rozière, B.; Goyal, N.; Hambro, E.; Azhar, F.; et al. Llama: Open and efficient foundation language models. arXiv 2023, arXiv:2302.13971. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Wei, J.; Bosma, M.; Zhao, V.Y.; Guu, K.; Yu, A.W.; Lester, B.; Du, N.; Dai, A.M.; Le, Q.V. Finetuned language models are zero-shot learners. arXiv 2021, arXiv:2109.01652. [Google Scholar]
- Ahmadian, A.; Dash, S.; Chen, H.; Venkitesh, B.; Gou, S.; Blunsom, P.; Üstün, A.; Hooker, S. Intriguing Properties of Quantization at Scale. arXiv 2023, arXiv:2305.19268. [Google Scholar]
- Chopra, S.; Hadsell, R.; LeCun, Y. Learning a similarity metric discriminatively, with application to face verification. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–26 June 2005; Volumne 1, pp. 539–546. [Google Scholar]
- Chicco, D. Siamese neural networks: An overview. In Artificial Neural Networks; Springer Nature: Berlin/Heidelberg, Germany, 2021; pp. 73–94. [Google Scholar]
- Weinberger, K.Q.; Saul, L.K. Distance metric learning for large margin nearest neighbor classification. J. Mach. Learn. Res. 2009, 10, 207–244. [Google Scholar]
- Schroff, F.; Kalenichenko, D.; Philbin, J. Facenet: A unified embedding for face recognition and clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 815–823. [Google Scholar]
- Cheng, K.H.; Chou, S.Y.; Yang, Y.H. Multi-label few-shot learning for sound event recognition. In Proceedings of the 2019 IEEE 21st International Workshop on Multimedia Signal Processing (MMSP), Kuala Lumpur, Malaysia, 27–29 September 2019; pp. 1–5. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Simon, C.; Koniusz, P.; Harandi, M. Meta-learning for multi-label few-shot classification. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 3951–3960. [Google Scholar]
- Rios, A.; Kavuluru, R. Few-shot and zero-shot multi-label learning for structured label spaces. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Conference on Empirical Methods in Natural Language Processing; NIH Public Access: Brussels, Belgium, 2018; Volume 2018, p. 3132. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Chalkidis, I.; Fergadiotis, M.; Malakasiotis, P.; Aletras, N.; Androutsopoulos, I. Extreme multi-label legal text classification: A case study in EU legislation. arXiv 2019, arXiv:1905.10892. [Google Scholar]
- Chalkidis, I.; Fergadiotis, M.; Malakasiotis, P.; Androutsopoulos, I. Large-scale multi-label text classification on EU legislation. arXiv 2019, arXiv:1906.02192. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Sumbul, G.; Ravanbakhsh, M.; Demir, B. Informative and representative triplet selection for multilabel remote sensing image retrieval. IEEE Trans. Geosci. Remote. Sens. 2021, 60, 1–11. [Google Scholar] [CrossRef]
- Biswas, S.; Gall, J. Multiple Instance Triplet Loss for Weakly Supervised Multi-Label Action Localisation of Interacting Persons. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 2159–2167. [Google Scholar]
- Melsbach, J.; Stahlmann, S.; Hirschmeier, S.; Schoder, D. Triplet transformer network for multi-label document classification. In Proceedings of the 22nd ACM Symposium on Document Engineering, San Jose, CA, USA, 20–23 September 2022; pp. 1–4. [Google Scholar]
- Nemeskey, D.M. Introducing huBERT. In Proceedings of the XVII. Magyar Számítógépes Nyelvészeti Konferencia (MSZNY2021), Szeged, Hungary, 28–29 January 2021; pp. 3–14. [Google Scholar]
- Csányi, G.M.; Vági, R.; Nagy, D.; Üveges, I.; Vadász, J.P.; Megyeri, A.; Orosz, T. Building a Production-Ready Multi-Label Classifier for Legal Documents with Digital-Twin-Distiller. Appl. Sci. 2022, 12, 1470. [Google Scholar] [CrossRef]
- Ghamrawi, N.; McCallum, A. Collective multi-label classification. In Proceedings of the 14th ACM International Conference on Information and Knowledge Management, Bremen, Germany, 31 October–5 November 2005; pp. 195–200. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Orosz, T.; Vági, R.; Csányi, G.M.; Nagy, D.; Üveges, I.; Vadász, J.P.; Megyeri, A. Evaluating Human versus Machine Learning Performance in a LegalTech Problem. Appl. Sci. 2021, 12, 297. [Google Scholar] [CrossRef]
- Ranaldi, L.; Ruzzetti, E.S.; Zanzotto, F.M. PreCog: Exploring the Relation between Memorization and Performance in Pre-trained Language Models. arXiv 2023, arXiv:2305.04673. [Google Scholar]



| Avg. | Avg. Coverage by BERT [%] | |
|---|---|---|
| Document character | 2955.96 | - |
| Document token | 613.95 | 85.12 |
| Sentence character | 253.68 | - |
| Sentence token | 53.42 | 99.95 |
| Multi-Labeled Dataset | Training Set | Test Set | |
|---|---|---|---|
| Count | 1084 | 675 | 409 |
| Avg. label per document | 1.149 | 1.151 | 1.144 |
| Label | Train Count | Test Count |
|---|---|---|
| Tax matters/Tax administration cases | 58 | 12 |
| Tax matters/Tax administration cases/ Tax audit | 38 | 11 |
| Tax matters/Personal income tax | 240 | 149 |
| Tax matters/Corporate tax | 194 | 103 |
| Tax matters/Value-added tax | 146 | 120 |
| Excise cases | 9 | 3 |
| Education cases | 26 | 4 |
| Gambling cases | 12 | 3 |
| Social administration and services cases | 41 | 10 |
| Customs duty cases | 13 | 6 |
| Count | Ratio | |
|---|---|---|
| Accounting cases | 272 | 60.31% |
| Non Accounting cases | 179 | 39.69% |
| Sum | 451 | 100% |
| Anchor | Positive | Negative |
|---|---|---|
| A, C | A | B, C |
| A | A, C | B, C |
| Approach | Micro | Macro | Accounting | Document Level | ||
|---|---|---|---|---|---|---|
| Cases | Complete Match | Partly Match | No Match | |||
| Classical | 88.66% | 76.62% | 53.19% | 77.49% | 16.49% | 6.02% |
| Few-shot | 81.67% | 68.33% | 59.00% | 78.73% | 6.93% | 14.35% |
| Precision | Recall | Train Count | Test Count | Training Set Overlap | Test Set Overlap | ||
|---|---|---|---|---|---|---|---|
| Tax matters/Tax administration cases | 0.62 | 0.67 | 0.63 | 58 | 12 | 0.19 | 0.25 |
| Tax matters/Tax administration cases/Tax audit | 0.83 | 0.45 | 0.71 | 38 | 11 | 0.24 | 0.36 |
| Tax matters/Personal income tax | 0.94 | 0.82 | 0.91 | 240 | 149 | 0.29 | 0.15 |
| Tax matters/Corporate Tax | 0.83 | 0.92 | 0.85 | 194 | 103 | 0.18 | 0.23 |
| Tax matters/Value-added tax | 0.91 | 0.88 | 0.90 | 146 | 120 | 0.19 | 0.18 |
| Excise cases | 1.00 | 1.00 | 1.00 | 9 | 3 | 0.11 | 0.00 |
| Education cases | 0.38 | 0.75 | 0.42 | 26 | 4 | 0.69 | 1.20 |
| Gambling cases | 0.50 | 0.67 | 0.53 | 12 | 3 | 0.50 | 0.33 |
| Social administration and services cases | 0.41 | 0.70 | 0.45 | 41 | 10 | 0.66 | 0.50 |
| Accounting cases | 0.62 | 0.66 | 0.63 | N/A | 47 | N/A | 0.74 |
| Customs duty cases | 0.57 | 0.67 | 0.59 | 13 | 6 | 0.62 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Csányi, G.M.; Vági, R.; Megyeri, A.; Fülöp , A.; Nagy, D.; Vadász, J.P.; Üveges, I. Can Triplet Loss Be Used for Multi-Label Few-Shot Classification? A Case Study. Information 2023, 14, 520. https://doi.org/10.3390/info14100520
Csányi GM, Vági R, Megyeri A, Fülöp A, Nagy D, Vadász JP, Üveges I. Can Triplet Loss Be Used for Multi-Label Few-Shot Classification? A Case Study. Information. 2023; 14(10):520. https://doi.org/10.3390/info14100520
Chicago/Turabian StyleCsányi, Gergely Márk, Renátó Vági, Andrea Megyeri, Anna Fülöp , Dániel Nagy, János Pál Vadász, and István Üveges. 2023. "Can Triplet Loss Be Used for Multi-Label Few-Shot Classification? A Case Study" Information 14, no. 10: 520. https://doi.org/10.3390/info14100520
APA StyleCsányi, G. M., Vági, R., Megyeri, A., Fülöp , A., Nagy, D., Vadász, J. P., & Üveges, I. (2023). Can Triplet Loss Be Used for Multi-Label Few-Shot Classification? A Case Study. Information, 14(10), 520. https://doi.org/10.3390/info14100520









