Abstract
Educational data mining is capable of producing useful data-driven applications (e.g., early warning systems in schools or the prediction of students’ academic achievement) based on predictive models. However, the class imbalance problem in educational datasets could hamper the accuracy of predictive models as many of these models are designed on the assumption that the predicted class is balanced. Although previous studies proposed several methods to deal with the imbalanced class problem, most of them focused on the technical details of how to improve each technique, while only a few focused on the application aspect, especially for the application of data with different imbalance ratios. In this study, we compared several sampling techniques to handle the different ratios of the class imbalance problem (i.e., moderately or extremely imbalanced classifications) using the High School Longitudinal Study of 2009 dataset. For our comparison, we used random oversampling (ROS), random undersampling (RUS), and the combination of the synthetic minority oversampling technique for nominal and continuous (SMOTE-NC) and RUS as a hybrid resampling technique. We used the Random Forest as our classification algorithm to evaluate the results of each sampling technique. Our results show that random oversampling for moderately imbalanced data and hybrid resampling for extremely imbalanced data seem to work best. The implications for educational data mining applications and suggestions for future research are discussed.
1. Introduction
As emerging technologies continue to advance at a rapid pace, modern education also benefits increasingly from leveraging educational data to enhance teaching practices through products such as early warning systems to notify teachers about at-risk, low-achieving students [1]. These data-driven innovations are based on the research field of educational data mining (EDM), which extracts insights from educational data (e.g., academic records, demographic data, and learning activities in digital learning environments) to inform learning and teaching decisions [2]. Insights extracted from EDM-based innovations typically come from a predictive model predicting a categorical target variable (e.g., passing or failing a course) from a set of relevant predictors, such as students’ activity data, formative assessment scores, and effective time use [3]. However, class imbalance in the target variable is a prevalent problem that negatively impacts the accuracy of predictive models in EDM, as many of these models are designed on the assumption that the predicted class is balanced [4,5]. This problem is especially prevalent and should be accounted for in the prediction of high-stakes educational outcomes, such as school dropout or grade repetition, where the discrepancy between two classes is often high due to the rare occurrence of a particular class [6,7,8]. For example, the students’ dropout rate may have an imbalance ratio of 21:1 between students who drop out and those who are able to complete their education degrees [6]. Similarly, students’ school failure status may have an imbalance ratio of 10:1 between students who pass and those who fail [8]. These class imbalances, if left unaddressed, could undermine a predictive model’s accuracy and thereby hamper its capacity to support decisions based on its output [6].
To mitigate the class imbalance problem, researchers have developed imbalance learning techniques to process and extract information from data with a severely skewed distribution [4]. Specifically, the imbalance learning technique enables the prediction algorithm to predict the outcome variable with a more realistic level of accuracy rather than ignoring minority classes (such as students who drop out) in the data. This technique addresses the aforementioned issue by either modifying the prediction algorithm itself or improving the dataset [5,6]. For example, to improve the input dataset for a predictive model, researchers can preprocess the data through oversampling by balancing the proportion between classes of the targeted variable [7]. Researchers can also create a classification algorithm that accounts for class imbalance in the dataset (e.g., using ensemble-based classifiers such as the bootstrapping aggregating method [9]). Note that we use the terms “imbalance learning technique” and “resampling technique” interchangeably since the imbalance learning approaches used in this study place more emphasis on enhancing the dataset than on modifying the predictive model.
Despite the availability of several imbalance learning techniques to address the class imbalance problem, the majority of the previous research focused on optimizing algorithms from a technical perspective of each technique (e.g., algorithms behind each technique), while only a few focused on the application aspect (e.g., the application of imbalance learning techniques in certain contexts) [4,7,10]. Furthermore, some studies compared the strategies using simulated data rather than actual data or used the imbalance learning techniques as a means to build a predictive model, without explaining the mechanism or underlying challenges during the model-building process [11]. Furthermore, while some research has been carried out on the application of imbalance learning techniques, very few studies have focused on imbalance learning in the context of education [7]. To address this gap, we performed a detailed comparison of imbalance learning techniques (i.e., oversampling, undersampling, hybrid) for an educational dataset of High School Longitudinal Study of 2009 and illustrate the mitigation of class imbalance with different imbalance ratios (i.e., moderately imbalanced and extremely imbalanced).
This paper illustrates and compares the capability of imbalance learning techniques in a real dataset with a mix of numeric and categorical variables. We investigate two typical cases of class imbalance in education, which are post-secondary enrollment for the moderately imbalanced class and school dropout for the extremely imbalanced class. Instead of using a simulated dataset, the current data present more realistic conditions with a large set of features (i.e., predictors), including categorical and numerical variables and common imbalance ratios in EDM. Furthermore, the features included in our predictive model were chosen based on educational and pedagogical theories such as Bronfenbrenner’s Ecological Systems Theory, which studies children’s development based on their environment [12], Tinto’s theoretical dropout model, which posits how students’ background and their approach to academic tasks affect drop out rates [13], and Slim et al. [14]’s framework, which predicts college enrollment based on real data from college students. The mentioned literature is used to inform our variable selection, as these works take students’ individual and ecological level factors into account to study academic retention and college enrollment. The usage of such frameworks could make our illustration representative of prediction tasks in the educational context. This illustrative example serves as a didactic guideline to help EDM researchers mitigate the problem of class imbalance, while also highlighting the proper techniques for handling data with various imbalance ratios.
2. Literature Review
2.1. Class Imbalance as a Threat to EDM
Class imbalance is described as a large discrepancy between two classes of the target variable, where one class is represented by many instances, while the other is only represented by a small number of instances [15]. This problem has become more prevalent in a variety of fields utilizing predictive models, including EDM, which applies data mining and machine learning to address problems in the educational context [11,16]. In fact, class imbalance frequently occurs in real-world situations that concern critical-but-rare instances of the population, instead of the majority group [17]. Some examples of class imbalance in the EDM discipline are the classification of school failure [8], school dropout [6], and students’ letter grade (i.e., A, B, C, D, and F) [18]. Minority populations in the aforementioned situations, such as dropout students, school failures, and F-grade students, are fewer in number, but must be quickly and accurately detected by educators in order to apply preventative measures. However, a predictive algorithm that learned from a dataset with class imbalance may fail to detect such cases due to its bias toward the minority class [4].
Specifically, class imbalance causes a machine learning algorithm to misclassify instances from the minority class despite being able to achieve high accuracy because it may simply classify all instances as the majority class in a dataset with class imbalance; this is because the algorithm tends to learn more from the majority class due to its large sample size and recognize less of the minority class because it is smaller in number [17]. This issue affects not only the algorithm’s prediction results, but also public confidence in the ramifications from the decision informed by the biased result [4]. For example, scholarship selection is an important decision that a university has to make almost every academic year, but the discrepancy in terms of sample size between successful and unsuccessful scholarship applicants is usually large. This class imbalance problem could hamper the credibility of the results from a predictive model if left unaddressed because the model may classify most students as unsuccessful scholarship applicants [19].
2.2. Addressing Class Imbalance with ROS, RUS, and SMOTE-NC + RUS Hybrid
To date, various imbalance learning techniques have been developed to address the class imbalance problem by (1) reducing the bias that a machine learning algorithm may have toward the majority class in a dataset or (2) configuring the algorithm to be sensitive toward the minority class [17]. Such techniques can be divided into three main categories: data-level approaches that emphasize data resampling (i.e., resampling techniques), algorithm-level approaches that emphasize the change of classification algorithms, and hybrid approaches that combine the capabilities of the first two [5]. This study focuses on comparing data-level approach techniques since one of the main applications of EDM is to leverage the power of computational algorithms to extract insights from educational datasets [2]. The data-level approach to imbalance learning aims to create a new dataset with an equal ratio between classes of the target variable to reduce the bias of the predictive algorithm [5,17]. This approach encompasses three umbrella resampling techniques: oversampling, undersampling, and hybrid sampling methods [5].
Under the data-level approach, each resampling method works differently to mitigate class imbalance. Oversampling works by replicating samples of the minority class through several variations of the oversampling technique, such as random oversampling (ROS), synthetic minority oversampling (SMOTE), borderline SMOTE, and support vector machine SMOTE [4]. Undersampling works by removing samples of the majority class [4]. Some popular variations of undersampling are random undersampling (RUS), repetitive undersampling based on ensemble models, and Tomek’s link undersampling [10,20]. Hybrid sampling combines the capability of both oversampling and undersampling together, thus allowing researchers to increase the number of minority classes and decrease the number of majority classes at the same time [9]. Some popular variations of hybrid resampling methods are the combination of SMOTE and edited nearest neighbor undersampling (ENN) and the combination of SMOTE and Tomek’s link undersampling [20].
The data-level approach is widely employed to mitigate class imbalance problems in practice. A systematic review Guo et al. [7] found that 156 out of 527 articles (accounting for 29.6% in total) utilized resampling techniques to address data imbalance problems across at least 12 disciplines. In addition, Kovács [11] empirically compared and evaluated 85 oversampling techniques across 104 datasets. The two studies show that the capability of resampling techniques to address class imbalance issues has been intensively researched in modern literature. Further, Kovács [11] also found that the capability of each resampling technique depends on not only its operating principle (i.e., how it balances classes of the target variable), but also the imbalance ratio between classes of the target variable as well. For example, oversampling works equally well as undersampling when used with moderately imbalanced data, but the former technique performs better than the latter when used with extremely imbalanced data [21]. Similarly, some variants of SMOTE such as cluster SMOTE or borderline SMOTE [22,23] and nearest-neighbor-based undersampling techniques such as ENN [24] were also found to work well for datasets with a low to moderate imbalance ratio, while the other SMOTE variants such as polynomial SMOTE [25] could handle both datasets with a moderately imbalanced class and an extremely imbalanced class equally well [11,26]. These results suggest that the imbalance ratio matters to the performance of each imbalance learning algorithm and should be accounted for when addressing class imbalance problems.
Among various resampling techniques available, the techniques of our interest are ROS for oversampling, RUS for undersampling, and the synthetic minority oversampling technique for nominal and continuous (SMOTE-NC) and RUS for hybrid sampling. Table 1 describes the operating principle, advantages, and drawbacks of each resampling technique. These techniques were selected based on the findings of Hassan et al. [9]’s, Pristyanto et al. [27]’s, and Rashu et al. [18] ’s research, suggesting that ROS, RUS, and the SMOTE hybrid work well with educational datasets. Specifically, Hassan et al. [9] addressed multi-class imbalance problems in students’ log data and found that ROS and SMOTE exhibited excellent and acceptable performance, respectively, with ensemble classifiers. Pristyanto et al. [27] also implemented a combination of SMOTE and one-sided selection undersampling to address the multi-class imbalance problem in EDM and found that the proposed hybrid algorithm achieves desirable results in reducing class imbalance. Finally, Rashu et al. [18] addressed the class imbalance problem to predict students’ final grades and found that SMOTE, ROS, and RUS work well in enhancing the performance of the classification models.

Table 1.
The comparison of resampling techniques utilized in this study.
As visualized in Figure 1, ROS operates by randomly duplicating data points of the minority class with replacement until the proportion of the two classes is balanced. In other words, instances that have a minority class in the target variable (e.g., students who dropped out) are randomly replicated until their number matches the instances of the majority class (e.g., students who did not drop out) [28]. ROS is the base method that underpins other oversampling techniques, such as SMOTE. It improves the overall accuracy of a predictive model by providing researchers with more samples of minority classes to lessen the class imbalance problem [28,29]. However, samples duplicated by ROS may have the same value and, therefore, increase the likelihood of overfitting [28]. Further, ROS also increases the training time of the predictive model as the dataset becomes larger with more minority samples [28,29].
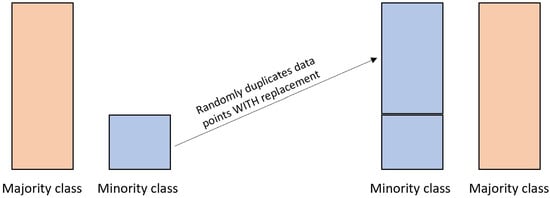
Figure 1.
Random oversampling process.
In contrast to ROS, RUS operates by randomly removing the data points of the majority class, either with or without replacement, until the proportion of the two classes is balanced. With this method, the instances of the majority class in the targeted variable are randomly removed until their number matches the instances of the minority class [28]. As the RUS method equalizes the majority and minority classes, it implements the following selection procedure:
where refers to the synthesized instances, refers to the samples of the minority class, is one of the k-nearest neighbors for , and is a random number generated between 0 and 1. Figure 2 demonstrates how RUS works. Other than improving model accuracy by balancing classes of the targeted variable, RUS decreases the training time of the predictive model as it reduces the size of the dataset, thereby making the project feasible for researchers to use complex predictive models such as a stacked ensemble algorithm [30]. However, by reducing the size of the dataset, RUS may exclude important information and patterns that could be helpful for the prediction and, consequently, reduce the predictive accuracy of the algorithm [28,31].
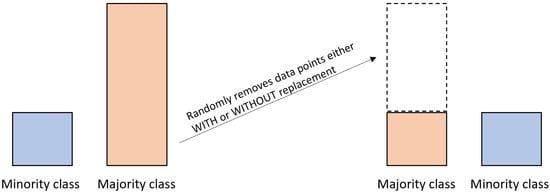
Figure 2.
Random undersampling process.
As visualized in Figure 3, the hybrid method works by implementing SMOTE-NC and RUS in two stages. Unlike ROS operating based on randomization, SMOTE-NC is an extension of SMOTE that operates based on (1) the base principle of SMOTE (see Equation (1)), which accounts for the nearest neighbors of the minority instances in the synthesis of new minority data points, (2) the median of the standard deviation of both nominal (in terms of frequency) and continuous variables, (3) the Euclidean distance between the minority instance and its k-nearest neighbors as determined by the researcher, and (4) the desired ratio of the minority class over the majority class as determined by the researcher (e.g., 80% of the number of majority class) [18,32]. Afterward, RUS is implemented to reduce the number of majority classes to match the number of minority classes. The hybrid method brings forth the advantages of both SMOTE-NC and RUS to enhance the dataset. SMOTE-NC is able to handle both numerical and categorical variables, whereas the base SMOTE can only handle numerical variables [20]. Further, SMOTE-NC possesses the advantage of the base SMOTE, which is its ability to synthesize minority samples that are different from the existing sample (i.e., non-replicated minority class), thereby reducing the chance of overfitting from several identical samples [29]. However, SMOTE-NC also has the same drawbacks as SMOTE, which are: (1) its sub-optimal performance with high-dimensional data [29], (2) its tendency to create overfitting as it could create potential noise in the data [29,33], and (3) its negligence of the local distribution of the minority samples as it only applies the same parameter K neighbors to the entire dataset while ignoring the fact that some minority samples may require more or less K neighbors to be identified [33]. Aside from SMOTE-NC, the hybrid method has advantages and drawbacks that RUS possesses as well; that is, RUS can reduce the number of majority instances to balance the classes of the targeted variable, thus reducing the computational time at the cost of losing potential useful information from the dataset, albeit not as much as implementing RUS alone [28].
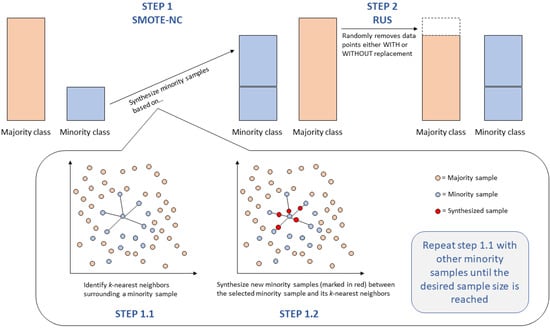
Figure 3.
Hybrid resampling process.
3. Present Study
Previous studies have indicated the importance of class imbalance problems, and most of them addressed this problem in a non-education context. Furthermore, the imbalance ratio was found to be impactful on the performance of predictive algorithms. Therefore, the current study seeks to answer the following research question: How do different imbalance learning techniques work in classification tasks of moderately and extremely imbalanced data? Specifically, this study compared the capability of ROS, RUS, and the hybrid method across two conditions, (1) moderate class imbalance, where the targeted variable is the enrollment of the post-secondary education of high school students (i.e., enroll and not enroll), and (2) extreme class imbalance, where the target variable is the dropout status of high school students (i.e., drop out and not drop out). To evaluate the effectiveness of each resampling condition, we implemented a tuned Random Forest classifier model and consulted the classification metrics of accuracy, precision, recall, receiver operating characteristic-area under curve (ROC-AUC), and F1-score. This study could inform educational researchers of appropriate resampling techniques to address class imbalance problems in educational datasets with different imbalance ratios.
4. Methods
4.1. Dataset and Data Preprocessing
This study used the the High School Longitudinal Study of 2009 (HSLS:09) dataset, which comes from a longitudinal study of 9th-grade students (n = 23,503) from the United States of America [34]. We utilized the R programming language with the tidyverse [35], readxl [36], DataExplorer [37], mice [38], Hmisc [39], and corrplot [40] packages for data preprocessing. From the original dataset with 4014 variables, we identified 67 variables that could be used as predictors of the two target variables (i.e., enrollment in a post-secondary institution and high school dropout status) based on the mentioned frameworks of Bronfenbrenner’s Ecological Systems Theory, Tinto’s theoretical dropout model, and Slim et al. [14]’s framework for college enrollment. To maintain the representativeness of the sample, we removed students for whom the HSLS:09 questionnaire was not completed by either a biological parent or a step-parent of the students. Next, variables with more than a 30% rate of missing data were dropped, and the rest was imputed with multiple imputations by chained equations [41]; this step dropped 16 variables. Then, variables that are not correlated with the targeted variables based on Pearson’s r and not related to the three mentioned frameworks were eliminated; this step further dropped 13 variables. The final dataset consisted of 16,137 students and 38 variables. Among the selected variables, 25 were categorical, and 13 were continuous (see Appendix A for the exhaustive list of the variables utilized in this study). For the moderately imbalanced condition, we used students’ post-secondary enrollment as the target variable, with 14,161 students enrolled in a post-secondary institution and 4676 students who did not enroll in a post-secondary institution (minority: majority = 1:3). For the extremely imbalanced condition, we used students’ school dropout rate as the target variable, with 2004 students who dropped out of their high school before graduation and 14,133 students who did not drop out (minority:majority = 1:7).
4.2. Imbalance Learning Techniques
For the comparison of the resampling techniques, this study used ROS, RUS, and the hybrid of SMOTE-NC and RUS with both moderately and extremely imbalanced datasets. For the SMOTE-NC configuration, this study synthesized the minority data points based on their five nearest neighbors and 0.8 resampling ratios. There was no configuration needed for ROS and RUS because their operation was fully randomized. We utilized the imbalanced-learn package [20] in Python to implement resampling techniques.
4.3. Classification Model
We used the Random Forest classifier from the scikit-learn package [30] in Python as our classification algorithm to evaluate the results of each resampling technique. The rationale behind our choice of this algorithm is as follows: (1) We first compared the performance of Random Forest with the adaptive boosting (Adaboost) classifier from scikit-learn package [30] in their default hyperparameter configuration. Both algorithms fall under the ensemble learning family and are successful in their application [42,43]. The two classifiers exhibited comparable results (i.e., equal F1-scores of 0.73 and 0.88 for the moderately imbalanced dataset and extremely imbalanced dataset, respectively). (2) The Random Forest classifier benefits from its nature of multiple smaller decision trees, being less prone to overfitting compared to Adaboost, which is a single tree with iterative fitting [43]. In fact, Random Forest tends to work well with real data as it is more robust to noise, while Adaboost could fit noise into its learning and, therefore, produce overfitting [43,44]. (3) Further, Random Forest is widely used in the field of educational data mining [45,46], which could attest to its high performance in the context of our interest.
To tune the classification algorithm, a randomized grid search was used, and 50 sets of hyperparameter values were fit with 3-fold cross-validation (3-fold CV), totaling 150 model fits. The candidate hyperparameter values were as follows: the options of max tree depth (max depth) values were 100, 140, 180, 220, 260, 300, 340, 380, 420, 460, 500, and none; the options of the number of trees (N estimator) were 200, 400, 600, 800, 1000, 1200, 1400, 1600, 1800, and 2000; the options of the max feature (max feature) when considering the best node split were “auto”, which takes all features at the split; and sqrt (i.e., square root), which takes the square root of the total number of features in a tree. After obtaining the optimal hyperparameter value, Each classification model was trained–tested–validated with repeated stratified K-folds CV. A 10-fold CV was performed repeatedly 3 times, totaling 30 fits, accounting for the class proportion of the targeted variable. Then, the mean and standard deviation (SD) of the accuracy, precision, recall, and ROC-AUC were extracted from 30 model fits.
5. Results
5.1. Resampling Results
Table 2 presents the results of each resampling technique. We used non-resampled data as the baseline to compare the ratio between the majority and minority classes. For the moderately imbalanced dataset, “0” indicates students who did not enroll in a post-secondary institution, while “1” indicates otherwise. For the extremely imbalanced dataset, “0” indicates students who did not drop out of their high school before graduation, while “1” indicates otherwise.

Table 2.
Class sizes by datasets and resampling techniques.
In Table 2, ROS increased the size of the minority class (0 for the moderately imbalanced dataset and 1 for the extremely imbalanced dataset) by randomly resampling to match the size of the majority class. That is, the sample size of students who did not enroll in a post-secondary institution was increased to 11,461, and the sample size of students who dropped out of high school was increased to 14,133. Conversely, RUS decreased the size of the majority class (1 for the moderately imbalanced dataset and 0 for the extremely imbalanced dataset) by randomly resampling to match the size of the minority class. That is, the sample size of students who enrolled in a post-secondary institution was decreased to 4676, and the sample size of students who did not drop out of their high school was decreased to 2004.
The hybrid resampling (SMOTE-NC+RUS) worked by synthesizing samples of the minority class based on their nearest neighbor, and then, RUS randomly reduced the majority sample to match the size of the minority class. For the moderately imbalanced dataset, the sample size of students who did not enroll in a post-secondary institution was increased to 9,168, while the sample of students who enrolled in a post-secondary institution was reduced to match. For the extremely imbalanced dataset, the sample size of students who dropped out of their high school was increased to 11,306, while the sample of students who did not drop out of their high school was reduced to match.
5.2. Algorithm Tuning and Classification Results
The tuning results of each classification model are displayed in Table 3, and the classification results of each classification condition are displayed in Table 4. The SD scores of all conditions were low, indicating stable performance across all iterations. For the moderately imbalanced dataset, RUS underperformed, as indicated by its lowest overall performance metric scores (mean accuracy = 0.705, mean precision = 0.724, mean recall = 0.662, mean ROC-AUC = 0.763, and mean F1-score = 0.692), compared to the other three conditions. The tuned baseline condition was in third place in its overall performance (mean accuracy = 0.736, mean precision = 0.773, mean recall = 0.888, mean ROC-AUC = 0.763, and mean F1-score = 0.827), followed by the second-best performer, the hybrid condition (mean accuracy = 0.779, precision = 0.796, recall = 0.749, ROC-AUC = 0.868, and mean F1-score = 0.772) and the ROS condition as the best performer (mean accuracy = 0.877, mean precision = 0.926, mean recall = 0.819, mean ROC-AUC = 0.968, and mean F1-score = 0.870).

Table 3.
Optimal hyperparameter values for each condition from randomized grid search.

Table 4.
Classification results for each resampling condition.
For the extremely imbalanced dataset, ROS exhibited an overfitting issue, as indicated by its metrics (mean accuracy = 0.984, mean precision = 0.971, mean recall = 0.999, mean ROC-AUC = 0.999, and mean F1-score = 0.985). This issue was expected as samples were only replicated without adjustments [47,48,49]. Among the remaining three conditions, the baseline condition had the lowest performance scores when considering its low precision, recall, and F1-score (mean accuracy = 0.887, mean precision = 0.665, mean recall = 0.193, mean ROC-AUC = 0.802, and mean F1 = 0.299), meaning that the model did not perform well in detecting positive instances (i.e., students who dropped out) in the extremely imbalanced dataset. RUS performed better due to its higher precision, recall, and F1-score, despite having lower accuracy than the baseline condition (mean accuracy = 0.731, mean precision = 0.736, mean recall = 0.721, mean ROC-AUC = 0.800, and mean F1-score = 0.728). The hybrid condition performed best among all conditions in the extremely imbalanced dataset (mean accuracy = 0.905, mean precision = 0.911, mean recall = 0.898, mean ROC-AUC = 0.967, and mean F1-score = 0.904).
6. Discussion and Conclusions
This study evaluated the performance of the three imbalance learning techniques (i.e., oversampling, undersampling, hybrid) in EDM-based classification tasks. Our goal was to illustrate the mitigation of class imbalance in an educational dataset with different imbalance ratios. The results from this study could inform EDM researchers of how the resampling techniques of our choice operate, including their advantages and drawbacks for their consideration of class imbalance mitigation. Additionally, our results from the comparison across different conditions of class imbalance ratios could guide researchers in choosing the appropriate resampling techniques for their educational datasets as well.
Our findings indicated that the effectiveness of imbalance learning techniques in classification tasks differs based on the skewness of class proportions in the target variable. For the moderately imbalanced case, RUS performed worse compared to the baseline condition of non-resampled data. On the other hand, the hybrid resampling method and ROS were able to enhance the performance of the Random Forest classifier, with ROS as the best performer. This finding suggests that, when the target variable is moderately imbalanced, oversampling could be more beneficial to the classification than undersampling [48]. For the extremely imbalanced case, ROS presented an overfitting issue, which might be due to the repeated replication of the minority class [47,48,49]. For the remaining three conditions, the baseline condition performed worst, while RUS was able to mitigate the issue to an extent and SMOTE-NC+RUS performed best in the enhancement of the classification results. Overall, the hybrid resampling approach seems to work well in an extremely imbalanced condition, whereas ROS is not recommended due to its vulnerability to overfitting [48,49]. Across both moderately and extremely imbalanced cases, RUS is not recommended as the first choice as it leads to the loss of potentially useful data for the classifier [4].
Overall, our results are consistent with the literature regarding how each imbalance learning technique performs on datasets of different imbalance ratios. We extended the findings of the previous literature by utilizing real data, rather than synthesized data, to reflect the patterns educational researchers are likely to come across in EDM research focused on critical target variables, such as school dropout status and post-secondary enrollment, which may have important consequences for both students and educators [6,7]. Further, the majority of our variables are categorical, which presents a challenge to several imbalance learning techniques as they only support continuous variables such as SMOTE or ENN [20]. We utilized SMOTE-NC as a novel workaround that can be applied to the actual situation as several education-related variables, such as parental expectations or the level of education, are either categorical or ordinal [50]. Our findings can serve as a set of guidelines for EDM researchers who want to mitigate the data imbalance issue in the development of data-driven innovations such as early warning systems in schools [1]. Finally, carefully addressing the class imbalance problem also contributes to improving fairness in the education field. For example, if a class imbalance in the underlying data results in biased predictions, such as underestimating college success for minority and low-income students, it might affect admissions decisions and negatively influence the consequences of the prediction model [51].
In addition, considering that the main focus of this study was to address class imbalance with resampling methods instead of testing the performance of predictive algorithms, the current study mainly focuses on comparing the effectiveness of each resampling method (i.e., ROS, RUS, and SMOTE-NC + RUS hybrid) on one classifier instead of many. However, given how results from the Random Forest and Adaboost classifiers are comparable in the initial analysis stage for algorithm selection, it is reasonable to deduce that the resampling algorithm should work similarly to classifiers other than Random Forest, which we used as the main evaluator. This point is supported by the literature: class imbalance is detrimental to the performance of predictive models as it makes the algorithm learn more from the majority class instead of the minority class, thus producing bias in the predictive model [4,17]. Therefore, reducing class imbalance could be beneficial to classifiers in general as it is the primary purpose of imbalance learning techniques [17].
This study has several limitations. First, we utilized a single dataset (HSLS:09) to illustrate the imbalance learning techniques and evaluate their performance in a classification task. However, each dataset has its own characteristics, such as the pattern of variables, the imbalance ratio, and the number of minority classes. The results of the imbalance learning algorithm may differ based on the uniqueness of each dataset. For example, the Programme for International Student Assessment dataset [52], despite being an educational dataset, might yield slightly different results with the same techniques demonstrated in this study. Thus, researchers are encouraged to explore the characteristics of their dataset carefully before selecting an imbalance learning algorithm to address the class imbalance issue. Second, finding an optimal set of hyperparameter values can be a challenging task in EDM. We used a randomized grid search in this study for feasibility reasons; however, using an exhaustive grid search and cross-validation with the same imbalance learning techniques might yield better classification results at the expense of more computational resources. Lastly, future research is needed to explore different combinations of resampling techniques (e.g., random oversampling example (ROSE)) and classification algorithms because the effectiveness of each resampling technique may partly depend on the classifier [53].
Author Contributions
Conceptualization, T.W., S.H. and O.B.; methodology, T.W., S.H. and O.B.; data curation, T.W., S.H. and O.B.; writing—original draft preparation, T.W., S.H. and O.B.; writing—review and editing, T.W., S.H. and O.B.; visualization, T.W.; supervision, O.B.; resources, T.W., S.H. and O.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study did not require ethical approval.
Informed Consent Statement
Not applicable.
Data Availability Statement
The dataset is available through the National Center for Education Statistics website (accessed on 6 January 2023): https://nces.ed.gov/surveys/hsls09/. The corresponding author can make the codes available upon request.
Acknowledgments
The authors would like to thank Ka-Wing Lai for her contributions to the initial conceptualization of this study.
Conflicts of Interest
The authors declare no conflict of interest in the writing of the manuscript.
Abbreviations
The following abbreviations are used in this manuscript:
| EDM | Educational data mining |
| ROS | Random oversampling |
| ROSE | Random oversampling example |
| RUS | Random undersampling |
| SMOTE-NC | Synthetic minority oversampling technique for nominal and continuous |
| ENN | Edited Nearest neighbor |
| ROC-AUC | Receiver operating characteristic-area under curve |
| ROSE | Random oversampling example |
Appendix A. List of Utilized Variables
| Variable Type | Variable Name (Variable Code) |
| Continuous | Students’ socio-economic status composite score (X1SES) |
| Students’ mathematics self-efficacy (X1MTHEFF) | |
| Students’ interest in fall 2009 math course (X1MTHINT) | |
| Students’ perception of science utility (X1SCIUTI) | |
| Students’ science self-efficacy (X1SCIEFF) | |
| Students’ interest in fall 2009 math course (X1SCIINT) | |
| Students’ sense of school belonging (X1SCHOOLBEL) | |
| Students’ school engagement (X1SCHOOLENG) | |
| Scale of school climate assessment (X1SCHOOLCLI) | |
| Scale of counselor’s perceptions of teacher’s expectations (X1COUPERTEA) | |
| Scale of counselor’s perceptions of counselor’s expectations (X1COUPERCOU) | |
| Scale of counselor’s perceptions of principal’s expectations (X1COUPERPRI) | |
| Students’ GPA in ninth grade (X3TGPA9TH) | |
| Categorical | Hours spent on homework/studying on typical school day (S1HROTHHOMWK) |
| Mother’s/female guardian’s highest level of education (X1MOMEDU) | |
| Father’s/male guardian’s highest level of education (X1DADEDU) | |
| How far in school 9th grader thinks he/she will get (X1STUEDEXPCT) | |
| How far in school parent thinks 9th grader will get (X1PAREDEXPCT) | |
| How often 9th grader goes to class without his/her homework done (S1NOHWDN) | |
| How often 9th grader goes to class without pencil or paper (S1NOPAPER) | |
| How often 9th grader goes to class without books (S1NOBOOKS) | |
| How often 9th grader goes to class late (S1LATE) | |
| 9th grader thinks studying in school rarely pays off later with a good job (S1PAYOFF) | |
| 9th grader thinks even if he/she studies, he/she will not get into college (S1GETINTOCLG) | |
| 9th grader thinks even if he/she studies, family cannot afford college (S1AFFORD) | |
| 9th grader thinks working is more important for him/her than college (S1WORKING) | |
| 9th grader’s closest friend gets good grades (S1FRNDGRADES) | |
| 9th grader’s closest friend is interested in school (S1FRNDSCHOOL) | |
| 9th grader’s closest friend attends classes regularly (S1FRNDCLASS) | |
| 9th grader’s closest friend plans to go to college (S1FRNDCLG) | |
| Hours spent on math homework/studying on typical school day (S1HRMHOMEWK) | |
| Hours spent on science homework/studying on typical school day (S1HRSHOMEWK) | |
| How sure 9th grader is that he/she will graduate from high school (S1SUREHSGRAD) | |
| How often parent contacted by school about problem behavior (P1BEHAVE) | |
| How often parent contacted by school about poor attendance (P1ATTEND) | |
| How often parent contacted by school about poor performance (P1PERFORM) | |
| Ever dropped out of high school in 2016 (X4EVERDROP) | |
| Post-secondary enrollment status in February 2016 (X4PSENRSTLV) |
References
- Jokhan, A.; Sharma, B.; Singh, S. Early warning system as a predictor for student performance in higher education blended courses. Stud. High. Educ. 2019, 44, 1900–1911. [Google Scholar] [CrossRef]
- Chen, G.; Rolim, V.; Mello, R.F.; Gašević, D. Let’s shine together! A comparative study between learning analytics and educational data mining. In Proceedings of the tenth International Conference on Learning Analytics & Knowledge, Frankfurt, Germany, 23–27 March 2020; pp. 544–553. [Google Scholar]
- Bulut, O.; Gorgun, G.; Yildirim-Erbasli, S.N.; Wongvorachan, T.; Daniels, L.M.; Gao, Y.; Lai, K.W.; Shin, J. Standing on the shoulders of giants: Online formative assessments as the foundation for predictive learning analytics models. Br. J. Educ. Technol. 2022. [CrossRef]
- Ma, Y.; He, H. Imbalanced Learning: Foundations, Algorithms, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Kaur, P.; Gosain, A. Comparing the behavior of oversampling and undersampling approach of class imbalance learning by combining class imbalance problem with noise. In ICT Based Innovations; Series Title: Advances in Intelligent Systems and Computing; Saini, A.K., Nayak, A.K., Vyas, R.K., Eds.; Springer: Singapore, 2018; Volume 653, pp. 23–30. [Google Scholar] [CrossRef]
- Barros, T.M.; SouzaNeto, P.A.; Silva, I.; Guedes, L.A. Predictive models for imbalanced data: A school dropout perspective. Educ. Sci. 2019, 9, 275. [Google Scholar] [CrossRef]
- Guo, H.; Li, Y.; Shang, J.; Gu, M.; Huang, Y.; Gong, B. Learning from class-imbalanced data: Review of methods and applications. Expert Syst. Appl. 2017, 73, 220–239. [Google Scholar] [CrossRef]
- Márquez-Vera, C.; Cano, A.; Romero, C.; Ventura, S. Predicting student failure at school using genetic programming and different data mining approaches with high dimensional and imbalanced data. Appl. Intell. 2013, 38, 315–330. [Google Scholar] [CrossRef]
- Hassan, H.; Ahmad, N.B.; Anuar, S. Improved students’ performance prediction for multi-class imbalanced problems using hybrid and ensemble approach in educational data mining. J. Phys. Conf. Ser. 2020, 1529, 052041. [Google Scholar] [CrossRef]
- Van Hulse, J.; Khoshgoftaar, T.M.; Napolitano, A. An empirical comparison of repetitive undersampling techniques. In Proceedings of the 2009 IEEE International Conference on Information Reuse & Integration, IEEE, Las Vegas, NA, USA, 10–12 August 2009; pp. 29–34. [Google Scholar] [CrossRef]
- Kovács, G. An empirical comparison and evaluation of minority oversampling techniques on a large number of imbalanced datasets. Appl. Soft Comput. 2019, 83, 105662. [Google Scholar] [CrossRef]
- Guy-Evans, O. Bronfenbrenner’s Ecological Systems Theory. 2020. Available online: https://www.simplypsychology.org/Bronfenbrenner.html (accessed on 3 January 2023).
- Nicoletti, M.d.C. Revisiting the Tinto’s Theoretical Dropout Model. High. Educ. Stud. 2019, 9, 52–64. [Google Scholar] [CrossRef]
- Slim, A.; Hush, D.; Ojah, T.; Babbitt, T. Predicting Student Enrollment Based on Student and College Characteristics. In Proceedings of the International Conference on Educational Data Mining (EDM), Raleigh, NC, USA, 16–20 July 2018. [Google Scholar]
- Japkowicz, N.; Stephen, S. The class imbalance problem: A systematic study. Intell. Data Anal. 2002, 6, 429–449. [Google Scholar] [CrossRef]
- Guo, B.; Zhang, R.; Xu, G.; Shi, C.; Yang, L. Predicting students performance in educational data mining. In Proceedings of the 2015 international symposium on educational technology (ISET), Wuhan, China, 27–29 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 125–128. [Google Scholar]
- Johnson, J.M.; Khoshgoftaar, T.M. Survey on deep learning with class imbalance. J. Big Data 2019, 6, 1–54. [Google Scholar] [CrossRef]
- Rashu, R.I.; Haq, N.; Rahman, R.M. Data mining approaches to predict final grade by overcoming class imbalance problem. In Proceedings of the 2014 17th International Conference on Computer and Information Technology (ICCIT), Dhaka, Bangladesh, 22–23 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 14–19. [Google Scholar]
- Sun, Y.; Li, Z.; Li, X.; Zhang, J. Classifier selection and ensemble model for multi-class imbalance learning in education grants prediction. Appl. Artif. Intell. 2021, 35, 290–303. [Google Scholar] [CrossRef]
- Lema, G. Imbalanced-learn: A python toolbox to tackle the curse of imbalanced datasets in machine learning. J. Mach. Learn. Res. 2017, 18, 1–5. [Google Scholar]
- Patel, H.; Singh Rajput, D.; Thippa Reddy, G.; Iwendi, C.; Kashif Bashir, A.; Jo, O. A review on classification of imbalanced data for wireless sensor networks. Int. J. Distrib. Sens. Netw. 2020, 16. [Google Scholar] [CrossRef]
- Cieslak, D.A.; Chawla, N.V.; Striegel, A. Combating imbalance in network intrusion datasets. In Proceedings of the GrC, Atlanta, GA, USA, 10–12 May 2006; pp. 732–737. [Google Scholar]
- Kovács, G. smote-variants: A Python Implementation of 85 Minority Oversampling Techniques. Neurocomputing 2019, 366, 352–354. [Google Scholar] [CrossRef]
- Wilson, D.L. Asymptotic properties of nearest neighbor rules using edited data. IEEE Trans. Syst. Man Cybern. 1972, SMC-2, 408–421. [Google Scholar] [CrossRef]
- Gazzah, S.; Amara, N.E.B. New oversampling approaches based on polynomial fitting for imbalanced data sets. In Proceedings of the 2008 the Eighth Iapr International Workshop on Document Analysis Systems, Nara, Japan, 16–19 September 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 677–684. [Google Scholar]
- Lin, W.C.; Tsai, C.F.; Hu, Y.H.; Jhang, J.S. Clustering-based undersampling in class-imbalanced data. Inf. Sci. 2017, 409–410, 17–26. [Google Scholar] [CrossRef]
- Pristyanto, Y.; Pratama, I.; Nugraha, A.F. Data level approach for imbalanced class handling on educational data mining multiclass classification. In Proceedings of the 2018 International Conference on Information and Communications Technology (ICOIACT), Yogyakarta, Indonesia, 6–7 March 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 310–314. [Google Scholar] [CrossRef]
- Menardi, G.; Torelli, N. Training and assessing classification rules with imbalanced data. Data Min. Knowl. Discov. 2014, 28, 92–122. [Google Scholar] [CrossRef]
- Dattagupta, S.J. A Performance Comparison of Oversampling Methods for Data Generation in Imbalanced Learning Tasks. Ph.D. Thesis, Universidade Nova de Lisboa, Lisbon, Portugal, 2018. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- García-Pedrajas, N.; Pérez-Rodríguez, J.; García-Pedrajas, M.; Ortiz-Boyer, D.; Fyfe, C. Class imbalance methods for translation initiation site recognition in DNA sequences. Knowl.-Based Syst. 2012, 25, 22–34. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority oversampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Cheng, K.; Zhang, C.; Yu, H.; Yang, X.; Zou, H.; Gao, S. Grouped SMOTE with noise filtering mechanism for classifying imbalanced data. IEEE Access 2019, 7, 170668–170681. [Google Scholar] [CrossRef]
- National Center for Educational Statistics [NCES]. High School Longitudinal Study of 2009. 2016. Available online: https://nces.ed.gov/surveys/hsls09/ (accessed on 6 January 2023).
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; McGowan, L.D.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J.; et al. Welcome to the tidyverse. J. Open Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef]
- Wickham, H.; Bryan, J. Readxl: Read Excel Files. 2022. Available online: https://readxl.tidyverse.org (accessed on 6 January 2023).
- Cui, B. DataExplorer. 2022. Available online: https://boxuancui.github.io/DataExplorer/ (accessed on 6 January 2023).
- van Buuren, S.; Groothuis-Oudshoorn, K. mice: Multivariate Imputation by Chained Equations in R. J. Stat. Softw. 2011, 45, 1–67. [Google Scholar] [CrossRef]
- Harrell, F.E., Jr.; Dupont, C. Hmisc: Harrell Miscellaneous. 2022. Available online: https://cran.r-project.org/web/packages/Hmisc/index.html (accessed on 6 January 2023).
- Wei, T.; Simko, V. Package ‘Corrplot’: Visualization of a Correlation Matrix , (Version 0.92); 2021. Available online: https://cran.r-project.org/web/packages/corrplot/vignettes/corrplot-intro.html (accessed on 6 January 2023).
- Buuren, S.V. Flexible Imputation of Missing Data, 2nd ed.; Chapman and Hall/CRC Interdisciplinary Statistics Series; CRC Press: Boca Raton, FL, USA; Taylor and Francis Group: Boca Raton, FL, USA, 2018. [Google Scholar]
- Shaik, A.B.; Srinivasan, S. A brief survey on random forest ensembles in classification model. In International Conference on Innovative Computing and Communications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 253–260. [Google Scholar]
- Wyner, A.J.; Olson, M.; Bleich, J.; Mease, D. Explaining the success of adaboost and random forests as interpolating classifiers. J. Mach. Learn. Res. 2017, 18, 1558–1590. [Google Scholar]
- Müller, A.C.; Guido, S. Introduction to Machine Learning with Python: A Guide for Data Scientists; O’Reilly Media, Inc.: Newton, MA, USA, 2016. [Google Scholar]
- Chau, V.T.N.; Phung, N.H. Imbalanced educational data classification: An effective approach with resampling and random forest. In Proceedings of the The 2013 RIVF International Conference on Computing & Communication Technologies-Research, Innovation, and Vision for Future (RIVF), Hanoi, Vietnam, 10–13 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 135–140. [Google Scholar]
- Ramaswami, G.; Susnjak, T.; Mathrani, A.; Lim, J.; Garcia, P. Using educational data mining techniques to increase the prediction accuracy of student academic performance. Inf. Learn. Sci. 2019, 120, 451–467. [Google Scholar] [CrossRef]
- Douzas, G.; Bacao, F.; Last, F. Improving imbalanced learning through a heuristic oversampling method based on k-means and SMOTE. Inf. Sci. 2018, 465, 1–20. [Google Scholar] [CrossRef]
- Mohammed, R.; Rawashdeh, J.; Abdullah, M. Machine learning with oversampling and undersampling techniques: Overview study and experimental results. In Proceedings of the 2020 11th International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 7–9 April 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 243–248. [Google Scholar] [CrossRef]
- Santos, M.S.; Soares, J.P.; Abreu, P.H.; Araujo, H.; Santos, J. Cross-validation for imbalanced datasets: Avoiding overoptimistic and overfitting approaches. IEEE Comput. Intell. Mag. 2018, 13, 59–76. [Google Scholar] [CrossRef]
- Islahulhaq, W.W.; Ratih, I.D. Classification of non-performing financing using logistic regression and synthetic minority oversampling technique-nominal continuous (SMOTE-NC). Int. J. Adv. Soft Comput. Its Appl. 2021, 13, 116–128. [Google Scholar] [CrossRef]
- Kizilcec, R.F.; Lee, H. Algorithmic fairness in education. arXiv 2020, arXiv:2007.05443. [Google Scholar]
- Organisation for Economic Co-operation and Development (OECD). PISA 2018 Results (Volume I): What Students Know and Can Do; OECD: Paris, France, 2018. [Google Scholar]
- Chakravarthy, A.D.; Bonthu, S.; Chen, Z.; Zhu, Q. Predictive models with resampling: A comparative study of machine learning algorithms and their performances on handling imbalanced datasets. In Proceedings of the 2019 18th IEEE International Conference On Machine Learning And Applications (ICMLA), Boca Raton, FL, USA, 16–19 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1492–1495. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).