A Method for UWB Localization Based on CNN-SVM and Hybrid Locating Algorithm
Abstract
1. Introduction
- (i)
- A complete method is proposed for NLOS/LOS classification and NLOS identification and mitigation, and a final accurate UWB coordinate solution is proposed through the integration of two machine learning algorithms and a hybrid localization algorithm, which can effectively mitigate signal propagation errors in indoor positioning and communication under strong NLOS interference. We call this innovative algorithm the C-T-CNN-SVM algorithm, which consists of three basic processes: an LOS/NLOS signal classification method based on SVM, an NLOS signal recognition and error elimination method based on CNN, and an accurate coordinate solution based on the hybrid weighting of the Chan–Taylor method.
- (ii)
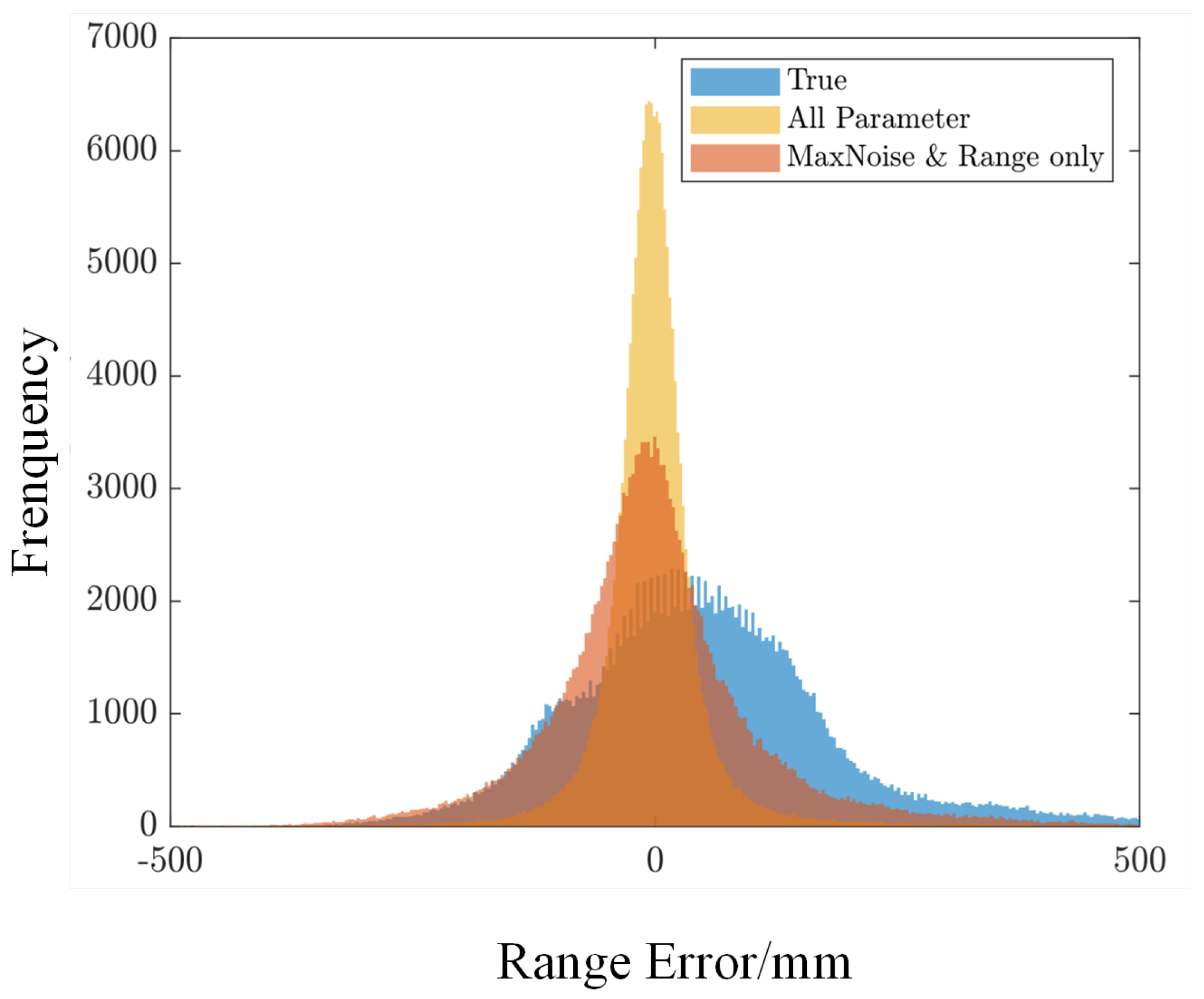
- After LOS/NLOS signal classification based on SVM and the CNN-based method for NLOS signal recognition and error elimination, using the testing data set and focusing on four main prediction errors (range measurements, maxNoise, stdNoise and rangeError), the standard deviation decreases from 13.65 cm to 4.35 cm, while the mean error decreases from 3.65 cm to 0.27 cm, and the errors are practically distributed normally, which demonstrates that after training a CNN for NLOS recognition and performing NLOS mitigation, the accuracy of UWB range measurements may be greatly increased.
- (iii)
- During the final accurate UWB coordinate solution based on the hybrid weighting of the Chan and Taylor algorithms, using a total number of 648 testing data sets that vary in the percentage of LOS and NLOS signals, after target positioning, this method can realize a one-dimensional X-axis and Y-axis accuracy within 175 mm and a Z-axis accuracy within 200 mm; a 2D () accuracy within 200 mm; and a 3D accuracy within 200 mm, most of which fall within (100 mm, 100 mm, 100 mm).
- (iv)
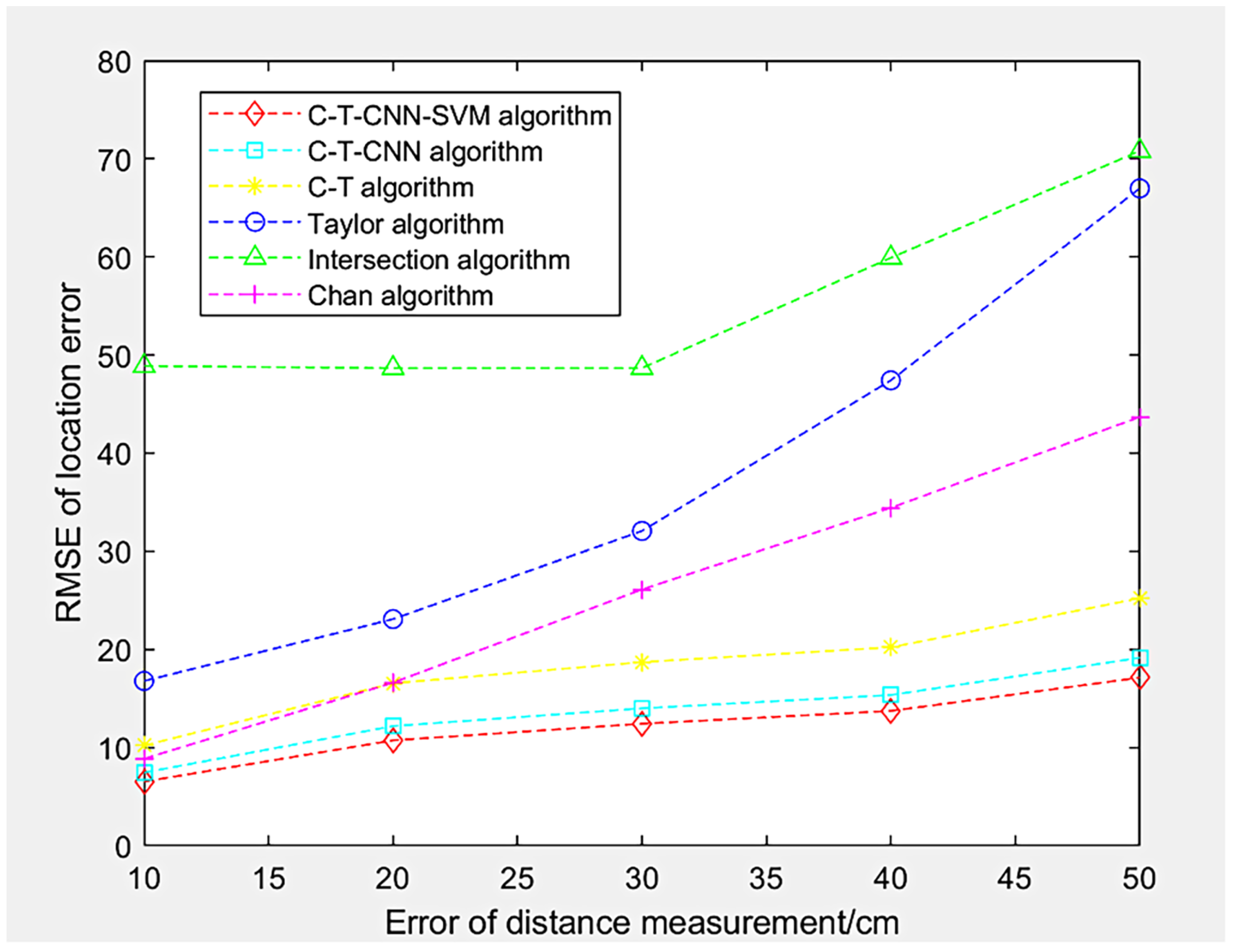
- Compared with the traditional Chan algorithm, Taylor algorithm, and intersection algorithm error, the proposed C-T-CNN-SVM algorithm performs better in location accuracy, cumulative error probability (CDF), and root-mean-square difference (RMSE): the 1D, 2D, and 3D accuracy of the proposed method is 2.5 times that of the traditional methods; when the location error is less than 10 cm, the CDF of the proposed algorithm only reaches , while that of the four-side intersection algorithm is as high as . When the positioning error reaches 30 cm, only the CDF of the proposed algorithm remains in an acceptable range; the RMSE of the proposed algorithm remains ideal when the distance error is greater than 30 cm, while that of the traditional algorithms grow very large when the distance error exceeds 10 cm.
- (v)
- The research result of this paper and the idea of a combination of machine learning methods with the classical locating algorithms for an improved UWB positioning under NLOS interference could meet the growing need for wireless indoor locating and communication, which indicates the possibility for the practical deployment of such a method in the future.
- (i)
- As stated in Section 2, we first create the UWB positioning model. From there, we investigate the NLOS error in the model and introduce standard UWB algorithms as well as the SVM and CNN technology that will be used in our method.
- (ii)
- The C-T-CNN-SVM algorithm, a particular UWB positioning technique, is described in detail in Section 3. It is separated into three sections: LOS/NLOS signal classification based on SVM, NLOS signal recognition and classification based on CNN, and final accurate UWB localization based on a hybrid locating algorithm.
- (iii)
- In Section 4, performance analysis and experimental findings are presented.
- (iv)
- Final remarks can be found in Section 5.
2. System Model, Assumptions and Notations
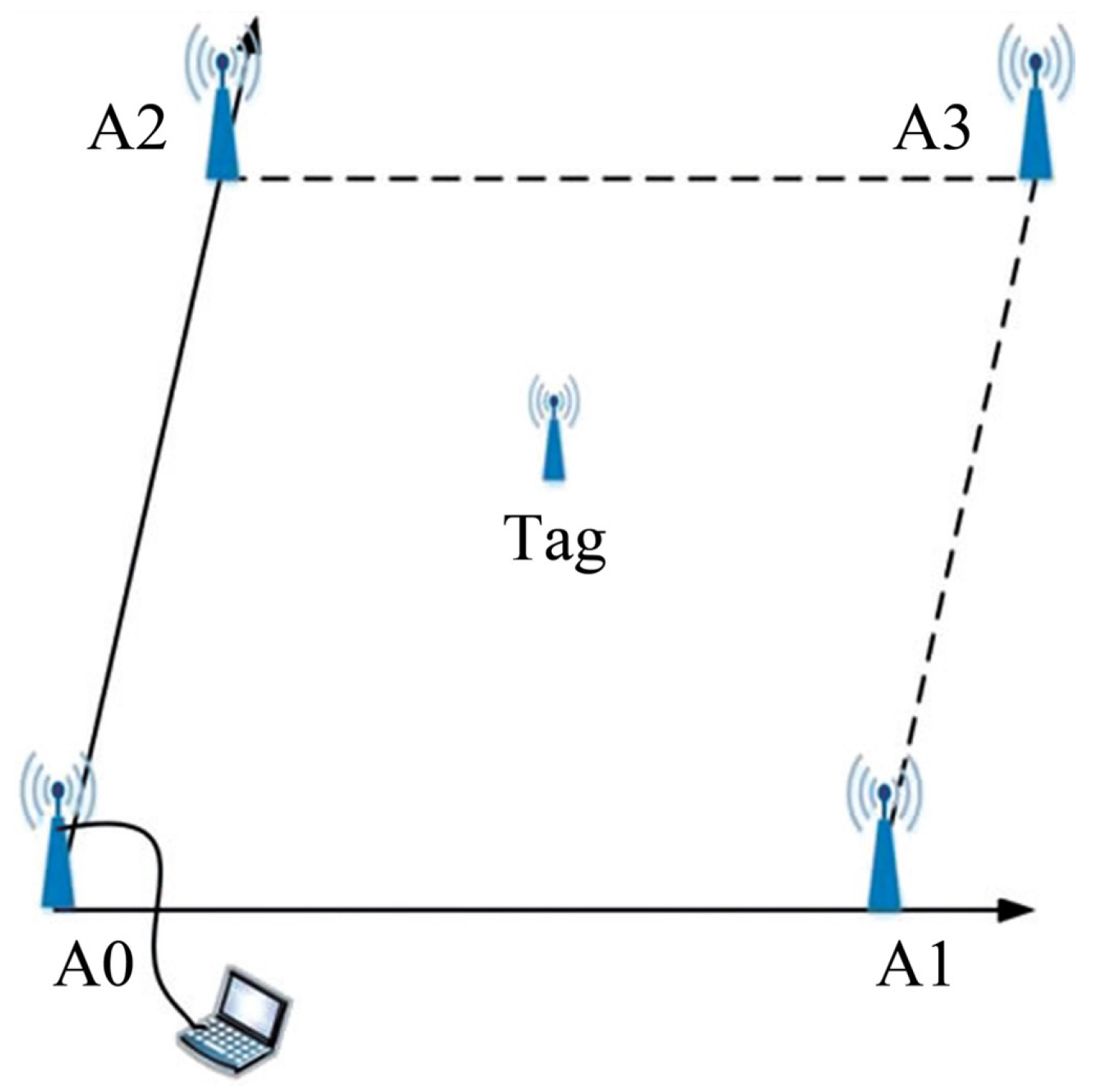
2.1. The Overall Model of Accurate UWB Localization
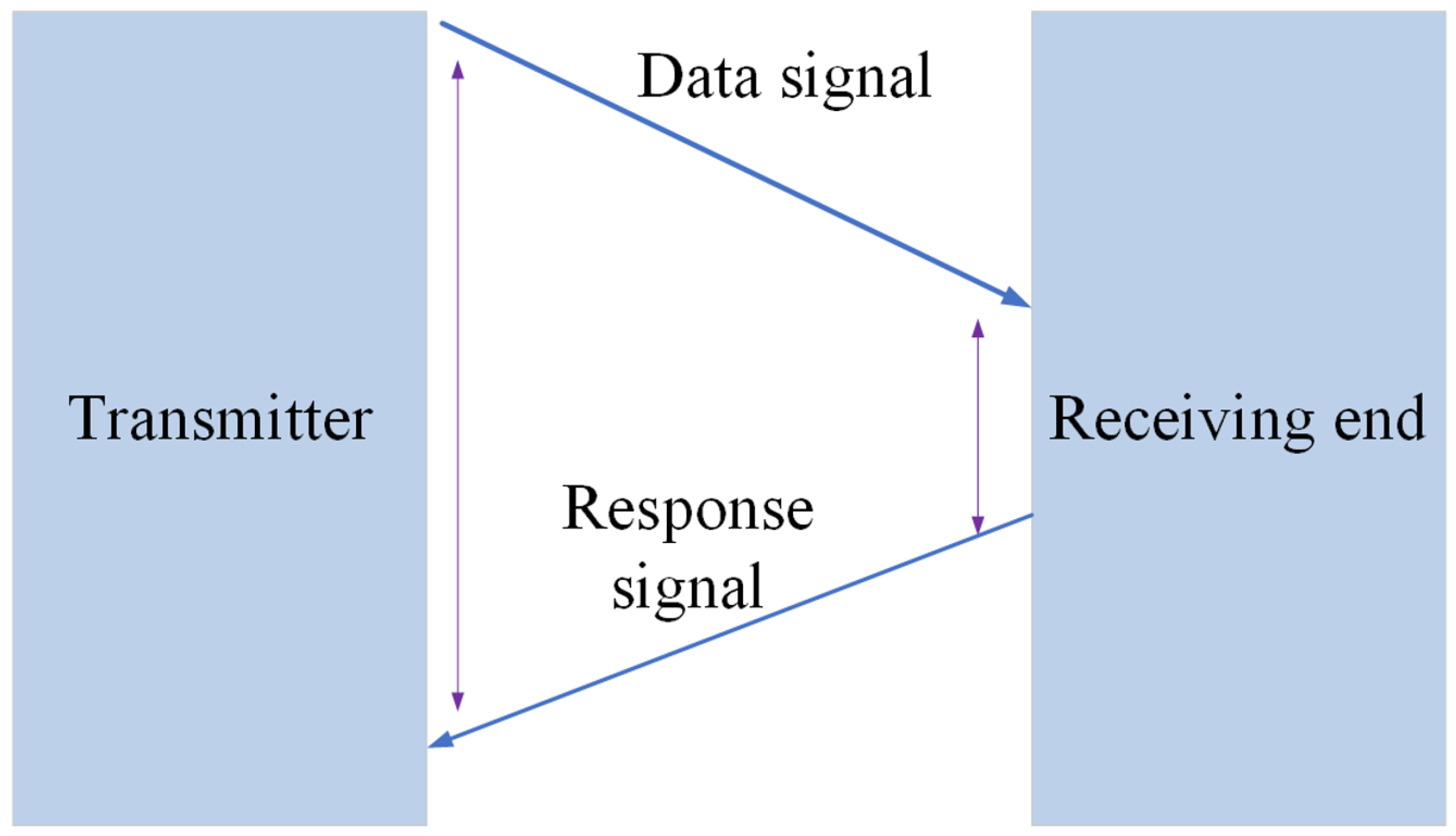
2.2. UWB Model Studied in This Paper
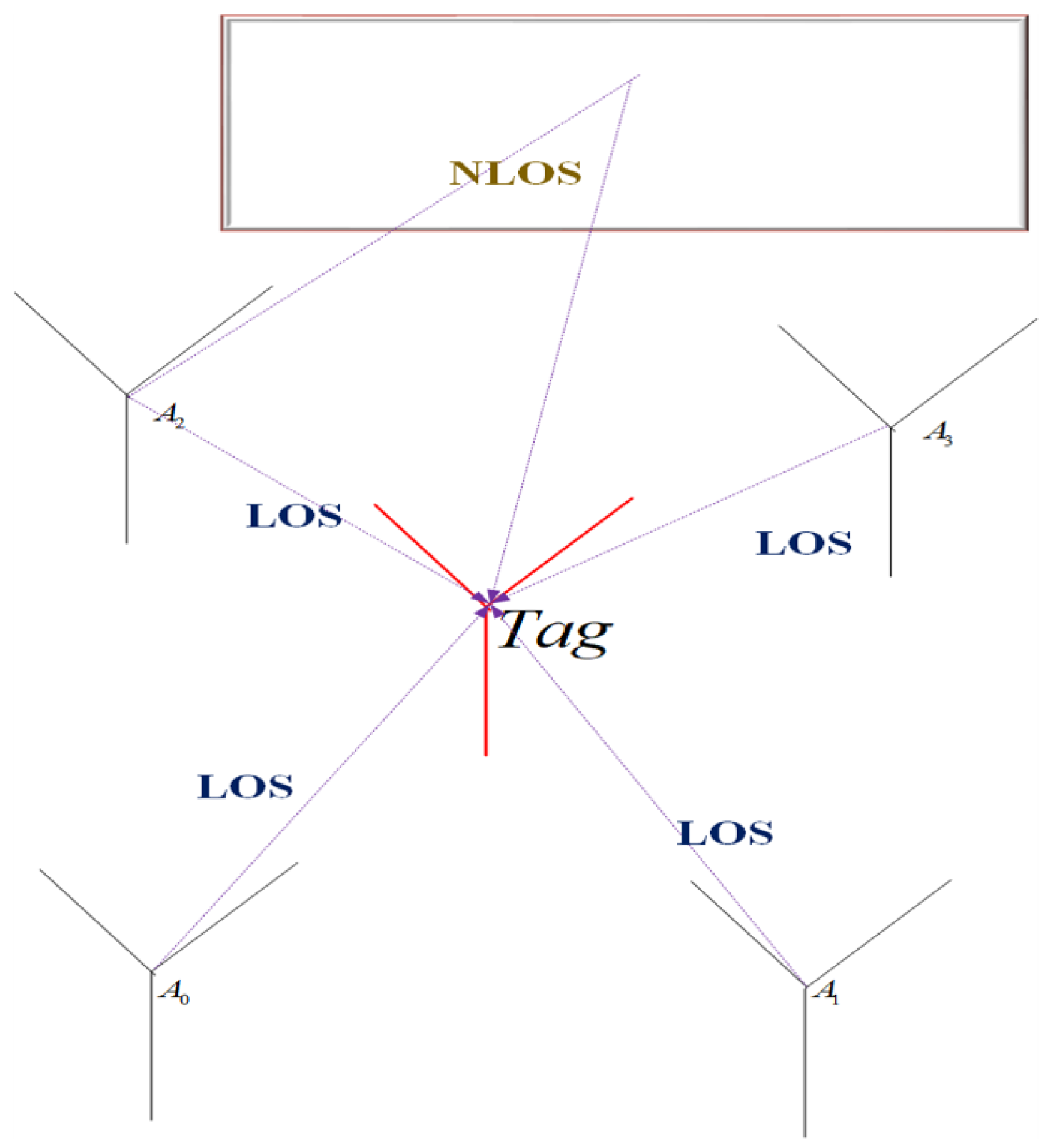
2.3. The NLOS Propogation Error Model in UWB
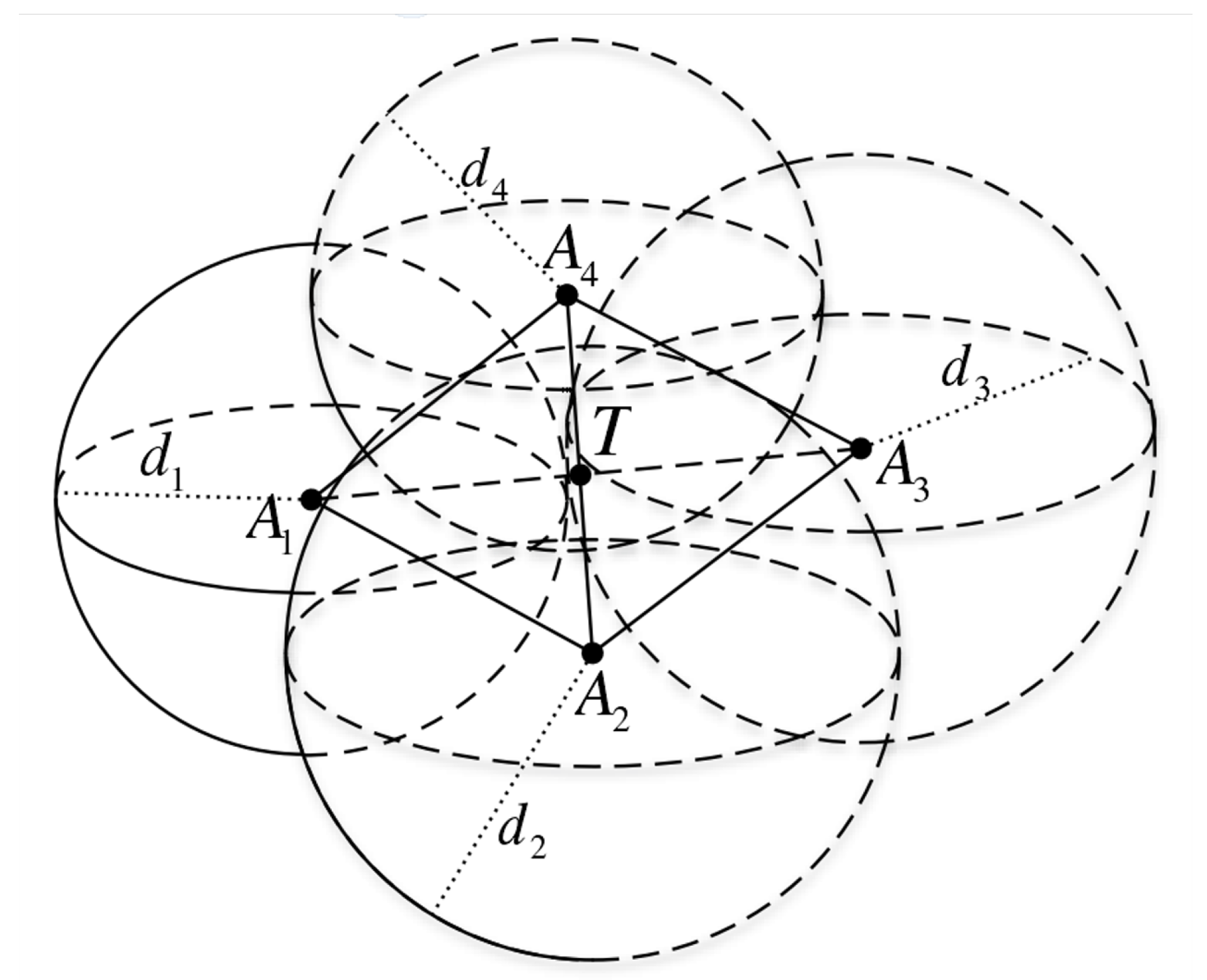
2.4. Traditional UWB Ranging Method of Quadrilateral Location Algorithm
2.5. UWB Ranging Method of Chan and Taylor Algorithm
2.6. Machine Learning-Based Ideas for UWB Localization
2.6.1. Technology of SVM
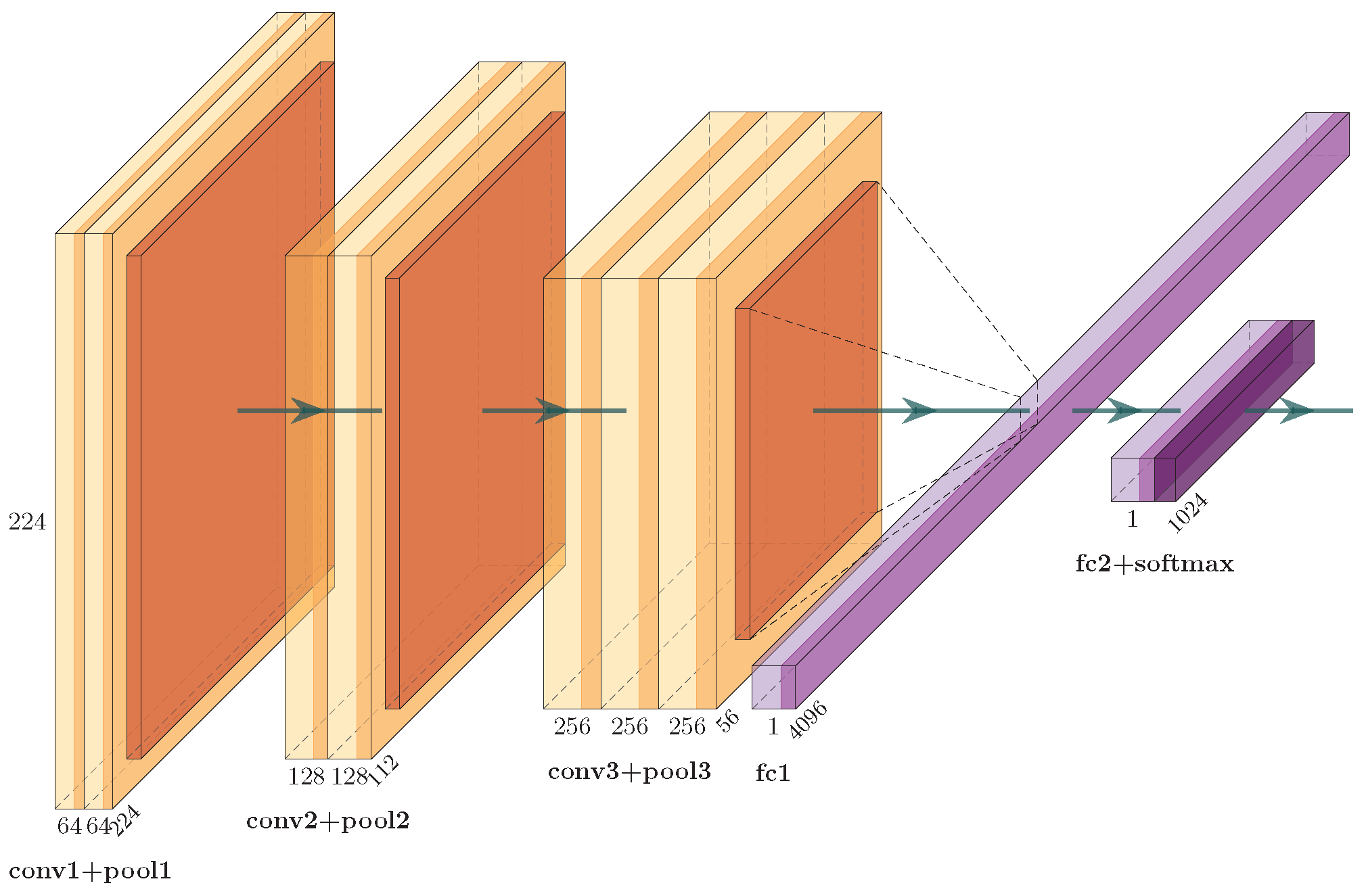
2.6.2. Technology of CNN
2.7. Assumptions
- (i)
- There is no other interference in the collected data other than that stated in the paper;
- (ii)
- Only the TOF-based ranging principle is considered;
- (iii)
- It is assumed that all interferences in the experimental design are of the same prototype;
- (iv)
- The effect of all interferences in the experimental design on the collected data remains stable.
2.8. Notations
3. Methods
3.1. Total Flow of C-T-CNN-SVM Algorithm
- (i)
- Firstly, SVM-based signal classification is used to distinguish between LOS and NLOS signals. The following stage for NLOS signal detection and error eradication will use the results as input.
- (ii)
- Next, a CNN-based approach for recognizing and mitigating NLOS signals is proposed, which draws on the concept of neural network pattern recognition.
- (iii)
- Following error correction, the UWB signal data will be sent into the following hybrid weighting algorithm, which uses the Chan algorithm to calculate the initial coordinates and the Taylor algorithm to calculate the final coordinates. The specific coordinates of the target point are solved by dividing the weights of these two algorithms.
3.2. LOS/NLOS Signal Classification Based on SVM
3.3. CNN-Based Method for NLOS Signal Recognition and Error Elimination
3.3.1. NLOS Signal Recognition
3.3.2. NLOS Error Mitigation
3.4. Final Accurate UWB Coordinate Solution Based on Hybrid Weighting of Chan and Taylor Algorithm
3.4.1. Target Coordinate Preliminary Solution Using Chan Algorithm
3.4.2. Taylor Series-Based Technique for the Accurate Coordinate Solution of the Anchor Point
3.4.3. Final Determination of Anchor Coordinates Based on Chan–Taylor Mixed Weighting Method
4. Experiment and Analysis
4.1. Analysis of NLOS Mitigation Performance
4.2. Accuracy Analysis of the Algorithms
4.2.1. 1D Accuracy Analysis of the Algorithms
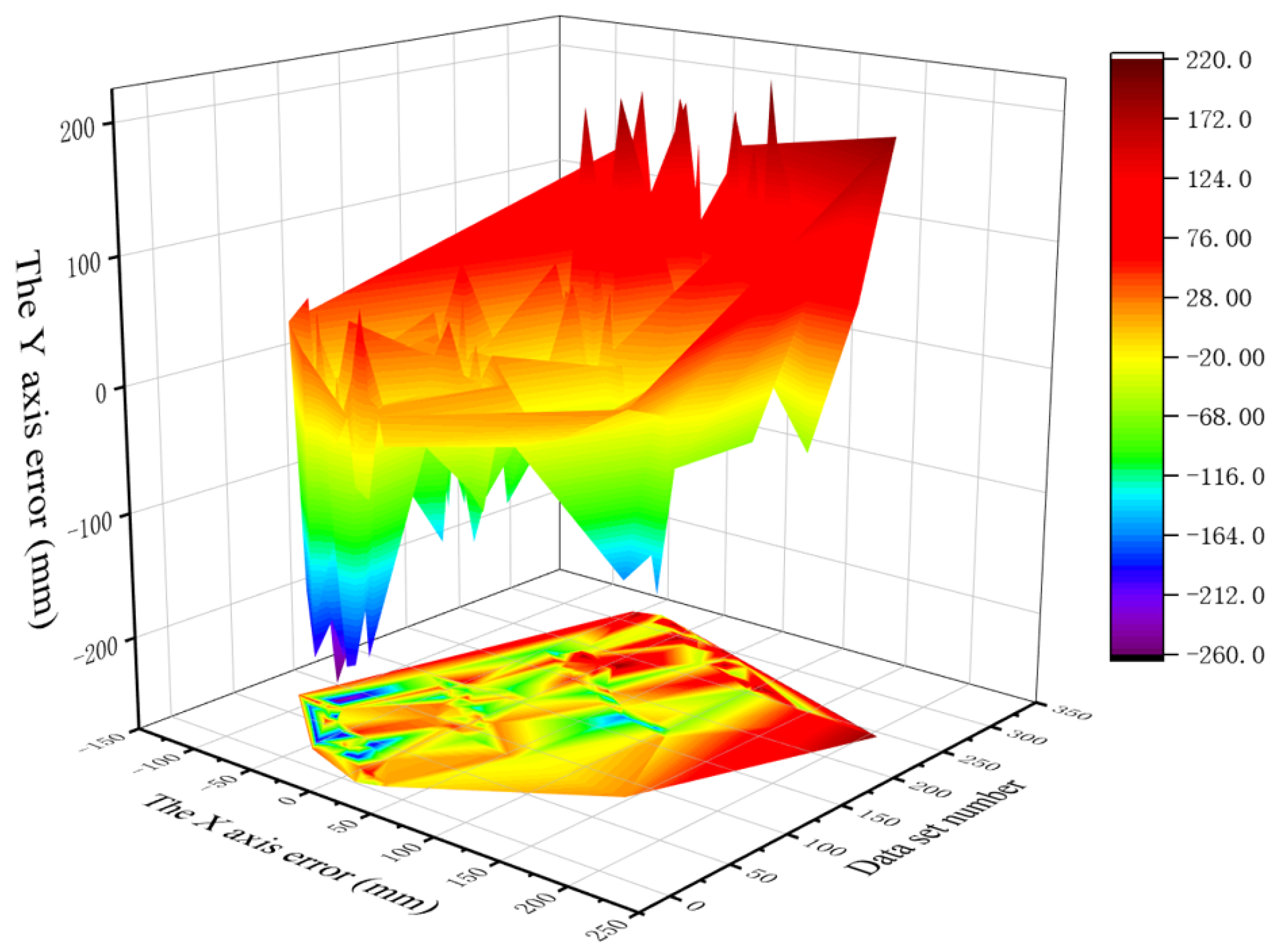
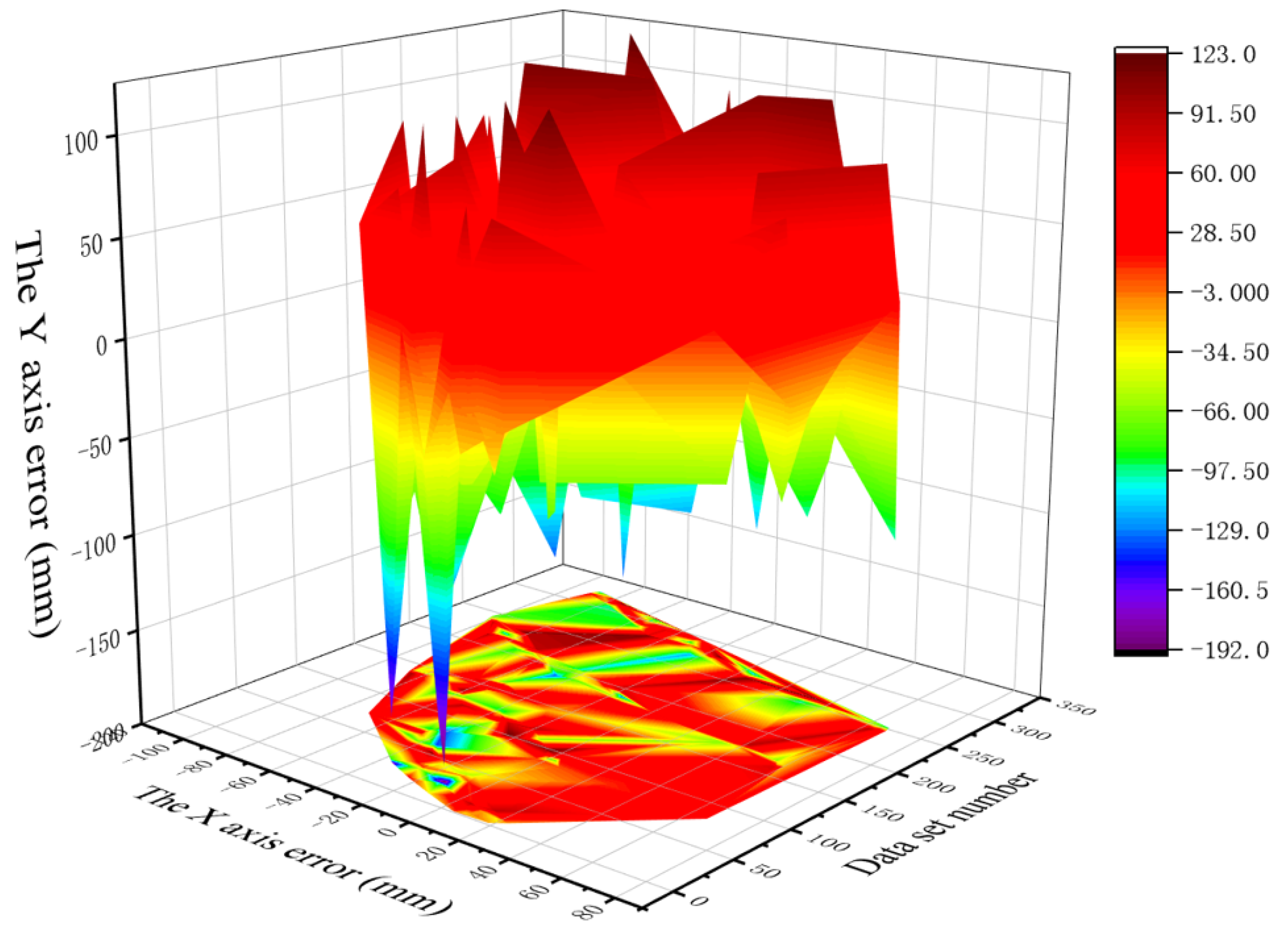
- (i)
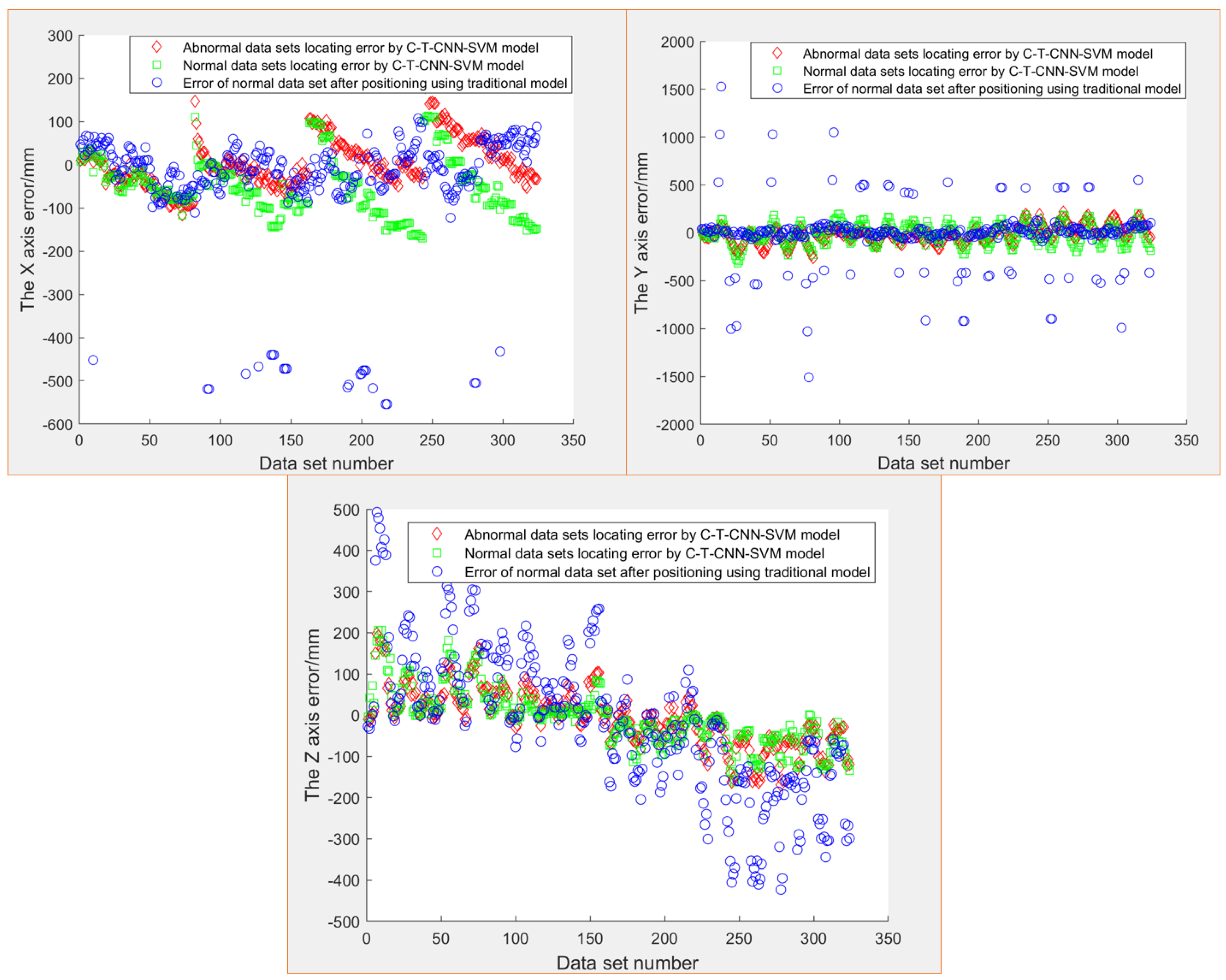
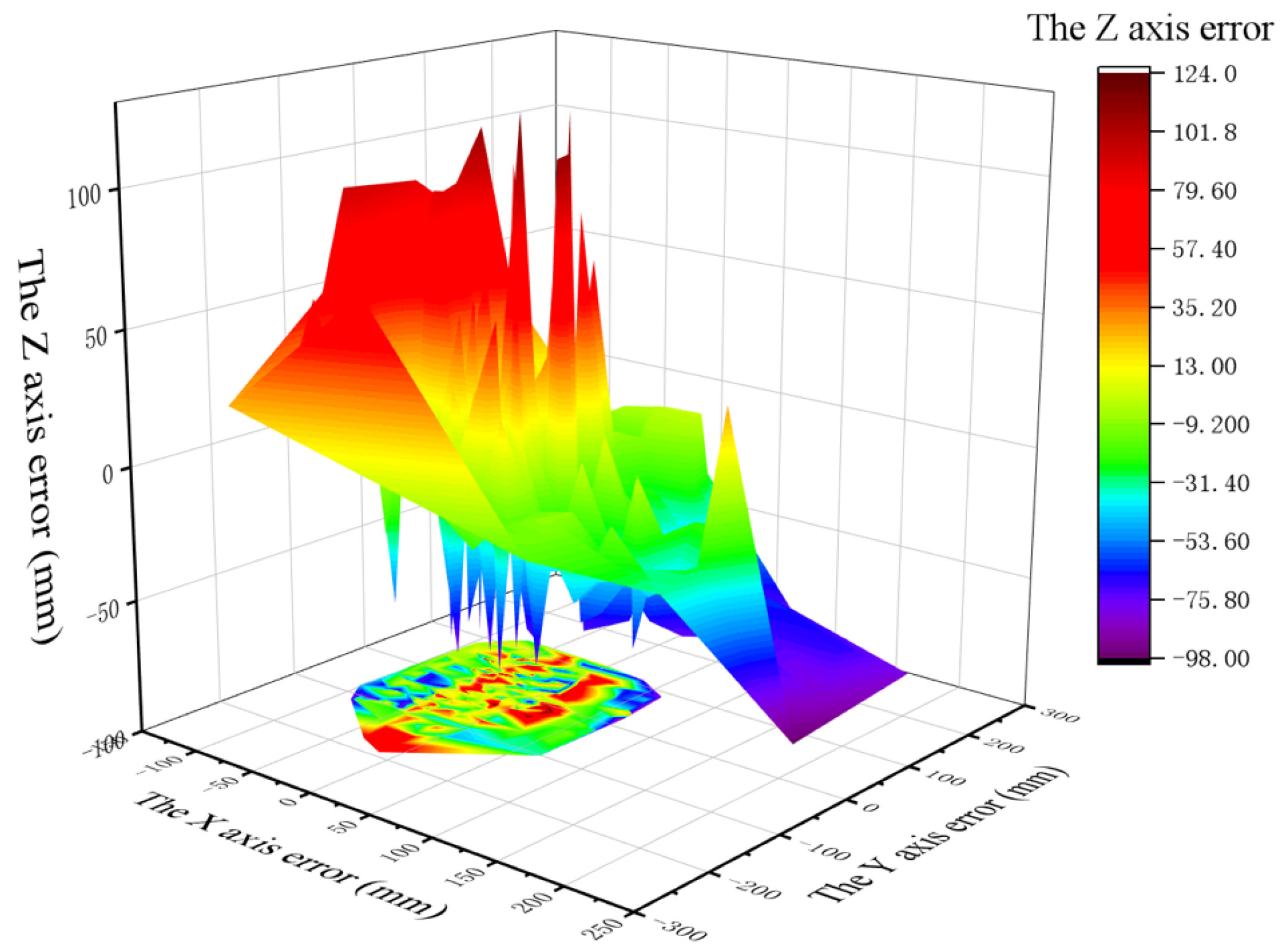
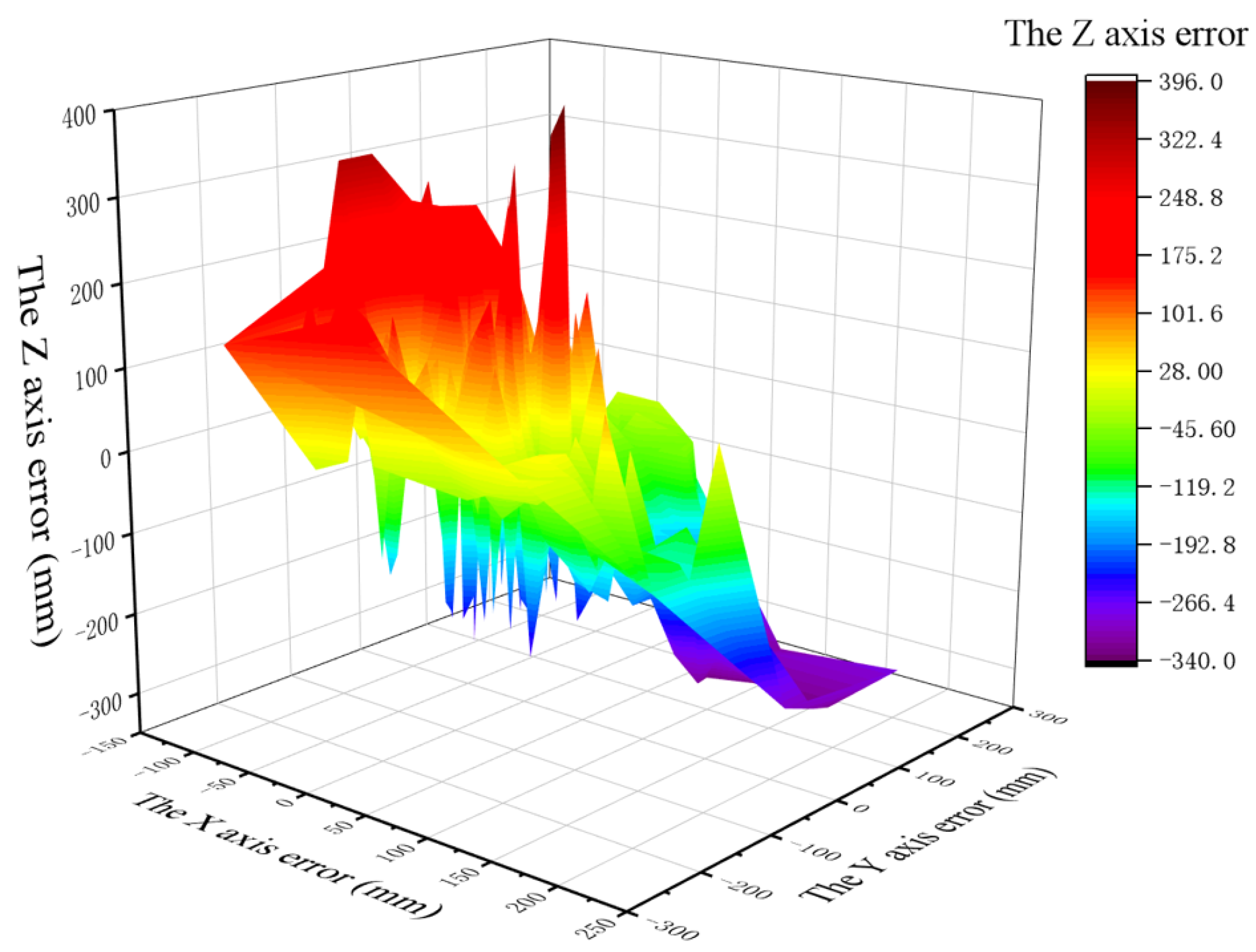
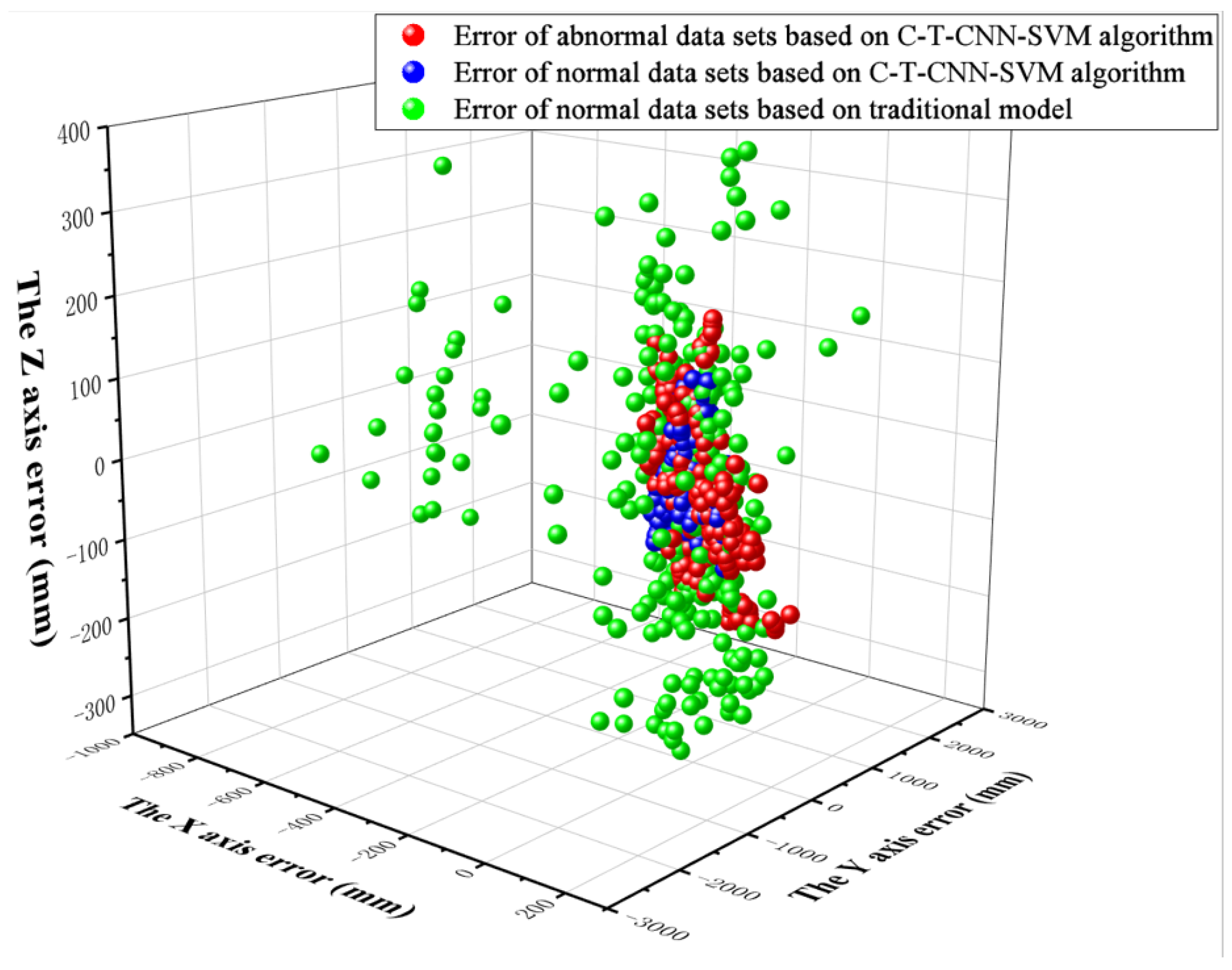
- It can be seen from Figure 10 that, under the model in this paper, the one-dimensional error after target positioning is within 175 mm on the X-axis and Y-axis. The X-axis error of normal data sets is generally less than 60 mm, and the Y-axis error is generally less than 75 mm. The error of the X-axis and Y-axis of an abnormal data set is generally less than 100 mm. The Z-axis error is larger than that of the X-axis and Y-axis, but generally less than 200 mm.
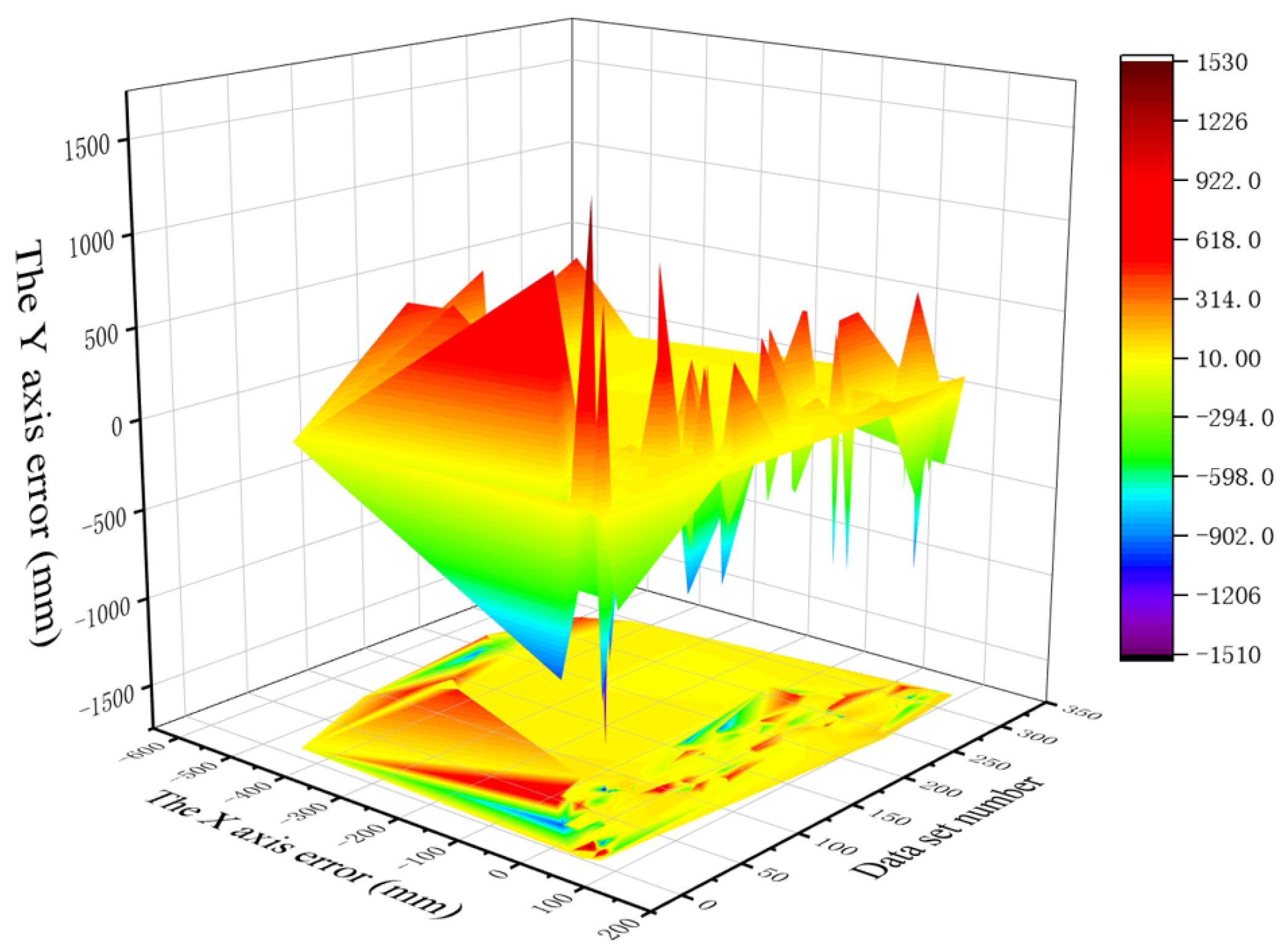
- (ii)
- For comparison, although the coordinate error obtained by the traditional model is within 200 mm under most data sets, it has an abnormal error as high as 600 mm. In terms of Y-axis error, compared with the C-T-CNN-SVM model, although the error of the traditional model is within 500 mm under most data sets, there exists an abnormal result of 1000 mm. In terms of Z-axis error, the coordinate errors obtained by the traditional model are all within 200 mm under most data sets, though there remains an error of 500 mm.
4.2.2. 2D Accuracy Analysis of the Algorithms
4.2.3. 3D Accuracy Analysis of the Algorithms
4.3. Validity Analysis of the Algorithms
4.3.1. Cumulative Error Probability Analysis of the Algorithms
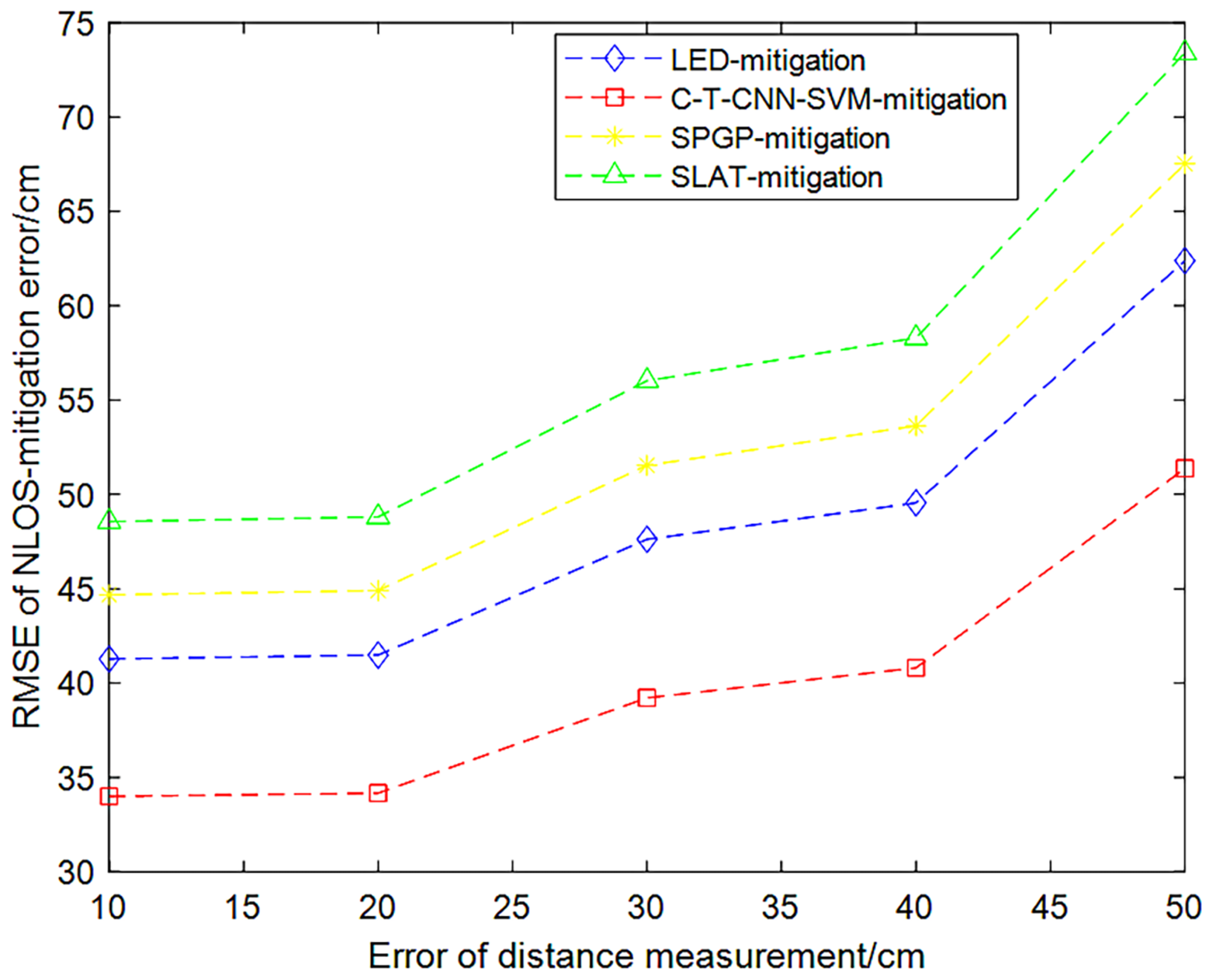
4.3.2. Root-Mean-Square Difference Analysis of the Algorithms
4.4. Complexity Analysis of the Proposed Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kok, M.; Hol, J.D.; Schon, T.B. Indoor Positioning Using Ultrawideband and Inertial Measurements. IEEE Trans. Veh. Technol. 2015, 64, 1293–1303. [Google Scholar] [CrossRef]
- Choi, J.W.; Quan, X.; Cho, S.H. Bi-Directional Passing People Counting System Based on IR-UWB Radar Sensors. IEEE Internet Things J. 2017, 5, 512–522. [Google Scholar] [CrossRef]
- Ahmed, S.; Wang, D.; Park, J.; Cho, S.H. UWB-gestures, a public dataset of dynamic hand gestures acquired using impulse radar sensors. Sci. Data 2021, 8, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Tiemann, J.; Pillmann, J.; Wietfeld, C. Ultra-Wideband Antenna-Induced Error Prediction Using Deep Learning on Channel Response Data. IEEE Veh. Technol. Conf. 2017. [Google Scholar] [CrossRef]
- Choliz, J.; Eguizabal, M.; Hernandez-Solana, A.; Valdovinos, A. Comparison of algorithms for uwb indoor location and tracking systems. In Proceedings of the 2011 IEEE 73rd Vehicular Technology Conference (VTC Spring), Budapest, Hungary, 15–18 May 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, J.; Wang, J.; Han, H.; Yang, D. An UWB/Vision Fusion Scheme for Determining Pedestrians’ Indoor Location. Sensors 2020, 20, 1139. [Google Scholar] [CrossRef]
- Shi, G.; Ming, Y. Survey of Indoor Positioning Systems Based on Ultra-wideband (UWB) Technology. In Wireless Communications, Networking and Applications; Lecture Notes in Electrical Engineering; Springer: New Delhi, India, 2015; pp. 1269–1278. [Google Scholar] [CrossRef]
- Liu, F.; Li, X.; Wang, J.; Zhang, J. An Adaptive UWB/MEMS-IMU Complementary Kalman Filter for Indoor Location in NLOS Environment. Remote. Sens. 2019, 11, 2628. [Google Scholar] [CrossRef]
- Guvenc, I.; Chong, C.-C. A survey on TOA based wireless localization and NLOS mitigation techniques. IEEE Commun. Surv. Tuts. 2009, 11, 107–124. [Google Scholar] [CrossRef]
- Guvenc, C.-C.; Chong, C.C.; Watanabe, F.; Inamura, H. NLOS identification and weighted least-squares localization for UWB systems using multipath channel statistics. EURASIP J. Adv. Signal Process. 2008, 36, 271984. [Google Scholar]
- Li, X.; Cai, X.; Hei, Y.; Yuan, R. NLOS identification and mitigation based on channel state information for indoor WiFi localisation. IET Commun. 2017, 11, 531–537. [Google Scholar] [CrossRef]
- Marano, S.; Gifford, W.M.; Wymeersch, H.; Win, M.Z. NLOS identification and mitigation for localization based on UWB experimental data. IEEE J. Sel. Areas Commun. 2010, 28, 1026–1035. [Google Scholar] [CrossRef]
- Wymeersch, H.; Marano, S.; Gifford, W.M.; Win, M.Z. A Machine Learning Approach to Ranging Error Mitigation for UWB Localization. IEEE Trans. Commun. 2012, 60, 1719–1728. [Google Scholar] [CrossRef]
- Zhu, Y.; Xia, W.; Yan, F.; Shen, L. NLOS Identification via AdaBoost for Wireless Network Localization. IEEE Commun. Lett. 2019, 23, 2234–2237. [Google Scholar] [CrossRef]
- Zhou, Z.; Yang, Z.; Wu, C.; Shangguan, L.; Cai, H.; Liu, Y.; Ni, L.M. WiFi-based indoor line-of-sight identification. IEEE Trans. Wireless Commun. 2015, 14, 6125–6136. [Google Scholar] [CrossRef]
- Xiao, F.; Guo, Z.; Zhu, H.; Xie, X.; Wang, R. AmpN: Real-time LOS/NLOS identification with WiFi. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017. [Google Scholar]
- Zhang, S.; Yang, C.; Jiang, D.; Kui, X.; Guo, S.; Zomaya, A.Y.; Wang, J. Nothing Blocks Me: Precise and Real-Time LOS/NLOS Path Recognition in RFID Systems. IEEE Internet Things J. 2019, 6, 5814–5824. [Google Scholar] [CrossRef]
- Wang, F.; Xu, Z.; Zhi, R.; Chen, J.; Zhang, P. Los/nlos channel identification technology based on cnn. In Proceedings of the 2019 6th NAFOSTED Conference on Information and Computer Science (NICS), Hanoi, Vietnam, 12–13 December 2019. [Google Scholar]
- Yu, K.; Wen, K.; Li, Y.; Zhang, S.; Zhang, K. A novel NLOS mitigation algorithm for UWB localization in harsh indoor environments. IEEE Trans. Veh. Technol. 2018, 68, 686–699. [Google Scholar] [CrossRef]
- Yozevitch, R.; Moshe, B.B.; Weissman, A. A Robust GNSS LOS/NLOS Signal Classifier. Navigation 2016, 63, 429–442. [Google Scholar] [CrossRef]
- Yang, X. NLOS Mitigation for UWB Localization Based on Sparse Pseudo-Input Gaussian Process. IEEE Sens. J. 2018, 18, 4311–4316. [Google Scholar] [CrossRef]
- Li, W.; Jia, Y.; Du, J.; Zhang, J. Distributed Multiple-Model Estimation for Simultaneous Localization and Tracking With NLOS Mitigation. IEEE Trans. Veh. Technol. 2013, 62, 2824–2830. [Google Scholar] [CrossRef]
- Van Nguyen, T.; Jeong, Y.; Shin, H.; Win, M.Z. Machine learning for wideband localization. IEEE J. Sel. Areas Commun. 2015, 33, 1357–1380. [Google Scholar] [CrossRef]
- Singh, A.; Kotiyal, V.; Sharma, S.; Nagar, J.; Lee, C.-C. A Machine Learning Approach to Predict the Average Localization Error With Applications to Wireless Sensor Networks. IEEE Access 2020, 8, 208253–208263. [Google Scholar] [CrossRef]
- AlHajri, M.I.; Ali, N.T.; Shubair, R.M. Indoor Localization for IoT Using Adaptive Feature Selection: A Cascaded Machine Learning Approach. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2306–2310. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhou, T. UWB indoor positioning algorithm based on TDOA technology. In Proceedings of the 2019 10th International Conference on Information Technology in Medicine and Education (ITME), Qingdao, China, 23–25 August 2019. [Google Scholar]
- Huan, L.; Bo, R. Wireless location for indoor based on UWB. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015. [Google Scholar]
- Badawika, A.; Kolakowski, J. UWB positioning system architecture based on paired anchor nodes. In Proceedings of the 2014 20th International Conference on Microwaves, Radar and Wireless Communications (MIKON), Gdansk, Poland, 16–18 June 2014; pp. 1–4. [Google Scholar] [CrossRef]
- He, K.; Sun, J. Convolutional neural networks at constrained time cost. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Wang, G.; Chen, H.; Li, Y.; Ansari, N. NLOS Error Mitigation for TOA-Based Localization via Convex Relaxation. IEEE Trans. Wirel. Commun. 2014, 13, 4119–4131. [Google Scholar] [CrossRef]
- Venkatesh, S.; Buehrer, R.M. NLOS Mitigation Using Linear Programming in Ultrawideband Location-Aware Networks. IEEE Trans. Veh. Technol. 2007, 56, 3182–3198. [Google Scholar] [CrossRef]
- Su, Z.; Shao, G.; Liu, H. Semidefinite Programming for NLOS Error Mitigation in TDOA Localization. IEEE Commun. Lett. 2017, 22, 1430–1433. [Google Scholar] [CrossRef]
- Bhatti, M.A.; Riaz, R.; Rizvi, S.S.; Shokat, S.; Riaz, F.; Kwon, S.J. Outlier detection in indoor localization and Internet of Things (IoT) using machine learning. J. Commun. Netw. 2020, 22, 236–243. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Y.; Gu, Y.; Yang, W. An efficient machine learning approach for indoor localization. China Commun. 2017, 14, 141–150. [Google Scholar] [CrossRef]
- Williamson, D.J.; Burn, G.L.; Simoncelli, S.; Griffié, J.; Peters, R.; Davis, D.M.; Owen, D.M. Machine learning for cluster analysis of localization microscopy data. Nat. Commun. 2020, 11, 1493. [Google Scholar] [CrossRef]
- Kristensen, J.B.; Ginard, M.M.; Jensen, O.K.; Shen, M. Non-line-of-sight identification for UWB indoor positioning systems using support vector machines. In Proceedings of the 2019 IEEE MTT-S International Wireless Symposium (IWS), Guangzhou, China, 19–22 May 2019. [Google Scholar] [CrossRef]
- Yin, Z.; Cui, K.; Wu, Z.; Yin, L. Entropy-Based TOA Estimation and SVM-Based Ranging Error Mitigation in UWB Ranging Systems. Sensors 2015, 15, 11701–11724. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Ahn, C.K.; Chen, X. Seamless indoor pedestrian tracking by fusing INS and UWB measurements via LS-SVM assisted UFIR filter. Neurocomputing 2020, 388, 301–308. [Google Scholar] [CrossRef]
- Ying, R.; Jiang, T.; Xing, Z. Classification of transmission environment in UWB communication using a support vector machine. In Proceedings of the 2012 IEEE Globecom Workshops, Anaheim, CA, USA, 3–7 December 2012; pp. 1389–1393. [Google Scholar] [CrossRef]
- Yin, W.; Yang, X.; Zhang, L.; Oki, E. ECG Monitoring System Integrated with IR-UWB Radar Based on CNN. IEEE Access 2016, 4, 1. [Google Scholar] [CrossRef]
- Abbasi, A.; Liu, H. Novel CNN and Hybrid CNN-LSTM Algorithms for UWB SNR Estimation. In Proceedings of the 2021 IEEE 11th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 27–30 January 2021. [Google Scholar]
- Maitre, J.; Bouchard, K.; Gaboury, S. Fall Detection With UWB Radars and CNN-LSTM Architecture. IEEE J. Biomed. Heal. Inform. 2021, 25, 1273–1283. [Google Scholar] [CrossRef] [PubMed]
- Schmid, L.; Salido-Monzú, D.; Wieser, A. Accuracy assessment and learned error mitigation of UWB ToF ranging. In Proceedings of the 2019 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Pisa, Italy, 30 September–3 October 2019. [Google Scholar]
- Niitsoo, A.; Edelhäußer, T.; Mutschler, C. Convolutional neural networks for position estimation in tdoa-based locating systems. In Proceedings of the 2018 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]




| Symbols | Description |
|---|---|
| c | The electromagnetic wave propagation speed |
| One-way flight time for TOF ranging | |
| Anchor point | |
| e | Error threshold |
| Data set to be processed | |
| Distance measurements of anchor to target | |
| X | Set of machine learning samples |
| Non-linear mapping | |
| Input vectors for machine learning samples | |
| Coordinates of the target point to be located | |
| Position of the target to be located in the hybrid weighting algorithm | |
| Error vector of the hybrid weighting algorithm | |
| Q | Covariance matrix of TOF range values |
| Coordinates of the target point calculated using the kth method | |
| Difference between coordinates of target point to anchor point i and 1 | |
| Square of the difference between true and measured values | |
| Weighting factor |
| SVM | CNN | C-T | C-T-CNN-SVM | |
|---|---|---|---|---|
| Time (FLOPS) | 20 G | 133.4 G | 15 G | 168.4 G |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Jiao, Y.; Yang, W.; Li, X.; Wang, Y. A Method for UWB Localization Based on CNN-SVM and Hybrid Locating Algorithm. Information 2023, 14, 46. https://doi.org/10.3390/info14010046
Gao Z, Jiao Y, Yang W, Li X, Wang Y. A Method for UWB Localization Based on CNN-SVM and Hybrid Locating Algorithm. Information. 2023; 14(1):46. https://doi.org/10.3390/info14010046
Chicago/Turabian StyleGao, Zefu, Yiwen Jiao, Wenge Yang, Xuejian Li, and Yuxin Wang. 2023. "A Method for UWB Localization Based on CNN-SVM and Hybrid Locating Algorithm" Information 14, no. 1: 46. https://doi.org/10.3390/info14010046
APA StyleGao, Z., Jiao, Y., Yang, W., Li, X., & Wang, Y. (2023). A Method for UWB Localization Based on CNN-SVM and Hybrid Locating Algorithm. Information, 14(1), 46. https://doi.org/10.3390/info14010046









