Abstract
When analyzing a financial asset, it is essential to study the trend of its time series. It is also necessary to examine its evolution and activity over time to statistically analyze its possible future behavior. Both retail and institutional investors base their trading strategies on these analyses. One of the most used techniques to study financial time series is to analyze its dynamic structure using auto-regressive models, simple moving average models (SMA), and mixed auto-regressive moving average models (ARMA). These techniques, unfortunately, do not always provide appreciable results both at a statistical level and as the Risk-Reward Ratio (RRR); above all, each system has its pros and cons. In this paper, we present CryptoNet; this system is based on the time series extraction exploiting the vast potential of artificial intelligence (AI) and machine learning (ML). Specifically, we focused on time series trends extraction by developing an artificial neural network, trained and tested on two famous crypto-currencies: Bitcoinand Ether. CryptoNet learning algorithm improved the classic linear regression model up to 31% of MAE (mean absolute error). Results from this work should encourage machine learning techniques in sectors classically reluctant to adopt non-standard approaches.
1. Introduction
Financial time series trend extraction is a common practice among traders and institutions [1,2,3]. For all of them, it is vital to understand that their future trend will be upward, downward, or sideways (i.e., lateral movements). Financial traders include the trend extraction activity within their trading framework or strategy. This algorithm deals with a single paramount purpose: maximizing the gains and minimizing the losses by executing entry and exit positions into the markets. It does not matter whether predicted trends provided by the models are upwards or downwards, as there are instruments such as options and futures, which enable the operator to speculate in both directions.
Traders use many different models to achieve this goal [4,5]. Very often, the simplest the model, the better because traders need to implement their analysis very quickly [6,7]. Proposing state-of-the-art systems that estimate classic patterns [8]. The most exciting aspect is that nowadays, 80% of the operations made in the financial markets are managed by software (programmed algorithms) developed after studying the mathematical and statistical level of all the financial instruments. Therefore, it is far easier to develop a strategy based on technical analysis and probabilistic models. Still, such systems are not always profitable, and each mathematical system has pros and cons. In contrast, AI models are very complex and time-consuming, so the eventual benefits do not outweigh the cost of implementing and using them. Machine learning and related models such as artificial neural networks are not so widespread among financial traders. This phenomenon is not limited to finance; there seems to be short confidence in machine learning-based models [9].
In this paper, we present CryptoNet, which is an Artificial Autoregressive Neural Network (ARNN) developed specifically for analyzing the weekly closing price time series of the two most popular cryptocurrencies by market capitalization, namely Bitcoin and Ether; they are giving a sense of digital revolution [10]. Institutional funds and retail traders need to understand if their future trend will be upward, downward, or stable (i.e., lateral movements). Sometimes the models are very complex and time-consuming, so the eventual benefits do not overcome the cost of implementing and using them. In addition, although cryptocurrencies have become very popular, few works propose time series estimates. In order to bridge the gap of difficulty, which is one of the major stumbling blocks in the application of machine learning-based algorithms in the financial domain, we propose an opensource, flexible and usable framework.
CryptoNet has been tested on the weekly closing prices of Bitcoin and Ether, the two major cryptocurrencies in the world for market capitalization. Cryptocurrencies are known for their highly volatile movements and tend to move in cycles through significant growth and contraction phases. Therefore, the problem linked with the heteroscedasticity of cryptocurrencies is far more relevant than in any other financial asset. Although cryptocurrencies are known for their highly volatile movements and the fact that they tend to move in cycles going through significant growth and contraction phases, we have demonstrated that CryptoNet manages to perform well. The choice of data on which CryptoNet was trained and tested is due to the etymology of cryptocurrency volatility. Generally, the higher the timeframe, the more evident the cycles and the trend; therefore, the price signal becomes more “predictable”. For this reason, we have chosen a weekly timeframe to reduce the noise caused by local highs and lows caused by market fluctuations.
The paper is organized as follows: related work will be described in Section 2; Section 3 describes methods used for forecasting; Section 4 presents the system architecture while Section 5 describes the experiments and experimental result respectively and a use case example; future work and conclusion are presented in Section 6.
2. Related Work
There are few relevant works published during the last 20 years regarding the application of machine learning to financial markets forecast. In 1990, Schoneburg et al. in [11] conducted the first studies using data from a randomly selected German stock market as a machine learning method for their back-propagation architecture, from which they, unfortunately, failed to get the best out of because of the limitations that arose, including parameterization. In the following years, many others tried to tackle this task by adapting data and algorithms to their purpose. Patel et al. [12] for predicting the direction of stock movement and price index of Indian stock markets have proposed an excellent overview comparing classical Machine Learning models such as Naive Bayes and Support Vector Machines and more advanced ones such as Neural Network. Reference [13] model cointegrated time series using the ARX (AutoRegressive with eXogenous inputs) model. Thus, by combining factors outside the model, they obtain good results. Until then, the representation of the input data was derived from the technical parameters of stock trading data (opening, high, low, and closing prices) and the representation of these technical parameters as deterministic trend data. However, the work of Patel et al. [12] has limitations. The authors acknowledge that there is a need to work on time series prediction by discretizing continuous data from index movements differently. Sometime later, Khaidem et al. [4] argued that the inherent volatility of the stock market makes the forecasting task challenging. In this regard, they proposed to use some of the derived technical indicators, such as the Relative Strength Index (RSI) and the stochastic oscillator, given by some NASDAQ stocks, by applying a Random Forest model. Khaidem et al. [4] highlight how the nature of the problem is non-linear, and although the proposed model obtains discrete results, they see technologies such as deep learning as the solution to their problems. One of the most advanced classification models developed recently and applied to financial market stock prediction was proposed by Kusuma et al. [5]. They generated complex deep convolutional artificial neural networks to recognize recent patterns in data to predict the short-term evolution of a few Indonesian companies’ stock prices. In addition to the technological innovation brought by the neural model used, the nature of the input also changes because it is a set of financially relevant image data as information (candlestick patterns) and provides future dynamics of price signals over a given period, achieving good results. Other neural network models applied with the same objective but with a regressive approach could be found in [14,15,16]. All the researchers above exploit the advantages of an intrinsic non-linear architecture of multi-layer neural networks to regress financial datasets to create valid substitutes for some mainstream models. This trust is rewarded by non-standard models such as artificial neural networks and machine vectoring, which seem to improve actual data with excellent results in terms of accuracy. Despite their power and efficiency, these approaches focus on the accuracy of short/medium-term price prediction. A series of parallel works add a set of indicators relative to sentiment to the numerical data. Behera et al. [17] propose a model that can estimate time series using heterogeneous data from online platforms, i.e., social media and time series. In contrast, Abayomi-Alli et al. [18] propose a model for data augmentation applicable in critical contexts, especially when financial patterns are still unknown and there are no long time series to analyze.
CryptoNet aims to use machine learning techniques by developing a flexible auto-regressive multi-layer Artificial Neural Network that is not limited to short-term trend extraction but focuses on trend extraction over a discrete period of time.
According to [19], the aim is not to produce accurate spot price forecasts, as they are not very useful in financial trading. What is more important is to anticipate long and sustained upward or downward movements, irrespective of the timeframe, to make the most of price bumps and falls.
Moreover, the discouraging complexity of some machine learning techniques pushes traders to prefer the use of classic trendlines, support, and resistance structures (the foundation of price action) which are discretionary variants of the well-known linear regression model. The simplicity, high-speed implementation, and computationally low-cost nature of the linear regression model have made it one of the most valuable tools for extracting trends on time series. Therefore our validation effort has been concentrated on demonstrating that machine learning cannot only replicate the power and flexibility of this mainstream model when extracting trends but also improve its data fitting capability, making it valid and not discouraging alternative for financial trading.
3. Methods Used For Forecasting
Before introducing CryptoNet are enumerated some available forecasting methods in predicting the stock prices. Starting from classical methods, technical analysis, through time series forecasting to CryptoNet.
3.1. Technical Analysis
Technical analysis (TA) consists of well-defined rules and indicators. The indicators and rules are committed to identifying and explaining the regularity of historical price dynamics. The moving average (MA) method is one of the most widely used TA methods. This method compares market prices or the index with the long MA. The MA method is easy to use and apply in investment decision-making, but it can generate significant forecast value errors [1]. TA is used during trading in the stock market to make “buy” and “sell” decisions. Technical specialists believe that a detailed study of stock price charts and graphs reveals regular and recurring patterns of price behavior, which are likely to be repeated in the future. In fact, this type of stock trader ignores all the fundamental data such as sales, earnings, profits, dividends, business prospects, etc. Traders who use TA fortuitously argue that these factors have already been taken into account by the market and are fully reflected in the current market price of a stock; this approach is suitable for speculators and short-term stock traders.
3.2. Fundamental Analysis
On the other side of the fence is fundamental analysis. Fundamental analysis, as stated in Section 2, is a type of analysis for making investment decisions. Traders on this site are called fundamentalists, who are long-term investors. These practitioners aim to estimate the intrinsic value of a company’s stock by studying its sales, earnings, profits, dividends, management competence, and a variety of other economic factors that affect the company’s profitability and business prospects. After making this study, the stock price of a particular company is outlined, and this price is considered the intrinsic or actual value of the stock, as it reflects the intrinsic value. Analysts, with the help of the intrinsic price judge whether the stock is currently overvalued or undervalued in the stock market.
3.3. Time Series Forecasting
The two theories of analyst thinking seem to have defined all possible methodologies for analyzing stock movements. In recent years, data processing has become fundamental in many applications. Time series forecasting by analyzing aggregate time series data and information attempts to predict the near future based on past data. Therefore, several time series analysis techniques have arisen, such as mixed moving average autoregression (ARMA) [20] and multiple regression models [21]. Time series prediction, such as most data-driven models, finds a trend in past data to predict future data. Consequently, as in all data-driven models, the more past data, the easier it is to find a pattern. However, if the history of action is short, accurate analysis and prediction for such sparse past data are complex. Therefore, neural networks are described as promising tools to use in this scenario.
3.4. Machine Learning in Stock Market
Although time series seems to have taken the scenario in mote applications, machine learning combined with human habits makes a difference. In particular, when it comes to financial trading, one timeframe might work better than another, meaning that one trader might record better results working with an hourly timeframe. At the same time, another might prefer a more relaxed approach by following price dynamics weekly (or monthly). It depends on personal attitudes and preferences, and the model adopted. Regressive models have the advantage of being somewhat neutral on the choice of timeframe. However, when it comes to financial analysis, they perform better in trend extraction when the timeframe is higher than usual (daily, weekly, monthly...) due to noise reduction and better handling of outliers.
3.5. Neural Networks in Stock Market
The vast field of Machine Learning shows multiple models, each with its peculiarities. In the field of stock market investment, there is high risk because of its indecision and volatility; consequently, predicting the behavior of stock prices is very difficult because of their nonlinear and complex demeanor. The main application of artificial neural networks is in areas where issues are ill-defined, data are incomplete or noisy, and the environment itself is dynamic. Because neural networks can adapt to noisy data and establish an input-output relationship of nonlinear data, it is possible to predict the behavior of stock prices. We will see later how these models can produce reasonable results.
3.6. CryptoNet
We propose CryptoNet, this framework uses a multi-layer Autoregressive Artificial Neural Network (The code is available at https://github.com/LeonardRanaldi/CryptoNet, accessed on 10 September 2022). Training this type of model requires the choice of a specific dataset that could influence the performance of the model and the effectiveness of its application. As introduced in Section 2, some patterns rather than timeframes may work better depending on end goals, trading habits, and other factors. CryptoNet is an elastic and performant machine learning model that follows the user through data retrieval (CryptoNet-1), pre-processing (CryptoNet-2) and training and predictions (CryptoNet-3).
4. Architecture
This section introduces our CryptoNet (Section 4.2) along its system (Section 4.3). CryptoNet our model is a lightweight and modular Neural Network. Its use is proposed with ETH and BTC but can be adapted to the needs of any other altcoin. Some preliminary notions on the model used are given in Section 4.1.
4.1. Autoregressive Model
In an autoregressive model, the goal is to predict the variable of interest using a linear combination of the past values of the variable “self” in Auto Regression (AR), which indicates that the variable is regressed against itself [22]. AR is similar to a multiple regression but with lagged values of the time-series as predictors. We refer to this as an model, an auto-regressive model of order n can be written as:
where are the n terms used to predict and b is the bias. The weights , by which each of the n lags are multiplied, are also referred to as the AR-coefficients.
4.2. Neural Network Auto-Regressive Model
We use the AR-Neural Network-based model (ARNN), which mimics the traditional AR process with a neural network.
It is not very far from the original AR because it is designed so that the parameters of its first layer are equivalent to the AR coefficients.
The ARNN we developed is a straightforward multi-layer auto-regressive artificial neural network implemented in a very intuitive and interactive simulator coded in Perl. ARNN can optionally be extended with hidden layers to achieve greater forecasting accuracy.
In order to fit the ARNN model to the same objective as Classic-AR optimized by least squares, the loss term is Mean Squared Error (MSE):
4.3. System Configuration
CryptoNet is very user-friendly and offers the possibility of changing the components of the Neural Network as the user chooses. In the following sections, the essential features are listed and described.
4.3.1. Outputs Neurons
The number of output neurons could be chosen via the command line at the beginning of the simulation. Each output neuron provides a prediction of the time series. The software will output the average value of the N neurons chosen by the user. Indeed, from a very architectural point of view, the neural model could be considered an overlap of N multi-layer auto-regressive neural networks.
4.3.2. Hidden Neurons
The number of hidden neurons has a significant impact on final results, but there is no fixed rule to follow in this respect [23]. Considering that a single layer is enough to approximate any function mapping a finite number of input variables into a finite number of output variables, the stochastic nature of the problem (which forced us to choose an arbitrary number of output neurons) led us to include several hidden neurons which is twice the number of inputs (bias excluded). The number of hidden neurons could not be huge as they would soar above computational costs during the training phase. Including an excessive number of hidden neurons could lead to overfitting, which is when a model is sticking too much to the actual values of the signal so that it becomes unable to extract its trend, which is the purpose of our model.
4.3.3. Input Neurons
The number of input neurons is the number of lagged values of the time series we want to analyze. The choice is even more discretionary than choosing the correct number of hidden neurons and is based on personal trading attitudes and the intrinsic dynamics of time series. From a trading perspective, the BTC and ETH weekly prices time series demonstrate, from previous experience, a clear trend (either upward or downward) by considering at most minuscule five lagged values. Therefore, we choose to include five input neurons (bias excluded). In the end, experience and discretionary analysis conducted on each time series are pivotal for the choice of net architecture and must be conducted at the early stages of the research.
4.3.4. Bias
The software allows the user to choose the number of predictions generated by the model. The projections are hugely influenced by the value of synaptic weights estimated during the training phase, including the bias. However, there is no clear guidance in the literature on the best way to treat them when generating trends over several epochs in the future. While [22] would suggest treating it as a pure white noise, delta-rule algorithm purists see it as a mere deterministic variable with its proper weight. The problem with the first approach is that the model could fail in extracting future trends, as the path is random. On the other hand, if we ignore the chaotic nature of financial signals, we could experience the opposite problem: the path does not demonstrate any randomness, which is unrealistic.To balance the two aspects above the time series forecast, we created a semi-deterministic bias, floating around the weight value estimated by the delta-rule algorithm. The purpose was to introduce a stochastic element into a purely deterministic model to make it more realistic when predicting financial time series.
5. Experiments
We aim to investigate whether CryptoNet can be used to create neural network architectures where the prediction is useful: (1) improve time-series predictions on non-linear data, and (2) give the user the possibility of modeling the model he uses. The rest of the section describes the time slot from which the data came and the reasons for the choice, the experimental set-up, the quantitative experimental results of CryptoNet and discusses how CryptoNet can be used to predict time series by neural networks over examples.
5.1. Dataset
In Figure 1, we can observe CryptoNet-1 and CryptoNet-2 where an ARNN is used to provide and pre-process. In this work, we have chosen to work with cryptocurrencies. The reason that led us to work on cryptocurrencies is the explicit cyclic behavior demonstrate by the BTC and ETH during the period, which could badly stress the classic prediction models. At the same time, we wanted to exalt the heuristic approach proper to machine learning by letting the model learn the intrinsic nonlinearities. As seen in Figure 2, we trained and tested the developed model over a sample of 172 weekly prices, where it is evident that the first speculative bubble attempt occurred in the middle of 2018 and 2020. In the Table 1, we reported the training and test periods of both BTC and ETH. The reason is that BTC, as the leader of the crypto sector, imposes itself as a trend generator for the other alternative coins. As the crypto market is not even close to getting off its maturity phase, the correlation between BTC and every successful altcoin is still very high and positive. In this regard, ETH does not make an exception, even if sometimes it exhibits different dynamics due to its technological framework and use cases, which differ substantially from those provided by BTC.
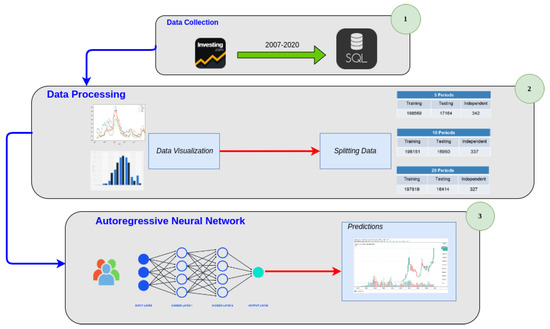
Figure 1.
The figure shows the different components of the CryptoNet.
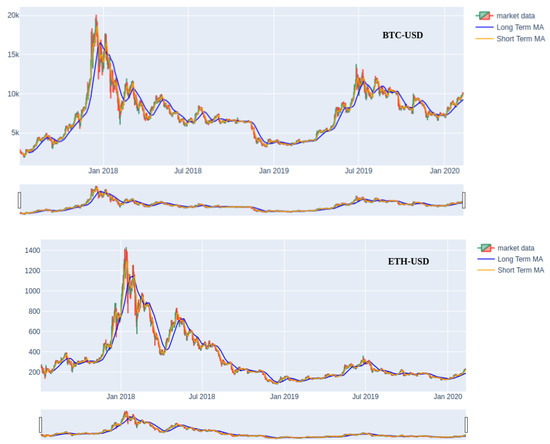
Figure 2.
Bitcoin (upper) and Ether (lower) time series.

Table 1.
ARNN time series parameters and main statistics.
Before the training phase took place, prices were scaled in order to speed up the backpropagation process. We have used the “maximum absolute value’’ scaler. The test set is formed by the remaining 20% of the original dataset, which includes the ongoing crypto bubble we have been experiencing since March 2020. The purpose was to train the neural model on a period when the expanding and contracting dynamics were fully completed to determine whether the model could have predicted the following expansion phase (trend extraction).
This is the reason why we concentrated our analysis on a weekly timeframe (closing prices) by choosing to regress Bitcoin (BTC) and Ether (ETH) on what we consider a significant period of their evolution going from 2007 to 2020.
5.2. Learning Algorithm
The ARNN is a backpropagation feedforward Artificial Neural Network.
In Figure 1, we can observe CryptoNet-3, where an ARNN is used to provide predictions about future movements.
Before starting the learning process, the weights are initialized stochastically with a linear congruential generator. Time-series values, as mentioned before, are passed through a time series value scaler to speed up the learning process. The learning process is applied to 80% of the whole dataset. The feedforward process is based on a non-linear sigmoid function, which generates the ultimate output of both hidden and output neurons. Hereafter, the delta rule is applied to propagate the error from the output layer back to the hidden one, and weights are updated accordingly. The process continues until the overall average error of every sample is minimized (online training). We choose the online training approach instead of a batch one because it is computationally cheaper, while the overall performance is almost the same. Moreover, based on an online supervised learning technique, it is easier to apply the net iteratively as a trend follower model instead of a trend extractor, even if this is not recommended in financial trading for a reason mentioned in the previous paragraphs. Once the training is finished, the net is tested on the remaining 20% of the dataset. The metric we used is the mean-absolute-error, which is useful whenever time series have many outliers and are affected by stochastic noise. This is the formula of MAE:
Moreover, near MAE we use the mean absolute percentage error (MAPE), also known as the mean absolute percentage deviation, which is a measure of prediction accuracy of a forecasting method in statistics. It usually expresses the accuracy as a ratio defined by the formula:
5.3. Simulator Architecture
The simulator we developed and named “predictor”, has been coded in Perl. We gave it a modular and easily expandable structure with few classes and one compact “main” routine in separate files. A user is asked to insert the number of output neurons that corresponds to the number of scenarios generated by the stochastic simulator, time-series id, cryptocurrency acronym, and the number of future epochs that should be generated.
5.4. Proposed Configurations
In order to simulate our model, we proposed three basic configurations. The first configuration, ARNN, is an ARNN with 3 input neurons, 3 layers, and 3 output neurons. The second ARNN, denoted by ARNN, is formed as 5 input neurons, 5 layers, and 5 output neurons. Finally, the third configuration, ARNN, is an ARNN with 10 input neurons, 10 layers, and 10 output neurons. In all proposed configurations, we kept the number of neurons in each hidden layer constant. For example, the hidden layer has three neurons in the small configuration. In the basic configuration, the inner layers have five neurons each, and so on. Recall that the number of input neurons coincides with the latest quotations. Consequently, if the number is 3, the last three quotations are considered. The other specific parameters are listed in Table 1.
6. Experimental Results and Discussions
In this section, we will demonstrate some experiments conducted on the ARNN for both Bitcoin and Ether on the period going from 3 July 2017 to 10 February 2020 (source https://tradingview.com accessed on 1 March 2020).
If we observe Figure 3, the cyclic structure of Bitcoin and Ether dynamics is evident. The 2017 speculative bubble bursts at the end of the same year. After a big downtrend move during 2018, the signal generated the first bump early in 2019 by initiating its ongoing rally in March 2020. To predict the recent price explosion from an un-trended period (June/July 2020, red circles in the charts below), we trained and tested the ARNN during a previous period dataset. Then, we used the synaptic weights to generate future trends simulations.
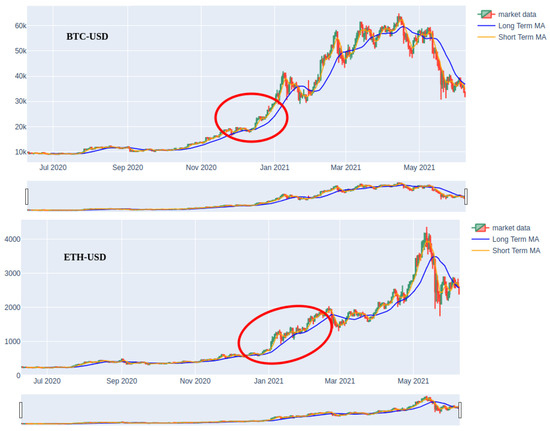
Figure 3.
Bitcoin (upper) and Ether (lower) parabolic moves and their previous lateral phase (red circles).
In particular, we generate 1000 simulations of future price dynamics by averaging them for both Bitcoin and Ether.
Main statistics and simulation parameters are reported in Table 1.
The extremely high volatility signals the risks of opening long or short positions in the crypto market. This could be noted by comparing the massive difference in value between the maximum and minimum price registered for each currency in a relatively short period (see Table above). For this reason, a trend extractor model (instead of a trend following one) is preferable, as it eliminates the intrinsic noise of financial time series and could also represent a strategic tool for opening long or short positions in the market. In this regard, a fundamental rule of financial trading is to open-close places as close in particular. Therefore, we generate 1000 simulations of future price dynamics by averaging them for Bitcoin and Ether.
Main statistics and simulation parameters are reported in the table as possible to generic areas of value, which are price ranges where the majority of trading volume took place on the previous trading day. Expected values generated by statistical models could represent areas used to formulate financial strategies. To clearly understand what price signals will do in the next ten weeks, starting from June 2020, we reported their average values over the entire dataset. As stated above, these values should be observed as a price attractor in the long term so that traders can formulate strategies accordingly. Moreover, they can set up long or short positions by comparing what comes out of ARNN with actual prices.
6.1. Use-Case Example
Bitcoin and Ether trends generated by the ARNN in the previous section are upward, indicating a possible bullish momentum within the coming weeks (then confirmed by the ongoing parabolic move). This could mean that a trader should consider opening long positions on Bitcoin and Ether. Speaking of Bitcoin, the dynamic attractor is higher than the average price, which signals solid bullish momentum over the period. On the contrary, the Ether dynamic attractor is lower than average, which is a weak bullish signal. This is maybe because all alternative coins investors, because of the positive correlation between them and the most capitalized cryptocurrency in the world, always wait for Bitcoin’s big moves to happen before taking any investment decision. Finally, it is important to stress that before getting any long or short positions on any financial assets, model outcomes should always be weighted with actual price action. For example, suppose prices are significantly above the increasing dynamic attractor. In that case, a generic trader should wait until it returns to it before entering an extended position to buy at lower prices. Vice versa, a situation when prices are well below a bullish dynamic attractor, should represent a reasonable opportunity of “buy low sell high” if price-action shows some good entry points. The simple linear regression model is maybe the most widespread trend-extractor in the world, applied at different levels in almost all fields of human action, from science (pure and applied) to finance. Speaking of financial trading, this model can speedily reveal the ongoing price trend of many assets. Admittedly, it is not the most advanced and complex model we could have been choosing for the validation phase. Still, it is the fastest, most flexible, and easily applicable model we can encounter in this sector. It is used by most traders worldwide and other consolidated techniques proper for price-action. The success of such a simple mathematical model is due to the advantageous ratio between its effectiveness in on-trend extraction and the low time cost when using or coding it for statistical analysis. The purpose of validating our ARNN against the simple regression model is to show how simple the application of a clear and well-conceived machine-learning technique could be, which usually scares people because of its heuristic nature, without renouncing performance.
The ARNN parameters estimated during the training phase described in the previous section are used here to calculate the MAE on the test set, consisting of 35 epochs (20 percent of the entire dataset). The simple regression model was estimated by applying the least squares method on 80 percent of the entire dataset, the same method used to estimate the weights of the ARNNs. The MAE was then calculated on the residual dataset.
As shown in Table 2, the ARNN outperforms the simple Linear Regression model on both Bitcoin and Ether time-series with a maximum performance improvement of 31% over the concerned period. The large and small, although they seem very close to the base, do not achieve optimal results, as we can see in Table 2. Finally, these results are also found with the MAPE metric, which demonstrated that the proposed base network achieves better results with more minor errors.

Table 2.
Comparison MAE and MAPE outputs.
6.2. Limitations
CryptoNet is an open-source framework that was built with the ultimate goal of empowering retail to use software for temporal data analysis and subsequent trend prediction. The newly proposed models can account for significant biases, such as the seesaw volatility of cryptocurrencies. Although these newly proposed models seem to work well, they are not guaranteed to work permanently, so they are not a sure means of making money.
7. Conclusions and Future Work
In this study, we developed CryptoNet, an auto-regressive multi-layer artificial neural network simulator to extract trends from financial time series. The CryptoNet has been applied to Bitcoin and Ether over a significant period to observe how a financial trader could use it to formulate investment strategies. The ARNN has been trained and tested on different (and statistically relevant) datasets. For example, the ongoing Bitcoin and Ether bull run have been predicted correctly by the trained CryptoNet. Finally, we validated the CryptoNet against the most widespread trend extractor model: the simple linear regression. The CryptoNet has improved the model’s performance up to 31% of MAE without renouncing simplicity and applicability easiness. The results show how a simply interactive Machine Learning software, easily applicable to any field of human knowledge, could replace the most used regression model in the world by improving its performance. For future works, we would like to extend this approach to other fields of science that are still reluctant to adopt it. We would also like to enable the human to insert particular rules into the neural network to control its behavior, as is widely performed in other fields with excellent results [24,25].
The greatest hope is that one day such a machine learning technique, which frightens the vast majority of practitioners because of its heuristic nature, may be more widely perceived as a viable alternative to other established models that are attractive because of their high effectiveness, low implementation costs and rapid exploitation.
Author Contributions
Conceptualization, L.R. and M.G.; methodology, F.F.; software, L.R.; validation, L.R. and M.G.; funding acquisition, L.R. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by L.R., M.G., F.F.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
All data are publicly available.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dzikevičius, A.; Saranda, S.; Kravcionok, A. The accuracy of simple trading rules in stock markets. Econ. Manag. 2010, 15, 910–916. [Google Scholar]
- Desai, M.A.; Foley, C.F.; Forbes, K.J. Financial Constraints and Growth: Multinational and Local Firm Responses to Currency Depreciations. Rev. Financ. Stud. 2007, 21, 2857–2888. [Google Scholar] [CrossRef]
- Rapach, D.E.; Strauss, J.K.; Zhou, G. Out-of-Sample Equity Premium Prediction: Combination Forecasts and Links to the Real Economy. Rev. Financ. Stud. 2009, 23, 821–862. [Google Scholar] [CrossRef]
- Khaidem, L.; Saha, S.; Dey, S.R. Predicting the direction of stock market prices using random forest. arXiv 2016, arXiv:cs.LG/1605.00003. [Google Scholar]
- Kusuma, R.M.I.; Ho, T.T.; Kao, W.C.; Ou, Y.Y.; Hua, K.L. Using Deep Learning Neural Networks and Candlestick Chart Representation to Predict Stock Market. arXiv 2019, arXiv:q-fin.GN/1903.12258. [Google Scholar]
- Tsantekidis, A.; Passalis, N.; Toufa, A.S.; Saitas-Zarkias, K.; Chairistanidis, S.; Tefas, A. Price Trailing for Financial Trading Using Deep Reinforcement Learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2837–2846. [Google Scholar] [CrossRef] [PubMed]
- Fülöp, M.T.; Gubán, M.; Gubán, Á.; Avornicului, M. Application Research of Soft Computing Based on Machine Learning Production Scheduling. Processes 2022, 10, 520. [Google Scholar] [CrossRef]
- Rubi, M.; Chowdhury, S.; Abdul Rahman, A.A.; Meero, A.; Zayed, N.; Islam, K.M. Fitting Multi-Layer Feed Forward Neural Network and Autoregressive Integrated Moving Average for Dhaka Stock Exchange Price Predicting. Emerg. Sci. J. 2022, 6, 1046–1061. [Google Scholar] [CrossRef]
- Ranaldi, L.; Fallucchi, F.; Zanzotto, F.M. Dis-Cover AI Minds to Preserve Human Knowledge. Future Internet 2022, 14, 10. [Google Scholar] [CrossRef]
- Cunha, P.R.; Melo, P.; Sebastião, H. From Bitcoin to Central Bank Digital Currencies: Making Sense of the Digital Money Revolution. Future Internet 2021, 13, 165. [Google Scholar] [CrossRef]
- Schöneburg, E. Stock price prediction using neural networks: A project report. Neurocomputing 1990, 2, 17–27. [Google Scholar] [CrossRef]
- Patel, J.; Shah, S.; Thakkar, P.; Kotecha, K. Predicting stock and stock price index movement using Trend Deterministic Data Preparation and machine learning techniques. Expert Syst. Appl. 2015, 42, 259–268. [Google Scholar] [CrossRef]
- Sidekerskienė, T.; Woźniak, M.; Damaševičius, R. Nonnegative Matrix Factorization Based Decomposition for Time Series Modelling. In Computer Information Systems and Industrial Management; Saeed, K., Homenda, W., Chaki, R., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 604–613. [Google Scholar]
- Selvamuthu, D.; Kumar, V.; Mishra, A. Indian stock market prediction using artificial neural networks on tick data. Financ. Innov. 2019, 5, 16. [Google Scholar] [CrossRef]
- Moghaddam, A.H.; Moghaddam, M.H.; Esfandyari, M. Stock market index prediction using artificial neural network. J. Econ. Financ. Adm. Sci. 2016, 21, 89–93. [Google Scholar] [CrossRef]
- Devadoss, A.; Ligori, A. Forecasting of Stock Prices Using Multi Layer Perceptron. Int. J. Web Technol. 2013, 002, 52–58. [Google Scholar] [CrossRef]
- Behera, R.; Das, S.; Rath, S.; Misra, S.; Damaševičius, R. Comparative Study of Real Time Machine Learning Models for Stock Prediction through Streaming Data. J. Univers. Comput. Sci. 2020, 26, 1128–1147. [Google Scholar] [CrossRef]
- Abayomi-Alli, O.O.; Sidekerskienundefined, T.; Damaševičius, R.; Siłka, J.; Połap, D. Empirical Mode Decomposition Based Data Augmentation for Time Series Prediction Using NARX Network. In Proceedings of the Artificial Intelligence and Soft Computing: 19th International Conference, ICAISC 2020, Zakopane, Poland, 12–14 October 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 702–711. [Google Scholar] [CrossRef]
- Jin, X. Do futures prices help forecast the spot price? J. Futur. Mark. 2017, 37, 1205–1225. [Google Scholar] [CrossRef]
- Box, G.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Palgrave Macmillan: London, UK, 1976. [Google Scholar]
- Huang, W.; Nakamori, Y.; Wang, S.Y. Forecasting stock market movement direction with support vector machine. Comput. Oper. Res. 2005, 32, 2513–2522. [Google Scholar] [CrossRef]
- Hyndman, R.; Athanasopoulos, G. Forecasting: Principles and Practice, 2nd ed.; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Heaton, J. The Number of Hidden Layers. Available online: https://www.heatonresearch.com/2017/06/01/hidden-layers.html (accessed on 28 October 2022).
- Ranaldi, L.; Fallucchi, F.; Santilli, A.; Zanzotto, F.M. KERMITviz: Visualizing Neural Network Activations on Syntactic Trees. In Metadata and Semantic Research; Garoufallou, E., Ovalle-Perandones, M.A., Vlachidis, A., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 139–147. [Google Scholar]
- Onorati, D.; Tommasino, P.; Ranaldi, L.; Fallucchi, F.; Zanzotto, F.M. Pat-in-the-Loop: Declarative Knowledge for Controlling Neural Networks. Future Internet 2020, 12, 218. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).