Abstract
The recent boom of artificial Neural Networks (NN) has shown that NN can provide viable solutions to a variety of problems. However, their complexity and the lack of efficient interpretation of NN architectures (commonly considered black box techniques) has adverse effects on the optimization of each NN architecture. One cannot simply use a generic topology and have the best performance in every application field, since the network topology is commonly fine-tuned to the problem/dataset in question. In this paper, we introduce a novel method of computationally assessing the complexity of the dataset. The NN is treated as an information channel, and thus information theory is used to estimate the optimal number of neurons for each layer, reducing the memory and computational load, while achieving the same, if not greater, accuracy. Experiments using common datasets confirm the theoretical findings, and the derived algorithm seems to improve the performance of the original architecture.
1. Introduction
One of the current biggest challenges in Deep Neural Networks (DNNs) is the limited memory bandwidth and capacity of DRAM devices that have to be used by modern systems to store the huge amounts of weights and activations in DNNs [1]. Neural networks require memory to store data, weight parameters and activations. Memory usage is high, especially during training, since the activations from a forward pass must be retained, until they can be used to calculate the error gradients in the backwards pass. A typical example is the ‘ResNet-50’ network, which has approximately 26 million weight parameters and computes approximately 16 million activations in the forward pass. Using the conventional 32-bit floating-point format, one would require almost 170 MB.
All the above clearly demonstrate an urgent need to reduce the memory requirements in modern DNN architectures. One way to address this is to reduce computation. A simple technique is to discard values that are relatively cheap to compute, such as activation functions, and re-compute them when necessary. Substantial reductions can be achieved by discarding retained activations in sets of consecutive layers of a network and re-computing them when they are required during the backwards pass, from the closest set of remaining activations [2]. However, this does not appear to be the optimal way to save on memory. A similar memory-reuse approach has been developed by researchers at Google DeepMind with Recurrent Neural Networks (RNNs). For RNNs, re-computation has shown to reduce memory by a factor of 20 for sequences of length 1000 with only a 0.3 performance overhead [3]. A third significant approach has been recently discovered by the Baidu Deep Speech team. Through various memory-saving techniques, they managed to obtain a 16× reduction in memory for activations, enabling them to train networks with 100 layers, instead of the previously attainable nine layers, using the same amount of memory [4].
The above three approaches mark a great improvement in memory handling; however, the greatest memory hog is the a-priori non optimised neural network topologies. Thus, another method to solve this general computational-resource problem is to choose the best network topology for each problem. However, in deep learning, the Neural Network topologies that are used are stochastically/empirically determined. Consequently, there is always room for improvement, either in terms of computational complexity, or model efficiency/accuracy.
There is a rule of thumb that can be applied on supervised learning problems [5]. One can usually prevent the network’s overfitting, provided the number of neurons are kept below a threshold value :
where denotes the number of input neurons, the number of output neurons, the number of samples in the training data set and a is an arbitrary scaling factor, usually in the range of 2–10. Usually, a value of 2 will often work without overfitting. One can consider a the effective branching factor or number of nonzero weights for each neuron. The degrees of freedom in the dataset are expressed by the number of samples, multiplied by the dimensions of each data sample or (assuming they are all independent). In this context, a acts as an indicator of how general a model is desired to be, or equivalently how much one needs to avoid overfitting to the training data. A hyper-parameter grid search could start with and test all the way up to 10, whether the error for the training dataset is significantly smaller than that of the test dataset, which means that the neural network does not generalise effectively.
The nature of hidden layers is defined by two distinct decisions. The number of the aforementioned hidden layers and the number of nodes (neurons/filters) in each layer. The question of the number of hidden layers used in the neural network will be answered first.
Problems that require two hidden layers, in theory, are rarely encountered. However, neural networks with two or more hidden layers can model functions with any kind of shape [6]. Hitherto, there was no theoretical reason to use neural networks with any more than two hidden layers, due to the universal approximation theorem that states that two-layer networks can perfectly approximate certain classes of functions. Nonetheless, it has been extensively reported [7] that deeper (more layers) networks produce more compact representations, compared to those produced by two-layer networks. In addition, using neural networks that are deeper is more efficient than using neural networks that are wider (more nodes per layer), since deeper networks capture the natural ‘hierarchy’ that is present in the observed phenomenon.
Deciding the number of hidden neuron layers is only a small part of the problem. One must also determine the number of neurons in each of these hidden layers. These layers may not directly interact with the external environment; however, they pose a huge impact on the final output and the network’s accuracy. The number of hidden layers and the number of nodes in each of these hidden layers has to be chosen wisely, as using too few nodes in the hidden layers will result in underfitting, which implies that the network cannot model the dataset’s complexity adequately. On the contrary, using too many neurons in the hidden layers can lead to even more damaging problems. First, too many neurons in the hidden layers may result in overfitting, which means that the neural network has so much information processing capacity that the limited amount of information contained in the training set is not enough to train all the neurons. The second problem is about efficiency, since a large number of nodes in the hidden layers can increase the training time of the network, even leading to inability of current technology to be used because of the memory size and bandwidth limitations. Generally, in order to secure the ability of the network to generalise, the number of nodes/neurons has to be kept as low as possible, to avoid creating a “memory bank” neural network that has mapped the training dataset one to one but cannot extrapolate. As a matter of fact, there is a region, a sweet spot, between the two situations, where the number of hidden layers and number of nodes in each layer is just right for the problem. The automatic finding of this sweet spot is the scope of this paper.
To this day, there are many rule-of-thumb methods for determining the correct number of neurons to use in the hidden layers, such as the following [8]:
- The number of hidden neurons should be between the size of the input layer and the size of the output layer;
- The number of hidden neurons should be 2/3 the size of the input layer, plus the size of the output layer;
- The number of hidden neurons should be less than twice the size of the input layer.
These three rules provide only a starting point, since the selection of an optimal architecture for the neural network in question would finally come down to trial and error, thus utilising valuable time and computational resources, and of course reduced efficiency.
Hitherto, the key strategy for obtaining good generalisation is finding the simplest model that explains the data. The idea is that, the more complex the model is, the greater the probability of error outcomes. In terms of neural networks, the simplest model is the one that contains the smallest number of free parameters (weights and biases), or, equivalently, the smallest number of nodes. To find a network that generalises well, we need to find the simplest network that fits the data.
There are at least five different approaches that people have used to produce simple networks: growing, pruning, global searches, regularisation and early stopping [9,10]. Growing methods start with no neurons in the network and then add neurons until the performance is adequate. Pruning methods start with large networks, which most likely overfit, and then remove neurons (or weights) one at a time, until the performance degrades significantly. Global searches, such as genetic algorithms, search the space of all possible network architectures to locate the simplest model that explains the data. However, these methods can either dynamically alter the size and topology of the network, while being highly computationally inefficient, or can only remove information, which, in turn, requires that the network starts from a bigger-than-required size.
The major differentiation, regarding pruning methods is (a) sparsity structure, (b) scoring, (c) scheduling and (d) fine-tuning.
- 1.
- Structure: The pruning of individual parameters is followed by some methods, and is called unstructured pruning. Following this method, a sparse neural network is produced, which although smaller in terms of parameter-count, may not be optimally arranged in a fashion conducive to speedups using modern libraries and hardware. Another popular method considers parameters in groups, removing entire neurons, filters, or even channels, exploiting hardware and software optimised for dense computation. This method is called structured pruning [11];
- 2.
- Scoring: One common method is scoring the parameters based on their absolute values, trained importance coefficients, or even contributions to network activations or gradients. One way to achieve this is to score locally, pruning a fraction of the parameters with the lowest scores within each structural sub-component of the network [9], while the other views scores globally, comparing scores to one another irrespective of the part of the network in which each parameter resides [10,12];
- 3.
- Scheduling: When considering the timing of each pruning algorithm, there are two schools of thought. Some pruning methods prune all targeted weights at once in a single step [13], while others prune a fixed fraction of the network iteratively over several steps [14] or vary the rate of pruning, according to a more complex function [15];
- 4.
- Fine-tuning: When a method utilises fine-tuning, the most common case is to train the network using the before-pruning trained weights. The other major school of thought rewinds the network to an earlier state [16] or even re-initialises the entire network [13].
In this paper, we propose a novel approach of dynamically calibrating the width of each layer, every arbitrary number of epochs. This is achieved using Shannon’s Channel Capacity Theory [17] and considering the NN’s weight matrix as an information transition matrix. A baseline complexity approximation of the dataset using Kolmogorov Complexity Theorem [18,19,20] (entropy approximation) is firstly performed. To evaluate the capacity of each layer, we utilise a novel optimized Blahut–Arimoto algorithm, since the original [21] is exponentially computationally expensive for a small increase in accuracy. For the dataset, we use an entropy approximation of the Kolmogorov Complexity Theorem, since the original is non computable, which converges to the entropy of the dataset. Experiments have shown that the above method can be effectively used for either convolutional layers or fully connected layers, treating each layer as a channel of information transformation/compression, while having enough capacity to encode the baseline information complexity of the input pattern.
2. Outline of the Proposed Algorithm
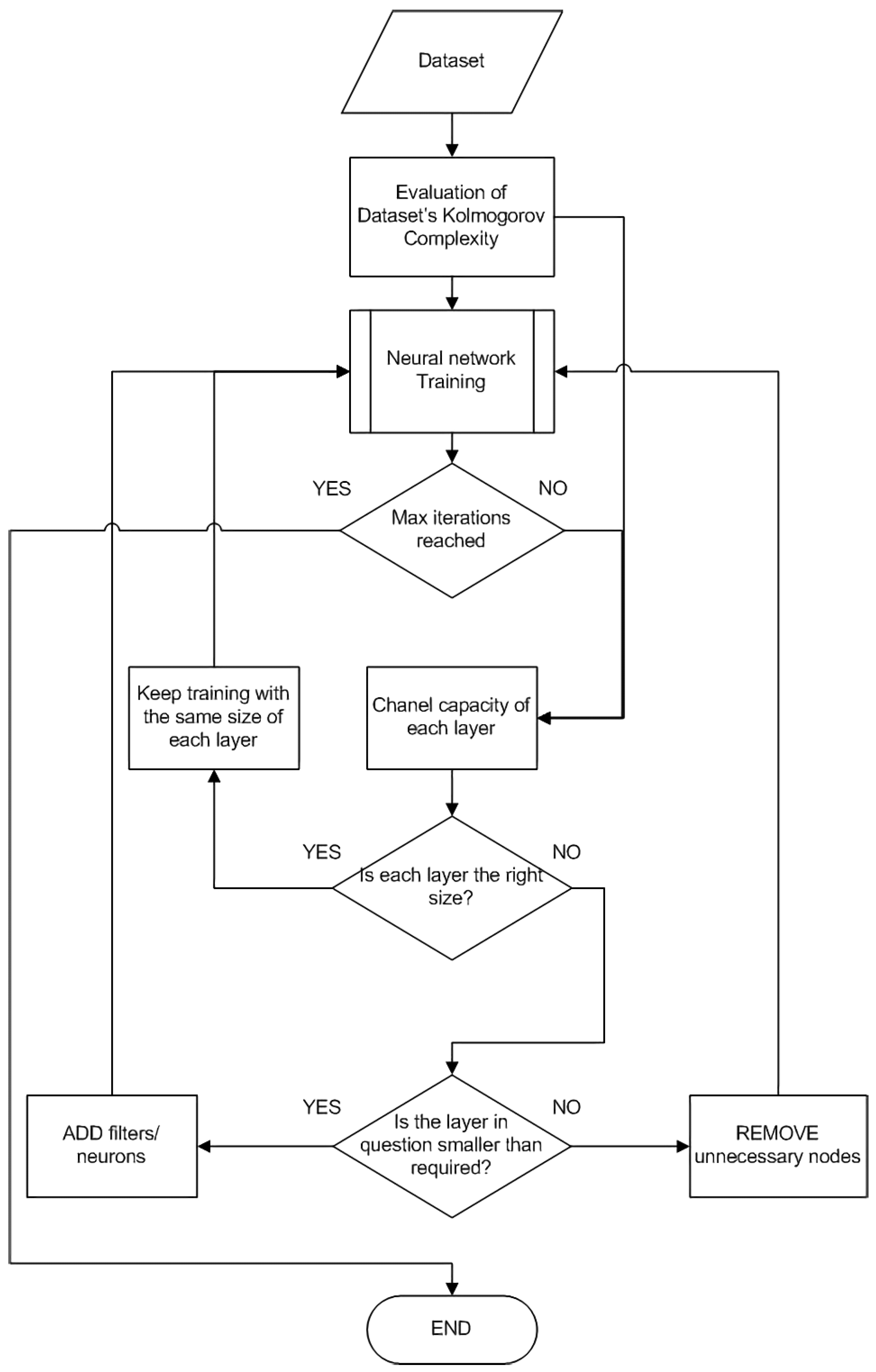
The proposed algorithm aims at optimising the topology of neural networks online during training, regardless of the dataset. The proposed algorithm consists of the following discrete steps:
- 1.
- At first, the complexity of the dataset is evaluated, using the average entropy, multiplied by the bits needed to depict each class (i.e., 3 bits for 8 classes).
- 2.
- The initial network topology is a common topology, i.e., a network topology used in the literature for similar datasets. The network is trained for a fixed number of epochs (e.g., 10), drifting from the random initialisation stage, in order to start encoding useful information in its layers.
- 3.
- After a number of epochs, the capacity of each layer is evaluated. Each layer is considered an information channel and the weight matrix can be viewed as a channel transition matrix (see (5)). We can then use a modified and optimized Blahut–Arimoto algorithm to estimate the information capacity of each layer. Based on the capacity of each layer and the given dataset complexity, extra filters are added with minimal weights (median 0, max 0.04 and min −0.04), so as not to undermine the training attained so far. In the case that the layer is found unable to contain the required information, we increase the width of those layers that are found to be too coarse, by adding new nodes with minimal weights. If a layer is found too wide, the nodes with the lowest entropy in their connections are removed. If the information capacity is found to lay within certain limits, no further action is taken. If there is no change of width of any layer for two consecutive iterations, the size of that layer freezes, and no computation takes place again for this specific part of the network.
- 4.
- The method terminates after a predefined number of epochs passes, or in the case that every layer size does not update.
The whole procedure is outlined in Figure 1. In the following sections, we will describe the operation of the algorithm in more detail.
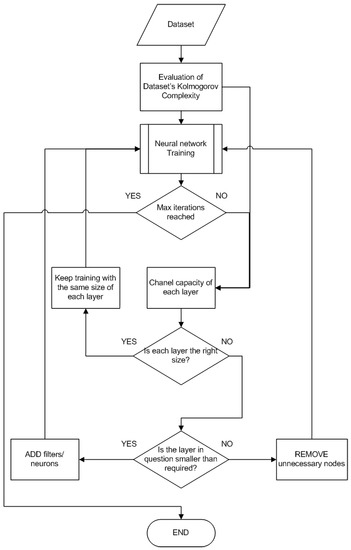
Figure 1.
Outline of the proposed Algorithm.
3. Dataset Complexity Estimation
The first step in our algorithm is to determine the complexity of the given dataset. We propose to estimate the complexity of the dataset using an approximation of the Kolmogorov complexity theorem, since computation of the actual Kolmogorov’s complexity theorem is impossible. Kolmogorov complexity can be defined for any information source. It can be shown [22,23,24] that, for the output of Markov information sources, Kolmogorov complexity is related to the entropy of the information source [25]. More precisely, the Kolmogorov complexity of the output of a Markov information source, normalised by the length of the output, converges almost surely (since the length of the output goes to infinity) to the entropy of the source [24,26].
Based on the above, we propose that one can evaluate the complexity of the dataset by the product of the mean entropy of each sample and the bits required to represent all categories (e.g., 6 bits for 60 classes, since ). This method is quite effective and fast, even for large image-based datasets. One could compute only a representative amount of samples from each class and not the full dataset, without losing accuracy in a meaningful way.
Assume that is a discrete Markov source with d symbols or classes. Let be a sequence of N symbols drawn from . One can estimate the number of occurrences of each symbol in the stream/dataset and thus calculate a histogram. If this histogram is normalised by the number of symbols N, this yields the approximate pdf . This can be used to estimate the entropy of the dataset, using Shannon’s formula:
We then estimate the number of bits required to encode the number of symbols/classes via
The dataset’s complexity can be estimated via:
The following Algorithm 1 outlines the proposed procedure.
| Algorithm 1 Dataset complexity estimation |
|
4. Neural Network as an Information Channel—Capacity Estimation
The number of columns of the weight matrix of a layer in a neural network is equal to the number of neurons in the hidden layer. The dimensions of the weight matrix between two layers are determined by the size of the two layers it connects. There is one weight for every input-to-neuron connection between the layers.
We can consider each neural network’s fully connected layer as an information channel that transmits information from its input to its output. The information capacity of a channel represents the upper bound of information that can be transmitted through the channel. Moving this concept to a layer in a neural network, information capacity denotes the information that can be transmitted through this layer, or equivalently the information that can be processed or stored through this layer. This is a novel concept presented in this work, and we intend to examine the effectiveness of information theory tools on automatically determining the optimal neural network architecture.
The inception of this idea is that, macroscopically, a neural network functions similarly to an information channel, transmitting and modifying the information of the input, to the output, as a decision or a continuous value, depending on the type of the neural network in question. In our quest to incorporate the information theory in the neural network, we made the assumption that every stage/layer of the neural network can be considered an information channel, as there are similarities in the usage of the weight matrix in a neural network and the transition matrix in an information channel. During experimentation, we discovered that the concept of viewing a neural network layer and an information channel as parallels is valid, as both can be regarded as ways of manipulating information.
An information channel is commonly described by the channel or transition matrix, which describes the conditional probabilities of any channel/layer’s output given any of the channel/layer’s input. For a discrete memoryless channel/layer with K inputs and L outputs , the transition matrix is given by:
Given this transition matrix , the capacity of the channel/layer is given by:
where refers to the mutual information between the inputs and and refers to the pdf of input x that achieves the maximum transmission rate.
As it is evident, the above definition is rather theoretical. There are many methods to estimate the information capacity of a channel/layer in practice. One method of channel capacity estimation is the Blahut–Arimoto algorithm [21,27,28,29]. The algorithm was independently invented by Suguru Arimoto [21] and Richard Blahut [27]. The algorithm is mostly applicable to the case of arbitrary finite alphabet sources. Recently, a version of the algorithm that accounts for continuous and multivariate outputs was proposed with applications in cellular signalling [30]. There also exists a version of the Blahut–Arimoto algorithm for directed information [29].
4.1. The Blahut–Arimoto Algorithm
Suppose we have a source X with probability of any given symbol and a network layer channel that translates X to Y with a transition matrix . In order to estimate the channel capacity C, we need to estimate the pdf of the source that maximises the mutual information between X and Y. The Blahut–Arimoto algorithm attempts to maximise (6) by reforming the original cost function and transforming it to the following equivalent alternating optimisation problem:
The Blahut–Arimoto algorithm resolves to an iterative algorithm that estimates the optimal source pdf that yields the maximum channel capacity C. The iterative procedure is defined as follows [31]:
- 1.
- Start with an arbitrary
- 2.
- , where is the Kullback–Leibler divergence between the distributions of and .
- 3.
- Iterate 2, until convergence.
The constant is a constant that controls the importance of the divergence function in the estimation of the prior distribution. For , we get the original Blahut–Arimoto algorithm. Once is estimated, we use the function of (7) to estimate the capacity of the network. The presented algorithm is a “squeezed” version [31] of the original Blahut–Arimoto algorithm, which is more possible to converge.
Our implementation of the Blahut–Arimoto algorithm is depicted in Algorithm 2. The algorithm had to be modified to reflect the fact that we are now modeling the layer of a neural network, instead of a communication channel. Since we are not interested in a very accurate estimate of the layer’s capacity, but rather get a valid and quick measurement, we lowered the accuracy from to and reduced the maximum number of iterations to 1000 ( of the original number of iterations).
| Algorithm 2 The modified Blahut–Arimoto algorithm |
|
Using the above two computations, the dataset information complexity is estimated only once at the beginning and the channel capacity after a set number of epochs.
4.2. The Mutual Information Algorithm
We also evaluated the idea of using mutual information as a method of determining the information capacity of each layer. However, during testing, we observed a large oscillation and a lack of temporal stability in the values, resulting in a non stable network topology with a sometimes wildly varying size of layers, which considerably hindered the training process. To estimate the mutual information, we need to use its definition [17]:
Since the transition matrix is known, we initially assume the uniform distribution for X. The following iterative algorithm (see Algorithm 3) is used to update the mutual information and the estimated distribution of X. The final estimate of the mutual information of each layer is provided as a final output.
A comparison between the two methods that led us to utilise the BA algorithm in favour of Mutual Information will follow after explaining the rest of the proposed algorithm in Section 5.2.
| Algorithm 3 The mutual information algorithm |
|
5. Automated Neural Network Topology Optimization
5.1. Proposed Method Description
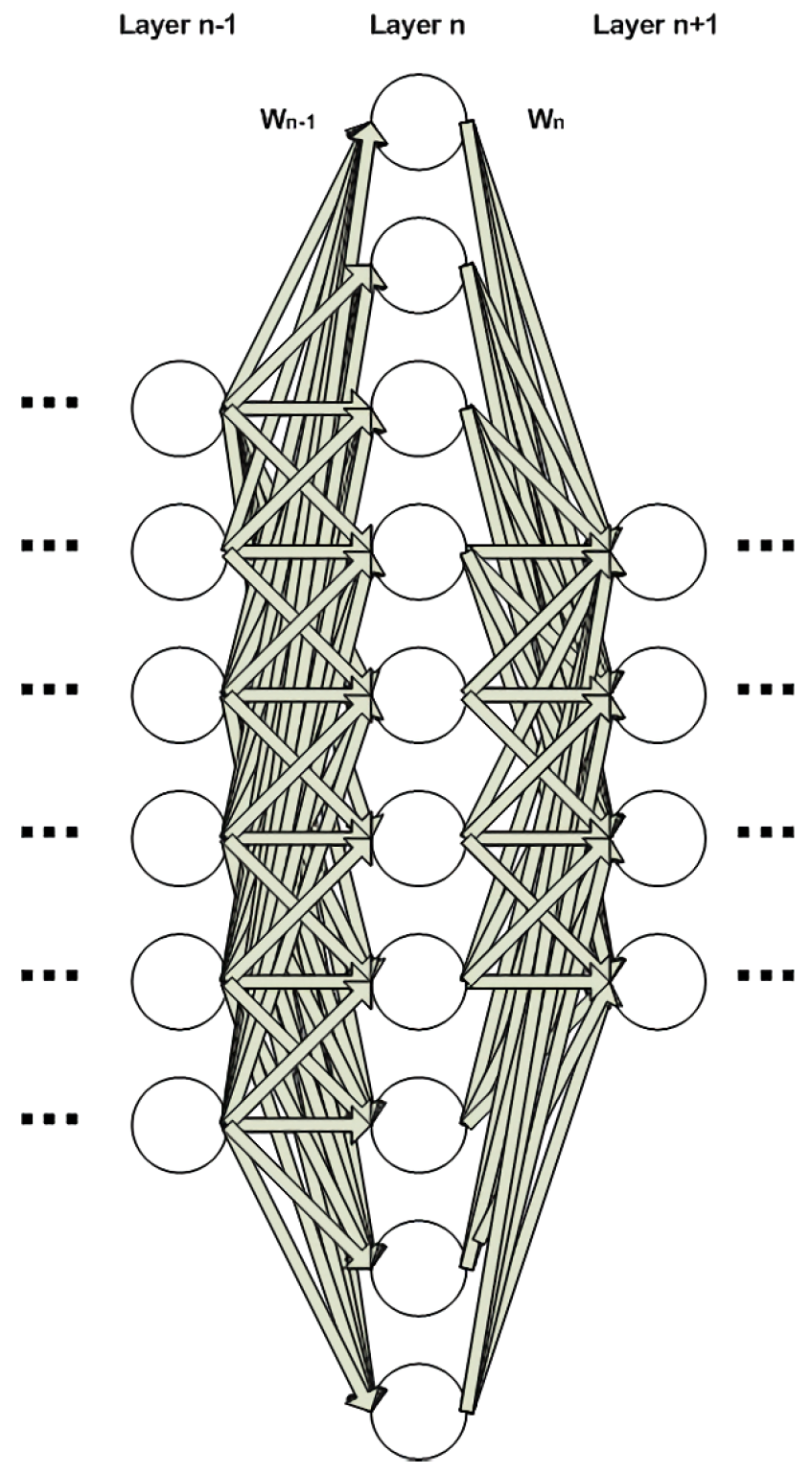
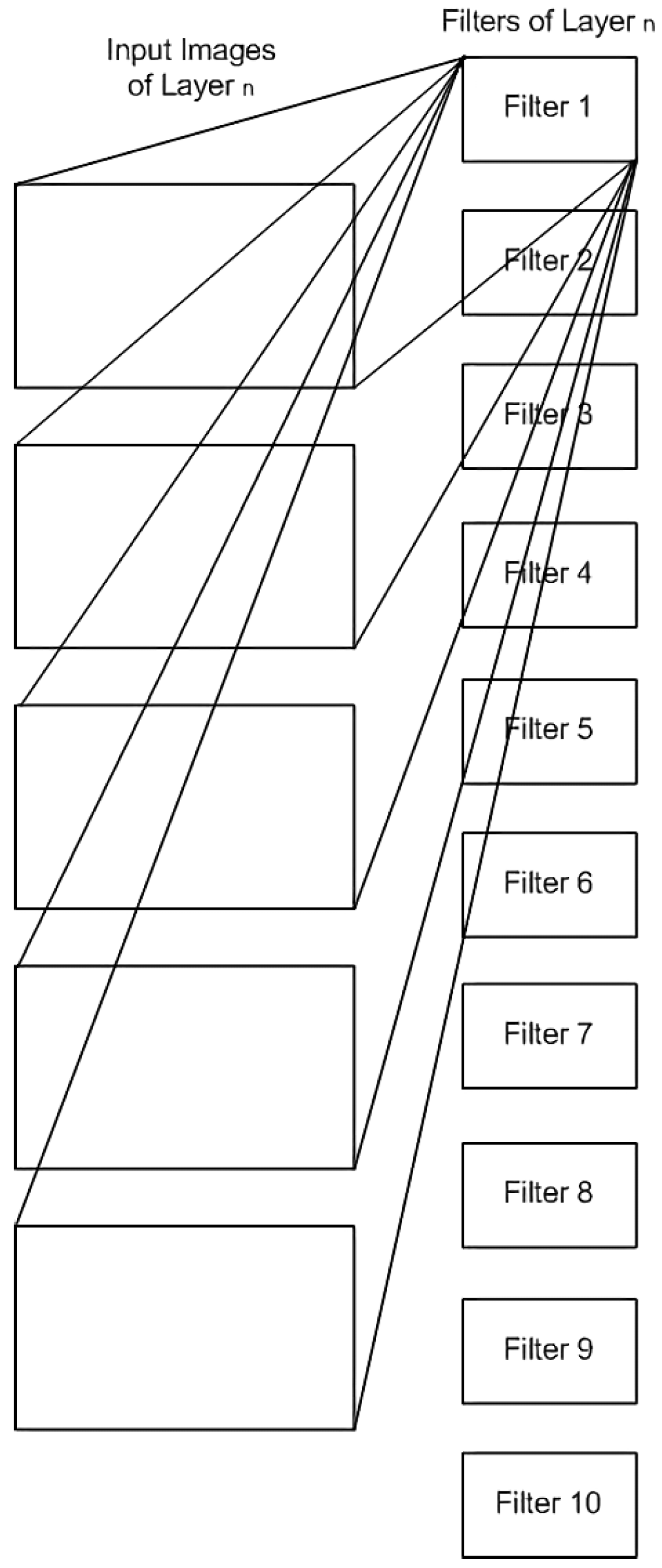
In this section, we describe the proposed automated procedure to optimize the topology of a neural network for a specific task. The proposed system is described in the block logical diagram in Figure 2. The process starts by evaluating the dataset’s complexity using Algorithm 1. The next step is to initialize NN training, based on an ad hoc topology, i.e., proposed in literature or used in a similar experiment and has been reported to perform well. The NN is left for a couple of epochs to commence its training. The information capacity of each layer is then computed using Algorithm 2 and compared to the complexity of the dataset that was already estimated earlier. In a fully connected neural network, the size of the layer connections/weight matrices are defined by the current and next layer’s number of neurons. In the example of Figure 2, the weight matrix of layer is and of layer n is . When evaluating the capacity of a convolutional layer (Figure 3), however, we must add the capacity of each individual filter, as calculated by the BA algorithm. In other words, the capacity of the layer is the sum of the capacities of all filters in each layer.
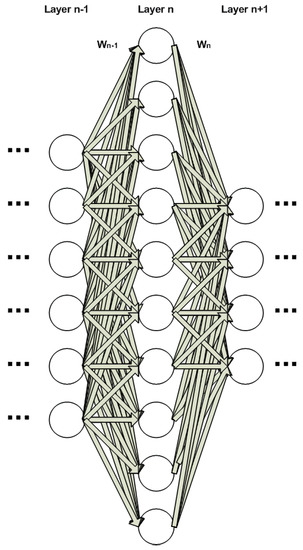
Figure 2.
Layers , n and of a fully-connected Neural Network.
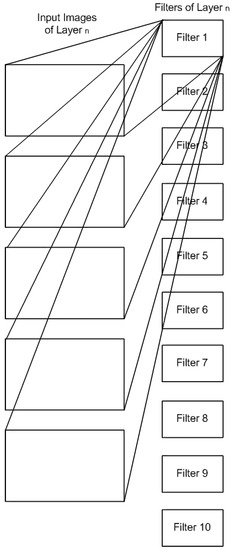
Figure 3.
Layer n of a Convolutional neural network.
The remaining details of the algorithms are discussed and validated over a specific convolutive network that classifies the MNIST dataset.
5.2. Method Application and Validation on the MNIST Dataset
5.2.1. Optimal Layer Size Estimation
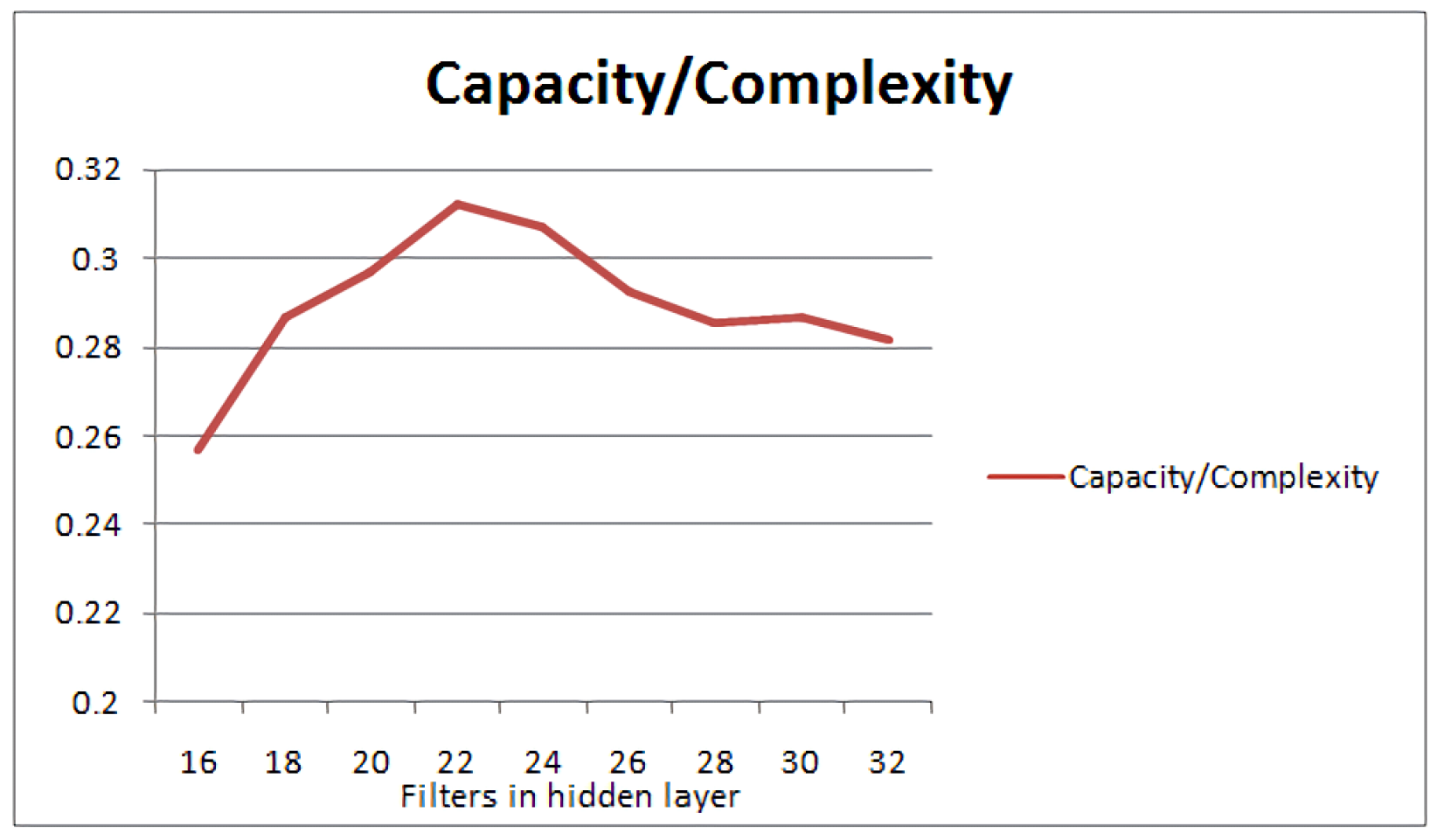
In the following experiment, we can uncover the connection between the dataset’s complexity and the layer capacity. For demonstration purposes, we will use a simple convolutional neural network with one hidden convolutional layer and 10 decision neurons to solve the MNIST classification problem. The dataset’s complexity is estimated to be 6.4102 using Algorithm 1. We will then vary the number of convolutional filters of the hidden convolutional layer and estimate the capacity of each network layer, the classification accuracy for each configuration and finally the corresponding capacity/layer complexity ratio. This ratio is equivalent to the ratio of capacity over the number of filters in the layer. This ratio demonstrates the amount of the dataset’s information that is stored by the current network’s capacity. In other words, the greater the value of the ratio, the better the utilization of the network’s resources for the corresponding classification problem. The experiment was executed 10 times, and the average of these is presented in Table 1. In addition, we denote the number of filters as the layer’s complexity. The ratio of Capacity over the Layer’s Complexity is also presented in Figure 4.

Table 1.
Accuracy, capacity and capacity/(layer’s complexity) with a varying number of filters in the hidden layer. The layer’s complexity is shown by the number of filters. The optimal ratio appears at 22 conv. filters.
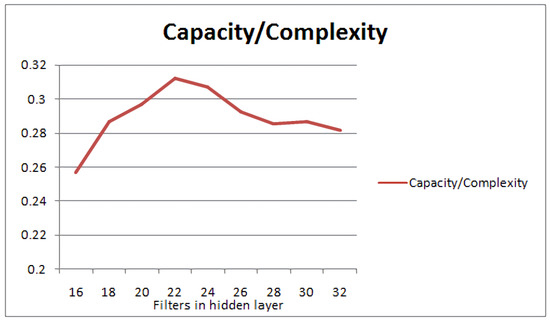
Figure 4.
Estimating the Capacity/Layer Complexity ratio for a varying number of filters in the hidden layer of a 1-layer convolutive NN. The configuration of 22 filters seems to yield the optimal ratio for the MNIST dataset.
We can observe in Figure 4 that the best Capacity/Layer Complexity ratio can clearly be achieved by the layer, whose capacity is the same as the dataset’s complexity. The configuration of 22 layers yields a capacity of 6.8649, which is closer to the complexity of the dataset, i.e., 6.4102. The aim here is to achieve the greatest information capacity capability, without resulting in a huge number of filters/neurons per layer. In other words, we are aiming at finding a configuration that maximises the ratio of Capacity/Layer Complexity, i.e., the best capacity match with the data’s complexity with the smallest number of filters (neurons) in the layer.
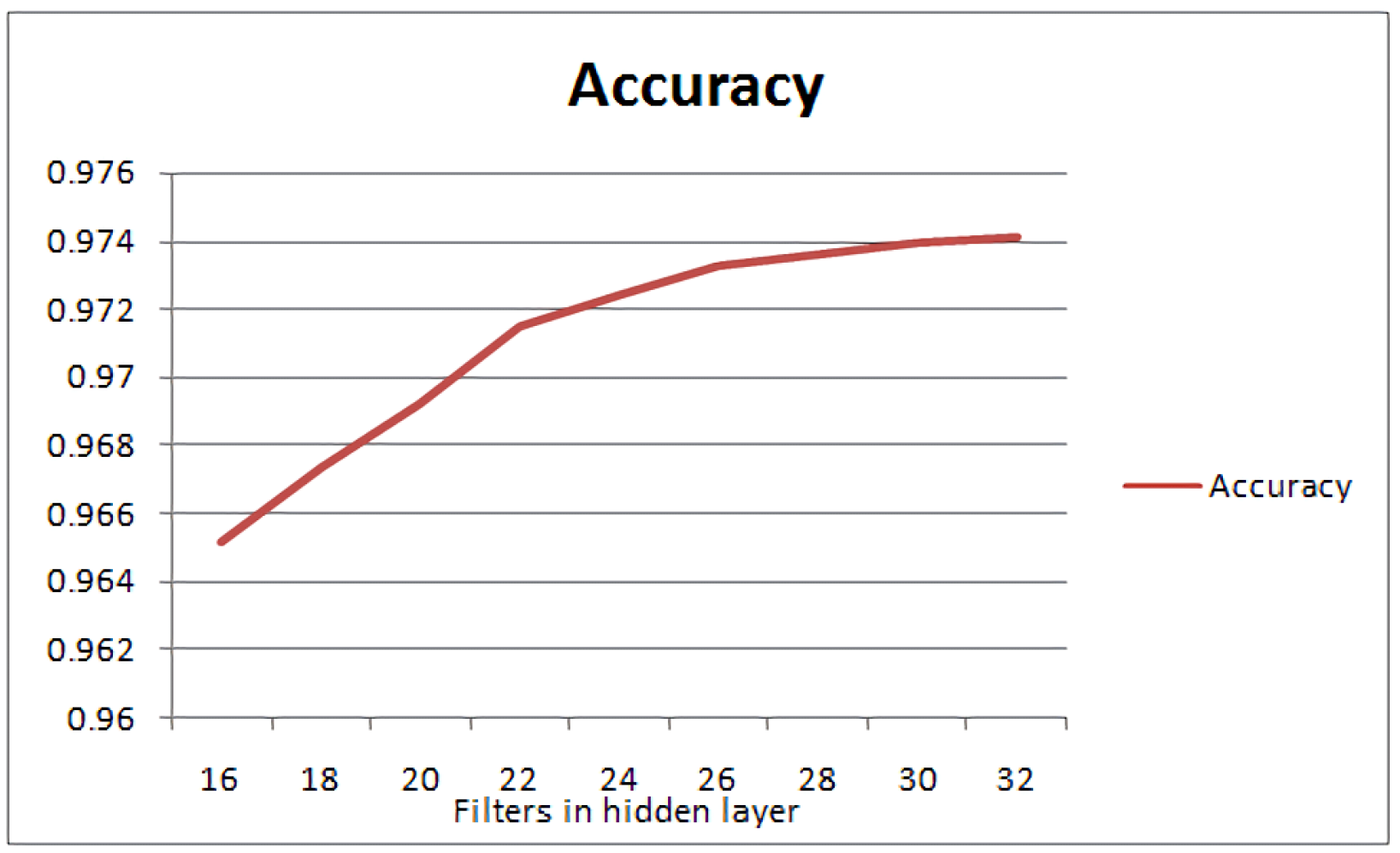
In Figure 5 and Table 2, the accuracy is depicted for a varying number of filters in the previous experiment. One can observe the decline of the slope after the optimal number of neurons in the hidden layer. To further support this, the first-order derivative of the accuracy chart is calculated, using the Mean Value Theorem, i.e., .
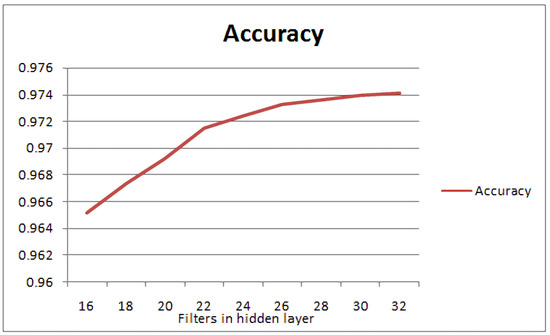
Figure 5.
Accuracy diagram for a varying number of filters in the hidden layer of a 1-layer convolutive NN for the MNIST dataset.

Table 2.
Accuracy values and first-order approximated derivative of accuracy. The slope of the curve reaches a maximum at the configuration of 22 filters, after which it is almost flat.
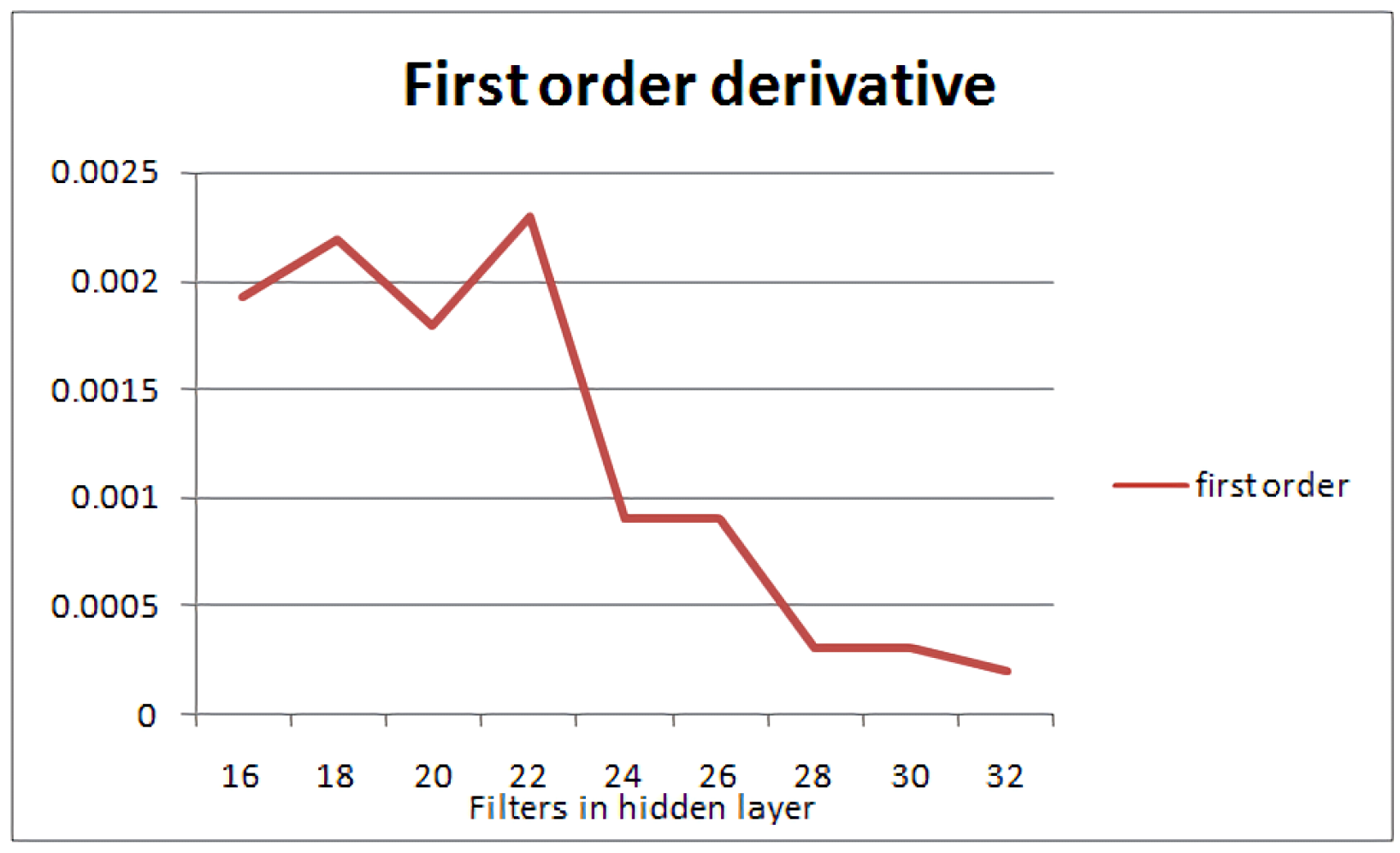
The first order derivative of the accuracy metric in Figure 6 shows that adding nodes beyond the number defined by the capacity of the layer in question has an adverse effect on the efficiency of the neural network. The accuracy may increase slightly, but the computation cost starts being disproportionately large. Thus, the further slight increase in accuracy entails the considerable increase of nodes in the configuration of the NN, which questions the overall efficiency of the network. In summary, the optimisation goal of this approach is to optimise the resource utilisation of the network, i.e., provide the smallest network that can perform efficient classification depending on the dataset. This will definitely increase accuracy but may not give the network with the best accuracy. As a result, the proposed scheme yields the best network configuration, in terms of resource allocation, with the best possible classification accuracy.
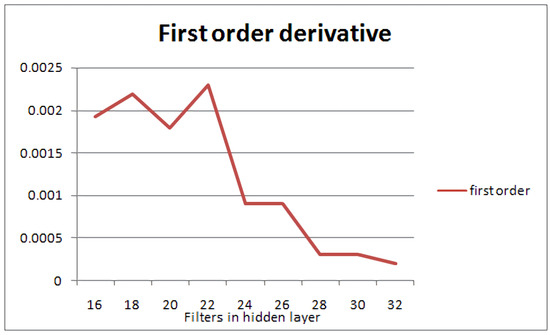
Figure 6.
First-order derivative diagram of accuracy for the 1-layer convolutive NN and the MNIST dataset. A clear peak is shown at the 22-filter configuration, after which the slope decreases considerably.
5.2.2. Information Capacity Evolution over More Layers and Network Adjustment
While it is not very clear how information theory can guide us in the relevance of capacity in each consecutive layer, it is clear that the last convolutional layer, before the fully connected decision layer, should be able to contain all the information complexity of the dataset, while the decision layer should be able to contain the information bits required to represent the categories in a classification task, or the stepping of the real values in the required accuracy. As mentioned above, only the last convolutional layer is required to store the whole information, as reviewed from layer hierarchical representation in [32,33], while all previous layers need to store exponentially less information. A natural logarithm is used as an information vanishing factor, depending on the number of layers. All units in (9) are measured in bits. Thus, we propose the following model to measure the capacity of each layer:
where i is the layer number and is the total number of layers in the network.
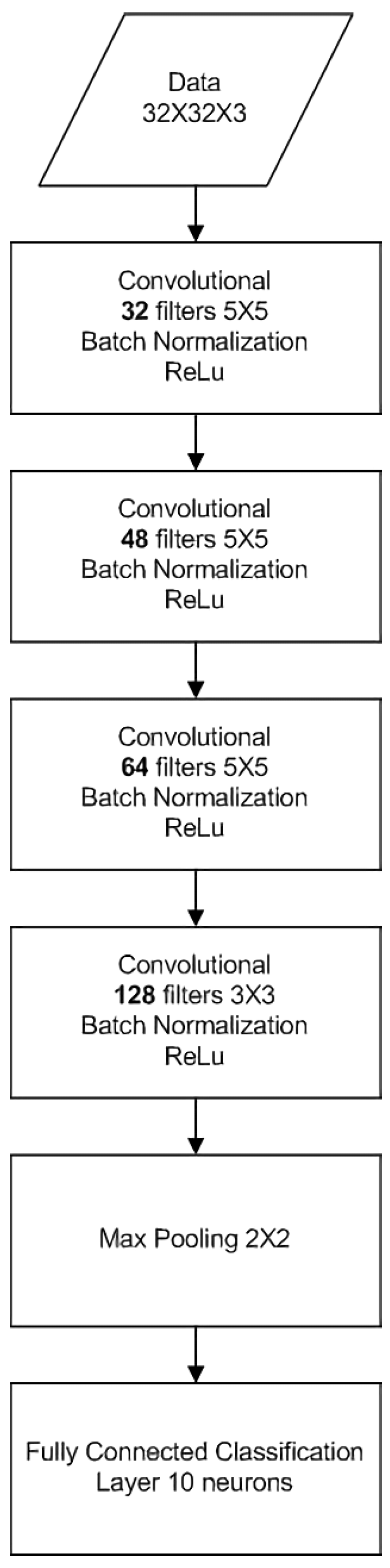
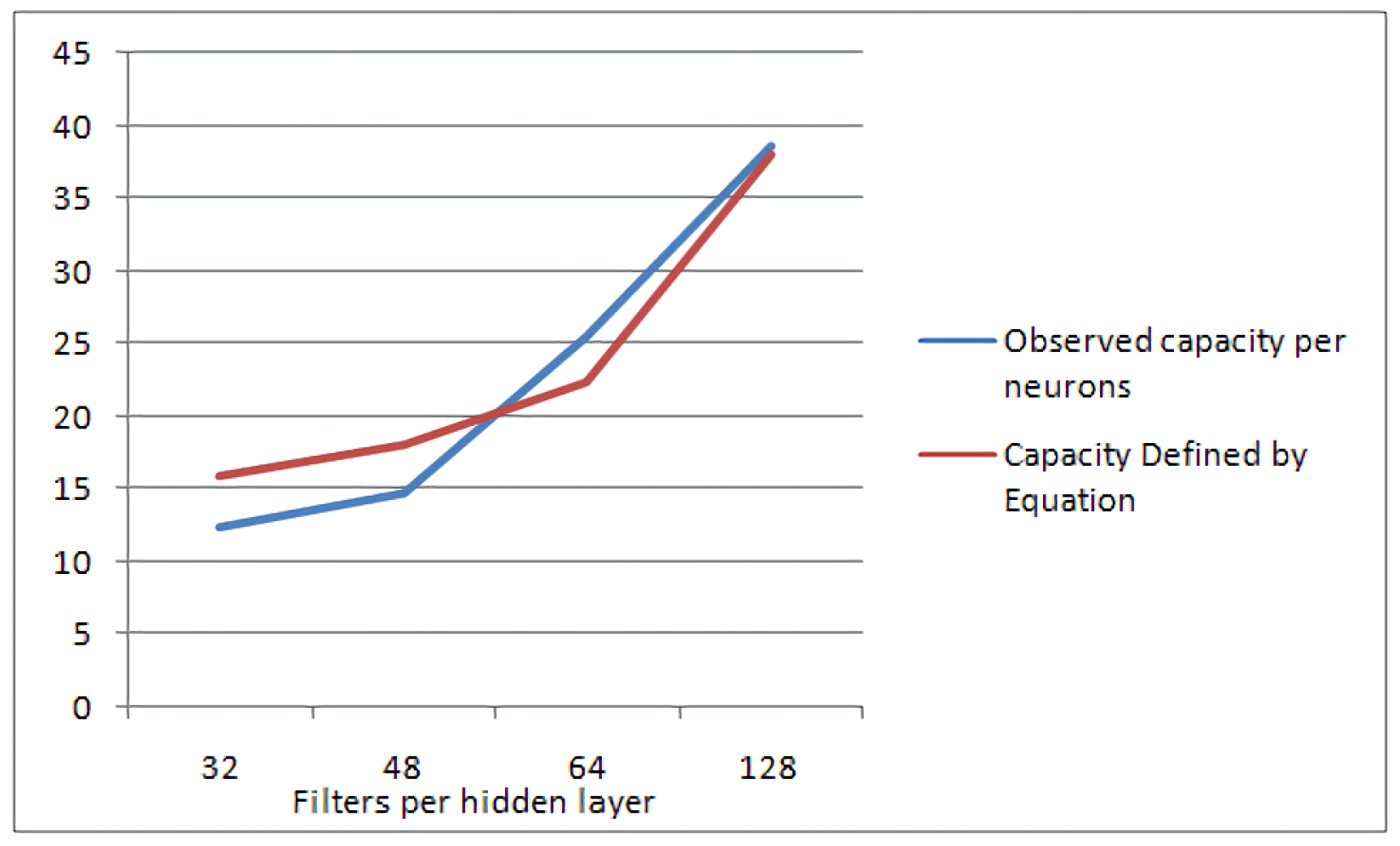
To test the validity of the proposed model in (9), we measure the capacity of each layer in a nearly optimised 4-layer convolutional neural network with 32, 48, 64 and 128 filters, respectively, classifying again the MNIST dataset. This NN architecture is depicted in Figure 7. The measured capacity of each layer is compared against the desired capacity, as predicted by the proposed model of (9). A comparison between the measurements and the predicted capacity is displayed in Figure 8. It is evident that the measured capacity is very close to the one predicted by the model, thus verifying the validity of Equation (9).
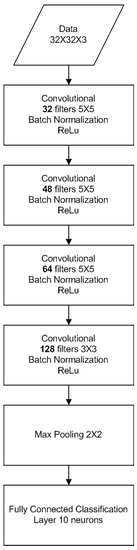
Figure 7.
Manually optimized CNN architecture to validate the layer capacity model of (9).
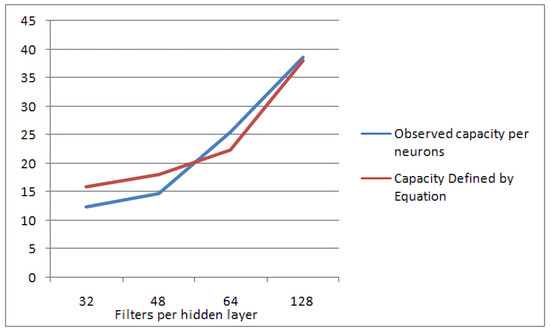
Figure 8.
Observed capacity of manually optimized neural network vs. theoretical optimal capacity calculations.
If the information capacity of the layer in question is larger than 1.05 of the required capacity of the given layer, the least significant nodes are identified and removed, along with their connection to and from the previous and next layer, respectively. The 0.05 margin is in place to prevent unnecessary oscillations during training, while the removal criterion for the excess nodes in the layer in question is the entropy of each connection. The nodes/filters/neurons that display the least amount of entropy are not contributing to the information holding capacity of the layer, as entropy is associated with information [34]. If the layer is found to be of an inadequate size, i.e., of lower information capacity than 0.95 of the desired capacity, compared to the dataset complexity, then nodes are added. The number of nodes depends on the difference of the information capacity and information complexity of the layer and dataset, respectively. The step of increase or decrease of filters/neurons is calculated as double the difference of channel capacity minus the dataset’s information complexity , for each layer i, i.e.,
The factor 2 in Equation (10) is used as an ad-hoc means to speed up the convergence process after extensive experimentation. The improved network is left for a couple of epochs to train and its performance is again evaluated using the procedure described above. If there is no visible improvement or the maximum number of epochs is reached, the improvement procedure stops, yielding the final optimised network. An overview of the proposed algorithm is shown in Figure 1.
The procedure can be outlined, as follows:
- Determine the complexity of the dataset;
- Set the desired capacity of the last layer equal to the dataset complexity;
- Set the desired capacity of each layer, according to (9);
- Begin training and, after a number of epochs, examine each layer independently;
- if the information capacity of the layer is larger than 1.05 of the desired capacity of the layer, remove nodes, according to (10);
- if the information capacity of the layer is smaller than 0.95 of the desired capacity of the layer, add nodes, according to (10);
- in all other cases, the layer stays the same;
- Go to 4 and continue the procedure, until the network is not updating or the accuracy is not improving.
5.2.3. Comparison between Blahut–Arimoto and Mutual Information for Layer Capacity Estimation
As mentioned earlier in the text, there are two methods to estimate channel capacity: one using the Blahut–Arimoto algorithm and one using mutual information. To compare the effectiveness between capacity estimation using the Blahut–Arimoto (BA) algorithm and mutual information, we set the following experiment. We set a simple convolutional neural network with three hidden layers, which we are trying to determine the optimal number of nodes/filters, using the proposed algorithm. We examine two cases, where the BA algorithm or the Mutual Information are used as a capacity estimation metric. We ran six training phases of five epochs each, for a total of 35 epochs. In Figure 9, one can observe the temporal oscillation on the number of nodes per layer, per training phase, especially, when observing layer 2 for this example. In contrast, one can clearly observe that, using the BA algorithm as an information capacity indication, the nodes per layer converge to a single value, without oscillations, as expected. Consequently, the BA algorithm seems to produce more stable estimates of information capacity, thus leading to more stable node predictions for the proposed algorithm. Therefore, the BA algorithm will be used to estimate channel capacity in the proposed approach.

Figure 9.
Number of nodes/filters per training phase when using mutual information (a) and Blahut–Arimoto (b) as an information capacity indication. The Blahut–Arimoto algorithm produces far less oscillations compared to Mutual Information.
6. Experimental Results
As stated in the previous chapters, due to the different approaches, followed by competing methods, we could not conduct any standardized testing. Our method is implemented to be used during training and not after training and during inference as the majority of the competing methods do. This can lead to difficulties in direct comparison; however, we believe that training topology optimization is of greater importance, given the vast memory and computation requirements during training. An optimal topology is paramount for the best utilization of the available computational resources.
Driven by the above-mentioned restrictions, our method is compared against vanilla neural networks used to solve popular datasets, whose topology would be used, if no topology optimization was available during training. The datasets used in our experiments are MNIST, Fashion MNIST, CIFAR-10 and Sign Language. The proposed method was developed on Matlab 2020a using GPU acceleration on a nVidia Tesla K10 graphics card. Below, a benchmark is followed for the proposed method over the commonly used datasets MNIST, Fashion MNIST, CIFAR-10 and Sign Language.
6.1. MNIST
The MNIST database (Modified National Institute of Standards and Technology database) is a large database of handwritten digits that is commonly used for training various image processing systems [35,36]. It is widely used for training and testing in machine learning models. The dataset was created from the samples from NIST’s original datasets and applying modifications on them [35]. The black and white images from NIST were resized into a pixel bounding box and anti-aliased and were converted to grayscale [37]. The MNIST database contains 60,000 training images and 10,000 testing images [38]. Half of the training set and half of the test set were taken from NIST’s training dataset, while the other half of the training set and the test set were taken from NIST’s testing dataset [38].
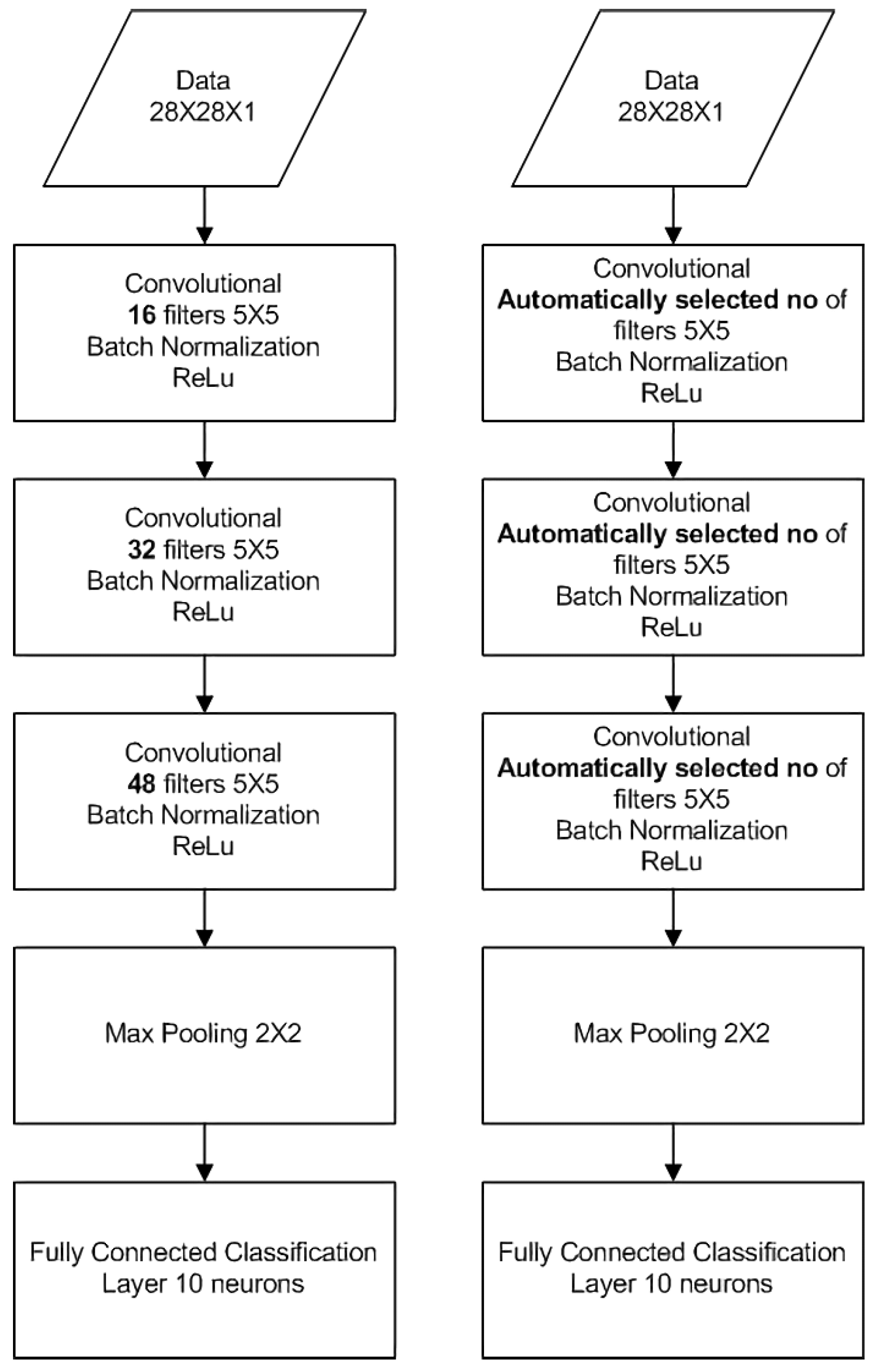
For our testing, we used five evaluations of the network’s capacity, once every five epochs for a total of 30 epochs. The conventional topology is based on three Convolutional Layers with max pooling only after the last layer and 10 neurons at the decision layer. The automatic topology optimized neural network used the same network as a baseline and further tuned each convolutional layer to the dataset’s needs using the proposed method.
The diagram in Figure 10 shows the neural network topology used in the MNIST and FashionMNIST datasets for the conventional and proposed method. Figure 11a illustrates the accuracy of 20 independent classification runs of the MNIST dataset, using the automatic topology optimization with the blue colour, and using the conventional topology with the red colour. It is obvious that the proposed method provides more consistent results with lower standard deviation among runs, 0.000652445 versus 0.001555263 of the conventional method, along with higher classification accuracy, 0.98426 versus 0.98029. The corresponding F1-scores are 0.9798 for the proposed method vs 0.9785 for the conventional one. Figure 11b illustrates the testing accuracy of the two competing network topologies every five epochs (one phase) up to the total of 30 epochs. The automatically optimized topology achieves an increase in accuracy, compared to the static topology, starting from the third phase of optimization.
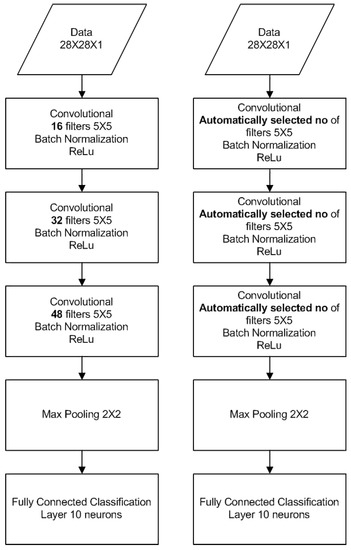
Figure 10.
Vanilla CNN for MNIST classification (left), Adaptive CNN for MNIST classification (right).

Figure 11.
(a) MNIST Testing accuracy variation over random independent runs of the optimized and the conventional NN; (b) MNIST Testing accuracy every five-epoch tranining (1 phase) for the optimized and the conventional NN.
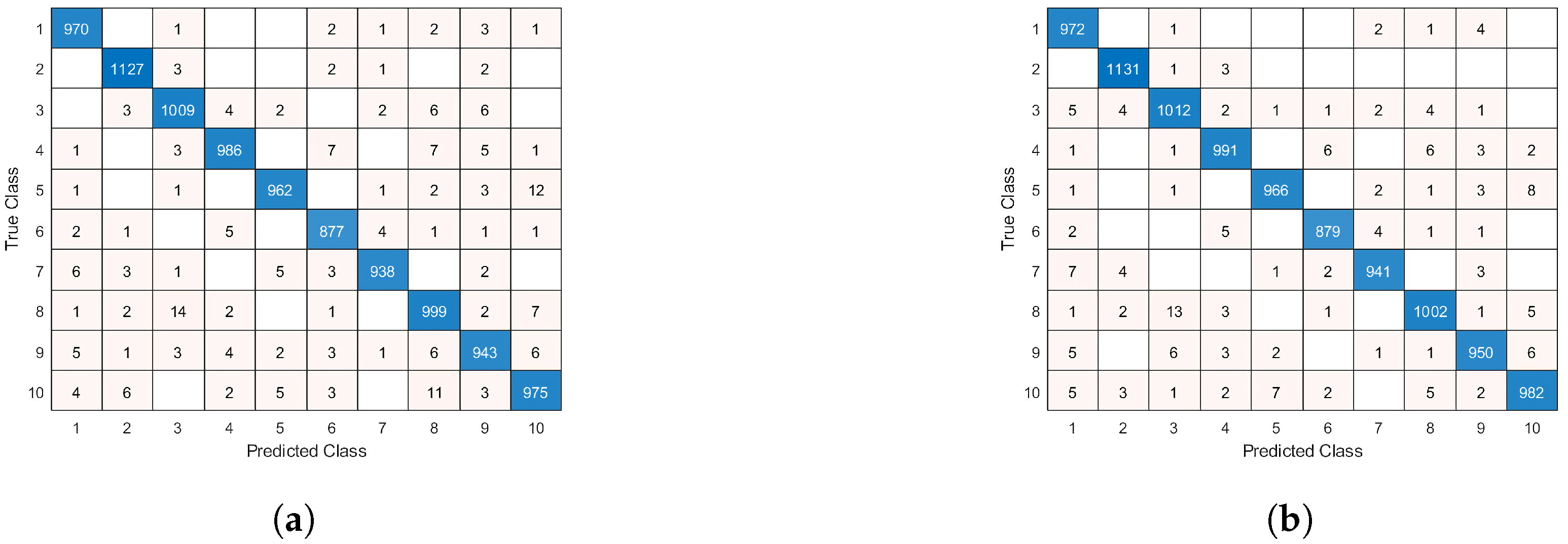
Figure 12 shows the confusion matrices of the vanilla MNIST network and the proposed network topology, respectively. Due to the low complexity of the dataset, the confusion matrix of the vanilla network is nearly diagonal, mostly confusing 8 with 3, which is expected. One can observe that the network, whose topology was automatically configured, is strongly diagonal, more than the vanilla network, which demonstrates the improvement offered by the proposed methodology.
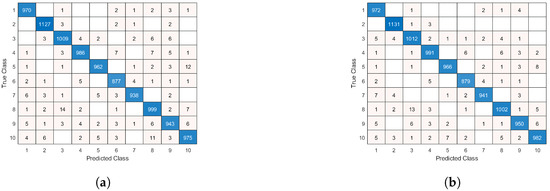
Figure 12.
Confusion matrix of (a) the vanilla MNIST network topology and (b) the adaptive MNIST network topology.
6.2. Fashion MNIST
Fashion-MNIST is a dataset of Zalando’s article [36], and it consists of a training set of 60,000 samples and a test set of 10,000 samples, with each sample being a grayscale image, associated with a label from 10 classes, just like the original MNIST dataset. Zalando intends Fashion-MNIST to serve as a direct drop-in replacement for the original MNIST dataset for benchmarking machine learning algorithms. For the fashion MNIST, we used the same neural network topology used on the numerical MNIST dataset, due to the size similarity of the two datasets.
Figure 13a illustrates the accuracy of 20 independent classification Runs of the Fashion MNIST dataset, using the automatic topology optimisation with the blue colour, and using the conventional topology with the red colour. The higher complexity of the dataset enables the proposed method to provide more consistent results with lower standard deviation among runs, 0.001720954 versus 0.002677681 of the original one, along with higher classification accuracy, 0.90002 versus 0.869445. The corresponding F1-scores are 0.8920 for the proposed method vs. 0.8721 for the conventional one. Figure 13b illustrates the testing accuracy of the two competing network topologies every five epochs up to the total of 30 epochs. Notice that, because the starting topologies are the same, the accuracy before any automatic change to the network topology is almost identical. However, we can observe a very different behaviour after the network decides its topology based on the dataset, achieving faster conversion and higher accuracy levels.

Figure 13.
(a) Fashion MNIST Testing Accuracy variation over random independent runs of the optimised and the conventional NN; (b) Fashion MNIST Accuracy every five-epoch training (1 phase) for the optimised and the conventional NN.
Figure 14 shows the confusion matrices of the vanilla fashion MNIST network and the proposed network topology, respectively. The confusion matrix of the vanilla network shows an inability to distinguish effectively some classes for the Fashion MNIST dataset, due to the slightly higher complexity compared to the regular MNIST. The optimized network shows a slightly stronger diagonal identity, due to the better suited topology, optimized by our proposed method.
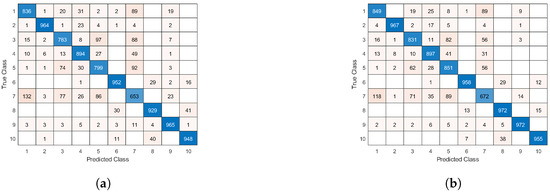
Figure 14.
Confusion matrix of (a) the vanilla Fashion MNIST network topology and (b) the adaptive Fashion MNIST network topology.
6.3. CIFAR-10 and CIFAR-100 Dataset
The CIFAR-10 dataset consists of 60,000 colour images in 10 classes, with 6000 images per class. The training set contains 50,000 training images and the test set 10,000 images. They were collected by Alex Krizhevsky, Vinod Nair and Geoffrey Hinton [32]. The dataset is divided into five training batches and one test batch, each with 10,000 images. The test batch contains exactly 1000 randomly-selected images from each class. The training batches contain the remaining images in random order, but some training batches may contain more images from one class than another. Between them, the training batches contain exactly 5000 images from each class.
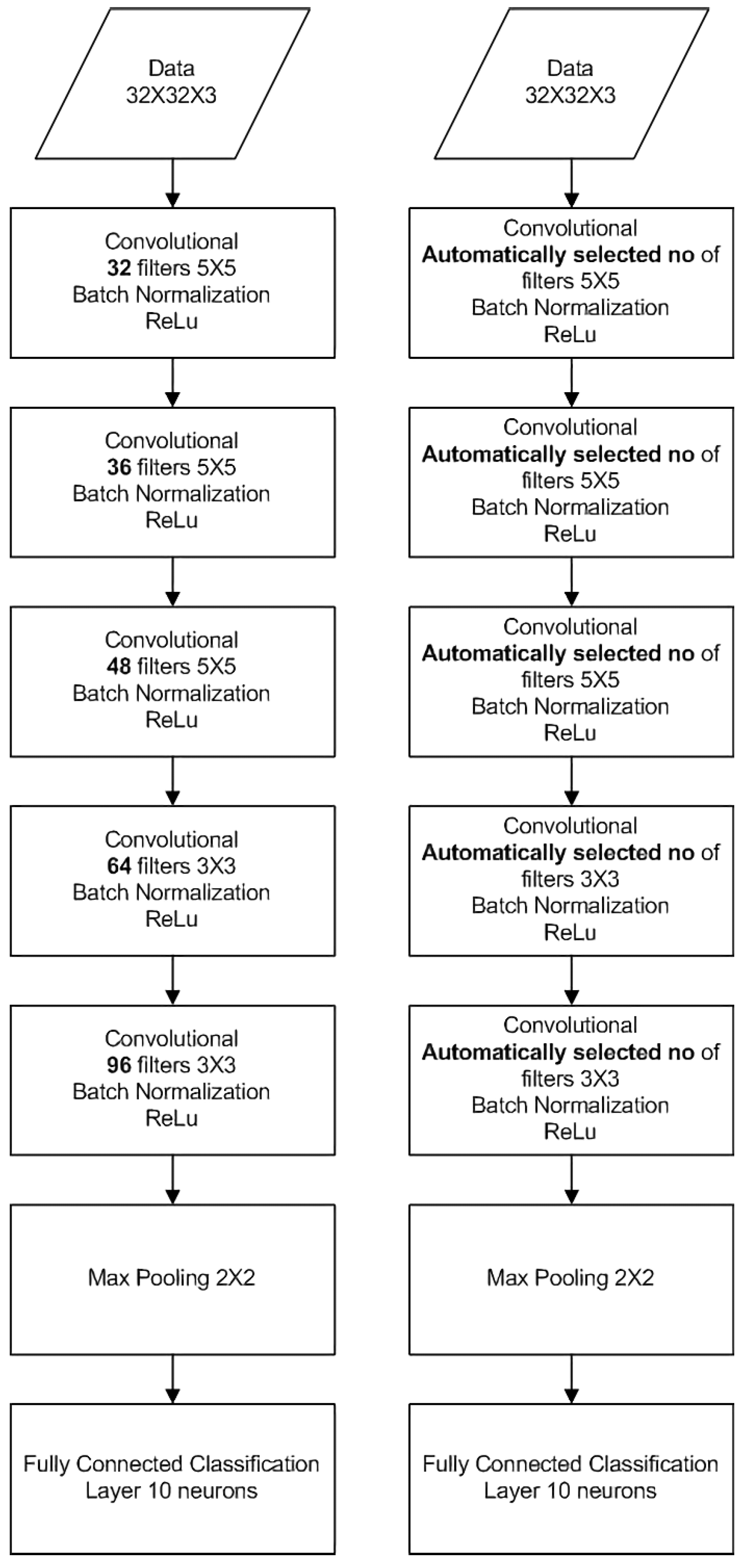
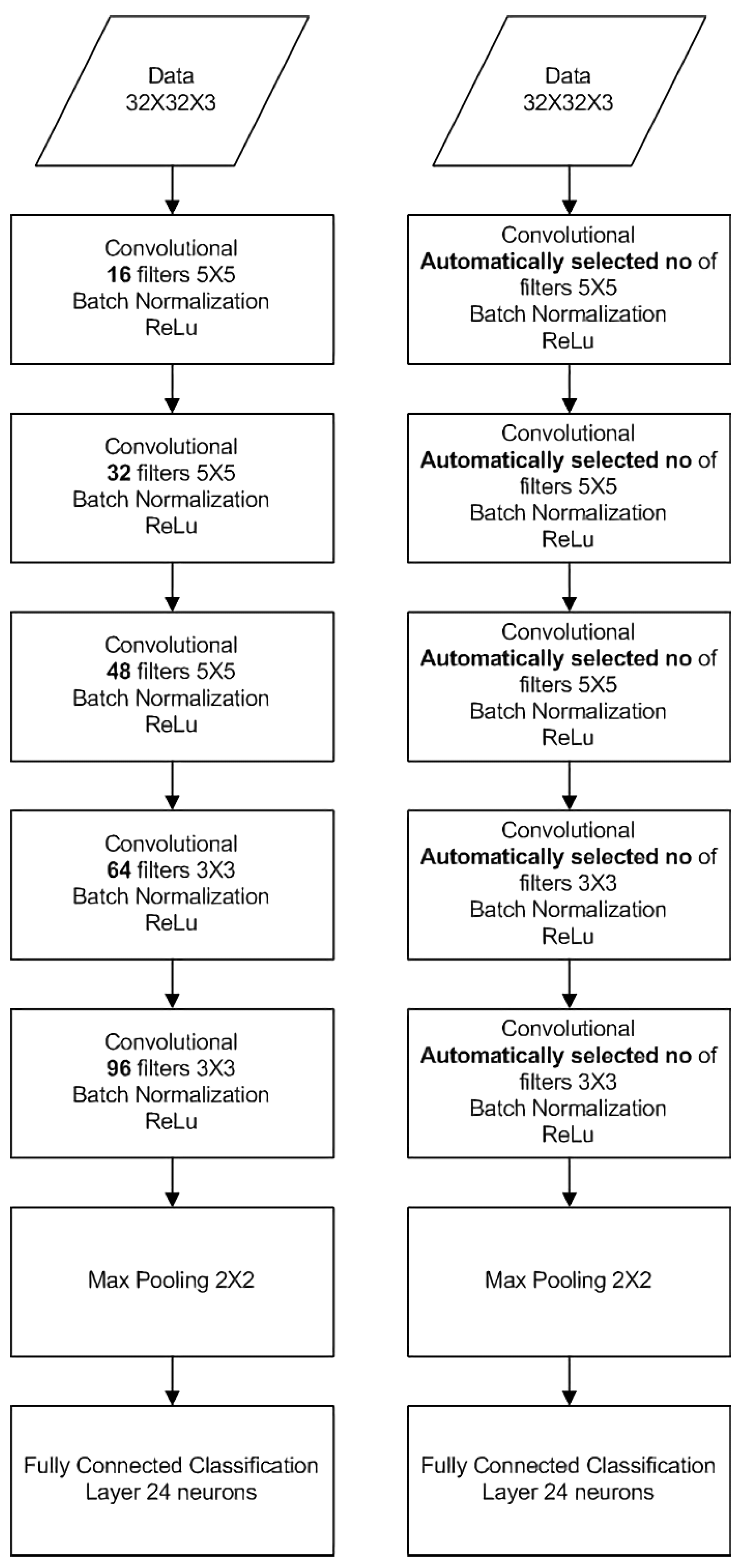
For the CIFAR-10 dataset, we used five evaluations of the network’s capacity, once every 10 epochs for a total of 50 epochs(Figure 15). The conventional topology is based on five Convolutional Layers with max pooling only after the last layer, and 10 neurons at the decision layer. The automatic topology optimized neural network used the same network as a baseline and further tuned each convolutional layer to the dataset’s needs.
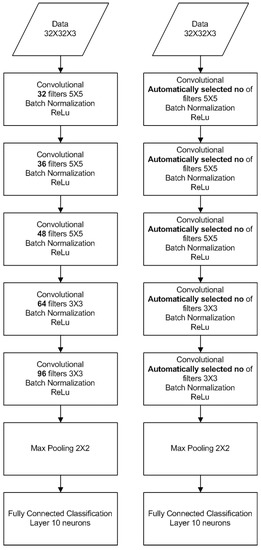
Figure 15.
Vanilla CNN for CIFAR10 classification (left), Adaptive CNN for CIFAR10 classification (right).
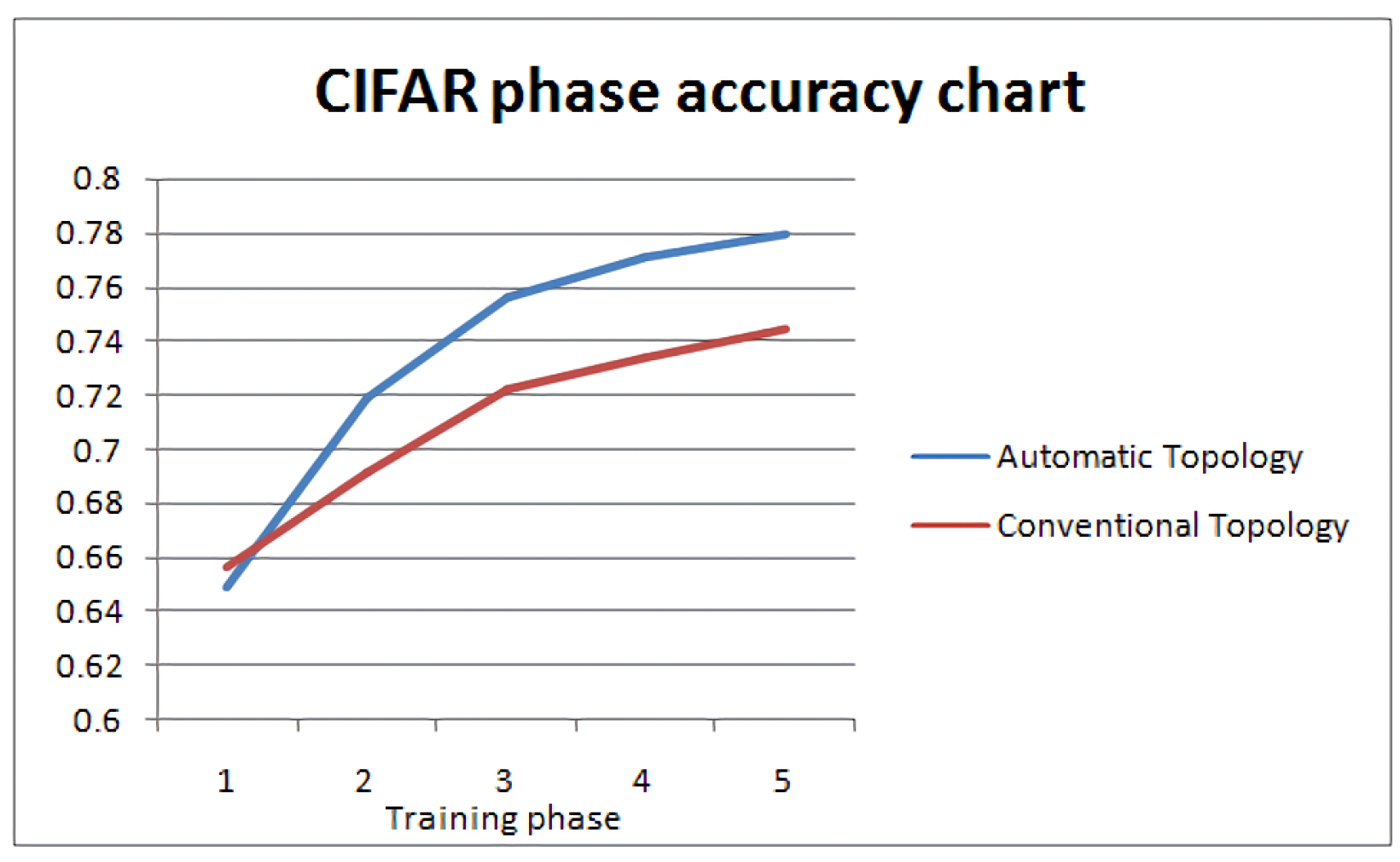
Figure 16 illustrates the testing accuracy per phase of topology tuning, of the two competing network topologies every ten epochs up to the total of 50 epochs. Even in this more complicated case, we can observe a very different behaviour after the network decides its topology based on the dataset, achieving faster conversion and higher accuracy levels. The corresponding F1-scores are 0.7708 for the proposed method vs. 0.6805 for the conventional one.
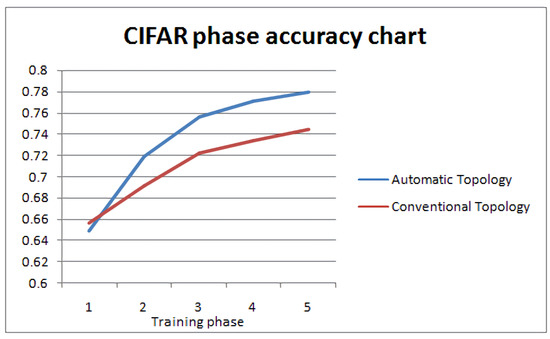
Figure 16.
CIFAR-10 testing Accuracy chart per phase of topology tuning.
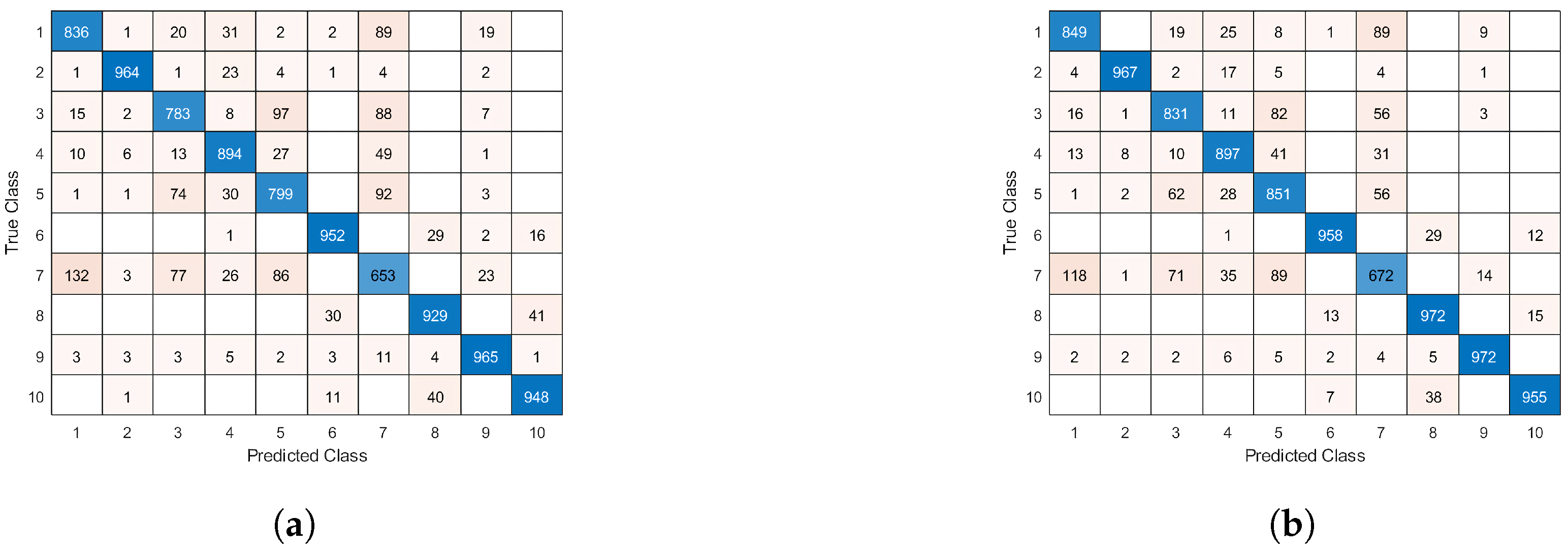
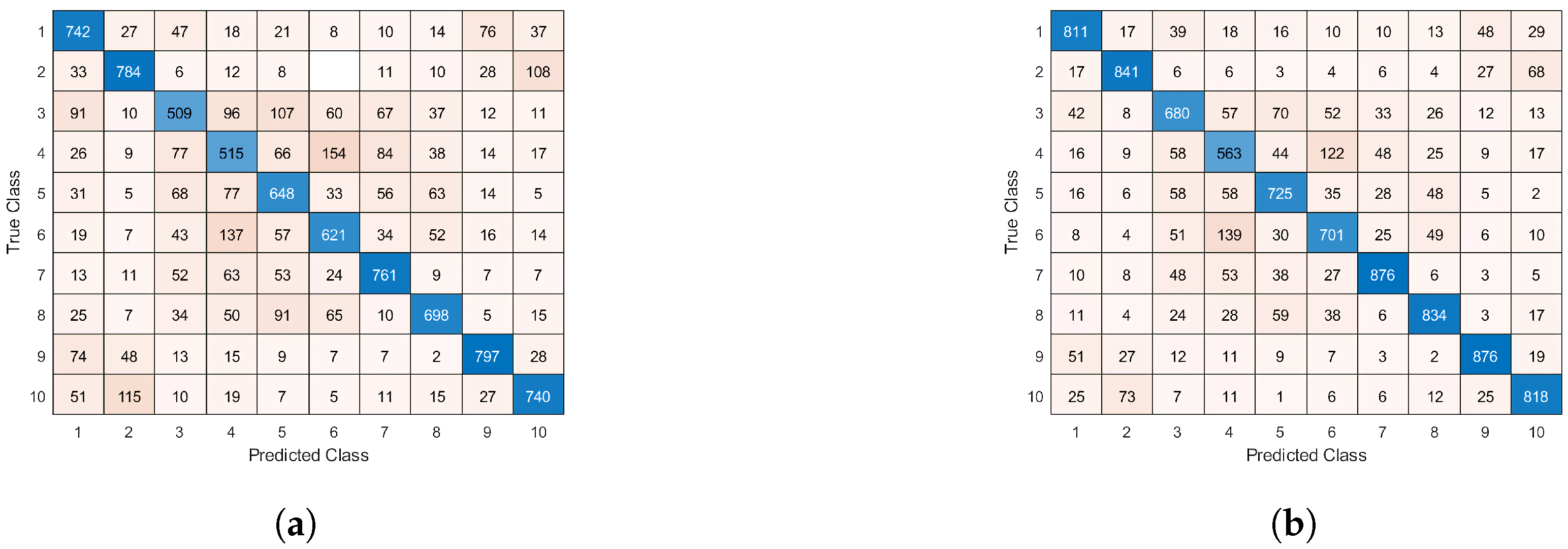
Figure 17 depicts the confusion matrices of the vanilla CIFAR-10 network and the proposed network topology, respectively. The confusion matrix of the conventional topology shows that the majority of the classification errors are between cats and dogs, and trucks and automobiles as expected, since the images of these classes are quite similar. The confusion matrix of the automatic topology shows that, while there are mostly classification errors between cats and dogs, and trucks and automobiles, there is an increase of correct classifications, due to the more optimal network topology.
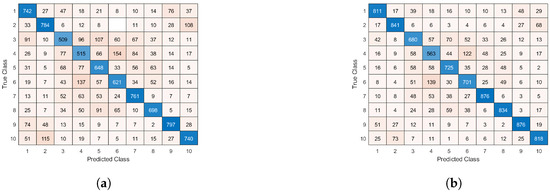
Figure 17.
Confusion matrix of (a) the vanilla CIFAR-10 network topology and (b) the adaptive CIFAR-10 network topology.
The CIFAR-100 dataset is very similar to the CIFAR-10, except that it has 100 classes containing 600 images each. There are 500 training images and 100 testing images per class. They were collected by Alex Krizhevsky, Vinod Nair and Geoffrey Hinton [32]. We used the same initial network that we used for the CIFAR-10 dataset. The only difference is that the last fully-connected layer contains 100 neurons, equal to the number of classes.
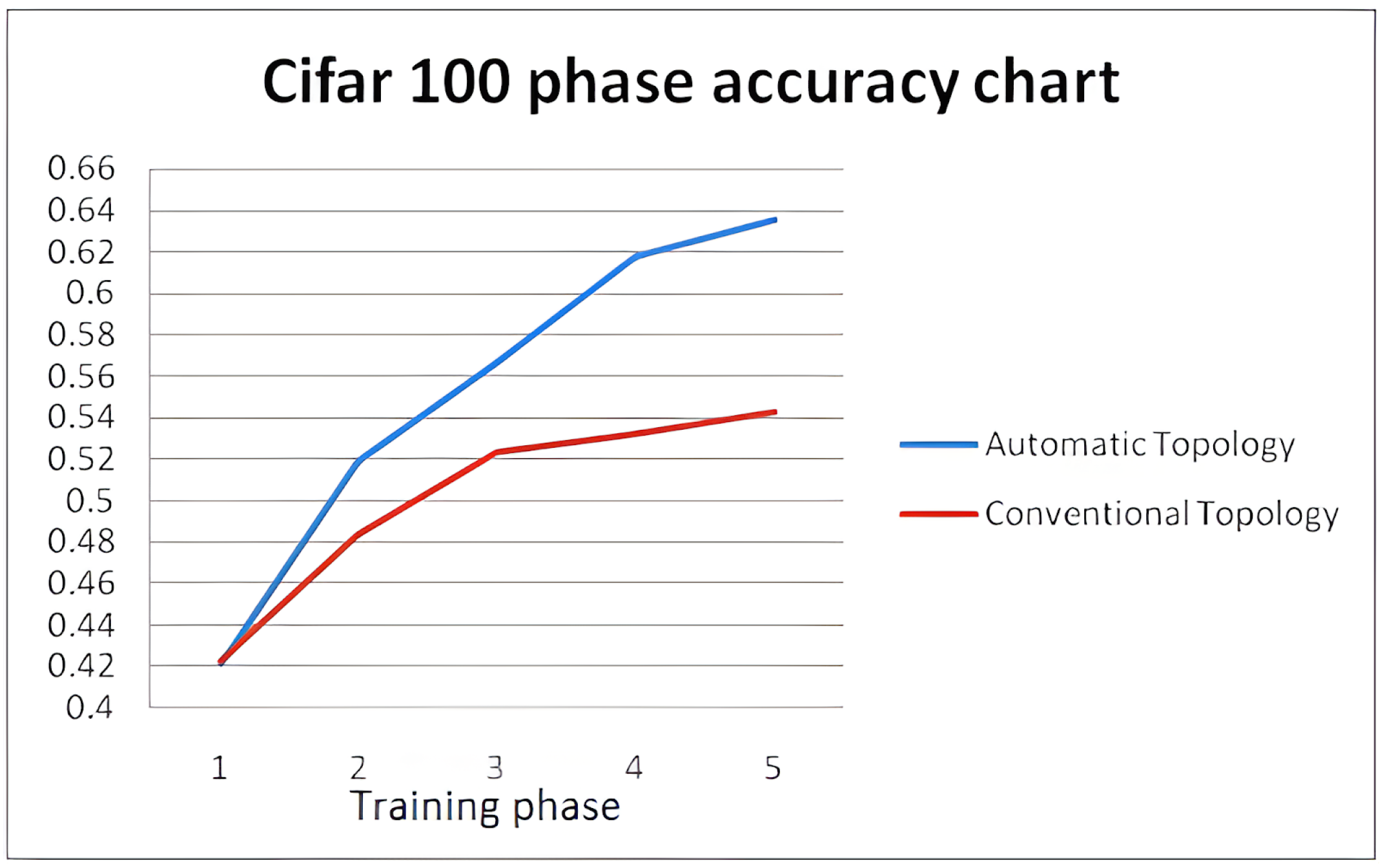
Figure 18 illustrates the testing accuracy per phase of topology tuning, of the two competing network topologies every ten epochs up to the total of 50 epochs. Despite the more complicated classification nature of CIFAR100, the proposed optimization algorithm improves the vanilla network, achieving faster conversion and higher accuracy levels of 0.6351 instead of 0.5421 of the vanilla network. The corresponding F1-scores are 0.6146 for the proposed method vs. 0.5240 for the conventional one.
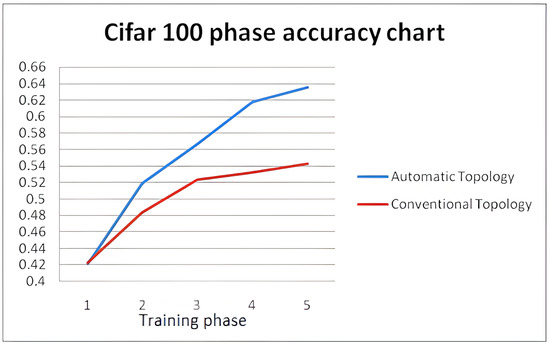
Figure 18.
Testing accuracy convergence of the vanilla CIFAR-100 network topology and the adaptive CIFAR-100 network topology.
6.4. Sign Language Dataset
The American Sign Language letter database of hand gestures represents a multi-class problem with 24 classes of letters (excluding J and Z which require motion). The Sign Language MNIST data came from greatly extending the small number (1704) of the colour images included as not cropped around the hand region of interest. To create new data, an image pipeline was used based on ImageMagick and included cropping to hands-only, gray-scaling, resizing, and then creating at least 50+ variations to enlarge the quantity. The modification and expansion strategy was filters (‘Mitchell’, ‘Robidoux’, ‘Catrom’, ‘Spline’, ‘Hermite’), along with 0.05 random pixelation, brightness/contrast, and finally three degrees of rotation. Because of the tiny size of the images, these modifications effectively alter the resolution and class separation in interesting, controllable ways.
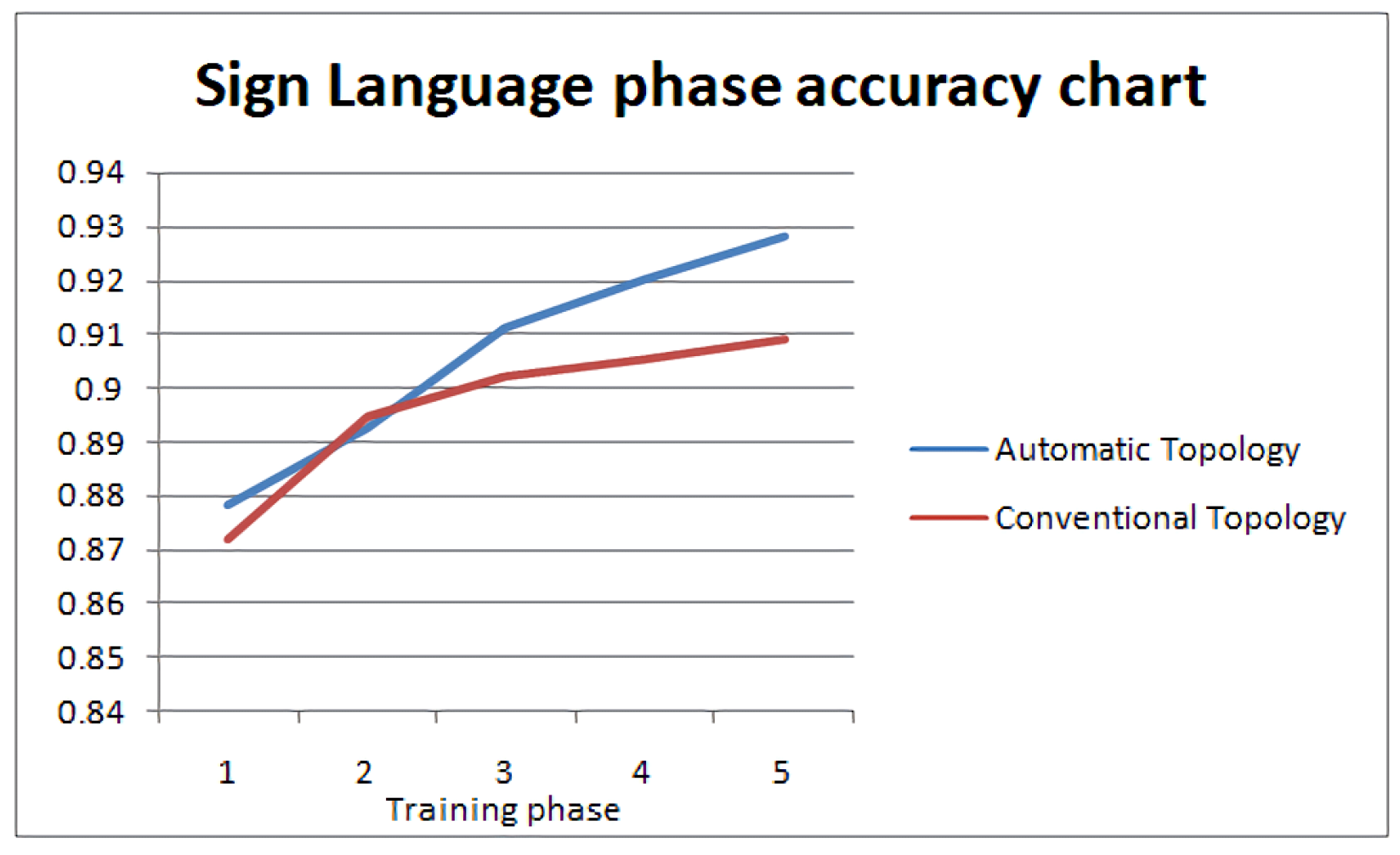
For the sign language dataset, we used the same number of layers as the CIFAR dataset, but with narrower layers, as the dataset’s complexity is lower. The two architectures are shown in Figure 19. The total number of epochs remained 30, with topology optimization every five epochs. The improvement of accuracy during optimization of the NN architecture is shown in Figure 20.
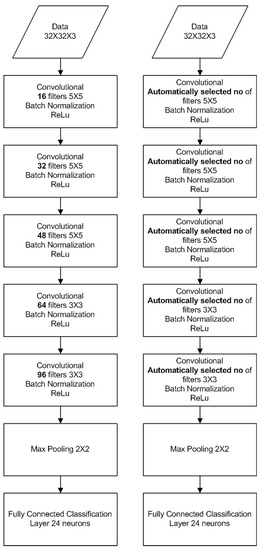
Figure 19.
Vanilla CNN for Sign Language classification (left), Adaptive CNN for Sign Language classification (right).
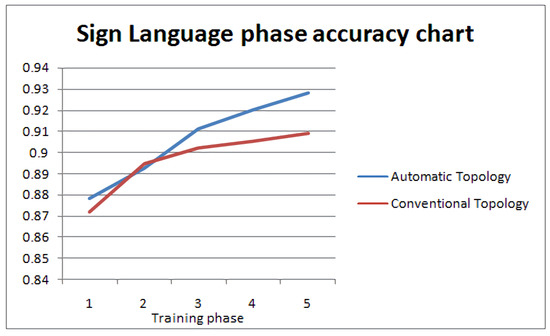
Figure 20.
Sign Language accuracy progression.
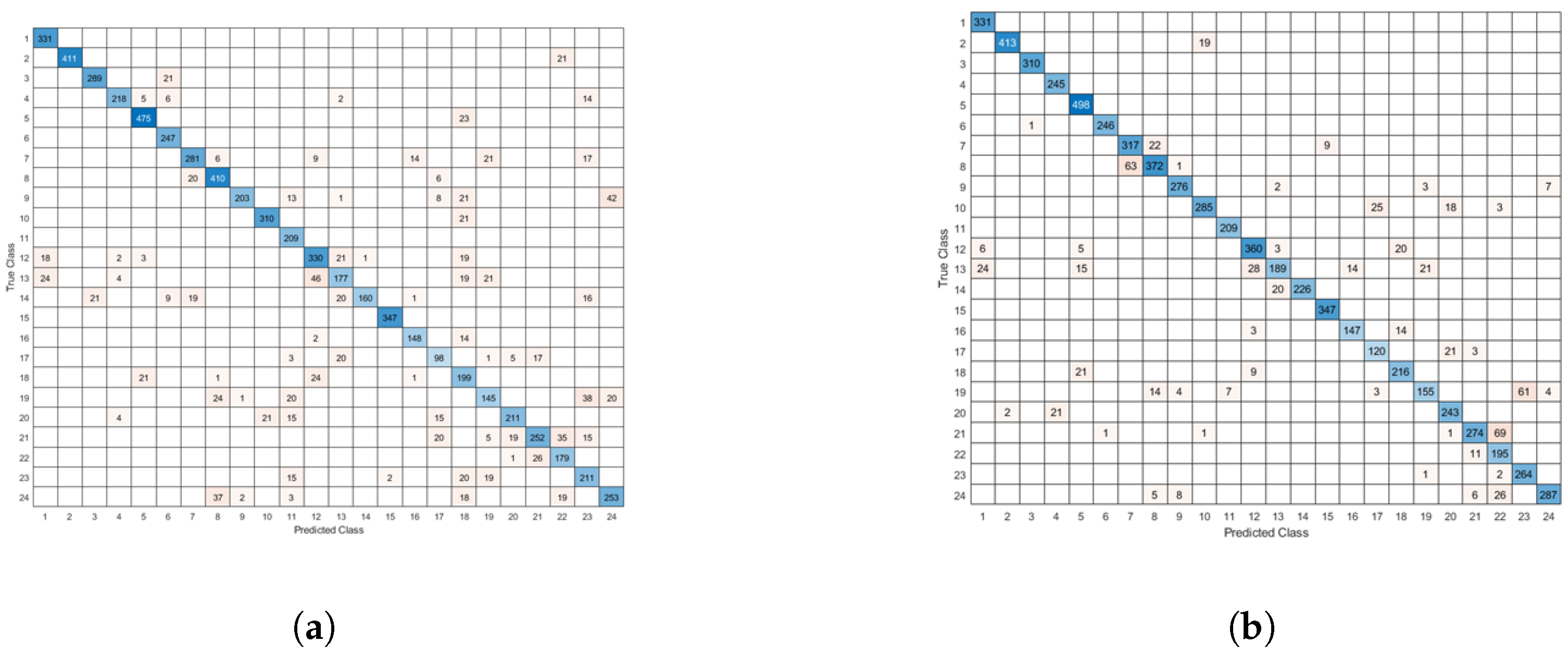
We can observe that the network achieves better accuracy by using the topology optimization proposed, compared to the vanilla network. We can spot a slight dip in accuracy the first time a change in topology takes place, as new random filters/neurons are integrated in the neural network. Figure 21 depicts the confusion matrices in both cases. We can observe that the improved topology features a decrease in misclassifications and a stronger diagonal behaviour, compared to the vanilla architecture. The corresponding F1-scores are 0.9033 for the proposed method vs. 0.8393 for the conventional one.
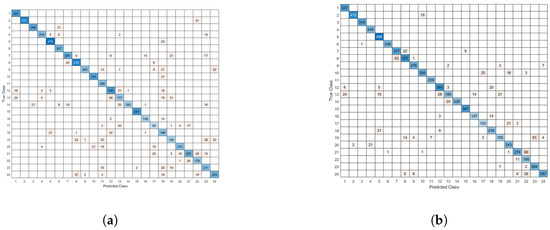
Figure 21.
Confusion matrix of (a) the vanilla Sign Language network topology and (b) the adaptive Sign Language network topology.
6.5. Computational Cost of the Proposed Algorithm
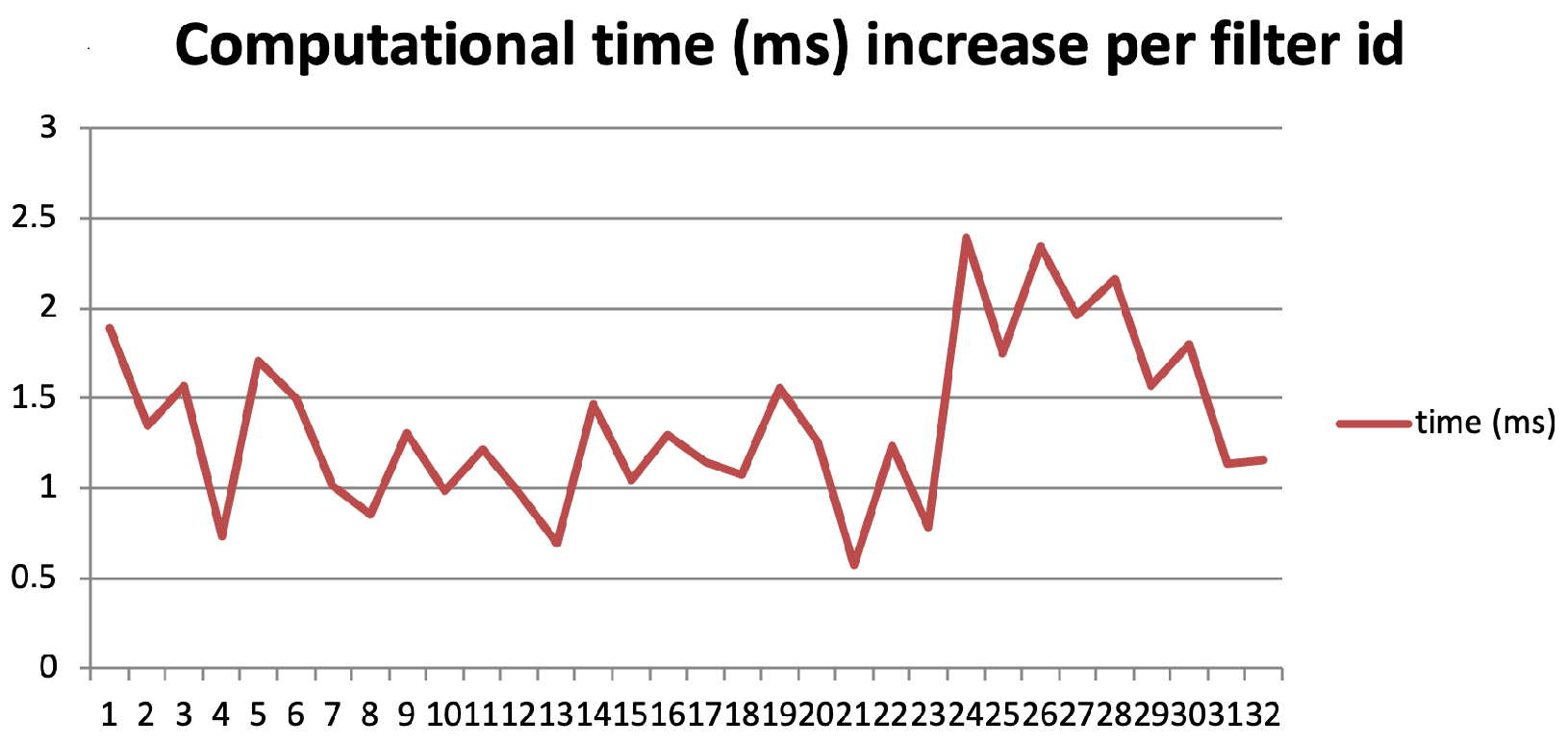
In this section, we attempt to evaluate the computational cost of the proposed algorithm. In other words, we investigate the complexity added by our method to a common NN architecture, in order to tune it up for better performance. In our measurements, we used a Windows 10 PC with an Intel i7-4770S processor, 8MB cache, 16 GB RAM, running MATLAB 2020a. We used the experiment described earlier for the MNIST dataset. More specifically, we compared the operations performed at the 2nd layer of the two architectures (vanilla and optimised), which contains 32 filters. The aim is to measure the difference in execution time for each filter update of this layer between the two architectures. The measurement is performed using the “tic-toc” MATLAB command. In our measurement, we have subtracted the computational cost of this command, in order to reflect the added computational cost only. Figure 22 depicts the increase in computational time per each of the 32 filters of the first layer, as induced by the proposed algorithm. We can see that the average delay for all filters is ms. The average delay per filter is relative small with minimal standard deviation, which demonstrated the stable added computational cost, required by the proposed algorithm. In order to make this figure independent of the specific CPU, where the measurement was taken, we take into account that an i7 4770S scores 447.7 single precision GFLOPS, according to the popular synthetic benchmark AIDA64. The average delay induced by the proposed algorithm is 1.359 ms, thus this accounts for an extra computational cost of GFLOP on average per filter. Consequently, the induced overhead is considered minimal for modern CPUs and GPUs. It is also important to mention that this overhead is applied only when the proposed algorithm optimises the NN’s architecture, which is every five epochs. Of course, this interval can be set to any number of epochs, according to the load of the system. In the meantime, there is no computational overhead between the vanilla and the optimised architecture. These figures are indicative due to the limitations induced by the measuring method, but clearly demonstrate that the induced computational burden by the algorithm is minimal, whereas the gain in computational efficiency is increased.
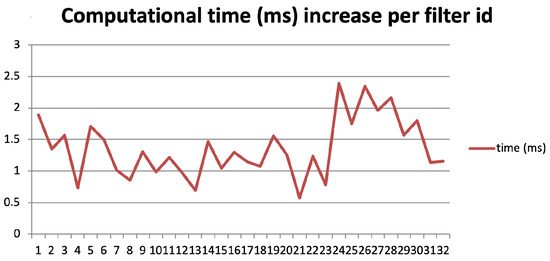
Figure 22.
Computational time (ms) increase per filter due to the proposed algorithm. The testbed is the MNIST dataset and the comparison entails the first layer of the vanilla and proposed architecture, as described earlier in the text.
7. Conclusions—Future Work
In this paper, we propose a strategy to improve the performance of any NN architecture. First, the complexity of the dataset is computed, and the neural network is initialized, as it would be if the automatic topology method was not used. Every fixed number of iterations, the information capacity of each layer is calculated, considering each layer as an information channel, using an optimized Blahut–Arimoto algorithm. If the layer is found to be unable to pass the required information to the next stage, it is expanded. In the opposite case in which the layer is found to encode the information sparsely, the extra nodes (neurons/filters) are removed, while maintaining the encoded information trained so far.
This strategy seems to be a viable, fast and computationally efficient method to boost performance and reduce computational and memory requirements in neural network architectures. One can use this method in order to achieve good accuracy without the trial and error required traditionally in order to find the most optimised topology for each problem.
As a next step, we will expand the method with the ability of adding whole layers, if the process of expanding wide-wise the current layers does not improve the performance considerably. Perhaps, adopting a greedy-wise search as the one presented in [39], but adapted to the information theoretic perspective might provide a solution. We also plan to combine this scheme with a previously proposed scheme [40], where the trained network is used to perform a rough classification of the testing dataset. Data with confident classification are used along with the training dataset to refine the training of the already trained network, which boosts the classification accuracy. These combined with an automatic topology network optimisation will be more likely to boost performance and usability even more.
Author Contributions
Conceptualization, A.M. and N.M.; methodology, A.M.; software, P.A. and A.M.; validation, P.A. and A.M.; formal analysis, A.M. and N.M.; investigation, A.M.; writing—original draft preparation, A.M.; writing—review and editing, A.M. and N.M.; supervision, N.M.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Siu, K.; Stuart, D.M.; Mahmoud, M.; Moshovos, A. Memory Requirements for Convolutional Neural Network Hardware Accelerators. In Proceedings of the 2018 IEEE International Symposium on Workload Characterization (IISWC), Raleigh, NC, USA, 30 September–2 October 2018; pp. 111–121. [Google Scholar] [CrossRef]
- Chen, T.; Li, M.; Li, Y.; Lin, M.; Wang, N.; Wang, M.; Xiao, T.; Xu, B.; Zhang, C.; Zhang, Z. MXNet: A Flexible and Efficient Machine Learning Library for Heterogeneous Distributed Systems. In Proceedings of the Neural Information Processing Systems, Workshop on Machine Learning Systems, Montreal, QC, Canada, 7–12 December 2015). [Google Scholar]
- Gruslys, A.; Munos, R.; Danihelka, I.; Lanctot, M.; Graves, A. Memory-Efficient Backpropagation Through Time. In Proceedings of the NIPS’16: 30th International Conference on Neural Information Processing Systems, Barcelona Spain, 5–10 December 2016. [Google Scholar]
- Diamos, G.; Sengupta, S.; Catanzaro, B.; Chrzanowski, M.; Coates, A.; Elsen, E.; Engel, J.; Hannun, A.; Satheesh, S. Persistent RNNs: Stashing recurrent weights on-chip. In Proceedings of the ICML’16: 33rd International Conference on International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; Volume 48, pp. 2024–2033. [Google Scholar]
- Hagan, M.; Demuth, H.B.; Beale, M.H.; De Jesus, O. Neural Network Design, 2nd ed.; Martin Hagan: Oklahoma, OK, USA, 2014; Available online: https://hagan.okstate.edu/nnd.html (accessed on 24 July 2022).
- Bishop, C. Neural Networks for Pattern Recognition; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Theodoridis, S. Machine Learning: A Bayesian Perspective, 1st ed.; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Heaton, J. Introduction to Neural Networks for Java, 2nd ed.; Heaton Research, Inc.: Dublin, Ireland, 2008. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep compression: Compressing deep neural network with pruning, trained quantization and huffman coding. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016, San Juan, Puerto Rico, 2–4 May 2016; Available online: http://arxiv.org/abs/1510.00149 (accessed on 24 July 2022).
- Lee, N.; Ajanthan, T.; Torr, P.H.S. Snip: Single-shot network pruning based on connection sensitivity. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019; Available online: https://openreview.net/forum?id=B1VZqjAcYX (accessed on 24 July 2022).
- Li, H.; Kadav, A.; Durdanovic, I.; Samet, H.; Graf, H.P. Pruning filters for efficient convnets. arXiv 2016, arXiv:1608.08710. [Google Scholar]
- Frankle, J.; Carbin, M. The lottery ticket hypothesis: Finding sparse, trainable neural networks. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019; Available online: https://openreview.net/forum?id=rJl-b3RcF7 (accessed on 24 July 2022).
- Liu, Z.; Sun, M.; Zhou, T.; Huang, G.; Darrell, T. Re-thinking the value of network pruning. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019; Available online: https://openreview.net/forum?id=rJlnB3C5Ym (accessed on 24 July 2022).
- Han, S.; Pool, J.; Tran, J.; Dally, W. Learning both weights and connections for efficient neural network. In Proceedings of the NIPS’15: Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 1135–1143. [Google Scholar]
- Gale, T.; Elsen, E.; Hooker, S. The state of sparsity in deep neural networks. arXiv 2016, arXiv:1902.09574. [Google Scholar]
- Frankle, J.; Dziugaite, G.K.; Roy, D.M.; Carbin, M. The lottery ticket hypothesis at scale. arXiv 2019, arXiv:1903.01611. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006; pp. 206–207. ISBN 978-0-471-24195-9. [Google Scholar]
- Kolmogorov, A. On Tables of Random Number. Theor. Comput. Sci. 1998, 207, 387–395. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Three Approaches to the Quantitative Definition of Information. Probl. Inform. Transm. 1965, 1, 1–7. [Google Scholar] [CrossRef]
- Kolmogorov, A.X. Logical basis for information theory and probability theory. IEEE Trans. Inf. Theory 1968, 14, 662–664. [Google Scholar] [CrossRef]
- Arimoto, S. An algorithm for computing the capacity of arbitrary discrete memoryless channels. IEEE Trans. Inf. Theory 1972, 18, 14–20. [Google Scholar] [CrossRef]
- Burgin, M. Generalized Kolmogorov complexity and duality in theory of computations. Not. Russ. Acad. Sci. 1982, 25, 19–23. [Google Scholar]
- Vitányi, P.M.B. Conditional Kolmogorov complexity and universal probability. Theor. Comput. Sci. 2013, 501, 93–100. [Google Scholar] [CrossRef]
- Kaltchenko, A. Algorithms for Estimating Information Distance with Application to Bioinformatics and Linguistics. arXiv 2004, arXiv:cs.CC/0404039. [Google Scholar]
- Solomonoff, R. A Preliminary Report on a General Theory of Inductive Inference; Report V-131; Revision Published November 1960; Zator Company: Cambridge, MA, USA, 1960. [Google Scholar]
- Rissanen, J. Information and Complexity in Statistical Modeling; Springer: Berlin/Heidelberg, Germany, 2007; p. 53. ISBN 978-0-387-68812-1. [Google Scholar]
- Blahut, R. Computation of channel capacity and rate-distortion functions. IEEE Trans. Inf. Theory 1972, 18, 460–473. [Google Scholar] [CrossRef]
- Vontobel, P.O. A Generalized Blahut–Arimoto Algorithm. In Proceedings of the IEEE International Symposium on Information Theory, Yokohama, Japan, 29 June–4 July 2003. [Google Scholar]
- Naiss, I.; Permuter, H.H. Extension of the Blahut–Arimoto Algorithm for Maximizing Directed Information. IEEE Trans. Inf. Theory 2013, 59, 204–222. [Google Scholar] [CrossRef]
- Jetka, T.; Nienaltowski, K.; Winarski, T.; Blonski, S.; Komorowski, M. Information-theoretic analysis of multivariate single-cell signaling responses. PLoS Comput. Biol. 2019, 15, e1007132. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y. Squeezing the Arimoto-Blahut Algorithm for Faster Convergence. IEEE Trans. Inf. Theory 2010, 56, 3149–3157. [Google Scholar] [CrossRef]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images. 2009. Available online: https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (accessed on 24 July 2022).
- Siddiqui, S.A.; Salman, A.; Malik, I.; Shafait, F. Automatic fish species classification in underwater videos: Exploiting pretrained deep neural network models to compensate for limited labelled data. ICES J. Mar. Sci. 2018, 75, 374–389. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Deng, L. The mnist database of handwritten digit images for machine learning research. IEEE Signal Proc. 2012, 29, 141–142. [Google Scholar] [CrossRef]
- Support Vector Machines Speed Pattern Recognition—Vision Systems Design. 2004. Available online: https://www.vision-systems.com/home/article/16737424/support-vector-machines-speed-pattern-recognition (accessed on 24 July 2022).
- LeCun, Y.; Cortez, C.; Burges, C.C.J. The MNIST Handwritten Digit Database. Yann LeCun’s Website. 2020. Available online: http://yann.lecun.com (accessed on 24 July 2022).
- Kussul, E.; Baidyk, T. Improved method of handwritten digit recognition tested on MNIST database. Image Vis. Comput. 2004, 22, 971–981. [Google Scholar] [CrossRef]
- Belilovsky, E.; Eickenberg, M.; Oyallon, E. Greedy Layerwise Learning Can Scale to ImageNet. arXiv 2019, arXiv:abs/1812.11446. [Google Scholar]
- Maniatopoulos, A.; Gazis, A.; Pallikaras, V.P.; Mitianoudis, N. Artificial Neural Network Performance Boost using Probabilistic Recovery with Fast Cascade Training. Int. J. Circuits Syst. Signal Process. 2020, 14, 847–854. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).