Prediction and Privacy Scheme for Traffic Flow Estimation on the Highway Road Network
Abstract
:1. Introduction
- Introduction of the privacy-preserving approach for traffic flow prediction. This method relies on FL to use the LSTM as a prediction model. As a consequence, the proposed method presents all the advantages offered by FL (cost-saving, privacy benefits, etc.)
- Proposition of the Local Differential Privacy mechanism to strengthen protections in the proposed method, by perturbing the shared model gradients to avoid the privacy threats during the communication phase.
- Evaluation of the proposed framework on a public traffic dataset, and comparison of the results with other centralized machine learning methods. Our proposed mechanism achieves good performance compared to other approaches.
2. Related Work
2.1. Traffic Flow Forecasting
2.2. Privacy and Security for Intelligent Transportation Systems
3. Preliminaries
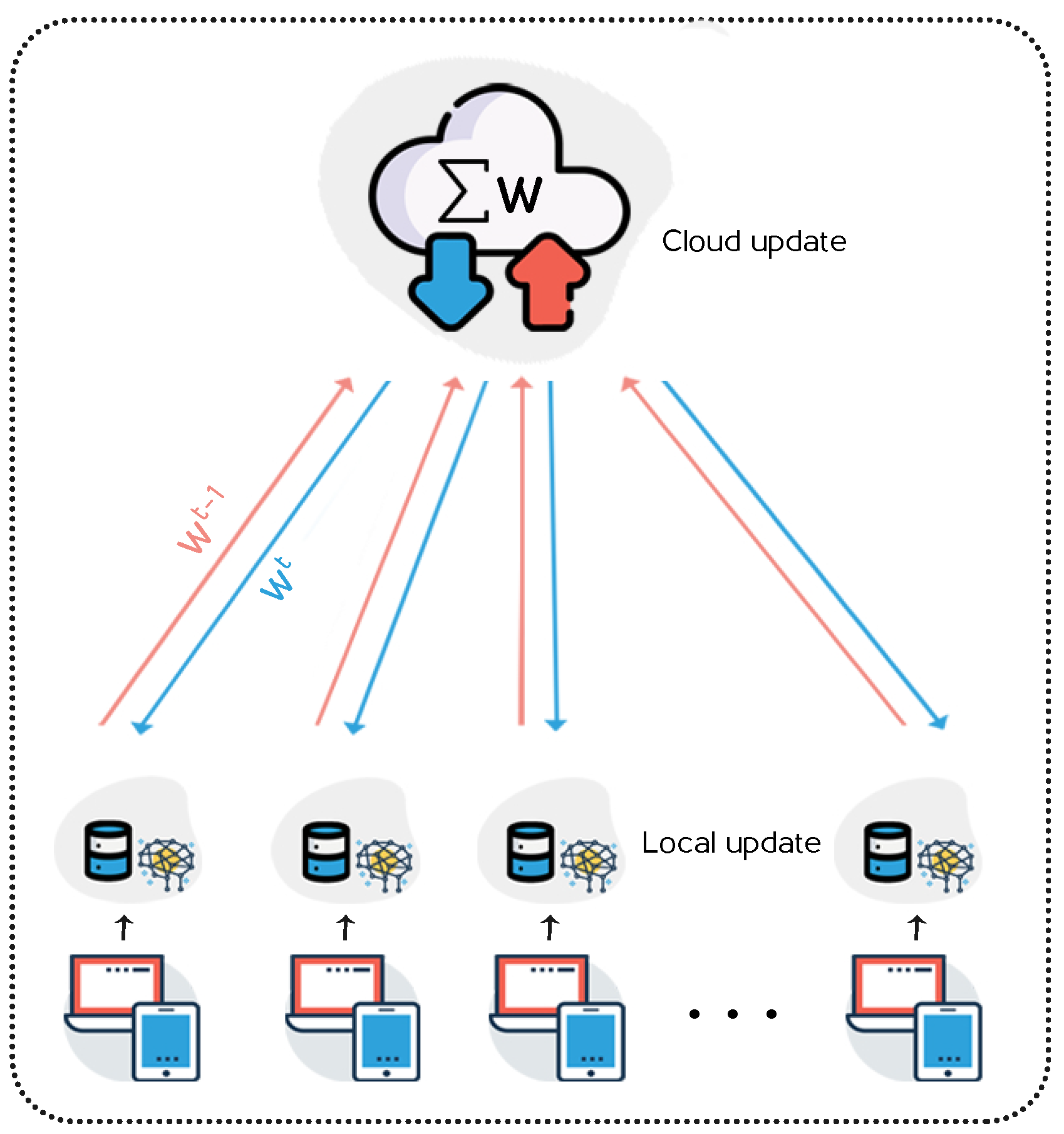
3.1. Federated Learning
3.2. Local Differential Privacy (LDP)
4. System Model and FL-LDP Protocol
4.1. System Model
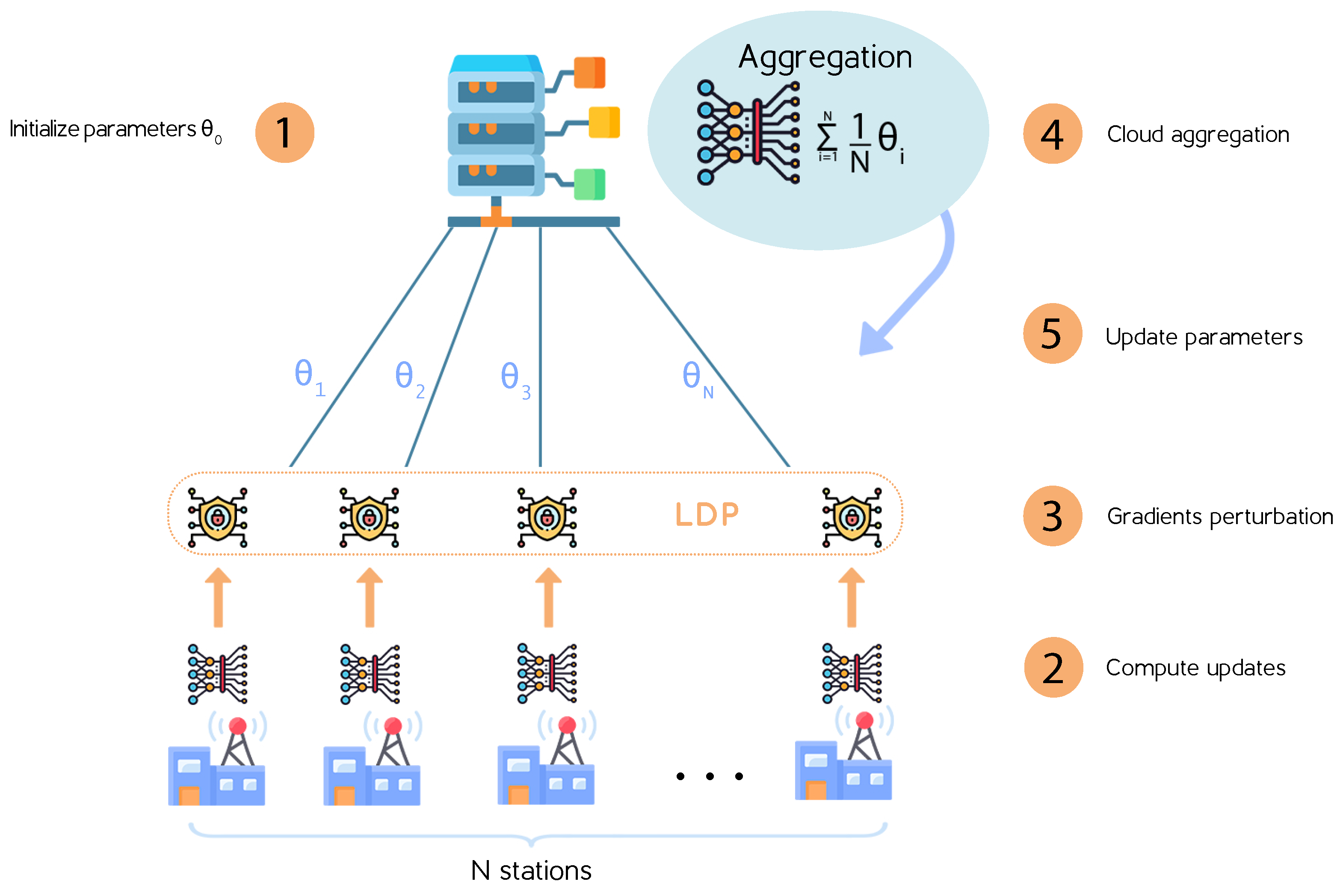
4.2. Federated Learning Based LDP: FL-LDP Protocol
- 1.
- Selects a subset of stations to participate in the current training round.
- 2.
- Distributes the initialized parameters to all participating stations.
- 3.
- Waits to receive gradients computed by the participating stations.
- 4.
- Aggregates the updated gradients sent by all stations using the aggregation protocol.
- 5.
- Shares the new global model to all stations.
| Algorithm 1:FL-LDP protocol: Server side |
 |
| Algorithm 2:FL-LDP protocol: Client side |
 |
- Initializes the local model.
- Trains the local model by locally computing the gradients on its private local dataset.
- Uses the LDP algorithm to compute the noisy gradient.
- Sends the noisy gradient to the cloud server.
- Waits to receive the aggregated gradient updates from the server.
5. Experiments
5.1. System Performance
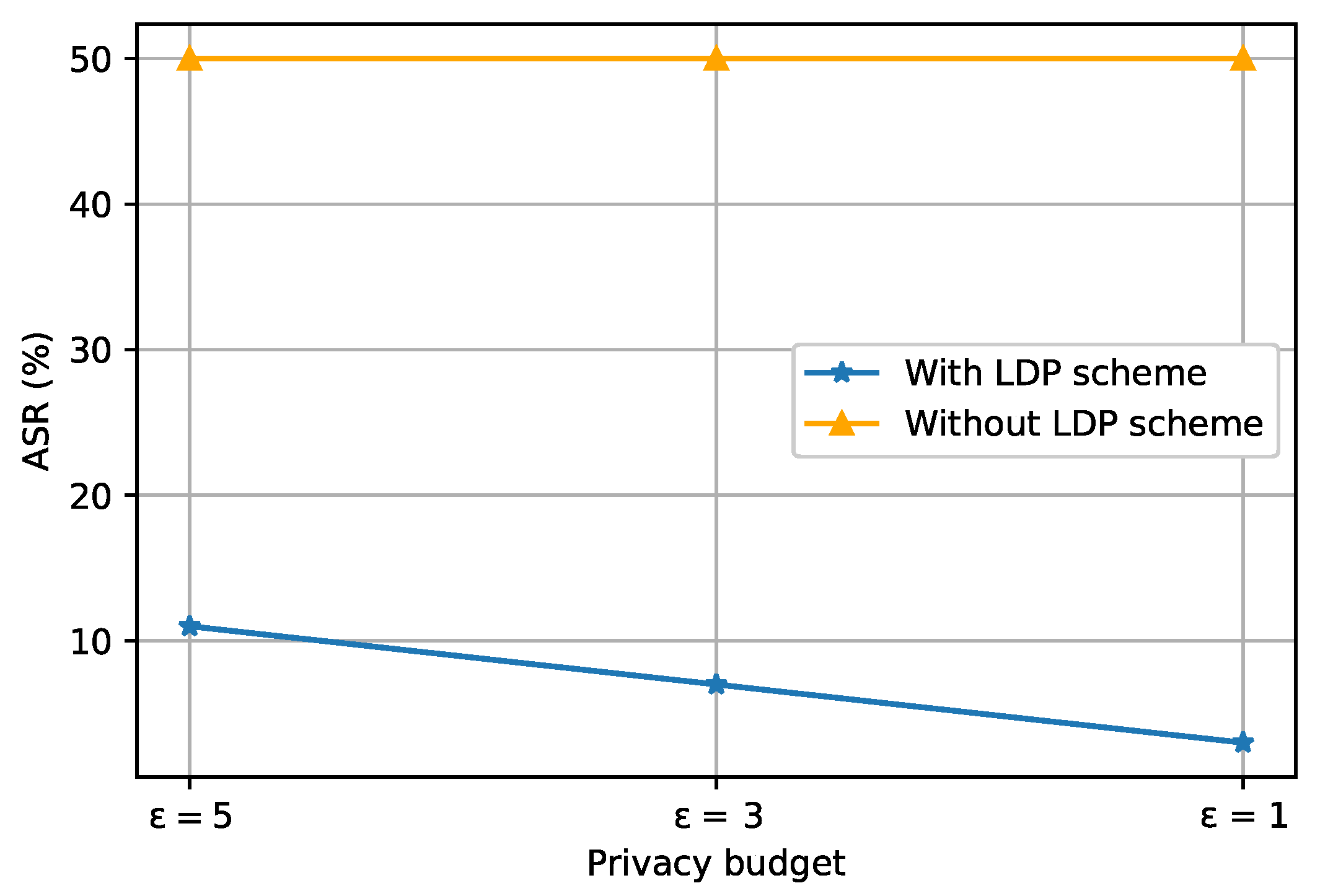
5.2. Privacy Budget Impact
5.3. Performance of Secure FL-LDP Model Training
5.4. Discussion
- -
- FL-LDP provides strong data protection and accurate traffic prediction, by combining local differential privacy (Gaussian noise) and federated learning (FedSGD). Specifically, the model achieves good performance by aggregating perturbed gradients, instead of the true gradient values, which guarantees user privacy protection.
- -
- Increasing the number of participants in each communication round may lead to some issues such as the communication overhead and model convergence due to the failure of synchronizing some stations.
- -
- The privacy budget affects the convergence of the model in some cases: decreasing the privacy budget can delay the convergence.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2014, 16, 865–873. [Google Scholar] [CrossRef]
- Aung, N.; Zhang, W.; Dhelim, S.; Ai, Y. T-Coin: Dynamic traffic congestion pricing system for the Internet of Vehicles in smart cities. Information 2020, 11, 149. [Google Scholar] [CrossRef] [Green Version]
- Konečnỳ, J.; McMahan, H.B.; Yu, F.X.; Richtárik, P.; Suresh, A.T.; Bacon, D. Federated learning: Strategies for improving communication efficiency. arXiv 2016, arXiv:1610.05492. [Google Scholar]
- Aono, Y.; Hayashi, T.; Wang, L.; Moriai, S. Privacy-preserving deep learning: Revisited and enhanced. In Proceedings of the International Conference on Applications and Techniques in Information Security, Auckland, New Zealand, 6–7 July 2017; Springer: New York, NY, USA, 2017; pp. 100–110. [Google Scholar]
- Phong, L.T.; Aono, Y.; Hayashi, T.; Wang, L.; Moriai, S. Privacy-preserving deep learning via additively homomorphic encryption. IEEE Trans. Inf. Forensics Secur. 2017, 13, 1333–1345. [Google Scholar]
- Bindschaedler, V.; Shokri, R.; Gunter, C.A. Plausible deniability for privacy-preserving data synthesis. arXiv 2017, arXiv:1708.07975. [Google Scholar] [CrossRef] [Green Version]
- Ojeda, L.L.; Kibangou, A.Y.; De Wit, C.C. Adaptive Kalman filtering for multi-step ahead traffic flow prediction. In Proceedings of the 2013 IEEE American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 4724–4729. [Google Scholar]
- Kumar, S.V. Traffic flow prediction using Kalman filtering technique. Procedia Eng. 2017, 187, 582–587. [Google Scholar] [CrossRef]
- Ghosh, B.; Basu, B.; O’Mahony, M. Multivariate short-term traffic flow forecasting using time-series analysis. IEEE Trans. Intell. Transp. Syst. 2009, 10, 246–254. [Google Scholar] [CrossRef]
- Olayode, I.O.; Tartibu, L.K.; Okwu, M.O.; Ukaegbu, U.F. Development of a hybrid artificial neural network-particle swarm optimization model for the modelling of traffic flow of vehicles at signalized road intersections. Appl. Sci. 2021, 11, 8387. [Google Scholar] [CrossRef]
- Wu, Y.; Tan, H.; Peter, J.; Shen, B.; Ran, B. Short-term traffic flow prediction based on multilinear analysis and k-nearest neighbor regression. In Proceedings of the COTA International Conference of Transportation Professionals (CICTP), Beijing, China, 24–27 July 2015; pp. 556–569. [Google Scholar]
- Kumar, K.; Parida, M.; Katiyar, V.K. Short term traffic flow prediction in heterogeneous condition using artificial neural network. Transport 2015, 30, 397–405. [Google Scholar] [CrossRef]
- Yang, H.F.; Dillon, T.S.; Chen, Y.P.P. Optimized structure of the traffic flow forecasting model with a deep learning approach. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2371–2381. [Google Scholar] [CrossRef]
- Polson, N.G.; Sokolov, V.O. Deep learning for short-term traffic flow prediction. Transp. Res. Part C Emerg. Technol. 2017, 79, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Tan, H.; Qin, L.; Ran, B.; Jiang, Z. A hybrid deep learning based traffic flow prediction method and its understanding. Transp. Res. Part C Emerg. Technol. 2018, 90, 166–180. [Google Scholar] [CrossRef]
- Fredianelli, L.; Carpita, S.; Bernardini, M.; Del Pizzo, L.G.; Brocchi, F.; Bianco, F.; Licitra, G. Traffic flow detection using camera images and machine learning methods in ITS for noise map and action plan optimization. Sensors 2022, 22, 1929. [Google Scholar] [CrossRef]
- Ma, X.; Dai, Z.; He, Z.; Ma, J.; Wang, Y.; Wang, Y. Learning traffic as images: A deep convolutional neural network for large-scale transportation network speed prediction. Sensors 2017, 17, 818. [Google Scholar] [CrossRef] [Green Version]
- Ul Abideen, Z.; Sun, H.; Yang, Z.; Ali, A. The Deep 3D Convolutional Multi-Branching Spatial-Temporal-Based Unit Predicting Citywide Traffic Flow. Appl. Sci. 2020, 10, 7778. [Google Scholar] [CrossRef]
- Ma, X.; Tao, Z.; Wang, Y.; Yu, H.; Wang, Y. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data. Transp. Res. Part C Emerg. Technol. 2015, 54, 187–197. [Google Scholar] [CrossRef]
- Tian, Y.; Pan, L. Predicting short-term traffic flow by long short-term memory recurrent neural network. In Proceedings of the 2015 IEEE international conference on smart city/SocialCom/SustainCom (SmartCity), Chengdu, China, 19–21 December 2015; pp. 153–158. [Google Scholar]
- Fu, R.; Zhang, Z.; Li, L. Using LSTM and GRU neural network methods for traffic flow prediction. In Proceedings of the 2016 IEEE 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC), Wuhan, China, 11–13 November 2016; pp. 324–328. [Google Scholar]
- Xiao, Y.; Yin, Y. Hybrid LSTM neural network for short-term traffic flow prediction. Information 2019, 10, 105. [Google Scholar] [CrossRef] [Green Version]
- Karimzadeh, M.; Schwegler, S.M.; Zhao, Z.; Braun, T.; Sargento, S. MTL-LSTM: Multi-Task Learning-based LSTM for Urban Traffic Flow Forecasting. In Proceedings of the 2021 IEEE International Wireless Communications and Mobile Computing (IWCMC), Harbin, China, 28 June–2 July 2021; pp. 564–569. [Google Scholar]
- Karpathy, A.; Fei-Fei, L. Deep visual-semantic alignments for generating image descriptions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3128–3137. [Google Scholar]
- Ren, J.; Hu, Y.; Tai, Y.W.; Wang, C.; Xu, L.; Sun, W.; Yan, Q. Look, listen and learn—A multimodal LSTM for speaker identification. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Chen, R.; Fung, B.; Desai, B.C. Differentially private trajectory data publication. arXiv 2011, arXiv:1112.2020. [Google Scholar]
- Hoh, B.; Gruteser, M. Protecting location privacy through path confusion. In Proceedings of the IEEE First International Conference on Security and Privacy for Emerging Areas in Communications Networks (SECURECOMM’05), Washington, DC, USA, 5–9 September 2005; pp. 194–205. [Google Scholar]
- Rass, S.; Fuchs, S.; Schaffer, M.; Kyamakya, K. How to protect privacy in floating car data systems. In Proceedings of the Fifth ACM International Workshop on VehiculAr Inter-NETworking, San Francisco, CA, USA, 15 September 2008; pp. 17–22. [Google Scholar]
- Hoh, B.; Gruteser, M.; Herring, R.; Ban, J.; Work, D.; Herrera, J.C.; Bayen, A.M.; Annavaram, M.; Jacobson, Q. Virtual trip lines for distributed privacy-preserving traffic monitoring. In Proceedings of the 6th International Conference on Mobile Systems, Applications, and Services, Breckenridge, CO, USA, 17–20 June 2008; pp. 15–28. [Google Scholar]
- Lu, S.; Yao, Y.; Shi, W. Collaborative learning on the edges: A case study on connected vehicles. In Proceedings of the 2nd USENIX Workshop on Hot Topics in Edge Computing (HotEdge 19), Renton, WA, USA, 9 July 2019. [Google Scholar]
- Fantacci, R.; Picano, B. Federated learning framework for mobile edge computing networks. CAAI Trans. Intell. Technol. 2020, 5, 15–21. [Google Scholar] [CrossRef]
- Saputra, Y.M.; Hoang, D.T.; Nguyen, D.N.; Dutkiewicz, E.; Mueck, M.D.; Srikanteswara, S. Energy demand prediction with federated learning for electric vehicle networks. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Big Island, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Zhang, C.; Zhang, S.; James, J.; Yu, S. FASTGNN: A topological information protected federated learning approach for traffic speed forecasting. IEEE Trans. Ind. Inform. 2021, 17, 8464–8474. [Google Scholar] [CrossRef]
- Hao, M.; Li, H.; Luo, X.; Xu, G.; Yang, H.; Liu, S. Efficient and privacy-enhanced federated learning for industrial artificial intelligence. IEEE Trans. Ind. Inform. 2019, 16, 6532–6542. [Google Scholar] [CrossRef]
- McMahan, H.B.; Ramage, D.; Talwar, K.; Zhang, L. Learning differentially private recurrent language models. arXiv 2017, arXiv:1710.06963. [Google Scholar]
- Truex, S.; Baracaldo, N.; Anwar, A.; Steinke, T.; Ludwig, H.; Zhang, R.; Zhou, Y. A hybrid approach to privacy-preserving federated learning. In Proceedings of the 12th ACM Workshop on Artificial Intelligence and Security, London, UK, 15 November 2019; pp. 1–11. [Google Scholar]
- Hu, R.; Guo, Y.; Li, H.; Pei, Q.; Gong, Y. Personalized federated learning with differential privacy. IEEE Internet Things J. 2020, 7, 9530–9539. [Google Scholar] [CrossRef]
- Triastcyn, A.; Faltings, B. Federated learning with bayesian differential privacy. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 2587–2596. [Google Scholar]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated machine learning: Concept and applications. ACM Trans. Intell. Syst. Technol. (TIST) 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Liu, Y.; James, J.; Kang, J.; Niyato, D.; Zhang, S. Privacy-preserving traffic flow prediction: A federated learning approach. IEEE Internet Things J. 2020, 7, 7751–7763. [Google Scholar] [CrossRef]
- Zeng, T.; Guo, J.; Kim, K.J.; Parsons, K.; Orlik, P.; Di Cairano, S.; Saad, W. Multi-task federated learning for traffic prediction and its application to route planning. In Proceedings of the 2021 IEEE Intelligent Vehicles Symposium (IV), Nagoya, Japan, 11–15 July 2021; pp. 451–457. [Google Scholar]
- Chen, J.; Pan, X.; Monga, R.; Bengio, S.; Jozefowicz, R. Revisiting distributed synchronous SGD. arXiv 2016, arXiv:1604.00981. [Google Scholar]
- Dewri, R. Local differential perturbations: Location privacy under approximate knowledge attackers. IEEE Trans. Mob. Comput. 2012, 12, 2360–2372. [Google Scholar] [CrossRef]
- Dwork, C.; Roth, A. The algorithmic foundations of differential privacy. Found. Trends Theor. Comput. Sci. 2014, 9, 211–407. [Google Scholar] [CrossRef]
- Lyu, L.; Yu, H.; Yang, Q. Threats to federated learning: A survey. arXiv 2020, arXiv:2003.02133. [Google Scholar]
- Chen, C. Freeway Performance Measurement System (PeMS); University of California: Berkeley, CA, USA, 2003. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Mohandes, M.A.; Halawani, T.O.; Rehman, S.; Hussain, A.A. Support vector machines for wind speed prediction. Renew. Energy 2004, 29, 939–947. [Google Scholar] [CrossRef]


| Symbol | Description |
|---|---|
| a specific loss function | |
| w | the weights of a deep neural network |
| the parameters of a deep neural network | |
| a deep neural network parameterized b | |
| perturbed f | |
| a dataset | |
| ∇ | Gradient optimization |
| randomized algorithm | |
| conditional probability distribution | |
| privacy budget | |
| S | station |
| T | training round |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akallouch, M.; Akallouch, O.; Fardousse, K.; Bouhoute, A.; Berrada, I. Prediction and Privacy Scheme for Traffic Flow Estimation on the Highway Road Network. Information 2022, 13, 381. https://doi.org/10.3390/info13080381
Akallouch M, Akallouch O, Fardousse K, Bouhoute A, Berrada I. Prediction and Privacy Scheme for Traffic Flow Estimation on the Highway Road Network. Information. 2022; 13(8):381. https://doi.org/10.3390/info13080381
Chicago/Turabian StyleAkallouch, Mohammed, Oussama Akallouch, Khalid Fardousse, Afaf Bouhoute, and Ismail Berrada. 2022. "Prediction and Privacy Scheme for Traffic Flow Estimation on the Highway Road Network" Information 13, no. 8: 381. https://doi.org/10.3390/info13080381
APA StyleAkallouch, M., Akallouch, O., Fardousse, K., Bouhoute, A., & Berrada, I. (2022). Prediction and Privacy Scheme for Traffic Flow Estimation on the Highway Road Network. Information, 13(8), 381. https://doi.org/10.3390/info13080381






