Computational Offloading of Service Workflow in Mobile Edge Computing

Abstract

Mobile edge computing (MEC) sinks the functions and services of cloud computing to the edge of the network to provide users with storage and computing resources. For workflow tasks, the interdependency and the sequence constraint being among the tasks make the offloading strategy more complicated. To obtain the optimal offloading and scheduling scheme for workflow tasks to minimize the total energy consumption of the system, a workflow task offloading and scheduling scheme based on an improved genetic algorithm is proposed in an MEC network with multiple users and multiple virtual machines (VMs). Firstly, the system model of the offloading and scheduling of workflow tasks in a multi-user and multi-VMs MEC network is built. Then, the problem of how to determine the optimal offloading and scheduling scheme of workflow to minimize the total energy consumption of the system while meeting the deadline constraint is formulated. To solve this problem, the improved genetic algorithm is adopted to obtain the optimal offloading strategy and scheduling. Finally, the simulation results show that the proposed scheme can achieve a lower energy consumption than other benchmark schemes.

1. Introduction

With the development of computer networks, cloud computing, and the Internet of Things (IoT), mobile devices (MDs) have become indispensable parts of people’s daily lives. However, due to the limited computing power and battery capacity, it is a great challenge to execute complex workflow application tasks on MDs with limited computation ability, such as interactive online games and image processing. Mobile cloud computing (MCC) offloads applications from MDs to the cloud for execution. It can solve the problems of insufficient computing capacity and poor storage capacity of MDs [1]. However, the cloud is usually located far away from mobile users, which may cause higher delay and energy consumption to data transmission, and reduce the quality of service (QoS) for users, especially for specific delay-sensitive applications [2].

To solve this problem, mobile edge computing (MEC) is proposed as a new computing model [3,4,5]. It extends edge clouds with solid computing capabilities to resource-constrained MDs to enhance the processing capabilities of MDs [6]. Thus, it can solve the problem of high transmission cost, high energy consumption, and large delay in traditional cloud computing [7]. MEC-enabled 5G wireless systems are expected to meet the real-time, low latency, and high bandwidth access requirements for IoT device who has time sensitive computation tasks to be executed. Thus, MEC has become a key technology of IoT and 5G. In MEC networks, many mobile applications, such as image processing applications and face recognition applications, perform typical business processes in which the entire task is split into multiple subtasks, with predetermined relationships and data dependencies between the subtasks [8]. Compared with general parallel tasks, MEC’s workflow scheduling problem is more complicated and challenging, since the execution order and execution position of subtasks will affect the latency and energy consumption of the entire workflow [9,10]. Thus, how to optimally allocate the subtasks in a workflow to the local node and the edge for execution to minimize the energy consumption of the entire system under the maximum tolerance latency constraint is an essential issue in MEC networks.

To address this issue, considering an MEC network with multiple users and multiple virtual machines (VMs), the problem of determining the optimal offloading strategy and scheduling scheme under the deadline constraint is solved through genetic algorithm. The main contributions of this paper can be summarized as follows:

• We study the offloading and scheduling problems of workflow tasks in an MEC scenario with multi-MD and multi-VM. A workflow model based on the directed acyclic graph which indicates execution order and execution location of workflow tasks is proposed.
• We propose a workflow scheduling strategy based on an adaptive genetic algorithm. In genetic algorithm, the offloading scheduling consisting of the execution order and execution location of workflow is defined as the individual. The optimal scheduling strategy for workflow in multi-user and multi-task scenarios is finally obtained through individual correction, competition for survival, selection, crossover, and mutation operations.
• The simulation results show that, compared with other benchmark methods, such as local offloading and random offloading, the proposed method can achieve optimal task scheduling for multi-user workflow to minimize the total energy consumption of the system.

The remainder of this paper is structured as follows: Section 2 discusses the related work in the past few years. Section 3 presents the system model. In Section 4, we formulate the problem of minimizing the total energy consumption in a multi-user multi-workflow MEC system, then propose an offloading and scheduling scheme to solve this problem. Section 5 presents extensive simulation experiments. Finally, Section 6 concludes this paper.

2. Related Work

There have been some studies conducted on the computation offloading strategy in MEC networks [11,12,13,14,15,16,17,18,19]. In [11], a new graph-based MEC workflow application strategy was proposed. It adopted a graph-based partitioning technology to obtain an offloading decision plan with the lowest energy consumption of terminal equipment under the deadline constraint. In [12], an online dynamic task allocation scheduling method was proposed to realize the high energy-efficient and low-latency communication in an MEC system. Considering the application scenario consisting of single-user and single MEC server, the authors of [13] used traditional genetic algorithm to reduce the execution time and energy consumption of workflow. In [14], the author studied the security problem in workflow task scheduling, and proposed a security and energy-aware workflow scheduling scheme. However, the above studies only considered single user scenario instead of multi-user scenario which was more common in real scene.

For the multi-user scenario, in [15], the authors proposed a heuristic algorithm to minimize the execution cost of the system in a multi-user MEC network. In [16], a dynamic offload and resource scheduling strategy is proposed to reduce energy consumption and execution time. In [17], the collaborative relationship between cloud computing and MEC in the IoT is considered comprehensively. They designed a heuristic algorithm to make the offloading decision considering the resource competition among MDs. In [18], the authors studied the makespan-minimization workflow scheduling problem in the Multi-user MEC system and proposed an improved composite heuristic (ICH) algorithm. However, they only considered single sever scenario. To enhance the computation ability of MEC sever, the BS station is always equipped with multiple VMs or MEC severs.

For the multi-sever or multi-VM scenario, in [19], the authors proposed a new multi-workflow scheduling method based on edge environment adopting a reliability estimation model and coevolutionary algorithm. The proposed method maximized the reliability of the success rate of workflow task offloading while reducing the cost of service invocation for users. However, they only considered execution latency and offloading efficiency, but did not considered the energy consumption. Energy consumption problem is an essential problem in IoT networks.

Above all, how to optimally offload and schedule the workflow tasks to minimize the total system energy consumption in a multi-user and multi-VM MEC network is still an open problem needed to be solved now.

3. System Model

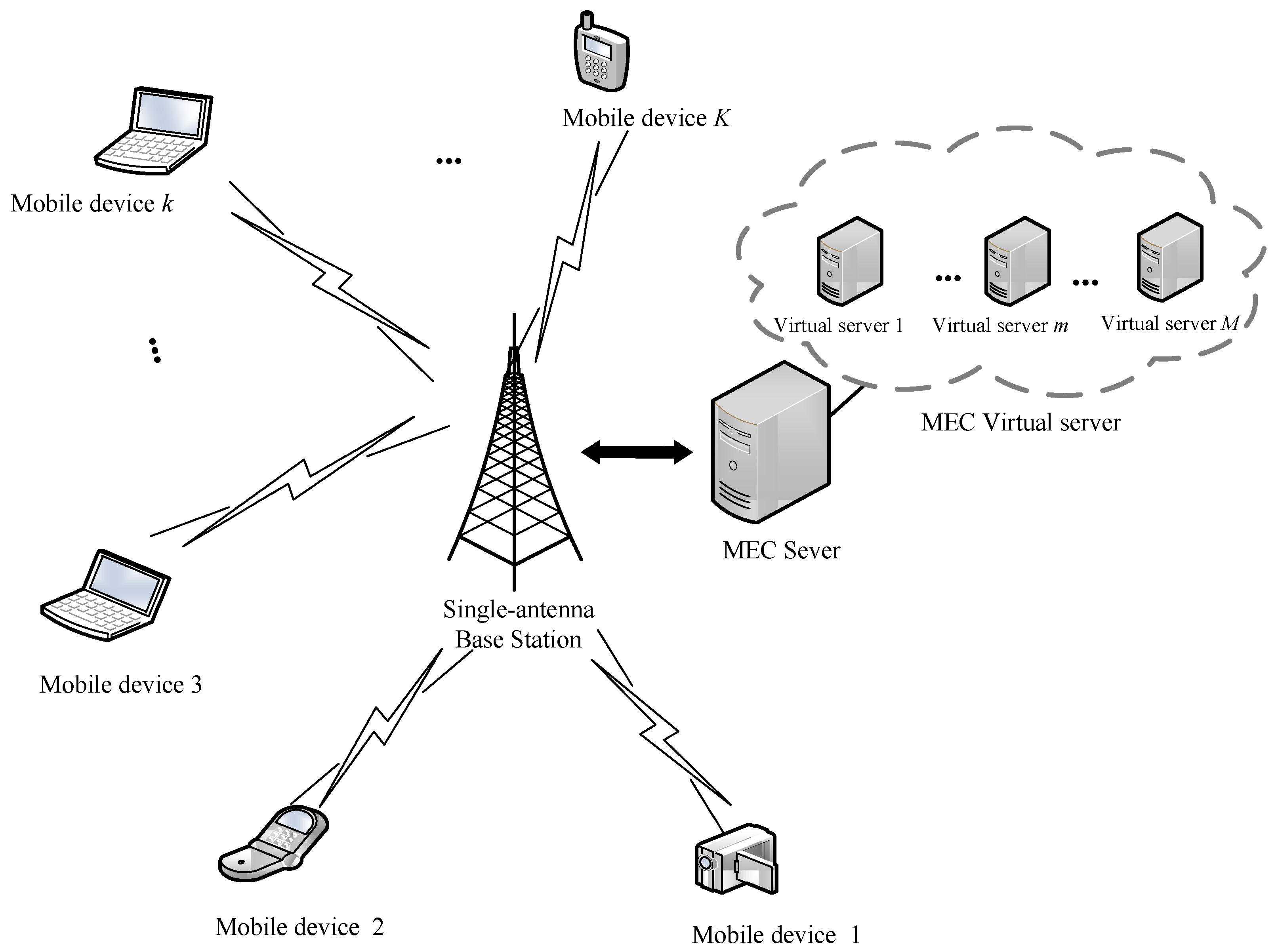
In a multi-user and multi-VM MEC network, as illustrated in Figure 1, there are a single-antenna base station (BS) and $\mathit{K}$ MDs denoted as set $\mathrm{U}=\{1,2,\dots ,K\}$ with some workflow tasks to be computed randomly located around the BS. The MEC server includes $\mathit{M}$ VMs denoted as $\mathrm{S}=\{1,2,\dots ,M\}$ for concurrent processing multiple computation tasks. Each VM works independently. The workflow processed by the MDs consists of $\mathit{I}$ subtasks. Each subtask can be scheduled to be executed locally or by MEC server through wireless access. MDs can offload all or part of the computation tasks to the MEC server for computing to the reduce energy consumption and the delay.

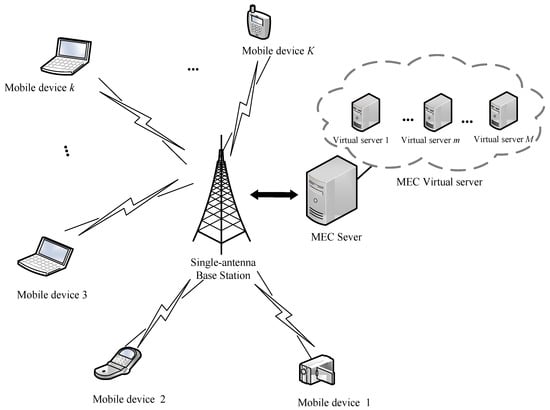
Figure 1. System model.

3.1. Workflow Task Model

In this paper, a weighted directed acyclic graph (DAG) is used to describe the execution sequence dependency of workflow in the MEC network.

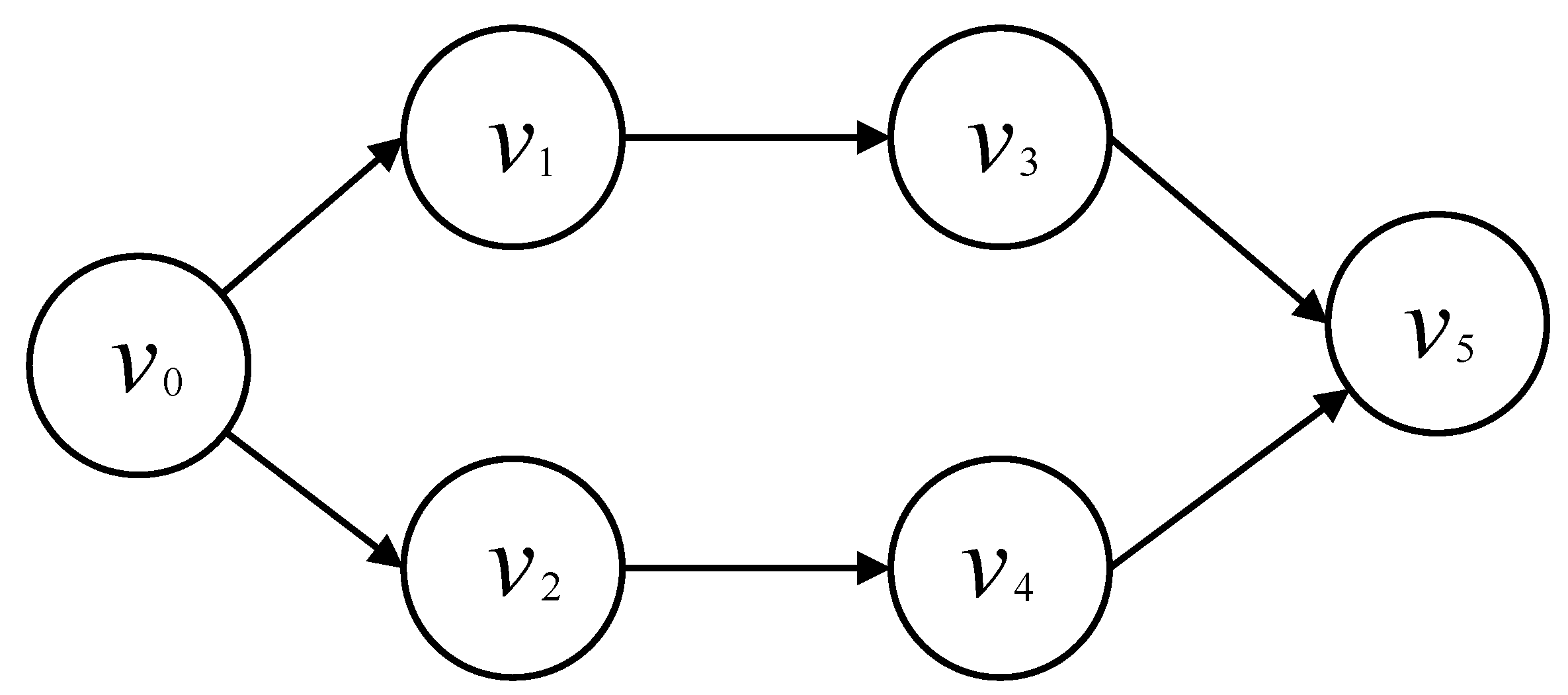
As show in Figure 2, let 2-tuples $W_k=\left\{V_k,E_k\right\}$ denote the DAG describing the execution sequence dependency of workflow $W_k$, where $V_k=\left\{v_{1,k},v_{2,k},\dots ,v_{I,K}\right\}$ is the set of I subtasks in the workflow $W_k$ and $E_k=\left\{e_{i,j}|i,j\in I\right\}$ is the set of edges between subtasks.

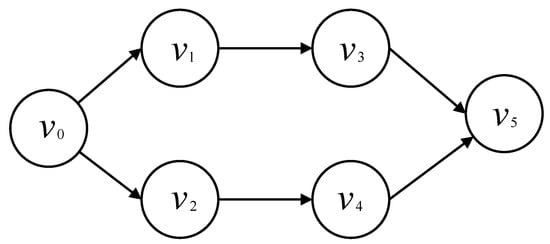
Figure 2. Workflow directed acyclic graph.

Each edge connecting two subtasks indicates that there is a priority constraint between them. For example, in the workflow $W_k$, $v_0$ is the entry subtask, and $v_1$ is the predecessor of subtask $v_0$. It means that subtask $v_1$ can only start when $v_0$ is finished computing. For each subtask $v_{i,k}$, we use a two-tuples ${\nu }_{i,k}=\left(w_{i,k}{c}_{i,k}\right)$ to represent the $ith$ subtask of MD k, in which $w_{i,k}$ is the input data size (bits) of subtask $v_{i,k}$, and $c_{i,k}$ is the number of CPU cycles needed to process one bit of data. It is assumed that all VMs have enough capacity to execute the computation tasks and execute the tasks until completion after the tasks are assigned.

3.2. Communication Model

We consider an MEC network where orthogonal frequency division multiple access (OFDMA) is adopted to offload tasks to the BS. When subtask $v_{i,k}$ is offloaded to the edge server, the uplink transmission rate $r_k^{\mathrm{u}}$ of MD k is given as

$$\begin{array}{c}\hfill r_k^{\mathrm{u}}=B_k{log}_2\left(1+\frac{g_k{p}_k^{\mathrm{trans}}}{{\sigma }_k^2}\right),\end{array}$$

(1)

where $B_k$ is the channel bandwidth between MD k and the MEC sever, $p_k^{\mathrm{trans}}$ is the transmission power of the MD k, and $g_k$ is the channel gain between the MD k and the MEC sever. In addition, the noise obeys the Gaussian distribution with zero expectation, and its variance is represented by ${\sigma }_k^2$.

We assume that the downlink channel has the same fading environment and noise; thus, the downlink transmission $r_k^{\mathrm{d}}$ rate of MD k is given as

$$\begin{array}{c}\hfill r_k^{\mathrm{d}}=B{log}_2\left(1+\frac{g_k{p}_m^{\mathrm{trans}}}{{\sigma }_k^2}\right).\end{array}$$

(2)

3.3. Computation Model

Let $W_k$ denote the workflow of MD k consisting of I subtasks. These subtasks can be computed locally or offloaded to VMs via a wireless channel for computation. $T_k^{max}$ represents the maximum deadline constraint of workflow $W_k$. In the following, the computation overhead will be discussed in terms of both execution time and energy consumption in local computing and offloading computing.

(1)

Local computing: We define $f_k^{\mathrm{loc}}$ as the local computation ability of the MD k. When the subtask is executed locally, the local computation time $T_{i,k}^{\mathrm{loc}}$ is

$$\begin{array}{c}\hfill T_{i,k}^{\mathrm{loc}}=\frac{{\omega }_{i,k}{c}_{i,k}}{f_k^{\mathrm{loc}}}.\end{array}$$

(3)

The energy consumption of computing the subtask can be calculated as

$$\begin{array}{c}\hfill E_{i,k}^{\mathrm{loc}}=\kappa {\left(f_k^{\mathrm{loc}}\right)}^2{\omega }_{i,k}{c}_{i,k},\end{array}$$

(4)

where $\kappa$ is the energy consumption factor related to the CPU chip architecture, $\kappa {\left(f_k^{\mathrm{loc}}\right)}^2$ is the energy consumption in each CPU cycle [20].

(2)

Offloading computing: If a subtask is offloaded to VM for computing, the total execution time consists of two parts. One is the transmission time that MD offloads the subtask to the MEC server. The other is the computation time on VMs. Then, the transmission time of offloading subtask to MEC can be calculated as follows

$$\begin{array}{c}\hfill T_{i,k}^{\mathrm{tr}}=\frac{{\omega }_{i,k}}{r_k^{\mathrm{u}}}.\end{array}$$

(5)

The energy consumption of uplink can be calculated as follows:

$$\begin{array}{c}\hfill E_{i,k}^{\mathrm{tr}}=p_k^{\mathrm{trans}}\frac{{\omega }_{i,k}}{r_k^{\mathrm{u}}},\end{array}$$

(6)

where $p_k^{\mathrm{trans}}$ is the transmission power of MD k. The computation time of subtasks on VM, which can be given as

$$\begin{array}{c}\hfill T_{i,m,k}^{\mathrm{com}}=\frac{{\omega }_{i,k}{c}_{i,k}}{f_m^{\mathrm{ser}}},\end{array}$$

(7)

where $f_m^{\mathrm{ser}}$ is the CPU frequency of the VMs m. Therefore, the total execution time for offloading can be expressed as

$$\begin{array}{c}\hfill T_{i,m,k}^{\mathrm{ser}}=T_{i,k}^{\mathrm{tr}}+T_{i,m,k}^{\mathrm{com}}=\frac{{\omega }_{i,k}}{r_k^{\mathrm{u}}}+\frac{{\omega }_{i,k}{c}_{i,k}}{f_m^{\mathrm{ser}}}.\end{array}$$

(8)

Similarly, in the case that a subtask is offloaded to VM, the energy consumption of MD includes transmission energy consumption and the circuit loss of the local device. Similar with [21], we only consider the energy consumption for offloading and ignore the circuit loss. Thus, the energy consumption of MD for offloading subtasks is given by

$$\begin{array}{c}\hfill E_{i,m,k}^{\mathrm{ser}}=E_{i,k}^{\mathrm{tr}}=p_k^{\mathrm{trans}}\frac{{\omega }_{i,k}}{r_k^{\mathrm{u}}}.\end{array}$$

(9)

Let $L=\mathrm{S}\cup \left\{0\right\}=\left\{0,1,2,\dots ,M\right\}$ denote the execution position set of the subtasks. Since a task can only be performed by one VM, an offloading decision $x_{i,k,m}\in \left\{0,1\right\}$ is utilized. If subtask $v_{i,k}$ is offloaded to the VM m ($m\in S$) for computation, $x_{i,k,m}=1$, otherwise $x_{i,k,m}=0$. Thus, the total time and the energy consumption of subtask $v_{i,k}$ for computation are given as follows

$$\begin{array}{c}\hfill T_{i,k}=\left[\left(1-x_{i,k,m}\right)T_{i,k}^{\mathrm{loc}}+x_{i,k,m,m}{T}_{i,m,k}^{\mathrm{gr}}\right],\end{array}$$

(10)

$$\begin{array}{c}\hfill E_{i,k}=\left[\left(1-x_{i,k,m}\right)E_{i,k}^{\mathrm{loc}}+x_{i,k,m}{E}_{i,m,k}^{\sec }\right].\end{array}$$

(11)

In the workflow, subtask $v_{j,k}$ is the immediate successor of subtask $v_{i,k}$. When subtask $v_{i,k}$ is finished computing, the output data $d_{i,j,k}$ of subtask $v_{i,k}$ is transmitted to successor subtask $v_{j,k}$. We assume that subtask $v_{i,k}$ is computed locally and $v_{j,k}$ is computed on VM m. The output data $d_{i,j,k}$ transmission time from $v_{i,k}$ to $v_{j,k}$ and transmission energy consumption are

$$\begin{array}{c}\hfill T_{i,j,k}^{\mathrm{tr}}=\frac{d_{i,j,k}}{r_k^{\mathrm{u}}}\end{array}$$

(12)

$$\begin{array}{c}\hfill E_{i,j,k}^{\mathrm{tr}}=p_k^{\mathrm{trans}}\frac{d_{i,j,k}}{r_k^{\mathrm{u}}}\end{array}$$

(13)

where $p_k^{\mathrm{trans}}$ is the transmission power of MD k, and $r_k^{\mathrm{u}}$ is the transmission rate of MD k.

Similarly, in the case that the subtask $v_{j,k}$ is executed on VM m and the subtask $v_{i,k}$ is executed locally, the local device needs to download the data from VM. Let $p_k^{\mathrm{re}}$ denote the downloading power of MD k. The data downloading time and the download energy consumption can be calculated respectively as

$$\begin{array}{c}\hfill T_{j,i,k}^{\mathrm{tr}}=\frac{d_{j,i,k}}{r_k^{\mathrm{d}}},\end{array}$$

(14)

$$\begin{array}{c}\hfill E_{j,i,k}^{\mathrm{tr}}=p_k^{\mathrm{re}}\frac{d_{j,i,k}}{r_k^{\mathrm{d}}}.\end{array}$$

(15)

The total computation time of workflow $W_k$ on MD k is the sum of computation time and data transmission time of the data transmitted between the associated subtasks. The total energy consumption of the workflow $W_k$ on MD k is the sum of the local computing energy consumption, offloading energy consumption, and the energy consumption for data transmission between associated subtasks. As mentioned above, the total computation time and the total energy consumption can be calculated respectively as

$$\begin{array}{c}\hfill T_k=\sum _{i=1}^I{T}_{i,k}+\sum _{i=1}^{I-1}\sum _{j=2}^I{\left|x_{i,k,m-x_{j,k,m}}\right|T_{i,j,k}^{\mathrm{tr}}}^{},\end{array}$$

(16)

$$\begin{array}{c}\hfill E_k=\sum _{i=1}^I{E}_{i,k}+\sum _{i=1}^{I-1}\sum _{j=2}^I\left|x_{i,k,m-x_{j,k,m}}\right|E_{i,j,k}^{\mathrm{tr}}.\end{array}$$

(17)

4. Problem Formulation

In this section, an optimization problem to minimize the total energy consumption in a multi-user multi-workflow MEC system is formulated. Considering the execution time and the energy consumption of each MD, the workflow offloading position and execution order are jointly studied.

The problem of minimizing the system energy consumption can be expressed as

$$\begin{array}{cc}\hfill & P1:\underset{x_{i,k,m}}{min}\sum _{k=1}^K{E}_k,\hfill \\ \hfill & s.t.\mathrm{C}1:T_k\le T_k^{max},\forall k\in U,\hfill \\ \hfill & \mathrm{C}2:x_{i,k,m}\in \left\{01\right\}\forall i\in I,k\in U,m\in L,\hfill \\ \hfill & \mathrm{C}3:\sum _{i\in I}\sum _{m\in L}{x}_{i,k,m}\le 1,\forall k\in U.\hfill \end{array}$$

(18)

where C1 is the deadline constraint of workflow $W_k$, C2 is the offloading decision variable constraint, and C3 is the offloading constraint of the subtasks, that is, each subtask in the workflow can only be executed locally or offloaded to one VM.

4.1. Algorithm Implementation

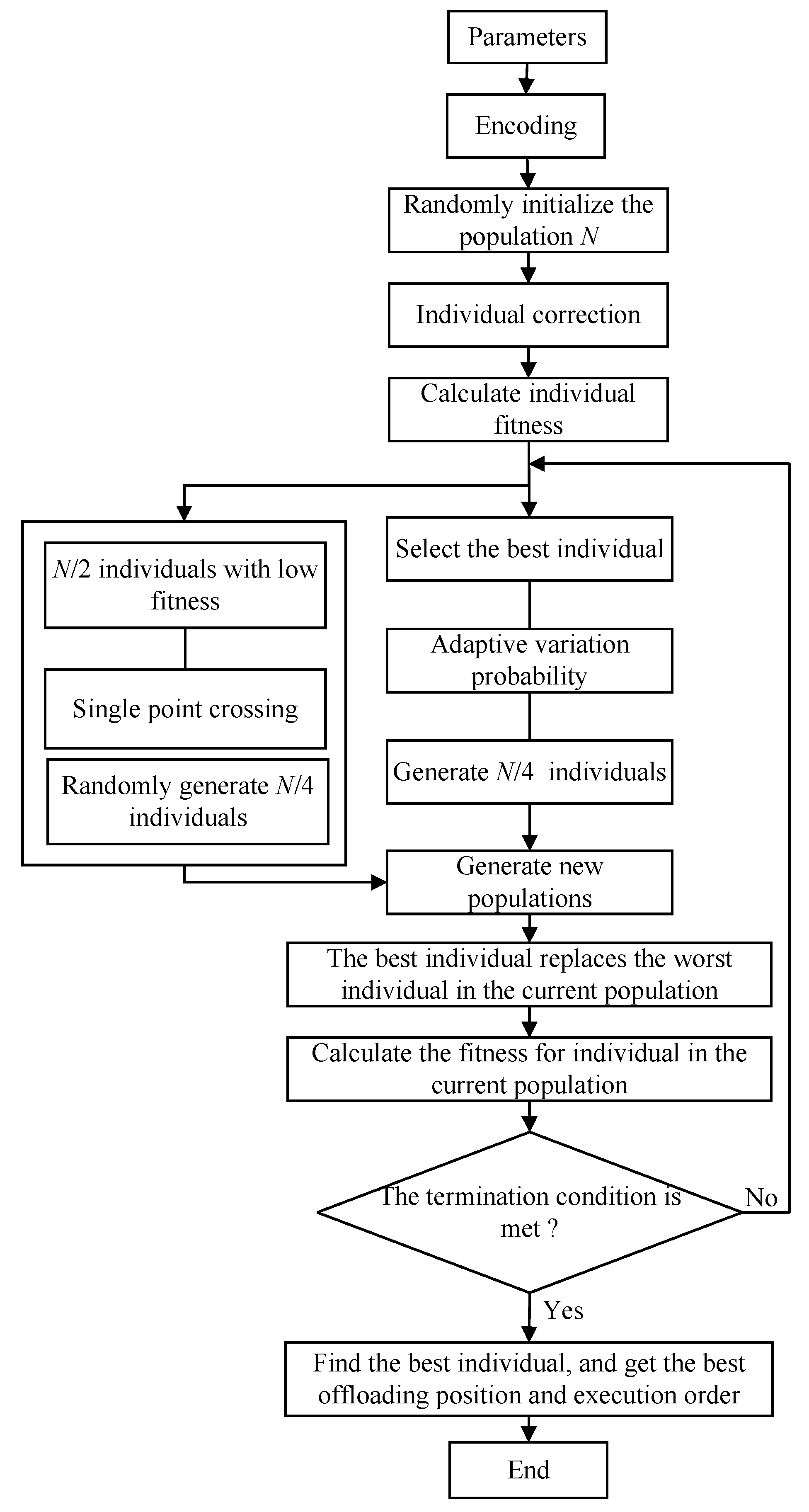
P1 is an NP-hard problem that is difficult to solve using traditional methods such as integer programming and convex optimization. In this section, we adopt a genetic algorithm to solve this problem. Genetic algorithm is an effective method for solving optimization problems based on the principle of evolution. It generates individuals with suitable fitness through selection, crossover, and mutation operations to obtain feasible solutions from a larger search space in a limited time. The implementation process of the algorithm is shown in Figure 3.

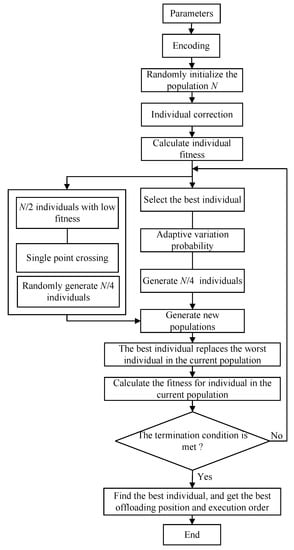
Figure 3. The algorithm flowchart.

4.1.1. Encoding

In the genetic algorithm, the task execution order and offloading position of the subtasks are jointly expressed as an individual’s gene. The coding method is shown in Figure 4. Assuming that there are k MDs and the workflow $W_k$ of each MD is divided into I subtasks, the length of the gene of an individual is $I\times K$. The subtask execution order is sorted in the workflow firstly, and then an offloading position is assigned to each subtask. The offloading position of a subtask is indicated by the value of the corresponding chromosome in the gene of this subtask. There are $M+1$ possibilities for the offloading position. If the subtask is executed locally, the value of this chromosome is set to be 0. If the subtask is executed on VM m, the value is set to be m, $m\in \left\{1,2,\dots ,M\right\}$.

Figure 4. Coding scheme in the genetic algorithm.

4.1.2. Population Initialization and Individual Correction

The initialization operation includes the random initialization of the offloading position and the execution order of the subtasks. Considering that the subtasks in the workflow must meet the priority constraints, the initialization of the subtask execution order is designed as follows: Let the set S denote the sortable subtasks, which are the tasks with no predecessor or the predecessor task to be executed. Firstly, a sortable task is randomly selected to join the set S. Then, another sortable task is selected to join the set S. This process keeps iterating until a feasible task sequence is generated. For the initialization of the task position, an integer range from 0 to M is randomly generated to indicate the offloading position of each subtask. All tasks are iteratively checked in the same way as that of the execution order to generate an initial set of task positions.

For each $W_k$, calculate the computation time according to Formula (16). The individual that meets the deadline constraint becomes a valid individual.

4.1.3. Select

An elite selection strategy is adopted to select the individual with the best fitness from the population. The individuals with the best fitness in the current population do not participate in crossover and mutation operations. It replaces the individuals with the worst fitness after crossover and mutation operations and enters the next generation.

4.1.4. Competition for Survival

In each generation, N individuals are randomly divided into $N/2$ pairs to compete for survival. In each pair, the individual with more fitness is selected for the next crossover operation. Then, $N/2$ individuals are obtained.

4.1.5. Crossover

The $N/2$ individuals obtained from the survival competition are randomly selected in pairs to perform single-point crossover with the crossover probability $P_c$. According to the adaptively varying probabilities of adjustment formula proposed by Srinivas [22], the adaptive crossover probability $P_c$ is

$$\begin{array}{c}\hfill P_c=\left\{\begin{array}{c}{p}_{c1}\frac{\left(p_{\mathrm{c}1}-p_{c2}\right)\left(f_{min}-f_c\right)}{f_{min}-f_{avg}},f_c\le f_{avg}\hfill \\ p_{c1},f_c>f_{avg}\hfill \end{array}\right.\end{array}$$

(19)

where $f_{min}$ and $f_{avg}$ are the minimum fitness and the average fitness in the population, respectively, and $f_c$ is the less fit of the two individuals in the crossover pair. $p_{\mathrm{c}1}$ and $p_{\mathrm{c}2}$ are the maximum and minimum crossover probabilities, respectively.

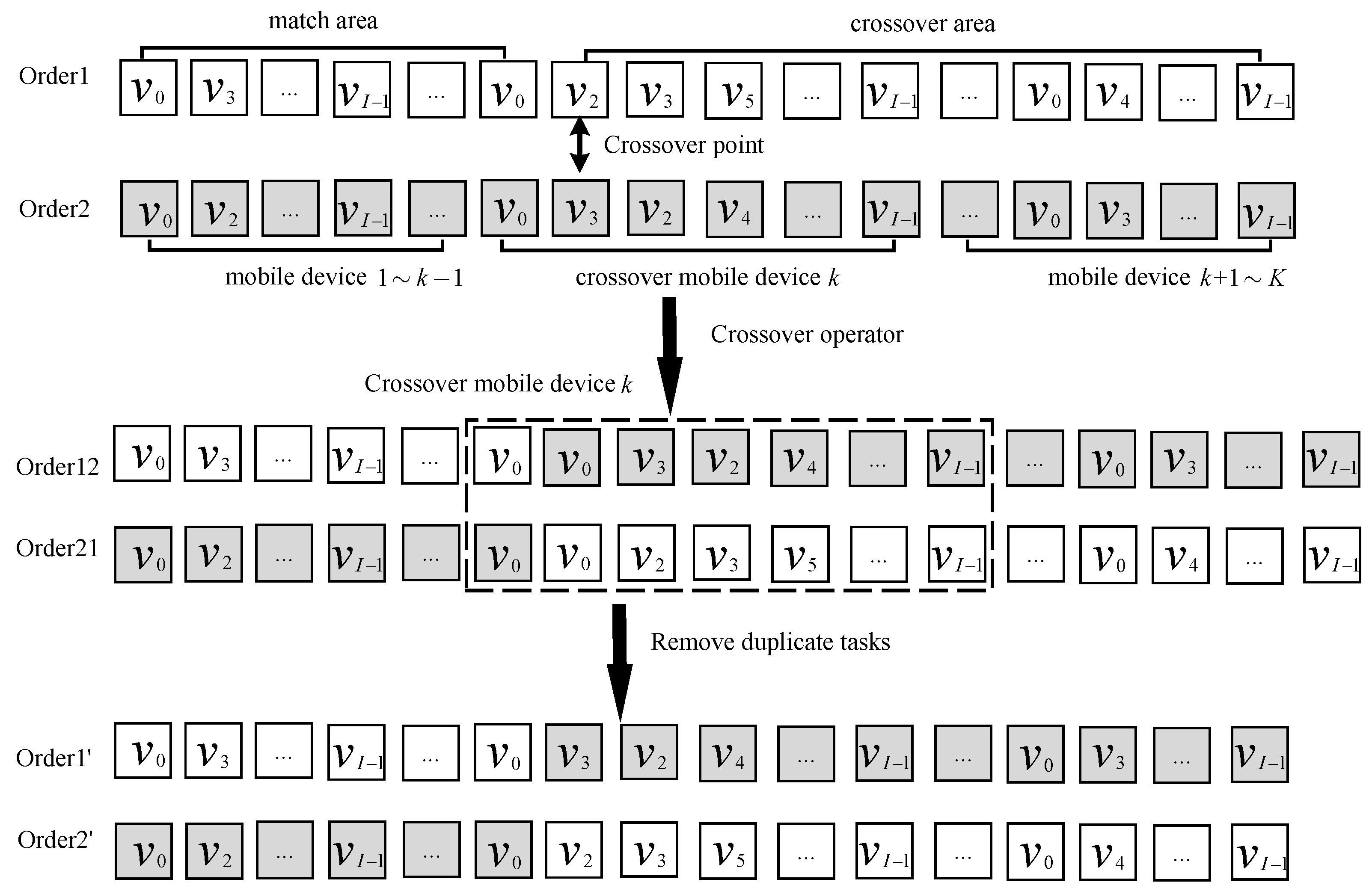
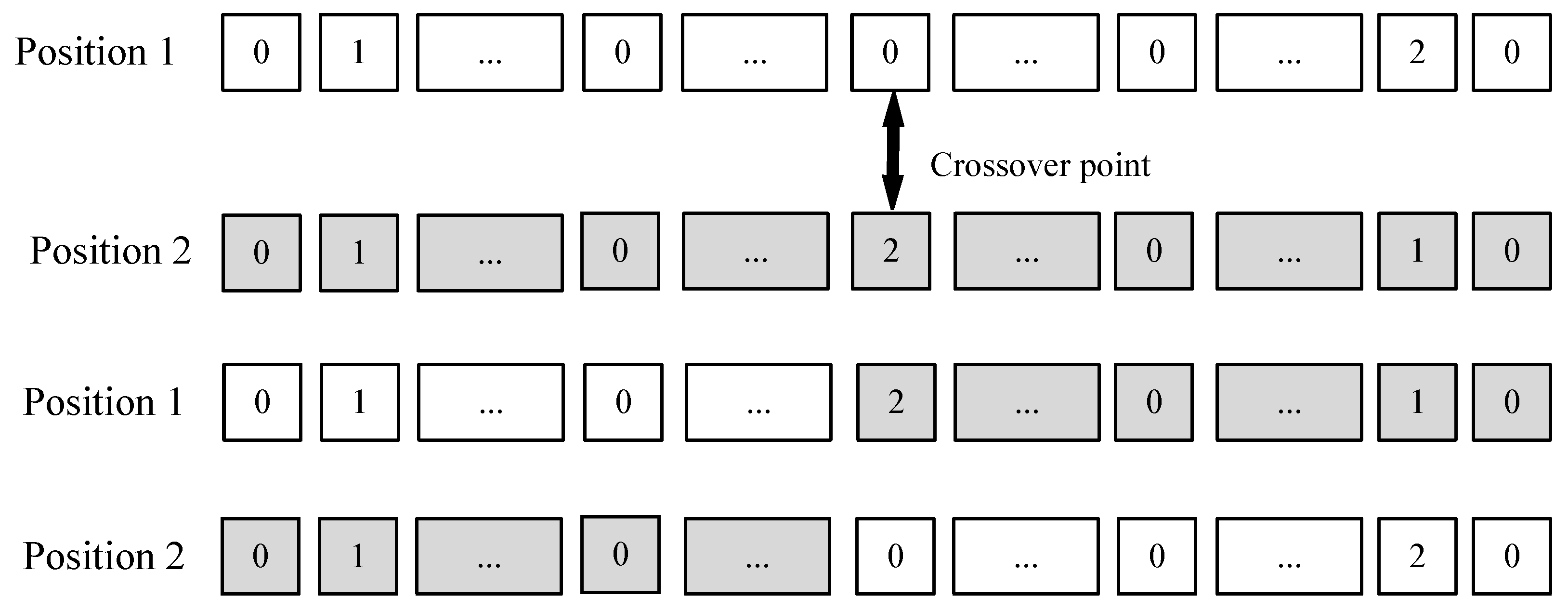
Since each subtask in the workflow needs to meet the particular order relationship, the new individuals generated by the crossover operation also need to follow the certain order relationship. The crossover operation of the execution order is shown in Figure 5. Take two execution orders denoted as Order1 and Order2, for example. Firstly, a crossover point is randomly generated. The crossover MD which is the MD involved in the crossover operation with the crossover point in it can be indicated. Secondly, the two execution orders cross each other to generate two temporary execution orders. Finally, each temporary execution order is scanned from the beginning to the end. The repetitive subtasks in each execution order are removed. Thus, two new execution orders are generated. The specific operation is shown in Algorithm 1.

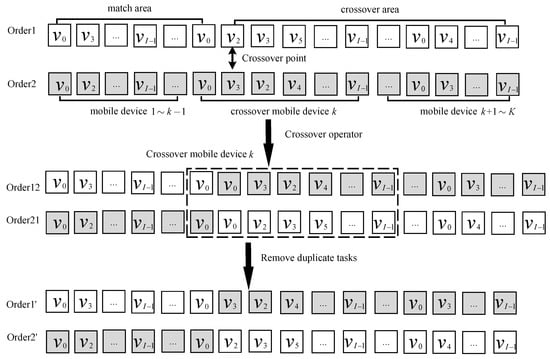
Figure 5. The single−point crossover operation of task execution order.

The process of the single-point crossing for the task offloading position is similar to that of the execution sequence, as shown in Figure 6. First, a cut-off crossing point is randomly selected in the task offloading position sequences. Then, the matching areas in the two execution position orders are swapped. The details of the process are shown in Algorithm 2.

Algorithm 1 Task execution order single-point crossover algorithm.

1: BEGIN 2:    $f_c=min\left(f_1,f_2\right)$; 3:    if $f_c\le f_{avg}$; 4:       $P_c=p_{c1}\left(p_{\mathrm{c}1}-p_{c2}\right)\left(f_{min}-f_c\right)/\left(f_{min}-f_{avg}\right)$; 5:    else 6:       $P_c=p_{c1}$; 7:    end if 8:    Randomly select the crossover user and crossover points; 9:    Execute the cross operations and remove the duplicate tasks in new individuals; 10: END

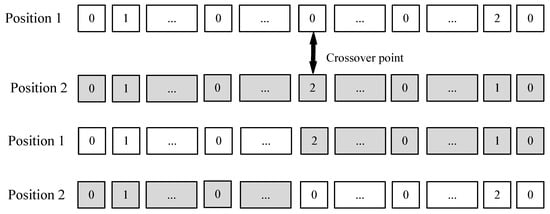
Figure 6. Single−point crossover operation of task offloading position.

Algorithm 2 Single-point crossover algorithm for task offloading position.

1: BEGIN 2:    $f_c=min\left(f_1,f_2\right)$; 3:    if $f_c\le f_{avg}$; 4:       $P_c=p_{c1}\left(p_{\mathrm{c}1}-p_{c2}\right)\left(f_{min}-f_c\right)/\left(f_{min}-f_{avg}\right)$; 5:    else 6:       $P_c=p_{c1}$; 7:    end if 8:    Randomly select the crossover points; 9:    Execute the cross operations; 10: END

4.1.6. Mutation

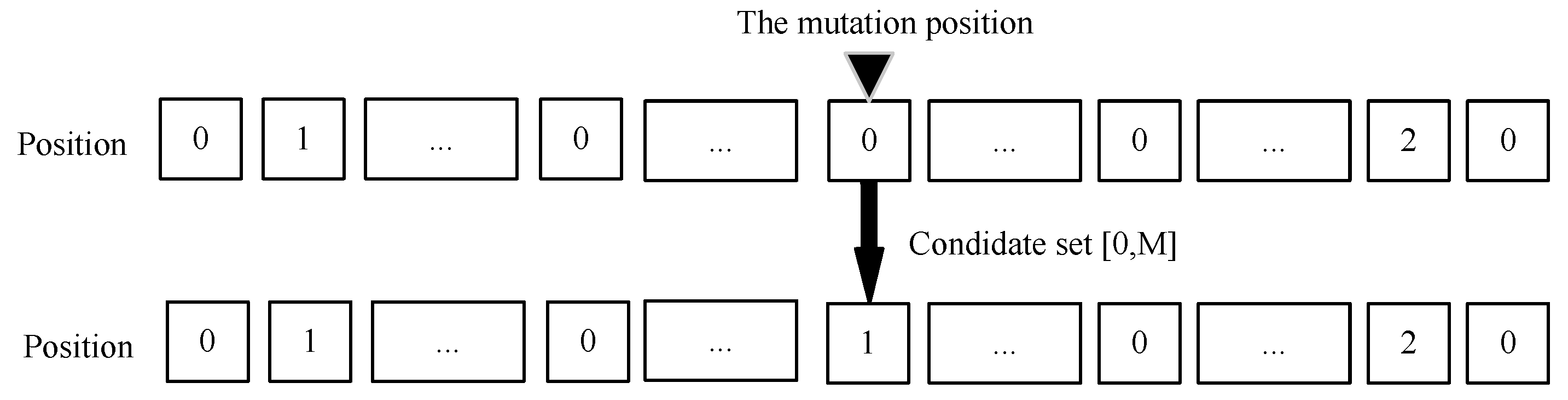
In the mutation operation, the genes of some individuals are randomly selected and changed to obtain new individuals with new characters. To maximize the chances of obtaining more excellent individuals, in this paper, the best individual with the most fitness in each generation is selected to be mutated. The best individual is mutated with mutation probability $P_m$ to generate $N/4$ individuals for the next generation. The mutation operation of the subtask offloading position is shown in Figure 7. For each individual, the mutation operation is performed with the mutation probability $P_m$. The value range of the mutation for each gene is 0∼M. The specific operation is shown in Algorithm 3.

Algorithm 3 Offloading position single-point mutation algorithm.

1: BEGIN 2:    if $f_m\le f_{avg}$; 3:       $P_m=p_{m1}\left(p_{m1}-p_{m2}\right)\left(f_{min}-f_m\right)/\left(f_{min}-f_{avg}\right)$; 4:    else 5:       $P_m=p_{m1}$; 6:    end if 7:    Randomly select the mutation points; 8:    Execute the cross operations; 9: END

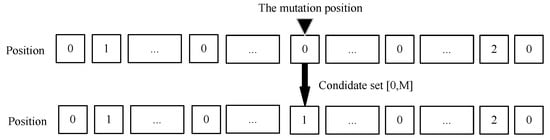
Figure 7. Single−point mutation operation of task offloading position.

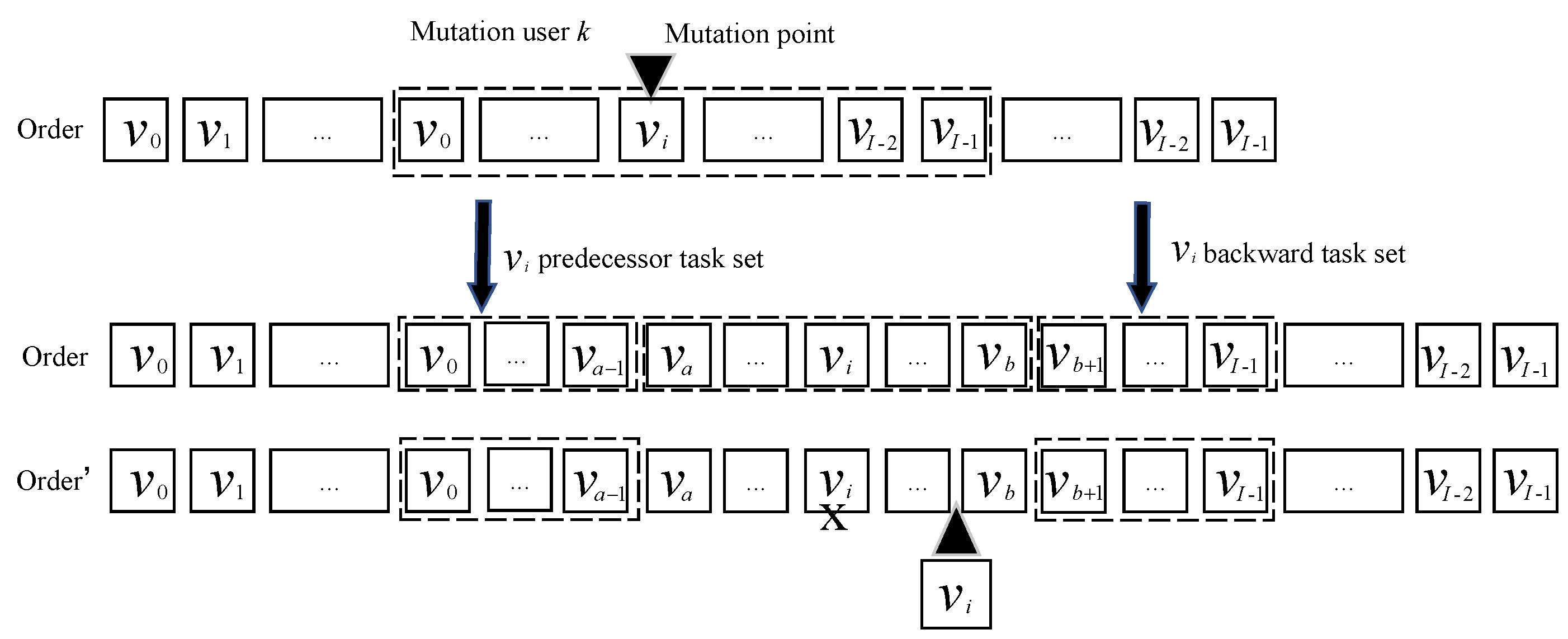
The mutation operation of the subtask execution order is shown in Figure 8 and Algorithm 4. As shown in Figure 8, firstly, a subtask $v_{i,k}$ is randomly selected from the workflow. Then, the predecessor subtasks subset $\left\{v_{0,k},v_{1,k},\dots ,v_{a,k}\right\}$ consisting of all predecessor subtasks of $v_{i,k}$ and the subset $\left\{v_{b,k},v_{b+1,k},\dots ,v_{I-1,k}\right\}$ consisting of all successors subtasks of $v_{i,k}$ are generated through forward searching and backward searching, respectively. As the mutation operation of subtask execution order must meet with the order constraint, the position of subtask $v_{i,k}$ must be inserted between $v_{a+1,k}$ and $v_{b-1,k}$ with any position. The set $\left\{v_{a+1,k},\dots ,v_{b-1,k}\right\}$ is called candidate set. Finally, the subtask $v_{i,k}$ can be placed in any position except the initial one. Similar to the crossover operation, the adaptive mutation probability is

$$\begin{array}{c}\hfill P_m=\left\{\begin{array}{c}{p}_{m1}\frac{\left(p_{m1}-p_{m2}\right)\left(f_{min}-f_m\right)}{f_{min}-f_{avg}},f_m\le f_{avg}\hfill \\ p_{m1},f_m>f_{avg}\hfill \end{array}\right.\end{array}$$

(20)

where $f_{min}$ represents the minimum fitness in the population, $f_{avg}$ represents the average fitness of the entire population, and $f_m$ represents the fitness of the individuals who choose to mutate. $p_{m1}$ and $p_{m2}$ are the maximum and minimum values of the mutation probability, respectively.

Algorithm 4 Single-point mutation for task execution order algorithm.

1: BEGIN 2:    if $f_m\le f_{avg}$; 3:       $P_m=p_{m1}\left(p_{m1}-p_{m2}\right)\left(f_{min}-f_m\right)/\left(f_{min}-f_{avg}\right)$; 4:    else 5:       $P_m=p_{m1}$; 6:    end if 7:    Find mutation user; 8:    Obtain the predecessor set of task $v_{mu\_p,user}$; 9:    Obtain the successors set of task $v_{mu\_p,user}$; 10:  Obtain the candidate set $\left\{v_{a+1,user},\dots ,v_{b-1,user}\right\}$; 11:  Randomly select a new position in set $\left\{v_{a+1,user},\dots ,v_{b-1,user}\right\}$ to insert $v_{mu\_p,user}$ to generate a new individual 12: END

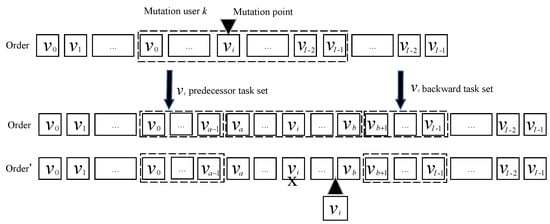
Figure 8. Task execution order single−point mutation operation.

5. Simulation Results and Discussion

This paper evaluates the performance of the proposed algorithm on the Python platform. Our simulation settings are described as follows. We consider a single-cell multi-user MEC network, where MDs are randomly located in a 60 m × 60 m area. The wireless access base stations are located in the center of this area. According to the path loss model considered in [23], the channel gain between MD k and the MEC is $g_{k,m}=d_{k,m}^{-\alpha }$, where $d_{k,m}^{}$ is the distance between MD k and the MEC, and $\alpha =4$ is the path loss factor. Every MD has a workflow task needed to be executed. To test the performance of the proposed scheme, in our simulation, we consider an image processing application with some workflow tasks needing to be executed. The simulation parameters are shown in Table 1.

Table 1. Simulation parameter.

Simulation Parameter	Value
Bandwidth	5 MHz
Transmission power of mobile device $p_i^{\mathrm{trans}}$	600 mW
Receive power of mobile device $p_k^{\mathrm{re}}$	100 mW
Background noise $\sigma$	−113 dBm
Mobile device execution power consumption coefficient $\kappa$	${10}^{-24}$ Joule/cycle
MEC execution power consumption coefficient ${\kappa }_1$	${10}^{-26}$ Joule/cycle
Data subtask $w_{i,k}$	[50, 300] kB
The weight between two subtasks $d_{i,j,k}$	[300, 500] kB
Needed CPU cycles to calculate 1 bit task $c_{i,k}$	1000–1200 (cycles/byte)
MD’s local computation capability $f_k^{\mathrm{loc}}$	[0.1, 1] GHz
MEC computation capability $f_m^{\mathrm{ser}}$	[2, 4] GHz
$p_{\mathrm{c}1}{p}_{\mathrm{c}2}{p}_{\mathrm{m}1}{p}_{\mathrm{m}2}$	0.9, 0.4, 0.1, 0.05
Population Size	80

To evaluate the performance, the proposed scheme is compared with some other computational offloading algorithms, which are introduced as follows:

(1)

Local computing (LC): The local execution involves no offloading. All tasks are executed locally on MDs;

(2)

Random offloading (RA): All subtasks in the workflow are randomly offloaded to some MEC servers for execution or executed locally;

(3)

Adaptive genetic algorithm (AGA): All tasks of the workflow are executed locally or offloaded to the MEC for execution based on the adaptive genetic algorithm in [24].

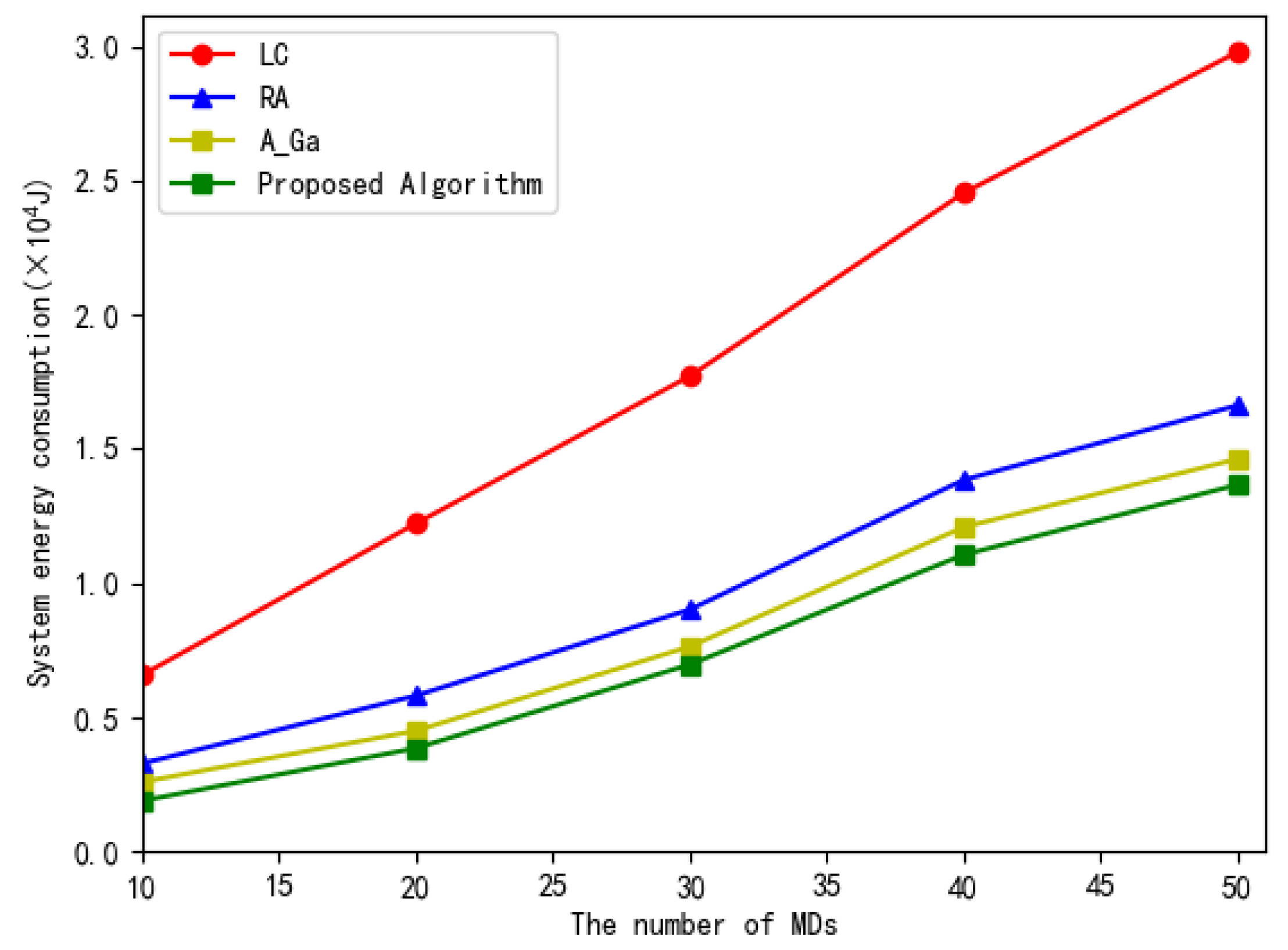
Figure 9 shows the total system energy consumption versus the number of MDs. The number of subtasks in each workflow is 10. It can be seen from Figure 9 that, when the number of MDs increases, the total system energy consumption of all the four methods increase to executing more subtasks. Our proposed scheme consumes less energy than other three compared algorithms due to its optimal allocation of the execution position for subtasks. For the adaptive genetic algorithm, the adaptive crossover and mutation probability can be dynamically adjusted with the adaptive value to avoid entering the local optimal solution. Therefore, the energy consumption of this algorithm is second only to that of our proposed algorithm.

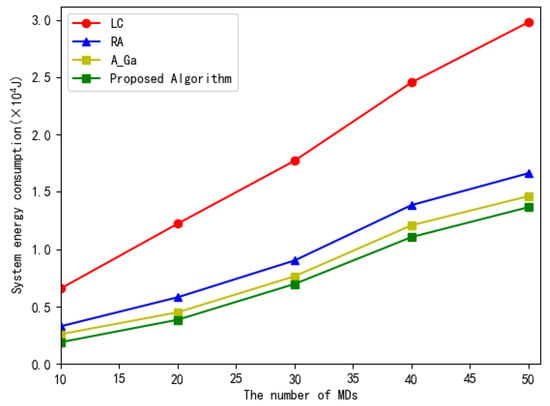
Figure 9. The total system energy consumption versus the number of MDs.

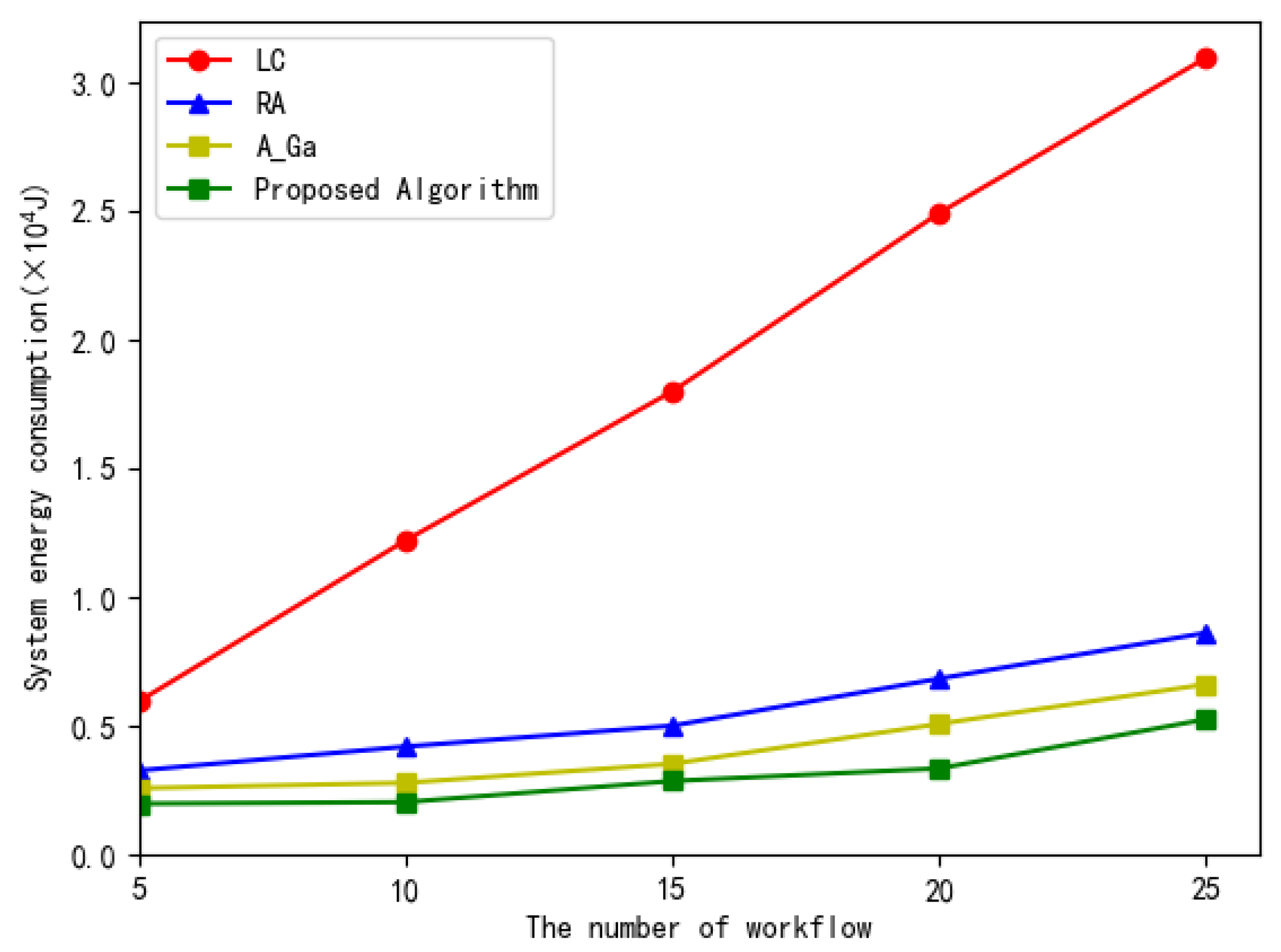
Figure 10 illustrates the total system energy consumption versus the number of the workflow subtasks in the four algorithms. From Figure 10, we can observe that as the number of tasks increases, the system total energy consumption increases accordingly. In four algorithms, the proposed scheme consumes less energy than other three algorithms. This is because the proposed scheme can optimally allocate the execution order and offload the position of each subtask in the workflow.

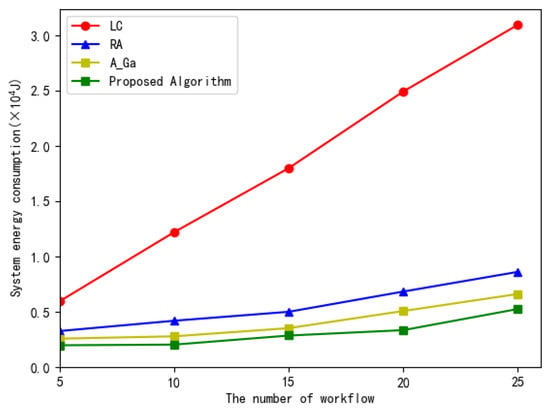
Figure 10. The total system energy consumption versus the number of workflow.

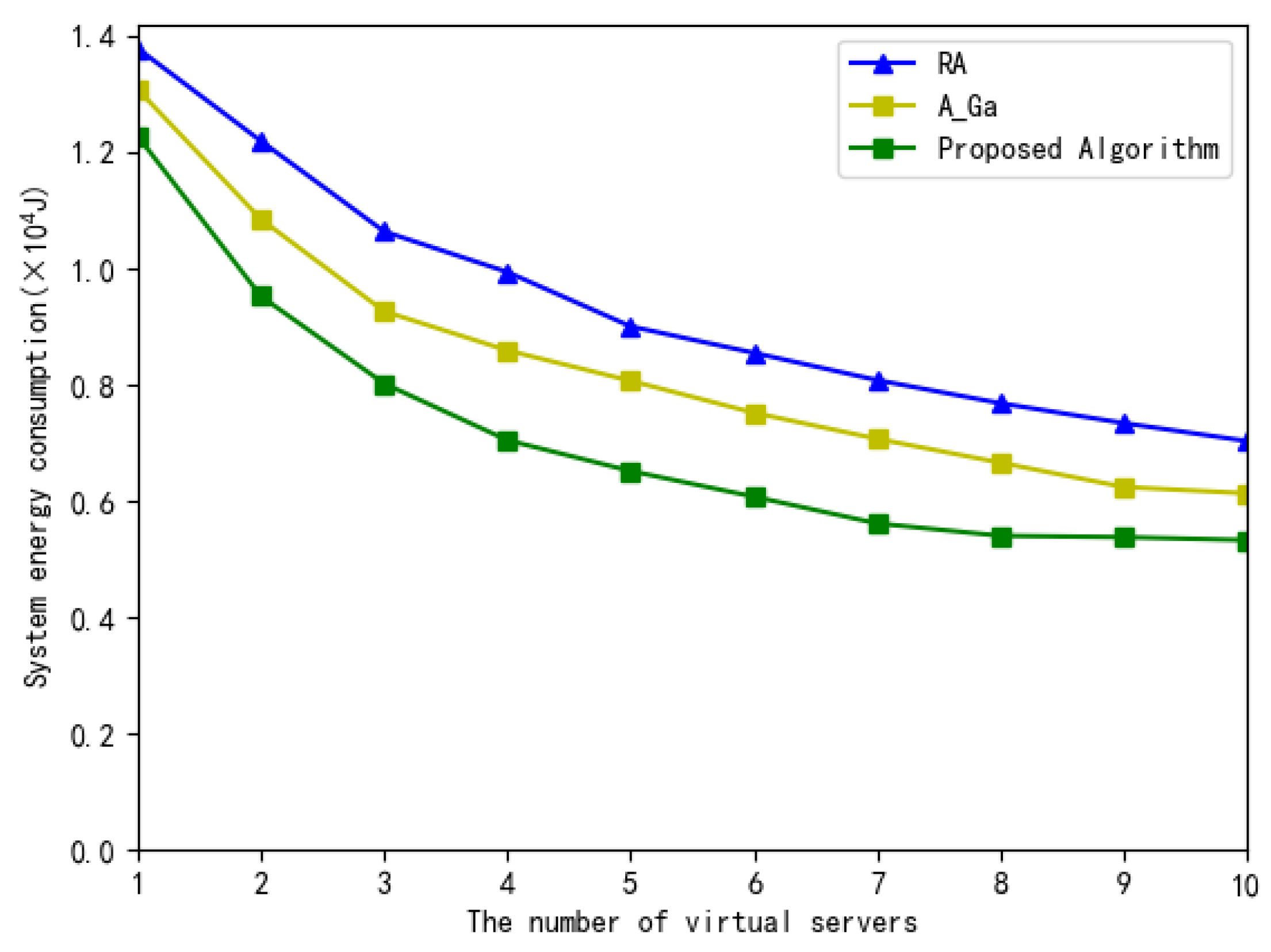
Figure 11 illustrates the total system energy consumption versus the number of MEC virtual servers. As shown in Figure 11, when the number of MEC virtual servers increases, the total system energy consumption of these four algorithms is decreased accordingly, since there are more virtual servers for the selection to minimize the energy consumption. The proposed scheme consumes less energy than the other two algorithms due to its optimal resource allocation. In addition, when the number of MEC virtual servers increases, especially those greater than 9, the decrease in the total system energy consumption slows down, since the number of virtual servers is large enough for subtasks to select to minimize the energy consumption and some virtual servers are idle.

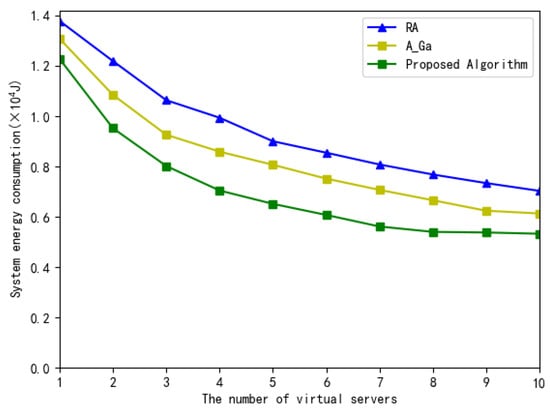
Figure 11. The total system energy consumption versus the number of virtual servers.

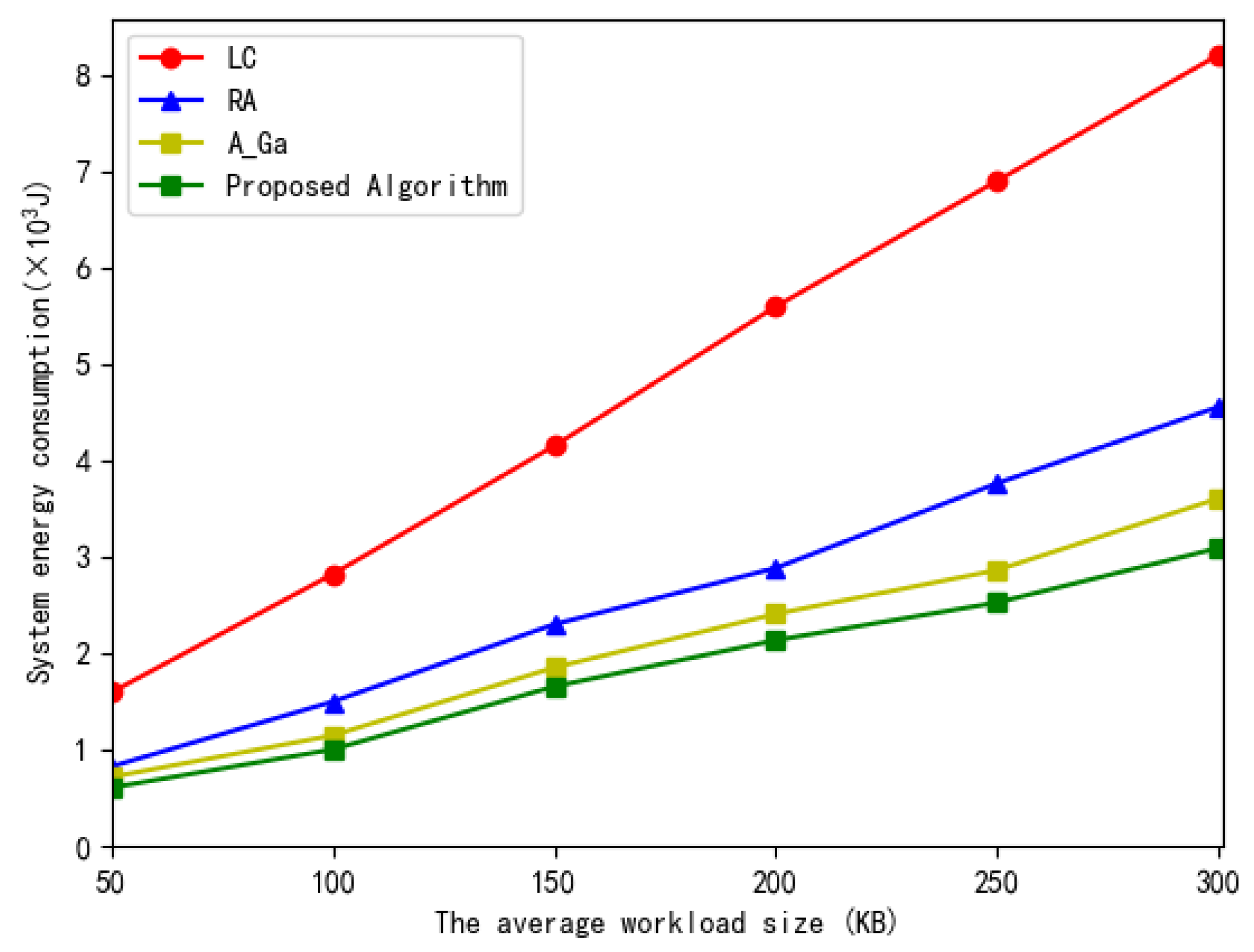
Finally, Figure 12 illustrates the total system energy consumption versus the average workload size. In Figure 12, we can seen that, when the workload size of the subtask increases, the energy consumption increases accordingly for computing more tasks. The proposed scheme consumes less energy than the other three algorithms due to its optimal resource allocation.

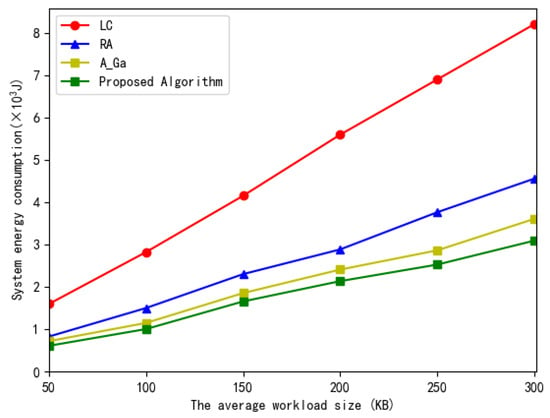
Figure 12. The total system energy consumption versus the average workload size.

6. Conclusions

In this paper, to solve the problem of how to determine the scheduling and execution position of the subtasks in a workflow, we propose a multi-user workflow task offloading decision and scheduling scheme based on genetic algorithm. Firstly, a system model of workflow scheduling and an offloading decision in a multi-user, multi-task scenario was built. Secondly, we formulated the problem of how to optimally determine the scheduling and the execution position of the subtasks to minimize the total energy consumption of the system under the deadline constraint as an optimization problem. Then, an improved genetic algorithm was adopted to obtain the optimal task execution order and offloading position to minimize the system energy consumption under the deadline constraint. Finally, the simulation results showed that, compared with other benchmark methods, our proposed scheme consumes less energy by optimally determining the scheduling and execution position of the subtasks.

7. Work Limitations

In our manuscript, we consider the resource allocation problem of how to minimize the total energy consumption of the system under a deadline constraint in a multi-user, single-BS static scenario. The major limitation of the present study is that we did not consider the resource allocation problem of the workflow task offloading in a multi-BS mobile MEC Network. Multiple BSs and the MDs with mobility will make the workflow schedule problem more complicated to solve. The workflow schedule problem in this scenario is an interesting problem which is worthy of being investigated in our future research.