Text Classification Using Intuitionistic Fuzzy Set Measures—An Evaluation Study
Abstract
:1. Introduction
2. Related Work
3. Materials and Methods
3.1. Important Definitions
3.1.1. Fuzzy Sets
3.1.2. Intuitionistic Fuzzy Sets
3.1.3. Distance Measure
- C1
- (coincidence);
- C2
- (symmetry);
- C3
- (triangle inequality).
3.1.4. Similarity Measure
- C1
- if and only if (coincidence);
- C2
- (symmetry);
- C3
- , then and (triangle inequality).
3.2. Evaluation Protocol
3.2.1. Bag-of-Words Representation
3.2.2. IFS Representation
3.2.3. IFS Pattern Learning
3.2.4. Document Classification
3.3. Experimental Setup
3.3.1. Distance and Similarity Measures
3.3.2. Datasets
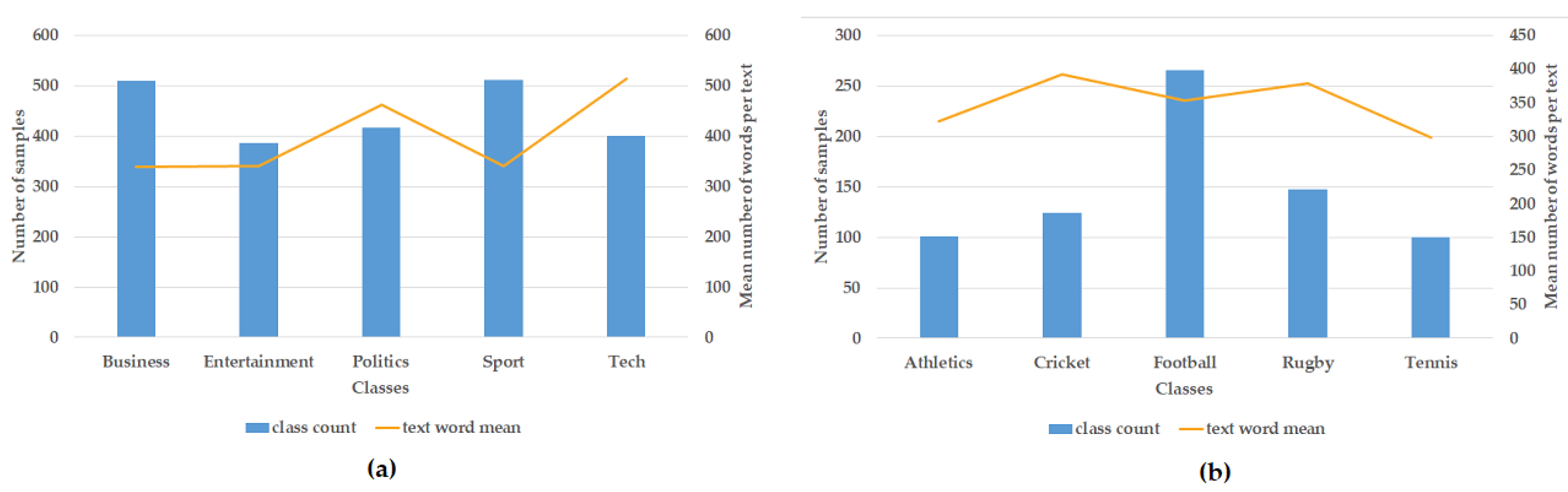
- BBC News: This consists of 2225 articles belonging to 5 topic areas (business, entertainment, politics, sports, and tech) from 2004 and 2005, with a total of 9635 words [50].
- BBC Sports: Similar to the previous one, it contains 737 articles from 5 areas, namely athletics, cricket, football, rugby, and tennis, having a total of 4613 words [50].
3.3.3. Data Preparation
- Documents’ conversion to bag-of-words;
- Word-by-word preprocessing:
- (a)
- Remove escape characters;
- (b)
- Convert to lower case;
- (c)
- Lemmatize word.
- Cut-off words with a document frequency lower than a frequency.
3.3.4. Performance Evaluation
4. Results
5. Discussion
5.1. BBC News Results
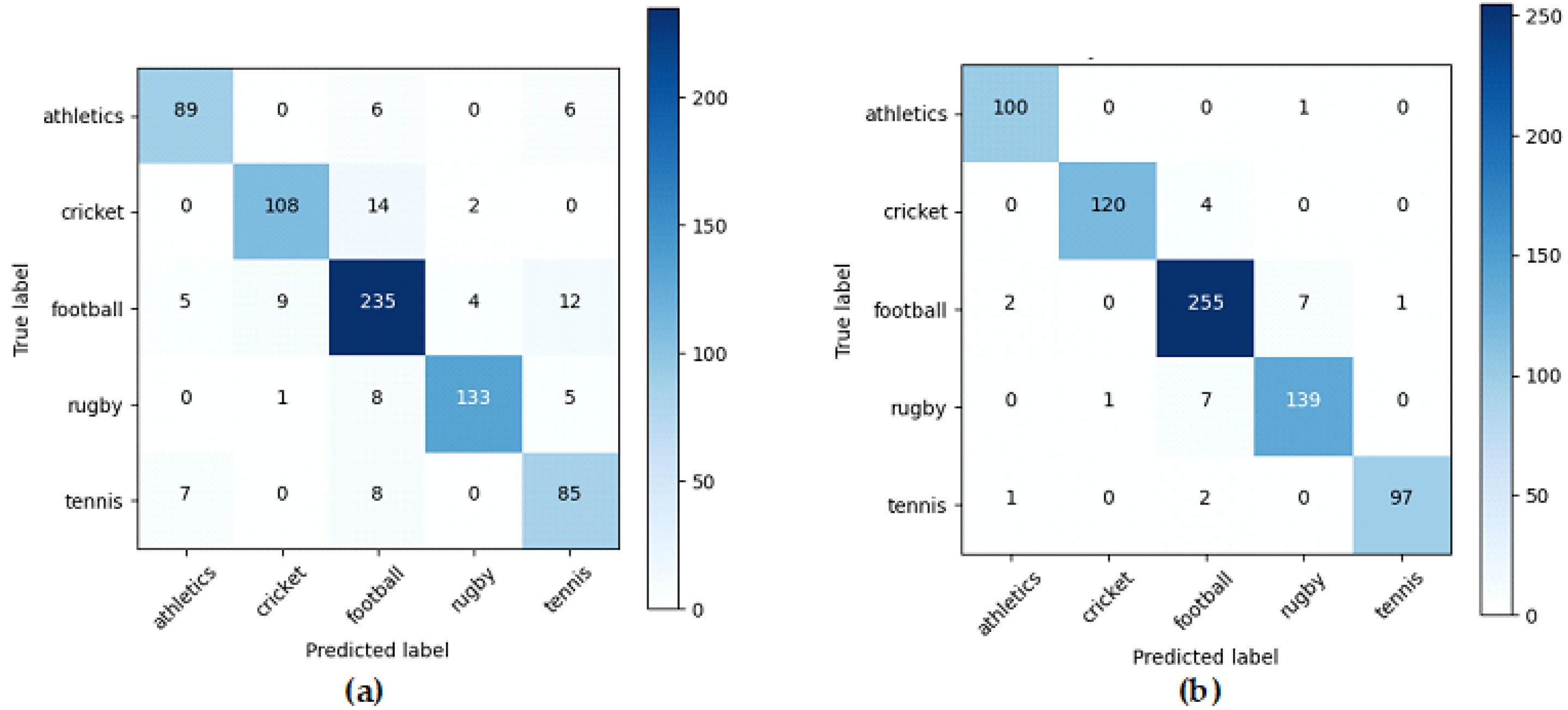
5.2. BBC Sports Results
5.3. Comparison with Standard Machine Learning Approaches
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Similarity Measure | Expression |
|---|---|
where | |
where | |
where , , , , | |
| T | where , and |
| S | where , , with |
where | |
| Similarity Measure | Expression |
|---|---|
where | |
where , , , with | |
where , with | |
where , | |
| Similarity Measure | Expression |
|---|---|
| Distance Measure | Expression |
|---|---|
| , where |
References
- Pang, B.; Lee, L. Opinion Mining and Sentiment Analysis. Found. Trends Inf. Retr. 2008, 2, 1–135. [Google Scholar] [CrossRef] [Green Version]
- Liu, B. Sentiment Analysis and Opinion Mining. 2012. Available online: https://www.cs.uic.edu/liub/FBS/SentimentAnalysis-and-OpinionMining.pdf (accessed on 14 March 2022).
- Řehůřek, R.; Kolkus, M. Language Identification on the Web: Extending the Dictionary Method; Springer: Berlin/Heidelberg, Germany, 2009; pp. 357–368. [Google Scholar] [CrossRef]
- Cai, W.; Cai, D.; Huang, S.; Li, M. Utterance-Level End-to-End Language Identification Using Attention-Based CNN-BLSTM. 2019. Available online: https://arxiv.org/abs/1902.07374 (accessed on 14 March 2022).
- Brenes, D.J.; Gayo-Avello, D.; Pérez-González, K. Survey and Evaluation of Query Intent Detection Methods. In Proceedings of the 2009 Workshop on Web Search Click Data WSCD ’09, Barcelona, Spain, 9–11 February 2009; Association for Computing Machinery: New York, NY, USA, 2009; pp. 1–7. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Blei, D.M. Collaborative Topic Modeling for Recommending Scientific Articles; ACM Press: New York, NY, USA, 2011; p. 448. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Małysiak-Mrozek, B. Uncertainty, imprecision, and many-valued logics in protein bioinformatics. Math. Biosci. 2019, 309, 143–162. [Google Scholar] [CrossRef] [PubMed]
- Atanassov, K.T. Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Intarapaiboon, P. A Framework for Text Classification Using Intuitionistic Fuzzy Sets; Springer: Berlin/Heidelberg, Germany, 2019; pp. 737–746. [Google Scholar] [CrossRef]
- Abbasi, B.Z.; Hussain, S.; Faisal, M.I. An Automated Text Classification Method: Using Improved Fuzzy Set Approach for Feature Selection; IEEE: Islamabad, Pakistan, 2019; p. 5. [Google Scholar]
- Widyantoro, D.H.; Yen, J. A Fuzzy Similarity Approach in Text Classification Task. 1998. Available online: https://www.researchgate.net/publication/3845652_A_fuzzy_similarity_approach_in_text_classification_task (accessed on 14 March 2022).
- Puri, S. A Fuzzy Similarity Based Concept Mining Model for Text Classification. 2012. Available online: https://arxiv.org/ftp/arxiv/papers/1204/1204.2061.pdf (accessed on 14 March 2022).
- Jiang, J.Y.; Liou, R.J.; Lee, S.J. A fuzzy self-constructing feature clustering algorithm for text classification. IEEE Trans. Knowl. Data Eng. 2011, 23, 335–349. [Google Scholar] [CrossRef]
- Jiang, J.Y.; Tsai, S.C.; Lee, S.J. Expert Systems with Applications FSKNN: Multi-label text categorization based on fuzzy similarity and k nearest neighbors q. Expert Syst. Appl. 2012, 39, 2813–2821. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Using Intuitionistic Fuzzy Sets in Text Categorization. In Artificial Intelligence and Soft Computing–ICAISC 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 351–362. [Google Scholar] [CrossRef]
- Bounabi, M.; Moutaouakil, K.E.; Satori, K. Text Classification Using Fuzzy TF-IDF and Machine Learning Models; ACM: Rabar, Morocco, 2019; p. 6. [Google Scholar]
- Behera, B. Text Document Classification Using Fuzzy Rough Set Based on Robust Nearest Neighbor (FRS-RNN). Soft Comput. 2021, 25, 9915–9923. [Google Scholar] [CrossRef]
- Puri, S. Efficient Fuzzy Similarity-Based Text Classification with SVM and Feature Reduction. In Proceedings of the Congress on Intelligent Systems, New Delhi, India, 5–6 September 2020; Sharma, H., Saraswat, M., Yadav, A., Kim, J.H., Bansal, J.C., Eds.; Springer: Singapore, 2020; pp. 341–356. [Google Scholar]
- Wang, W.; Xin, X. Distance measure between Intuitionistic Fuzzy Sets. Pattern Recognit. Lett. 2005, 26, 2063–2069. [Google Scholar] [CrossRef]
- Kacprzyk, J. Multistage Fuzzy Control: A Prescriptive Approach, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1997. [Google Scholar]
- Atanassov, K.T. Intuitionistic Fuzzy Sets. In Studies in Fuzziness and Soft Computing; Physica-Verlag HD Fuzzy Sets and Systems: Berlin/Heidelberg, Germany, 1999; Volume 35. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Distances between Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 2000, 114, 505–518. [Google Scholar] [CrossRef]
- Li, D.; Cheng, C. New Similarity Measures of Intuitionistic Fuzzy Sets and Application to Pattern Recognitions. Pattern Recognit. Lett. 2002, 23, 221–225. [Google Scholar] [CrossRef]
- Mitchell, H. On the Dengfeng–Chuntian Similarity Measure and Its Application to Pattern Recognition. Pattern Recognit. Lett. 2003, 24, 3101–3104. [Google Scholar] [CrossRef]
- Hung, W.L.; Yang, M.S. Similarity Measures of Intuitionistic Fuzzy Sets Based on Hausdorff Distance. Pattern Recognit. Lett. 2004, 25, 1603–1611. [Google Scholar] [CrossRef]
- Chen, S.M. Measures of similarity between vague sets. Fuzzy Sets Syst. 1995, 74, 217–223. [Google Scholar] [CrossRef]
- Sidiropoulos, G.K.; Apostolidis, K.D.; Damianos, N.; Papakostas, G.A. Fsmpy: A Fuzzy Set Measures Python Library. Information 2022, 13, 64. [Google Scholar] [CrossRef]
- Grzegorzewski, P. Distances between Intuitionistic Fuzzy Sets and/or Interval-Valued Fuzzy Sets Based on the Hausdorff Metric. Fuzzy Sets Syst. 2004, 148, 319–328. [Google Scholar] [CrossRef]
- Chen, S.-M. Similarity Measures between Vague Sets and between Elements. IEEE Trans. Syst. Man Cybern. Part Cybern. 1997, 27, 153–158. [Google Scholar] [CrossRef]
- Hong, D.H.; Kim, C. A Note on Similarity Measures between Vague Sets and between Elements. Inf. Sci. 1999, 115, 83–96. [Google Scholar] [CrossRef]
- Liang, Z.; Shi, P. Similarity Measures on Intuitionistic Fuzzy Sets. Pattern Recognit. Lett. 2003, 24, 2687–2693. [Google Scholar] [CrossRef]
- Liu, H.W. New Similarity Measures between Intuitionistic Fuzzy Sets and between Elements. Math. Comput. Model. 2005, 42, 61–70. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, H. Similarity Measures on Three Kinds of Fuzzy Sets. Pattern Recognit. Lett. 2006, 27, 1307–1317. [Google Scholar] [CrossRef]
- Hung, W.L.; Yang, M.S. Similarity Measures of Intuitionistic Fuzzy Sets Based on Lp Metric. Int. J. Approx. Reason. 2007, 46, 120–136. [Google Scholar] [CrossRef] [Green Version]
- Park, J.H.; Park, J.S.; Kwun, Y.C.; Lim, K.M. New Similarity Measures on Intuitionistic Fuzzy Sets. In Fuzzy Information and Engineering; Cao, B.Y., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 40, pp. 22–30. [Google Scholar] [CrossRef]
- Hung, W.L.; Yang, M.S. On Similarity Measures between Intuitionistic Fuzzy Sets. Int. J. Intell. Syst. 2008, 23, 364–383. [Google Scholar] [CrossRef]
- Hung, W.L.; Yang, M.S. On the J-divergence of Intuitionistic Fuzzy Sets with Its Application to Pattern Recognition. Inf. Sci. 2008, 178, 1641–1650. [Google Scholar] [CrossRef]
- Ye, J. Cosine Similarity Measures for Intuitionistic Fuzzy Sets and Their Applications. Math. Comput. Model. 2011, 53, 91–97. [Google Scholar] [CrossRef]
- Hwang, C.M.; Yang, M.S. Modified Cosine Similarity Measure between Intuitionistic Fuzzy Sets. In Artificial Intelligence and Computational Intelligence; Lei, J., Wang, F., Deng, H., Miao, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7530, pp. 285–293. [Google Scholar]
- Julian, P.; Hung, K.C.; Lin, S.J. On the Mitchell Similarity Measure and Its Application to Pattern Recognition. Pattern Recognit. Lett. 2012, 33, 1219–1223. [Google Scholar] [CrossRef]
- Iancu, I. Intuitionistic Fuzzy Similarity Measures Based on Frank T-Norms Family. Pattern Recognit. Lett. 2014, 42, 128–136. [Google Scholar] [CrossRef]
- Deng, G.; Jiang, Y.; Fu, J. Monotonic Similarity Measures between Intuitionistic Fuzzy Sets and Their Relationship with Entropy and Inclusion Measure. Inf. Sci. 2015, 316, 348–369. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Lei, L.; Xue, A. A Novel Similarity Measure on Intuitionistic Fuzzy Sets with Its Applications. Appl. Intell. 2015, 42, 252–261. [Google Scholar] [CrossRef]
- Chen, S.M.; Cheng, S.H.; Lan, T.C. A Novel Similarity Measure between Intuitionistic Fuzzy Sets Based on the Centroid Points of Transformed Fuzzy Numbers with Applications to Pattern Recognition. Inf. Sci. 2016, 343–344, 15–40. [Google Scholar] [CrossRef]
- Muthukumar, P.; Sai Sundara Krishnan, G. A Similarity Measure of Intuitionistic Fuzzy Soft Sets and Its Application in Medical Diagnosis. Appl. Soft Comput. 2016, 41, 148–156. [Google Scholar] [CrossRef]
- Yang, Y.; Chiclana, F. Consistency of 2D and 3D Distances of Intuitionistic Fuzzy Sets. Expert Syst. Appl. 2012, 39, 8665–8670. [Google Scholar] [CrossRef]
- Vlachos, I.K.; Sergiadis, G.D. Intuitionistic Fuzzy Information–Applications to Pattern Recognition. Pattern Recognit. Lett. 2007, 28, 197–206. [Google Scholar] [CrossRef]
- Nguyen, H. A Novel Similarity/Dissimilarity Measure for Intuitionistic Fuzzy Sets and Its Application in Pattern Recognition. Expert Syst. Appl. 2016, 45, 97–107. [Google Scholar] [CrossRef]
- Greene, D.; Cunningham, P. Practical Solutions to the Problem of Diagonal Dominance in Kernel Document Clustering. In Proceedings of the 23rd International Conference on Machine Learning (ICML’06), Pittsburgh, PA, USA, 25–29 June 2006; pp. 377–384. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Müller, A.; Nothman, J.; Louppe, G. Scikit-Learn: Machine Learning in Python. Available online: https://arxiv.org/abs/1201.0490 (accessed on 11 August 2021).
- Bird, S.; Klein, E.; Loper, E. Natural Language Processing with Python, 1st ed.; O’Reilly: Newton, MA, USA, 2009. [Google Scholar]
- Hatzimichailidis, A.; Papakostas, G.; Kaburlasos, V. A novel distance measure of Intuitionistic Fuzzy Sets and its application to pattern recognition problems. Int. J. Intell. Syst. 2012, 27, 396–409. [Google Scholar] [CrossRef]
- Xu, Z. Some Similarity Measures of Intuitionistic Fuzzy Sets and Their Applications to Multiple Attribute Decision Making. Fuzzy Optim. Decis. Mak. 2007, 6, 109–121. [Google Scholar] [CrossRef]

| Authors Names | Parameters | Measure Name | Reference |
|---|---|---|---|
| S. M. Chen | weights, a, b, c | [30] | |
| D.H. Hong, C. Kim | weights, a, b, c | [31] | |
| L. Dengfeng, C. Chuntian | p, weights | [24] | |
| Z. Liang, P. Shi | p, weights | , | [32] |
| H.B. Mitchell | p, weights | [25] | |
| W.L. Hung, M.S. Yang | weights | , , | [26] |
| H.W. Liu | p, weights, a, b, c | T | [33] |
| C. Zhang, H. Fu | - | S | [34] |
| W.L. Hung, M.S. Yang | a | , , | [35] |
| S. Park, Y.C. Kwun, K.M. Lim | p, weights | [36] | |
| W.L. Hung, M.S. Yang | - | , , , , , | [37] |
| W.L. Hung, M.S. Yang | p | , , | [38] |
| J. Ye | weights | [39] | |
| C.M. Hwang, M.S. Yang | - | [40] | |
| P. Julian, K.C. Hung, S. Lin | p, weights | [41] | |
| I. Iancu | lamda | , , , , , , , | [42] |
| G. Deng, Y. Jiang, J. Fu | weights, p, u, v | , , , , | [43] |
| Y. Song, X. Wang, L. Lei, A. Xue | weights | [44] | |
| S.M. Chen, S. Cheng, T.C. Lan | weights | [45] | |
| P. Muthukumar, G.S.S. Krishnan | weights | [46] |
| Authors Names | Parameters | Measure Name | Reference |
|---|---|---|---|
| K.T. Atanassov | - | , , , | [22] |
| E. Szmidt, A. Kacprzyk | - | , , , | [23] |
| P. Grzegorzewski | - | , , , | [29] |
| W. Wang, X. Xin | weights, p | , | [20] |
| Y. Yang, F. Chiclana | - | , , , | [47] |
| I.K. Vlachos, G.D. Sergiadis | - | [48] |
| Distance Measures | Parameters | Weights (, ) | Accuracy % | Precision % | Recall % | F1 % | DoC |
|---|---|---|---|---|---|---|---|
| - | (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0903 | |
| - | (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 3.9711 | |
| - | (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0018 | |
| - | (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 0.0016 | |
| - | (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0903 | |
| - | (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 3.9711 | |
| - | (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0018 | |
| - | (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 0.0016 | |
| (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 0.0016 | ||
| (, ) | 88.94 | 90.45 | 88.98 | 88.63 | 0.0031 | ||
| - | (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0903 | |
| - | (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 3.9711 | |
| - | (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0018 | |
| - | (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 0.0016 | |
| - | (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0903 | |
| - | (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 3.9711 | |
| - | (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0018 | |
| - | (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 0.0016 | |
| - | (, ) | 94.25 | 94.10 | 93.98 | 94.02 | 5.5846 |
| Similarity Measures | Parameters | Weights (, ) | Accuracy % | Precision % | Recall % | F1 % | DoC |
|---|---|---|---|---|---|---|---|
| , , | (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 0.0016 | |
| , , | (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 0.0016 | |
| (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0018 | ||
| (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0018 | ||
| (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0018 | ||
| (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0018 | ||
| - | (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 0.0016 | |
| - | (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 0.0025 | |
| - | (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 0.0031 | |
| T | , , , | (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0018 |
| S | - | (, ) | 50.65 | 61.21 | 49.05 | 39.49 | 0.0091 |
| (, ) | 94.83 | 94.67 | 94.62 | 94.63 | 0.0019 | ||
| (, ) | 94.83 | 94.67 | 94.62 | 94.63 | 0.0021 | ||
| (, ) | 94.83 | 94.67 | 94.62 | 94.63 | 0.0022 | ||
| (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0025 | ||
| - | (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 0.0023 | |
| - | (, ) | 50.47 | 60.86 | 48.9 | 39.26 | 0.0293 | |
| - | (, ) | 75.06 | 77.75 | 74.99 | 74.56 | 0.0418 | |
| - | (, ) | 50.47 | 60.86 | 48.9 | 39.26 | 0.0157 | |
| - | (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 0.0017 | |
| - | (, ) | 49.17 | 39.46 | 47.68 | 37.84 | 0 | |
| (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 0.0026 | ||
| (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 0.0033 | ||
| , , | (, ) | 49.66 | 61.04 | 48.18 | 38.51 | 0.0016 | |
| - | (, ) | 94.74 | 94.67 | 94.57 | 94.56 | 0.0033 | |
| - | (, ) | 93.71 | 93.44 | 93.47 | 93.44 | 0.0019 | |
| (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0040 | ||
| - | (, ) | 71.91 | 80.40 | 73.01 | 73.03 | 0.0097 | |
| - | (, ) | 59.78 | 75.68 | 60.60 | 61.30 | 0.0112 | |
| - | (, ) | 75.55 | 84.69 | 74.10 | 73.14 | 0.0007 | |
| - | (, ) | 91.69 | 92.20 | 91.84 | 91.49 | 0.0006 | |
| - | (, ) | 55.33 | 58.77 | 56.51 | 55.42 | 0.0091 | |
| - | (, ) | 93.48 | 93.36 | 93.45 | 93.29 | 0.0012 | |
| - | (, ) | 64.9 | 76.35 | 65.71 | 66.39 | 0.0056 | |
| - | (, ) | 90.25 | 91.11 | 89.72 | 89.72 | 0 | |
| , , | (, ) | 94.29 | 94.24 | 94.09 | 94.10 | 0.0289 | |
| , , | (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0018 | |
| , , | (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0006 | |
| , , | (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0 | |
| , , | (, ) | 93.17 | 93.19 | 92.76 | 92.86 | 0.0028 | |
| - | (, ) | 94.47 | 94.26 | 94.23 | 94.24 | 0.0005 | |
| - | (, ) | 49.93 | 60.98 | 48.42 | 38.74 | 0.0083 | |
| - | (, ) | 65.75 | 81.88 | 63.86 | 59.92 | 0.0285 |
| Similarity Measures | Parameters | Weights (, ) | Accuracy % | Precision % | Recall % | F1 % | DoC |
|---|---|---|---|---|---|---|---|
| , , | (, ) | 25.10 | 83.07 | 33.90 | 25.50 | 0.0014 | |
| , , | (, ) | 25.10 | 83.07 | 33.90 | 25.50 | 0.0014 | |
| (, ) | 96.34 | 96.54 | 96.47 | 96.48 | 0.0028 | ||
| (, ) | 96.34 | 96.54 | 96.47 | 96.48 | 0.0028 | ||
| (, ) | 96.34 | 96.54 | 96.47 | 96.48 | 0.0028 | ||
| (, ) | 96.34 | 96.54 | 96.47 | 96.48 | 0.0028 | ||
| - | (, ) | 25.10 | 83.07 | 33.90 | 25.50 | 0.0014 | |
| - | (, ) | 25.10 | 83.07 | 33.90 | 25.50 | 0.0023 | |
| - | (, ) | 25.10 | 83.07 | 33.90 | 25.50 | 0.0028 | |
| T | , , , | (, ) | 96.34 | 96.54 | 96.47 | 96.48 | 0.0028 |
| S | - | (, ) | 28.49 | 83.19 | 36.36 | 29.31 | 0.0081 |
| (, ) | 96.47 | 96.69 | 96.78 | 96.72 | 0 | ||
| (, ) | 96.47 | 96.69 | 96.78 | 96.72 | 0 | ||
| (, ) | 96.47 | 96.69 | 96.78 | 96.72 | 0 | ||
| (, ) | 96.34 | 96.54 | 96.47 | 96.48 | 0.0045 | ||
| - | (, ) | 25.10 | 83.07 | 33.90 | 25.50 | 0.0021 | |
| - | (, ) | 26.46 | 83.12 | 35.38 | 27.44 | 0.0269 | |
| - | (, ) | 79.65 | 81.51 | 77.73 | 78.79 | 0.0489 | |
| - | (, ) | 26.46 | 83.12 | 35.38 | 27.44 | 0.0144 | |
| - | (, ) | 25.10 | 83.07 | 33.90 | 25.50 | 0.002 | |
| - | (, ) | 24.42 | 81.04 | 33.44 | 24.17 | 0 | |
| (, ) | 25.10 | 83.07 | 33.90 | 25.50 | 0.0024 | ||
| (, ) | 25.10 | 83.07 | 33.90 | 25.50 | 0.003 | ||
| , , | (, ) | 25.10 | 83.07 | 33.90 | 25.50 | 0.0014 | |
| - | (, ) | 96.47 | 96.99 | 96.71 | 96.84 | 0.0023 | |
| - | (, ) | 95.93 | 96.54 | 96.11 | 96.31 | 0.0067 | |
| (, ) | 96.34 | 96.54 | 96.47 | 96.48 | 0.0064 | ||
| - | (, ) | 69.61 | 76.86 | 72.68 | 71.01 | 0.0072 | |
| - | (, ) | 50.47 | 78.02 | 54.83 | 54.77 | 0.0096 | |
| - | (, ) | 82.36 | 86.95 | 87.83 | 84.91 | 0.0012 | |
| - | (, ) | 94.44 | 93.89 | 95.63 | 94.61 | 0.0006 | |
| - | (, ) | 40.30 | 58.81 | 47.36 | 43.41 | 0.0072 | |
| - | (, ) | 94.30 | 93.71 | 95.61 | 94.50 | 0.0018 | |
| - | (, ) | 63.50 | 73.42 | 66.40 | 65.26 | 0.004 | |
| - | (, ) | 90.09 | 89.41 | 91.95 | 89.84 | 0 | |
| , , | (, ) | 96.20 | 96.46 | 96.34 | 96.37 | 0.0371 | |
| , , | (, ) | 96.34 | 96.54 | 96.47 | 96.48 | 0.0028 | |
| , , | (, ) | 96.34 | 96.54 | 96.47 | 96.48 | 0.0009 | |
| , , | (, ) | 96.20 | 96.36 | 96.40 | 96.35 | 0 | |
| , , | (, ) | 96.34 | 96.54 | 96.47 | 96.48 | 0.0045 | |
| - | (, ) | 95.93 | 97.33 | 95.64 | 96.42 | 0.0006 | |
| - | (, ) | 25.78 | 83.09 | 34.40 | 26.22 | 0.0075 | |
| - | (, ) | 62.82 | 84.04 | 65.53 | 64.82 | 0.0261 |
| Distance Measures | Parameters | Weights (, ) | Accuracy % | Precision % | Recall % | F1 % | DoC |
|---|---|---|---|---|---|---|---|
| - | (, ) | 93.62 | 96.32 | 92.79 | 94.28 | 0.1001 | |
| - | (, ) | 25.1 | 83.07 | 33.9 | 25.5 | 3.423 | |
| - | (, ) | 93.62 | 96.32 | 92.79 | 94.28 | 0.002 | |
| - | (, ) | 25.1 | 83.07 | 33.9 | 25.5 | 0.0014 | |
| - | (, ) | 93.62 | 96.32 | 92.79 | 94.28 | 0.1001 | |
| - | (, ) | 25.1 | 83.07 | 33.9 | 25.5 | 3.423 | |
| - | (, ) | 93.62 | 96.32 | 92.79 | 94.28 | 0.002 | |
| - | (, ) | 25.1 | 83.07 | 33.9 | 25.5 | 0.0014 | |
| (, ) | 25.1 | 83.07 | 33.9 | 25.5 | 0.0014 | ||
| (, ) | 95.66 | 95.54 | 96.15 | 95.77 | 0.0034 | ||
| - | (, ) | 93.62 | 96.32 | 92.79 | 94.28 | 0.1001 | |
| - | (, ) | 25.1 | 83.07 | 33.9 | 25.5 | 3.423 | |
| - | (, ) | 93.62 | 96.32 | 92.79 | 94.28 | 0.002 | |
| - | (, ) | 25.1 | 83.07 | 33.9 | 25.5 | 0.0014 | |
| - | (, ) | 93.62 | 96.32 | 92.79 | 94.28 | 0.1001 | |
| - | (, ) | 25.1 | 83.07 | 33.9 | 25.5 | 3.423 | |
| - | (, ) | 93.62 | 96.32 | 92.79 | 94.28 | 0.002 | |
| - | (, ) | 25.1 | 83.07 | 33.9 | 25.5 | 0.0014 | |
| - | (, ) | 95.39 | 97.07 | 95.02 | 95.94 | 3.6342 |
| BBC News | BBC Sports | |||||||
|---|---|---|---|---|---|---|---|---|
| Model/ Measure | Accuracy (%) | Precision (%) | Recall (%) | F1 (%) | Accuracy (%) | Precision (%) | Recall (%) | F1 (%) |
| Decision Tree | 81.61 | 81.85 | 81.04 | 81.31 | 88.19 | 88.14 | 87.87 | 87.96 |
| KNN | 82.69 | 86.47 | 81.63 | 82.79 | 88.46 | 92.96 | 87.42 | 89.16 |
| 94.83 | 94.67 | 94.62 | 94.63 | 96.47 | 96.69 | 96.78 | 96.72 | |
| 94.74 | 94.67 | 94.57 | 94.56 | 96.47 | 96.99 | 96.71 | 96.84 | |
| 94.25 | 94.10 | 93.98 | 94.02 | 95.39 | 97.07 | 95.02 | 95.94 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sidiropoulos, G.K.; Diamianos, N.; Apostolidis, K.D.; Papakostas, G.A. Text Classification Using Intuitionistic Fuzzy Set Measures—An Evaluation Study. Information 2022, 13, 235. https://doi.org/10.3390/info13050235
Sidiropoulos GK, Diamianos N, Apostolidis KD, Papakostas GA. Text Classification Using Intuitionistic Fuzzy Set Measures—An Evaluation Study. Information. 2022; 13(5):235. https://doi.org/10.3390/info13050235
Chicago/Turabian StyleSidiropoulos, George K., Nikolaos Diamianos, Kyriakos D. Apostolidis, and George A. Papakostas. 2022. "Text Classification Using Intuitionistic Fuzzy Set Measures—An Evaluation Study" Information 13, no. 5: 235. https://doi.org/10.3390/info13050235
APA StyleSidiropoulos, G. K., Diamianos, N., Apostolidis, K. D., & Papakostas, G. A. (2022). Text Classification Using Intuitionistic Fuzzy Set Measures—An Evaluation Study. Information, 13(5), 235. https://doi.org/10.3390/info13050235







