A Forward-Looking Approach to Compare Ranking Methods for Sports
Abstract
:1. Introduction
2. Rating and Ranking Methods
2.1. Winning Percentage (WP)
2.2. Rating Percentage Index (RPI)
2.3. Massey’s Least Squares Method (M)
2.4. Colley’s Least Squares Method (C)
2.5. Keener Method (K)
2.6. PageRank Method (PR)
2.7. Graph Representation of the Methods
3. Evaluation and Comparison of Rating Methods
3.1. Rolling Window Approach
3.2. Expanding Window Approach
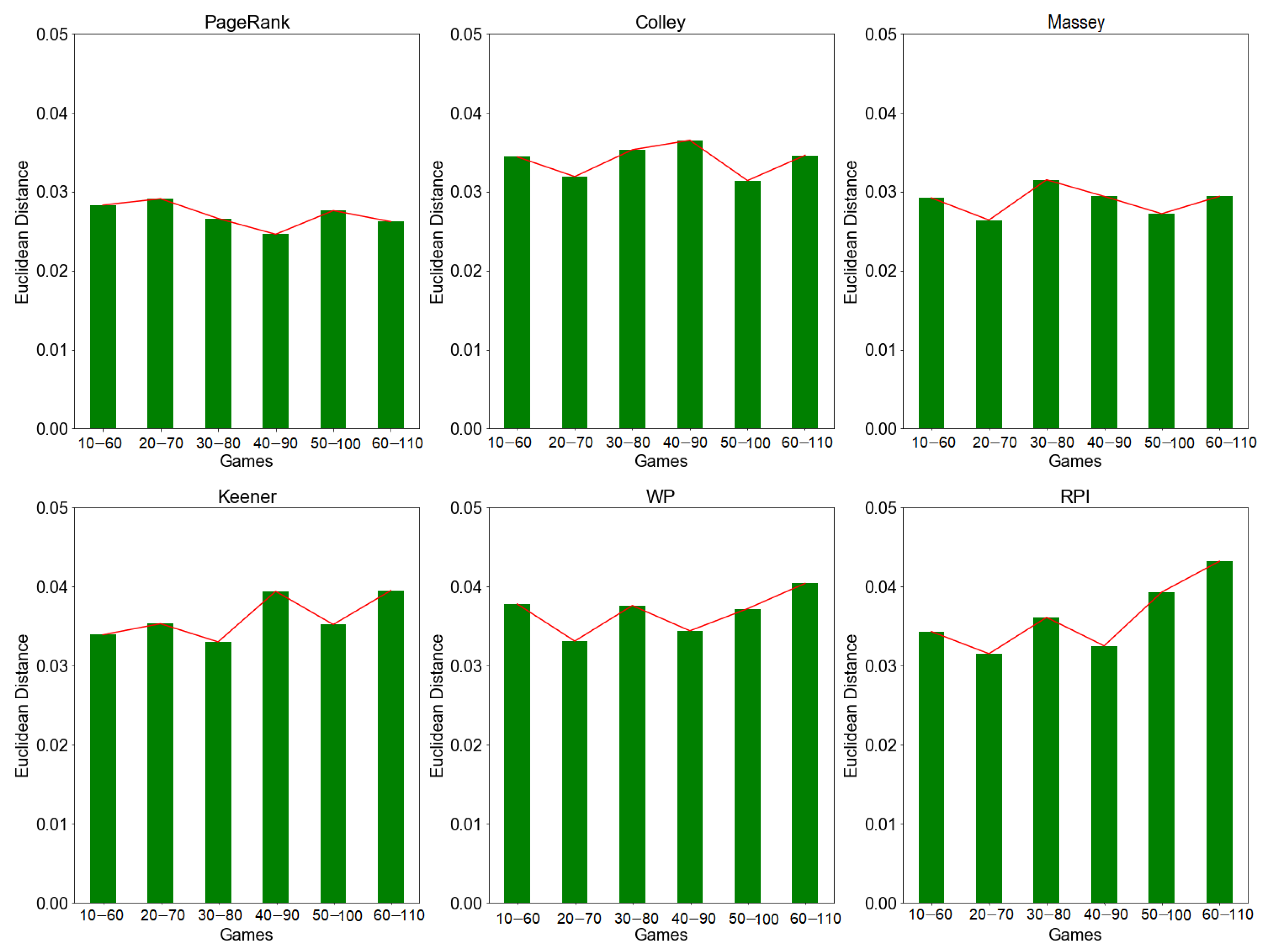
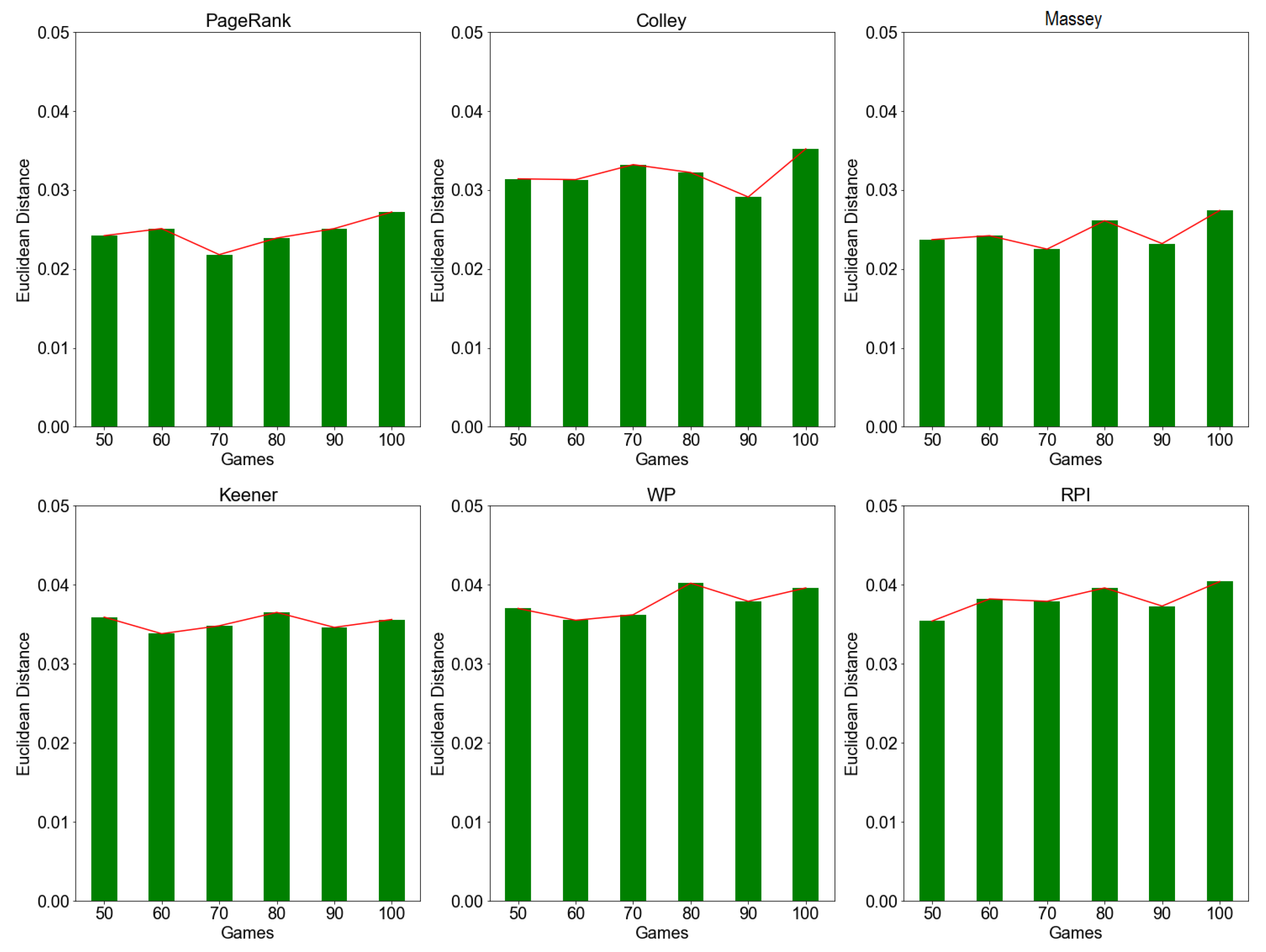
3.3. Rating Stability
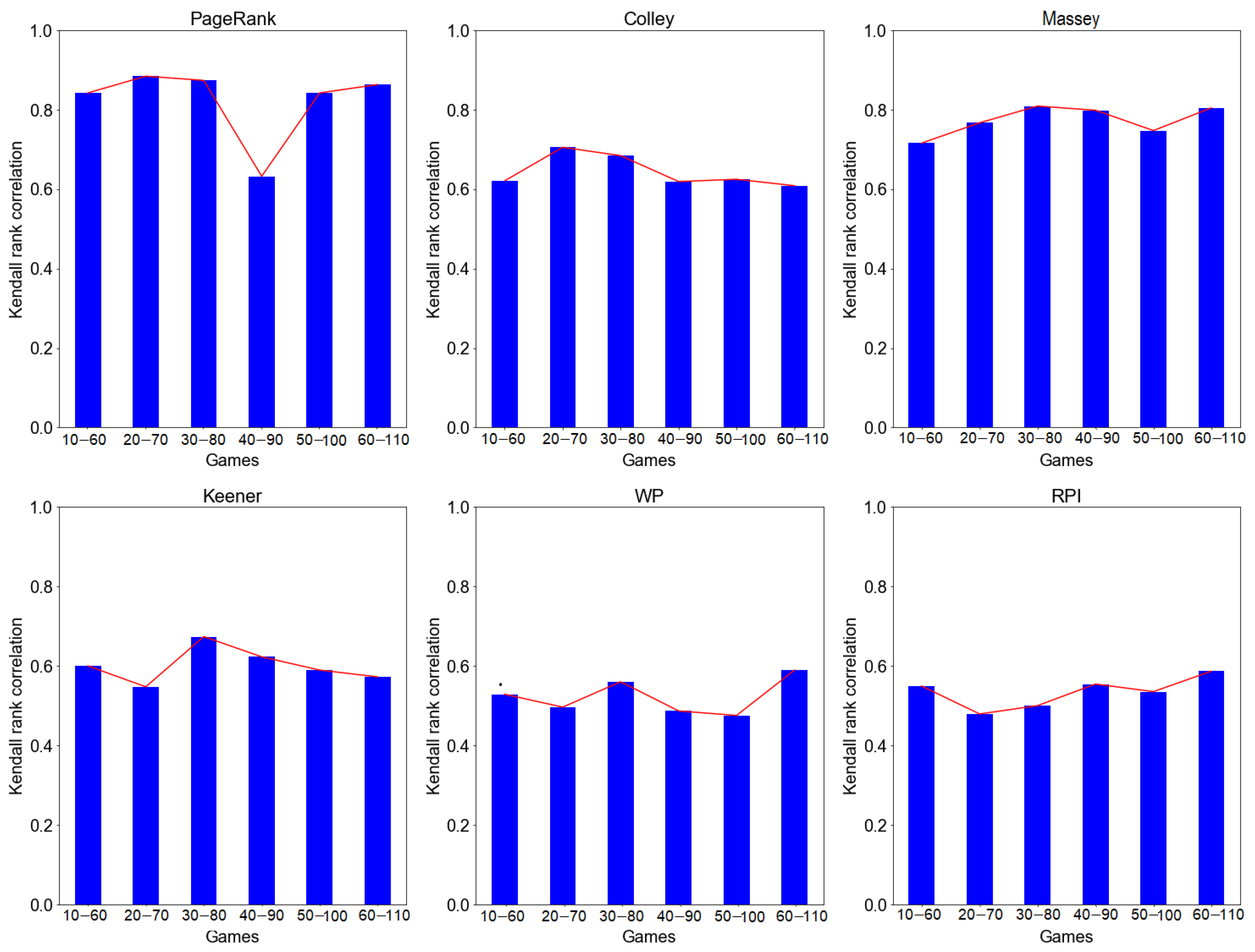
3.4. Ranking Stability
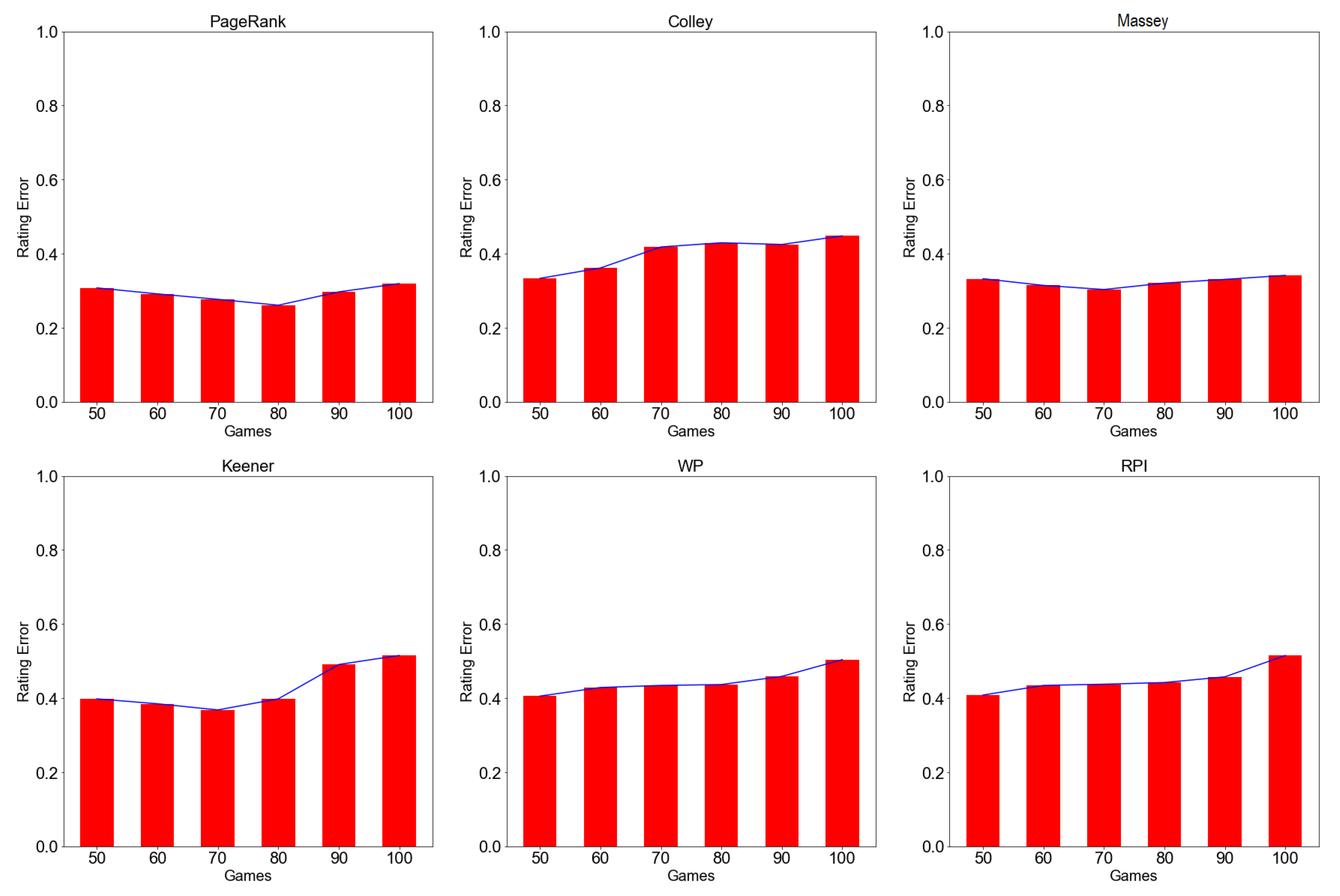
3.5. Rating Error
4. Results
4.1. Comparison of Top-5 Teams Ranking by Rolling Window Approach
4.2. Comparison of Top-5 Teams Ranking by Expanding Window Approach
4.3. Rating Stability
4.3.1. Evaluation by Rolling Window Approach
4.3.2. Evaluation by Expanding Window Approach
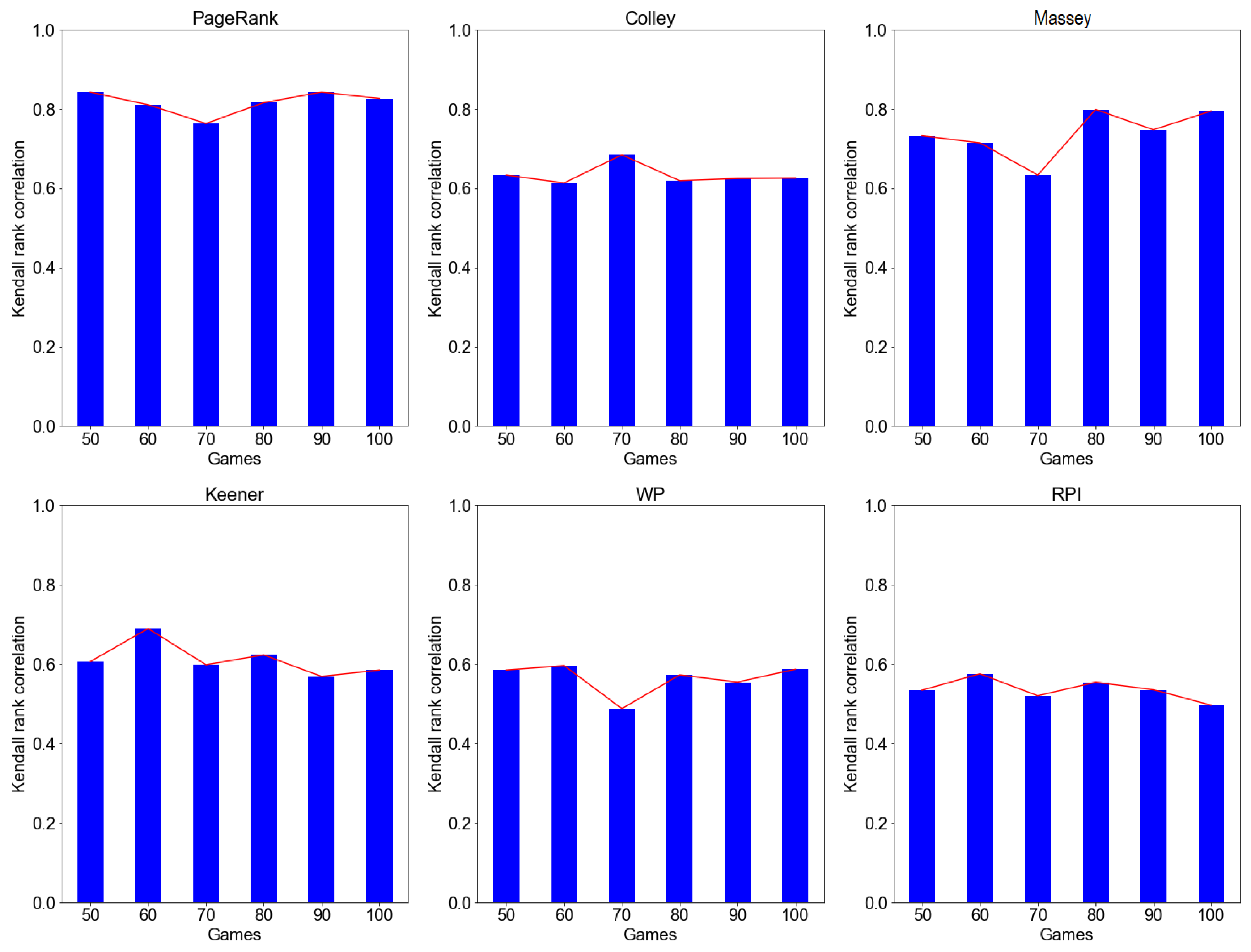
4.4. Ranking Stability
4.4.1. Evaluation by Rolling Window Approach
4.4.2. Evaluation by Expanding Window Approach
4.5. Rating Error
5. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Rank–Rate Comparison of Top-5 Teams by Rolling Window Approach
Appendix A.2. Rank–Rate Comparison of Top-5 Teams by Expanding Window Approach
| 10–60 Games | 20–70 Games | 30–80 Games | 40–90 Games | 50–100 Games | 60-110 Games | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Teams | Ranks | Ratings | Teams | Ranks | Ratings | Teams | Ranks | Ratings | Teams | Ranks | Ratings | Teams | Ranks | Ratings | Teams | Ranks | Ratings | |
| PageRank | ‘Man. City’ | 1 | 0.0696 | ‘Man. City’ | 1 | 0.0894 | ‘Man. City’ | 1 | 0.0895 | ‘Man. City’ | 1 | 0.0894 | ‘Man. City’ | 1 | 0.0944 | ‘Man. City’ | 1 | 0.0002 |
| ‘Man. United’ | 2 | 0.0067 | ‘Arsenal’ | 2 | 0.0815 | ‘Arsenal’ | 2 | 0.083 | ‘Arsenal’ | 2 | 0.0805 | ‘Arsenal’ | 2 | 0.0820 | ‘Man. United’ | 2 | 0.0000 | |
| ‘Arsenal’ | 3 | 0.1564 | ‘Man. United’ | 3 | 0.0671 | ‘Man. United’ | 3 | 0.068 | ‘Man. United’ | 3 | 0.0683 | ‘Man. United’ | 3 | 0.0716 | ‘Arsenal’ | 3 | 0.0004 | |
| ‘Tottenham’ | 4 | 0.0544 | ‘Newcastle’ | 4 | 0.0612 | ‘Newcastle’ | 4 | 0.0655 | ‘Newcastle’ | 4 | 0.0644 | ‘Newcastle’ | 4 | 0.0661 | ‘Tottenham’ | 4 | 0.0002 | |
| ‘Chelsea ’ | 5 | 0.1344 | ‘Tottenham’ | 5 | 0.0635 | ‘Tottenham’ | 5 | 0.0639 | ‘Tottenham’ | 5 | 0.0625 | ‘Tottenham’ | 5 | 0.0651 | ‘Chelsea’ | 5 | 0.0004 | |
| sd ± 0.0522 | sd ± 0.0116 | sd ± 0.0125 | sd ± 0.0122 | sd ± 0.0251 | sd ± 0.0185 | |||||||||||||
| Colley | ‘Man. City’ | 1 | 0.1923 | ‘Man. United’ | 1 | −0.042 | ‘Arsenal’ | 1 | −0.0368 | ‘Tottenham’ | 1 | −0.0198 | ‘Tottenham’ | 1 | −0.0187 | ‘Man. City’ | 1 | 0.1847 |
| ‘Man. United’ | 2 | −0.0138 | ‘Man. City’ | 2 | −0.0579 | ‘Man. City’ | 2 | 0.057 | ‘Man. City’ | 2 | 0.0489 | ‘Man. City’ | 2 | 0.0472 | ‘Man. United’ | 2 | -0.0291 | |
| ‘Arsenal’ | 3 | −0.1511 | ‘Newcastle’ | 3 | 0.1823 | ‘Tottenham’ | 3 | 0.2564 | ‘Man. United’ | 3 | 0.2119 | ‘Man. United’ | 3 | 0.2121 | ‘Arsenal’ | 3 | −0.1408 | |
| ‘Tottenham’ | 4 | −0.0149 | ‘Arsenal’ | 4 | 0.0206 | ‘Man. United’ | 4 | −0.1074 | ‘Arsenal’ | 4 | −0.0829 | ‘Arsenal’ | 4 | −0.0811 | ‘Tottenham’ | 4 | −0.0114 | |
| ‘Newcastle’ | 5 | 0.061 | ‘Tottenham’ | 5 | −0.0821 | ‘Newcastle’ | 5 | 0.1348 | ‘Newcastle’ | 5 | 0.1111 | ‘Newcastle’ | 5 | 0.1131 | ‘Newcastle’ | 5 | −0.0030 | |
| sd ± 0.1104 | sd ± 0.1267 | sd ± 0.1333 | sd ± 0.1303 | sd ± 0.1135 | sd± 0.0797 | |||||||||||||
| Massey | ‘Man. City’ | 1 | −0.0696 | ‘Man. City’ | 1 | −0.1379 | ‘Man. City’ | 1 | −0.1053 | ‘Man. City’ | 1 | −0.0961 | ‘Man. City’ | 1 | −0.0002 | ‘Man. City’ | 1 | −0.0961 |
| ‘Man. United’ | 2 | −0.0067 | ‘Man. United’ | 2 | −0.0599 | ‘Man. United’ | 2 | −0.2243 | ‘Tottenham’ | 2 | 0.0494 | ‘Man. United’ | 2 | 0.0000 | ‘Tottenham’ | 2 | 0.0494 | |
| ‘Arsenal’ | 3 | −0.1564 | ‘Arsenal’ | 3 | 0.7011 | ‘Arsenal’ | 3 | 0.8573 | ‘Man. United’ | 3 | 0.4733 | ‘Tottenham’ | 4 | −0.0002 | ‘Arsenal’ | 3 | −0.0004 | |
| ‘Tottenham’ | 4 | −0.0544 | ‘Tottenham’ | 4 | −0.3316 | ‘Tottenham’ | 4 | −0.314 | ‘Arsenal’ | 4 | −0.2376 | ‘Arsenal’ | 5 | 0.4678 | ‘Man. United’ | 3 | 0.4733 | |
| ‘Newcastle’ | 5 | 0.1344 | ‘Newcastle’ | 5 | 0.4368 | ‘Chelsea’ | 5 | 0.4633 | ‘Chelsea’ | 5 | 0.4678 | ‘Newcastle’ | 5 | 0.0004 | ‘Fulham’ | 4 | −0.2376 | |
| sd ± 0.0333 | sd ± 0.0409 | sd ± 0.0418 | sd ± 0.0427 | sd ± 0.0412 | sd ± 0.05328 | |||||||||||||
| Keener | ‘Man. City’ | 1 | 0.1843 | ‘Man. City’ | 1 | 0.1612 | ‘Man. City’ | 1 | 0.1617 | ‘Man. City’ | 1 | 0.1589 | ‘Man. City’ | 1 | 0.1589 | ‘Man. City’ | 1 | 0.2211 |
| ‘Man. United’ | 2 | 0.2164 | ‘Man. United’ | 2 | 0.2157 | ‘Man. United’ | 2 | 0.2145 | ‘Man. United’ | 2 | 0.2164 | ‘Man. United’ | 2 | 0.2164 | ‘Man. United’ | 2 | 0.2231 | |
| ‘Arsenal’ | 3 | 0.2415 | ‘Tottenham’ | 3 | 0.2238 | ‘Tottenham ’ | 3 | 0.2258 | ‘Tottenham’ | 3 | 0.2237 | ‘Everton’ | 3 | 0.2237 | ‘Arsenal’ | 3 | 0.2248 | |
| ‘Tottenham’ | 4 | 0.2348 | ‘Arsenal’ | 4 | 0.2496 | ‘Arsenal’ | 4 | 0.2465 | ‘Arsenal’ | 4 | 0.2347 | ‘Arsenal’ | 4 | 0.2347 | ‘Tottenham’ | 4 | 0.2244 | |
| ‘Newcastle’ | 5 | 0.2065 | ‘Newcastle’ | 5 | 0.1889 | ‘Newcastle’ | 5 | 0.1759 | ‘Newcastle’ | 5 | 0.1768 | ‘Newcastle’ | 5 | 0.1768 | ‘Newcastle’ | 5 | 0.2222 | |
| sd ± 0.0328 | sd ± 0.0434 | sd ± 0.0482 | sd ± 0.0428 | sd ± 0.0306 | sd ± 0.0515 | |||||||||||||
| WP | ‘Man. United’ | 1 | 0.0513 | ‘Man. United’ | 1 | 0.0511 | ‘Man. United’ | 1 | 0.0509 | ‘Man. United’ | 1 | 0.0508 | ‘Man. United’ | 1 | 0.0506 | ‘Man. City’ | 1 | 0.0487 |
| ‘Man. City’ | 2 | 0.0484 | ‘Man. City’ | 2 | 0.0485 | ‘Man. City’ | 2 | 0.0484 | ‘Man. City’ | 2 | 0.0486 | ‘Man. City’ | 2 | 0.0485 | ‘Man. United’ | 2 | 0.0505 | |
| ‘Arsenal’ | 3 | 0.0514 | ‘Arsenal’ | 3 | 0.0518 | ‘Arsenal’ | 3 | 0.0513 | ‘Arsenal’ | 3 | 0.0520 | ‘Arsenal’ | 3 | 0.0519 | ‘Arsenal’ | 3 | 0.0518 | |
| ‘Tottenham’ | 4 | 0.0509 | ‘Tottenham’ | 4 | 0.0502 | ‘Tottenham’ | 4 | 0.0508 | ‘Tottenham ’ | 4 | 0.0512 | ‘Tottenham’ | 4 | 0.0511 | ‘Tottenham’ | 4 | 0.0512 | |
| ‘Newcastle’ | 5 | 0.0531 | ‘Newcastle’ | 5 | 0.0519 | ‘Newcastle’ | 5 | 0.0515 | ‘Swansea City’ | 5 | 0.0504 | ‘Swansea City’ | 5 | 0.0505 | ‘Chelsea’ | 5 | 0.0488 | |
| sd ± 0.2418 | sd ± 0.2256 | sd ± 0.02097 | sd ± 0.1941 | sd ± 0.2024 | sd ± 0.2668 | |||||||||||||
| RPI | ‘Man. City’ | 1 | 0.0489 | ‘Man. City’ | 1 | 0.0484 | ‘Man. City’ | 1 | 0.0483 | ‘Man. City’ | 1 | 0.0485 | ‘Man. United’ | 1 | 0.0508 | ‘Tottenham’ | 1 | 0.0515 |
| ‘Man. United’ | 2 | 0.0490 | ‘Man. United’ | 2 | 0.0510 | ‘Man. United’ | 2 | 0.0514 | ‘Tottenham’ | 2 | 0.0515 | ‘Man. City’ | 2 | 0.0486 | ‘Man. City’ | 2 | 0.0486 | |
| ‘Arsenal’ | 3 | 0.0526 | ‘Arsenal’ | 3 | 0.0510 | ‘Arsenal’ | 3 | 0.0521 | ‘Man. United’ | 3 | 0.0510 | ‘Newcastle’ | 3 | 0.0523 | ‘Man. United’ | 3 | 0.0508 | |
| ‘Tottenham’ | 4 | 0.0482 | ‘Tottenham’ | 4 | 0.0514 | ‘Tottenham’ | 4 | 0.0508 | ‘Arsenal’ | 4 | 0.0512 | ‘Arsenal’ | 4 | 0.0523 | ‘Arsenal’ | 4 | 0.0523 | |
| ‘Newcastle’ | 5 | 0.0523 | ‘Newcastle’ | 5 | 0.0533 | ‘Chelsea’ | 5 | 0.0491 | ‘Chelsea’ | 5 | 0.0492 | ‘Tottenham’ | 5 | 0.0515 | ‘Newcastle’ | 5 | 0.0523 | |
| sd ± 0.2122 | sd ± 0.2819 | sd ± 0.3418 | sd ± 0.3435 | sd ± 0.1752 | sd ± 0.1769 | |||||||||||||
| 50 Games | Afer 60 Games | After 70 Games | After 80 Games | After 90 Games | After 100 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Teams | Ranks | Ratings | Teams | Ranks | Ratings | Teams | Ranks | Ratings | Teams | Ranks | Ratings | Teams | Ranks | Ratings | Teams | Ranks | Ratings | |
| PageRank | ‘Man. City’ | 1 | 0.1217 | ‘Man. City’ | 1 | 0.1226 | ‘Man. City’ | 1 | 0.1237 | ‘Man. City’ | 1 | 0.1249 | ‘Man. City’ | 1 | 0.1263 | ‘Man. City’ | 1 | 0.1566 |
| ‘Chelsea’ | 2 | 0.0889 | ‘Chelsea’ | 2 | 0.0898 | ‘Chelsea’ | 2 | 0.0907 | ‘Chelsea’ | 2 | 0.0919 | ‘Chelsea’ | 2 | 0.0932 | ‘Chelsea’ | 2 | 0.1211 | |
| ‘Man. United’ | 3 | 0.0757 | ‘Man. United’ | 3 | 0.0758 | ‘Man. United’ | 3 | 0.0759 | ‘Man. United’ | 3 | 0.0759 | ‘Man. United’ | 3 | 0.0760 | ‘Man. United’ | 3 | 0.0781 | |
| ‘Newcastle’ | 4 | 0.0670 | ‘Arsenal’ | 4 | 0.0668 | ‘Arsenal’ | 4 | 0.0666 | ‘Arsenal’ | 4 | 0.0663 | ‘Arsenal’ | 4 | 0.0659 | ‘Arsenal’ | 4 | 0.0706 | |
| ‘Tottenham’ | 5 | 0.0640 | ‘Tottenham’ | 5 | 0.0641 | ‘Tottenham’ | 5 | 0.0643 | ‘Tottenham’ | 5 | 0.0646 | ‘Tottenham’ | 5 | 0.0648 | ‘Tottenham’ | 5 | 0.0669 | |
| sd ± 0.0165 | sd ± 0.0174 | sd ± 0.0176 | sd ± 0.0179 | sd ± 0.0213 | sd ± 0.0244 | |||||||||||||
| Colley | ‘Arsenal’ | 1 | 0.1923 | ‘Arsenal’ | 1 | 0.1815 | ‘Arsenal’ | 1 | 0.1846 | ‘Arsenal’ | 1 | 0.1848 | ‘Arsenal’ | 1 | 0.1847 | ‘Arsenal’ | 1 | 0.1847 |
| ‘Man. City’ | 2 | −0.0138 | ‘Man. City’ | 2 | −0.0205 | ‘Man. City’ | 2 | −0.0290 | ‘Man. City’ | 2 | −0.0291 | ‘Man. City’ | 2 | −0.0292 | ‘Man. City’ | 2 | −0.0291 | |
| ‘Man. United’ | 3 | −0.1511 | ‘Man. United’ | 3 | −0.1462 | ‘Man. United’ | 3 | −0.1436 | ‘Man. United’ | 3 | −0.1408 | ‘Man. United’ | 3 | −0.1437 | ‘Man. United’ | 3 | −0.1408 | |
| ‘Tottenham’ | 4 | −0.0149 | ‘Tottenham’ | 4 | −0.0085 | ‘Tottenham’ | 4 | −0.0113 | ‘Tottenham’ | 4 | −0.0113 | ‘Tottenham’ | 4 | −0.0114 | ‘Tottenham’ | 4 | −0.0114 | |
| ‘Newcastle’ | 5 | 0.0610 | ‘Chelsea’ | 5 | 0.0030 | ‘Chelsea’ | 5 | 0.0001 | ‘Chelsea’ | 5 | −0.0029 | ‘Chelsea’ | 5 | −0.0030 | ‘Newcastle’ | 5 | −0.0030 | |
| sd ± 0.0773 | sd ± 0.0754 | sd ± 0.0775 | sd ± 0.0747 | sd ± 0.0783 | sd ± 0.0778 | |||||||||||||
| Massey | ‘Man. City’ | 1 | −0.0696 | ‘Man. City’ | 1 | −0.0569 | ‘Man. United’ | 1 | 0.1560 | ‘Man. City’ | 1 | −0.0380 | ‘Man. City’ | 1 | −0.0310 | ‘Man. City’ | 1 | −0.0002 |
| ‘Arsenal’ | 2 | −0.0067 | ‘Man. United’ | 2 | −0.0055 | ‘Man. City’ | 2 | −0.0509 | ‘Man. United’ | 2 | −0.0037 | ‘Man. United’ | 2 | −0.0030 | ‘Man. United’ | 2 | 0.0000 | |
| ‘Man. United’ | 3 | −0.1564 | ‘Arsenal’ | 3 | −0.1278 | ‘Arsenal’ | 3 | −0.1044 | ‘Arsenal’ | 3 | −0.0853 | ‘Arsenal’ | 3 | −0.0697 | ‘Arsenal’ | 3 | −0.0004 | |
| ‘Tottenham’ | 4 | −0.0544 | ‘Tottenham’ | 4 | −0.0444 | ‘Newcastle’ | 4 | 0.0121 | ‘Tottenham’ | 4 | −0.0297 | ‘Tottenham’ | 4 | −0.0242 | ‘Tottenham’ | 4 | −0.0002 | |
| ‘Newcastle’ | 5 | 0.1344 | ‘Newcastle’ | 5 | 0.1098 | ‘Chelsea’ | 5 | 0.0464 | ‘Newcastle’ | 5 | 0.0733 | ‘Newcastle’ | 5 | 0.0599 | ‘Newcastle’ | 5 | 0.0004 | |
| sd ± 0.0242 | sd ± 0.0226 | sd ± 0.0210 | sd ± 0.0518 | sd ± 0.0337 | sd ± 0.0296 | |||||||||||||
| Keener | ‘Man. United’ | 1 | 0.1843 | ‘Man. United’ | 1 | 0.1870 | ‘Man. United’ | 1 | 0.1897 | ‘Man. United’ | 1 | 0.1923 | ‘Man. United’ | 1 | 0.1948 | ‘Man. United’ | 1 | 0.2211 |
| ‘Man. City’ | 2 | 0.2164 | ‘Man. City’ | 2 | 0.2169 | ‘Man. City’ | 2 | 0.2173 | ‘Man. City’ | 2 | 0.2178 | ‘Man. City’ | 2 | 0.2183 | ‘Man. City’ | 2 | 0.2231 | |
| ‘Arsenal’ | 3 | 0.2415 | ‘Arsenal’ | 3 | 0.2403 | ‘Arsenal’ | 3 | 0.2391 | ‘Arsenal’ | 3 | 0.2380 | ‘Arsenal’ | 3 | 0.2369 | ‘Arsenal’ | 3 | 0.2248 | |
| ‘Tottenham’ | 4 | 0.2348 | ‘Tottenham’ | 4 | 0.2341 | ‘Tottenham’ | 4 | 0.2333 | ‘Tottenham’ | 4 | 0.2326 | ‘Tottenham’ | 4 | 0.2319 | ‘Tottenham’ | 4 | 0.2244 | |
| ‘Newcastle’ | 5 | 0.2065 | ‘Newcastle’ | 5 | 0.2073 | ‘Newcastle’ | 5 | 0.2081 | ‘Swansea City’ | 5 | 0.2090 | ‘Swansea City’ | 5 | 0.2098 | ‘Newcastle’ | 5 | 0.2222 | |
| sd ± 0.0326 | sd ± 0.0408 | sd ± 0.0418 | sd ± 0.0394 | sd ± 0.0314 | sd ± 0.0416 | |||||||||||||
| WP | ‘Man. City’ | 1 | 0.0555 | ‘Man. City’ | 1 | 0.0553 | ‘Man. City’ | 1 | 0.0550 | ‘Man. City’ | 1 | 0.0486 | ‘Man. City’ | 1 | 0.0487 | ‘Arsenal’ | 1 | 0.0511 |
| ‘Man. United’ | 2 | 0.0490 | ‘Man. United’ | 2 | 0.0490 | ‘Man. United’ | 2 | 0.0490 | ‘Man. United’ | 2 | 0.0511 | ‘Man. United’ | 2 | 0.0510 | ‘Man. City’ | 2 | 0.0488 | |
| ‘Arsenal’ | 3 | 0.0483 | ‘Tottenham’ | 3 | 0.0497 | ‘Tottenham’ | 3 | 0.0497 | ‘Tottenham’ | 3 | 0.0508 | ‘Everton’ | 3 | 0.0504 | ‘Man. United’ | 3 | 0.0509 | |
| ‘Tottenham’ | 4 | 0.0497 | ‘Arsenal’ | 4 | 0.0483 | ‘Arsenal’ | 4 | 0.0484 | ‘Arsenal’ | 4 | 0.0512 | ‘Arsenal’ | 4 | 0.0511 | ‘Tottenham’ | 4 | 0.0507 | |
| ‘Newcastle ’ | 5 | 0.0502 | ‘Newcastle’ | 5 | 0.0501 | ‘Newcastle’ | 5 | 0.0501 | ‘Newcastle’ | 5 | 0.0526 | ‘Newcastle’ | 5 | 0.0525 | ‘Chelsea’ | 5 | 0.0489 | |
| sd ± 0.0971 | sd ± 0.0865 | sd ± 0.0737 | sd ± 0.0626 | sd ± 0.0885 | sd ± 0.0571 | |||||||||||||
| RPI | ‘Man. City’ | 1 | 0.0573 | ‘Man. United’ | 1 | 0.0497 | ‘Man. United’ | 1 | 0.0497 | ‘Arsenal’ | 1 | 0.0491 | ‘Arsenal’ | 1 | 0.0491 | ‘Arsenal’ | 1 | 0.0508 |
| ‘Man. United’ | 2 | 0.0497 | ‘Man. City’ | 2 | 0.0570 | ‘Man. City’ | 2 | 0.0567 | ‘Man. City’ | 2 | 0.0563 | ‘Man. City’ | 2 | 0.0559 | ‘Man. City’ | 2 | 0.0487 | |
| ‘Arsenal’ | 3 | 0.0490 | ‘Arsenal’ | 3 | 0.0490 | ‘Arsenal’ | 3 | 0.0490 | ‘Man. United’ | 3 | 0.0497 | ‘Man. United’ | 3 | 0.0497 | ‘Man. United’ | 3 | 0.0508 | |
| ‘Tottenham’ | 4 | 0.0494 | ‘Newcastle’ | 4 | 0.0499 | ‘Tottenham’ | 4 | 0.0495 | ‘Tottenham’ | 4 | 0.0495 | ‘Tottenham’ | 4 | 0.0496 | ‘Tottenham’ | 4 | 0.0511 | |
| ‘Newcastle’ | 5 | 0.0499 | ‘Chelsea’ | 5 | 0.0479 | ‘Swansea City’ | 5 | 0.0503 | ‘Chelsea’ | 5 | 0.0481 | ‘Chelsea’ | 5 | 0.0482 | ‘Chelsea’ | 5 | 0.0487 | |
| sd ± 0.0506 | sd ± 0.0831 | sd ± 0.0843 | sd ± 0.0662 | sd ± 0.0706 | sd ± 0.0805 | |||||||||||||
Appendix B

References
- Langville, A.N.; Meyer, C.D. Google’s PageRank and Beyond: The Science of Search Engine Rankings; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Rubinstein, A. Ranking the participants in a tournament. SIAM J. Appl. Math. 1980, 38, 108–111. [Google Scholar] [CrossRef]
- Bouyssou, D.; Perny, P. Ranking methods for valued preference relations: A characterization of a method based on leaving and entering flows. Eur. J. Oper. Res. 1992, 61, 186–194. [Google Scholar] [CrossRef]
- Chebotarev, P.Y.; Shamis, E. Characterizations of scoring methodsfor preference aggregation. Ann. Oper. Res. 1998, 80, 299–332. [Google Scholar] [CrossRef]
- Vaziri, B.; Dabadghao, S.; Yih, Y.; Morin, T.L. Properties of sports ranking methods. J. Oper. Res. Soc. 2018, 69, 776–787. [Google Scholar] [CrossRef]
- Constantinou, N.E.F.; Neil, M. Pi-football: A bayesian network model for forecasting association football match outcomes. Knowl.-Based Syst. 2012, 36, 322–339. [Google Scholar] [CrossRef]
- Barrow, D.; Drayer, I.; Elliott, P.; Gaut, G.; Osting, B. Ranking rankings: An empirical comparison of the predictive power of sports ranking methods. J. Quant. Anal. Sport 2013, 9, 187–202. [Google Scholar] [CrossRef]
- Chartier, T.P.; Kreutzer, E.; Langville, A.N.; Pedings, K.E. Sensitivity and stability of ranking vectors. SIAM J. Sci. Comput. 2011, 33, 1077–1102. [Google Scholar] [CrossRef]
- Kardos, O.; London, A.; Vinkó, T. Stability of network centrality measures: A numerical study. Soc. Netw. Anal. Min. 2020, 10, 1–17. [Google Scholar] [CrossRef]
- Segarra, S.; Ribeiro, A. Stability and continuity of centrality measures in weighted graphs. IEEE Trans. Signal Process. 2015, 64, 543–555. [Google Scholar] [CrossRef] [Green Version]
- Costenbader, E.; Valente, T.W. The stability of centrality measures when networks are sampled. Soc. Netw. 2003, 25, 283–307. [Google Scholar] [CrossRef]
- Langville, A.N.; Meyer, C.D. Who’s# 1?: The Science of Rating and Ranking; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Jiang, X.; Lim, L.H.; Yao, Y.; Ye, Y. Statistical ranking and combinatorial Hodge theory. Math. Program. 2011, 127, 203–244. [Google Scholar] [CrossRef] [Green Version]
- Pickle, D.; Howard, B. Computer to Aid in Basketball Championship Selection. NCAA News. 1981, Volume 4. Available online: https://scholar.google.com/scholar?q=Pickle%2C+D.%3B+Howard%2C+B+Computer+to+aid+in+basketball+championship+selection.+NCAA+News%2C+1981%3B+Volume+4.&hl=en&as_sdt=0%2C5&as_ylo=&as_yhi= (accessed on 15 March 2022).
- Massey, K. Statistical Models Applied to the Rating of Sports Teams. Unpublished. Bachelor’s Thesis, Bluefield College, Bluefield, VA, USA, 1997. [Google Scholar]
- Colley, W. Colleyâs Bias Free College Football Ranking Method; Princeton University Princeton, NJ, USA. 2002. Available online: https://scholar.google.com/scholar?hl=en&as_sdt=0%2C5&q=Colley%2C+W.+Colley+%C3%A2s+Bias+Free+College+Football+Ranking+Method%3B+2002.&btnG= (accessed on 15 March 2022).
- Keener, J.P. The Perron-Frobenius Theorem and the Ranking of Football Teams. SIAM Rev. 1993, 35, 80–93. [Google Scholar] [CrossRef]
- Page, L.; Brin, S.; Motwani, R.; Winograd, T. The PageRank Citation Ranking: Bringing Order to the Web; Technical Report; Stanford InfoLab: Stanford, CA, USA, 1999. [Google Scholar]
- Franceschet, M.; Bozzo, E. The Massey’s method for sport rating: A network science perspective. arXiv 2017, arXiv:1701.03363. [Google Scholar]
- Liberti, L.; Lavor, C.; Maculan, N.; Mucherino, A. Euclidean distance geometry and applications. SIAM Rev. 2014, 56, 3–69. [Google Scholar] [CrossRef]
- Kendall, M. A new measure of rank correlationâ? Biometrica 1938, 30, 81–93. [Google Scholar] [CrossRef]
- HA, D. Ranking the players in a round robin tournament. Rev. Int. Stat. Inst. 1971, 39, 137–147. [Google Scholar]
- Borodin, A.; Roberts, G.O.; Rosenthal, J.S.; Tsaparas, P. Link analysis ranking: Algorithms, theory, and experiments. ACM Trans. Internet Technol. 2005, 5, 231–297. [Google Scholar] [CrossRef]
- Lasek, J.; Szlávik, Z.; Bhulai, S. The predictive power of ranking systems in association football. Int. J. Appl. Pattern Recognit. 2013, 1, 27–46. [Google Scholar] [CrossRef]
- London, A.; Németh, J.; Németh, T. Time-dependent network algorithm for ranking in sports. Acta Cybern. 2014, 21, 495–506. [Google Scholar] [CrossRef] [Green Version]
- Avron, H.; Horesh, L. Community Detection Using Time-Dependent Personalized Pagerank. In International Conference on Machine Learning; PMLR; 2015; pp. 1795–1803. Available online: https://scholar.google.com/scholar?hl=en&as_sdt=0%2C5&q=Avron%2C+H.%3B+Horesh%2C+L.+Community+detection+using+time-dependent+personalized+pagerank.+In+International+Conference+on+Machine+Learning%3B+PMLR%3A+2015%3B+pp.+1795%E2%80%931803&btnG= (accessed on 15 March 2022).
- Zhou, Y.; Wang, R.; Zhang, Y.C.; Zeng, A.; Medo, M. Improving PageRank using sports results modeling. Knowl.-Based Syst. 2022, 2022, 108168. [Google Scholar] [CrossRef]
| 10–60 Games | 20–70 Games | 30–80 Games | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | Teams | Ranks | Rating | Teams | Ranks | Rating | Teams | Ranks | Rating |
| PageRank | ‘Man. City’ | 1 | 0.0696 | ‘Man. City’ | 1 | 0.0894 | ‘Man. City’ | 1 | 0.0895 |
| ‘Man. United’ | 2 | 0.0067 | ‘Arsenal’ | 2 | 0.0815 | ‘Arsenal’ | 2 | 0.083 | |
| ‘Arsenal’ | 3 | 0.1564 | ‘Man. United’ | 3 | 0.0671 | ‘Man. United’ | 3 | 0.068 | |
| ‘Tottenham’ | 4 | 0.0544 | ‘Newcastle’ | 4 | 0.0612 | ‘Newcastle’ | 4 | 0.0655 | |
| ‘Chelsea’ | 5 | 0.1344 | ‘Tottenham’ | 5 | 0.0635 | ‘Tottenham’ | 5 | 0.0639 | |
| sd ± 0.0522 | sd ± 0.0116 | sd ± 0.0125 | |||||||
| Colley | ‘Man. City’ | 1 | 0.1923 | ‘Man. United’ | 1 | −0.042 | ‘Arsenal’ | 1 | −0.0368 |
| ‘Man. United’ | 2 | −0.0138 | ‘Man. City’ | 2 | −0.0579 | ‘Man. City’ | 2 | 0.057 | |
| ‘Arsenal’ | 3 | −0.1511 | ‘Newcastle’ | 3 | 0.1823 | ‘Tottenham’ | 3 | 0.2564 | |
| ‘Tottenham’ | 4 | −0.0149 | ‘Arsenal’ | 4 | 0.0206 | ‘Man. United’ | 4 | −0.1074 | |
| ‘Newcastle’ | 5 | 0.061 | ‘Tottenham’ | 5 | −0.0821 | ‘Newcastle’ | 5 | 0.1348 | |
| sd ± 0.1104 | sd ± 0.1267 | sd ± 0.1333 | |||||||
| Massey | ‘Man. City’ | 1 | −0.0696 | ‘Man. City’ | 1 | −0.1379 | ‘Man. City’ | 1 | −0.1053 |
| ‘Man. United’ | 2 | −0.0067 | ‘Man. United’ | 2 | −0.0599 | ‘Man. United’ | 2 | −0.2243 | |
| ‘Arsenal’ | 3 | −0.1564 | ‘Arsenal’ | 3 | 0.7011 | ‘Arsenal’ | 3 | 0.8573 | |
| ‘Tottenham’ | 4 | −0.0544 | ‘Tottenham’ | 4 | −0.3316 | ‘Tottenham’ | 4 | −0.314 | |
| ‘Newcastle ’ | 5 | 0.1344 | ‘Newcastle’ | 5 | 0.4368 | ‘Chelsea’ | 5 | 0.4633 | |
| sd ± 0.0333 | sd ± 0.0409 | sd ± 0.0418 | |||||||
| Keener | ‘Man. City’ | 1 | 0.1843 | ‘Man. City’ | 1 | 0.1612 | ‘Man. City’ | 1 | 0.1617 |
| ‘Man. United’ | 2 | 0.2164 | ‘Man. United’ | 2 | 0.2157 | ‘Man. United’ | 2 | 0.2145 | |
| ‘Arsenal’ | 3 | 0.2415 | ‘Tottenham’ | 3 | 0.2238 | ‘Tottenham’ | 3 | 0.2258 | |
| ‘Tottenham’ | 4 | 0.2348 | ‘Arsenal’ | 4 | 0.2496 | ‘Arsenal’ | 4 | 0.2465 | |
| ‘Newcastle’ | 5 | 0.2065 | ‘Newcastle’ | 5 | 0.1889 | ‘Newcastle’ | 5 | 0.1759 | |
| sd ± 0.0328 | sd ± 0.0434 | sd ± 0.0482 | |||||||
| WP | ‘Man. United’ | 1 | 0.0513 | ‘Man. United’ | 1 | 0.0511 | ‘Man. United’ | 1 | 0.0509 |
| ‘Man. City’ | 2 | 0.0484 | ‘Man. City’ | 2 | 0.0485 | ‘Man. City’ | 2 | 0.0484 | |
| ‘Chelsea’ | 3 | 0.0514 | ‘Arsenal’ | 3 | 0.0518 | ‘Chelsea’ | 3 | 0.0513 | |
| ‘Arsenal’ | 4 | 0.0509 | ‘Tottenham’ | 4 | 0.0502 | ‘Arsenal’ | 4 | 0.0508 | |
| ‘Tottenham’ | 5 | 0.0531 | ‘Newcastle’ | 5 | 0.0519 | ‘Tottenham’ | 5 | 0.0515 | |
| sd ± 0.2418 | sd ± 0.2256 | sd ± 0.2097 | |||||||
| RPI | ‘Man. City’ | 1 | 0.0489 | ‘Man. United’ | 1 | 0.0484 | ‘Man. United’ | 1 | 0.0483 |
| ‘Man. United’ | 2 | 0.0490 | ‘Chelsea’ | 2 | 0.0510 | ‘Chelsea’ | 2 | 0.0514 | |
| ‘Arsenal’ | 3 | 0.0526 | ‘Man. City’ | 3 | 0.0510 | ‘Man. City’ | 3 | 0.0527 | |
| ‘Tottenham’ | 4 | 0.0482 | ‘Arsenal’ | 4 | 0.0514 | ‘Arsenal’ | 4 | 0.0508 | |
| ‘Newcastle’ | 5 | 0.0523 | ‘Tottenham’ | 5 | 0.0533 | ‘Tottenham’ | 5 | 0.0491 | |
| sd ± 0.2122 | sd ± 0.2819 | sd ± 0.3418 | |||||||
| After 60 Games | After 70 Games | After 80 Games | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | Teams | Ranks | Rating | Teams | Ranks | Rating | Teams | Ranks | Rating |
| PageRank | ‘Man. City’ | 1 | 0.1217 | ‘Man. City’ | 1 | 0.1226 | ‘Man. City’ | 1 | 0.1237 |
| ‘Chelsea’ | 2 | 0.0889 | ‘Chelsea’ | 2 | 0.0898 | ‘Chelsea’ | 2 | 0.0907 | |
| ‘Man. United’ | 3 | 0.0757 | ‘Man. United’ | 3 | 0.0758 | ‘Man. United’ | 3 | 0.0759 | |
| ‘Newcastl’ | 4 | 0.0670 | ‘Arsenal’ | 4 | 0.0668 | ‘Arsenal’ | 4 | 0.0666 | |
| ‘Tottenham’ | 5 | 0.0640 | ‘Tottenham’ | 5 | 0.0641 | ‘Tottenham’ | 5 | 0.0643 | |
| sd ± 0.0165 | sd ± 0.0174 | sd ± 0.0176 | |||||||
| Colley | ‘Arsenal’ | 1 | 0.1923 | ‘Arsenal’ | 1 | 0.1815 | ‘Arsenal’ | 1 | 0.1846 |
| ‘Man. City’ | 2 | −0.0138 | ‘Man. City’ | 2 | −0.0205 | ‘Man. City’ | 2 | −0.0290 | |
| ‘Man. United’ | 3 | −0.1511 | ‘Man. United’ | 3 | −0.1462 | ‘Man. United’ | 3 | −0.1436 | |
| ‘Tottenham’ | 4 | −0.0149 | ‘Tottenham’ | 4 | −0.0085 | ‘Tottenham’ | 4 | −0.0113 | |
| ‘Newcastle’ | 5 | 0.0610 | ‘Chelsea’ | 5 | 0.0030 | ‘Chelsea’ | 5 | 0.0001 | |
| sd ± 0.0773 | sd ± 0.0754 | sd ± 0.0775 | |||||||
| Massey | ‘Man. City’ | 1 | −0.0696 | ‘Man. City’ | 1 | −0.0569 | ‘Man. United’ | 1 | 0.1560 |
| ‘Arsenal’ | 2 | −0.0067 | ‘Man. United’ | 2 | −0.0055 | ‘Man. City’ | 2 | −0.0509 | |
| ‘Man. United’ | 3 | −0.1564 | ‘Arsenal’ | 3 | −0.1278 | ‘Arsenal’ | 3 | −0.1044 | |
| ‘Tottenham’ | 4 | −0.0544 | ‘Tottenham’ | 4 | −0.0444 | ‘Newcastle’ | 4 | 0.0121 | |
| ‘Newcastle’ | 5 | 0.1344 | ‘Newcastle’ | 5 | 0.1098 | ‘Chelsea’ | 5 | 0.0464 | |
| sd ± 0.0242 | sd ± 0.0226 | sd ± 0.0210 | |||||||
| Keener | ‘Man. United’ | 1 | 0.1843 | ‘Man. United’ | 1 | 0.1870 | ‘Man. United’ | 1 | 0.2382 |
| ‘Man. City’ | 2 | 0.2164 | ‘Man. City’ | 2 | 0.2169 | ‘Man. City’ | 2 | 0.2150 | |
| ‘Arsenal’ | 3 | 0.2415 | ‘Arsenal’ | 3 | 0.2403 | ‘Chelsea’ | 3 | 0.2109 | |
| ‘Tottenham’ | 4 | 0.2348 | ‘Tottenham’ | 4 | 0.2341 | ‘Arsenal’ | 4 | 0.1791 | |
| ‘Newcastle’ | 5 | 0.2065 | ‘Newcastle’ | 5 | 0.2073 | ‘Tottenham’ | 5 | 0.1947 | |
| sd ± 0.0326 | sd ± 0.0408 | sd ± 0.0418 | |||||||
| WP | ‘Man. City’ | 1 | 0.0555 | ‘Man. City’ | 1 | 0.0553 | ‘Man. City’ | 1 | 0.0550 |
| ‘Man. United’ | 2 | 0.0490 | ‘Man. United’ | 2 | 0.0490 | ‘Man. United’ | 2 | 0.0490 | |
| ‘Arsenal’ | 3 | 0.0483 | ‘Tottenham’ | 3 | 0.0497 | ‘Tottenham’ | 3 | 0.0497 | |
| ‘Tottenham’ | 4 | 0.0497 | ‘Arsenal’ | 4 | 0.0483 | ‘Arsenal’ | 4 | 0.0484 | |
| ‘Newcastle’ | 5 | 0.0502 | ‘Newcastle’ | 5 | 0.0501 | ‘Newcastle’ | 5 | 0.0501 | |
| sd ± 0.0971 | sd ± 0.0865 | sd ± 0.0737 | |||||||
| RPI | ‘Man. City’ | 1 | 0.0573 | ‘Man. United’ | 1 | 0.0497 | ‘Man. United’ | 1 | 0.0497 |
| ‘Man. United’ | 2 | 0.0497 | ‘Man. City’ | 2 | 0.0570 | ‘Man. City’ | 2 | 0.0567 | |
| ‘Arsenal’ | 3 | 0.0490 | ‘Arsenal’ | 3 | 0.0490 | ‘Arsenal’ | 3 | 0.0490 | |
| ‘Tottenham’ | 4 | 0.0494 | ‘Newcastle’ | 4 | 0.0499 | ‘Tottenham’ | 4 | 0.0495 | |
| ‘Newcastle’ | 5 | 0.0499 | ‘Chelsea’ | 5 | 0.0479 | ‘Swansea’ | 5 | 0.0503 | |
| sd ± 0.0506 | sd ± 0.0831 | sd ± 0.0843 | |||||||
| PageRank | Colley | Massey | Keener | WP | RPI | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | sd | RMSE | sd | RMSE | sd | RMSE | sd | RMSE | std | RMSE | sd | |
| RW | 0.2568 | 0.0188 | 0.4133 | 0.1156 | 0.2819 | 0.0318 | 0.4067 | 0.0435 | 0.4722 | 0.0927 | 0.4809 | 0.2220 |
| EW | 0.2826 | 0.0193 | 0.4025 | 0.0765 | 0.3237 | 0.0172 | 0.3859 | 0.0573 | 0.4446 | 0.0489 | 0.4425 | 0.0692 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ochieng, P.J.; London, A.; Krész, M. A Forward-Looking Approach to Compare Ranking Methods for Sports. Information 2022, 13, 232. https://doi.org/10.3390/info13050232
Ochieng PJ, London A, Krész M. A Forward-Looking Approach to Compare Ranking Methods for Sports. Information. 2022; 13(5):232. https://doi.org/10.3390/info13050232
Chicago/Turabian StyleOchieng, Peter Juma, András London, and Miklós Krész. 2022. "A Forward-Looking Approach to Compare Ranking Methods for Sports" Information 13, no. 5: 232. https://doi.org/10.3390/info13050232
APA StyleOchieng, P. J., London, A., & Krész, M. (2022). A Forward-Looking Approach to Compare Ranking Methods for Sports. Information, 13(5), 232. https://doi.org/10.3390/info13050232






